Известия РАН. Механика твердого тела, 2020, № 6, стр. 93-100
МОДЕЛЬ СДВИГОВОГО УПРУГОПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ ТОНКОГО АДГЕЗИОННОГО СЛОЯ
В. В. Глаголев a, *, А. А. Маркин a, **
a Тульский государственный университет
Тула, Россия
* E-mail: vadim@tsu.tula.ru
** E-mail: markin-nikram@yandex.ru
Поступила в редакцию 10.06.2020
После доработки 21.07.2020
Принята к публикации 14.08.2020
Аннотация
Исследуется напряженно-деформированное состояние тонкого адгезионного слоя в слоистом композите при сдвиговом характере нагружения с учетом его возможного упругопластического деформирования. Толщина слоя рассматривается в качестве линейного параметра. Проанализировано аналитическое решение, полученное на основе упрощенной постановки задачи в дифференциальном виде. Для малых толщин слоя предложен локальный критерий перехода в состояние пластичности, связанный с линейным параметром.
Введение. В настоящее время основным подходом при определении прочности адгезионных соединений является представление адгезионного слоя слоем нулевой толщины и использование критериальной базы механики квазихрупкого разрушения [1–4]. В этом случае пренебрегают толщиной адгезива, а его механические свойства сводятся к адгезионным силам взаимодействия [5] сопряженных слоем материалов, которые могут иметь разные механические [6] или прочностные свойства [7, 8]. Аналитические решения в этом случае получаются, как правило, в рамках упрощающих гипотез [9–11].
Наряду с данными моделями имеет место подход, учитывающий толщину адгезионного слоя (АС), в рамках модели контактного слоя [12, 13] и модели слоя взаимодействия [14, 15]. В модели контактного слоя пренебрегают напряжением, действующим ортогонально отрыву, которое может учитываться при формулировке условий возможного перехода слоя в состояние пластического деформирования. Отметим, что в настоящее время в состав адгезионных слоев могут входить пластификаторы. Данное обстоятельство требует описания поведения слоев в рамках упругопластической модели. В статье предлагается постановка и приближенное аналитическое решение задачи нагружения адгезионного соединения близкого к регламентной схеме испытания на адгезионную прочность ГОСТ 14759-69.
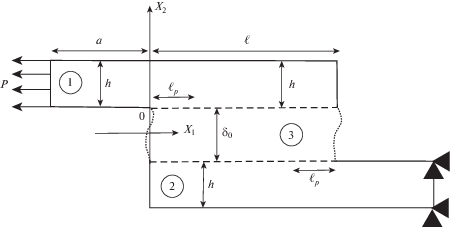
1. Постановка задачи. Рассмотрим композитную пластину, состоящую из двух консолей 1 и 2 длиной $\ell + a$, с одинаковыми толщинами h и механическими свойствами. Консоли сопряжены AC толщиной δ0 по отрезку $\ell $ согласно рисунку. На левом торце консоли 1 действует горизонтальная распределенная нагрузка постоянной интенсивности P. Правый торец пластины жестко закреплен от перемещений. Вся остальная поверхность пластины свободна от напряжений. Считаем материал пластин линейно упругим, а материал AC – идеально упругопластическим. Полагаем, что пластические деформации, как и упругие [16], распределены симметрично по длине слоя ${{{\text{x}}}_{1}} \in [0;{{\ell }_{p}}) \cup (\ell - {{\ell }_{p}};\ell ]$. При значении интенсивности внешней нагрузки, соответствующей пластическому течению в вершине слоя, необходимо определить напряженно-деформированное состояние (НДС) в данном композите.
Для описания взаимодействия слоя 3 с телами 1 и 2 применим концепцию “слоя взаимодействия”, развитую в работах [14–17]. В этом случае равновесие тел 1 и 2, согласно [14, 17] запишем в вариационной форме для тела 1:
(1.1)
$\begin{gathered} \int\limits_{{{S}_{1}}} {\sigma \cdot \cdot \,\delta {\mathbf{\varepsilon }}ds} + \int\limits_l {{{{\bar {\sigma }}}_{{22}}}\delta u_{2}^{ + }d{{{\text{x}}}_{1}}} + \int\limits_l {{{{\bar {\sigma }}}_{{12}}}\delta u_{1}^{ + }d{{{\text{x}}}_{1}}} + \\ \, + 0.5{{\delta }_{0}}\left( {\int\limits_l {{{{\bar {\sigma }}}_{{11}}}\frac{{\partial \delta u_{1}^{ + }}}{{\partial {{{\text{x}}}_{1}}}}d{{{\text{x}}}_{1}}} + \int\limits_l {{{{\bar {\sigma }}}_{{12}}}\frac{{\partial \delta u_{2}^{ + }}}{{\partial {{{\text{x}}}_{1}}}}d{{{\text{x}}}_{1}}} } \right) = A \\ \end{gathered} $(1.2)
$\begin{gathered} \int\limits_{{{S}_{2}}} {\sigma \cdot \cdot \,\delta {\mathbf{\varepsilon }}ds} - \int\limits_l {{{{\bar {\sigma }}}_{{22}}}\delta u_{2}^{ - }d{{{\text{x}}}_{1}}} - \int\limits_l {{{{\bar {\sigma }}}_{{12}}}\delta u_{1}^{ - }d{{{\text{x}}}_{1}}} + \\ \, + 0.5{{\delta }_{0}}\left( {\int\limits_l {{{{\bar {\sigma }}}_{{11}}}\frac{{\partial \delta u_{1}^{ - }}}{{\partial {{{\text{x}}}_{1}}}}d{{{\text{x}}}_{1}}} + \int\limits_l {{{{\bar {\sigma }}}_{{12}}}\frac{{\partial \delta u_{2}^{ - }}}{{\partial {{{\text{x}}}_{1}}}}d{{{\text{x}}}_{1}}} } \right) = 0 \\ \end{gathered} $(1.3)
${{\sigma }_{{22}}} = \frac{1}{{{{\delta }_{0}}}}\int\limits_{ - 0.5{{\delta }_{0}}}^{0.5{{\delta }_{0}}} {{{\sigma }_{{22}}}\left( {{{{\text{x}}}_{{\text{1}}}}{\text{,}}{{{\text{x}}}_{2}}} \right)d{{{\text{x}}}_{2}}} ,\quad {{\bar {\sigma }}_{{11}}} = \frac{1}{{{{\delta }_{0}}}}\int\limits_{ - 0.5{{\delta }_{0}}}^{0.5{{\delta }_{0}}} {{{\sigma }_{{11}}}\left( {{{{\text{x}}}_{{\text{1}}}}{\text{,}}{{{\text{x}}}_{2}}} \right)d{{{\text{x}}}_{2}}} $(1.4)
${{\bar {\varepsilon }}_{{21}}} = {{\bar {\varepsilon }}_{{12}}} = 0.5\left( {\frac{{u_{1}^{ + }\left( {{{{\text{x}}}_{{\text{1}}}}} \right) - u_{1}^{ - }\left( {{{{\text{x}}}_{1}}} \right)}}{{{{\delta }_{0}}}} + 0.5\left( {\frac{{\partial u_{2}^{ + }\left( {{{{\text{x}}}_{1}}} \right)}}{{\partial {{{\text{x}}}_{1}}}} + \frac{{\partial u_{2}^{ - }\left( {{{{\text{x}}}_{1}}} \right)}}{{\partial {{{\text{x}}}_{1}}}}} \right)} \right)$Уравнения (1.1) и (1.2) замкнем определяющими соотношениями в форме закона Гука:
(1.5)
${{\sigma }_{{ij}}} = \frac{E}{{1 + \nu }}\left( {{{\varepsilon }_{{ij}}} + \frac{\nu }{{1 - 2\nu }}\varepsilon {{\delta }_{{ij}}}} \right)$Для материала АС определяющие соотношения считаем справедливыми для средних компонент тензоров напряжений и деформаций. В области упругого деформирования определяющие соотношения примут вид:
(1.6)
${{\bar {\sigma }}_{{ij}}} = \frac{{{{E}_{3}}}}{{1 + {{\nu }_{3}}}}\left( {{{{\bar {\varepsilon }}}_{{ij}}} + \frac{{{{\nu }_{3}}}}{{1 - 2{{\nu }_{3}}}}\bar {\varepsilon }{{\delta }_{{ij}}}} \right)$В области упругопластического деформирования АС определяющие соотношения для средних по толщине слоя напряжений принимаем в виде критерия Треска–Сен-Венана [18]:
где ${{\bar {\sigma }}^{{\max }}}$ – максимальное касательное напряжение; ${{\tau }_{0}}$ – предел текучести.Таким образом, решение системы (1.1)–(1.7) сводится к определению поля перемещений $u\left( {{{{\text{x}}}_{{\text{1}}}}{\text{,}}{{{\text{x}}}_{2}}} \right)$ в телах 1 и 2 (см. рисунок) при заданных граничных условиях.
Для упрощения задачи и получения аналитического решения принимаем, что поле перемещений согласно концепции “дифференциального сдвига” [19] определено следующим образом в теле 1:
(1.8)
${{u}_{1}}\left( {{{{\text{x}}}_{{\text{1}}}}{\text{,}}{{{\text{x}}}_{2}}} \right) = u_{1}^{ + }\left( {{{{\text{x}}}_{1}}} \right);\quad {{u}_{2}}\left( {{{{\text{x}}}_{{\text{1}}}}{\text{,}}{{{\text{x}}}_{2}}} \right) = 0$(1.9)
${{u}_{1}}\left( {{{{\text{x}}}_{{\text{1}}}}{\text{,}}{{{\text{x}}}_{2}}} \right) = u_{1}^{ - }\left( {{{{\text{x}}}_{1}}} \right);\quad {{u}_{2}}\left( {{{{\text{x}}}_{{\text{1}}}}{\text{,}}{{{\text{x}}}_{2}}} \right) = 0$При данной схеме нагружения для средних напряжений в слое в случае плоской деформации реализуется напряженное состояние следующего вида:
(1.10)
${{\bar {\sigma }}_{{11}}} \ne 0;\quad {{\bar {\sigma }}_{{22}}} \ne 0;\quad {{\bar {\sigma }}_{{12}}} \ne 0;\quad {{\bar {\sigma }}_{{33}}} \ne 0$Полагаем, что имеет место упругая сжимаемость $\bar {\sigma } = 3K\bar {\varepsilon }$, где $\bar {\sigma } = {{\bar {\sigma }}_{{11}}} + {{\bar {\sigma }}_{{22}}} + {{\bar {\sigma }}_{{33}}}$; K – коэффициент объемного расширения. Для материала слоя в состоянии плоской деформации, как и в работе [20], пластические и упругие деформации в направлении базисного вектора e3 равны нулю: $\varepsilon _{{33}}^{p} = 0$, $\varepsilon _{{33}}^{e} = 0$. В силу условий (1.8) и (1.9) полагаем равенство нулю пластических $\varepsilon _{{22}}^{p} = 0$ и упругих компонент деформаций $\varepsilon _{{22}}^{e} = 0$ в направлении базисного вектора e2. Считаем деформации малыми и для стадии упругопластического деформирования справедливым следующее разложение: ${{\varepsilon }_{{ii}}} = \varepsilon _{{ii}}^{e} + \varepsilon _{{ii}}^{p}$. Пренебрегая пластической составляющей, получаем: $\bar {\varepsilon } = {{\varepsilon }_{{11}}} = \varepsilon _{{11}}^{e}$. В результате диагональные напряжения в слое и на стадии упругопластического деформирования могут быть определены в виде (1.6). Используя связь ${{\bar {\sigma }}_{{22}}} = {{\bar {\sigma }}_{{33}}} = \frac{{{{\nu }_{3}}}}{{(1 - {{\nu }_{3}})}}{{\bar {\sigma }}_{{11}}}$, перейдем к главным напряжениям. В результате из (1.7) получим связь касательных напряжений слоя с пределом текучести и осевым напряжением:
(1.11)
${{\bar {\sigma }}_{{12}}} = - \frac{{\sqrt {4\tau _{0}^{2} - \beta \bar {\sigma }_{{11}}^{2}} }}{2}$С учетом (1.3)–(1.11) преобразуем систему (1.1), (1.2) к следующим дифференциальным уравнениям для тела 1:
(1.12)
$\frac{{d\sigma _{{11}}^{{\left( 1 \right)}}}}{{d{{{\text{x}}}_{1}}}} = 0\quad {\text{на}}\;{\text{участке}}\quad {{{\text{x}}}_{1}} \in \left[ { - a;0} \right)$(1.13)
$h\frac{{d\sigma _{{11}}^{{\left( 1 \right)}}}}{{d{{{\text{x}}}_{1}}}} + 0.5{{\delta }_{0}}\frac{{d{{{\bar {\sigma }}}_{{11}}}}}{{d{{{\text{x}}}_{1}}}} = - \frac{{\sqrt {4\tau _{0}^{2} - \beta \bar {\sigma }_{{11}}^{2}} }}{2}\quad {\text{на}}\;{\text{участке}}\quad {{{\text{x}}}_{1}} \in \left( {0;{{l}_{p}}} \right)$(1.14)
$h\frac{{d\sigma _{{11}}^{{\left( 1 \right)}}}}{{d{{{\text{x}}}_{1}}}} + 0.5{{\delta }_{0}}\frac{{d{{{\bar {\sigma }}}_{{11}}}}}{{d{{{\text{x}}}_{1}}}} = {{\bar {\sigma }}_{{21}}}\quad {\text{на}}\;{\text{участке}}\quad {{{\text{x}}}_{1}} \in \left( {{{\ell }_{p}};\ell - {{\ell }_{p}}} \right)$(1.15)
$h\frac{{d\sigma _{{11}}^{{\left( 1 \right)}}}}{{d{{{\text{x}}}_{1}}}} + 0.5{{\delta }_{0}}\frac{{d{{{\bar {\sigma }}}_{{11}}}}}{{d{{{\text{x}}}_{1}}}} = - \frac{{\sqrt {4\tau _{0}^{2} - \beta \bar {\sigma }_{{11}}^{2}} }}{2}\quad {\text{на}}\;{\text{участке}}\quad {{{\text{x}}}_{1}} \in \left( {\ell - {{\ell }_{p}};\ell } \right]$(1.16)
$h\frac{{d\sigma _{{11}}^{{\left( 2 \right)}}}}{{d{{{\text{x}}}_{1}}}} + 0.5{{\delta }_{0}}\frac{{d{{{\bar {\sigma }}}_{{11}}}}}{{d{{{\text{x}}}_{1}}}} = \frac{{\sqrt {4\tau _{0}^{2} - \beta \bar {\sigma }_{{11}}^{2}} }}{2}\quad {\text{на}}\;{\text{участке}}\quad {{{\text{x}}}_{1}} \in \left( {0;{{l}_{p}}} \right)$(1.17)
$h\frac{{d\sigma _{{11}}^{{\left( 2 \right)}}}}{{d{{{\text{x}}}_{1}}}} + 0.5{{\delta }_{0}}\frac{{d{{{\bar {\sigma }}}_{{11}}}}}{{d{{{\text{x}}}_{1}}}} = - {{\bar {\sigma }}_{{21}}}\quad {\text{на}}\;{\text{участке}}\quad {{{\text{x}}}_{1}} \in \left( {{{\ell }_{p}};\ell - {{\ell }_{p}}} \right)$(1.18)
$h\frac{{d\sigma _{{11}}^{{\left( 2 \right)}}}}{{d{{{\text{x}}}_{1}}}} + 0.5{{\delta }_{0}}\frac{{d{{{\bar {\sigma }}}_{{11}}}}}{{d{{{\text{x}}}_{1}}}} = \frac{{\sqrt {4\tau _{0}^{2} - \beta \bar {\sigma }_{{11}}^{2}} }}{2}\quad {\text{на}}\;{\text{участке}}\quad {{{\text{x}}}_{1}} \in \left( {\ell - {{\ell }_{p}};\ell } \right)$(1.19)
$\frac{{d\sigma _{{11}}^{{\left( 2 \right)}}}}{{d{{{\text{x}}}_{1}}}} = 0\quad {\text{на}}\;{\text{участке}}\quad {{{\text{x}}}_{1}} \in \left( {\ell ;a} \right]$Решения уравнений сопрягаются в точках ${{{\text{x}}}_{1}} = 0$:
(1.20)
${{\left. {h{\sigma }_{{11}}^{{\left( 1 \right)}}} \right|}_{{{\text{x}}{}_{1} = 0 - 0}}} = {{\left. {(h{\sigma }_{{11}}^{{\left( 1 \right)}} + 0.5{{\delta }_{0}}{{{\bar {\sigma }}}_{{11}}})} \right|}_{{{\text{x}}{}_{1} = 0 + 0}}},\quad {{\left. {u_{1}^{ + }} \right|}_{{{{{\text{x}}}_{1}} = 0 - 0}}} = {{\left. {u_{1}^{ + }} \right|}_{{{{{\text{x}}}_{1}} = 0 + 0}}}$(1.21)
${{\left. {(h{\sigma }_{{11}}^{{\left( 1 \right)}} + 0.5{{\delta }_{0}}{{{{\bar {\sigma }}}}_{{11}}})} \right|}_{{{\text{x}}{}_{1} = {{\ell }_{p}} - 0}}} = {{\left. {(h{\sigma }_{{11}}^{{\left( 1 \right)}} + 0.5{{\delta }_{0}}{{{{\bar {\sigma }}}}_{{11}}})} \right|}_{{{\text{x}}{}_{1} = {{\ell }_{p}} + 0}}},\quad {{\left. {u_{1}^{ + }} \right|}_{{{{{\text{x}}}_{1}} = {{\ell }_{p}} - 0}}} = {{\left. {u_{1}^{ + }} \right|}_{{{{{\text{x}}}_{1}} = {{\ell }_{p}} + 0}}}$(1.22)
${{\left. {(h{\sigma }_{{11}}^{{\left( 2 \right)}} + 0.5{{{\delta }}_{0}}{{{{\bar {\sigma }}}}_{{11}}})} \right|}_{{{\text{x}}{}_{1} = {{\ell }_{p}} - 0}}} = {{\left. {(h{\sigma }_{{11}}^{{\left( 2 \right)}} + 0.5{{{\delta }}_{0}}{{{{\bar {\sigma }}}}_{{11}}})} \right|}_{{{\text{x}}{}_{1} = {{\ell }_{p}} + 0}}},\quad {{\left. {u_{1}^{ - }} \right|}_{{{{{\text{x}}}_{1}} = {{\ell }_{p}} - 0}}} = {{\left. {u_{1}^{ - }} \right|}_{{{{{\text{x}}}_{1}} = {{\ell }_{p}} + 0}}}$(1.23)
${{\left. {(h{\sigma }_{{11}}^{{\left( 1 \right)}} + 0.5{{{\delta }}_{0}}{{{{\bar {\sigma }}}}_{{11}}})} \right|}_{{{\text{x}}{}_{1} = \ell - {{\ell }_{p}} - 0}}} = {{\left. {(h{\sigma }_{{11}}^{{\left( 1 \right)}} + 0.5{{{\delta }}_{0}}{{{{\bar {\sigma }}}}_{{11}}})} \right|}_{{{\text{x}}{}_{1} = \ell - {{\ell }_{p}} + 0}}},\quad {{\left. {u_{1}^{ + }} \right|}_{{{{{\text{x}}}_{1}} = \ell - {{\ell }_{p}} - 0}}} = {{\left. {u_{1}^{ + }} \right|}_{{{{{\text{x}}}_{1}} = \ell - {{\ell }_{p}} + 0}}}$(1.24)
${{\left. {(h{\sigma }_{{11}}^{{\left( 2 \right)}} + 0.5{{{\delta }}_{0}}{{{{\bar {\sigma }}}}_{{11}}})} \right|}_{{{\text{x}}{}_{1} = \ell - {{\ell }_{p}} - 0}}} = {{(h{\sigma }_{{11}}^{{\left( 2 \right)}} + 0.5{{{\delta }}_{0}}{{{\bar {\sigma }}}_{{11}}})}_{{{\text{x}}{}_{1} = \ell - {{\ell }_{p}} + 0}}},\quad {{\left. {u_{1}^{ - }} \right|}_{{{{{\text{x}}}_{1}} = \ell - {{\ell }_{p}} - 0}}} = {{\left. {u_{1}^{ - }} \right|}_{{{{{\text{x}}}_{1}} = \ell - {{\ell }_{p}} + 0}}}$(1.25)
${{\left. {(h{\sigma }_{{11}}^{{\left( 2 \right)}} + 0.5{{{\delta }}_{0}}{{{{\bar {\sigma }}}}_{{11}}})} \right|}_{{{\text{x}}{}_{1} = \ell - 0}}} = {{\left. {h{\sigma }_{{11}}^{{\left( 2 \right)}}} \right|}_{{{\text{x}}{}_{1} = \ell + 0}}},\quad {{\left. {u_{1}^{ - }} \right|}_{{{{{\text{x}}}_{1}} = \ell - 0}}} = {{\left. {u_{1}^{ - }} \right|}_{{{{{\text{x}}}_{1}} = \ell + 0}}}$(1.26)
$\begin{gathered} {{\left. {{\sigma }_{{11}}^{{\left( 1 \right)}}} \right|}_{{{{{\text{x}}}_{1}} = - a}}} = P,\quad {{\left. {(h{\sigma }_{{11}}^{{\left( 2 \right)}} + 0.5{{{\delta }}_{0}}{{{\bar {\sigma }}}_{{11}}})} \right|}_{{x{}_{1} = 0}}} = 0 \\ {{\left. {(h{\sigma }_{{11}}^{{\left( 1 \right)}} + 0.5{{{\delta }}_{0}}{{{\bar {\sigma }}}_{{11}}})} \right|}_{{{\text{x}}{}_{1} = \ell }}} = 0,\quad {{\left. {u_{1}^{ - }} \right|}_{{{{{\text{x}}}_{1}} = \ell + a}}} = 0 \\ \end{gathered} $Определяющие соотношения (1.5), (1.6) для состояния плоской деформации приобретают вид:
для консолей:
(1.27)
$\sigma _{{11}}^{{\left( 1 \right)}} = D\frac{{du_{1}^{ + }}}{{d{{{\text{x}}}_{1}}}};\quad \sigma _{{11}}^{{\left( 2 \right)}} = D\frac{{du_{1}^{ - }}}{{d{{{\text{x}}}_{1}}}}$(1.28)
${{\bar {\sigma }}_{{12}}} = L\frac{{(u_{1}^{ + } - u_{1}^{ - })}}{{{{\delta }_{0}}}};\quad {{\bar {\sigma }}_{{11}}} = {{D}_{1}}\left( {\frac{{du_{1}^{ + }}}{{d{{{\text{x}}}_{1}}}} + \frac{{du_{1}^{ - }}}{{d{{{\text{x}}}_{1}}}}} \right)$На участках ${{{\text{x}}}_{1}} \in \left[ {0;{{\ell }_{p}}} \right) \cup \left( {\ell - {{\ell }_{p}};\ell } \right]$ имеет место связь компонент средних напряжений и производных граничных перемещений:
(1.29)
${{\bar {\sigma }}_{{12}}} = - \frac{{\sqrt {4\tau _{0}^{2} - \beta \bar {\sigma }_{{11}}^{2}} }}{2};\quad {{\bar {\sigma }}_{{11}}} = {{D}_{1}}\left( {\frac{{du_{1}^{ + }}}{{d{{{\text{x}}}_{1}}}} + \frac{{du_{1}^{ - }}}{{d{{{\text{x}}}_{1}}}}} \right)$1. Локальное предельное состояние. Аналитическое решение задачи (1.12)–(1.29) приведено в работе [21]. Связь между длиной пластической зоны и внешней нагрузкой определена из полей перемещений при условии достижения в точке ${{{\text{x}}}_{1}} = {{\ell }_{p}}$ предельного касательного напряжения
(2.1)
${{\left. {{{{\bar {\sigma }}}_{{12}}}} \right|}_{{{{x}_{1}} = {{\ell }_{p}}}}} = {{\left. {L\frac{{(u_{1}^{ + } - u_{1}^{ - })}}{{{{\delta }_{0}}}}} \right|}_{{{{x}_{1}} = {{\ell }_{p}}}}} = - \frac{{\sqrt {4\tau _{0}^{2} - \beta \bar {\sigma }_{{11}}^{2}} }}{2}$Связь (2.1) приводит к следующему выражению внешней нагрузки [21]:
(2.2)
$P = \frac{{2{{\tau }_{0}}\left( {hD + {{\delta }_{0}}{{D}_{1}}} \right)m}}{{h\sqrt {(\beta {{{\left( {{{D}_{1}}m} \right)}}^{2}} + m_{1}^{2})} }}$Считаем, что ${{e}^{{kl}}},{h \mathord{\left/ {\vphantom {h {{{\delta }_{0}}}}} \right. \kern-0em} {{{\delta }_{0}}}} \gg 1$. При этом в момент достижения условия пластичности для малых δ0 критическая нагрузка при ${{\ell }_{p}} = 0$ из (2.2) принимает вид:
В соответствии с (2.3) при δ0 → 0 переход в пластичность происходит при сколь угодно малой внешней нагрузке. Данный парадокс следует из зависимости (2.3) внешней нагрузки от толщины слоя при малых значениях δ0. Сформулируем условие пластичности, используя в качестве характеристики напряженного состояния слоя обобщенное касательное напряжение
(2.4)
${{\tau }_{{{{\delta }_{0}}}}} = \frac{{\sqrt {(4\bar {\sigma }_{{12}}^{2} + \beta \bar {\sigma }_{{11}}^{2}){{\delta }_{0}}} }}{2}$Полагаем, что в слое достигается пластическое состояние, если выполняется условие:
(2.5)
$\mathop {\lim }\limits_{{{\delta }_{0}} \to 0} {{\tau }_{{{{\delta }_{0}}}}} = \tau _{{{{\delta }_{0}}}}^{s}$Потребуем, чтобы на интервале $0 \leqslant {{\delta }_{0}} \leqslant \delta _{0}^{*}$ выполнялось условие (2.5). В этом случае внешняя нагрузка, соответствующая переходу слоя в состояние пластичности равна:
Считаем, что при ${{\delta }_{0}} = \delta _{0}^{*}$ выполняется условие (1.7). Тогда из (2.4) и (2.5) следует, что
Таким образом, на интервале $0 \leqslant {{\delta }_{0}} \leqslant \delta _{0}^{*}$ критическая внешняя нагрузка имеет конечное значение (2.6). При ${{\delta }_{0}} > \delta _{0}^{*}$ критическая нагрузка определяется по формуле (2.2).
Для определения характерного размера можно использовать эксперименты, реализуемые по схеме рисунка. Установив $P_{s}^{{\left( 0 \right)}}$ для малых толщин АС и характеристик консолей, находим $\tau _{{{{\delta }_{0}}}}^{s}$. Из (2.7) определяем $\delta _{0}^{*} = {{(\tau _{{{{\delta }_{0}}}}^{s}{\text{/}}{{\tau }_{0}})}^{2}}$.
Данный подход позволяет определить значение внешней нагрузки, соответствующее переходу в пластическое состояние во всем диапазоне толщин АС.
Заключение. Предложена модель упругопластического деформирования тонкого адгезионного слоя в слоистом композите. Показано, что учет толщины слоя существенен при расчете внешней нагрузки. Для малых толщин слоя предложен локальный критерий перехода в состояние пластичности, связанный с линейным параметром. В отличие от классических условий пластичности, данный критерий позволяет выделить стадию упругого деформирования и установить значение внешней нагрузки, соответствующее переходу в пластическое состояние. При этом выделяется диапазон толщин, включая нулевую, в котором внешняя нагрузка, соответствующая переходу в пластическое состояние постоянна.
Исследование выполнено при финансовой поддержке РФФИ и правительства Тульской области в рамках научного проекта № 19-41-710001 р_а.
Список литературы
Болотин В.В., Новичков Ю.Н. Механика многослойных конструкций. М.: Машиностроение, 1980. 375 с.
Черепанов Г.П. Механика разрушения композиционных материалов. М.: Наука, 1974. 640 с.
Allen H.G., Feng Z. Classification of Structural Sandwich Panel Behaviour // Mechanics of Sandwich Structures. Springer, Dordrecht. 1998. P. 1–12.
Ивлев Д.Д. О теории трещин квазихрупкого разрушения // ПМТФ. 1967. № 6. С. 88–128.
Фроленкова Л.Ю., Шоркин В.С. Поверхностная энергия и энергия адгезии упругих тел // Изв. РАН. МТТ. 2017. № 1. С. 76–91.
Астапов И.С., Астапов Н.С., Корнев В.М. Модель расслоения композита при поперечном сдвиге // Механика композиционных материалов и конструкций. 2015. № 2 (21). С. 149–161.
Baldan A. Adhesively-bonded joints in metallic alloys, polymers and composite materials: Mechanical and environmental durability performance // Journal of Materials Science. 2004. V. 39. № 15. P. 4729–4797.
Sun C.T., Jih C.J. On strain energy release rates for interfacial cracks in bi-material media // Engineering Fracture Mechanics. 1987. № 1 (28). P. 13–20.
Timoshenko S., Woinowsky-Krieger S. Theory of plate and shells. New York, Toronto, London: McGraw-Hill, 1959. Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки. М.: Физматгиз, 1963. 636 с.
Fang X., Charalambides P.G. The fracture mechanics of cantilever beams with an embedded sharp crack under end force loading // Engineering Fracture Mechanics. 2015. V. 149. P. 1–17.
Mattei O., Bardella L. A structural model for plane sandwich beams including transverse core deformability and arbitrary boundary conditions // Eur. J. Mech. A-Solid. 2016. V. 58. P. 172–186.
Андреев В.И., Цыбин Н.Ю., Турусов Р.А. Анализ краевого эффекта касательных напряжений при сдвиге двухконсольной балки // Строительная механика инженерных конструкций и сооружений. 2018. № 3 (14). С. 180–186.
Андреев В.И., Цыбин Н.Ю., Турусов Р.А. Определение напряженно-деформированного состояния трехслойной балки с применением контактного слоя // Вестник МГСУ. 2016. № 4. С. 17–26.
Глаголев В.В., Маркин А.А., Фурсаев А.А. Моделирование процесса разделения композита с адгезионным слоем // Вестник ПНИПУ. Механика. 2016. № 2. С. 34–44.
Глаголев В.В., Маркин А.А., Пашинов С.В. Биметаллическая пластина в однородном температурном поле // Механика композиционных материалов и конструкций. 2017. № 3 (23). С. 331–343.
Абдурахманов А.А., Глаголев В.В., Фурсаев А.А. О сдвиге адгезионного слоя в композиционной пластине // Вестник ТулГУ. Серия: Дифференциальные уравнения и прикладные задачи. 2017. № 1. С. 51–60.
Glagolev V.V., Markin A.A. Fracture models for solid bodies, based on a linear scale parameter // International Journal of Solids and Structures. 2019. V. 158. P. 141–149.
Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. М.: ФИЗМАТЛИТ, 2001. 704 с.
Volkersen O. Die Nietkraftverteilung in zugbeanspruchten Nietverbindungen mit konstanten Laschenquerschnitten. Luftfahrtforschung. 1938. V. 15. P. 41–47.
Глаголев В.В., Маркин А.А. Об одной постановке задачи упругопластического разделения // ПМТФ. 2009. № 4 (50). С. 187–195.
Абдурахманов А.А., Глаголев В.В., Инченко О.В. Упругопластическое деформирование адгезива при сдвиге // Вестник Чувашского государственного педагогического университета. Серия: Механика предельного состояния. 2019. № 4 (42). С. 34–45.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела