Известия РАН. Механика твердого тела, 2021, № 3, стр. 42-61

1. Введение. Последнее десятилетие активно развивается экспериментальная методика исследования ударно-волновых процессов в тонких (порядка и меньше микрометра) пленках металлов под действием мощных фемтосекундных импульсов лазерного излучения [1–8]. Уменьшение времени воздействия и дистанции распространения ударных волн позволяет получить сильно неравновесные состояния вещества [9]. Такие состояния характеризуются аномально высокой откольной и сдвиговой прочностью [10]. Регистрируемые в экспериментах напряжения на упругом предвестнике достигают 7.5–12.5 ГПа для алюминия [1, 2, 7], 23 ГПа для хрома [8], 28 ГПа для железа [3] и даже 43 ГПа для тантала [6]. Столь высокие значения напряжений на предвестнике и соответствующей сдвиговой прочности объясняются сверхвысокими скоростями деформации в этих экспериментах – порядка 10⁹ с^–1. Инерционность развития пластической деформации позволяет материалу на короткое время зайти в область больших сдвиговых напряжений. В большинстве металлов пластическая релаксация происходит за счет скольжения дислокаций, конечная плотность и скорость которых ограничивает скорость релаксации.

Развитие методов математического моделирования актуально для более полного понимания неравновесных ударно-волновых процессов, особенностей возникающего метастабильного состояния и динамики выхода из него. На малых пространственных и временных масштабах возможно непосредственное применение молекулярно-динамического (МД) моделирования возникновения и распространения ударной волны. Для исследования эволюции структуры волны в широком диапазоне пространственных масштабов необходимо развитие континуальных моделей.

Последовательная адаптация дислокационных моделей пластичности [11–14] на случай сверхвысоких скоростей деформации требует учета двух важных факторов. Первый фактор связан с большой по величине упругой деформацией, что приводит к нелинейному росту напряжений на упругой стадии. Как следствие, необходимо учитывать нелинейную зависимость давления и девиатора напряжений от деформации. Для давления это можно осуществить с помощью хорошо разработанного аппарата уравнений состояния, в том числе широкодиапазонных [15–17]. Для девиаторов такой аппарат отсутствует и в большинстве моделей используется линейный закон Гука [11, 18, 19]. Согласно результатам МД-моделирования [20] сдвиговая деформация влияет на давление, что не учитывается в существующих уравнениях состояния. Все это требует развития аппарата нелинейных тензорных уравнений состояния, связывающих тензоры напряжений и деформаций на нелинейной упругой стадии.

Второй фактор – возможность гомогенной нуклеации как дополнительного источника дислокаций в материале [21–23]. В большинстве случаев этот процесс подавлен по сравнению с размножением существующих дислокаций. В упругих предвестниках большой амплитуды он может реализовываться за счет сверхвысокой скорости деформации, дефицита существующих дислокаций и, как следствие, высокого уровня сдвиговых напряжений. Гомогенная нуклеация будет выступать ограничителем сдвиговых напряжений и амплитуды упругого предвестника. Согласно результатам МД-исследований [24–27] порог гомогенной нуклеации дислокаций сложным образом зависит от характера нагружения, в частности от направления сдвиговой деформации относительно кристаллографических осей. Для ударно-волновых задач важно, что порог нуклеации зависит от давления и температуры. Это требует нахождения порога нуклеации как функции тензора деформации и температуры.

В последние годы в механике материалов все более широкое распространение находит применение искусственных нейронных сетей [28–32] как мощного дополнительного инструмента, позволяющего повысить точность используемых моделей. Нейронные сети эффективны при анализе трендов данных и построении аппроксимаций сложных зависимостей, что позволяет использовать их при решении поставленных выше задач.

В данной работе мы используем МД-моделирование деформации репрезентативного объема монокристалла алюминия для исследования связи деформаций и напряжений и порога гомогенной нуклеации дислокаций. Рассматриваются осесимметричные деформированные состояния, которые реализуются в плоских ударных волнах. Состояние характеризуется двумя независимыми компонентами тензора деформаций. Ось симметрии совпадает с направлением [100 ] монокристалла. Полученные данные МД-моделирования используются для обучения нейронных сетей. Обученные нейронные сети выступают в качестве тензорного уравнения состояния и функции порога нуклеации (аппроксимируют эти сложные зависимости). Они используются в составе континуальной модели дислокационной пластичности. Результаты расчетов по модели сравниваются с прямым МД-моделированием распространения ударной волны и используются для анализа затухания упругого предвестника в алюминии в зависимости от начальной плотности дислокаций.

2. Континуальная модель. 2.1. Кинематика деформации. При высокоскоростном соударении пластин металлов от плоскости соударения распространяется ударная волна. За исключением краевых областей, в которых важна боковая разгрузка [33], ударная волна является плоской и приводит к одноосной деформации материала вдоль нормали к фронту волны (направим ось x₁ вдоль этой нормали). За счет пластической релаксации напряженное состояние меняется от того, что соответствует одноосной упругой деформации, до состояния, близкого к гидростатическому случаю. Первое реализуется на упругом предвестнике, а второе – за фронтом ударной волны. Чтобы учесть этот переход будем рассматривать осесимметричный случай, когда упругие деформации в поперечных направлениях (вдоль x₂ и x₃) равны друг другу, но могут быть отличны от нуля и от деформации в продольном направлении (вдоль оси x₁).

Эксперименты [1–3] и расчеты [13] показывают, что упругий предвестник ударной волны имеет большую амплитуду на малых расстояниях от плоскости соударения. Это значит, что упругие деформации могут быть большими и необходимо использовать формализм конечных деформаций. Также необходимо учитывать нелинейную зависимость давления и девиатора напряжений от деформации.

Рассмотрим деформацию, связанную с макроскопическим движением вещества. В результате перемещения макроскопических частей вещества (содержащих много атомов) точки с начальными координатами ${\mathbf{X}}$ заняли текущие положения x. Тензор градиента макроскопической деформации ${\mathbf{F}}$ вводится как [34]

В начальном недеформированном состоянии этот тензор сводится к единичной матрице ${{\left. {\mathbf{F}} \right|}_{{t = 0}}} = {\mathbf{I}}$ или ${{\left. {{{F}_{{ik}}}} \right|}_{{t = 0}}} = {{{{\delta }}}_{{ik}}}$, где ${{{{\delta }}}_{{ik}}}$ – символы Кронекера. При одноосной деформации в плоской ударной волне продольная компонента ${{F}_{{11}}}$ может быть рассчитана через текущую ${{\rho }}$ и начальную ${{{{\rho }}}_{0}}$ плотности как ${{F}_{{11}}} = {{{{\rho }_{0}}} \mathord{\left/ {\vphantom {{{{\rho }_{0}}} \rho }} \right. \kern-0em} \rho }$, поперечные компоненты остаются единичными, а недиагональные компоненты – нулевыми. Поэтому вместо (2.1) запишем:

Макроскопическая деформация ${\mathbf{F}}$ представляется комбинацией упругой ${{{\mathbf{F}}}^{{\text{e}}}}$ и пластической ${{{\mathbf{F}}}^{{\text{p}}}}$ частей [35]:

При известных ${\mathbf{F}}$ и ${{{\mathbf{F}}}^{{\text{p}}}}$ из (2.3) находится упругая часть деформации, определяющая действующие в материале напряжения. В начальном недеформированном состоянии ${{{\mathbf{F}}}^{{\text{p}}}}{{{\text{|}}}_{{t = 0}}} = {\mathbf{I}}$, а его производная от времени определяется как [36]:

где ${\mathbf{\dot {w}}}$ есть тензор скоростей пластической деформации за счет скольжения дислокаций. В осесимметричном случае с учетом того, что пластическая деформация за счет скольжения дислокаций не приводит к изменению объема, этот тензор сводится к следующей диагональной матрице: где $\dot {w}$ есть скорость пластической деформации, которая будет определена далее. Из (2.4), (2.5) и начальных условий для ${{{\mathbf{F}}}^{{\text{p}}}}$ следует, что этот тензор остается диагональным, причем $F_{{22}}^{{\text{p}}} = F_{{33}}^{{\text{p}}}$ и

С учетом диагональности ${{{\mathbf{F}}}^{{\text{p}}}}$ из (2.2) и (2.3) следует:

Таким образом, при известной $\dot {w}$ уравнения (2.6) и (2.7) позволяют найти компоненты упругого градиента деформации $F_{{11}}^{{\text{e}}}$ и $F_{{22}}^{{\text{e}}}$. Саму упругую деформацию характеризуем тензором конечных деформаций Грина [34]:

где т означает транспонирование. Из (2.7) и (2.8) получаем следующий диагональный вид для тензора деформаций:

Выпишем основные уравнения, описывающие кинематику упругопластической деформации в плоской ударной волне:

2.2. Напряжения и тензорное уравнение состояния. Напряженное состояние вещества в текущей конфигурации характеризуем тензором напряжений Коши, который с учетом осевой симметрии приобретает следующий вид:

где $P$ – давление, $S$ – девиатор напряжений. В случае малых деформаций применим закон Гука, устанавливающий линейную связь между деформациями и напряжениями [37]: где $K$ – объемный модуль упругости, $G$ – модуль сдвига. В общем случае связь между $P$, $S$ и ${{L}_{{11}}}$, ${{L}_{{22}}}$ является нелинейной и зависит от температуры. При решении уравнений механики сплошной среды из закона сохранения энергии вычисляется не температура, а внутренняя энергия E, поэтому удобно представить зависимости в следующем виде:

Набор переменных $\left\{ {{{L}_{{11}}},{{L}_{{22}}},E} \right\}$ полностью характеризует термодинамическое состояние элемента вещества. Поскольку функции (2.13) определяют не только давление, но и девиаторную часть напряжений, будем называть их тензорным уравнением состояния. В рассматриваемом осесимметричном случае есть всего две независимых компоненты тензора напряжений. В общем случае тензорное уравнение состояния должно определять все шесть независимых компонент. Помимо самих напряжений для замыкания модели и численного решения потребуются текущие значения упругих модулей, которые, опираясь на (2.12), можно определить как

Полученные в соответствии с (2.14) производные также образуют зависимости

являющиеся частью тензорного уравнения состояния. Помимо напряжений (2.13) и упругих модулей (2.15) уравнение состояния должно определять температуру $T$ и теплоемкость ${{C}^{{\text{V}}}}$ при постоянном объеме и форме тела (при постоянных деформациях ${{L}_{{11}}}$ и ${{L}_{{22}}}$):

Совокупность зависимостей (2.13), (2.15) и (2.16) представляет собой тензорное уравнение состояния. Для его построения было проведено МД-моделирование деформации репрезентативного объема монокристалла алюминия при различных температурах и траекториях изменения ${{L}_{{11}}}$ и ${{L}_{{22}}}$, выбрана упругая часть траекторий до нуклеации дислокации и полостей (при растяжении). Далее эти упругие состояния использовались для обучения искусственной нейронной сети: на вход сети подавался набор $\left\{ {{{L}_{{11}}},{{L}_{{22}}},E} \right\}$, а на выход набор $\{ P,S,T,{{C}^{{\text{V}}}},{\kern 1pt} \;K,G\} $. После обучения нейронная сеть использовалась как аппроксимирующая функция для зависимостей (2.13), (2.15) и (2.16), то есть в качестве тензорного уравнения состояния. Подробнее структура, алгоритм обучения нейронной сети и его результаты описаны в разделе 3.

2.3. Законы сохранения. Запишем законы сохранения массы, импульса и энергии в лагранжевых переменных. Поле макроскопических скоростей имеет только одну компоненту $u$ вдоль оси $x \equiv {{x}_{1}}$. Закон сохранения массы приводит к уравнению непрерывности

Закон сохранения импульса приводит к уравнению движения

Закон сохранения энергии приводит к уравнению для внутренней энергии

В (2.19) E – удельная внутренняя энергия бездефектного кристалла, ${{E}^{{\text{D}}}}$ – энергия дислокаций в единице массы материала. Их сумма $(E + {{E}^{{\text{D}}}})$ – это полная внутренняя энергия, ее изменение определяется работой механических напряжений на макроскопических деформациях. Пластическое течение переводит энергию упругих деформаций в тепловую часть [13, 38], но полная внутренняя энергия при этом не меняется. Отметим, что в (2.19) не учтена теплопроводность.

2.4. Модель дислокационной пластичности. На микроуровне пластическая деформация кристаллических материалов в большинстве случаев реализуется за счет скольжения дислокаций. Полная дислокационная модель пластичности [11–13] включает уравнение Орована, связывающее скорость пластической деформации $\dot {w}$ со скоростью скольжения дислокаций и их плотностью. В [14] показано, что структура фронта ударной волны может быть описана при помощи упрощенного подхода с использованием релаксационной модели Максвелла. В рамках этого подхода скорость пластической деформации определяется уравнением

где $H\left( \centerdot \right)$ – функция Хэвисайда. Статический предел текучести ${{Y}^{{\text{p}}}}$ зависит от плотности дислокаций ${{\rho }^{{\text{D}}}}$ согласно закону упрочнения Тэйлора: где ${{Y}^{0}}$ – предел текучести бездефектного материала, $A = 0.3$ – коэффициент упрочнения, $b$ – модуль вектора Бюргерса. Параметр “вязкости” ${{\eta }}$, обратно пропорциональный времени релаксации [39], определяется текущей плотностью дислокаций ${{{{\rho }}}^{{\text{D}}}}$ как где B – коэффициент фононного трения дислокаций, температурная зависимость которого для алюминия найдена в [40] из результатов МД-моделирования.

Для определения ${{Y}^{{\text{p}}}}$ и ${{\eta }}$ необходима текущая плотность дислокаций, которая находится из модели кинетики дислокационного ансамбля [12–14]. Для простоты используем здесь уравнение только для подвижных дислокаций:

Последнее слагаемое в правой части (2.23) отвечает за ограничение плотности дислокаций процессом аннигиляции, здесь ${{k}^{{\text{a}}}} = 40$ – коэффициент аннигиляции (безразмерная величина). Второе слагаемое в правой части (2.23) описывает размножениe существующих дислокаций, на что тратится определенная часть работы пластической деформации. В общем случае эта доля может меняться и достигать единицы при большом дефиците дислокаций, то есть при больших действующих напряжениях сдвига, которые необходимо снять за счет пластического течения. Здесь ${{{{\varepsilon }}}^{{\text{D}}}}$ – энергия единицы длины дислокационной линии, которая включает энергию ядра и энергию окружающего упругого поля [41], ограниченного характерным междислокационным расстоянием ${1 \mathord{\left/ {\vphantom {1 {\sqrt {{{{{\rho }}}^{{\text{D}}}}} }}} \right. \kern-0em} {\sqrt {{{{{\rho }}}^{{\text{D}}}}} }}$:

где ${{\nu }} = 0.33$ – коэффициент Пуассона.

Первое слагаемое в правой части (2.23), $q$, представляет собой скорость гомогенной нуклеации дислокаций. Вероятность тепловой флуктуации, приводящей к нуклеации дислокационной петли, тем больше, чем меньше работа ее образования. Анализ результатов МД-моделирования показывает, что работа образования дислокационной петли сложным образом зависит от деформации и резко уменьшается до определенной величины вблизи порога нуклеации [42]. Поэтому будем использовать следующее выражение для q:

где ${{c}^{{\text{t}}}} = \sqrt {{G \mathord{\left/ {\vphantom {G {{\rho }}}} \right. \kern-0em} {{\rho }}}} $ – поперечная скорость звука, (ρ/m) – концентрация атомов, m – масса одного атома, ${{k}^{{\text{B}}}}$ – постоянная Больцмана, $W = 0.3$ эВ – характерная величина энергетического барьера образования петли вблизи порога нуклеации. Функция Хэвисайда в (2.25) учитывает пороговый характер нуклеации, то есть резкий рост вероятности нуклеации вблизи предельной упругой деформации. Функция ${{Q}_{{{\text{DN}}}}}\left( {{{L}_{{11}}},{{L}_{{22}}},E} \right)$ задает порог нуклеации и представляет собой искусственную нейронную сеть, обученную так, чтобы принимать значение 0 в упругой области и 1 за порогом нуклеации (см. раздел 3).

Изменение энергии дислокаций связано с изменением их плотности:

Результаты МД-моделирования показывают, что при динамическом нагружении пластическая деформация в ГЦК металлах связана с образованием и движением частичных дислокаций Шокли. Такие дислокации имеют меньшее значение модуля вектора Бюргерса и меньшую энергию образования, см. (2.24). Поэтому они доминируют в дислокационном ансамбле, хотя их скольжение и приводит к образованию поверхностей дефекта упаковки. Для частичных дислокаций Шокли текущее значение вектора Бюргерса может быть вычислено через плотность вещества как

Входящие в модель дифференциальные по времени уравнения решались явным методом Эйлера с временным шагом, определяемым согласно условию Куранта–Фридрихса–Леви. Для стабилизации решения использовалась искусственная вязкость в форме, предложенной в [43].

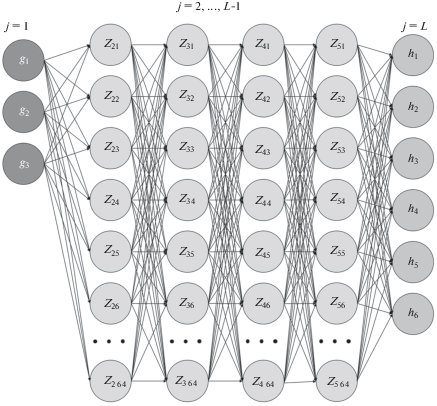
3. МД-моделирование и обучение нейронных сетей. 3.1. Структура нейронной сети и алгоритм обучения. Искусственная нейронная сеть может рассматриваться как универсальная функция (отображение). Она вычисляет выходной вектор (значение) по входному вектору (аргументу). В рассматриваемом случае входной вектор – это набор величин $\left\{ {{{L}_{{11}}},{{L}_{{22}}},E} \right\}$, а выходной вектор – набор $\{ P,S,T,{{C}^{{\text{V}}}},K,G\} $ для тензорного уравнения состояния и одно значение $\left\{ {{{Q}_{{{\text{DN}}}}}} \right\}$ для функции порога нуклеации. Каждый нейрон сети также является функцией, причем достаточно простой, и вычисляет единственный выходной сигнал по нескольким входным сигналам. Под сигналом понимается число, передаваемое от одного нейрона к другому. Нейроны упорядочены в слои как показано на рис. 1. Первый слой  j = 1 является входным и просто распределяет входные значения нейронам следующего слоя. Последний слой j = L является выходным и окончательно формирует выходные значения. Число нейронов входного и выходного слоя определяется размерностью входного и выходного вектора, соответственно. Промежуточные слои $1 < j < L$ называют скрытыми. Число скрытых слоев (L – 2) и число нейронов в каждом из них в общем случае может быть произвольным. В данной работе использовалось четыре (L = 6) скрытых слоя по 64 нейрона в каждом. Сигналы передавались только в одном направлении – от нейронов предыдущего слоя к нейронам последующего, такая структура называется искусственной нейронной сетью с прямой связью.

Обозначим число нейронов в $j$-м слое как ${{N}_{j}}$, а сигнал, формируемый k-м нейроном в $j$-м слое как ${{Z}_{{jk}}}$. Сигналы, формируемые нейронами всех слоев кроме входного можно записать как:

где ${{a}_{{jk,m}}}$ (веса) и ${{b}_{{jk}}}$ (смещения) – параметры, подбираемые в ходе обучения сети; ${{f}_{j}}\left( \centerdot \right)$ – передаточная функция j-го слоя. Мы используем ‘Leaky ReLU’ для нейронов скрытых слоев $j \in \left[ {2,L - 1} \right]$: и сигмоидальную функцию для выходного слоя:

Для ‘Leaky ReLU’ нейронов вычисление самих функций и их производных требует минимум ресурсов. Вычислительно более емкие, но немногочисленные сигмоидальные нейроны выходного слоя сглаживают выходные значения.

Уравнение (3.1) демонстрирует, что нейронная сеть как функция является сложной композицией простых передаточных функций отдельных нейронов. Каждый набор параметров $\{ {{a}_{{jk,m}}},{{b}_{{jk}}}\} $ определяет конкретное частное отображение. Большое количество параметров (порядка 13000 для рассматриваемых нейронных сетей) приводит к чрезвычайной гибкости, практически универсальности задаваемого сетью отображения и широким возможностям ее использования для аппроксимации сложных зависимостей. Процесс обучения состоит в подгонке параметров так, чтобы задаваемое сетью отображение было максимально близко к ожидаемому отображению.

Обучающие данные можно представить как набор пар векторов $\{ ({{{\mathbf{g}}}^{{{\beta }}}},{{{\mathbf{h}}}^{{{\beta }}}}),{{\beta }} \in {\rm B}\} $, где g^β есть входной вектор, а h^β – соответствующий ему выходной вектор. Текущее состояние нейронной сети с текущим набором параметров отображает входной вектор в некоторый другой выходной вектор ${{{\mathbf{g}}}^{{{\beta }}}} \to {{{\mathbf{h}}}^{{{\text{ANN}}}}}({{{\mathbf{g}}}^{{{\beta }}}})$ для каждого ${{\beta }} \in {\rm B}$. За текущую ошибку аппроксимации обычно принимают сумму квадратов отклонений результатов сети от ожидаемых выходных данных:

Обучение сети предполагает минимизацию ошибки (3.4) путем подбора параметров $\left\{ {{{a}_{{jk,m}}},{{b}_{{jk}}}} \right\}$. Для этого необходимо знать значения производных ошибки $e$ по этим параметрам. Дифференцирование (3.4) приводит к формулам:

Используя правило дифференцирования композиции функций, находим производные выхода сети $h_{n}^{{{\text{ANN}}}}({{{\mathbf{g}}}^{{{\beta }}}})$ по параметрам:

где вспомогательные матрицы $D_{k}^{{j,n}}$ находятся через серию матричных перемножений (алгоритм обратного распространения):

Для краткости за z_jk обозначен аргумент передаточной функции соответствующего нейрона:

Алгоритм обучения нейронной сети производит многократные последовательные изменения случайно выбранной части параметров в направлении, обеспечивающем уменьшение ошибки аппроксимации (3.4). Обычно шаг изменения параметров делают пропорциональным соответствующей производной (3.5). Такой алгоритм позволяет замедлить и остановить изменение параметров вблизи минимума, когда производные стремятся к нулю. С другой стороны, он приводит к медленному схождению, если начальное приближение попало в область плато. Более эффективным оказалось изменение параметров с фиксированным малым шагом в направлении против градиента. Параметр увеличивается на фиксированный шаг, если производная по нему отрицательна, и наоборот. Проблема прохождения мимо минимума решалась сохранением набора параметров, соответствующего минимальному значению ошибки. Три последовательных этапа минимизации с уменьшением шага изменения параметров на порядок на каждом последующем этапе оказалось достаточным для достижения приемлемой точности аппроксимации (средняя ошибка менее 1%, максимальная ошибка менее 10%). На последующих этапах обучения алгоритм стартовал с обеспечивающего минимальную ошибку набора параметров предыдущих этапов. Алгоритм обучения был написан на языке программирования FORTRAN. Обучение нейронной сети по набору данных из 8 тысяч пар вход-выход требовало порядка 3 часов работы в однопоточном режиме.

3.2. МД-моделирование для создания обучающих данных. Чем более полный набор данных используется для обучения нейронной сети, тем более детальным будет настроенное отображение, задаваемое сетью. МД-моделированиe является оптимальным инструментом для генерации больших наборов обучающих данных. В свою очередь, нейронные сети как очень гибкие отображения оптимальны для фиксации сложных закономерностей, выявляемых при помощи МД-моделирования.

МД-моделирование проводилось при помощи пакета LAMMPS [44] с использованием межатомного потенциала [45] типа EAM, учитывающего помимо парных взаимодействий также взаимодействие атомов с плотностью обобществленных свободных электронов в металле. Компоненты тензора напряжений Коши рассчитывались через кинетическую энергию атомов и вириал [46]. Визуализация МД-систем проводилась при помощи программы OVITO [47], селекция дефектных областей осуществлялась по величине центрально-симметричного параметра [48], также применялся алгоритм “DXA” для поиска дислокационных линий [49].

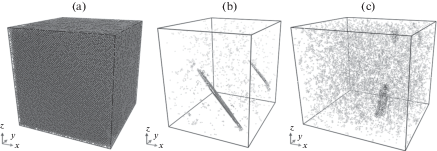
Начальный вид МД-системы показан на рис. 2,a. Она представляет собой кубический образец (репрезентативный объем) монокристалла алюминия (ГЦК структура) с кристаллографическими направлениями [100 ] , [010] и [001], ориентированными вдоль осей $x \equiv {{x}_{1}}$, $y \equiv {{x}_{2}}$ и $z \equiv {{x}_{3}}$, соответственно. Расчетная область содержит полмиллиона атомов, на всех границах заданы периодические граничные условия. После начальной термализации и релаксации напряжений к нулю МД-система подвергается однородной изотермической деформации сжатия/растяжения вдоль осей координат с постоянными инженерными скоростями деформации ${{{{\dot {\varepsilon }}}}_{1}}$, ${{{{\dot {\varepsilon }}}}_{2}}$ и ${{{{\dot {\varepsilon }}}}_{3}}$, причем ${{{{\dot {\varepsilon }}}}_{2}} = {{{{\dot {\varepsilon }}}}_{3}}$, что обеспечивает обсуждаемое выше осесимметричное деформированное состояние. Деформация осуществляется командой “deform” пакета LAMMPS, которая масштабирует координаты атомов. Таким образом, при фиксированной температуре справедливо преобразование:

где $t$ – время с начала деформации. При расчете тензора напряжений за недеформированное состояние принималось состояние без напряжений при температуре 300 K. До образования дефектов и начала пластического течения упругие градиенты деформации можно вычислить как где ${{l}_{0}}$ – размер расчетной области без напряжений при температуре 300 K, а l(T) – ее размер при температуре T. Отношение ${{l\left( T \right)} \mathord{\left/ {\vphantom {{l\left( T \right)} {{{l}_{0}}}}} \right. \kern-0em} {{{l}_{0}}}}$ учитывает тепловое расширение.

На определенной стадии деформации происходит образование дефектов – частичных дислокаций Шокли со следами в виде поверхностей дефектов упаковки (см. рис. 2,b для одноосного сжатия и рис. 2,c для одноосного растяжения – показаны только дефектные атомы). При растяжении вскоре после начала пластического течения образуются и начинают расти полости. Для построения уравнения состояния необходимы данные только об упругой стадии деформации. Для построения порога нуклеации дислокаций нужно отделить упругую и пластическую стадии. В качестве индикатора начала пластического течения использовались всплески температуры. Во время деформации температура системы контролируется термостатом Нозье–Гувера [50], который на упругой стадии обеспечивает флуктуации в пределах десятых долей Кельвина вблизи целевого значения. Начало пластического течения приводит к резкому тепловыделению, термостат не справляется и температура растет на единицы Кельвин при сжатии и даже десятки Кельвин при растяжении (за счет роста полостей). Анализ атомных конфигураций показывает, что момент начала всплеска температуры совпадает с образованием дефектов.

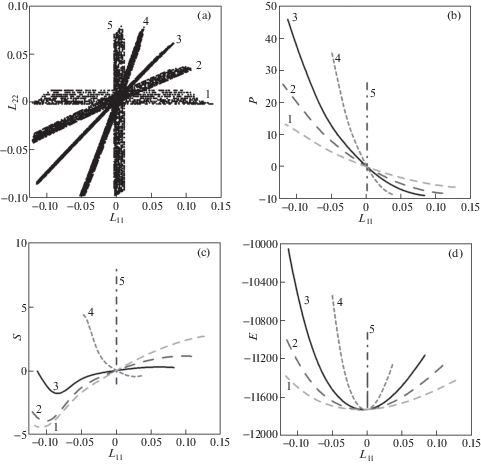
Скорости деформации по осям выбирались одного знака так, чтобы выполнялось ${{{{\dot {\varepsilon }}}}_{1}} + 2{{{{\dot {\varepsilon }}}}_{2}} = {{\dot {\varepsilon }}} = \pm 1$ нс^–1 (знак “–” соответствует сжатию, знак “+” – расширению). Соотношение между ${{{{\dot {\varepsilon }}}}_{1}}$ и ${{{{\dot {\varepsilon }}}}_{2}}$ определяет траекторию деформации. Рассматривалось пять различных траекторий, их список приведен в таблице, в которой значения ${{{{\dot {\varepsilon }}}}_{1}}$ и ${{{{\dot {\varepsilon }}}}_{2}}$ даны в обратных наносекундах для случая растяжения; номера траекторий ${{N}^{{{\text{TR}}}}}$ совпадают с обозначениями на рис. 3. Отметим, что траектория ${{N}^{{{\text{TR}}}}} = 1$ соответствует одноосному растяжению/сжатию, а траектория ${{N}^{{{\text{TR}}}}} = 3$ – наиболее близка к всестороннему растяжению/сжатию. Исследованные траектории деформации в плоскости $\left\{ {{{L}_{{11}}},\;{{L}_{{22}}}} \right\}$ для всех температур представлены на рис. 3,a. Смещение траекторий одной группы для разных температур связано с учетом в (3.10) теплового расширения. Границы приведенных траекторий соответствуют предельной упругой деформации, после которой начинается пластическое течение.

Для каждой траектории деформации расчеты проводились при целевых температурах от 100 до 900 K с шагом 100 K. Всего было проведено 90 МД-расчетов: 5 траекторий по 2 направления (сжатие/растяжение) и 9 температур. Термодинамические параметры МД-систем записывались с временным шагом $\Delta t = 0.1$ пс, что соответствует шагу объемной инженерной деформации ${{\dot {\varepsilon }}} \cdot \Delta t = {{10}^{{ - 4}}}$. После отсечения пластических участков траекторий на оставшихся упругих участках случайным образом равномерно по длине выбиралось 5% точек (от 150 до 250 точек для каждой траектории и температуры), которые использовались в качестве обучающих данных. Использование дополнительно промежуточных точек увеличит время обучения, но в силу гладкости аппроксимируемых зависимостей не добавит новой информации. Примеры рассчитанных в МД-моделировании зависимостей давления (в ГПа), девиатора напряжений (в ГПа) и внутренней энергии (в Дж/г) для 300 K приведены на рис. 3,b–d. Видно, что не только давление (рис. 3,b) но и девиатор напряжений (рис. 3,c) нелинейно зависит от деформации на упругой стадии. Примечательна немонотонная зависимость девиатора при сжатии для траекторий 1–3 вблизи границы упругой стадии. Зависимость внутренней энергии от деформации (рис. 3,d) близка к квадратичной.

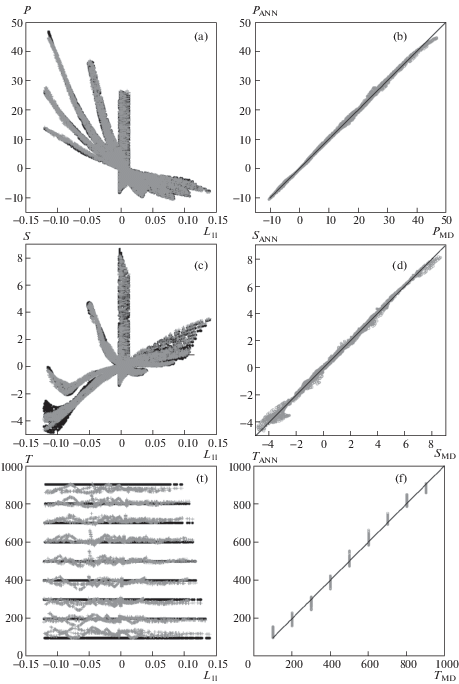
Полученный обучающий массив для тензорного уравнения состояния содержит 8300 пар: входной вектор $\left\{ {{{L}_{{11}}},{{L}_{{22}}},E} \right\}$ – выходной вектор $\{ P,S,T,{{C}^{{\text{V}}}},K,G\} $. Результаты обучения нейронной сети в сравнении с обучающими данными представлены на рис. 4. На рис. 4,a, 4,c и 4,e приведено, соответственно, давление (в ГПа), девиатор напряжений (в ГПа) и температура (в K) как функции продольной деформации L₁₁; темные кружки – данные МД-моделирования, светлые крестики – результаты нейронной сети для тех же входных векторов $\left\{ {{{L}_{{11}}},{{L}_{{22}}},E} \right\}$. На рис. 4,b, 4,d и 4,f светлыми кружками приведена корреляция между данными МД-моделирования (горизонтальная ось) и результатами обученной нейронной сети (вертикальная ось). Можно отметить приемлемую степень корреляции. В МД-моделировании контролируемым параметром является температура, но для более удобного использования в рамках континуальной модели входным параметром уравнения состояния выбрана внутренняя энергия.

Для функции порога нуклеации обучающий набор строился следующим образом. Вдоль каждой полутраектории (сжатие/растяжение) с равным шагом по деформации записывалось 20 точек до определенного из МД-моделирования порога начала пластического течения с парами: входной вектор $\left\{ {{{L}_{{11}}},{{L}_{{22}}},E} \right\}$ – выходной вектор {0}. Далее с тем же шагом в том же направлении записывалось 11 точек (включая сам порог нуклеации и более сильные деформации) с парами: входной вектор $\left\{ {{{L}_{{11}}},{{L}_{{22}}},E} \right\}$ – выходной вектор {1}. Получившийся набор из порядка 2800 точек использовался для обучения нейронной сети, аппроксимирующей функцию ${{Q}_{{{\text{DN}}}}}\left( {{{L}_{{11}}},{{L}_{{22}}},E} \right)$, см. уравнение (2.25) и комментарии. Как следует из определения, эта функция должна принимать значение 0 в упругой области и 1 за порогом нуклеации.

4. Ударные волны в монокристалле алюминия. 4.1. Сравнение континуальной модели и прямого МД-моделирования. На основе континуальной модели и обученных нейронных сетей была написана программа на языке программирования FORTRAN. На первом этапе результаты континуальных расчетов сравнивались с данными прямого МД-моделирования [38] симметричного соударения монокристаллов алюминия толщиной 0.5 мкм каждый с относительной скоростью 2 км/с. Скачек скорости на фронте ударной волны составляет 1 км/с. В поперечных направлениях размер МД-системы составляет 0.02 мкм; в этих направлениях заданы периодические граничные условия, что обеспечивает одноосную макроскопическую деформацию. МД-система содержит 26 миллионов атомов. Рисунок 5 показывает сечение МД-системы в моменты времени 10, 20, 30, 40 и 50 пс (сверху вниз). Раскраска атомов проведена в соответствии со значением центрально-симметричного параметра [48], так что темные области обозначают дефекты упаковки – следы скольжения дислокаций. Видно распространение по изначально идеальному монокристаллу ударной волны, за фронтом которой образуются дислокации.

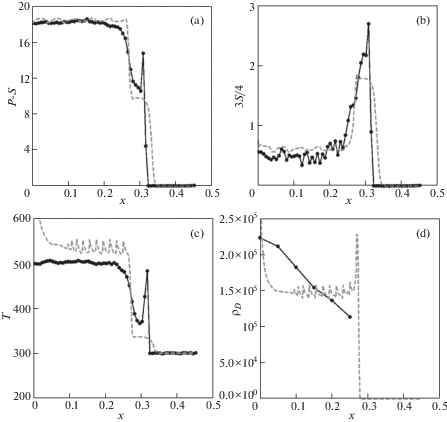
На рис. 6 приведено сравнение пространственных распределений продольных напряжений в ГПа (рис. 6,a), касательных напряжений в ГПа (рис. 6,b), температуры в Кельвинах (рис. 6,c) и плотности дислокаций в мкм^–2 (рис. 6,d), найденных из МД-моделирования (темная сплошная линия с точками) и рассчитанных при помощи континуальной модели (светлая штриховая линия) для момента времени 50 пс с начала соударения. Координата $x$ отсчитывается от плоскости соударения и приведена в микрометрах. Рассчитанные по континуальной модели распределения находятся в соответствии с данными МД-моделирования. Перед основной ударной волной формируется упругий предвестник. Предвестник распространяется по идеальному монокристаллу, и деформация в нем остается упругой вплоть до достижения порога гомогенной нуклеации дислокаций. Полученные в расчетах продольные напряжения на предвестнике согласуются с экспериментальными оценками: от 7.5 ГПа [7] до 12.5 ГПа [1].

После достижения предельной упругой деформации начинается резкий рост плотности дислокаций (рис. 6,d), как за счет нуклеации, так и за счет последующего их размножения. При деформации плотность дислокаций может меняться на порядки величины, поэтому полученное совпадение модели и МД (рис. 6,d) является хорошим. Скольжение дислокаций приводит к релаксации сдвиговых напряжений (рис. 6,c). Далее следует фронт основной ударной волны, на котором деформация происходит уже в пластическом режиме. За фронтом ударной волны касательные напряжения поддерживаются на уровне порядка 0.5 ГПа, определяемом статическим пределом текучести, уравнение (2.21), который высок из-за крайне высокой плотности дислокаций – порядка 10⁵ мкм^–2 (рис. 6,c). Температура за фронтом волны составляет 500 K по данным МД и порядка 535 K согласно континуальной модели; различие может быть связано с конечной точностью аппроксимации нейронной сети (рис. 4,f).

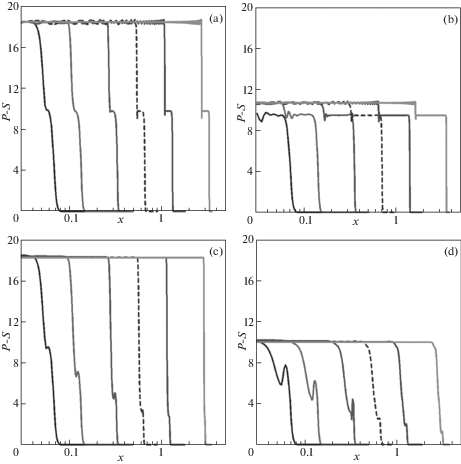
4.2. Эволюция структуры ударной волны в идеальном и деформированном монокристалле. С помощью континуальной модели проведено исследование эволюции предвестника ударной волны. Распределения продольных напряжений в ГПа приведены на рис. 7 для моментов времени (слева направо): 10, 20, 50, 100, 200 и 500 пс. Координата $x$ отсчитывается от плоскости соударения и приведена в микрометрах. Рассматривался случай идеального монокристалла (рис. 7,a,b) и деформированного монокристалла с начальной плотностью дислокаций 100 мкм^–2 (рис. 7,c,d). Такая плотность дислокаций соответствует уже сильно деформированному материалу. При меньших плотностях на рассматриваемых масштабах (от 0.1 мкм) нагружаемый объем может быть свободен от дислокаций. Приведены результаты для ударных волн со скачками скорости 1 км/с (рис. 7,a,c) и 0.6 км/с (рис. 7,b,d).

Основная особенность структуры ударной волны в бездефектном монокристалле – постоянная амплитуда упругого предвестника, не затухающего с удалением от плоскости соударения (рис. 7,a,b). Амплитуда предвестника не зависит и от амплитуды последующей ударной волны, если она достаточна для достижения порога гомогенной нуклеации (скачек скорости более 0.47 км/с). Принципиально иное поведение демонстрирует деформированный монокристалл: упругий предвестник быстро затухает. В то же время, на малых расстояниях от плоскости соударения амплитуда предвестника близка к случаю идеального монокристалла.

5. Заключение. Разработана методика применения искусственных нейронных сетей для описания нелинейной связи компонент напряжений и деформаций (тензорное уравнение состояния) и начала пластического течения (гомогенная нуклеация дислокаций) в монокристаллах металлов на примере алюминия. Наборы данных для обучения нейронных сетей генерируются при помощи МД-моделирования однородной деформации репрезентативных объемов монокристалла. Рассматриваются осесимметричные деформированные состояния, когда ось симметрии совпадает с направлением [100 ] монокристалла. Обученные нейронные сети используются в качестве аппроксимирующих функций в рамках модели дислокационной пластичности, обобщенной на случай конечных деформаций. С ее помощью проводится моделирование распространения ударных волн, возникающих при соударении пластин. В случае наноразмерных пластин проводится сравнение с прямым МД-моделированием процесса. Полученные в расчетах продольные напряжения на упругом предвестнике согласуются с экспериментальными оценками: от 7.5 ГПа [7] до 12.5 ГПа [1]. Проведено исследование эволюции предвестника ударной волны в идеальном и деформированном монокристалле. В идеальном монокристалле упругий предвестник сохраняет постоянную амплитуду, соответствующую порогу гомогенной нуклеации дислокаций; амплитуда предвестника не зависит от амплитуды последующей ударной волны, если она достаточна для достижения порога гомогенной нуклеации (скачек скорости более 0.47 км/с). В деформированном монокристалле упругий предвестник имеет существенно меньшую амплитуду и быстро затухает с расстоянием.

Разработанная континуальная модель с использованием нейронных сетей позволяет исследовать ударные волны в тонких пленках металлов с учетом конечности деформаций и нелинейной связи тензора напряжений и деформаций, а также гомогенной нуклеации дислокаций, как фактора, ограничивающего предельную упругую деформацию. Развитием работы может стать применение разработанной методики для других металлов и сплавов, а также рассмотрение более общего случая деформации.

Благодарности. Описание гомогенной нуклеации дислокации на основе нейронной сети и исследование роли гомогенной нуклеации в распространении ударных волн выполнено за счет гранта Российского научного фонда (проект № 20-11-20153). Разработка тензорного уравнения состояния на основе нейронной сети поддержана Минобрнауки РФ в рамках гос. задания на выполнение НИР ЧелГУ (№ 075-00250-20-03).