Известия РАН. Механика твердого тела, 2021, № 3, стр. 36-41

ОБ ЭВОЛЮЦИИ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА, ПОДВЕШЕННОГО НА НИТИ В ОДНОРОДНОМ ПОЛЕ ТЯЖЕСТИ

А. П. Маркеев^a, b, *

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

^b Московский авиационный институт (национальный исследовательский университет)
Москва, Россия

^* E-mail: anat-markeev@mail.ru

Поступила в редакцию 25.04.2020
После доработки 25.07.2020
Принята к публикации 07.08.2020

DOI: 10.31857/S0572329921020124

Полный текст (PDF)

Аннотация

Изучается плоское движение твердого тела в однородном поле тяжести. Тело подвешено на невесомой нерастяжимой нити, которая во все время движения остается натянутой. Предполагается, что длина нити имеет большую величину ($\sim {{\varepsilon }^{{ - 1/2}}}$), а расстояние от точки подвеса тела до его центра тяжести является малым (~ε). Уравнения движения представлены как уравнения системы с одной быстро вращающейся фазой. Эта система исследуется при помощи классической теории возмущений и КАМ-теории. Показано, что для всех значений времени движение мало (на величины ~ε) отличается от медленных колебаний нити в окрестности нисходящей вертикали и вращения тела относительно точки подвеса с почти постоянной угловой скоростью. Мера множества движений, отличных от упомянутых движений, оценивается сверху величиной порядка $\exp \left( { - c{\text{/}}\varepsilon } \right)$ ($c > 0$ – const).

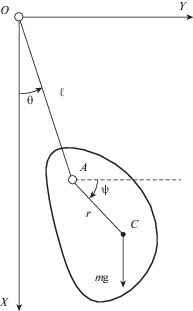
Ключевые слова: система Гамильтона, маятник, колебания, вращения, устойчивость

Введение. Рассмотрим твердое тело весом $mg$, подвешенное при помощи невесомой нерастяжимой нити длиной $\ell $. Движение тела таково, что векторы скоростей всех его точек параллельны неподвижной вертикальной плоскости $OXY$, проходящей через центр тяжести $C$ тела и его точку подвеса $A$ (см. рис. 1). Считаем, что во все время движения нить натянута.

Рис. 1

Рассматриваемая материальная система имеет две степени свободы. За обобщенные координаты примем угол $\theta $, который составляет направление нити $OA$ с вертикалью $OX$, и угол $\psi $ между отрезком $AC$ и горизонтальной осью OY.

Целью статьи является исследование эволюции движения на бесконечном интервале времени при следующих двух предположениях: расстояние $r$ от точки $A$ до центра тяжести $C$ является малой величиной, длина нити $\ell $ – большая величина. Анализ проводится при помощи классических и современных методов теории возмущений [1–4].

Динамика твердого тела на невесомой идеально гибкой нерастяжимой нити (струне) к настоящему времени получила значительное развитие. Подробно исследован вопрос о существовании, устойчивости и бифуркациях периодических, стационарных и прецессионных движений, рассмотрен также случай, когда струна не является идеальной [5–8]. В статьях [9, 10] исследованы некоторые задачи динамики твердого тела, в которых нить рассматривается как идеальная неудерживающая связь.

1. Уравнения движения. Кинетическая и потенциальная энергия тела вычисляются по формулам

(1.1)

$T = \frac{1}{2}m({{\dot {x}}^{2}} + {{\dot {y}}^{2}}) + \frac{1}{2}{{J}_{c}}{{\dot {\psi }}^{2}},\quad \Pi = - mg{{x}_{c}}$

(1.2)

${{x}_{c}} = \ell \cos \theta + r\sin \psi ,\quad {{y}_{c}} = \ell \sin \theta + r\cos \psi $

Здесь точкой обозначается дифференцирование по времени t, а ${{J}_{c}}$ – момент инерции тела относительно оси, проходящей через его центр тяжести перпендикулярно плоскости $OXY$.

Из (1.1) и (1.2) имеем выражение для функции Лагранжа $L = T - \Pi $:

$L = \frac{1}{2}({{J}_{c}} + m{{r}^{2}}){{\dot {\psi }}^{2}} - mr\ell \sin (\theta + \psi )\dot {\psi }\dot {\theta } + \frac{1}{2}m{{\ell }^{2}}{{\dot {\theta }}^{2}} + mg(\ell \cos \theta + r\sin \psi )$

В дальнейшем будет использоваться гамильтонова форма уравнений движения. Функция Гамильтона $\Gamma $ задается равенством $\Gamma = T + \Pi $, в правой части которого величины $\dot {\psi }$ и $\dot {\theta }$ должны быть выражены через обобщенные импульсы ${{p}_{\psi }}$, ${{p}_{\theta }}$:

${{p}_{\psi }} = \tfrac{{\partial L}}{{\partial{ \dot {\psi }}}},\quad {{p}_{\theta }} = \tfrac{{\partial L}}{{\partial{ \dot {\theta }}}}$

После несложных выкладок получаем функцию Гамильтона в следующем виде:

(1.3)

$\begin{gathered} \Gamma = \frac{1}{{2[{{J}_{c}} + m{{r}^{2}}{{{\cos }}^{2}}(\theta + \psi )]}}\left[ {p_{\psi }^{2} + 2\frac{r}{\ell }\sin (\theta + \psi ){{p}_{\psi }}{{p}_{\theta }} + \frac{{J_{c}^{2} + m{{r}^{2}}}}{{m{{\ell }^{2}}}}p_{\theta }^{2}} \right] - \\ - \;mg(\ell \cos \theta + r\sin \psi ) \\ \end{gathered} $

2. Малый параметр. Представление функции Гамильтона в виде ряда. Вместо ${{p}_{\psi }}$, ${{p}_{\theta }}$ введем безразмерные импульсы ${{p}_{\chi }}$, ${{p}_{\delta }}$ при помощи канонического (с валентностью ${{(m\ell \sqrt {g\ell } )}^{{ - 1}}}$) преобразования вида

(2.1)

${{p}_{\psi }} = {{(m\ell \sqrt {g\ell } )}^{{ - 1}}}{{p}_{\chi }},\quad {{p}_{\theta }} = {{(m\ell \sqrt {g\ell } )}^{{ - 1}}}{{p}_{\delta }},\quad \psi = \chi ,\quad \theta = \delta $

и перейдем к новой (безразмерной) независимой переменной τ:

(2.2)

$\tau = (m\ell \sqrt {g\ell } {\text{/}}{{J}_{c}})t$

Новым переменным отвечает функция G, вычисляемая по формуле

(2.3)

$G = {{{{J}_{c}}} \mathord{\left/ {\vphantom {{{{J}_{c}}} {({{m}^{2}}g{{\ell }^{3}})}}} \right. \kern-0em} {({{m}^{2}}g{{\ell }^{3}})}}\Gamma $

где $\Gamma $ – функция (1.3), в которой сделана замена (2.1).

В соответствии с принятыми (см. Введение) предположениями введем в уравнения движения малый параметр $\varepsilon $ ($0 < \varepsilon \ll 1$), положив

(2.4)

$r = \varepsilon {\text{ a,}}\quad \ell = {{\varepsilon }^{{ - 1/2}}}\sqrt {{{{{J}_{c}}} \mathord{\left/ {\vphantom {{{{J}_{c}}} m}} \right. \kern-0em} m}} $

где a – величина порядка единицы, имеющая размерность длины.

Функция Гамильтона (2.3) представима в виде ряда по степеням параметра ε:

(2.5)

$G = {{G}_{0}} + \varepsilon {{G}_{1}} + {{\varepsilon }^{2}}{{G}_{2}} + O({{\varepsilon }^{3}})$

${{G}_{0}} = \frac{1}{2}p_{\chi }^{2},\quad {{G}_{1}} = - \frac{1}{2}\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}p_{\chi }^{2}{{\cos }^{2}}(\delta + \chi ) + \frac{a}{\ell }{{p}_{\chi }}{{p}_{\delta }}\sin (\delta + \chi ) + \frac{1}{2}p_{\delta }^{2} - \cos \delta ,$

$\begin{gathered} {{G}_{2}} = - \frac{a}{\ell }\sin \chi + \frac{1}{2}\frac{{{{a}^{4}}}}{{{{\ell }^{4}}}}p_{\chi }^{2}{{\cos }^{4}}(\delta + \chi ) - \\ - \;\frac{{{{a}^{3}}}}{{{{\ell }^{3}}}}{{p}_{\chi }}{{p}_{\delta }}\sin (\delta + \chi ){{\cos }^{2}}(\delta + \chi ) + \frac{1}{2}\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}p_{\delta }^{2}{{\sin }^{2}}(\delta + \chi ) \\ \end{gathered} $

3. Упрощение функции Гамильтона. Система с функцией Гамильтона (2.5) имеет быстро вращающуюся фазу χ. При помощи классической теории возмущений можно построить близкое к тождественному каноническое преобразование χ, δ, p_χ, ${{p}_{\delta }} \to x,y$, p_x, p_y, которое исключает зависимость функции Гамильтона от быстрой фазы в любом конечном приближении по ε. Приведем явный вид канонической замены, исключающей быструю фазу в членах до второй степени ε включительно. Производящую функцию $S({{p}_{x}},{{p}_{y}},\chi ,\delta )$ возьмем в виде

(3.1)

$S = {{p}_{x}}\chi + {{p}_{y}}\delta + \varepsilon {{S}_{1}}({{p}_{x}},{{p}_{{y,}}}\chi ,\delta ) + {{\varepsilon }^{2}}{{S}_{2}}({{p}_{x}},{{p}_{{y,}}}\chi ,\delta )$

Из (3.1) и соотношений

$x = \tfrac{{\partial S}}{{\partial {{p}_{x}}}},\quad y = \tfrac{{\partial S}}{{\partial {{p}_{y}}}},\quad {{p}_{\chi }} = \tfrac{{\partial S}}{{\partial \chi }},\quad {{p}_{\delta }} = \tfrac{{\partial S}}{{\partial \delta }}$

следует, что

(3.2)

$\begin{gathered} \chi = x - \varepsilon \frac{{\partial {{S}_{1}}}}{{\partial {{p}_{x}}}} + O({{\varepsilon }^{2}}),\quad \delta = y - \varepsilon \frac{{\partial {{S}_{1}}}}{{\partial {{p}_{y}}}} + O({{\varepsilon }^{2}}), \\ {{p}_{\delta }} = {{p}_{y}} + \varepsilon \frac{{\partial {{S}_{1}}}}{{\partial y}} + O({{\varepsilon }^{2}}) \\ \end{gathered} $

(3.3)

${{p}_{\chi }} = {{p}_{x}} + \varepsilon \frac{{\partial {{S}_{1}}}}{{\partial x}} + {{\varepsilon }^{2}}\left( {\frac{{\partial {{S}_{2}}}}{{\partial x}} - \frac{{{{\partial }^{2}}{{S}_{1}}}}{{\partial {{x}^{2}}}}\frac{{\partial {{S}_{1}}}}{{\partial {{p}_{x}}}} - \frac{{{{\partial }^{2}}{{S}_{1}}}}{{\partial x\partial y}}\frac{{\partial {{S}_{1}}}}{{\partial {{p}_{y}}}}} \right) + O({{\varepsilon }^{3}})$

где ${{S}_{i}} = {{S}_{i}}({{p}_{x}},{{p}_{{y,}}}x,y)$ ($i = 1,\;2$).

Подставив выражения (3.2) и (3.3) в правую часть равенства (2.5) и проведя несложные вычисления, получим, что для исключения быстрой фазы $x$ из членов до второй степени включительно в разложении новой функции Гамильтона $F({{p}_{x}},{{p}_{{y,}}}x,y,\varepsilon )$ в ряд по $\varepsilon $ функции ${{S}_{1}}$ и ${{S}_{2}}$ следует взять такими:

${{S}_{1}} = \frac{a}{\ell }{{p}_{y}}\cos (x + y) + \frac{1}{8}\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}{{p}_{x}}\sin (2x + 2y)$

${{S}_{2}} = - {\text{ }}\frac{a}{{2\ell {{p}_{x}}}}{\text{ }}\cos x - \frac{a}{{8\ell {{p}_{x}}}}{\text{ }}\left( {\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}p_{x}^{2} + 8p_{y}^{2}} \right)\cos (x + y) - {\text{ }}\frac{a}{{2\ell {{p}_{x}}}}{\text{ }}\cos (x + 2y) + $

$ + \;\frac{1}{{24}}\frac{{{{a}^{3}}}}{{{{\ell }^{3}}}}{{p}_{x}}\cos (3x + 3y) - \frac{1}{{16}}\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}\left( {\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}{{p}_{x}} + 6{{p}_{y}}} \right)\sin (2x + 2y) - \frac{1}{{256}}\frac{{{{a}^{4}}}}{{{{\ell }^{4}}}}{{p}_{x}}\sin (4x + 4y)$

Новая функция Гамильтона записывается в следующем виде:

(3.4)

$F = \frac{1}{2}{{A}_{0}}p_{x}^{2} - \frac{1}{2}{{\varepsilon }^{2}}\frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}{{p}_{x}}{{p}_{y}} + \varepsilon \left( {\frac{1}{2}p_{y}^{2} - \cos y} \right) + {{\varepsilon }^{3}}{{F}_{3}}({{p}_{x}},{{p}_{y}},x,y,\varepsilon )$

где введено обозначение

(3.5)

${{A}_{0}} = 1 - \frac{1}{2}\varepsilon \frac{{{{a}^{2}}}}{{{{\ell }^{2}}}} + \frac{9}{{32}}{{\varepsilon }^{2}}\frac{{{{a}^{4}}}}{{{{\ell }^{4}}}}$

Структуру функции Гамильтона (3.4) можно упростить, если сделать унивалентное каноническое преобразование $x,y,{{p}_{x}},{{p}_{y}} \to {{w}_{0}},q,{{I}_{0}},p$ по формулам

(3.6)

$x = {{w}_{0}} - \frac{1}{2}\varepsilon \frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}q,\quad y = q,\quad {{p}_{x}} = {{I}_{0}},\quad {{p}_{y}} = p + \frac{1}{2}\varepsilon \frac{{{{a}^{2}}}}{{{{\ell }^{2}}}}{{I}_{0}}$

Преобразование (3.6) уничтожает в функции (3.4) второе слагаемое, и в новых переменных уравнения движения задаются функцией Гамильтона

(3.7)

$F = \frac{1}{2}{{A}_{0}}I_{0}^{2} + \varepsilon \left( {\frac{1}{2}{{p}^{2}} - \cos q} \right) + {{\varepsilon }^{3}}{{A}_{3}}({{I}_{0}},p,{{w}_{0}},q,\varepsilon ),\quad {{A}_{3}} = {{F}_{3}} - \frac{1}{8}\frac{{{{a}^{4}}}}{{{{\ell }^{4}}}}I_{0}^{2}$

Здесь ${{F}_{3}}$ – функция из (3.4), в которой сделана замена (3.6).

Еще большего упрощения можно добиться, приняв в качестве независимой переменной величину ${{\tau }_{*}} = {{A}_{0}}\tau $. Это приводит к делению функции Гамильтона (3.7) на ${{A}_{0}}$.

Если еще вместо $\varepsilon $ ввести новый малый параметр $\mu $ по формуле $\mu = \varepsilon {\text{/}}{{A}_{0}}$, то вместо функции $F$ из (3.7) получим функцию $H$ вида

(3.8)

$H = {{H}^{{(0)}}}({{I}_{0}}) + \mu {{H}^{{(1)}}}(p,q) + {{\mu }^{3}}{{H}^{{(3)}}}({{I}_{0}},p,{{w}_{0}},q,\mu )$

(3.9)

${{H}^{{(0)}}} = \frac{1}{2}I_{0}^{2},\quad {{H}^{{(1)}}} = \frac{1}{2}{{p}^{2}} - \cos q$

4. Анализ системы с функцией Гамильтона (3.8). В приближенной системе с функцией ${{H}^{{(0)}}} + \mu {{H}^{{(1)}}}$ переменная I₀ постоянна, а угловая координата ${{w}_{0}}$ равномерно меняется со временем. Переменные же q, $p$ отвечают движению математического маятника. Будем предполагать, что реализуется колебательный режим его движения. Амплитуду колебаний обозначим через ${{q}_{{\max }}}$ $(0 < {{q}_{{\max }}} < \pi {\text{/}}2)$. Для описания колебаний введем переменные действие-угол I, $w$. Переменная I вычисляется [11] по формуле

(4.1)

$I = \frac{8}{\pi }[E(k) - (1 - {{k}^{2}})K(k)]$

Здесь и далее используются общепринятые обозначения для эллиптических интегралов и функций. В (4.1) $k = \sin ({{q}_{{\max }}}{\text{/}}2)$ ($0 < {{k}^{2}} < 1{\text{/}}2$).

Каноническое преобразование $q,p \to w,I$ задается формулами [11]:

(4.2)

$q = 2\arcsin (k{\text{sn}}(u,k)),\quad p = 2k{\text{cn}}(u,k),\quad u = (2K(k){\text{/}}\pi )w$

в которых $k = k(I)$ – функция, обратная функции (4.1).

Функцию Гамильтона (3.8) можно теперь записать в виде

(4.3)

$H = {{H}^{{(0)}}}({{I}_{0}}) + \mu {{H}^{{(1)}}}(I) + {{\mu }^{3}}{{H}^{{(3)}}}({{I}_{0}},p,{{w}_{0}},q,\mu )$

Здесь функция ${{H}^{{(1)}}} = - 1 + 2{{k}^{2}}(I)$, она представима сходящимся рядом по степеням I. Переменные p и q в функции ${{H}^{{(3)}}}$должны быть заменены по формулам (4.2).

Функция (4.3) аналитична по всем своим аргументам и $2\pi $ – периодична по ${{w}_{0}}$ и $w$. При этом имеет место случай собственного вырождения [1], так как при μ = 0 в системе есть только одна отличная от нуля частота:

(4.4)

$\tfrac{{\partial {{H}^{{(0)}}}}}{{\partial {{I}_{0}}}} = {{I}_{0}} \ne 0$

Для производных функции H⁽¹⁾ из (4.3) справедливы неравенства

(4.5)

$\tfrac{{\partial {{H}^{{(1)}}}}}{{\partial I}} \ne 0,\quad \tfrac{{{{\partial }^{2}}{{H}^{{(1)}}}}}{{\partial {{I}^{2}}}} \ne 0$

Действительно,

$\tfrac{{\partial {{H}^{{(1)}}}}}{{\partial I}} = \frac{\pi }{{2K(k)}} = 1 - \frac{1}{8}I - \frac{3}{{256}}{{I}^{2}} - \frac{5}{{2048}}{{I}^{3}} + O({{I}^{4}}) > 0$

$\tfrac{{{{\partial }^{2}}{{H}^{{(1)}}}}}{{\partial {{I}^{2}}}} = - {{\pi }^{2}}\frac{{E(k) - (1 - {{k}^{2}})K(k)}}{{16{{k}^{2}}(1 - {{k}^{2}}){{K}^{3}}(k)}} = - \frac{1}{8} - \frac{3}{{128}}I - \frac{{15}}{{2048}}{{I}^{2}} + O({{I}^{3}}) < 0$

Так как приближенная система с функцией Гамильтона ${{H}^{{(0)}}} + \mu {{H}^{{(1)}}}$ удовлетворяет условиям (4.4), (4.5), то [2] в полной системе с функцией Гамильтона (4.3) переменные действия I₀, I при всех значениях $t$ остаются вблизи своих начальных значений и отличаются от них на величины порядка $\mu $ (или порядка $\varepsilon $, что одно и то же). При этом мера инвариантных торов приближенной системы, разрушающихся при учете возмущения ${{H}^{{(3)}}}$ в (4.3), имеет порядок $\exp \left( { - c{\text{/}}\varepsilon } \right)$ ($c > 0$ – const).

Основной результат анализа. Из сказанного следует, что при малых $\varepsilon $ движение твердого тела, подвешенного на идеальной нити в однородном поле тяжести, устойчиво по отношению к возмущениям величин $\theta $, $\dot {\theta }$, $\dot {\psi }$. В частности, если начальные значения θ и $\dot {\theta }$ имеют, например, порядок ${{\varepsilon }^{{1 - \sigma }}}$ ($0 < \sigma < 1$), то $\theta $ и $\dot {\theta }$ при всех $t$ остаются малыми того же порядка.

Замечание. В статье [12], посвященной динамике маятника Максвелла, утверждается, что “отклонение маятника от вертикали имеют конечный размах при соответствующих сколь угодно малых начальных значениях координат и скоростей нити. Причиной этой неустойчивости является достаточно быстрое переходное движение маятника при перемене его движения снизу вверх”. В приведенной в статье [12] попытке обоснования этого утверждения содержатся неточности, а само утверждение ошибочно.

Работа выполнена за счет гранта Российского научного фонда (проект № 19-11-00116) в Московском авиационном институте (Национальном исследовательском университете) и в Институте проблем механики им. А.Ю. Ишлинского РАН.

Список литературы

Арнольд В.И., Козлов В.В., Нейштадт А.И. Математические аспекты классической и небесной механики. М.: Эдиториал УРСС, 2002. 414 с.
Нейштадт А.И. Оценки в теореме Колмогорова о сохранении условно-периодических движений // ПММ. 1981. Т. 45. Вып. 6. С. 1016–1025.
Giacaglia G.E.O. Perturbation Methods in Non-Linear Systems. N.Y.etc. Springer, 1972. = Джакалья Г.Е.О. Методы теории возмущений для нелинейных систем. М.: Наука, 1979. 320 с.
Журавлев В.Ф., Климов Д.М. Прикладные методы в теории колебаний. М.: Наука, 1988. 328 с.
Ишлинский А.Ю., Стороженко В.А., Темченко М.Е. Вращение твердого тела на струне и смежные задачи. М.: Наука, 1991. 330 с.
Ишлинский А.Ю., Стороженко В.А., Темченко М.Е. Динамика быстровращающихся на струне тел и некоторые смежные вопросы (обзор) // Прикладная механика. 1994. Т. 30. № 8. С. 3–30.
Мирер С.А., Сарычев В.А. О стационарных движениях тела на струнном подвесе // Нелинейная механика: сб. статей. М.: Физматлит, 2001. С. 281–322.
Маркеев А.П. О периодических движениях твердого тела, подвешенного на нити в однородном поле тяжести // Вестник Удм. ун-та. Математика. Механика. Компьютерные науки. 2019. Т. 29. Вып. 2. С. 245–260.
Иванов А.П. Об устойчивости перманентных вращений тела, подвешенного на струне, при наличии ударных взаимодействий // Изв. АН СССР. МТТ. 1985. № 6. С. 47–50.
Маркеев А.П. Об устойчивости периодического движения стержня, подвешенного на идеальной нити // Изв. РАН. МТТ. 2007. № 4. С. 3–13.
Маркеев А.П. Теоретическая механика. Москва–Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2007. 592 с.
Розенблат Г.М. О неустойчивости движения маятника Максвелла // Изв. РАН. МТТ. 2018. № 5. С. 59–67.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал