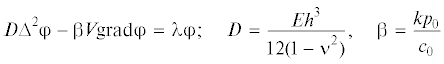Известия РАН. Механика твердого тела, 2021, № 3, стр. 62-67
О ФЛАТТЕРЕ ЭЛЛИПТИЧЕСКОЙ ПЛАСТИНЫ
С. Д. Алгазин a, *, Ж. Г. Ингтем b, **
a Институт проблем механики им. А.Ю. Ишлинского Российской aкадемии наук
Москва, Россия
b Московский государственный университет им. М.В. Ломоносова
Москва, Россия
* E-mail: algazinsd@mail.ru
** E-mail: j-g.ingtem@cs.msu.ru
Поступила в редакцию 04.12.2019
После доработки 19.03.2020
Принята к публикации 22.05.2020
Аннотация
Методом математического моделирования исследуется флаттер пластины эллиптической формы в плане при разных направлениях угла атаки набегающего потока. Для численного моделирования неустойчивых колебаний пластины предложен эффективный численный алгоритм без насыщения, который позволяет на редкой сетке получить приемлемую точность в приближенном решении. Численно исследована зависимость критической скорости от безразмерной скорости звука в пластине, толщины пластины и угла направления вектора скорости набегающего потока.
Введение. Рассматривается флаттер пластины, обтекаемой, с одной стороны, потоком воздуха. Принята математическая модель флаттера пластины построена А.А. Ильюшиным, И.А. Кийко [1]. Эффективный алгоритм решения задачи разработан автором и Кийко И.А. [2]. Основу программы составляет построение дискретного бигармонического оператора по методике [3]. Конформное отображение строится по программе Э.П. Казанджана [4]. Программный комплекс устроен таким образом, что если известны параметрические уравнения границы области, то возможно найти критическую скорость флаттера и построить соответствующую собственную форму. Стандартно критическая скорость флаттера ищется на двух сетках 9 × 15 и 15 × 31; критерием правильности расчета является близость полученных значений, возможно задать произвольную сетку.
1. Математическая постановка задачи. Исследование устойчивости колебаний тонкой пластины произвольной формы в плане, которая в плоскости x, y занимает область G с границей $\partial G$ и обдувается потоком газа, приводит к спектральной задаче [1] для амплитудного значения прогибов ${{\varphi }} = {{\varphi }}(x,y)$, $(x,y) \in G$.
(1.2)
${{\left. {{\varphi }} \right|}_{{\partial G}}} = 0,\quad {{\left. {M{{\varphi }}} \right|}_{{\partial G}}} = 0$Здесь Е, ν – модуль Юнга и коэффициент Пуассона материала пластины, h – ее толщина, V = (Vx, Vy) – вектор скорости газа, р0, с0 – давление и скорость звука в невозмущенном потоке, k – показатель политропы газа.
Собственное число λ связано с частотой колебаний соотношением
в котором ρ – плотность материала пластины.Оператор М в (1.2) – это известный в теории пластин дифференциальный оператор, определяемый типом граничных условий. Методика решения спектральной задачи (1.1)– (1.3) описана для произвольного оператора М.
Колебания пластины будут устойчивыми или нет в зависимости от того, будет ли Reω < 0 или Reω > 0; если ${{{{\lambda }}}_{1}} = {{{{\alpha }}}_{1}} + i{{{{\beta }}}_{1}}$ – наименьшее по модулю собственное значение, то вследствие (1.3) выписанным неравенствам соответствуют $F\left( {{{{{\alpha }}}_{1}},{{{{\beta }}}_{1}}} \right) > 0$ или $F({{{{\alpha }}}_{1}},{{{{\beta }}}_{1}})$ < 0, где $F\left( {{{{{\alpha }}}_{1}},{{{{\beta }}}_{1}}} \right) = {{{{\alpha }}}_{1}}{{\beta }}_{1}^{2} - {{\rho }}h{{\beta }}_{1}^{2}$. Поскольку ${{{{\alpha }}}_{1}} = {{{{\alpha }}}_{1}}\left( V \right)$, ${{{{\beta }}}_{1}} = {{{{\beta }}}_{1}}\left( V \right)$ уравнение $F({{{{\alpha }}}_{1}},{{{{\beta }}}_{1}})$ = 0 определяет нейтральную кривую и соответствующую ей критическую скорость флаттера. Речь идет, следовательно, о нахождении нулей функции F(α1(V), ${{{{\beta }}}_{1}}(V))$ при заданном направлении вектора скорости потока.
Обозначим через l характерный размер области G и введем безразмерные (со штрихами) координаты и параметры: $x = x{\kern 1pt} '{\kern 1pt} l$, $y = y{\kern 1pt} '$, $E = E{\kern 1pt} '{\kern 1pt} {{p}_{0}}$, $h = h{\kern 1pt} '{\kern 1pt} l$, ${{\rho }} = \frac{{{{\rho }}{\kern 1pt} {\text{'}}{{p}_{0}}}}{{c_{0}^{2}}}$, ${{\omega }} = \frac{{{{\omega '}}{{c}_{0}}}}{l}$, $V = V{\kern 1pt} '{\kern 1pt} {{c}_{0}}$, ${{\varphi }} = {{\varphi '}}l$.
Подставив в (1.1) (1.3), убеждаемся, что в безразмерной форме система сохраняет свой вид, если параметр β заменить на безразмерный параметр k. В дальнейшем изложении штрихи будем опускать.
Введем вместо декартовых координат х, у криволинейные координаты r, θ по формулам $x = u~\left( {r,~{{\theta }}} \right)$, $y = {\text{\;}}{v}(r,~{{\theta }})$; если выполнены условия Коши–Римана
(1.5)
$D{{\Delta }}({{\left| {{{\psi '}}\left( {{\zeta }} \right)} \right|}^{{ - 2}}}{{\Delta \varphi }}) = {{\Phi }}\left( {r,{{\varphi }}} \right) + {{\lambda }}{{\left| {{{\psi '}}\left( {{\zeta }} \right)} \right|}^{2}}{{\varphi }}$Теперь очевидно, что дискрeтизация краевой задачи (1.5), (1.2) вполне аналогична описанной ранее [5] для бигармонического оператора.
2. Вычислительные эксперименты. Рассматривалась эллиптическая пластина с большой полуосью a = 1 и эксцентриситетом e = 0.7 для 4-х материалов: титан $({{c}_{2}}$ = 14.773, сталь $({{c}_{2}} = 15.131)$, алюминий $({{c}_{2}} = 15.214){\text{\;}}$ и дюралюминий $\left( {{{c}_{2}} = 15.257} \right)$, где c2 – безразмерная скорость звука в пластине (отношение скорости звука в пластине к скорости звука в воздухе). Величина $h \times {{10}^{3}}$ менялась от 1 до 5 с шагом 1, где h – толщина пластины (безразмерная, a – характерный размер). Критическая скорость флаттера ищется на двух сетках 9 × 15 и 15 × 31; критерием правильности расчета является близость полученных значений. Было произведено 80 расчетов. Проводились 4 серии расчетов (по 20 расчетов в серии):
Первая краевая задача (защемленная по контуру пластинка). Рассматривается случай θ = 0, где θ – угол направления вектора потока с осью Ox. По результатам численных расчетов подбиралась аналитическая зависимость критической скорости флаттера $z = {{{v}}_{{{\text{кр}}}}}$, от двух безразмерных параметров $x = {{c}_{2}}$ – безразмерная скорость звука в пластине (отношение скорости звука в пластине к скорости звука в воздухе), $y = h \times {{10}^{3}}$, где h – толщина пластины (безразмерная, a – характерный размер) в результате получено:
Первая краевая задача (защемленная по контуру пластинка). Рассматривается случай ${{\theta }} = \pi {\text{/}}2$. Получена та же зависимость (2.1), где $a = 10.889836$, $b = - 0.71384416$, c = = $0.023068911$.
Вторая краевая задача (свободно опертая по контуру пластинка). Рассматривается случай θ = 0. Получена та же зависимость (2.1), где $a = 1.4538196$, $b = - 0.089596533$, $c = 0.011091714$.
Вторая краевая задача (свободно опертая по контуру пластинка). Рассматривается случай θ = π/2. Получена та же зависимость (2.1), где $a = 3.885002$, $b = - 0.25079837$, $c = 0.019491586$.
Дальнейшие расчеты проводились для алюминиевой пластины с разными направлениями вектора скорости потока.
В этих таблицах в левой колонке приведены углы ${{\theta }}$ направления вектора потока с осью Оx. Запись 9 × 15 означает сетку в круге из 9 окружностей по 15 точек на каждой окружности и т.п. Число в круглых скобках указывает номер собственного значения, по которому исследовалась устойчивость.
По таблицам 1, 3–6 подбиралась аналитическая зависимость критической скорости флаттера от двух параметров h – толщина пластины и θ – направление вектора скорости с осью абсцисс. В приведенных формулах первый параметр x = h, а y – доля π в θ. Например, для ${{\theta }} = {{\pi /}}8$, $y = 1{\text{/}}8$.
Таблица 1
| (a = 1, e = 0.7); Al: $E = 0.7 \times {{10}^{6}}$ кгс/см2, $\rho = 2.7 \times {{10}^{3}}$ кг/м3 | ||||
|---|---|---|---|---|
| θ | 1-я краевая задача | 2-я краевая задача | ||
| 9 × 15 | 15 × 31 | 9 × 15 | 15 × 31 | |
| 0 | 0.3626 | 0.3622 | 0.2789 | 0.2783 |
| π/16 | 0.3652 | 0.3652 | 0.2796 | 0.2796 |
| π/8 | 0.3735 | 0.3742 | 0.2821 | 0.2833 |
| 3π/16 | 0.3873 | 0.3887 | 0.2867 | 0.2887 |
| π/4 | 0.4061 | 0.4076 | 0.2925 | 0.2946 |
| 5π/16 | 0.4260 | 0.4280 | 0.2974 | 0.2992 |
| 3π/8 | 0.4432 | 0.4441 | 0.2994 | 0.3006 |
| 7π/16 | 0.4498 | 0.4502 | 0.2989 | 0.2996 |
| π/2 | 0.4503 | 0.4505 | 0.2985 | 0.2987 |
Таблица 2
| a = 1, e = 0.7; Ti: $E = 1.1 \times {{10}^{6}}$ кгс/см2, $\rho = 4.5 \times {{10}^{3}}$ кг/м3 | ||||
|---|---|---|---|---|
| θ | 1-я краевая задача | 2-я краевая задача | ||
| 9 × 15 | 15 × 31 | 9 × 15 | 15 × 31 | |
| 0 | 0.4438 | 0.4434 | 0.3011 | 0.3005 |
| π/16 | 0.4481 | 0.4478 | 0.3036 | 0.3032 |
| π/8 | 0.4609 | 0.4611 | 0.3112 | 0.3115 |
| 3π/16 | 0.4829 | 0.4837 | 0.3241 | 0.3250 |
| π/4 | 0.5144 | 0.5157 | 0.3419 | 0.3435 |
| 5π/16 | 0.5545 | 0.5559 | 0.3627 | 0.3646 |
| 3π/8 | 0.5980 | 0.5993 | 0.3884 | 0.3828 |
| 7π/16 | 0.6291 | 0.6298 | 0.3894 | 0.3902 |
| π/2 | 0.6344 | 0.6346 | 0.3899(2) | 0.3902(2) |
Таблица 3
| a = 1, e = 0.7; Al: $E = 0.7 \times {{10}^{6}}$ кгс/см2, ${{\rho }} = 2.7 \times {{10}^{3}}$ кг/м3, h = 0.001 | ||||
|---|---|---|---|---|
| θ | 1-я краевая задача | 2-я краевая задача | ||
| 9 × 15 | 15 × 31 | 9 × 15 | 15 × 31 | |
| 0 | 0.0992046(3) | 0.0906550(5) | 0.0869917(2) | 0.127044(4) |
| π/8 | 0.0752673(3) | 0.0922430(5) | 0.0699500(4) | 0.108846(5) |
| π/4 | 0.0953305(5) | 0.0948778(4) | 0.125775(3) | 0.137177(5) |
| 3π/8 | 0.099404(4) | 0.0979349(5) | 0.129950(5) | 0.164949(5) |
| π/2 | 0.137070(3) | 0.122857(5) | 0.127777(5) | 0.175892(5) |
Таблица 4
| a = 1, e = 0.7; Al: $E = 0.7 \times {{10}^{6}}$ кгс/см2, ${{\rho }} = 2.7 \times {{10}^{3}}$кг/м3, $h = 0.002$ | ||||
|---|---|---|---|---|
| Θ | 1-я краевая задача | 2-я краевая задача | ||
| 9 × 15 | 15 × 31 | 9 × 15 | 15 × 31 | |
| 0 | 0.185628 | 0.185868 | 0.151815(2) | 0.152090(2) |
| π/8 | 0.194063 | 0.190921 | 0.163442 | 0.155237(2) |
| π/4 | 0.206059 | 0.203922 | 0.168332 | 0.163886(2) |
| 3π/8 | 0.215977 | 0.216651 | 0.175135(2) | 0.176313(2) |
| π/2 | 0.220158 | 0.220423 | 0.184554 | 0.185116 |
Таблица 5
| a = 1, e = 0.7; Al: $E = 0.7\,~ \times \,~{{10}^{6}}{\text{\;}}$ кгс/см2, ${{\rho }} = 2.7 \times {{10}^{3}}$ кг/м3, $h = 0.004$ | ||||
|---|---|---|---|---|
| θ | 1-я краевая задача | 2-я краевая задача | ||
| 9 × 15 | 15 × 31 | 9 × 15 | 15 × 31 | |
| 0 | 0.647881 | 0.647201 | 0.904399 | 0.902115 |
| π/8 | 0.673244 | 0.673408 | 1.24598 | 1.19275 |
| π/4 | 0.752941 | 0.754649 | 1.38964(2) | 1.55694(2) |
| 3π/8 | 0.881436 | 0.883365 | 1.62488(3) | 1.77013 |
| π/2 | 0.945176 | 0.945504 | 1.82248(3) | 1.75265(2) |
Таблица 6
| a = 1, $e = 0.7$; Al: $E = 0.7 \times {{10}^{6}}$ кгс/см2, ${{\rho }} = 2.7 \times {{10}^{3}}$ кг/м3, $h = 0.005$ | ||||
|---|---|---|---|---|
| θ | 1-я краевая задача | 2-я краевая задача | ||
| 9 × 15 | 15 × 31 | 9 × 15 | 15 × 31 | |
| 0 | 1.14191 | 1.14054 | 1.76638 | 1.76194 |
| π/8 | 1.18812 | 1.18791 | 2.09717(2) | 2.32947 |
| π/4 | 1.33485 | 1.33702 | 2.71417(2) | 3.04075(2) |
| 3π/8 | 1.58769 | 1.59103 | 3.01609(3) | 3.37000(3) |
| π/2 | 1.77902 | 1.78041 | 3.43821(3) | 3.41858(2) |
3. Выводы. I. Во всех проведенных расчетах подтвердилось, что зависимость критической скорости флаттера $z = {{{v}}_{{cr}}}$, от двух безразмерных параметров $x = {{с}_{2}}$ – безразмерная скорость звука в пластине (отношение скорости звука в пластине к скорости звука в воздухе), $y = h \times {{10}^{3}}$, где h – толщина пластины (безразмерная, a – характерный размер) есть $z = a + bx + c{{y}^{3}}$. Это утверждение не противоречит ранее полученному соотношению (2.1) $z = a + с{{y}^{3}}$ для алюминиевой пластины, т.е. когда варьировалась только толщина пластины, bx – поправка на материал.
Можно сказать, что решена задача табулирования: вместо того, чтобы хранить громоздкие таблицы со значениями критической скорости флаттера, зависящей от двух параметров, достаточно воспользоваться простой формулой (2.1).
II. Максимум критической скорости флаттера для алюминиевой пластины достигается при обтекании вдоль малой полуоси эллипса, а минимум при обтекании вдоль большой оси эллипса для обеих краевых задач: 1-я краевая задача – защемленная пластинка; 2-я краевая задача – свободно опертая пластинка. В первом случае критическая скорость флаттера монотонно возрастает от значения 0.3622 до значения 0.4505 (при $h = 0.003$). Во втором случае монотонного возрастания критической скорости флаттера для алюминия нет, а для титана есть. Видимо это связано с тем, что первый материал более мягкий.
Для алюминия зависимость критической скорости флаттера от двух параметров h – толщина пластины и θ – направление вектора скорости с осью абсцисс представляется рациональной функцией (для обеих краевых задач):
Первая краевая задача $z = \frac{{(a + bx + c{{x}^{2}} + dy)}}{{(1 + ex + fy + g{{y}^{2}} + h{{y}^{3}})}}$,
Вторая краевая задача
Эти формулы содержат 8 параметров, которые могут быть определены в методических расчетах (для других значений эксцентриситета).
Благодарность. Работа выполнена по теме государственного задания № АААА-А20-120011690132-4.
Список литературы
Ильюшин А.А., Кийко И.А. Новая постановка задачи о флаттере пологой оболочки // ПММ. 1994. Т. 58. Вып. 3. С. 167–171.
Алгазин С.Д., Кийко И.А. Численно-аналитическое исследование флаттера пластины произвольной формы в плане // ПММ. 1997. Т. 61. Вып. 1. С. 171–174.
Алгазин С.Д. Численные алгоритмы классической матфизики. II. Спектральные задачи для бигармонического уравнения // Препр. ИПМех. М.: 2001. № 678. 27 с.
Казанджан Э.П. Об одном численном методе конформного отображения односвязных областей // Препр. ИПМ. М., 1977. № 82. 59 с.
Алгазин С.Д., Бабенко К.И. Численное решение задачи об изгибе и свободных колебаниях пластинки // ПММ.1982. Т. 46. Вып. 6. С. 1011–1015.
Алгазин С.Д., Кийко И.А. Флаттер пластин и оболочек. Издание 2-е, переработанное и дополненное. М.: “URSS”, 2016, 278 с. ISBN 978-5-9710-4188-7.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела