Известия РАН. Механика твердого тела, 2021, № 3, стр. 26-35
ВИБРОАКУСТИЧЕСКИЙ ЭФФЕКТ ЗАПОЛНЕНИЯ ДЕФЕКТОВ В СТЕРЖНЯХ И ПЛАСТИНАХ
И. М. Лебедев a, М. Н. Перельмутер a, А. Л. Попов a, *, Д. А. Челюбеев a, Е. И. Шифрин a
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: popov@ipmnet.ru
Поступила в редакцию 25.04.2020
После доработки 25.07.2020
Принята к публикации 07.08.2020
Аннотация
Диагностика дефектов является первым шагом к их “залечиванию” – частичному или полному устранению влияния дефектов на напряженно-деформированное состояние конструкции. В работе рассмотрено “залечивание” полостных дефектов путем заполнения различными материалами. Оценка эффективности такого залечивания производится по виброакустическим критериям на примерах кольцевых дефектов в стержне и малого отверстия в пластине.
1. Введение. Актуальным для разных областей техники является не только диагностика дефектов в конструкциях, но и их “залечивание”, например, путем заполнения различными материалами. Очевидно, что полноценное заполнение полостных дефектов основным материалом не создает концентрации напряжений в месте залечивания, однако некоторые способы такого заполнения, такие как сварка или наплавка, повреждают окрестность исправляемого дефекта, создавая ослабленную зону и тем самым фактически расширяя дефект. Ликвидировать ослабленную зону можно только применив термическую обработку всей конструкции в целом. Более щадящие способы заполнения, такие как пайка и вклеивание, часто не позволяют использовать для заполнения основной материал конструкции. Подбор альтернативного материала должен осуществляться с учетом условия минимизации концентрации напряжений после залечивания. В статье рассматривается эффективность такого залечивания на примере кольцевых дефектов в стержне и малого отверстия в пластине по виброакустическим критериям на основе спектров частот продольных колебаний стержня и концентрации напряжений по контуру дефекта в пластине при прохождении по ней плоской изгибной волны.
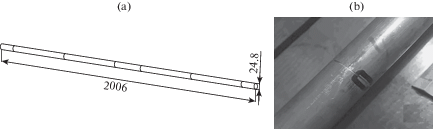
2. Дефекты в виде кольцевых проточек в стержне круглого поперечного сечения. В качестве первой модели для залечивания дефектов рассмотрим металлический стержень круглого поперечного сечения с искусственно созданными дефектами – кольцевыми проточками малой протяженности и глубины. На рис. 1,a приведен эскиз этого стержня с размерами в мм и обозначениями мест расположения проточек, а на рис. 1,b – фото одной из проточек протяженностью 0.6 мм и глубиной 1 мм.
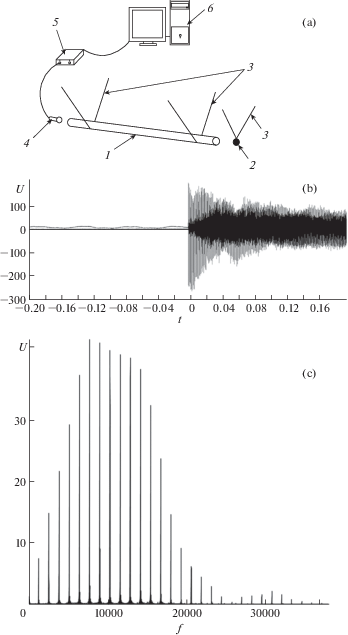
Возбуждение продольных колебаний стержня осуществлялось ударом шарика из закаленной стали по одному из торцов подвешенного на двух нитях стержня. Регистрация колебаний производилась бесконтактно микрофоном по звукоизлучению с другого торца стержня. Аналоговый сигнал с микрофона, пропорциональный среднему акустическому давлению на площади мембраны микрофона, подавался на спектроанализатор, а с него – в компьютер, где сохранялся в форме оцифрованных амплитудно-временной и амплитудно-частотной зависимостей (АЧЗ). На рис. 2,а показана схема экспериментальной установки (1 – стержень, 2 – шарик, 3 – нити подвесов, 4 – измерительный микрофон, 5 – спектроанализатор A19-U2, 6 – персональный компьютер), а на рис. 2,b,c – графические отображения характерных временной (b) и амплитудно-частотной (c) зависимостей колебаний стержня из алюминиевого сплава Д16, построенные программным обеспечением ZETLAB спектроанализатора. Значения t по оси абсцисс на рис. 2,b – секунды, значения f на рис. 2,c – в Гц; значения U по осям ординат отложены в мВ электрического сигнала, передаваемого с микрофона. На рис. 2,b виден момент начала регистрации сигнала после ударного воздействия и фрагмент его в записи на протяжении 0.2 с. Из рис. 2,c видно, что расстояния между пиками в спектре частот колебаний стержня практически одинаковы, что характерно для спектра свободных продольных колебаний стержня [1].
При наличии небольших дефектов измеренный спектр продольных колебаний стержня визуально повторяет картину, изображенную на рис. 2,c. Для оценки отличий частот колебаний стержня с дефектами от частот бездефектного стержня приведена табл. 1, в которой сопоставлены 14 первых, наиболее заметных, частот соответствующих спектров. В первой строке табл. 1 приведены номера частот n в порядке возрастания, во второй – значения частот бездефектного стержня, в третьей строке – значения частот стержня с тремя парами кольцевых проточек протяженностью 0.6 мм, расположенных симметрично середины оси стержня на расстояниях 100, 500 и 900 мм от торцов стержня. Проточки, находящиеся на расстояниях 100 и 900 мм от торцов стержня, были сделаны глубиной 1 мм, а проточки, находящиеся на расстояниях 500 мм от торцов стержня, – глубиной 1.5 мм. Такое расположение дефектов позволило из спектра собственных частот стержня со свободными концами выделить собственные частоты для свободного и жестко-свободного стержня половинной длины, используемые в примененном методе диагностики множественных дефектов по двум спектрам продольных колебаний стержня.
Таблица 1
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| f0n/Гц | 1297.8 | 2595.0 | 3893.2 | 5191.1 | 6488.5 | 7785.0 | 9080.9 |
| fdn/Гц | 1295.7 | 2591.8 | 3887.1 | 5188.6 | 6479.4 | 7765.9 | 9069.3 |
| n | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| f0n/Гц | 10377.1 | 11672.1 | 12965.3 | 14260.0 | 15551.0 | 16842.8 | 18133.0 |
| fdn/Гц | 10363.7 | 11658.8 | 12927.6 | 14242.5 | 15532.2 | 16821.3 | 18090.6 |
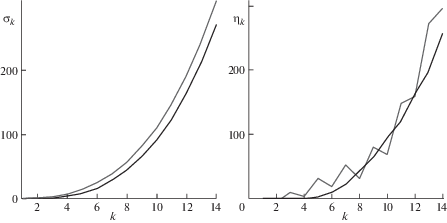
О наличии малых дефектов в стержне можно судить по присутствующим в табл. 1 небольшим отличиям в распределениях частот бездефектного стержня и стержня с дефектами. Так как эти отличия на фоне 10-килогерцовых частот малозаметны, то введены были их комбинации, показывающие, во-первых, отличие в распределении частот от равномерного с шагом, равным удвоенной первой частоте консольного стержня половинной длины, а, во-вторых, изменения в этих отличиях, вызванные наличием дефектов. Данные комбинации задавались формулами:
На рис. 3 показаны эти отличия (верхняя кривая на рис. 3 слева и пилообразная кривая на рис. 3 справа – для консольного стержня, нижние кривые слева и справа – для стержня со свободными краями): слева – для стержня без дефектов, справа – для стержня с тремя дефектами. Видно, что на частотах консольного стержня наличие дефектов почти не отразилось, в то время как распределение частот стержня со свободными краями превратилось из гладкой функции в пилообразную.
Отмеченный признак характеризует только факт наличия дефектов. Для нахождения их положения вдоль оси стержня используется алгоритм, разработанный в [2].
Основные идеи предложенного алгоритма состоят в следующем. Рассматривается конечно-элементная модель стержня. Предполагается, что дефект снижает жесткость содержащего ее элемента, но не влияет на плотность. Такое предположение является общепринятым в случае трещиноподобных и других локализованных дефектов [2]. Предполагается, что в результате эксперимента определены собственные значения ${{\lambda }}_{m}^{*}$ и ${{\mu }}_{m}^{*}$, $m = 1, \ldots ,M$, соответствующие свободным и жестко-свободным условиям на концах стержня. Собственные значения связаны с круговой частотой ${{\omega }}$ соотношением ${{\lambda }} = {{\rho }}{{{{\omega }}}^{2}}{\text{/}}E$, где ρ – плотность, $E$ – модуль Юнга материала стержня, ${{\lambda }}$ равно ${{\lambda }}_{m}^{*}$ или ${{\mu }}_{m}^{*}$ в зависимости от рассматриваемых условий на концах стержня. Стержень разбивается на N элементов. Эти элементы могут не совпадать с конечными элементами, а содержать несколько конечных элементов. Модуль Юнга k-го элемента обозначим ${{E}_{k}}$. Далее рассматривается последовательность минимизационных задач с целевыми функциями ${{F}_{N}}\left( {\mathbf{p}} \right)$, где $N \leqslant M$, ${\mathbf{p}} = \left( {{{p}_{1}},\; \ldots ,\;{{p}_{K}}} \right)$, ${{p}_{k}} = {{E}_{k}}{\text{/}}E$, $K \leqslant N$.
Здесь ${{{{\lambda }}}_{k}}\left( {\mathbf{p}} \right)$ и ${{{{\mu }}}_{k}}\left( {\mathbf{p}} \right)$ – собственные числа, получаемые в результате конечно-элементного расчета для стержня со свободными и жестко-свободными концами, соответственно.
Минимизация функции FN(p) осуществляется с помощью алгоритма Левенберга–Марквардта. В качестве начального приближения берется ${\mathbf{p}} = {{{\mathbf{p}}}^{0}} = \left( {1, \cdots ,1} \right)$, что соответствует неповрежденному стержню. Поврежденными считаются элементы, у которых полученные в результате минимизации значения pk оказываются меньше единицы. Для уточнения положения дефектов количество элементов удваивается, но переменными считаются только pk, относящиеся к новым элементам, находящимся внутри старых элементов, которые на предыдущем шаге были определены как поврежденные. Процедура продолжается до стабилизации результатов по определению положения дефектов. В большинстве случаев при начальном количество элементов равном N = 10, процедура продолжалась до использования 80 элементов.
Для расчета использовались спектры продольных колебаний стержня длиной 1003 мм со свободно-свободными и свободно-закрепленными концами (табл. 1). Эти спектры были извлечены из спектра колебаний стержня длиной 2006 мм со свободно-свободными концами. Как и ожидалось, численный расчет по алгоритму поиска дефектов не выявил дефектов. По первой собственной частоте было определено отношение модуля Юнга к плотности, которое использовалось в дальнейшем.
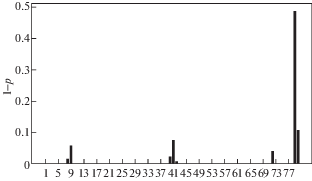
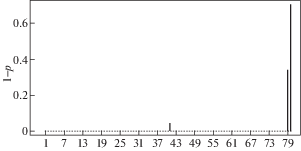
На рис. 4 представлены результаты идентификации описанных выше дефектов на стержне половинной длины. По оси абсцисс отложены номера элементов, а по оси ординат – величины $1 - {{p}_{k}}$, соответствующие податливостям элементов. Эти величины в местах обнаружения дефектов изображены черными столбиками. Помимо мест нахождения дефектов, виден большой всплеск у правого (свободного) конца стержня связанный со скачком жесткости на этом конце.
“Залечивание” дефектов состояло в закладке в проточки стального, алюминиевого и медного колец, полученных расплющиванием проволок из этих материалов до толщины 0.55 мм, затягиванием их в проточках и фиксацией эпоксидной смолой. На рис. 5 приведены фотографии “залеченных” дефектов.
По спектрам частот продольных колебаний стержня с “залеченными” дефектами была проведена их идентификация на основе описанного выше алгоритма. Результаты идентификации представлены на рис. 6. Видно, что крайние дефекты перестали опознаваться.
Единственный всплеск на диаграмме рис. 6 сохранился у среднего, наиболее глубокого дефекта, “залеченного” материалом с иными свойствами (медью), чем алюминиевый сплав Д16.
Таким образом, заполнение дефектов металлическими вставками оказалось достаточно эффективным средством “залечивания” дефектов с точки зрения акустической регистрации изменений в спектре продольных колебаний стержня, вызванных дефектами, и диагностики на их основе мест расположения дефектов.
2. Дефект в виде отверстия в пластине. Второй моделью дефекта и его залечивания может служить задача о дефекте в виде отверстия в плоской пластине, заполняемого упругим материалом с теми же, или отличными от пластины механическими характеристиками. В статической постановке эта задача была рассмотрена в [3]. Задача о дифракции изгибной волны на круговом препятствии в пластине рассмотрена в [4]. Звуковое поле в акустической среде, контактирующей с пластиной, восстановленное по полю изгибных волн в пластине с включением, без учета обратной реакции среды на колебания пластины, рассмотрена в [5].
Установившиеся изгибные колебания основной пластины и включения толщины h описываются уравнениями
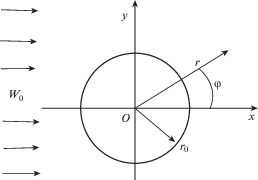
Пусть по основной пластине распространяется изгибная волна (рис. 7):
где r, φ – полярные координаты, A – заданная амплитуда.Рассеянное поле ищется в виде суммы расходящихся и быстрозатухающих волн:
Поле в упругом заполнителе представляется в виде
Постоянные ${{\alpha }_{n}}$, ${{\beta }_{n}}$, ${{\gamma }_{n}}$, ${{\eta }_{n}}$ определяются решением системы из четырех уравнений, полученных из граничных условий при r = r0:
Эти условия означают непрерывность функции прогиба, угла поворота, радиальной компоненты изгибающего момента и приведенной перерезывающей силы на окружности контакта основной пластины и заполнения.
В качестве условия залечивания примем снижение концентрации напряжений вокруг отверстия при его заполнении материалами с разными свойствами. Об этом можно судить по величине коэффициента концентрации напряжений, равного отношению окружного момента
Расчеты проводились для случая пластины толщиной h = 1 мм с круглым отверстием радиуса r0 = 10 мм при падающей волне с частотой 1000 Гц. Длина изгибной волны в пластине при этих параметрах составляет около 100 мм.
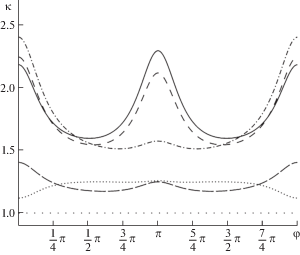
На рис. 8 представлены кривые распределения по контуру отверстия коэффициента концентрации напряжений K при заполнении отверстия различными материалами: для стальной пластины и пустого отверстия (сплошная линия), при заполнении сталью (редкий пунктир), алюминием (частый пунктир), висмутом (штрих-пунктир), пластиком (короткие штрихи) и медью (длинные штрихи).
Как видно из рис. 8, максимальные коэффициенты концентрации имеют место в точках входа (φ = 0) и выхода падающей волны (φ = π). Численные значения приведены в табл. 2.
Таблица 2
| Материал заполнения | φ | |
|---|---|---|
| 0 | π | |
| Незаполненное отверстие | 2.19 | 2.30 |
| Сталь | 1.00 | 1.00 |
| Алюминий | 1.12 | 1.26 |
| Висмут | 2.41 | 1.58 |
| Пластик | 2.25 | 2.12 |
| Медь | 1.40 | 1.25 |
Как следует из табл. 2, при свободном отверстии максимум K = 2.3. Наименьшее значение коэффициента концентрации напряжений (исключая заполнение сталью) получается при заполнении отверстия в стали алюминием (K = 1.26) и медью (K = 1.4). При заполнении висмутом концентрация напряжений даже усиливается (K = 2.5). Заполнение легким материалом (пластик) влияет на концентрацию напряжений незначительно.
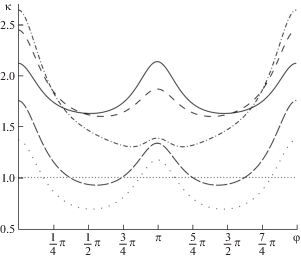
На рис. 9 показано распределение коэффициента концентрации напряжений K для аналогичной пластины из алюминия для тех же условий, что и на рис. 8. Обозначения те же, что на рис. 8.
Численные значения максимальных коэффициентов концентрации напряжений приведены в табл. 3.
Таблица 3
| Материал заполнения | φ | |
|---|---|---|
| 0 | π | |
| Незаполненное отверстие | 2.12 | 2.14 |
| Сталь | 1.37 | 1.17 |
| Алюминий | 1.00 | 1.00 |
| Висмут | 2.64 | 1.39 |
| Пластик | 2.45 | 1.87 |
| Медь | 1.75 | 1.34 |
Видно, что в случае алюминиевой пластины при свободном отверстии K = 2.2. Наименьшее значение коэффициента концентрации напряжений (не считая заполнения алюминием) получается при заполнении отверстия сталью (K = 1.37) и медью (K = 1.75). При заполнении висмутом и пластиком концентрация напряжений усиливается (K = 2.64 для висмута и K = 2.45 для пластика).
Таким образом, подбирая физические и механические характеристики материала заполнения – плотность, модуль Юнга и коэффициент Пуассона, можно значительно снизить концентрацию напряжений в окрестности дефекта. При этом остается некоторая свобода в выборе типа материала, которую можно использовать для улучшения технологической и эксплуатационной совместимости материалов основы и заполнителя.
Исследование И.М. Лебедевa, М.Н. Перельмутерa, А.Л. Поповa и Д.А. Челюбеева выполнено за счет гранта Российского научного фонда (проект № 19-19-00616).
Список литературы
Тимошенко С.П. Колебания в инженерном деле. М.: Наука, 1967. 444 с.
Лебедев И.М., Шифрин Е.И. Решение обратной спектральной задачи для стержня, ослабленного поперечными трещинами, с помощью оптимизационного алгоритма Левенберга-Марквардта // Изв. РАН. МТТ. 2019. № 4. С. 8–26.
Перельмутер М.Н., Попов А.Л., Челюбеев Д.А., Бухалов В.И. Анализ эффективности залечивания дефектов при их заполнении различными материалами // Актуальн. пробл. прикл. матем., информат. и механ.: Сб. тр. Междунар. научн. конф., Воронеж, 11–13 ноября 2019 г. Воронеж: Научно-исслед. публ., 2020. С. 1488–1492.
Коненков Ю.К. Дифракция изгибной волны на круговом препятствии в пластине // Акустический журнал. 1964. Т. 10. С. 186–190.
Боровиков В.А., Попов А.Л., Челюбеев Д.А. Звуковое поле, возбужденное изгибными колебаниями упругой пластины с круглым включением // Акустический журнал. 2007. Т. 53. № 6. С. 749–759.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела