1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 3, 2021

Известия РАН. Механика твердого тела, 2021, № 3, стр. 13-25

ПРИМЕНЕНИЕ ПОДХОДА МЕХАНИКИ КОНЕЧНЫХ ТРЕЩИН ДЛЯ ОЦЕНКИ РАЗРУШЕНИЯ КВАЗИХРУПКОГО МАТЕРИАЛА С КРУГОВЫМ ОТВЕРСТИЕМ

С. В. Сукнев *

Институт горного дела Севера им. Н.В. Черского СО РАН
Якутск, Россия

* E-mail: suknyov@igds.ysn.ru

Поступила в редакцию 17.02.2020
После доработки 20.02.2020
Принята к публикации 25.02.2020

Полный текст (PDF)

Аннотация

Масштабный эффект прочности структурно-неоднородных материалов проявляется, в частности, в зависимости разрушающей нагрузки от размера зоны концентрации напряжений, возникающей вблизи материальных или геометрических неоднородностей (включений, пор, вырезов, галтелей). Хотя размер зоны концентрации напряжений определяется, в первую очередь, размерами и формой неоднородности, определенное влияние оказывают также условия нагружения. Кроме этого, прогностическая ценность теории разрушения определяется не только способностью учета масштабного эффекта, но и возможностью распространения теории на возможно более широкий круг краевых условий. Теоретически и экспериментально исследовано влияние краевых условий и диаметра отверстия на возникновение трещин отрыва у кругового отверстия в квазихрупком геоматериале при неравномерно распределенном сжатии с учетом масштабного фактора. На основе подхода механики конечных трещин предложен критерий квазихрупкого разрушения. Проведено сопоставление результатов расчета критического напряжения с полученными экспериментальными данными.

Ключевые слова: квазихрупкое разрушение, геоматериал, масштабный эффект, отверстие, механика конечных трещин

1. Введение. Для геоматериалов и горных пород характерно влияние масштабного фактора на параметры прочности [1]. Наиболее сильно масштабный эффект проявляется в условиях концентрации напряжений у отверстий, полостей, выработок, когда характерный размер неоднородности напряжений сопоставим с размерами структурных составляющих материала. Для оценки прочности и прогнозирования разрушения структурно-неоднородных материалов используют различные нелокальные и градиентные модели со структурным параметром [2–9]. В последнее время получили распространение нелокальные критерии разрушения, реализующие подходы и методы теории критических расстояний и механики трещин [10–15].

Общим свойством нелокальных критериев является введение внутреннего размера (константы) материала d0, характеризующего его структуру, что позволяет описать масштабный эффект, свойственный структурно-неоднородным материалам. На практике это дает возможность прогнозировать наступление разрушения при варьировании размера зоны концентрации напряжений ${{L}_{e}}$. При этом полагают, что за пределами малой области (зоны предразрушения) возле наиболее напряженной точки материал деформируется упруго. Размер этой области d0 определяется микроструктурой материала и является малым по отношению к размерам деформируемого тела. Появление трещины в наиболее напряженной области и ее рост не сопровождаются сколько-нибудь заметными неупругими деформациями, поэтому говорят, что имеет место хрупкое разрушение.

Применение подхода механики трещин (fracture mechanics) состоит в том, что зона предразрушения моделируется трещиной длиной d0, которая предполагается изначально существующей в теле. Такую трещину называют фиктивной или воображаемой. Для трещины, находящейся в неоднородном поле напряжений, рассчитывается коэффициент интенсивности напряжений K, при достижении которым критического значения ${{K}_{c}}$ происходит страгивание трещины (разрушение).

На первый взгляд, модель твердого тела с распределенными в нем микротрещинами (preexisting microcracks) выглядит вполне реалистичной и согласующейся с общепринятыми представлениями о реальном твердом теле, обладающем изначальной, присущей ему дефектностью (эти микротрещины часто называют трещинами Гриффитса). Но в действительности такая модель может быть использована только для оценки прочности твердого тела, содержащего большой ансамбль гладких дефектов, например, пор. Чтобы применить модель для оценки прочности однородного тела, содержащего одиночный дефект произвольного размера, трещины Гриффитса должны заполнять объем всего тела, что физически абсурдно. Поэтому в рамках модели твердого тела с распределенными микротрещинами могут рассматриваться только достаточно большие отверстия, вырезы или полости, размер которых намного превышает размер микротрещин, а также расстояние между ними.

Проблема существования в твердом теле воображаемых микротрещин снимается в механике конечных трещин (finite fracture mechanics) [16–18], получившей в последнее время широкое распространение [19–24]. В настоящей работе подход механики конечных трещин применяется для решения задачи о разрушении хрупкого или квазихрупкого материала с круговым отверстием под действием двухосного нагружения сжимающими и растягивающими усилиями.

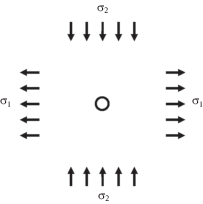
2. Постановка задачи. Рассматривается пропорциональное нагружение изотропной однородной линейно-упругой пластины из хрупкого или квазихрупкого материала равномерно распределенными на бесконечности растягивающими ${{\sigma }_{1}} \equiv {{k}_{1}}p$ и сжимающими ${{\sigma }_{2}} \equiv {{k}_{2}}p$ напряжениями. В центре пластины находится малое круговое отверстие радиуса a (рис. 1). Требуется определить критическую нагрузку ${{p}_{c}}$, при которой в пластине будет достигнуто предельное состояние (образование трещин отрыва, исходящих от отверстия) в зависимости от диаметра отверстия.

Рис. 1

Материал пластины характеризуется масштабным эффектом прочностных свойств. В присутствии концентратора напряжений (отверстия) эффективный нагруженный объем определяется размером зоны концентрации напряжений ${{L}_{e}}$. Стандартные механические свойства материала пластины характеризуются предельным напряжением ${{\sigma }_{0}}$, которое определяется при одноосном растяжении пластины без отверстия.

3. Критерий разрушения. В механике конечных трещин постулируется, что рост трещины, включая момент ее возникновения у выреза, происходит скачкообразно. Разрушение происходит, если энергия, высвобождаемая при скачкообразном изменении длины трещины, достигнет критического значения. Для хрупких материалов конечный размер приращения длины трещины, характеризующий зону предразрушения, рассматривается в качестве константы материала: $\delta l = d = {\text{const}}$. Условие разрушения имеет вид [10]:

(3.1)
$\int\limits_l^{l + d} {{{K}^{2}}dl} = K_{c}^{2}d$

Важным преимуществом инкрементального условия разрушения (3.1) перед обычным дифференциальным условием $K = {{K}_{c}}$ является то, что оно может быть применено не только в качестве условия роста уже существующей в теле трещины, но и для предсказания появления трещины у гладкого выреза в теле, не содержащем начальных трещин. Для этого в уравнении (3.1) достаточно принять l = 0. При этом не требуется делать никаких дополнительных допущений о существовании в теле фиктивных или воображаемых трещин, которые, как было показано выше, приводят к определенным физическим противоречиям.

Чтобы применить критерий разрушения (3.1) необходимо сначала найти зависимость коэффициента интенсивности напряжений от длины трещины, исходящей от выреза. Для рассматриваемой задачи можно воспользоваться решением Бови [25], но оно не обеспечивает сшивку с классической механикой сплошной среды при больших диаметрах отверстия. Покажем это на примере одноосного растяжения пластины с отверстием усилиями ${{\sigma }_{1}}$. Представим коэффициент интенсивности напряжений в виде

$K = {{\sigma }_{1}}\sqrt {\pi l} f(l{\text{/}}a)$

Критическое напряжение

(3.2)
${{\sigma }_{c}} = \frac{{{{K}_{c}}}}{{\sqrt {\pi l} f(l{\text{/}}a)}}$

В отсутствии отверстия (a = 0) функция $f(l{\text{/}}a)$ принимает значение 1. Поскольку при этом критическое напряжение характеризует не что иное, как прочность гладкого (без отверстия) образца ${{\sigma }_{0}}$, то можно записать:

(3.3)
${{\sigma }_{0}} = \frac{{{{K}_{c}}}}{{\sqrt {\pi l} }}$

С учетом формулы (3.3) запишем выражение (3.2) в виде

(3.4)
${{\sigma }_{c}} = \frac{{{{\sigma }_{0}}}}{{f(l{\text{/}}a)}}$

Функцию $f(l{\text{/}}a)$ можно интерпретировать как эффективный коэффициент концентрации напряжений, зависящий от радиуса отверстия и некоторого структурного параметра. Было бы справедливо ожидать, что для очень больших отверстий эффективный коэффициент концентрации напряжений совпадет с теоретическим коэффициентом Kt, рассчитанным по теории упругости. Однако в пределе $l{\text{/}}a \to 0$ функция $f(l{\text{/}}a)$ принимает значение 3.36, в то время как решение задачи Кирша о растяжении бесконечной плоскости с круговым отверстием дает ${{K}_{t}} = 3$.

Следует подчеркнуть, что эта ситуация характерна для любых вырезов, а не только для круговых отверстий. Действительно, в классическом пределе, когда размеры выреза намного больше l, мы приходим к задаче о краевой трещине длиной l в однородном поле растягивающих напряжений ${{\sigma }_{1}} \cdot {{K}_{t}}$. Коэффициент интенсивности напряжений для такой трещины [26]

$K = 1.12{{\sigma }_{1}}{{K}_{t}}\sqrt {\pi l} $

Отсюда, с учетом формулы (3.3), для критического напряжения получим выражение ${{\sigma }_{c}} = {{\sigma }_{0}}{\text{/}}\left( {1.12{{K}_{t}}} \right)$ вместо ожидаемого по классической теории упругости ${{\sigma }_{c}}$ = = σ0/Kt.

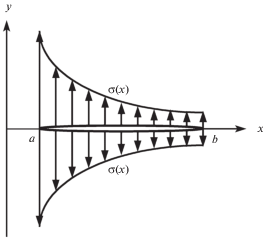
Чтобы обеспечить сшивку с классической механикой сплошной среды, воспользуемся приближенным способом вычисления коэффициента интенсивности напряжений, предложенным Тирошем [27]. Он рассмотрел круговое отверстие с одной трещиной, исходящей от контура, а для приближенного определения коэффициента интенсивности напряжений использовал известный прием [26], в соответствии с которым исходная задача заменяется задачей о трещине, к берегам которой приложено распределенное давление ${{\sigma }_{y}}(x)$ (рис. 2). Общее выражение для коэффициента интенсивности напряжений в этой задаче (K вычисляется в точке x = b) имеет вид [28]:

(3.5)
$K = \sqrt {\frac{2}{{\pi (b - a)}}} \int\limits_a^b {{{\sigma }_{y}}(x)\sqrt {\frac{{x - a}}{{b - x}}} dx} $
Рис. 2

Напряжение ${{\sigma }_{y}}(x)$ определяется из решения исходной задачи при отсутствии трещины, т.е. в данном примере – из решения задачи Кирша, которое имеет вид [29]:

(3.6)
${{\sigma }_{y}} = \frac{{{{\sigma }_{1}}}}{2}\left( {2 + \frac{{{{a}^{2}}}}{{{{x}^{2}}}} + 3\frac{{{{a}^{4}}}}{{{{x}^{4}}}}} \right)$

Подставив выражение (3.6) в формулу (3.5) и выполнив интегрирование, приняв $b = a + l$, получим:

(3.7)
${{K}_{1}} = {{\sigma }_{1}}\sqrt {\frac{{\pi l}}{2}} \left( {1 + \frac{1}{2}{{{\left( {1 + \frac{l}{a}} \right)}}^{{ - 3/2}}} + \frac{3}{2}{{{\left( {1 + \frac{l}{a}} \right)}}^{{ - 7/2}}}\left( {1 + \frac{l}{{2a}} + \frac{{{{l}^{2}}}}{{8{{a}^{2}}}}} \right)} \right)$

Теперь подставим выражение (3.7) в левую часть уравнения (3.1) и выполним интегрирование в пределах $[0,d]$:

(3.8)
$\int\limits_0^d {K_{1}^{2}dl} = \pi {{J}_{1}}{{\left( {\frac{{a{{\sigma }_{1}}}}{{32}}} \right)}^{2}}$
где

${{J}_{1}} = - 1533 - 512\gamma + 256{{\gamma }^{2}} + 1408{{\gamma }^{{0,5}}} + 640{{\gamma }^{{ - 0,5}}} - 384{{\gamma }^{{ - 1,5}}} + 384{{\gamma }^{{ - 2,5}}} - $
$ - \;242{{\gamma }^{{ - 1}}} - 11{{\gamma }^{{ - 2}}} - 156{{\gamma }^{{ - 3}}} + 93{{\gamma }^{{ - 4}}} - 18{{\gamma }^{{ - 5}}} + 75{{\gamma }^{{ - 6}}},\quad \gamma = 1 + d{\text{/}}a$

В отсутствие отверстия выражение (3.1) определяет условие разрушение гладкого образца. Отсюда, с учетом формулы (3.7), найдем связь между прочностными свойствами материала в механике конечных трещин:

(3.9)
${{K}_{c}} = {{\sigma }_{0}}\sqrt {\pi d{\text{/}}4} $

В классическом пределе $d{\text{/}}a \to 0$ интегрирование дает следующий результат:

(3.10)
$\int\limits_0^d {K_{1}^{2}dl} = \pi {{\left( {\frac{{3{{\sigma }_{1}}d}}{2}} \right)}^{2}}\quad {\text{при}}\quad d{\text{/}}a \to 0$

Подставив результат интегрирования (3.10) в условие разрушения (3.1), получим выражение для критического напряжения:

(3.11)
${{\sigma }_{c}} = \frac{{2{{K}_{c}}}}{{3\sqrt {\pi d} }}\quad {\text{при}}\quad d{\text{/}}a \to 0$

Теперь подставим соотношение (3.9) в формулу (3.11) и убедимся в том, что σc = ${{\sigma }_{0}}{\text{/}}{{K}_{t}}$, где Kt = 3 в соответствии с решением задачи Кирша. Таким образом, сшивка с классической механикой сплошной среды обеспечивается.

С учетом (3.8) и (3.9) из уравнения (3.1) получим формулу для расчета критического напряжения при произвольных значениях радиуса отверстия:

(3.12)
${{\sigma }_{c}} = {{\sigma }_{0}}\frac{{16\left( {\gamma - 1} \right)}}{{\sqrt {{{J}_{1}}} }}$

В отсутствие отверстия (a = 0) критическое напряжение ожидаемо равно пределу прочности гладкого образца.

При одноосном сжатии пластины по оси x распределение напряжения ${{\sigma }_{y}}$ вдоль линии y = 0 имеет вид [29]:

(3.13)
${{\sigma }_{y}} = \frac{{{{\sigma }_{2}}}}{2}\left( {3\frac{{{{a}^{4}}}}{{{{x}^{4}}}} - \frac{{{{a}^{2}}}}{{{{x}^{2}}}}} \right)$

Здесь ${{\sigma }_{2}}$ – приложенное сжимающее напряжение, которое принято положительным. Подставив выражение (3.13) в формулу (3.5), получим:

(3.14)
${{K}_{2}} = {{\sigma }_{2}}\sqrt {\frac{{\pi l}}{2}} \left( { - \frac{1}{2}{{{\left( {1 + \frac{l}{a}} \right)}}^{{ - 3/2}}} + \frac{3}{2}{{{\left( {1 + \frac{l}{a}} \right)}}^{{ - 7/2}}}\left( {1 + \frac{l}{{2a}} + \frac{{{{l}^{2}}}}{{8{{a}^{2}}}}} \right)} \right)$

Теперь подставим выражение (3.14) в левую часть уравнения (3.1) и выполним интегрирование в пределах [0, d]:

(3.15)
$\int\limits_0^d {K_{2}^{2}dl} = \pi {{J}_{2}}{{\left( {\frac{{a{{\sigma }_{2}}}}{{32}}} \right)}^{2}}$
где

${{J}_{2}} = 19 - 50{{\gamma }^{{ - 1}}} + 85{{\gamma }^{{ - 2}}} + 36{{\gamma }^{{ - 3}}} - 147{{\gamma }^{{ - 4}}} - 18{{\gamma }^{{ - 5}}} + 75{{\gamma }^{{ - 6}}},\quad \gamma = 1 + d{\text{/}}a$

С учетом выражений (3.9) и (3.15) из уравнения (3.1) получим формулу для расчета критического напряжения:

(3.16)
${{\sigma }_{c}} = {{\sigma }_{0}}\frac{{16\left( {\gamma - 1} \right)}}{{\sqrt {{{J}_{2}}} }}$

При $d{\text{/}}a \to 0$ из формулы (3.16) следует ${{\sigma }_{c}} = {{\sigma }_{0}}$, т.е. обеспечивается сшивка с классической механикой сплошной среды. При уменьшении радиуса отверстия критическая величина приложенного давления, при котором на контуре отверстия образуются трещины отрыва, стремится к неограниченному значению. В действительности, это значение, очевидно, ограничено пределом прочности материала на сжатие, откуда следует, что существует критическое значение размера отверстия, ниже которого трещины отрыва на контуре отверстия не образуются.

При совместном действии растягивающей нагрузки ${{\sigma }_{1}} \equiv {{k}_{1}}p$ и сжимающей нагрузки ${{\sigma }_{2}} \equiv {{k}_{2}}p$ коэффициент интенсивности напряжений

(3.17)
$K = {{K}_{1}} + {{K}_{2}},$
где K1 и K2 определяются по формулам (3.7) и (3.14), соответственно. Подставив формулу (3.17) в левую часть уравнения (3.1) и выполнив интегрирование в пределах [0, d], получим:
(3.18)
$\int\limits_0^d {{{{\left( {{{K}_{1}} + {{K}_{2}}} \right)}}^{2}}dl} = \pi k_{1}^{2}{{J}_{1}}{{\left( {\frac{{ap}}{{32}}} \right)}^{2}} + 2\pi {{k}_{1}}{{k}_{2}}{{J}_{{12}}}{{\left( {\frac{{ap}}{{32}}} \right)}^{2}} + \pi k_{2}^{2}{{J}_{2}}{{\left( {\frac{{ap}}{{32}}} \right)}^{2}}$
где

${{J}_{{12}}} = 1035 - 320{{\gamma }^{{0.5}}} - 704{{\gamma }^{{ - 0.5}}} - 192{{\gamma }^{{ - 1.5}}} + 192{{\gamma }^{{ - 2.5}}} + $
$ + \;110{{\gamma }^{{ - 1}}} - 91{{\gamma }^{{ - 2}}} - 60{{\gamma }^{{ - 3}}} - 27{{\gamma }^{{ - 4}}} - 18{{\gamma }^{{ - 5}}} + 75{{\gamma }^{{ - 6}}},\quad \gamma = 1 + d{\text{/}}a$

С учетом (3.9) и (3.18) из уравнения (3.1) получим формулу для расчета критической нагрузки ${{p}_{c}}$:

(3.19)
${{p}_{c}} = \chi {{C}_{0}}\frac{{16\left( {\gamma - 1} \right)}}{{\sqrt {k_{1}^{2}{{J}_{1}} + 2{{k}_{1}}{{k}_{2}}{{J}_{{12}}} + k_{2}^{2}{{J}_{2}}} }}$
где $\chi = {{\sigma }_{0}}{\text{/}}{{C}_{0}}$.

4. Размер зоны предразрушения. Как уже было сказано, для хрупких материалов конечный размер приращения длины трещины, характеризующий размер зоны предразрушения, рассматривается в качестве константы материала, определяемой его структурой: $d = {{d}_{0}} = const$. Для квазихрупких материалов в работе [30] предложено следующее выражение для размера зоны предразрушения:

(4.1)
$d = {{d}_{0}} + \beta {{L}_{e}}$

Здесь $\beta $ – безразмерный параметр, характеризующий пластичность материала. Для хрупких материалов β = 0, для пластичных материалов $\beta \gg 1$. При $\beta $ ∼ 1 материал характеризуется умеренными пластическими свойствами. Первое слагаемое в выражении (4.1) характеризует собственно структуру материала, а второе отражает вклад неупругих деформаций. Таким образом, пластические свойства материала начинают проявляться при $d > {{d}_{0}}$ и проявляются тем сильнее, чем больше d по отношению к d0. Если $d = {{d}_{0}}$ будем говорить о хрупком разрушении, если $d > {{d}_{0}}$ – о квазихрупком разрушении, которое в пределе $d \gg {{d}_{0}}$ переходит в вязкое разрушение. При вязком разрушении критическое напряжение не зависит от размера выреза, поэтому размер зоны предразрушения пропорционален размеру выреза и, соответственно, размеру Le (при неизменных граничных условиях). При хрупком разрушении, напротив, размер зоны предразрушения не зависит от выреза и определяется структурой материала.

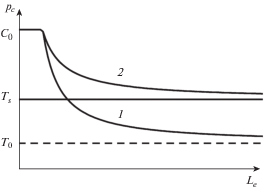
При одноосном сжатии поведение разрушающего напряжения, характеризующего образование трещин отрыва у выреза, имеет вид, изображенный на рис. 3. В соответствии с современными представлениями о реальном твердом теле, обладающем изначальной, присущей ему дефектностью малые искусственные дефекты, размеры которых сопоставимы с размерами структурных составляющих материала, не оказывают влияния на его прочность до тех пор, пока их размеры не достигнут определенного (критического) значения. Поэтому при малых значениях ${{L}_{e}}$ материал не чувствует присутствия концентратора напряжений и разрушается как гладкий образец при достижении критическим давлением предела прочности при сжатии ${{C}_{0}}$. После достижения критического размера концентратора разрушающее давление ${{p}_{c}}$ уменьшается, асимптотически приближаясь к напряжению ${{T}_{0}}$, равному пределу прочности материала при растяжении в случае хрупкого разрушения (кривая 1), и к напряжению ${{T}_{s}}$ (${{C}_{0}} > {{T}_{s}} > {{T}_{0}}$) в случае вязкого разрушения (кривая 2). Напряжение ${{T}_{s}}$ связано с величиной параметра пластичности $\beta $ в выражении (4.1).

Рис. 3

Для описания квазихрупкого разрушения размер d будем определять по формуле (4.1), в которой размер зоны концентрации напряжений рассчитывается в точке максимума эквивалентного напряжения ${{\sigma }_{e}}$ по формуле ${{L}_{e}} = {{\sigma }_{e}}{\text{/}}\left| {grad{{\sigma }_{e}}} \right|$. В рассматриваемой задаче ${{\sigma }_{e}} = {{\sigma }_{y}}$ и ${{L}_{e}} = a\frac{{3{{k}_{1}} + {{k}_{2}}}}{{7{{k}_{1}} + 5{{k}_{2}}}}$. Соответственно выражение для параметра γ в формуле (3.19) принимает вид:

(4.2)
$\gamma = 1 + \frac{{{{d}_{0}}}}{a} + \beta \frac{{3{{k}_{1}} + {{k}_{2}}}}{{7{{k}_{1}} + 5{{k}_{2}}}}$

При значении параметра $\gamma = 1$ формула (3.19) дает расчет критического напряжения согласно традиционному критерию разрушения.

Асимптотическое (при $a \to \infty $) значение критического напряжения:

(4.3)
${{T}_{s}} = {{T}_{0}}\frac{{16\left( {{{\gamma }_{s}} - 1} \right)(3{{k}_{1}} + {{k}_{2}})}}{{\sqrt {k_{1}^{2}{{J}_{1}}\left( {{{\gamma }_{s}}} \right) + 2{{k}_{1}}{{k}_{2}}{{J}_{{12}}}\left( {{{\gamma }_{s}}} \right) + k_{2}^{2}{{J}_{2}}\left( {{{\gamma }_{s}}} \right)} }}$
где ${{\gamma }_{s}} = 1 + \beta \frac{{3{{k}_{1}} + {{k}_{2}}}}{{7{{k}_{1}} + 5{{k}_{2}}}}$, ${{T}_{0}} = \frac{{\chi {{C}_{0}}}}{{3{{k}_{1}} + {{k}_{2}}}}$ – асимптотическое значение критического напряжения для хрупкого материала. Для квазихрупких материалов, характеризующихся умеренными пластическими свойствами, ${{T}_{s}} \approx {{T}_{0}}\left( {1 + \beta {\text{/}}2} \right)$.

Проверку применимости критерия квазихрупкого разрушения проведем на экспериментальных данных о разрушении плоских образцов с отверстием, подверженных неравномерно распределенному сжатию.

5. Испытания образцов с круговым отверстием. Программа экспериментальных исследований включала проведение двух серий испытаний образцов под действием сжимающей нагрузки, которая распределялась неравномерно (ступенчато) по верхней и нижней граням образца. Методика эксперимента описана в работе [31]. В качестве модельного материала использовали дигидрат сульфата кальция (двухводный гипс), приготовленный из водного раствора высокопрочного гипса марки ГВВС-16 (гипс 1) и из водного раствора строительного гипса марки Г-5 (гипс 2). Образцы представляли собой квадратные плиты размером 200 × 200 мм или 100 × 100 мм и толщиной 40 мм (гипс 1) и 36 мм (гипс 2). Перед испытанием в центре образцов высверливали круговые отверстия различного диаметра.

Для первой серии экспериментов было изготовлено по 5 образцов размером 200 × 200 мм с отверстиями каждого диаметра: 1, 2, 5, 10, 15 и 20 мм. Нагрузка p прикладывалась к образцу через жесткие вставки размером 120 мм, помещенные между образцом и нагружающими плитами. При этом в центральной части образца (вне зоны влияния отверстия) реализовывалось достаточно однородное двухосное напряженное состояние: растяжение по горизонтальной оси и сжатие по вертикальной оси образца (рис. 1). В процессе испытания образцов в зонах концентрации растягивающих напряжений на контуре отверстия наблюдали внезапное образование трещин отрыва, которое сопровождалось локальной разгрузкой образца, что отражалось на диаграмме деформирования в виде появления зубца. Критическую нагрузку в момент образования трещин определяли по вершине зубца на диаграмме.

Для определения прочности материала при одноосном сжатии использовали такие же квадратные образцы размером 200 × 200 мм без отверстия, нагружение производили через вставки размером 200 мм. По результатам испытания 4 образцов из гипса 1 определено среднее значение предела прочности 34.11 МПа; по результатам испытания 7 образцов из гипса 2 определено среднее значение предела прочности 11.53 МПа. Предел прочности материала при одноосном растяжении определяли прямым методом на образцах типа “dog-bone” (dog-bone shaped specimens). Было испытано по 10 образцов, изготовленных из гипса 1 и гипса 2. По результатам испытания образцов из гипса 1 определено среднее значение предела прочности 5.38 МПа; для гипса 2 среднее значение предела прочности составило 2.61 МПа.

Значения ${{k}_{1}}$ и ${{k}_{2}}$ рассчитывали методом конечных элементов в центре образцов, нагруженных через вставки заданного размера и не содержащих отверстия. Для использованных в первой серии экспериментов вставок ${{k}_{1}} = 0.143$, ${{k}_{2}} = 0.764$.

Во второй серии экспериментов испытывали образцы размером 100 × 100 мм с отверстиями диаметром 2 мм. Нагружение образцов производили через вставки размером 20, 40, 60 и 80 мм. Было испытано от 5 до 7 образцов со вставками каждого размера. Также как в первой серии испытаний, в зонах концентрации растягивающих напряжений на контуре отверстия наблюдали образование трещин отрыва, которое носило внезапный характер и сопровождалось локальной разгрузкой образца. Рассчитанные для испытанных образцов значения ${{k}_{1}}$, ${{k}_{2}}$ и $\alpha = {{k}_{1}}{\text{/}}{{k}_{2}}$ приведены в таблице.

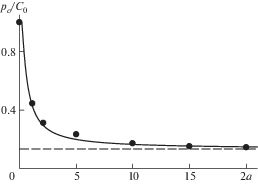
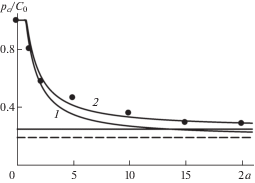
6. Результаты и обсуждение. На рис. 4 представлены экспериментальные данные (точки) о величине нагрузки в момент образования трещин отрыва на контуре отверстия в зависимости от его диаметра 2a [мм], полученные на образцах из гипса 1, и результаты расчета критического давления (кривая) по формуле (3.19) при β = 0. Размер ${{d}_{0}}$ определялся исходя из наилучшего соответствия результатов расчета и экспериментальных данных. Он составил 0.6 мм и оказался сопоставимым с размером наиболее крупных пор. Штриховая прямая рассчитана согласно традиционному критерию разрушения при γ = 1.

Рис. 4

На рис. 5 приведены экспериментальные данные (точки) и результаты расчета критического давления для гипса 2 при значениях β = 0 (кривая 1) и $\beta = 0.6$ (кривая 2). Размер ${{d}_{0}}$ составил 1.0 мм. В соответствии с формулой (4.3), напряжение ${{T}_{s}}$ в первом случае равно ${{T}_{0}}$ (штриховая прямая), во втором случае ${{T}_{s}} = 1.3{{T}_{0}}$ (сплошная прямая).

Рис. 5

Рисунки 4, 5 иллюстрируют существенный масштабный эффект, т.е. влияние диаметра отверстия на локальную прочность материала. С его уменьшением критическое давление возрастает, достигая предела прочности на сжатие, с увеличением – асимптотически приближается к напряжению ${{T}_{0}}$ для гипса 1 и к напряжению ${{T}_{s}}$ для гипса 2. Такое поведение хорошо описывается модифицированным нелокальным критерием конечной трещины, в котором размер трещины d определяется по формуле (4.1).

Результаты второй серии экспериментов удобно представить в виде зависимости критической величины напряжения ${{\sigma }_{2}}$ от величины двухосности нагружения, характеризуемой параметром $\alpha = {{k}_{1}}{\text{/}}{{k}_{2}}$. Из формулы (3.19) получим:

(6.1)
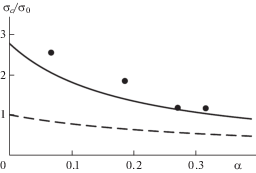
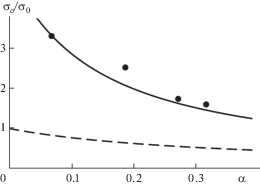
${{\sigma }_{c}} = {{\sigma }_{0}}\frac{{16\left( {\gamma - 1} \right)}}{{\sqrt {{{\alpha }^{2}}{{J}_{1}} + 2\alpha {{J}_{{12}}} + {{J}_{2}}} }}$

На рис. 6 представлены экспериментальные данные (точки) о величине напряжения ${{\sigma }_{2}}$ в момент образования трещин отрыва на контуре отверстия в образцах из гипса 1 в зависимости от двухосности нагружения и результаты расчета критического напряжения по формуле (6.1). Для выполнения расчетов использовали параметры материала ${{d}_{0}}$ и $\beta $, определенные по результатам первой серии испытаний. Штриховая кривая рассчитана согласно традиционному критерию разрушения при γ = 1. Результаты, полученные для гипса 2, представлены на рис. 7.

Рис. 6
Рис. 7

Как видно из рис. 4 хрупкое разрушение образцов из гипса 1, характеризующееся внезапным образованием на контуре отверстия и быстрым распространением вдоль оси сжатия трещин отрыва, может быть описано в рамках общепринятого подхода механики конечных трещин. Критерий разрушения хорошо описывает зависимость критического давления от диаметра отверстия во всем исследованном диапазоне от 1 до 20 мм.

В то же время, его применение для описания экспериментальных данных, полученных на образцах из гипса 2, позволяет получить удовлетворительные оценки величины критического давления только при малых (1–2 мм) диаметрах отверстия (рис. 5). Результаты расчетов, выполненных для больших диаметров отверстия, дают заниженные значения критического давления. Полученные экспериментальные данные свидетельствуют о том, что при увеличении диаметра отверстия критическое давление асимптотически стремится к значению, превышающему на 30% значение, рассчитанное для упругого тела. При этом, как и в первом случае, разрушение образцов из гипса 2 характеризуется внезапным образованием на контуре отверстия и быстрым распространением вдоль оси сжатия трещин отрыва. Все это позволяет охарактеризовать разрушение данного материала как квазихрупкое, с развитой зоной предразрушения, размер которой значительно превышает характерный размер структуры материала d0. Такое поведение хорошо описывается модифицированным критерием конечной трещины, в котором структурный параметр определяется по формуле (4.1).

Из рис. 6, 7 видно, что модифицированный критерий конечной трещины также хорошо описывает хрупкое и квазихрупкое разрушение материалов с круговым отверстием при изменении условий нагружения (краевых условий).

7. Заключение. Теоретически и экспериментально исследовано хрупкое и квазихрупкое разрушение геоматериалов с круговым отверстием различного диаметра при неравномерно распределенном сжатии, и выполнен анализ возможности применения подхода механики конечных трещин для оценки разрушающей нагрузки. При хрупком разрушении, когда размер зоны предразрушения является константой материала и определяется его структурой, общепринятый критерий конечной трещины хорошо описывает масштабный эффект прочности, проявляющийся в зависимости критической нагрузки от размера зоны концентрации упругих напряжений. Показано, что применение подхода механики конечных трещин может быть распространено на случай квазихрупкого разрушения с развитой зоной предразрушения. В модифицированном критерии «структурный» параметр представляется в виде суммы двух слагаемых. Первое их них характеризует собственно структуру материала и является константой, а второе отражает формирование зоны неупругих деформаций, или зоны поврежденности, и зависит от пластических свойств материала, геометрии концентратора напряжений (отверстия, полости, выработки) и условий нагружения (краевых условий). На основе проведенных исследований установлены закономерности образования трещин отрыва на контуре отверстия, и показано хорошее соответствие результатов расчета критической нагрузки по модифицированному критерию конечной трещины и полученных экспериментальных данных.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 18-05-00323). Автор выражает благодарность А.И. Рукавишникову и Н.В. Попову за помощь в подготовке образцов и проведении испытаний.

Таблица 1.
Размер образца, мм Размер вставки, мм ${{k}_{1}}$ ${{k}_{2}}$ α
100 20 0.110 0.349 0.317
100 40 0.164 0.602 0.272
100 60 0.143 0.764 0.187
100 80 0.060 0.883 0.068

Список литературы

  1. Осипенко Н.М. О масштабной зависимости трещиностойкости структурированных тел (на примере морского ледяного покрова) // Изв. РАН. МТТ. 2019. № 5. С. 70–85.

  2. Mikhailov S.E. A functional approach to non-local strength condition and fracture criteria // Eng. Fract. Mech. 1995. V. 52. P. 731–754.

  3. Петров Ю.В., Груздков А.А., Братов В.А. Структурно-временная теория разрушения как процесса, протекающего на разных масштабных уровнях // Физическая мезомеханика. 2012. Т. 15. № 2. С. 15–21.

  4. Lecampion B. Modeling size effects associated with tensile fracture initiation from a wellbore // Int. J. Rock Mech. Min. Sci. 2012. V. 56. P. 67–76.

  5. Корнев В.М., Зиновьев А.А. Модель квазихрупкого разрушения горных пород // ФТПРПИ. 2013. № 4. С. 74–82.

  6. Васильев В.В., Лурье С.А. О корректных нелокальных обобщенных теориях упругости // Физическая мезомеханика. 2016. Т. 19. № 1. С. 47–59.

  7. Ревуженко А.Ф. Об одном варианте линейной теории упругости со структурным параметром // ПМТФ. 2016. Т. 57. № 5. С. 45–52.

  8. Кулиев В.Д., Морозов Е.М. Градиентный деформационный критерий хрупкого разрушения // ДАН. 2016. Т. 470. № 5. С. 528–530.

  9. Кургузов В.Д. Сравнительный анализ критериев разрушения искусственных строительных материалов и горных пород // ФТПРПИ. 2019. № 5. С. 79–89.

  10. Taylor D. The theory of critical distances: a new perspective in fracture mechanics. Oxford: Elsevier, 2007. 284 p.

  11. Negru R., Marsavina L., Voiconi T., Linul E., Filipescu H., Belgiu G. Application of TCD for brittle fracture of notched PUR materials // Theor. Appl. Fract. Mech. 2015. V. 80. P. 87–95.

  12. Li W., Susmel L., Askes H., Liao F., Zhou T. Assessing the integrity of steel structural components with stress raisers using the Theory of Critical Distances // Eng. Fail. Anal. 2016. V. 70. P. 73–89.

  13. Fuentes J.D., Cicero S., Procopio I. Some default values to estimate the critical distance and their effect on structural integrity assessments // Theor. Appl. Fract. Mech. 2017. V. 90. P. 204–212.

  14. Justo J., Castro J., Cicero S., Sánchez-Carro M.A., Husillos R. Notch effect on the fracture of several rocks: Application of the Theory of Critical Distances // Theor. Appl. Fract. Mech. 2017. V. 90. P. 251–258.

  15. Taylor D. The Theory of Critical Distances applied to multiscale toughening mechanisms // Eng. Fract. Mech. 2019. V. 209. P. 392–403.

  16. Leguillon D. Strength or toughness? A criterion for crack onset at a notch // Eur. J. Mech. A/Solids. 2002. V. 21. P. 61–72.

  17. Pugno N.M., Ruoff R.S. Quantized fracture mechanics // Philos. Mag. 2004. V. 84. P. 2829–2845.

  18. Taylor D., Cornetti P., Pugno N. The fracture mechanics of finite crack extension // Eng. Fract. Mech. 2005. V. 72. P. 1021–1038.

  19. Yavari A., Wnuk M.P. Finite Fracture Mechanics for fractal cracks // IUTAM Symposium on Scaling in Solid Mechanics. Iutam Bookseries. V. 10. Dordrecht: Springer, 2009. P. 223–231.

  20. Carpinteri A., Cornetti P., Sapora A. Brittle failures at rounded V-notches: a finite fracture mechanics approach // Int. J. Fract. 2011. V. 172. P. 1–8.

  21. Sapora A., Mantič V. Finite Fracture Mechanics: a deeper investigation on negative T-stress effects // Int. J. Fract. 2016. V. 197. P. 111–118.

  22. Weißgraeber P., Leguillon D., Becker W. A review of Finite Fracture Mechanics: crack initiation at singular and non-singular stress raisers // Arch. Appl. Mech. 2016. V. 86. P. 375–401.

  23. Strobl M., Dowgiałło P., Seelig T. Analysis of Hertzian indentation fracture in the framework of finite fracture mechanics // Int. J. Fract. 2017. V. 206. P. 67–79.

  24. Martin E., Leguillon D., Carrère N. Finite Fracture Mechanics: a useful tool to analyze cracking mechanisms in composite materials // The structural integrity of carbon fiber composites. Cham: Springer, 2017. P. 529–548.

  25. Bowie O.L. Analysis of an infinite plate containing radial cracks originating at the boundary of an internal circular hole // Journal of Mathematics and Physics. 1956. V. 35. P. 60–71.

  26. Хеллан К. Введение в механику разрушения. М.: Мир, 1988. 364 с.

  27. Tirosh J. On the tensile and compressive strength of solids weakened (strengthened) by an inhomogeneity // Trans. ASME. J. Appl. Mech. 1977. V. 44. P. 449–454.

  28. Черепанов Г.П. Механика хрупкого разрушения. М.: Наука, 1974. 640 с.

  29. Седов Л.И. Механика сплошной среды. М.: Наука, 1984. Т. 2. 560 с.

  30. Сукнев С.В. Нелокальные и градиентные критерии разрушения квазихрупких материалов при сжатии // Физическая мезомеханика. 2018. Т. 21. № 4. С. 22–32.

  31. Сукнев С.В. Разрушение хрупкого геоматериала с круговым отверстием при двухосном нагружении // ПМТФ. 2015. Т. 56. № 6. С. 166–172.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал