Известия РАН. Механика твердого тела, 2021, № 3, стр. 118-127

Введение. Поверхностное упрочнение деталей, являющееся штатной технологией в авиадвигателестроении, энергетическом машиностроении, самолетостроении и других отраслях, является одним из методов повышения показателей надежности изделий (предела сопротивления усталости, износостойкости, микротвердости и других характеристик). Положительное влияние поверхностного пластического деформирования связывают с созданием в тонком приповерхностном слое сжимающих остаточных напряжений (ОН), с которыми и связывают повышение ресурса упрочненных деталей по сравнению с неупрочненными. Это показано в необозримом количестве публикаций отечественных и зарубежных исследователей, например, в [1–4] и многих других.

Одной из важных задач является реконструкция напряженно-деформированного состояния после процедуры упрочнения, поскольку эта информация является решающей при разработке методов решения краевых задач для упрочненных элементов конструкций в условиях ползучести. Различные экспериментальные методы применительно к цилиндрическим и призматическим деталям позволяют определить распределение лишь одной или двух компонент тензора ОН по глубине упрочненного слоя [2], но не позволяют установить распределение компонент тензора остаточных пластических деформаций (ПД).

Развитие теоретических методов реконструкции полей ОН и ПД на основе непосредственного моделирования конкретного технологического процесса, в первую очередь, связано с появлением мощных вычислительных комплексов, что и стимулировало появление ряда работ, в которых рассмотрено решение контактных динамических и квазистатических упругопластических задач [5–7]. Однако учесть в полном объеме все параметры технологий упрочнения поверхности деталей практически невозможно. Поэтому полученные результаты носят преимущественно качественный характер.

Второй важной проблемой является оценка кинетики наведенных остаточных напряжений в поле температурно-силовых (эксплуатационных) нагрузок, поскольку вследствие деформации ползучести происходит релаксация ОН. Как следствие, возникает необходимость разработки методов решения краевых задач с начальным напряженно-деформированным состоянием в условиях ползучести. Анализ публикаций свидетельствует, что данная тематика находится в стадии становления и развивается в основном в научной школе Самарского государственного технического университета при участии авторов настоящей статьи. Выделим здесь работу [8], в которой реализован метод решения краевой задачи релаксации ОН в упрочненном цилиндре при действии растягивающей осевой нагрузки и крутящего момента. Однако в прикладных исследованиях возникают задачи и другого рода, когда поверхностно упрочненные стержни в начальный момент получают осевые и окружные деформации, которые в дальнейшем жестко фиксируются. Техническим примером такого режима эксплуатации являются бандажированные рабочие лопатки компрессора и турбины авиационного двигателя (разумеется, с более сложной геометрической конструкцией). В связи с вышеизложенным целью настоящей работы является обобщение метода, предложенного в [8], на случай релаксации ОН в сплошном поверхностно упрочненном цилиндрическом образце в условиях ползучести при жестких (зафиксированных) ограничениях на линейные и угловые деформации.

1. Постановка задачи. Рассматривается сплошной цилиндрический образец радиуса R, в поверхностном слое которого методом поверхностного пластического деформирования наведены ОН и ПД при нормальной (“комнатной”) температуре $T = {{T}_{0}}$. На первом этапе решается обратная краевая задача реконструкции полей ОН и ПД по частично известной (экспериментальной) информации об одной или двух (в зависимости от технологии упрочнения) компонентах тензора ОН. Далее происходит изменение температуры до рабочей $T = {{T}_{1}}{\text{\;}}({{T}_{1}} > {{T}_{0}})$; прикладываются осевая растягивающая нагрузка F₀ и крутящий момент M₀, приводящие к линейной однородной осевой и угловой деформациям (соответственно), которые в дальнейшем жестко фиксируются. Затем решается краевая задача о релаксации усилий $~F = F\left( t \right)$ ($F\left( 0 \right) = {{F}_{0}}$) и $M = M\left( t \right)$ ($M\left( 0 \right) = {{M}_{0}})$, на фоне которой происходит релаксация ОН в приповерхностном слое цилиндра вследствие ползучести материала. Рассматривается осесимметричная постановка в цилиндрической системе координат $\left( {r,~{{\theta }},~z} \right)$, поэтому все компоненты тензоров напряжений и деформаций зависят лишь от координаты $r \in \left[ {0,~R} \right]$.

2. Реконструкция напряженно-деформированного состояния в сплошном цилиндре после процедуры упрочнения. Первый этап решения поставленной задачи состоит в реконструкции полей ОН и ПД после упрочнения. Обозначим через ${{\sigma }}_{r}^{{{\text{res}}}}$, ${{\sigma }}_{{{\theta }}}^{{{\text{res}}}}$, ${{\sigma }}_{z}^{{{\text{res}}}}$ радиальную, окружную и осевую компоненты тензора ОН, а через ${{q}_{r}}$, ${{q}_{{{\theta }}}}$, ${{q}_{z}}$ соответствующие компоненты тензора ПД. Для определения ОН и ПД воспользуемся феноменологическим методом [9], исходной информацией для которого в зависимости от технологии упрочнения являются одна (${{\sigma }}_{{{\theta }}}^{{{\text{res}}}}$) или две (${{\sigma }}_{{{\theta }}}^{{{\text{res}}}}$ и ${{\sigma }}_{z}^{{{\text{res}}}}$) экспериментально определенные эпюры ОН по глубине упрочненного слоя.

Как и для любой обратной краевой задачи, необходимо ввести ряд ограничений на компоненты тензоров ОН и ПД для получения единственного решения. В данном методе вводятся следующие гипотезы: 1) недиагональные компоненты тензоров ОН и ПД на порядок и более меньше (по модулю) нормальных компонент [10], поэтому ими можно пренебречь; 2) осевая и окружная компоненты тензора ПД пропорциональны: ${{q}_{z}}(r) = {{\alpha }}{{q}_{{{\theta }}}}(r)$, где α – феноменологический параметр анизотропии упрочнения [9]; 3) в области сжатия материала вторичные пластические деформации отсутствуют. Тогда для компонент тензоров ОН и ПД справедливы следующие соотношения [9]:

где E₀ – модуль Юнга материала при температуре упрочнения T₀, µ – коэффициент Пуассона.

Искомые компоненты тензоров ОН и ПД в поверхностно упрочненном сплошном цилиндре определяются в следующей последовательности:

здесь над стрелками указаны номера формул, по которым рассчитываются соответствующие величины.

Исходной информацией для применения схемы (2.6) являются зависимость для окружной компоненты тензора остаточных напряжений ${{\sigma }}_{{{\theta }}}^{{{\text{res}}}} = {{\sigma }}_{{{\theta }}}^{{{\text{res}}}}\left( r \right)$ и параметр анизотропии упрочнения α.

Экспериментальными методами распределение компоненты ${{\sigma }}_{{{\theta }}}^{{{\text{res}}}} = {{\sigma }}_{{{\theta }}}^{{{\text{res}}}}\left( r \right)$ можно определить лишь в тонком поверхностном слое. Для получения непрерывных полей ОН и ПД по схеме (2.6) эту информацию необходимо экстраполировать на всю область интегрирования $r \in \left[ {0,~R} \right]$. Для этого предлагается следующая аппроксимация:

где ${{\sigma }}_{0}^{{}}$, ${{\sigma }}_{1}^{{}}$, h*, b – параметры, подлежащие определению.

Методика идентификации параметра α также изложена в работе [9], причем для методов изотропного упрочнения поверхности (пневмодробеструйная обработка, ультразвуковое упрочнение и др.) величина α = 1 и эпюры напряжений ${{\sigma }}_{{{\theta }}}^{{{\text{res}}}} = {{\sigma }}_{{{\theta }}}^{{{\text{res}}}}\left( r \right)$ и ${{\sigma }}_{z}^{{{\text{res}}}} = {{\sigma }}_{z}^{{{\text{res}}}}\left( r \right)$ практически совпадают, а для методов анизотропного упрочнения (обкатка роликом, алмазное выглаживание и др.) параметр α ≠ 1 и наблюдается существенное различие эпюр осевой и окружной компонент тензора ОН в упрочненном слое [9].

3. Определение характеристик напряженно-деформированного состояния в поверхностно упрочненном сплошном цилиндре при температурно-силовом нагружении. Вначале рассмотрим режим температурного нагружения цилиндрического образца с температуры при упрочнении T₀ (как правило, “комнатная” температура), при которой модуль Юнга материала равен E₀, до температуры “эксплуатации” ${{T}_{1}}{\text{\;}}({{T}_{1}} > {{T}_{0}})$, при которой в материале развиваются деформации ползучести и которой соответствует значение модуля Юнга ${{E}_{1}}{\text{\;}}({{E}_{1}} < {{E}_{0}})$.

Предполагая, что при температурном нагружении дополнительных пластических деформаций не возникает, а, следовательно, величина ${{q}_{{{\theta }}}} = {{q}_{{{\theta }}}}\left( r \right)$ не зависит от температуры, запишем соотношение (2.2) для момента полного прогрева образца до температуры T₁ в виде

Соотношение (3.1) по форме будет аналогично (2.2), если все эпюры ОН после процедуры упрочнения умножить на коэффициент E₁/E₀. Таким образом, получаем распределения ОН при температуре T₁. Отметим, что температурные деформации здесь не учитываются, поскольку мы условно считаем, что прогрев образца выполнился мгновенно, а однородное температурное поле приводит лишь к объемному изменению геометрии образца и не влияет на напряженное состояние.

Теперь рассмотрим нагружение упрочненного цилиндра в момент времени $t$ = 0 + 0 осевой силой F₀ и крутящим моментом M₀. Предполагается, что при повторной нагрузке цилиндрического образца (после упрочнения) его материал находится в упругой области. При этом происходит ступенчатое изменение осевого и касательного напряжений на величину “рабочих” напряжений, возникающих за счет внешних нагрузок, и напряженное состояние задается соотношениями:

а компоненты тензора полных деформаций будут иметь вид:

Здесь и далее через ${{{{\sigma }}}_{i}} = {{{{\sigma }}}_{i}}\left( {r,t} \right)$ и ${{{{\varepsilon }}}_{i}} = {{{{\varepsilon }}}_{i}}\left( {r,t} \right){\text{\;}}\left( {i = r,~\;{{\theta }},{\text{\;}}z} \right)$ обозначены зависимости для компонент тензоров напряжений и полных деформаций от пространственной и временной координат; ${{\sigma *}} = {{{{\sigma }}}_{z}}\left( {r,0 + 0} \right) + {{{{\sigma }}}_{{{\theta }}}}\left( {r,0 + 0} \right) + {{{{\sigma }}}_{r}}\left( {r,0 + 0} \right)$; ${{\tau }}\left( {r,t} \right) = {{{{\sigma }}}_{{{{\theta }}z}}}\left( {r,t} \right)$ – касательное напряжение; ${{\gamma }}\left( {r,t} \right) = 2{{{{\varepsilon }}}_{{{{\theta }}z}}}\left( {r,t} \right)$ – деформация сдвига; $J = {{\pi }}{{R}^{4}}{\text{/}}2$ – момент инерции сечения относительно оси цилиндра, G₁ – модуль сдвига материала при температуре T₁.

Для описания процесса релаксации остаточных напряжений, осевой силы и крутящего момента необходимо решить краевую задачу ползучести поверхностно упрочненного цилиндра при температуре T₁ в режиме жесткого ограничения на осевую деформацию и угол поворота с начальным напряженно-деформированным состоянием, определяемым напряжениями (3.2) и деформациями (3.3).

4. Методика решения краевой задачи ползучести поверхностно упрочненного сплошного цилиндра, нагруженного осевой силой и крутящим моментом, в режиме жесткого ограничения на линейные и угловые деформации. Опишем процесс релаксации остаточных напряжений, осевой силы $F = F\left( t \right)$ и крутящего момента $M = M\left( t \right)$ в процессе ползучести поверхностно упрочненного сплошного цилиндра в режиме жесткого нагружения, когда заданы полная осевая деформация ${{{{\varepsilon }}}_{z}}\left( {r,t} \right) = {{{{\varepsilon }}}_{z}}\left( {r,0 + 0} \right) = {{\varepsilon }}_{z}^{*} = {\text{const}}$ и относительный угол закручивания ${{\varphi }}\left( t \right) = {{\varphi }}\left( {0 + 0} \right) = {{\varphi *}} = {\text{const}}$. Постановка соответствующей краевой задачи ползучести включает в себя следующие соотношения:

– уравнения равновесия:

– уравнение совместности деформаций:

– гипотеза плоских сечений:

– гипотеза прямых радиусов:

где ${{\varphi *}} = {{\gamma }}\left( {r,0 + 0} \right){\text{/}}r = {\text{const}}$;

– краевые условия:

Поскольку время t входит в соотношения (4.1)–(4.7) параметрически, здесь и в дальнейшем для производных компонент тензоров напряжений и деформаций по r используется оператор полной производной.

Опишем процесс релаксации остаточных напряжений вследствие ползучести при температуре $T = {{T}_{1}}$. Запишем соотношения для компонент тензора полных деформаций в виде

где e_z, ${{e}_{{{\theta }}}}$, e_r, ${{{{\gamma }}}^{e}}$ – компоненты тензора упругих деформаций; p_z, ${{p}_{{{\theta }}}}$, p_r, ${{{{\gamma }}}^{p}}$ – компоненты тензора деформаций ползучести. При этом в начальный момент времени компоненты тензора деформаций ползучести равны нулю для всех $r \in \left[ {0,~R} \right]$:

Задача сводится к разрешению системы (4.8), (4.9) относительно компонент тензора напряжений.

Запишем закон Гука для упругих деформаций:

где ${{\bar {\sigma }}} = {{{{\sigma }}}_{z}}\left( {r,t} \right) + {{{{\sigma }}}_{{{\theta }}}}\left( {r,t} \right) + {{{{\sigma }}}_{r}}\left( {r,t} \right)$.

Подставляя (4.5) и (4.10) при i = z в соотношение (4.8) при i = z, находим зависимость для осевой компоненты тензора напряжений:

Применяя далее методику работы [8], в которой реализован метод решения краевой задачи релаксации ОН в упрочненном цилиндре при действии растягивающей осевой нагрузки и крутящего момента, с использованием (4.1), (4.4), (4.5), (4.12) в системе уравнений (4.8), (4.9) последовательно исключаются компоненты тензора напряжений ${{{{\sigma }}}_{{{\theta }}}}$ и ${{{{\sigma }}}_{z}}$. В итоге получаем неоднородное дифференциальное уравнение второго порядка относительно ${{{{\sigma }}}_{r}}$:

с правой частью

Решение уравнения (4.13) при граничных условиях (4.7) записывается следующим образом:

При известном ${{{{\sigma }}}_{r}}$ из уравнения (4.1) находим зависимость для окружной компоненты тензора напряжений:

Зная величины ${{{{\sigma }}}_{r}}$ и ${{{{\sigma }}}_{{{\theta }}}}$ можно определить ${{{{\sigma }}}_{z}}$ по формуле (4.12) и далее – значение F(t) из уравнения (4.2).

Подставляя (4.11) в соотношение (4.9) с учетом (4.6), получаем распределение касательной компоненты тензора напряжений:

после чего определяем величину M(t) из соотношения (4.3).

5. Результаты расчетов и их анализ. В модельных расчетах использовались цилиндрические образцы из сплава ЖС6КП радиуса $R = 3.76$ мм (r ∈ [0, 3.76] мм), упрочненные пневмодробеструйной обработкой поверхности, которая является штатной технологией упрочнения деталей из этого сплава, например, в двигателестроении.

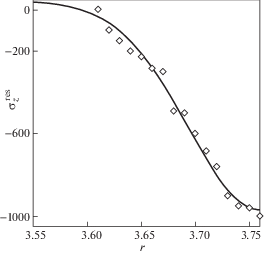
В расчетах полагалось ${{T}_{0}} = 20~^\circ {\text{C}}$, ${{T}_{1}} = 900~^\circ {\text{C}}$, ${{E}_{0}} = 2 \times {{10}^{5}}~$ МПа, ${{E}_{1}} = 1.364 \times {{10}^{5}}~$ МПа, μ = 0.3. В качестве исходной информации использовались экспериментальные данные для компоненты ${{\sigma }}_{z}^{{{\text{res}}}} = {{\sigma }}_{z}^{{{\text{res}}}}\left( r \right)$ в поверхностном слое, приведенные в работе [8]. При пневмодробеструйной обработке поверхности коэффициент анизотропии упрочнения α = 1 и эпюры для окружных и осевых ОН близки. Поэтому для идентификации параметров аппроксимации (2.7) в первом приближении использовались экспериментальные данные для осевой компоненты тензора ОН (точки на рис. 1). Затем параметры ${{\sigma }}_{0}^{{}}$, ${{\sigma }}_{1}^{{}}$ и b в (2.7) варьировались, и для каждого набора значений реализовывался алгоритм (2.6) до достижения минимума функционала среднеквадратического отклонения расчетных данных для ${{\sigma }}_{z}^{{{\text{res}}}}$ от экспериментальных значений. В результате получены следующие значения параметров аппроксимации (2.7) для ${{\sigma }}_{{{\theta }}}^{{{\text{res}}}}$: ${{{{\sigma }}}_{0}} = 22.554$ МПа, ${{{{\sigma }}}_{1}} = 1027.454$ МПа и $b = 9.313$ × 10^–2 мм. Величина h* = 0 изначально, поскольку $h{\text{*}} \ne 0$ только в случае, если экстремум зависимости ${{\sigma }}_{{{\theta }}}^{{{\text{res}}}} = {{\sigma }}_{{{\theta }}}^{{{\text{res}}}}\left( r \right)$ находится не на поверхности, а в подповерхностном слое [9]. На рис. 1 сплошной линией показана зависимость для ${{\sigma }}_{z}^{{{\text{res}}}} = {{\sigma }}_{z}^{{{\text{res}}}}\left( r \right)$ (МПа).

Для моделирования процесса релаксации ОН и усилий $F = F\left( t \right)$ и $M = M\left( t \right)$ использовалась теория установившейся ползучести:

где S – интенсивность напряжений; c, m – константы материала. Для сплава ЖС6КП при температуре ${{T}_{1}} = 900~^\circ {\text{C}}$ имеем [8]: $c = 1.5 \times {{10}^{{ - 20}}}$ (МПа)^–m ч^–1, $m = 6.62$.

Отметим, что задача ползучести решалась численно известным методом – “шагами по времени” [8], при этом соотношения (5.1) интегрировались по методу Эйлера.

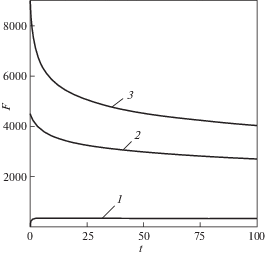
Расчеты выполнены при различных комбинациях первоначальных растягивающей нагрузки ${{F}_{0}}$ и закручивающего момента M₀. На рис. 2 приведена типичная картина релаксации осевого усилия $F = F\left( t \right)$ ($t \in \left[ {0,~\;100} \right]$ ч) при фиксированном значении первоначального угла закручивания моментом ${{M}_{0}} = 16700$ Н · мм. Сплошные линии 1, 2, 3 соответствуют значениям $F = F(t)$ при первоначальных значениях ${{F}_{0}} = \{ 0,4441.5$, 8882.9} Н соответственно.

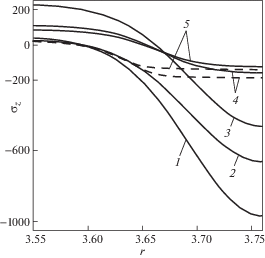
На рис. 3 в качестве иллюстрации результатов расчетов сплошными линиями приведено типичное распределение ${{{{\sigma }}}_{z}} = {{{{\sigma }}}_{z}}\left( {r,t} \right)$ (МПа) при ${{F}_{0}} = 8882.9$ Н, ${{M}_{0}} = 16700$ Н·мм в различные моменты времени. Цифра 1 соответствует исходному состоянию после упрочнения ($t = 0 - 0$), цифра 2 – температурному нагружению, цифра 3 – силовому нагружению ($t = 0 + 0$), цифры 4 и 5 – моментам времени t = 20 ч и t = 100 ч соответственно. Здесь же штриховыми линиями показано распределение этой же компоненты тензора ОН в условиях чистой термоэкспозиции при ${{T}_{1}} = 900~^\circ {\text{C}}$.

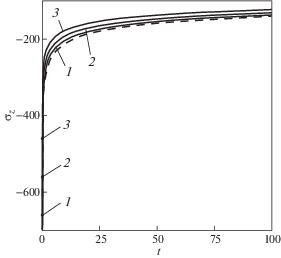
На рис. 4 сплошными линиями приведены зависимости для напряжения ${{{{\sigma }}}_{z}} = {{{{\sigma }}}_{z}}$(R, t) (МПа) на поверхности цилиндра после температурно-силового нагружения при $t \in \left[ {0,~\;100} \right]$ ч (цифры 1, 2, 3 соответствуют режимам нагружения на рис. 2). Здесь же для сравнения штриховой линией показана зависимость для этого же напряжения в условиях термоэкспозиции (чисто температурное нагружение при ${{F}_{0}} = 0$, ${{M}_{0}} = 0$ и ${{T}_{1}} = 900~^\circ {\text{C}}$). Отметим, что для окружной компоненты происходит ступенчатое изменение ее величины лишь вследствие изменения температуры, а при приложении внешних силовых возмущений ступенчатого изменения ${{{{\sigma }}}_{{{\theta }}}} = {{{{\sigma }}}_{{{\theta }}}}\left( {r,t} \right)$ не происходит, в отличие от компоненты ${{{{\sigma }}}_{z}} = {{{{\sigma }}}_{z}}\left( {r,t} \right)$.

Детально выполненное параметрическое исследование задачи релаксации ОН ${{{{\sigma }}}_{z}}$, ${{{{\sigma }}}_{{{\theta }}}}$, ${{{{\sigma }}}_{r}}$ показало несущественное влияние первоначально заданных (и жестко зафиксированных) упругих осевой и угловой деформаций на кинетику всех компонент тензора ОН.

Выводы. Разработана методика решения краевых задач релаксации ОН в поверхностно упрочненных сплошных цилиндрах в условиях ползучести с начальным напряженно-деформированным состоянием (НДС), вызванным заданными (и жестко зафиксированными) осевой и угловой деформациями. Анализ модельных расчетов для упрочненных образцов из сплава ЖС6КП при $T = 900~^\circ {\text{C}}$ показал несущественное влияние первоначального НДС на процесс релаксации ОН по отношению к случаю чистой термоэкспозиции, что является позитивным фактором в прикладном плане с точки зрения инженерной практики, например, в авиадвигателестроении, где поверхностное пластическое упрочнение является штатной технологической операцией.

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 19-19-00062).