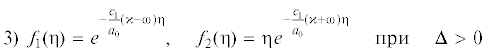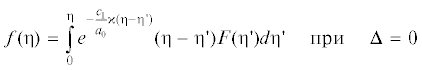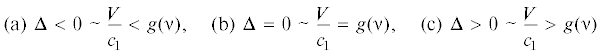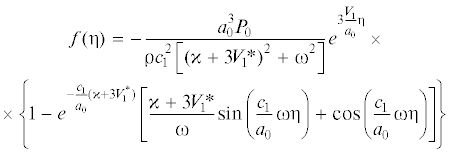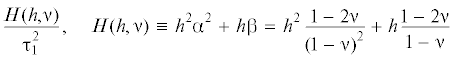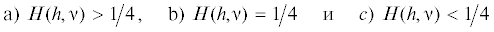Известия РАН. Механика твердого тела, 2021, № 3, стр. 100-117

1. Введение. Работа посвящена исследованию нестационарных процессов, возникающих в упругих средах, в частности, в грунтах под действием динамической нагрузки (давления), приложенного на границе сферической полости. Считается, что полость расширяется с течением времени с постоянной и произвольной по величине скоростью, которая может принимать значения вплоть до скорости объемных упругих волн. Если при этом поверхность полости идентифицируется с поверхностью раздавливания, дробления и обрушения грунта, то описанная задача служит в некоторых случаях приемлемой моделью камуфлетного подземного взрыва, например, взрыва в скальных грунтах. В других случаях, эта задача является одним из важных этапов (элементов) в более сложной модели подземного взрыва и ее решение позволяет оценивать действие взрыва в “дальней зоне”, на расстояниях, значительно превышающих первоначальный размер полости.

Практически во всех существующих постановках данной проблемы с динамическим расширением полости в упругой среде, когда отсутствуют или пренебрегается наличием зон пластических деформаций вокруг полости, деформации считаются малыми и граничные условия с текущей поверхности полости сносятся на ее первоначальное положение в момент возникновения ударной нагрузки от взрыва. Такая постановка сильно упрощает задачу, сводя ее к дифференциальному уравнению с постоянными коэффициентами. В настоящем исследовании допускается возможность быстрого расширения полости с большими скоростями, когда краевые условия удовлетворяются на подвижной границе полости; снесение их на начальное положение полости привело бы к значительным ошибкам. Формулировка краевых условий задачи на движущейся границе приводит к необходимости интегрирования дифференциального уравнения второго порядка с переменными коэффициентами. Дж. Ахенбах и С. Сан [1] нашли приближенное решение этой задачи в случае присутствия большого параметра в полученном дифференциальном уравнении с переменными коэффициентами, когда возможно использование метода Горна для его интегрирования.

Однако, работа Дж. Ахенбаха и С. Сана содержит ряд существенных недостатков, которые требуется исправить, ввиду практической важности данной задачи.

1. Рассматривая в качестве основного расчетного примера случай полости, расширяющейся с постоянной скоростью, авторы не заметили, что в этом случае дифференциальное уравнение с переменными коэффициентами, к которому они свели задачу, является уравнением типа Эйлера, допускающем точное решение.

2. За большой параметр в дифференциальном уравнении принимается размерная величина, а именно, скорость распространения в среде объемных упругих волн, что некорректно и не позволяет судить о точности и границах применимости полученного приближенного решения.

3. Для возможности применения метода Горна необходимо, чтобы введенный нами ниже безразмерный параметр $h$, равный отношению скорости объемных упругих волн среды к “приведенной” скорости расширения полости, был хотя бы больше единицы или, иначе, чтобы скорость расширения полости была меньше половины скорости объемной упругой волны. Но даже если это условие ($h > 1$) выполнено, то, как мы покажем, существует интервал изменения параметра Пуассона среды ${{\nu }}$, примыкающий к точке ${{\nu }} = 0.5$ (слабосжимаемые среды), на котором представление решения в форме метода Горна не справедливо (на этом интервале решение имеет другой аналитический вид). Правда при малых скоростях расширения полости этот интервал весьма мал. Тем не менее из сказанного следует, что решение Дж. Ахенбаха и С. Сана не является полным.

2. Постановка задачи. 2.1. Физические предпосылки. Пусть в начальный момент времени (t = 0) в неограниченной изотропной упругой среде имеется сферическая полость радиуса ${{a}_{0}}$. Предполагается, что полость с течением времени расширяется и имеет в текущий момент времени $t$ радиус $r = a(t)$ в сферической системе координат ($r$, ${{\theta }}$, ${{\varphi }}$) с полюсом в центре полости. Рассматривается случай, когда расширяющаяся граница полости является, подобно фронту волны, геометрической или нематериальной поверхностью в том смысле, что в разные моменты времени она состоит из разных физических частиц среды. К границе полости с момента времени t = 0 приложено равномерное, т.е. не зависящее от координат ${{\theta }}$ и ${{\varphi }}$, и переменное по времени давление $P(t)$. Задача состоит в исследовании возникающих в этом случае динамических возмущений в среде или, иными словами, в нахождении волн, распространяющихся по среде от расширяющейся нагруженной полости.

Физическим явлением, описываемым рассматриваемой задачей, служит, например, камуфлетный подземный взрыв, когда под действием высокого давления в газообразных продуктах взрыва, возникающего при детонации взрывчатого вещества в объеме $r \leqslant {{a}_{0}}$, происходит раздавливание и обрушение грунта. Такая ситуация, когда в результате взрыва образуется расширяющаяся до некоторого предела зона обрушения (или разрушения), а вне этой зоны сохраняется область чисто упругих деформаций характерна для взрывов в скальных грунтах или хрупких средах. При этом в самой упругой области к расширяющейся полости (зоне разрушения) может примыкать зона, в которой после прохождения взрывной волны образовались микро- или макротрещины и дефекты, которые не приводят к макроразрушению. Будем считать также, что эти трещины и дефекты не изменяют заметно упругие свойства грунта.

Представленная картина последствий подземного взрыва в общем случае для произвольных грунтов разумеется не является полной. Достаточно полное и основанное на экспериментальных данных описание явлений, возникающих при подземных взрывах, включая ядерные взрывы, можно найти в общирной литературе по данному вопросу (см., например, обзорные работы [2–5]). Главное отличие результатов этих исследований от представленной выше картины явления состоит в том, что за областью обрушения для многих грунтов имеется зона чисто пластических или упругопластических деформаций. Однако, можно избежать решения этой более сложной задачи, пренебрегая существованием пластической зоны, если интересоваться эффектом подземного взрыва в “дальней зоне”, на расстояниях от места взрыва значительно (на многие порядки) превышающих ширину пластической зоны. Очевиден и практический интерес таких постановок задач в связи с вопросами обнаружения и оценок мощности подземных взрывов.

Упомянем теперь и другое упрощающее предположение, которое принимается нами в постановке задачи, – это то, что полость считается расширяющейся на бесконечном промежутке времени. В реальности при расширении полости давление во взрывных газах падает и при падении его до некоторого значения (своего для каждого типа грунта) процесс дробления и обрушения грунта прекращается. Тем самым, полость имеет максимальный размер или максимальный радиус (в предположении сферической симметрии процесса). В силу сказанного, давление газов в полости принимает максимальное значение в начальный момент времени при полной детонации к этому моменту времени взрывчатого вещества, заложенного в объеме шара радиуса ${{a}_{0}}$ (тогда взрывные газы имеют минимально возможный объем), либо максимальное значение давления достигается очень скоро после взрыва до момента “остановки” полости как, например, в случае подземных ядерных взрывов [6, 7]. Таким образом, если интересоваться максимальными напряжениями при подземном взрыве в дальней зoне упругой области, то можно считать полость расширяющейся на всем рассматриваемом промежутке времени. Что касается задачи с полостью, расширяющейся на конечном интервале времени (задачи “с остановкой”), метод ее точного аналитического решения дан в диссертации Х. Хамиду [8] (более полное и детальное изложение решения этой задачи авторы намереваются опубликовать в скором времени).

2.2. Уравнения, начальные и краевые условия. Считая среду (грунт) линейно упругой, перейдем к математической формулировке задачи. В этом случае предполагаются малыми деформации и перемещения (в сравнении, скажем, с первоначальным радиусом полости ${{a}_{0}}$), а также скорости физических частиц (материальных точек) среды (в сравнении со скоростью распространения упругой волны от полости). Тогда лагранжевы и эйлеровы координаты точек среды неразличимы и в выражении ускорения при записи уравнений движения в эйлеровой (пространственной) системе координат можно пренебречь конвективным членом, то есть считать, что ускорение материальных точек дается, как и в лагранжевых координатах, частной производной вектора скорости по времени. Что касается скорости нематериальной поверхности разрушения (границы полости) $V = {{da} \mathord{\left/ {\vphantom {{da} {dt \equiv \dot {a}(t)}}} \right. \kern-0em} {dt \equiv \dot {a}(t)}}$, то, как было сказано, мы не накладываем на ее величину никаких ограничений, кроме естественного ограничения, что она должна быть меньше скорости распространения объемных волн в среде: $0 < V < {{c}_{1}}$. В то время как в работе Дж. Ахенбаха и С. Сана [1] эта скорость считается малой, что связано с методом решения задачи (максимальное значение ее в рассмотренных в [1] примерах составляет $V = 0.05{{c}_{1}}$).

В силу сферической симметрии задачи только одна (радиальная) компонента вектора перемещения точек среды отлична от нуля и она есть только функция координаты $r$ и времени $t$, т.е.

Тензор малых деформации в криволинейной системе координат определяется теми же формулами Коши, что и в декартовой системе координат, только необходимо в них частные производные по координатам заменить на ковариантные производные (см., например, [9], Ch. III); по повторяющимся дважды латинским индексам принято, если не оговорено противное, правило суммирования по всем значениям, принимаемым индексами):

Здесь (q¹, q², q³) – криволинейные координаты, а величины ${{\Gamma }}_{{ij}}^{n}$, называемые символами Кристоффеля, являются коэффициентами в выражениях производных по координате от базисных векторов ${{{\mathbf{G}}}_{i}}$, т.е. в равенствах ${{{{\partial {{{\mathbf{G}}}_{i}}} \mathord{\left/ {\vphantom {{\partial {{{\mathbf{G}}}_{i}}} {\partial q}}} \right. \kern-0em} {\partial q}}}^{j}} = {{\Gamma }}_{{ij}}^{n}{{{\mathbf{G}}}_{n}}$. При этом базисные или координатные вектора в произвольной точке (q¹, q², q³) определяются как производные радиус-вектора ${\mathbf{r}}$ этой точки по криволинейным координатам, т.е. G_i = ${{\partial {\mathbf{r}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}} {\partial {{q}^{i}}}}} \right. \kern-0em} {\partial {{q}^{i}}}}$. Не все из этих векторов являются единичными и безразмерными, и потому, не все компоненты тензора деформаций, определенного формулой (2.2), будут безразмерными. Чтобы избавиться от этого неудобства, вводят в рассмотрение физические компоненты тензора деформаций (аналогично и других тензоров второго порядка) равенствами ${{{{\tilde {\varepsilon }}}}_{{ij}}} = $ ${{{{{{\varepsilon }}}_{{ij}}}} \mathord{\left/ {\vphantom {{{{{{\varepsilon }}}_{{ij}}}} {\sqrt {{{G}_{{ii}}}{{G}_{{jj}}}} }}} \right. \kern-0em} {\sqrt {{{G}_{{ii}}}{{G}_{{jj}}}} }}$ (по индексам i и j не суммировать), где ${{G}_{{ii}}}$ и ${{G}_{{jj}}}$ есть квадраты длин координатных векторов ${{{\mathbf{G}}}_{i}}$ и ${{{\mathbf{G}}}_{j}}$ или, иначе, компоненты метрического тензора, определяемого как скалярное произведение координатных векторов: ${{G}_{{ij}}} = {{{\mathbf{G}}}_{i}} \cdot {{{\mathbf{G}}}_{j}}$. Переход к физическим компонентам тензоров имеет еще и то преимущество, что ковариантные и контрвариантные физические компоненты совпадают друг с другом (и потому, индексы у физических компонент можно всегда писать внизу), однако, есть и неудобство, связанное с тем, что физические компоненты не образуют тензора, т.е. они при переходе к новой системе координат не преобразуются по правилам преобразования компонент тензора.

В случае сферической системы координат, пользуясь известными значениями для символов Кристоффеля и ко- и контрвариантных компонент метрического тензора (см., например, [10]), получаем из (2.2) следующие выражения для физических компонент тензора деформаций:

Как легко показать, закон Гука, связывающий тензоры напряжений и деформаций и записываемый в декартовой системе координат для изотропной упругой среды в виде

в котором ${{\lambda }}$ и ${{\mu }}$ – постоянные, называемые параметрами Ламе, будет иметь аналогичный вид и в любой криволинейной ортогональной системе координат с заменой единичного тензора Кронекера ${{{{\delta }}}_{{ij}}}$ (принимающего значение 1 при i = j и 0 при $i \ne j$) на метрический тензор G_ij криволинейной системы (${{{{\delta }}}_{{ij}}}$ $ \to $ ${{G}_{{ij}}}$). Отсюда следует, что физические компоненты тензора напряжений ${{{{\tilde {\sigma }}}}_{{ij}}}$ и деформаций ${{{{\tilde {\varepsilon }}}}_{{ij}}}$ (к которым, в силу указанных выше причин, удобно перейти в криволинейных координатах), связаны ровно соотношением (2.4). На указанную разницу в написании закона Гука не всегда обращается внимание; так, например, в книге В.Б. Поручикова [11] (с. 8) ошибочно полагается, что соотношение между тензорами напряжений и деформаций в виде (2.4) справедливо кроме декартовой и в любой ортогональной криволинейной системе координат.

В нашем случае, когда физические компоненты тензора деформаций определены формулами (2.3), получаем из закона Гука (2.4), записанного в физических переменных

В соотношениях закона Гука (2.4), (2.5) величины ${{{{\sigma }}}_{{ij}}}$ и ${{{{\tilde {\sigma }}}}_{{ij}}}$ можно понимать как компоненты и физические компоненты тензора условных напряжений, когда вектора внутренних усилий (напряжений), возникающие на элементарных (т.е. бесконечно малых) координатных площадках в текущем деформированном состоянии, отнесены к соответствующим площадкам до деформации, поскольку в случае малых деформаций (и малых перемещений) физических частиц эти компоненты мало отличаются от компонент тензора истинных напряжений, в котором вектора внутренних усилий отнесены к деформированным площадкам, т.е. к площадкам, на которых эти усилия возникают.

Дифференциальные уравнения движения (или равновесия) сплошной среды в криволинейных, в частности, сферических эйлеровых координатах, вытекающие из закона сохранения или изменения количества движения любого объема тела и выраженные через физические компоненты тензора напряжений, получены в курсах по механике сплошной среды и теории упругости (см., например, [12, 13]. Легко проверить, что при отсутствии массовых сил, наличии сферической симметрии и равенстве нулю касательных напряжений (2.5), два из этих уравнений тождественно выполнены, а остающимся является уравнение

где ${{\rho }}$ – плотность среды.

Подставляя в (2.6) выражения (2.5), следующие из закона Гука, приходим для радиального перемещения точек упругого грунта к уравнению

в котором через ${{c}_{1}} = \sqrt {{{({{\lambda }} + 2{{\mu }})} \mathord{\left/ {\vphantom {{({{\lambda }} + 2{{\mu }})} {{\rho }}}} \right. \kern-0em} {{\rho }}}} $ обозначена скорость распространения в среде объемных волн.

Уравнение (2.7) решается в области $r > a(t)$, т.е. во внешности полости переменного радиуса, при нулевых начальных условиях

К уравнению (2.7) и начальным условиям (2.8) необходимо присоединить краевое условие

означающее, что на расширяющейся полости задано давление P(t) (знак минус характеризует то обстоятельство, что сила ${\mathbf{P}}(t)$ и внешняя по отношению к области $r > a(t)$ нормаль n к границе полости направлены в разные стороны).

Используя выражение для ${{{{\tilde {\sigma }}}}_{{rr}}}$ из закона Гука (2.5), можно переписать краевое условие в терминах функции перемещения u:

Некоторые авторы [14, 15] сносят краевое условие (2.9) на начальное положение полости $r = {{a}_{0}}$, что существенно упрощает задачу в математическом отношении. Однако, в большинстве случаев при сильных взрывах область разрушения значительна, радиус полости заметно увеличивается и снесение краевого условия на начальное положение полости может привести к не приемлемым ошибкам.

2.3. Приведение краевой задачи (2.7)–(2.9) к задаче Коши для обыкновенного дифференциального уравнения. Если ввести в рассмотрение потенциал перемещений по формуле

то, как нетрудно видеть, уравнение (2.7) сведется к уравнению сферических волн

Как известно, общее решение волнового уравнения (2.11) дается формулой

в которой произвольные функции  f и $g$ являются дважды непрерывно дифференцируемыми функциями в случае классического решения (f, $g \in {{C}^{2}}$) или дважды кусочно непрерывно дифференцируемыми функциями, если рассматриваются решения с разрывами (волны).

Если функции $f({{{{\xi }}}_{ - }})$ и $g({{{{\xi }}}_{ + }})$, ${{{{\xi }}}_{ \mp }} \equiv t \mp {r \mathord{\left/ {\vphantom {r {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}$ таковы, что они равны тождественно нулю при отрицательных значениях аргументов ${{{{\xi }}}_{ \mp }} < 0$, то первое слагаемое в (2.12) есть волна уходящая на бесконечность, а вторая – идущая из бесконечности. Тогда, в силу начальных условий (2.8), решение краевой задачи (2.7)–(2.9) должно быть представимо в виде волны, уходящей от полости на бесконечность, т.е. в виде первого слагаемого в (2.12). Выполняя в этом слагаемом сдвиг по времени на величину $ - {{{{a}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}} {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}$, чтобы волна зарождалась на границе полости в тот же момент времени t = 0, с которого действует давление $P(t)$, получим решение указанной выше краевой задачи в виде

Подставляя это решение в краевое условие (2.9), приходим после ряда элементарных преобразований к обыкновенному дифференциальному уравнению для неизвестной функции f:

в котором $f{\text{'}}$, $f{\text{''}}$ означают производные функции  f  по аргументу.

Обозначим в этом уравнении аргумент неизвестной функции через

Поскольку функция ${{\tau }}(t)$, определенная равенством (2.14), есть непрерывная монотонно возрастающая функция $t$, то существует однозначная непрерывная обратная функция $t = t({{\tau }})$. Тогда, вводя обозначения $a(t) = a(t({{\tau }})) \equiv \bar {a}({{\tau }}),$ $P(t) = P(t({{\tau }})) \equiv \bar {P}({{\tau }})$ и константу

перепишем полученное выше уравнение для $f$ в виде

В уравнении (2.16) ${{\tau }} \geqslant 0$ (что соответствует моментам времени $t \geqslant 0$) и для выделения единственного его решения нужно поставить два начальных условия. В работе Дж. Ахенбаха и С. Сана и многочисленных работах с полостью постоянного радиуса (когда уравнение подобное (2.16) является уравнением с постоянными коэффициентами) в качестве начальных условий для функции $f$ ставятся однородные условия

ограничиваясь замечанием, что они следуют из нулевых начальных условий (2.8), означающих, что среда в момент времени t = 0 (и в более ранние моменты времени) находилась в состоянии покоя. Однако, этот вывод не столь очевиден и требует разъяснений. Для этого от функции  f  вернемся к функции, имеющей физический смысл, а именно к функции перемещений точек среды по формуле (2.10), в которую подставим выражение (2.13). Тогда имеем где $f{\text{'}} \equiv {{df} \mathord{\left/ {\vphantom {{df} {ds}}} \right. \kern-0em} {ds}}$.

Заметим, что значению аргумента s = 0 соответствует, в силу определения $s$ в (2.13), значение функции на фронте волны. Следовательно, условие непрерывности перемещений в упругой области при переходе через фронт волны (условие сплошности подразумевается), согласно первому начальному условию в (2.8) и (2.18), записывается в виде

Здесь и далее за $f{\text{'}}(0)$ и $f(0)$ принимаются предельные значения этих функций при $s \to 0 + $, т.е. их значения за фронтом волны; соответствующие значения перед фронтом тождественно равны нулю, поскольку перед фронтом среда находится в состоянии покоя (условия (2.8)).

Получим теперь второе начальное условие. Нужно ожидать, что потенциал перемещений $\Phi $, а значит и f, более гладкие функции, чем перемещение $u$. Действительно, равенство (2.10), используя (2.13), можно переписать в виде

или, интегрируя по s, в виде ($0 < s < t$)

При этом, константа интегрирования в (2.20) положена равной нулю, поскольку потенциал перемещений (2.10) определен с точностью до константы.

Из (2.20) следует, что при s = 0 (на фронте волны) $f(0) = 0$. Объединяя этот результат с условием (2.19), получаем, что функция f должна удовлетворять однородным начальным условиям (2.17). Таким образом, краевая задача (2.7)–(2.9) сведена к задаче Коши (2.16), (2.17) для линейного обыкновенного дифференциального уравнения с переменными коэффициентами.

3. Точное решение задачи в случае полости, расширяющейся с постоянной скоростью. 3.1. Преобразование уравнения и сведение проблемы к задаче Коши для уравнения с постоянными коэффициентами. В уравнении (2.16) перейдем к новой независимой переменной ${{\eta }}$, задаваемой равенствами

Тогда

и уравнение (2.16) переписывается в виде

Уравнение (3.2) будет уравнением с постоянными коэффициентами, если величина $\bar {a}{\text{'}}({{\tau }}) \equiv \frac{{d\bar {a}({{\tau }})}}{{d{{\tau }}}}$ есть константа. Последнее имеет место при равномерном расширении полости (расширении с постоянной скоростью). Действительно, пусть

В этом случае, в силу (2.14),

Следовательно,

Кроме того, когда переменные t, τ и переменный радиус полости a(t) связаны соотношениями (3.3)–(3.5), закон преобразования (3.1) может быть выражен в явном виде. Для этого первое соотношение из (3.5) подставим во второе равенство в (3.1). Тогда приходим к равенству

интегрирование которого дает явное выражение между переменными ${{\tau }}$ и ${{\eta }}$:

Заметим, что здесь константа интегрирования выбрана равной нулю, чтобы значению τ = 0 соответствовало значение η = 0. Видно также, что ${{\eta }} \to {{\tau }}$ при ${{V}_{1}} \to 0$.

Обозначая правую часть уравнения (3.2) через $F({{\eta }})$, выразим ее через переменную ${{\eta }}$; имеем в соответствии с (3.5) и (3.6)

В частном случае, когда давление в полости постоянно, т.е. $P(t) = {{P}_{0}}H(t)$, ${{P}_{0}} = {\text{const}}$ ($H(t)$ – единичная функция Хевисайда, равная 1 при $t > 0$ и 0 при $t < 0$)

Следовательно, при расширении полости с постоянной скоростью уравнение (3.2) принимает вид

в котором правая часть $F({{\eta }})$ определена выражением (3.7) (или (3.8)), а безразмерная приведенная скорость расширения полости $V_{1}^{ * }$ определена равенством

Наконец, поскольку значению переменной τ = 0 соответствует значение η = 0, то при переходе к новой независимой переменной начальные условия остаются однородными и совпадают с (2.17). Таким образом, наша задача с полостью, расширяющейся с постоянной скоростью, свелась к задаче Коши (3.9), (2.17) для обыкновенного линейного дифференциального уравнения с постоянными коэффициентами.

3.2. Точное решение задачи Коши. Известно (см., например, [16]), что общее решение $f({{\eta }})$ линейного неоднородного уравнения (3.9) легко выписывается, если известна фундаментальная система решений соответствующего (3.9) однородного уравнения, состоящего из двух линейно независимых решений ${{f}_{1}}({{\eta }})$ и ${{f}_{2}}({{\eta }})$. Тогда

где через $W({{f}_{1}},{{f}_{2}})$ обозначен вронскиан функций $\left\{ {{{f}_{1}},{{f}_{2}}} \right\}$, т.е. определитель (штрих у функций означает производную по аргументу)

Последнее слагаемое в (3.11) есть частное решение неоднородного уравнения (3.9), а два первых слагаемых, содержащие произвольные константы D₁ и D₂, образуют общее решение соответствующего (3.9) однородного уравнения.

Легко показать, что решение (3.11) удовлетворяет нулевым начальным условиям (2.17) когда ${{D}_{1}} = {{D}_{2}} = 0$. Следовательно, последнее слагаемое в (3.11) является решением сформулированной в предыдущем пункте задачи Коши. Для явного выражения этого решения найдем фундаментальную систему решений $\left\{ {{{f}_{1}},{{f}_{2}}} \right\}$ уравнения (3.9) с нулевой правой частью.

Вид функций ${{f}_{1}}({{\eta }})$ и ${{f}_{2}}({{\eta }})$ зависит от корней характеристического уравнения

Корни уравнения (3.12) даются формулой

где обозначено

В зависимости от значения величины Δ имеем случаи, когда корни (3.13) являются комплексными и сопряженными (Δ < 0), оба корня совпадают и являются действительными (Δ = 0) и случай двух различных действительных корней (Δ > 0).

Соответствующие этим корням фундаментальные решения имеют следующий вид (${{\omega }} \equiv \sqrt {\left| {{\Delta }} \right|} $):

Подставляя найденные фундаментальные системы решений (3.15)–(3.17) в (3.11) и проводя элементарные вычисления, получаем решение исходной задачи Коши в каждом из возникающих здесь случаев, а именно

В формулы (3.18)–(3.20) необходимо подставить значение правой части уравнения (3.9), выраженное формулой (3.7) при произвольном давлении на поверхности полости и (3.8), если это давление постоянно.

Условия наличия разных типов корней характеристического уравнения и различного представления решения задачи Коши, выраженные выше через равенство нулю или знак величины ${{\Delta }}$, полезно представить в виде условий на величину скорости расширения полости. Подставляя в (3.14) выражение (3.10) для $V_{1}^{ * }$ и затем (2.15) для ${{\beta }}$, легко установить эквивалентность следующих неравенств:

где

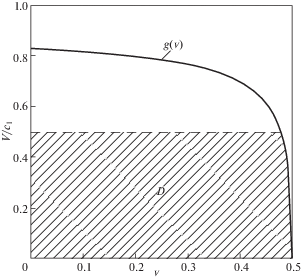
На рис. 1 представлен график функции ${V \mathord{\left/ {\vphantom {V {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}} = g({{\nu }})$, задаваемой формулой (3.22), в зависимости от коэффициента Пуассона грунта ${{\nu }}$, изменяющегося на интервале от нуля до 0.5. Графиком является кривая, проходящая через точки $g(0) = 2(\sqrt 2 - 1) \approx $ 0.82 и $g(0.5) = 0$. Если относительная скорость расширения полости ${V \mathord{\left/ {\vphantom {V {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}$принадлежит области под кривой $g({{\nu }})$, то имеется два комлексно-сопряженных корня характеристического уравнения (3.12), в точках самой кривой имеется один кратный действительный корень этого уравнения и в точках области между кривой $g({{\nu }})$ и горизонтальной прямой ${V \mathord{\left/ {\vphantom {V {{{c}_{1}} = 1}}} \right. \kern-0em} {{{c}_{1}} = 1}}$, определяющей предельное значение скорости расширения полости, существуют два различных действительных корня уравнения (3.12). Как видно из рис. 1, неверно считать, что при малых отношениях ${V \mathord{\left/ {\vphantom {V {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}$ имеются только комплексные корни: при коэффициенте Пуассона среды ${{\nu }}$ близких к 0.5 (слабо сжимаемые среды) и при малых значениях ${V \mathord{\left/ {\vphantom {V {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}$ существуют действительные корни уравнения (3.12). Отметим здесь сразу же, что в силу особенности использованного метода, Дж. Ахенбах и С. Сан [1] при приближенном рассмотрении данной задачи смогли выписать только решение, соответствующее комплексным корням. Потому полученное ими решение не является полным даже для малых значений ${V \mathord{\left/ {\vphantom {V {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}$. Это обстоятельство тем более важно, поскольку динамический коэффициент Пуассона (при вибрациях) для песчаных и глинистых грунтов оказывается несколько большим, чем при статических испытаниях и для глинистых грунтов он может принимать значения из интервала $0.40{\kern 1pt} \div {\kern 1pt} 0.50$ ([17], с. 354).

Чтобы найти окончательную форму решений необходимо в формулы (3.18)–(3.20) подставить выражение (3.7) (или (3.8)) для правой части $F({{\eta }})$ и вернуться от переменной ${{\eta }}$ и функции $f({{\eta }})$ к переменной s и функции (потенциалу перемещений среды) $\Phi (r,t)$, определенными формулами (2.13).

В некоторых частных случаях задания закона изменения давления P(t) на границе полости интегралы в (3.18)–(3.20) вычисляются в конечном виде, что приводит к простым аналитическим решениям, удобным для исследования. Имея ввиду сравнение точного решения с приближенным решением Дж. Ахенбаха и С. Сана [1], ниже мы получим окончательную форму решения для случая, когда давление P(t) в полости является постоянным, т.е. $P(t) = {{P}_{0}}H(t)$. Тогда правая часть в уравнении (3.9) , входящая в решения (3.18)–(3.20), определена формулой (3.8). Подставляя это выражение для $F({{\eta )}}$ в (3.18) и интегрируя, получаем в области (а), определенной в (3.21),

Используя формулы (3.14), введем обозначения

Возвращаясь теперь в решении (3.23) от переменной ${{\eta }}$ к переменной τ по формуле (3.6), а затем и к переменной s и потенциалу перемещений $\Phi $, определенными соотношениями (2.13), имеем окончательно

Заметим здесь же, что в случае полости постоянного радиуса (V = 0) корни характеристического уравнения (3.12) являются комплексно сопряженными и преобразование (3.6) является тождественным, т.е. ${{\eta }} \to {{\tau }}$ при $V \to 0$ $({{V}_{1}} \to 0)$.

Следовательно, решение задачи с полостью постоянного радиуса получается непосредственно из решения (3.23), полагая в нем ${{\eta }} = s$ и $V_{1}^{ * } = 0$. В результате приходим к известному результату [18] (${{\alpha }}$ такое же, как и в (3.24)).

Таким же образом, вычисляя интегралы, входящие в решения (3.19), (3.20) при $F({{\eta }})$, определяемом выражением (3.8), получаем в замкнутой форме решения и для случаев (b) и (с) из (3.21), а именно

4. О приближенном решении задачи по методу Горна. Сравнение с точным решением. 4.1. Преобразование уравнения к виду, пригодному для применения схемы Горна, недостатки метода. Дж. Ахенбах и С. Сан [1] также, используя автомодельность, сводят проблему о динамическом расширении сферической полости в упругой среде к задаче Коши для уравнения (2.16) при начальных условиях (2.17). Однако, решение последней предлагается искать путем, отличным от предложенного нами в п. 3. Этот путь состоит в переходе в уравнении (2.16) к новой неизвестной функции $w(\tau )$, определяемой преобразованием

Здесь и далее, если обозначения работы Дж. Ахенбаха и С. Сана не совпадают с нашими, то они заменены на обозначения, принятые в настоящей работе. Напомним, что переменная τ определена равенством (2.14) и что $\bar {a}({{\tau }}) = a(t({{\tau }})).$

В результате перехода к новой неизвестной функции по формуле (4.1) уравнение (2.16) сводится к следующему

Проблема состоит в нахождении фундаментальной системы решений однородного уравнения (4.2), с правой частью равной нулю. Когда эта система решений найдена, решение задачи Коши для неоднородного уравнения (4.2) выписывается так, как указано выше в п. 3.2 (формулой (3.11)).

Целью преобразования уравнения (2.16) к виду (4.2) является использование для его решения метода асимптотического интегрирования, предложенного Горном [19] и получившего дальнейшее развитие в ряде статей [20] и монографии [21]. Как следует из этих работ, метод применим к уравнениям типа (4.2) без правой части, когда коэффициент при $w({{\tau }})$ (выражение в квадратных скобках) содержит большой параметр $h$ и имеет форму

Дж. Ахенбах и С. Сан приняли в своей работе за большой параметр скорость распространения объемных волн c₁. Формально это приводит в данной задаче к правильному результату (в области $D$ рис. 1, как будет установлено ниже), однако, принятие за большой параметр размерной величины не является корректным и не выявляет области применимости метода.

Хотя безразмерный параметр $h$ (который при определенных условиях может рассматриваться как большой) может быть введен строго и при произвольном законе расширения полости, мы ограничимся случаем полости, расширяющейся с постоянной скоростью, когда имеется возможность сравнения приближенных результатов, получаемых по методу большого параметра с точным решением, представленным в предыдущих разделах.

В случае линейно расширяющейся полости в уравнении (4.2) нужно положить

в силу соотношений (3.3)–(3.5). Тогда, выполняя в уравнении (4.2) замену ${{\tau }} \to {{{{\tau }}}_{1}}$, ${{{{\tau }}}_{1}} = {{a}_{0}} + {{V}_{1}}{{\tau }}$, $\frac{\partial }{{\partial {{\tau }}}} = {{V}_{1}}\frac{\partial }{{\partial {{{{\tau }}}_{1}}}}$ приводим однородное уравнение (4.2) к виду

В этом месте, прежде всего, отметим следующее. Хотя авторы работы [1] рассмотрели подробно случай линейного расширения полости в качестве основного примера на приложение метода Горна, они, однако, не заметили, что соответствующее линейному расширению однородное уравнение (4.5) (которое в работе [1] не выписано) является уравнением типа Эйлера, допускающим точное решение (см., например, [22], часть 2, уравнение 2.148). Кроме того, из вида коэффициента перед $w$ в уравнении (4.5) следует, что большой параметр при расширении полости с постоянной скоростью может быть введен строго как отношение

т.е. как отношение скорости распространения объемных волн в грунте к приведенной скорости расширения полости (4.4), вместо некорректного принятия за большой параметр размерной скорости распространения упругих волн c₁. Это позволило бы определить область применимости приближенного метода, о чем Дж. Ахенбах и С. Сан ничего не смогли сказать в своей работе. При введении большого параметра формулой (4.6), коэффициент при w записывается в виде имеющим форму (4.3) с ${{{{\chi }}}_{2}} = 0$ и уравнение (4.5) подпадает под тип, к которому можно применить метод Горна (при $h \gg 1$). Однако использование данного метода в нашей задаче имеет следующие ограничения, которые заслуживают быть отмеченными.

1. Точное решение уравнения (4.5) имеет (три) различные формы в случаях, когда

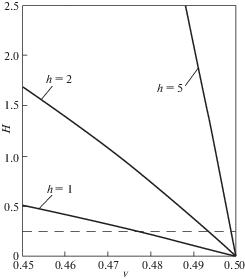
Эти формы как раз соответствуют решениям (3.15)–(3.17), полученным в п. 3 в случаях комплексных и действительных корней характеристического уравнения, а условия (4.8) совпадают с условиями существования таких корней. Между тем метод Горна позволяет выписать только решение, соответствующее случаю (a) из (4.8), что и выполнено в работе [1]. Однако, сколь бы большим ни был параметр h, в силу определения функции $H(h,{{\nu }})$ формулой (4.7), существует, хотя и весьма малая, левая полуокрестность точки ${{\nu }} = 0.5$, в которой $H(h,{{\nu }}) < {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}$ и на левой границе которой $H(h,{{\nu }})$ = 1/4; на рис. 2, где изображены функции $H(1,{{\nu }})$, $H(2,{{\nu }})$ и $H(5,{{\nu }})$ названная окрестность определяется интервалами, на которых графики этих функций лежат ниже пунктирной прямой. На этих интервалах и в их левых концах решение имеет другие представления и метод Горна не применим (т.е. решения (3.26), (3.27) не могут быть получены по методу Горна).

2. В области, где решение в форме метода Горна правомерно (т.е. там, где функция $H(h,{{\nu }})$ принимает значения большие, чем 0.25), использование метода ограничено другим условием, а именно требованием, что параметр h должен быть большим или, по крайней мере, большим единицы. Таким образом, метод Горна применим и приближенное решение Дж. Ахенбаха и С. Сана для полости, расширяющейся с постоянной скоростью, справедливо, когда ${{\nu }}$ и ${V \mathord{\left/ {\vphantom {V {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}$ определены точками заштрихованной на рис. 1 области $D$.

Имея ввиду эти ограничения, изложим в краткой форме способ получения решения и приведем полученный в [1] результат для линейного расширения полости. Решение уравнения (4.5) с коэффициентом при $w$, определенным формулой (4.7) и содержащим большой параметр $h$, в методе Горна разыскивается в форме [21]

Подстановка представления (4.9) в уравнение (4.5) и приравнивание членов при одинаковых степенях $h$, приводит к уравнениям для неизвестных функций, содержащихся в этом представлении. В частности, приравнивание коэффициентов при h² и $h$ дает следующие уравнения для первого приближения с Ψ = 1:

Уравнение (4.11) есть линейное уравнение относительно ${\text{Q}}$. Интегрируя это уравнение с учетом алгебраического уравнения (4.10) для ${{\omega '}}$ и подставляя результат в (4.9), получаем общее решение уравнения (4.5) в первом приближении

где ${{{{\chi }}}_{0}}$ и ${{{{\chi }}}_{1}}$ определены в (4.10) и (4.11).

Находя теперь, пользуясь (4.11), общее решение неоднородного уравнения (4.2) (так же, как и в п. 3) и константы ${{D}_{1}}$, ${{D}_{2}}$ из однородных начальных условий, приходим в случае постоянного давления на границе полости к результату Дж. Ахенбаха и С. Сана [1], который в наших обозначениях имеет вид

Все величины здесь имеют те же значения, что и в полученном в п. 3 точном решении (3.25), а через B₁ обозначена величина

4.2. Сравнение приближенного решения с точным. Как видно, приближенное выражение (4.13) для потенциала перемещений, полученное по методу Горна, отличается в области его справедливости D (рис. 1) от точного решения (3.25) только тем, что в него входит величина ${{B}_{1}}$, определенная формулой (4.14), вместо $B$ в точном решении.

При сравнении точного и приближенного решений примем для коэффициента Пуассона грунта численное значение ${{\nu }} = 0.3$; тогда параметры ${{\alpha }}$ и ${{\beta }}$, от которых зависят константы в уравнениях (3.25) и (4.13), принимают численные значения

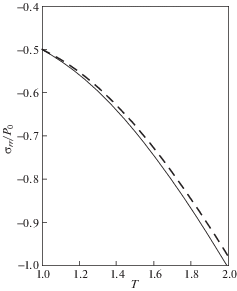
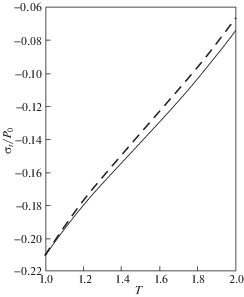
Близость приближенного и точного решений демонстрируют графики радиальных и окружных напряжений, представленные на рис. 3, 4. Напряжения вычисляются в точке с координатой $r = {{r}_{0}} = 2{{a}_{0}}$ по формулам (2.5), (2.10) путем вполне элементарных, но довольно длинных выкладок, и даны как функции от аргумента $T \in [1,2]$:

где $t* = \frac{t}{{{{{{a}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}} {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}}} = {{{{c}_{1}}t} \mathord{\left/ {\vphantom {{{{c}_{1}}t} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}}$ есть безразмерное время, отнесенное к времени прохождения первоначального радиуса полости объемной упругой волной и отсчитываемое от момента времени $t_{1}^{ * } = 1$ прибытия волны в точку $r = 2{{a}_{0}}$ до момента $t_{2}^{ * } = \frac{{{{{{a}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}} V}} \right. \kern-0em} V}}}{{{{{{a}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}} {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}}} = {{{{c}_{1}}} \mathord{\left/ {\vphantom {{{{c}_{1}}} V}} \right. \kern-0em} V}$ поглощения этой точки фронтом разрушения (расширяющейся полостью).

Изображенные на рис. 3, 4 графики радиальных и окружных напряжений относятся к значению параметра h = 1 (или ${{{{V}_{1}}} \mathord{\left/ {\vphantom {{{{V}_{1}}} {{{c}_{1}} = 1}}} \right. \kern-0em} {{{c}_{1}} = 1}}$, ${V \mathord{\left/ {\vphantom {V {{{c}_{1}} = 0.5}}} \right. \kern-0em} {{{c}_{1}} = 0.5}}$), т.е. к случаю, когда h не является большим параметром и формально метод Горна не применим. При этом, сплошные линии соответствуют точному решению, а штриховые – приближенному. Тот факт, что даже в этом случае приближенное решение весьма близко к точному объясняется тем, что, согласно формулам (3.24) и (4.14), $B \approx {{B}_{1}}$ и ${{\tilde {\Phi }}}$ служит приближением для Φ, если ${{{\beta }} \mathord{\left/ {\vphantom {{{\beta }} {{{{{\alpha }}}^{2}}h < 1}}} \right. \kern-0em} {{{{{\alpha }}}^{2}}h < 1}}$ или $h > {{{\beta }} \mathord{\left/ {\vphantom {{{\beta }} {{{{{\alpha }}}^{2}}}}} \right. \kern-0em} {{{{{\alpha }}}^{2}}}}$. Последнее условие приводит к тому, что для численных значений параметров (4.15) близость решений, на самом деле, имеет место при $h > \; \approx {\kern 1pt} 0.7$ или при ${V \mathord{\left/ {\vphantom {V {{{c}_{1}} < \; \approx {\kern 1pt} 0.58}}} \right. \kern-0em} {{{c}_{1}} < \; \approx {\kern 1pt} 0.58}}$ в силу определения (4.6), а не только когда ${V \mathord{\left/ {\vphantom {V {{{c}_{1}} < 0.5}}} \right. \kern-0em} {{{c}_{1}} < 0.5}}$ и метод Горна применим (рис. 1). Как показывают расчеты, для больших значений параметра h решения в напряжениях еще меньше отличаются друг от друга.

Работа является частью материала, доложенного на семинаре “Лаборатории прочности и разрушения материалов и конструкций” в Институте проблем механики РАН и семинаре по “Механике деформируемого твердого тела” в Институте механики Московского университета. Авторы выражают благодарность участникам этих семинаров, в особенности академику РАН Горячевой И.Г., профессору Шифрину Е.И. и профессору Тарлаковскому Д.В. за полезные замечания.