Известия РАН. Механика твердого тела, 2021, № 3, стр. 128-142
ЧИСЛЕННО-АНАЛИТИЧЕСКИЙ МЕТОД ПОИСКА АВТОРОТАЦИЙ МЕХАНИЧЕСКОЙ СИСТЕМЫ С ДВУМЯ ВРАЩАТЕЛЬНЫМИ СТЕПЕНЯМИ СВОБОДЫ
Л. А. Климина a, *, А. А. Мастерова a, В. А. Самсонов a, Ю. Д. Селюцкий a
a НИИ механики МГУ
Москва, Россия
* E-mail: klimina@imec.msu.ru
Поступила в редакцию 20.05.2020
После доработки 14.06.2020
Принята к публикации 03.07.2020
Аннотация
Рассматривается механическая система с двумя вращательными степенями свободы. Математическая модель представлена в форме динамической системы четвертого порядка. Предложен численно-аналитический итерационный метод поиска близких к периодическим решений, соответствующих режимам авторотации механической системы. В качестве нулевого приближения используются неподвижные точки (в том числе седла) системы, усредненной по двум углам. На каждой итерации численно строятся периодические решения двух вспомогательных подсистем с использованием подхода, родственного методу Андронова–Понтрягина. При условии сходимости метода получается набор периодических функций, которые предположительно приближенно описывают близкие к периодическим траектории, в частности, квазипериодические. Обсуждаются условия применимости подхода. Предложенный метод проиллюстрирован на примере отыскания авторотационных режимов двух взаимодействующих роторов Савониуса.
1. Введение. Рассмотрим автономную механическую систему с двумя вращательными степенями свободы. В частности, такие системы возникают при моделировании двухроторных ветроэнергетических установок. Существенную фундаментальную и прикладную значимость имеет описание установившихся движений таких систем.
Пусть требуется найти режимы движения, при которых по обеим угловым координатам происходит авторотация. Под авторотацией будем подразумевать режим движения, на котором обе угловые скорости сколь угодно долго не меняют знак (для системы с одной степенью свободы термин “авторотация” введен, например, в [1]).
Рассмотрим случай, когда обе угловые координаты явно входят в уравнения движения. Соответствующая автономная динамическая система имеет четвертый порядок. Режимам авторотации могут отвечать периодические, а также близкие к периодическим решения динамической системы.
Для поиска периодических решений можно принять за новое время одну из угловых координат и рассмотреть задачу поиска периодического (по этой координате) решения неавтономной динамической системы. Тогда в случае наличия соответствующего малого параметра можно использовать классический метод усреднения [2]. Если же малый параметр отсутствует, можно использовать, например, обобщение [3] метода усреднения [2] или другие методы поиска периодических решений неавтономных динамических систем: метод пристрелки с применением прямого численного интегрирования, проекционные методы, методы, основанные на продолжении по параметру решений порождающей системы, и другие подходы [4–8].
В данной работе остановимся на задаче поиска режимов авторотации, которым отвечают не периодические, а в некотором смысле близкие к периодическим, например, квазипериодические решения динамической системы. Если при этом обе угловые скорости можно считать медленными переменными, а углы – быстрыми, то естественно в качестве первого приближения для авторотаций рассмотреть неподвижные точки системы, усредненной по двум углам (как, например, в [9] для задачи о вращении тела в среде). Тем самым, на первом этапе задача сводится к рассмотрению “порождающей системы”, в которой обе координаты циклические. Подробно такой подход описан в работах [2, 10–14].
При отсутствии малого параметра можно попытаться использовать неподвижные точки “порождающей” системы, чтобы при помощи численно-аналитических методов искать установившиеся решения полной системы “вблизи” таких точек. На практике этот подход хорошо работает для многих задач. Например, в работе [15] он реализован на основе продолжения по параметру и метода сечений Пуанкаре. При этом обнаружены не только аттракторы, но и такие квазипериодические решения, которые соответствуют седловым точкам усредненной системы и не являются притягивающими ни в прямом, ни в обратном времени.
Отметим, что систематизированный анализ методов поиска квазипериодических решений и описание соответствующих исторических фактов приведены в [16]. При этом выделены такие направления, как метод спектрального баланса [17, 18], который расширяет метод гармонического баланса (Фурье–Галеркина); метод обобщенных сечений Пуанкаре [19]; подходы, опирающиеся на вычисление инвариантных торов, в том числе метод ускоренной сходимости [20, 21], непрерывная по Липшицу аппроксимация нормального расслоения [22], естественная параметризация [16, 23]. Помимо этого можно привести примеры относительно новых подходов: метод гармонического баланса с переменными коэффициентами [24]; комбинация метода гармонического баланса и продолжения по длине дуги [25]; комплексификация c выделением быстрой и медленной компонент и усреднением [26], продолжение по параметру порождающего решения усредненной системы [15], комбинаторно-топологический анализ [27], численные алгоритмы построения седловых инвариантных торов [28].
В настоящей работе предлагается метод поиска близкого к периодическому решения, “порожденного” неподвижной точкой усредненной системы, но при этом используется не численное продолжение по параметру, а процедура, сочетающая усреднение и итерационный алгоритм построения периодических решений, предложенный в [29]. Наличие малого параметра не предполагается. В результате применения метода формируется набор торов в фазовом пространстве; около каждого такого тора можно ожидать существования близкой к периодической траектории.
Метод отличается простотой численной реализации по сравнению с перечисленными выше подходами. Но при этом он применим только к системам определенного вида.
Рассматривается пример применения предложенной методики для отыскания авторотаций в модели ветроэнергетической установки, состоящей из двух соосных роторов Савониуса. При этом для описания зависимости аэродинамического момента, действующего на ротор Савониуса, от угла поворота ротора используется функция, построенная на основе аппроксимации экспериментальных данных [30]. Найдены приближения для режимов авторотации ветротурбины. Дана оценка скорости сходимости метода.
2. Постановка задачи. Рассматривается автономная неконсервативная механическая система с двумя вращательными степенями свободы. Пусть в безразмерных переменных динамика системы описывается уравнениями следующего вида (точкой обозначена производная по безразмерному времени):
(2.1)
$\begin{gathered} {{{\dot {\varphi }}}_{i}} = {{\omega }_{i}},\quad i = 1,\;2 \\ {{{\dot {\omega }}}_{1}} = a\left( {{{f}_{1}}({{\varphi }_{1}},{{\omega }_{1}}) - {{\omega }_{2}}{{q}_{1}}({{\varphi }_{1}},{{\omega }_{1}})} \right) \\ {{{\dot {\omega }}}_{2}} = a\left( {{{f}_{2}}({{\varphi }_{2}},{{\omega }_{2}}) - {{\omega }_{1}}{{q}_{2}}({{\varphi }_{2}},{{\omega }_{2}})} \right) \\ \end{gathered} $Здесь φi – обобщенные координаты (углы), ${{\omega }_{i}}$ – соответствующие обобщенные скорости (угловые скорости); $a$ – параметр, характеризующий инерционные свойства, который рассматривается как бифуркационный параметр модели и не предполагается малым. Все функции в правой части $2\pi $-периодические по переменным φi. Дополнительно предположим, что ${{\omega }_{i}}{{q}_{i}}({{\varphi }_{i}},{{\omega }_{i}}) > 0$ при ${{\omega }_{i}} \ne 0$.
Уравнения вида (2.1) возникают, например, в некоторых задачах ветроэнергетики. Одна из таких задач будет рассмотрена подробно далее в примере реализации метода.
Задача состоит в том, чтобы приближенно описать посредством периодических функций те траектории системы (2.1), которые в некотором смысле близки к периодическим, например, являются квазипериодическими. Будем рассматривать систему (2.1) в области $G = \left\{ {{{\omega }_{1}} \in \left[ {{{A}_{1}},{{B}_{1}}} \right],\;{{\omega }_{2}} \in \left[ {{{A}_{2}},{{B}_{2}}} \right]} \right\}$ фазового пространства, где ${{A}_{i}}$, ${{B}_{i}}$ – некоторые положительные значения. Случаи, когда обе или одна из переменных ωi отрицательны, можно рассмотреть аналогично. Близким к периодическим траекториям, расположенным в области G, отвечают авторотации механической системы.
Будем искать траектории близкие к периодическим, но не являющиеся периодическими.
3. Система нулевого приближения. Рассмотрим вспомогательную усредненную систему вида:
(3.1)
$\begin{gathered} {{{\dot {\Omega }}}_{1}} = a\left( {{{F}_{1}}({{\Omega }_{1}}) - {{\Omega }_{2}}{{Q}_{1}}({{\Omega }_{1}})} \right),\quad {{F}_{i}}({{\Omega }_{i}}) = {{(2\pi )}^{{ - 1}}}\int\limits_0^{2\pi } {{{f}_{i}}(\varphi ,{{\Omega }_{i}})d\varphi } \\ {{{\dot {\Omega }}}_{2}} = a\left( {{{F}_{2}}({{\Omega }_{2}}) - {{\Omega }_{1}}{{Q}_{2}}({{\Omega }_{2}})} \right),\quad {{Q}_{i}}({{\Omega }_{i}}) = {{(2\pi )}^{{ - 1}}}\int\limits_0^{2\pi } {{{q}_{i}}(\varphi ,{{\Omega }_{i}})d\varphi } \\ \end{gathered} $Здесь ${{\Omega }_{i}}$ отвечают переменным ωi системы (2.1). Функции ${{F}_{i}}({{\Omega }_{i}})$ и ${{Q}_{i}}({{\Omega }_{i}})$ – усредненные по соответствующим углам слагаемые правой части системы (2.1).
Отметим, что, по крайней мере, при $a \ll 1$ можно установить соответствие между поведением переменных ωi в системе (2.1) и переменных ${{\Omega }_{i}}$ в системе (3.1). При $a \ll 1$ в области $G$ оба угла φi являются быстрыми переменными, а безразмерные угловые скорости ωi – медленными. Формальное усреднение по быстрым переменным (без учета влияния резонансов) приводит к системе (3.1). Более того, и в окрестности резонансного соотношения частот усреднение тоже приводит к системе (3.1). Это легко показать, следуя методике, описанной в [10, 13]: в окрестности резонанса можно ввести дополнительную медленную переменную и усреднить систему по единственной быстрой переменной ([2]), при этом потребуется использовать то, что каждое слагаемое в правой части системы (2.1) зависит не более чем от одной из переменных ${{\varphi }_{i}}$. В работе [31] приведены соответствующие выкладки для частного случая системы (2.1).
В силу вышесказанного для системы (2.1) при $a \ll 1$ и начальных условиях из области $G$ вид усредненной системы вдали от резонансов и вблизи резонансов совпадает с (3.1). Следовательно, если для системы (2.1) выполнены условия теоремы [10], то на интервале времени порядка a–1 отличие между решением ${{\omega }_{i}}(t)$ системы (2.1) и решением ${{\Omega }_{i}}(t)$ системы (3.1) с аналогичными начальными условиями имеет порядок a.
Вопрос о соответствии между решениями систем (2.1) и (3.1) на бесконечном интервале времени в общем случае остается открытым. Однако естественно рассмотреть неподвижные точки системы (3.1) в качестве нулевого приближения для периодических и близких к периодическим траекторий системы (2.1). Например, подобный подход используется в работах [9, 15].
4. Описание метода построения приближенного решения. Предложим метод построения приближения для близкого к периодическому решения $({{\hat {\varphi }}_{1}}(t),{{\hat {\varphi }}_{2}}(t),{{\hat {\omega }}_{1}}(t),{{\hat {\omega }}_{2}}(t))$ системы (2.1), если такое решение существует.
Метод состоит из трех этапов:
1) построение вспомогательных систем, отыскание $2\pi $-периодических по φi траекторий этих систем;
2) выбор тех периодических траекторий вспомогательных систем, которым могут соответствовать близкие к периодическим решения системы (2.1);
3) проверка наличия соответствия между найденными периодическими траекториями вспомогательных систем и близкими к периодическим траекториями системы (2.1).
Опишем каждый этап подробно.
4.1. Вспомогательные системы и их периодические траектории. Рассмотрим вспомогательную систему вида:
(4.1)
$\begin{gathered} {{{\dot {\varphi }}}_{1}} = {{\omega }_{1}} \\ {{{\dot {\omega }}}_{1}} = a\left( {{{f}_{1}}({{\varphi }_{1}},{{\omega }_{1}}) - {{\Omega }_{2}}{{q}_{1}}({{\varphi }_{1}},{{\omega }_{1}})} \right) \\ \end{gathered} $Здесь значение ${{\Omega }_{2}}$ – константа (параметр). Система (4.1) относится к классу, рассмотренному в [29]. При изменении параметра ${{\Omega }_{2}}$ происходит поворот векторного поля системы (4.1) (используем определение поворота поля, данное в [1, 32]). Будем рассматривать различные начальные значения ${{\omega }_{{10}}}$ переменной ${{\omega }_{1}}$, лежащие на отрезке $\left[ {{{A}_{1}},{{B}_{1}}} \right]$.
Для заданного значения ${{\omega }_{{10}}}$ будем искать такое значение ${{\Omega }_{2}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{2}}({{\omega }_{{10}}})$, при котором система (4.1) имеет $2\pi $-периодическую по ${{\varphi }_{1}}$ траекторию ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{1}}({{\varphi }_{1}};{{\omega }_{{10}}})$, проходящую через точку ${{\varphi }_{1}} = 0$, ${{\omega }_{1}} = {{\omega }_{{10}}}$. В силу свойств поворота векторного поля такое значение ${{\Omega }_{2}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{2}}({{\omega }_{{10}}})$, если существует, единственно. Для отыскания ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{2}}({{\omega }_{{10}}})$ можно воспользоваться разнообразными методами (в том числе методом стрельбы, методом гармонического баланса, методом [3]). В настоящей работе используем метод [29], который основан на построении последовательности “порождающих” гамильтоновых систем. На нулевой итерации метода [29] приближение для ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{2}}({{\omega }_{{10}}})$ задается следующим образом:
На каждой итерации алгоритма [29] приближение для значения ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{2}}({{\omega }_{{10}}})$ определяется как явная функция от ${{\omega }_{{10}}}$. Если для некоторых ${{\omega }_{{10}}}$ не удалось построить ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{2}}({{\omega }_{{10}}})$ (не сошелся итерационный процесс, примененный для поиска), то при таких значениях аргумента функция ${{\Omega }_{2}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{2}}({{\omega }_{{10}}})$ не определена.
В результате выполнения итерационной процедуры [29] для каждого ${{\omega }_{{10}}}$, при котором найдена ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{2}}({{\omega }_{{10}}})$, будет построена соответствующая $2\pi $-периодическая по углу ${{\varphi }_{1}}$ траектория ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{1}}({{\varphi }_{1}};{{\omega }_{{10}}})$ системы (4.1). Вычислим среднее по времени за период значение переменной ${{\omega }_{1}}$ вдоль этой траектории (отметим, что это значение в общем случае отличается от среднего по углу):
Итак, пусть на отрезке ${{\omega }_{{10}}} \in \left[ {{{A}_{1}},{{B}_{1}}} \right]$ построены функции ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{2}}({{\omega }_{{10}}})$ и ${{\bar {\Omega }}_{1}}({{\omega }_{{10}}})$ (возможно, не везде определены). Рассмотрим на плоскости $({{\Omega }_{1}},{{\Omega }_{2}})$ кривую Γ1 = = $\{ ({{\Omega }_{1}},{{\Omega }_{2}}){\text{:}}\;{{\Omega }_{1}} = {{\bar {\Omega }}_{1}}({{\omega }_{{10}}})$, ${{\Omega }_{2}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{2}}({{\omega }_{{10}}})\} $, заданную параметрически. В силу свойств поворота векторного поля кривую ${{\Gamma }_{1}}$ можно представить в виде некоторой явной функции ${{\Omega }_{2}} = {{\tilde {\Omega }}_{2}}({{\Omega }_{1}})$, при этом каждому значению аргумента ${{\Omega }_{1}}$ отвечает не более одного значения ${{\Omega }_{2}}$ (доказательство аналогично утверждению из [33]).
Аналогично рассмотрим различные начальные значения ${{\omega }_{{20}}} \in \left[ {{{A}_{2}},{{B}_{2}}} \right]$ переменной ${{\omega }_{2}}$. Построим функции ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{1}}({{\omega }_{{20}}})$ и ${{\bar {\Omega }}_{2}}({{\omega }_{{20}}})$, вводя для переменных ${{\varphi }_{2}}$ и ${{\omega }_{2}}$ систему, аналогичную (4.1), и используя для нее метод [29]. На плоскости $({{\Omega }_{1}},{{\Omega }_{2}})$ эти функции задают параметрически кривую ${{\Gamma }_{2}} = \{ ({{\Omega }_{1}},{{\Omega }_{2}}){\text{:}}\;{{\Omega }_{1}} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{1}}({{\omega }_{{20}}}),\;{{\Omega }_{2}} = {{\bar {\Omega }}_{2}}({{\omega }_{{20}}})\} $, которая может быть описана явной однозначной функцией ${{\Omega }_{1}} = {{\tilde {\Omega }}_{1}}({{\Omega }_{2}})$.
4.2. Выбор “особых” траекторий. Каждая точка $(\Omega _{1}^{*},\Omega _{2}^{*})$ пересечения кривых ${{\Gamma }_{1}}$ и ${{\Gamma }_{2}}$, полученных в результате решения подзадачи, определяет пару $(\omega _{{10}}^{*},\omega _{{20}}^{*})$:
(4.2)
$\begin{gathered} {{{\bar {\Omega }}}_{1}}(\omega _{{10}}^{*}) = {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }}_{1}}(\omega _{{20}}^{*}) \\ {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }}_{2}}(\omega _{{10}}^{*}) = {{{\bar {\Omega }}}_{2}}(\omega _{{20}}^{*}) \\ \end{gathered} $Пусть значения $(\omega _{{10}}^{*},\omega _{{20}}^{*})$ удовлетворяют системе (4.2). Тогда можно ожидать, что в системе (2.1) существует близкая к периодической траектория $({{\hat {\varphi }}_{1}}(t),{{\hat {\varphi }}_{2}}(t),{{\hat {\omega }}_{1}}(t),{{\hat {\omega }}_{2}}(t))$, проекции которой на плоскости $({{\varphi }_{i}},{{\omega }_{i}})$ расположены в окрестностях кривых ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{i}}({{\varphi }_{i}};\omega _{{i0}}^{*})$.
Рассмотрим некоторую пару $(\Omega _{1}^{{**}},\Omega _{2}^{{**}})$, для которой определены функции ${{\tilde {\Omega }}_{2}}(\Omega _{1}^{{**}})$, ${{\tilde {\Omega }}_{1}}(\Omega _{2}^{{**}})$ и при этом точка $(\Omega _{1}^{{**}},\Omega _{2}^{{**}})$ не является общей точкой кривых ${{\Gamma }_{1}}$ и ${{\Gamma }_{2}}$ (при $a \ll 1$ это означает, что точка $(\Omega _{1}^{{**}},\Omega _{2}^{{**}})$ не является неподвижной точкой системы (3.1)). Можно ожидать, что в системе (2.1) отсутствует близкая к периодической траектория, на которой средние по времени значения переменных ${{\omega }_{1}}$ и ${{\omega }_{2}}$ равны $\Omega _{1}^{{**}}$ и $\Omega _{2}^{{**}}$. Это предположение основано на том, что соответствующее значение ${{\Omega }_{2}} = \Omega _{2}^{{**}}$ приводит во вспомогательной системе вида (4.1) к росту/убыванию среднего значения ${{\Omega }_{1}}$ переменной ${{\omega }_{1}}$.
Замечание 1. Предложенный алгоритм не предназначен для отыскания периодических траекторий системы (2.1), поскольку учитывает только усредненные перевязки между уравнениями без учета согласованного изменения фазовых координат, свойственного периодическим решениям.
Замечание 2. Отметим, что в случае $a \ll 1$ алгоритм [29] сводится только к нулевой итерации, которая представляет собой не что иное, как применение метода Андронова–Понтрягина [1, 34]. В результате при $a \ll 1$ получаем: ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{2}}({{\omega }_{{10}}}) = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Omega } }_{{20}}}$, ${{\bar {\Omega }}_{1}}({{\omega }_{{10}}}) = {{\omega }_{{10}}}$ и аналогично для ${{\omega }_{{20}}}$. Таким образом, в случае $a \ll 1$ кривая ${{\Gamma }_{i}}$ представляет собой кривую, на которой обращается в нуль правая часть $i$-го уравнения системы (3.1). Тем самым, при $a \ll 1$ предложенный алгоритм сводится к поиску неподвижных точек системы (3.1).
Замечание 3. Пусть в точке $(\Omega _{1}^{*},\Omega _{2}^{*})$ определены значения производных α1 = = ${{d{{{\tilde {\Omega }}}_{2}}} \mathord{\left/ {\vphantom {{d{{{\tilde {\Omega }}}_{2}}} {d{{\Omega }_{1}}}}} \right. \kern-0em} {d{{\Omega }_{1}}}}$, ${{{{\alpha }_{2}} = d{{{\tilde {\Omega }}}_{1}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}} = d{{{\tilde {\Omega }}}_{1}}} {d{{\Omega }_{2}}}}} \right. \kern-0em} {d{{\Omega }_{2}}}}$. Если выполнено ${{\alpha }_{1}} < 0$, ${{\alpha }_{2}} < 0$, ${{\alpha }_{1}}{{\alpha }_{2}} > 1$, то будем условно называть такую точку $(\Omega _{1}^{*},\Omega _{2}^{*})$ “притягивающим узлом”. При ${{\alpha }_{1}} > 0$, ${{\alpha }_{2}} > 0$, ${{\alpha }_{1}}{{\alpha }_{2}} > 1$ будем условно называть такую точку $(\Omega _{1}^{*},\Omega _{2}^{*})$ “неустойчивым узлом” (замена времени $t$ на $ - t$ делает эту точку “притягивающим узлом”). При ${{\alpha }_{1}}{{\alpha }_{2}} < 1$ будем условно называть точку $(\Omega _{1}^{*},\Omega _{2}^{*})$ “седлом”. В случае $a \ll 1$ таким точкам отвечают неподвижные точки системы (3.1), в прямом смысле являющиеся точками соответствующих типов. Нетрудно показать, что неподвижные точки типа центра и фокуса в системе (3.1) отсутствуют.
4.3. Этап проверки. Пусть построены траектории ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{i}}({{\varphi }_{i}};\omega _{{i0}}^{*})$ систем вида (4.1). Проверим численно, существует ли в системе (2.1) притягивающее близкое к периодическому решение, проекции которого на фазовые плоскости расположены в окрестностях кривых ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{i}}({{\varphi }_{i}};\omega _{{i0}}^{*})$. Выполним прямое численное интегрирование системы (2.1) с начальными условиями ${{\varphi }_{i}}(0) = 0$, ${{\omega }_{i}}(0) = \omega _{{i0}}^{*}$ на относительно большом интервале времени T. Проверим, остаются ли проекции решения вблизи кривых ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{i}}({{\varphi }_{i}};\omega _{{i0}}^{*})$.
Для проверки наличия в системе (2.1) близкой к периодической траектории, притягивающей в обратном времени, можно выполнить аналогичную процедуру, заменив в системе (2.1) время t на $ - t$.
Отметим, что особый интерес представляет вопрос о решениях, “порожденных” седловыми точками усредненной системы (подобно [15]). Естественно предположить, что в полной системе соответствующее близкое к периодическому решение, если существует, не является притягивающим ни в прямом, ни в обратном времени. Непосредственно наблюдать такое решение при численном интегрировании полной системы в общем случае не представляется возможным. В данной работе используем следующий подход: если для пары ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{i}}({{\varphi }_{i}};\omega _{{i0}}^{*})$ не обнаружена соответствующая ей близкая к периодической траектория системы (2.1), притягивающая в прямом/обратном времени, то проверим, проходит ли в окрестности тора ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{1}}({{\varphi }_{1}};\omega _{{10}}^{*}) \times {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{2}}({{\varphi }_{2}};\omega _{{20}}^{*})$ граница между областями притяжения различных аттракторов. Для этого выполним прямое численное интегрирование системы (2.1) с различными начальными условиями, расположенными в окрестности кривых ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{i}}({{\varphi }_{i}};\omega _{{i0}}^{*})$.
5. Пример применения алгоритма (поиск авторотаций ветротурбины). Проиллюстрируем возможности предложенного алгоритма на примере задачи отыскания авторотаций ветротурбины, состоящей из двух соосных роторов Савониуса. Математическая модель такой системы построена по аналогии с моделями [35–39] для однороторных ветроэнергетических устройств и моделями [31, 40] для двухроторных ветротурбин других типов.
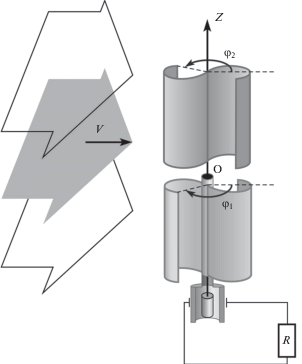
5.1. Описание механической системы, уравнения движения. Рассмотрим механическую систему, которая состоит из двух вертикально-осевых роторов Савониуса. Схема системы представлена на рис. 1. Валы роторов соосны. Лопасти ориентированы так, чтобы воздействие потока поддерживало вращение роторов в противоположных направлениях. Система помещена в поток воздуха постоянной скорости V. На оси одного ротора Савониуса жестко закреплен статор электрогенератора ветроустановки, на оси другого – ротор того же электрогенератора. Генератор подключен к локальной электрической цепи с внешним сопротивлением R.
Ось вращения роторов обозначим Oz. Положительные направления отсчета углов ${{\varphi }_{1}}$ и ${{\varphi }_{2}}$ поворота роторов выберем противоположными друг другу в соответствии с ожидаемыми направлениями вращения роторов. Оба угла отсчитываются от направления скорости V ветра, как показано на рис. 1.
Будем считать, что геометрические размеры и форма роторов одинаковы. Радиус каждого ротора обозначим r. Пусть ${{J}_{1}}$ и ${{J}_{2}}$ – моменты инерции роторов относительно оси Oz.
Будем считать, что аэродинамическое воздействие на каждый из роторов определяется текущими значениями угла поворота и угловой скорости этого ротора и не зависит напрямую от характеристик движения другого ротора. Аэродинамический момент ${{M}_{i}}$ (i = 1, 2), действующий на ротор Савониуса, будем описывать при помощи подхода [39], основанного на квазистатической модели:
Здесь $\rho $ – плотность воздуха, S – площадь, ометаемая ротором, ${{\omega }_{i}}$ – быстроходность ротора (безразмерная угловая скорость). Функция ${{C}_{m}}\left( {{{\varphi }_{i}},{{\omega }_{i}}} \right)$ – безразмерный коэффициент аэродинамического момента, $\pi $-периодический по переменной ${{\varphi }_{i}}$. Эта функция может быть идентифицирована по экспериментальным данным. Соответствующие эксперименты были проведены в НИИ механики МГУ. Результаты экспериментов описаны и проанализированы в статье [30], где построена кусочно-гладкая аппроксимация для функции ${{C}_{m}}\left( {{{\varphi }_{i}},{{\omega }_{i}}} \right)$ аэродинамического момента в широком диапазоне $\omega $. В настоящей статье для того, чтобы избежать необходимости работать с кусочно-гладкими (хотя и непрерывными) функциями, упростим аппроксимационные формулы. Построим гладкую функцию, которая может быть использована для приближенного описания аэродинамического момента при $\omega > 0$:
Электромагнитные процессы в генераторе приводят к тому, что на его ротор и статор действуют равные по величине противоположно направленные моменты. Величина ${{M}_{e}}$ каждого из этих моментов описывается следующим выражением (следуя модели [36]):
Здесь K – коэффициент электромеханического взаимодействия, $\sigma $ – внутреннее сопротивление генератора (положительные константы, определяемые характеристиками генератора).
Введем безразмерное время $\tau = {{r}^{{ - 1}}}Vt$ и запишем уравнения движения системы в безразмерной форме (точкой обозначена производная по безразмерному времени):
(5.1)
$\begin{gathered} {{{\dot {\varphi }}}_{i}} = {{\omega }_{i}},\quad i = 1,\;2 \\ {{{\dot {\omega }}}_{1}} = a({{C}_{m}}({{\varphi }_{1}},{{\omega }_{1}}) - b({{\omega }_{1}} + {{\omega }_{2}})) \\ {{{\dot {\omega }}}_{2}} = ap({{C}_{m}}({{\varphi }_{2}},{{\omega }_{2}}) - b({{\omega }_{1}} + {{\omega }_{2}})) \\ {\text{ }}a = 0.5J_{1}^{{ - 1}}\rho S{{r}^{3}},\quad p = J_{2}^{{ - 1}}J_{1}^{{}},\quad b = 2{{V}^{{ - 1}}}{{\rho }^{{ - 1}}}{{S}^{{ - 1}}}{{r}^{{ - 2}}}{{(\sigma + R)}^{{ - 1}}}K \\ \end{gathered} $Уравнения движения имеют форму системы (2.1). В данном примере f1 = = $\left( {{{C}_{m}}({{\varphi }_{1}},{{\omega }_{1}}) - b{{\omega }_{1}}} \right)$, ${{f}_{2}} = p\left( {{{C}_{m}}({{\varphi }_{2}},{{\omega }_{2}}) - b{{\omega }_{2}}} \right)$, ${{q}_{1}} \equiv b$, ${{q}_{2}} \equiv pb$. Отметим, что при физически осмысленных значениях параметров выполнено a < 1. Параметр b характеризует внешнюю электрическую нагрузку в цепи генератора.
Если значение p близко к единице, то можно ожидать проявления эффектов синхронизации, поскольку при p = 1 система состоит из двух идентичных подсистем. Предложенный метод не предназначен для описания таких эффектов, для этого существуют специальные подходы (например, [41]). Для иллюстрации работы метода положим p = 0.8.
5.2. Анализ системы нулевого приближения. Система (3.1) нулевого приближения имеет в данной задаче вид:
(5.2)
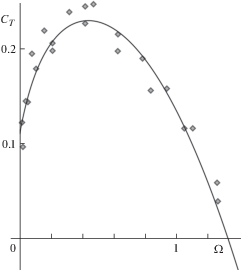
$\begin{array}{*{20}{c}} {{{{\dot {\Omega }}}_{1}} = a({{C}_{T}}({{\Omega }_{1}}) - b({{\Omega }_{1}} + {{\Omega }_{2}})),} \\ {{{{\dot {\Omega }}}_{2}} = ap({{C}_{T}}({{\Omega }_{2}}) - b({{\Omega }_{1}} + {{\Omega }_{2}})),} \end{array}\quad {{C}_{T}}(\Omega ) = \frac{1}{\pi }\int\limits_0^\pi {{{C}_{m}}(\varphi ,\Omega )d\varphi } $График функции ${{C}_{T}}(\Omega )$ усредненного аэродинамического момента приведен на рис. 2; точки соответствуют экспериментальным данным для ротора радиуса $r = 0.2$ м при скоростях ветра 6 и 8 м/с [30].
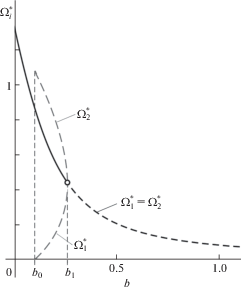
У системы (5.2) для каждой неподвижной точки $(\Omega _{1}^{*},\Omega _{2}^{*})$ существует симметричная ей: $(\Omega _{2}^{*},\Omega _{1}^{*})$. Таким образом, достаточно описать неподвижные точки, в которых $\Omega _{1}^{*} \leqslant \Omega _{2}^{*}$. Зависимости $\Omega _{i}^{*}(b)$ при $0 < \Omega _{1}^{*} \leqslant \Omega _{2}^{*}$ представлены на рис. 3. Пунктиром обозначены семейства седловых точек, сплошной кривой – семейство устойчивых узлов. Черным цветом обозначено семейство неподвижных точек, для которых $\Omega _{1}^{*} = \Omega _{2}^{*}$. Серым цветом – семейство, на котором $\Omega _{1}^{*} < \Omega _{2}^{*}$. Для него существует симметричное семейство с $\Omega _{1}^{*} > \Omega _{2}^{*}$.
При $b > {{b}_{1}}$ у системы (5.2) есть только одна неподвижная точка в области ${{G}_{1}} = \{ {{\Omega }_{i}}$ > 0}, и это седло с $\Omega _{1}^{*}(b) = \Omega _{2}^{*}(b)$. При уменьшении параметра b до значения $b = {{b}_{1}} \approx $ 0.2611 происходит бифуркация: седло распадается на три неподвижные точки: устойчивый узел с $\Omega _{1}^{*}(b) = \Omega _{2}^{*}(b)$ и два седла. Эти седла на плоскости $({{\Omega }_{1}},{{\Omega }_{2}})$ расположены симметрично друг другу относительно прямой ${{\Omega }_{1}} = {{\Omega }_{2}}$. При $b \in ({{b}_{0}},{{b}_{1}})$ существуют три неподвижные точки в области ${{G}_{1}}$. При уменьшении параметра b до значения $b = {{b}_{0}}$ обе седловые точки выходят из области ${{G}_{1}}$ (для одной из них обращается в нуль $\Omega _{1}^{*}$, для симметричной ей: $\Omega _{2}^{*}$).
При $b = 0.262 > {{b}_{1}}$ у системы (5.2) в области ${{G}_{1}}$ есть единственная неподвижная точка – седло с $\Omega _{1}^{*} = \Omega _{2}^{*} \approx 0.433$ – и, соответственно, отсутствуют циклы, расположенные целиком в ${{G}_{1}}$. Таким образом, при таком b и достаточно малом a можно ожидать, что у системы (5.1) нет аттракторов в области, где ${{\omega }_{i}}$ положительны и отделены от нуля.
5.3. Поиск авторотаций при конечных значениях a. Далее будем рассматривать систему (5.1) при $b = 0.262$. Применим предложенный итерационный метод. Начнем с рассмотрения относительно небольших конечных значений параметра a. При $a = 0.1$ получаем одну точку ${{P}_{1}}$ пересечения кривых ${{\Gamma }_{1}}$ и ${{\Gamma }_{2}}$ на плоскости $({{\Omega }_{1}},{{\Omega }_{2}})$: $\Omega _{1}^{*} = 0.40$, $\Omega _{2}^{*}$ = 0.48. В этом случае для определения $\Omega _{i}^{*}$ с точностью до второго знака после запятой достаточно одной итерации метода [29], применяемого на этапе построения периодических траекторий вспомогательных систем (п. 4.1). Найденная точка “седловая” (в терминах Замечания 3). Численное интегрирование (этап проверки п. 4.3) системы (5.1) показывает, что при небольших отклонениях начальных значений ${{\omega }_{i}}$ от $\Omega _{i}^{*}$ в ту или иную сторону реализуется один из двух сценариев: или ${{\omega }_{1}}$ значительно возрастает, при этом ${{\omega }_{2}}$ убывает до нуля, или наоборот. Продолжать численное интегрирование в области, где угловая скорость хотя бы одной турбины отрицательна, нецелесообразно, поскольку используемая функция аэродинамического момента хорошо согласуется с экспериментальными данными только в области $\{ {{\omega }_{i}} > 0\} $.
При увеличении параметра a возникают и начинают “расходиться” друг от друга еще две точки ${{P}_{2}}$ и ${{P}_{3}}$ пересечения кривых ${{\Gamma }_{1}}$ и ${{\Gamma }_{2}}$. Эти “дополнительные” точки появляются при $a \approx 0.3$ около точки $(0.47,0.40)$; при этом точка ${{P}_{1}}$ примерно описывается координатами (0.36, 0.50).
Рассмотрим подробно случай $a = 0.5$. В этом случае на плоскости $({{\Omega }_{1}},{{\Omega }_{2}})$ есть три точки $(\Omega _{1}^{*},\Omega _{2}^{*})$: ${{P}_{1}} = (0.36,0.51)$ – “седло”, ${{P}_{2}} = (0.46,0.42)$ – “устойчивый узел”, ${{P}_{3}}$ = = (0.50, 0.37) – “седло” (для получения этих значений выполнено 10 итераций на этапе поиска периодических решений вспомогательных систем). Здесь и далее одинаково обозначены точки, которые непрерывно переходят друг в друга при изменении параметра a.
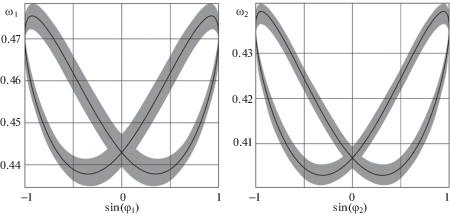
Для точки $(\Omega _{1}^{*},\Omega _{2}^{*})$ = $(0.46,0.42)$ на рис. 4 черным показаны проекции на плоскость $(\sin {{\varphi }_{i}},{{\omega }_{i}})$ найденного приближения ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{i}}({{\varphi }_{i}};\omega _{{i0}}^{*})$ для близкой к периодической траектории. Прямое численное интегрирование системы (5.1) с начальными условиями ${{\varphi }_{i}}(0) = 0$, ${{\omega }_{i}}(0) = \omega _{{i0}}^{*}$ показывает наличие аттрактора “близкого к периодическому”, проекции которого на соответствующие плоскости показаны на рис. 4 серым цветом.
Из рис. 4 видно, что при $(\Omega _{1}^{*},\Omega _{2}^{*})$ = (0.46, 0.42) построенные итерационным методом кривые ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{i}}({{\varphi }_{i}};\omega _{{i0}}^{*})$ позволяют достаточно точно описать местоположение аттрактора, который представляет собой близкую к периодической траекторию.
Несоизмеримость значений $\Omega _{i}^{*}$ приводит к тому, что на плоскости $(\sin {{\varphi }_{1}},\sin {{\varphi }_{2}})$ близкое к периодическому решение “заполняет” единичный квадрат.
Отметим, что при $b = 0.262$, $a = 0.5$ поведение решений системы (5.2) и переменных ${{\omega }_{i}}$ полной системы (5.1) принципиально отличается: в последней существует аттрактор, не имеющий аналога в системе (5.2). Этот аттрактор удается найти и описать предложенным методом.
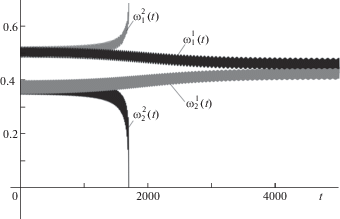
Рассмотрим поведение системы (5.1) в окрестности тора ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{1}}({{\varphi }_{1}};\omega _{{10}}^{*}) \times {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega } }_{2}}({{\varphi }_{2}};\omega _{{20}}^{*})$, соответствующего “седловой” точке ${{P}_{3}} = (0.50,0.37)$ пересечения кривых ${{\Gamma }_{1}}$ и ${{\Gamma }_{2}}$, “аналог” которой отсутствует в системе (5.2). На рис. 5 показаны зависимости ${{\omega }_{i}}(t)$, полученные путем прямого численного интегрирования системы (5.1) методом Рунге–Кутты с начальными условиями ${{\varphi }_{i}}(0) = 0$, ${{\omega }_{i}}(0) = \omega _{{i0}}^{*}$ (кривые $\omega _{i}^{1}(t)$) и с начальными условиями ${{\varphi }_{i}}(0) = 0$, ${{\omega }_{1}}(0) = \omega _{{10}}^{*} + 0.002$, ${{\omega }_{2}}(0) = \omega _{{20}}^{*} - 0.002$ (кривые $\omega _{i}^{2}(t)$).
С течением времени решение $(\varphi _{1}^{1}(t),\;\varphi _{2}^{1}(t),\;\omega _{1}^{1}(t),\;\omega _{2}^{1}(t))$ системы (5.1), представленное на рис. 5 кривыми $\omega _{i}^{1}(t)$, выходит на близкое к периодическому решение, соответствующее точке ${{P}_{2}}$ (оно было рассмотрено выше). Решение $(\varphi _{1}^{2}(t),\;\varphi _{2}^{2}(t),\;\omega _{1}^{2}(t),\;\omega _{2}^{2}(t))$, изображенное кривыми $\omega _{i}^{2}(t)$, пересекает гиперплоскость ${{\omega }_{2}} = 0$. Далее расчет не проводился, поскольку вне области $\{ {{\omega }_{i}} > 0\} $ правая часть системы (5.1) не задана. При численном интегрировании в обратном времени в окрестности тора, отвечающего “седловой” точке ${{P}_{3}}$, были обнаружены начальные условия, при которых обе угловые скорости неограниченно возрастают, а также начальные условия, при которых обе угловые скорости убывают к нулю. Таким образом, в указанной окрестности проходит граница областей притяжения различных аттракторов системы (5.1) и в прямом, и в обратном времени.
При увеличении параметра a точки ${{P}_{1}}$ и ${{P}_{2}}$ сближаются и при $a \approx 0.95$ исчезают около точки (0.42, 0.45) (когда координаты точки ${{P}_{3}}$ примерно равны (0.50, 0.38)).
6. Обсуждение результатов. При помощи предложенного метода описаны близкие к периодическим траектории системы (5.1). В том числе не только решения, которые при уменьшении параметра a непрерывно переходят в неподвижные точки системы (5.2), но и “дополнительные” решения – такие, которые при уменьшении параметра a разрушаются, сливаясь друг с другом.
Отметим, что ряд известных методов поиска квазипериодических траекторий (например, [15]) основан на продолжении по параметру решений, порожденных неподвижными точками усредненной системы. Наличие/введение нескольких параметров (в рассмотренном примере: a и b) позволяет организовать продолжение по параметрам так, чтобы отследить эволюцию “дополнительных” близких к периодическим траекторий. Так, например, в [15] помимо параметра, аналогичного a, используются еще два параметра.
Возникновение “дополнительных” близких к периодическим траекторий при увеличении параметра a можно рассматривать в контексте эволюции диаграммы $\Omega _{i}^{*}(b)$ с ростом параметра a. Так, в представленном примере траектории, возникающие в случае $b = 0.262$ при $a \approx 0.3$, можно рассматривать как “продолжение” по параметрам a и b неподвижных точек усредненной системы (5.2), существующих при меньших значениях b: $b < 0.261$. Отметим, что при $b \geqslant 0.264$ “дополнительные” траектории обнаружены не были.
Диапазон значений параметров a и b, при которых обнаружен “дополнительный” аттрактор рассмотренной системы, очень узкий. Тем не менее, предложенный метод позволил его отыскать.
Помимо возможности описания “дополнительных” решений, к преимуществам предложенного метода можно отнести то, что он не зависит от свойств притяжения искомого решения. В частности, он позволяет выявлять траектории, являющиеся аттракторами (в прямом или обратном времени), а также порожденные седловыми точками усредненной системы кривые, расположенные вблизи границы областей притяжения различных аттракторов. Более того, метод, в отличие от прямого численного интегрирования, не использует область притяжения аттракторов. В частности трудоемкость предложенного алгоритма не зависит от того, содержит ли область притяжения неподвижные точки системы.
Предложенный метод можно распространить на системы более общего вида, чем (2.1). Для этого на этапе построения вспомогательных систем можно ввести дополнительные слагаемые, отвечающие за поворот векторного поля, в методе [29]. Однако это обобщение выходит за рамки данной работы. Помимо этого, среди путей развития предложенного метода можно выделить создание алгоритма для поиска автоколебаний в системах вида (2.1), а также режимов, при которых по одному из углов происходит ротация, а по другому углу – колебания. В этом случае на начальном этапе алгоритма (п. 4.1) можно применить итерационные методы поиска автоколебаний, предложенные в работах [42, 43].
Возможно развитие метода в направлении отыскания режимов, которым на плоскости $({{\Omega }_{1}},{{\Omega }_{2}})$ усредненных скоростей отвечают не точки, а замкнутые кривые.
7. Заключение. Для механических систем с двумя угловыми координатами предложен метод отыскания авторотаций, основанный на усреднении и применении итерационной процедуры [29].
Метод родственен подходам, использующим в качестве нулевого приближения для режимов авторотации неподвижные точки системы, усредненной по двум углам.
Приведен пример применения метода к математической модели двухроторной ветротурбины Савониуса. Описаны некоторые тенденции эволюции режимов авторотации при изменении параметров модели. В частности, обнаружен аттрактор, которому не отвечает ни одна неподвижная точка усредненной системы. Помимо этого, построены кривые, расположенные вблизи границы областей притяжения различных аттракторов. Такие кривые можно взять за основу при построении границы областей притяжения аттракторов методом продолжения по начальным условиям.
Работа выполнена при финансовой поддержке РФФИ: гранты № 18-31-20029, 19-31-90073.
Список литературы
Андронов А.А., Леонтович Е.А., Гордон И.И., Майер А.Г. Теория бифуркаций динамических систем на плоскости. М.: Наука, 1967. 488 с.
Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. Изд. 2-е. М.: Наукa, 1974. 408 с.
Самойленко А.М. Численно-аналитический метод исследования периодических систем обыкновенных дифференциальных уравнений. I // Укр. мат. журн. 1965. Т. 17. № 4. С. 82–93.
Delamotte B. Nonperturbative (but Approximate) Method for Solving Differential Equations and Finding Limit Cycles // Physical Review Letters. 1993. V. 70. Iss. 22. P. 3361.
Buonomo A., Schiavo A.L. A Constructive Method for Finding the Periodic Response of Nonlinear Circuits // IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. 2003. V. 50. Iss. 7. P. 885–893.
Bindel D., Friedman M., Govaerts W., Hughes J., Kuznetsov Y.A. Numerical Computation of Bifurcations in Large Equilibrium Systems in Matlab // Journal of Computational and Applied Mathematics. 2014. V. 261. P. 232–248.
Dudkowski D., Jafari S., Kapitaniak T., Kuznetsov N.V., Leonov G.A., Prasad A. Hidden Attractors in Dynamical Systems // Physics Reports. 2016. V. 637. P. 1–50.
Renson L., Kerschen G., Cochelin B. Numerical Computation of Nonlinear Normal Modes in Mechanical Engineering // Journal of Sound and Vibration. 2016. V. 364. P. 177–206.
Акуленко Л.Д., Лещенко Д.Д., Черноусько Ф.Л. Быстрое движение вокруг неподвижной точки тяжелого твердого тела в сопротивляющейся среде // Изв. РАН. МТТ. 1982. № 3. С. 5–13.
Волосов В.М. О методе усреднения // ДАН. 1961. Т. 137. № 1. С. 21–24.
Волосов В.М., Моргунов Б.И. Метод осреднения в теории нелинейных колебательных систем. М.: Изд-во Московского университета, 1971. 508 с.
Арнольд В.И. Математические методы классической механики. М.: Наука, 1974. 432 с.
Моисеев Н.Н. Асимптотические методы нелинейной механики. М.: Наука, 1981. 400 с.
Sanders J.A., Verhulst F., Murdock J. Averaging Methods in Nonlinear Dynamical Systems. New York: Springer, 2007. 433 p.
Kamiyama K., Komuro M., Endo T. Bifurcation of Quasi-Periodic Oscillations in Mutually Coupled Hard-Type Oscillators: Demonstration of Unstable Quasi-Periodic Orbits // International Journal of Bifurcation and Chaos. 2012. V. 22. Iss. 6. P. 1230022.
Schilder F., Osinga H.M., Vogt W. Continuation of Quasi-Periodic Invariant Tori // SIAM Journal on Applied Dynamical Systems. 2005. V. 4. Iss. 3. P. 459–488.
Chua L.O., Ushida A. Algorithms for Computing Almost Periodic Steadystate Response of Nonlinear Systems to Multiple Input Frequencies // IEEE Trans. Circuits and Systems. 1981. V. 28. Iss. 10. P. 953–971.
Parker T.S., Chua L.O. Practical Numerical Algorithms for Chaotic Systems. New York: Springer-Verlag, 1989. 348 p.
Kaas-Petersen Chr. Computation of Quasiperiodic Solutions of Forced Dissipative Systems // J. Comput. Phys. 1985. V. 58. Iss. 3. P. 395–408.
Боголюбов Н.Н., Митропольский Ю.А., Самойленко А.М. Метод ускоренной сходимости в нелинейной динамике. Киев: Наукова думка, 1969. 248 с.
Самойленко А.М. Элементы математической теории многочастотных колебаний: Инвариантные торы. М.: Наукa, 1987. 301 с.
Broer H., Hagen A., Vegter G. Multiple Purpose Algorithms for Invariant Manifolds // Dynamics of Continuous, Discrete and Impulsive Systems Series B: Applications & Algorithms. 2003. V. 10. P. 331–344.
Schilder F., Vogt W., Schreiber S., Osinga H.M. Fourier Methods for Quasi-Periodic Oscillations // International journal for numerical methods in engineering. 2006. V. 67. Iss. 5. P. 629–671.
Zhou B., Thouverez F., Lenoir D. A Variable-Coefficient Harmonic Balance Method for the Prediction of Quasi-Periodic Response in Nonlinear Systems // Mechanical Systems and Signal Processing. 2015. V. 64. P. 233–244.
Chen G., Dunne J.F. A Fast Continuation Scheme for Accurate Tracing of Nonlinear Oscillator Frequency Response Functions // Journal of Sound and Vibration. 2016. V. 385. P. 284–299.
Kerschen G., Gendelman O., Vakakis A.F., Bergman L.A., McFarland D.M. Impulsive Periodic and Quasi-Periodic Orbits of Coupled Oscillators with Essential Stiffness Nonlinearity // Communications in Nonlinear Science and Numerical Simulation. 2008. V. 13. Iss. 5. P. 959–978.
Bush J., Gameiro M., Harker S., Kokubu H., Mischaikow K., Obayashi I., Pilarczyk P. Combinatorial-Topological Framework for the Analysis of Global Dynamics // Chaos: An Interdisciplinary Journal of Nonlinear Science. 2012. V. 22. Iss. 4. P. 047508.
Kamiyama K., Komuro M., Endo T. Algorithms for Obtaining a Saddle Torus Between Two Attractors // International Journal of Bifurcation and Chaos. 2013. V. 23. Iss. 9. P. 1330032.
Климина Л.А. Метод построения периодических решений в управляемой динамической системе с цилиндрическим фазовым пространством // Изв. РАН. ТИСУ. 2020. № 2. С. 5–16.
Masterova A., Selyutskiy Yu., Zubkov A. Garziera R. On Empirical Model of Aerodynamic Torque Acting on Savonius Rotor // 2020 15th International Conference on Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiy’s Conference) (STAB). IEEE. 2020. P. 1–3.
Досаев М.З., Климина Л.А., Локшин Б.Я., Селюцкий Ю.Д., Шалимова Е.С. О режимах авторотации двухроторной ветротурбины Дарье // Изв. РАН. МТТ. 2021. № 2. С. 133–147.
Баутин Н.Н., Леонтович Е.А. Методы и приемы качественного исследования динамических систем на плоскости. М.: Наука, 1990. 486 с.
Черкас Л.А., Гринь А.А., Булгаков В.И. Конструктивные методы исследования предельных циклов автономных систем второго порядка (численно-алгебраический подход). Гродно: ГрГУ, 2013. 489 с.
Понтрягин Л.С. О динамических системах, близких к гамильтоновым // ЖЭТФ. 1934. Т. 4. № 9. С. 234–238.
Досаев М.З., Самсонов В.А., Селюцкий Ю.Д. О динамике малой ветроэлектростанции // ДАН. 2007. Т. 416. № 1. С. 50–53.
Досаев М.З., Самсонов В.А., Селюцкий Ю.Д., Вен-Лон Лю, Чин-Хуэй Линь. Бифуркации режимов функционирования малых ветроэлектростанций и оптимизация их характеристик // Изв. РАН. МТТ. 2009. № 2. С. 59–66.
Самсонов В.А., Селюцкий Ю.Д. Математическая модель поведения малых ветровых электростанций // Математическое моделирование. 2015. Т. 27. № 2. С. 85–95.
Селюцкий Ю.Д. О динамике малых ветроэнергетических установок // Математическое моделирование. 2018. Т. 30. № 1. С. 31–39.
Selyutskiy Y.D., Klimina L.A., Masterova A.A., Hwang S.S., Lin C.H. Savonius Rotor as a Part of Complex Systems // J. Sound and Vibration. 2019. V. 442. P. 1–10.
Климина Л.А., Шалимова Е.С. Двухпропеллерная ветроэнергетическая установка с дифференциальной планетарной передачей // Мехатроника, автоматизация, управление. 2017. Т. 18. № 10. С. 679–684.
Барабанов И.Н., Тхай В.Н. Конструирование устойчивого цикла в слабо связанных идентичных системах // Автоматика и телемеханика. 2017. № 2. С. 27–35.
Климина Л.А. Метод поиска периодических траекторий центрально-симметричных динамических систем на плоскости // Дифференц. уравнения. 2019. Т. 55. № 2. С. 159–168.
Климина Л.А., Селюцкий Ю.Д. Метод построения периодических решений в управляемой динамической системе второго порядка // Изв. РАН. ТиСУ. 2019. № 4. С. 3–15.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела