Известия РАН. Механика твердого тела, 2021, № 3, стр. 90-99
ПЛАСТИЧЕСКОЕ КРУЧЕНИЕ ПРИ ВЫСОКОМ ДАВЛЕНИИ С НЕОДНОРОДНЫМ НАПРЯЖЕННЫМ СОСТОЯНИЕМ
Г. М. Севастьянов *
Хабаровский федеральный исследовательский центр ДВО РАН
Комсомольск-на-Амуре, Россия
* E-mail: akela.86@mail.ru
Поступила в редакцию 18.06.2020
После доработки 04.07.2020
Принята к публикации 13.08.2020
Аннотация
Получено аналитическое решение для кручения при высоком давлении цилиндрического образца, помещенного в жесткую обойму. Деформируемый материал полагается изотропным идеально пластическим. Учтена зависимость предела текучести от давления. Используется модель неассоциированного пластического течения, включающая пластический потенциал Треска и условие текучести Мора–Кулона. Решение прогнозирует неоднородность тензора напряжений в образце. Напряженное состояние соответствует гипотезе Хаара–Кармана (условию полной пластичности). Определены крутящий момент, среднее нормальное давление на торце цилиндрического образца, а также распределение среднего напряжения по радиусу образца. Указаны условия, при которых отсутствует проскальзывание на контактной поверхности.
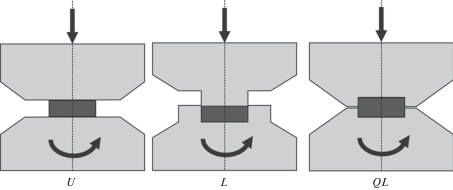
Введение. Влияние высокого давления на способность материалов сопротивляться пластическому сдвигу, вероятно, впервые было рассмотрено в работах Бриджмена [1, 2]. Его опыты по кручению образцов, подвергнутых сильному сжатию, показывают, что для самых разных материалов (в том числе, металлических) кривые крутящего момента и предельная разрушающая нагрузка зависят от величины приложенного гидростатического давления. Дальнейшие экспериментальные исследования в этом направлении проводились различными научными группами [3–5]. Достаточно полный исторический обзор представлен в работе [6]. В 1988 году группой профессора Валиева было сообщено о получении в алюминиевом сплаве размера зерна меньше 1 микрометра при обработке образца кручением под высоким давлением [5]. С этих пор процессы кручения под высоким давлением (HPT – high-pressure torsion) интенсивно исследуются методами механики твердого тела, материаловедения и физики материалов [7, 8]. Схемы деформирования при кручении под высоким давлением различаются по степени ограниченности течения образца [9] (рис. 1, U – неограниченная, L – ограниченная, QL – квазиограниченная). Неограниченная схема никак не препятствует радиальному течению материала, при этом образец в ходе деформирования существенно изменяет толщину и диаметр. Квазиограниченная схема [10] допускает некоторое радиальное течение, однако основной объем образца не слишком сильно изменяет свою геометрию. При полностью ограниченной схеме деформирования образец может менять свои размеры только за счет изменения плотности и деформирования оснастки. Различные варианты деформирования, близкие к полностью ограниченной схеме описаны, например, в работах [4, 11, 12]. Как правило, используются цилиндрические образцы с достаточно большим отношением диаметра к толщине. Процесс проводят в два этапа. На первом к образцу прикладывается начальное давление путем сведения наковален. При этом для ограниченных схем деформирования создается начальное давление, близкое к однородному гидростатическому [9]. На втором этапе одна или обе наковальни сообщают образцу деформации кручения.
Для прогнозирования напряженного состояния образца и его итоговых свойств широко используются различные аналитические и вычислительные модели. Отметим здесь работу [13], в которой учитываются процессы фазовых превращений в материалах, протекание которых связано с накоплением пластической деформации и зависит от локальной величины давления, а также их влияние на механические характеристики образца. Также учитываются контактные условия между образцом и наковальнями, деформирование оснастки. А, кроме того, в численных расчетах учтено влияние давления на предел текучести образца при изохорной пластической деформации. В ряде работ строятся жестко-пластические решения для различных постановок задачи. В [14] для упрочняющегося по степенному закону материала рассмотрено кручение, нелинейное по высоте образца, с учетом дополнительного кругового сдвига (упомянем, что для комбинации кручения с круговым сдвигом есть точное нелинейно-упругое решение [15]); модель [14] прогнозирует однородное распределение давления. В [16] рассмотрено влияние сдвига в радиальном направлении, вызванного радиальным течением материала, и на основе упрощенного уравнения равновесия получено неоднородное распределение давления в образце. Также упомянем некоторые результаты, связанные с использованием градиентных теорий пластичности [17, 18].
Следует отметить, что для полностью закрепленной схемы деформирования принятие пластического потенциала Мизеса приводит к тому, что напряженное состояние образца в цилиндрическом координатном базисе $\left( {{{{\mathbf{e}}}_{{\mathbf{r}}}},{{{\mathbf{e}}}_{{\mathbf{\varphi }}}},{{{\mathbf{e}}}_{{\mathbf{z}}}}} \right)$ представляется тензором напряжений Коши вида
Здесь ${{p}_{0}} = {\text{const}}$ – величина начального гидростатического давления в образце перед фазой кручения. Таким образом, полагается, что давление в образце однородно и постоянно в течение всего процесса деформирования.
В экспериментах с использованием квазиограниченной схемы деформирования, которые, как правило, проводятся при постоянном давлении, в фазе кручения наблюдается уменьшение толщины образца (по сравнению с гидростатически сжатым образцом перед началом кручения) за счет радиального течения. Это дает основания ожидать, что если в начале фазы кручения расстояние между наковальнями (и, следовательно, высота образца) будет зафиксировано, то нормальное давление на наковальни и среднее давление в образце будут снижаться, а радиальное течение материала будет сведено к минимуму. Это ничего не говорит об однородности среднего давления в образце, но, тем не менее, не соответствует указанному выше напряженному состоянию, поскольку величина ${{p}_{0}}$ остается неизменной в ходе деформирования. Отметим также, что проведенные непосредственные измерения на контактной поверхности между образцом и наковальней в ходе процесса [19] демонстрируют неоднородность давления по радиусу образца. По косвенным данным, в частности, по распределению микротвердости по радиусу обработанного образца, теоретически возможно оценить степень неоднородности давления. Однако, при том условии, что ключевым механизмом изменения твердости является выделение новых фаз материала, связанное с локальной величиной давления. Эта оценка, однако, представляет собой достаточно нетривиальную задачу. Кроме того, данные МКЭ-моделирования также говорят о достаточно сильной неоднородности давления в образце. В качестве причин называются: радиальное течение материала, деформирование оснастки, фазовые превращения и соответствующая им объемная деформация, а также изменение механических свойств, начальная неоднородность давления и другие факторы. Тем не менее, кажется интересным, что даже на базе очень простой жестко-пластической модели можно построить решение указанной проблемы, которое не приводит к однородности давления в образце.
Далее будет использована модель изотропного идеально-пластического несжимаемого материала. Это положение основывается на том, что заметное изменение предела текучести материалов из-за деформационного упрочнения (или разупрочнения) прекращается после некоторой степени деформации (которая обычно имеет порядок единицы) [20]. При обработке кручением при высоком давлении величины деформации могут превышать это значение на 1–2 порядка. В таком случае будет разумно использовать в качестве предела текучести при чистом сдвиге его предельную величину.
В этих же условиях вызванная пластической деформацией анизотропия также не проявляется при монотонном нагружении, если исходный (недеформированный) материал изотропен. Эти положения нашли подтверждение при деформировании самых различных материалов [20]. Кроме этого, мы не рассматриваем процессы фазовых превращений в материале, однако учитываем, что давление может оказывать существенное влияние на локальный предел текучести в образце. Последнее утверждение верно в той или иной значимой степени для самых различных материалов – металлических стекол, полимеров, а также металлов в твердом состоянии. Для металлов зависимость предела текучести от величины всестороннего сжатия нехарактерна при обычных условиях, однако отметим, что в случае рассматриваемого процесса речь может идти о давлениях в десятки гигапаскаль. Пластическая несжимаемость компактных материалов в процессе интенсивной деформации является естественным допущением. Отметим, что для кручения с конечными деформациями изотропного неупрочняющегося несжимаемого материала нечувствительного к среднему напряжению имеются аналитические упруго-пластические решения [21–23]. Также отметим недавнее исследование [24], в котором построено приближенное аналитическое решение, которое учитывает зависимость предела текучести от давления.
1. Постановка задачи и уравнения модели. Рассмотрим изохорную деформацию кручения цилиндрического образца высотой $h$ и радиусом $R$, подвергнутого начальному однородному гидростатическому сжатию величиной ${{p}_{0}}$. Будем рассматривать идеализированный случай полностью ограниченного деформирования и пренебрегать обратимыми деформациями. Тензор скорости (пластической) деформации имеет вид
(1.1)
$2{\mathbf{\varepsilon }} = 2{{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} = \left( {\nabla \otimes {\mathbf{v}}} \right) + {{\left( {\nabla \otimes {\mathbf{v}}} \right)}^{T}} = 2r{{\theta }_{t}}\left( {{{{\mathbf{e}}}_{{\mathbf{\varphi }}}} \otimes {{{\mathbf{e}}}_{{\mathbf{z}}}} + {{{\mathbf{e}}}_{{\mathbf{z}}}} \otimes {{{\mathbf{e}}}_{{\mathbf{\varphi }}}}} \right)$Здесь вектор скорости ${\mathbf{v}} = rz{{\theta }_{t}}{{{\mathbf{e}}}_{{\mathbf{\varphi }}}}$, ${{\theta }_{t}} = {{\partial \theta } \mathord{\left/ {\vphantom {{\partial \theta } {\partial t}}} \right. \kern-0em} {\partial t}}$, t – время, θ(t) – угол кручения на единицу высоты цилиндрического образца.
Напряженное состояние характеризуется тензором Коши вида
(1.2)
${\mathbf{\sigma }} = {{\sigma }_{{rr}}}{{{\mathbf{e}}}_{{\mathbf{r}}}} \otimes {{{\mathbf{e}}}_{{\mathbf{r}}}} + {{\sigma }_{{\varphi \varphi }}}{{{\mathbf{e}}}_{{\mathbf{\varphi }}}} \otimes {{{\mathbf{e}}}_{{\mathbf{\varphi }}}} + {{\sigma }_{{zz}}}{{{\mathbf{e}}}_{{\mathbf{z}}}} \otimes {{{\mathbf{e}}}_{{\mathbf{z}}}} + {{\sigma }_{{\varphi z}}}\left( {{{{\mathbf{e}}}_{{\mathbf{\varphi }}}} \otimes {{{\mathbf{e}}}_{{\mathbf{z}}}} + {{{\mathbf{e}}}_{{\mathbf{z}}}} \otimes {{{\mathbf{e}}}_{{\mathbf{\varphi }}}}} \right)$Условие равновесия $\nabla \cdot {\mathbf{\sigma }} = {\mathbf{0}}$ приводит к уравнению
(1.3)
$r\frac{{\partial {{\sigma }_{{rr}}}}}{{\partial r}} + \left( {{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}} \right) = 0$Мы используем неассоциированную пластическую модель, которая включает условие текучести Мора–Кулона
(1.4)
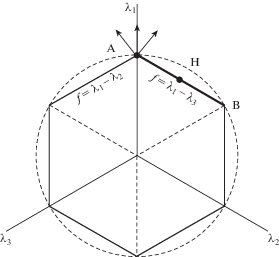
$\left( {{{\sigma }_{1}} - {{\sigma }_{3}}} \right) + \vartheta \left( {{{\sigma }_{1}} + {{\sigma }_{3}}} \right) = 2\kappa $Здесь ${{\sigma }_{1}}$, ${{\sigma }_{3}}$ – наибольшее и наименьшее собственные значения тензора напряжений Коши, $\vartheta \in (0,1)$ – параметр материала. Функция (1.5) дифференцируема везде, кроме угловых точек [25] (рис. 2): ${{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} = \Lambda {{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial {\mathbf{\sigma }}}}} \right. \kern-0em} {\partial {\mathbf{\sigma }}}}$, где Λ – скалярный пластический множитель. Правило определения тензора скорости пластической деформации в угловых точках функции пластического потенциала оговорим далее отдельно. Уравнение равновесия (1.3), условие текучести (1.4) и ассоциированный с пластическим потенциалом (1.5) закон должны исчерпывающе определять компоненты тензоров (1.1) и (1.2) с учетом граничного условия ${{\left. {{{\sigma }_{{rr}}}} \right|}_{{r = R}}} = - {{p}_{0}}$.
2. Анализ напряженного состояния. Исходя из (1.2), собственные значения тензора напряжений выражаются в следующем виде (нумерация произвольная):
(2.1)
${{\lambda }_{2}} = {{\sigma }_{{rr}}},\quad {{\lambda }_{{1,3}}} = {{\left( {{{\sigma }_{{\varphi \varphi }}} + {{\sigma }_{{zz}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\sigma }_{{\varphi \varphi }}} + {{\sigma }_{{zz}}}} \right)} 2}} \right. \kern-0em} 2} \pm \sqrt {{{{{{\left( {{{\sigma }_{{\varphi \varphi }}} - {{\sigma }_{{zz}}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {{{\sigma }_{{\varphi \varphi }}} - {{\sigma }_{{zz}}}} \right)}}^{2}}} 4}} \right. \kern-0em} 4} + \sigma _{{\varphi z}}^{2}} $Согласно правилу нормальности ${{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} = \Lambda {{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial {\mathbf{\sigma }}}}} \right. \kern-0em} {\partial {\mathbf{\sigma }}}}$ и (9), из первого равенства в (2.1) следует, что радиальная компонента тензора скорости пластической деформации может быть нулевой, только если напряженное состояние соответствует либо стороне AB с примыкающими узловыми точками (рис. 2), либо симметричной ей стороне. Последний случай исключен, поскольку ${{\lambda }_{1}} > {{\lambda }_{3}}$. Будем полагать, что в пластическом состоянии при достаточно большой величине деформации напряженное состояние всех точек образца соответствует одной и той же точке на AB.
Для угловых точек пластического потенциала Койтер [26] ввел обобщенное правило нормальности, которое говорит о том, что собственный вектор тензора скорости деформации принадлежит вееру, ограниченному нормалями к смежным сторонам шестиугольника (рис. 2). В рассматриваемой задаче кинематические ограничения (1.1) приводят к тому, что и в угловых точках A или B собственный вектор тензора скорости деформации ортогонален AB. Тогда тензор скорости деформации имеет вид [27]
С учетом (2.1) и (1.2), имеем
(2.2)
${{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}} = \frac{\Lambda }{{\sqrt {{{{\left( {{{\sigma }_{{\varphi \varphi }}} - {{\sigma }_{{zz}}}} \right)}}^{2}} + 4\sigma _{{\varphi z}}^{2}} }}\left( {\frac{{{{\sigma }_{{\varphi \varphi }}} - {{\sigma }_{{zz}}}}}{2}\left( {{{{\mathbf{e}}}_{{\mathbf{\varphi }}}} \otimes {{{\mathbf{e}}}_{{\mathbf{\varphi }}}} - {{{\mathbf{e}}}_{{\mathbf{z}}}} \otimes {{{\mathbf{e}}}_{{\mathbf{z}}}}} \right) + {{\sigma }_{{\varphi z}}}\left( {{{{\mathbf{e}}}_{{\mathbf{\varphi }}}} \otimes {{{\mathbf{e}}}_{{\mathbf{z}}}} + {{{\mathbf{e}}}_{{\mathbf{z}}}} \otimes {{{\mathbf{e}}}_{{\mathbf{\varphi }}}}} \right)} \right)$Из (2.2) и (1.1) следует ${{\sigma }_{{\varphi \varphi }}} = {{\sigma }_{{zz}}}$. Условие пластичности (1.4) с учетом ${{\sigma }_{{\varphi z}}} > 0$ имеет вид
Введем параметр напряженного состояния
(2.4)
$L = \frac{{{{\lambda }_{1}} - {{\lambda }_{2}}}}{{{{\lambda }_{2}} - {{\lambda }_{3}}}} = \frac{{{{\sigma }_{{\varphi z}}} - \left( {{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}} \right)}}{{{{\sigma }_{{\varphi z}}} + \left( {{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}} \right)}}$Значение L = 1 соответствует точке H и состоянию гидростатического сжатия с наложенной деформацией сдвига, значение L = 0 соответствует угловой точке B, значение $L \to + \infty $ – угловой точке A. Из (2.4) следует
(2.5)
${{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}} = - {{\sigma }_{{\varphi z}}}\frac{{L - 1}}{{L + 1}}$Из (2.3) и (2.5) следует
(2.6)
${{\sigma }_{{\varphi \varphi }}} = {{\sigma }_{{zz}}} = \left( {{{\sigma }_{{rr}}} + \kappa \frac{{L - 1}}{{L + 1}}} \right){{\left( {1 + \vartheta \frac{{L - 1}}{{L + 1}}} \right)}^{{ - 1}}}$Тогда, согласно уравнению равновесия (1.3), при $0 \leqslant L < 1$ ${{\partial {{\sigma }_{{rr}}}} \mathord{\left/ {\vphantom {{\partial {{\sigma }_{{rr}}}} {\partial r}}} \right. \kern-0em} {\partial r}} < 0$, а также ${{\partial {{\sigma }_{{\varphi \varphi }}}} \mathord{\left/ {\vphantom {{\partial {{\sigma }_{{\varphi \varphi }}}} {\partial r}}} \right. \kern-0em} {\partial r}} < 0$ и ${{\partial \operatorname{tr} {\mathbf{\sigma }}} \mathord{\left/ {\vphantom {{\partial \operatorname{tr} {\mathbf{\sigma }}} {\partial r}}} \right. \kern-0em} {\partial r}} < 0$, что не согласуется с расчетными и экспериментальными данными. Таким образом, мы будем рассматривать только напряженные состояния, которым соответствуют точки из отрезка AH.
Поскольку параметр L неизвестен, промежуточное главное напряжение остается неопределенным, система уравнений не имеет однозначного решения без принятия дополнительных условий.
В качестве такого условия может выступать уже упомянутое предположение ${{\sigma }_{{rr}}}$ = = σφφ = σzz = –p0. В этом случае напряженное состояние однородно (соответствует точке H на рис. 2):
(2.7)
${\mathbf{\sigma }} = - {{p}_{0}}{\mathbf{I}} + \left( {\kappa + \vartheta {{p}_{0}}} \right)\left( {{{{\mathbf{e}}}_{{\mathbf{\varphi }}}} \otimes {{{\mathbf{e}}}_{{\mathbf{z}}}} + {{{\mathbf{e}}}_{{\mathbf{z}}}} \otimes {{{\mathbf{e}}}_{{\mathbf{\varphi }}}}} \right)$Другой возможный вариант – принятие условия полной пластичности [28] (гипотезы Хаара–Кармана). В этом случае напряженное состояние соответствует угловой точке A ($L \to + \infty $). Уравнение равновесия принимает вид
(2.8)
${{\sigma }_{{rr}}}\left( r \right) = {\kappa \mathord{\left/ {\vphantom {\kappa \vartheta }} \right. \kern-0em} \vartheta } - \left( {{{p}_{0}} + {\kappa \mathord{\left/ {\vphantom {\kappa \vartheta }} \right. \kern-0em} \vartheta }} \right){{\left( {{r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R}} \right)}^{{{{ - \vartheta } \mathord{\left/ {\vphantom {{ - \vartheta } {\left( {1 + \vartheta } \right)}}} \right. \kern-0em} {\left( {1 + \vartheta } \right)}}}}}$Напряженное состояние в этом случае неоднородно. Среднее напряжение согласно (2.8) и (2.6) равно
(2.9)
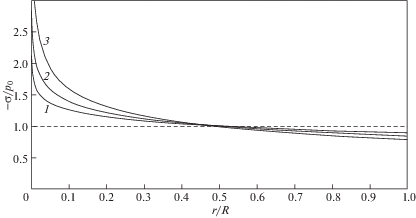
$\sigma = {{\left( {\operatorname{tr} {\mathbf{\sigma }}} \right)} \mathord{\left/ {\vphantom {{\left( {\operatorname{tr} {\mathbf{\sigma }}} \right)} 3}} \right. \kern-0em} 3} = \frac{\kappa }{\vartheta } - \frac{{3 + \vartheta }}{{3\vartheta \left( {1 + \vartheta } \right)}}\left( {\kappa + \vartheta {{p}_{0}}} \right){{\left( {\frac{r}{R}} \right)}^{{{{ - \vartheta } \mathord{\left/ {\vphantom {{ - \vartheta } {\left( {1 + \vartheta } \right)}}} \right. \kern-0em} {\left( {1 + \vartheta } \right)}}}}}$На рис. 3 приведено распределение среднего напряжения при различных значениях параметра ϑ, полученное по формуле (2.9) при ${\kappa \mathord{\left/ {\vphantom {\kappa {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}} = 0.15$; кривая 1 соответствует значению $\vartheta = 0.01$, кривая 2 значению $\vartheta = 0.1$, кривая 3 значению $\vartheta = 0.25$.
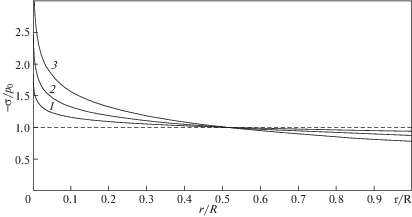
На рис. 4 приведено распределение среднего напряжения при различных значениях параметра ${\kappa \mathord{\left/ {\vphantom {\kappa {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}}$, полученное по формуле (2.9) при $\vartheta = 0.05$; кривая 1 соответствует значению ${\kappa \mathord{\left/ {\vphantom {\kappa {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}} = 0.05$, кривая 2 значению ${\kappa \mathord{\left/ {\vphantom {\kappa {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}} = 0.15$, кривая 3 значению ${\kappa \mathord{\left/ {\vphantom {\kappa {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}} = 0.3$.
Касательное напряжение
(2.10)
${{\sigma }_{{\varphi z}}} = \frac{{\kappa + \vartheta {{p}_{0}}}}{{1 + \vartheta }}{{\left( {\frac{r}{R}} \right)}^{{ - {\vartheta \mathord{\left/ {\vphantom {\vartheta {\left( {1 + \vartheta } \right)}}} \right. \kern-0em} {\left( {1 + \vartheta } \right)}}}}}$Крутящий момент
(2.11)
$M = 2\pi \int\limits_0^R {{{r}^{2}}{{\sigma }_{{\varphi z}}}dr} = \frac{{2\pi {{R}^{3}}\left( {\kappa + \vartheta {{p}_{0}}} \right)}}{{3 + 2\vartheta }}$Среднее осевое давление
3. Заключительные замечания. Соответствующее решению (2.8) напряженное состояние следует трактовать как предельное при неограниченном росте пластической деформации. В таком случае сингулярность тензора напряжений в центре образца просто отражает тот факт, что для упруго-пластического материала условие пластичности никогда не выполнится в точке r = 0.
Предельный переход $\vartheta \to 0$ в (2.9) дает $\mathop {\lim }\limits_{\vartheta \to 0} \sigma = - {{p}_{0}} + 2{\kappa \mathord{\left/ {\vphantom {\kappa 3}} \right. \kern-0em} 3} + \kappa \ln \left( {{R \mathord{\left/ {\vphantom {R r}} \right. \kern-0em} r}} \right)$. Интересно вспомнить работу [29], в которой полученное напряженное состояние в задаче о кручении материала, не чувствительного к среднему напряжению, также имеет логарифмическую сингулярность на оси симметрии.
Крутящий момент, согласно (2.11) несколько ниже, чем прогнозируется решением с однородным напряженным состоянием ($M = 2\pi {{R}^{3}}{{\left( {\kappa + \vartheta {{p}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {\kappa + \vartheta {{p}_{0}}} \right)} 3}} \right. \kern-0em} 3}$). Учет неоднородности напряженного состояния в частности может повлиять на результаты определения величины $\vartheta $ по экспериментальным данным крутящего момента. Среднее осевое давление ниже начального значения, причем снижение существеннее для материалов с большим пределом текучести при чистом сдвиге $\kappa $. Локальная величина среднего напряжения на периферии образца также может быть существенно ниже p0. Среднее напряжение должно мало отличаться от p0 в средней зоне образца (${r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R} \approx {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$) в достаточно широком диапазоне используемых параметров материала.
Приведенное аналитическое решение может реализоваться при ограничении на величину ${\kappa \mathord{\left/ {\vphantom {\kappa {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}}$. Отношение локального касательного напряжения ${{\sigma }_{{\varphi z}}}$ к локальному осевому давлению ${{\sigma }_{{zz}}}$ согласно (2.6), (2.8) и (2.10) есть
Эта функция растет с ростом координаты $r$, для отсутствия кругового сдвига, вызванного проскальзыванием между образцом и наковальнями, требуется, чтобы выполнялось
Предельное (при неограниченном росте деформации кручения) напряженное состояние в упруго-пластическом материале может существенно отличаться как от однородного, так и от прогнозируемого решением (2.8). Отметим, что для материала нечувствительного к давлению с условием текучести Треска локальное значение параметра напряженного состояния L в каждой точке образца не меняется после прохождения упруго-пластической границы через эту точку [22]. При этом распределение параметра L однородно в пластической зоне, значение L конечно и больше единицы (то есть напряженное состояние соответствует некоторой точке между A и H, рис. 2). В этой же задаче, но с учетом изменения свойств материала (из-за нагрева вследствие пластической диссипации [23]) параметр L изменяется в ходе необратимого деформирования. Вместе с тем, учет чувствительности материала к давлению приводит к практически стационарному, но неоднородному распределению параметра L в пластической области [24].
Работа выполнена в рамках государственного задания ХФИЦ ДВО РАН.
Список литературы
Bridgman P.W. Effects of high shearing stress combined with high hydrostatic pressure // Phys. Rev. 1935. V. 48. P. 825–847. https://doi.org/10.1103/PhysRev.48.825
Bridgman P.W. Studies in large plastic flow and fracture: With special emphasis on the effects of hydrostatic pressure. New York-London: McGraw-Hill, 1952. 362 p.
Верещагин Л.Ф., Шапочкин В.А. Влияние гидростатического давления на сопротивление сдвигу в твердых телах // ФММ. 1960. Т. 9. С. 258–264.
Бланк В.Д., Коняев Ю.С., Кузнецов А.И., Эстрин Э.И. Алмазная камера для исследования влияния деформации сдвига на структуру и свойства твердых тел при давлении до 43 ГПа // ПТЭ. 1984. № 5. С. 178–180.
Валиев P.3., Кайбышев О.А., Кузнецов Р.И., Мусалимов Р.Ш., Ценев Н.К. Низкотемпературная сверхпластичность металлических материалов // Докл. АН СССР. 1988. Т. 301. С. 864–866.
Edalati K., Horita Z. A review on high-pressure torsion (HPT) from 1935 to 1988 // Mat. Sci. Eng. A – Struct. 2016. V. 652. P. 325–352. https://doi.org/10.1016/j.msea.2015.11.074
Valiev R.Z., Islamgaliev R.K., Alexandrov I.V. Bulk nanostructured materials from severe plastic deformation // Prog. Mater. Sci. 2000. V. 45. P. 103–189. https://doi.org/10.1016/S0079-6425(99)00007-9
Levitas V.I. High-pressure phase transformations under severe plastic deformation by torsion in rotational anvils // Mater. Trans. 2019. V. 60(7). P. 1294–1301. https://doi.org/10.2320/matertrans.MF201923
Zhilyaev A.P., Langdon T.G. Using high-pressure torsion for metal processing: Fundamentals and applications // Prog. Mater. Sci. 2008. V. 53. P. 893–979. https://doi.org/10.1016/j.pmatsci.2008.03.002
Wadsack R., Pippan R., Schedler B. Structural refinement of chromium by severe plastic deformation // Fusion Eng. Des. 2003. V. 66–68. P. 265–269. https://doi.org/10.1016/S0920-3796(03)00136-4
Ma Y., Levitas V.I., Hashemi J. X-ray diffraction measurements in a rotational diamond anvil cell // J. Phys. Chem. Solids. 2006. V. 67 (9). P. 2083–2090. https://doi.org/10.1016/j.jpcs.2006.05.052
Joo S.-H., Kim H.S. Ring-constraint high-pressure torsion process // Metall. Mater. Trans. A. 2016. V. 47 (7). P. 3473–3478. https://doi.org/10.1007/s11661-016-3518-3
Feng B., Levitas V.I., Li W. FEM modeling of plastic flow and strain-induced phase transformation in BN under high pressure and large shear in a rotational diamond anvil cell // Int. J. Plasticity. 2019. V. 113. P. 236–254. https://doi.org/10.1016/j.ijplas.2018.10.004
Beygelzimer Y., Kulagin R., Toth L.S., Ivanisenko Y. The self-similarity theory of high pressure torsion // Beilstein J. Nanotechnol. 2016. V. 7. P. 1267–1277. https://doi.org/10.3762/bjnano.7.117
Sevastyanov G.M. Torsion with circular shear of a Mooney – Rivlin solid // Mech. Solids. 2020. V. 55 (2). P. 273–276. https://doi.org/10.3103/S0025654420020156
Levitas V.I. High-pressure mechanochemistry: Conceptual multiscale theory and interpretation of experiments // Phys. Rev. B. 2004. V. 70, 184118. https://doi.org/10.1103/PhysRevB.70.184118
Estrin Y., Molotnikov A., Davies C.H.J., Lapovok R. Strain gradient plasticity modelling of high-pressure torsion // J. Mech. Phys. Solids. 2008. V. 56 (4). P. 1186–1202. https://doi.org/10.1016/j.jmps.2007.10.004
Lubarda V.A. Rigid-plastic torsion of a hollow tube in strain-gradient plasticity // Int. J. Solids Struct. 2016. V. 100–101. P. 127–137. https://doi.org/10.1016/j.ijsolstr.2016.07.029
Levitas V.I., Ma Y., Hashemi J., Holtz M., Guven N. Strain-induced disorder, phase transformations, and transformation-induced plasticity in hexagonal boron nitride under compression and shear in a rotational diamond anvil cell: In situ x-ray diffraction study and modeling // J. Chem. Phys. 2006. V. 125, 044507. https://doi.org/10.1063/1.2208353
Levitas V.I. Large deformation of materials with complex rheological properties at normal and high pressure. N.-Y.: Nova Science Publishers, 1996. 385 p.
Arutyunyan N.Kh., Radayev Yu.N. Elastoplastic torsion of a cylindrical rod for finite deformations // J. Appl. Math. Mech. 1989. V. 53 (6). P. 804–811. https://doi.org/10.1016/0021-8928(89)90090-7
Sevastyanov G.M., Burenin A.A. Finite strain upon elastic–plastic torsion of an incompressible circular cylinder // Dokl. Phys. 2018. V. 63. P. 393–395. https://doi.org/10.1134/S1028335818090094
Sevast’yanov G.M., Burenin A.A. Local adiabatic heating effect in finite-strain elastic-plastic torsion // J. Appl. Mech. Tech. Phys. 2019. V. 60. P. 1104–1114. https://doi.org/10.1134/S0021894419060166
Sevastyanov G.M. Analytical solution for high-pressure torsion in the framework of geometrically nonlinear non-associative plasticity // Int. J. Solids Struct. 2020. V. 206. P. 383–395. https://doi.org/10.1016/j.ijsolstr.2020.09.028
He Q.-C., Vallée C., Lerintiu C. Explicit expressions for the plastic normality-flow rule associated to the Tresca yield criterion // Z. Angew. Math. Phys. 2005. V. 56 (2). P. 357–366. https://doi.org/10.1007/s00033-005-4121-4
Koiter W.T. Stress-strain relations, uniqueness and variational theorems for elasto-plastic materials with a singular yield surface // Quart. Appl. Math. 1953. V. 11. P. 350–354. https://doi.org/10.1090/qam/59769
Itskov M. Tensor algebra and tensor analysis for engineers with applications to continuum mechanics. Springer, 2015. 300 p.
Ивлев Д.Д. Механика пластических сред. Т. 1. Теория идеальной пластичности. М.: Физматлит, 2001.
Seth B.R. Elastic-plastic transition in torsion // Z. Angew. Math. Mech. 1964. V. 44 (6). P. 229–233. https://doi.org/10.1002/zamm.19640440602
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела