Известия РАН. Механика твердого тела, 2021, № 3, стр. 68-89

1. Описание модели и основные уравнения. Пусть гладкая поверхность, на которой находится нерастяжимая тяжелая нить, задана уравнением $h(x,y,z) = 0$. Натяжение в точке нити с естественной координатой $s$ обозначим через $T(s) \geqslant 0$, внешние силы, действующие на единицу длины нити, в проекциях на оси системы координат $Oxyz$ обозначим x, y, z. Тогда уравнения равновесия нити на указанной поверхности суть (см. [1, 2, 9–16])

В (1.1) штрих “$'$” означает производную по параметру $s$ – длине дуги нити (естественная координата), а $\lambda > 0$ – неопределенный множитель, характеризующий нормальную реакцию поверхности (односторонней связи $h \geqslant 0$). К уравнениям (1.1) следует добавить еще два уравнения

Первое из уравнений системы (1.2) характеризует свойство нерастяжимости нити (неголономная связь). Пять скалярных уравнений систем (1.1) и (1.2) полностью определяют пять неизвестных функций ($x$, $y$, $z$, $T$, $\lambda $) параметра s, которые реализуются при равновесии нити.

2. Формулировки и решения задач равновесия. Далее рассмотрим два случая: 1) поверхность – круговой конус, 2) поверхность – сфера.

2.1. Круговой конус. Рассмотрим круговой конус, ось симметрии которого вертикальна, а половина угла его раствора равна α. Пусть система координат $Oxyz$ выбрана так, что точка O совпадает с вершиной конуса, ось его симметрии совпадает с осью Oz, которая направлена вертикально вниз (т.е. по направлению силы тяжести), а оси Ox и Oy лежат в горизонтальной плоскости. Тогда уравнение поверхности конуса будет таким

Пусть на этот конус (односторонняя связь) положена нерастяжимая тяжелая однородная замкнутая нить плотности ρ. Исследуем возможность ее равновесия при отсутствии сил трения.

В этом случае имеем X = 0, Y = 0, $Z = \rho g$, и уравнения равновесия (1.1) принимают вид

Система (2.2) имеет следующий интеграл натяжений (“энергии”)

Кроме того, (так как внешние силы, приложенные в каждой точке нити, создают нулевой момент относительно оси $z$) имеется следующий интеграл момента сил натяжения в любой точке нити относительно оси Oz

Введем полярные координаты (r, $\varphi $) в плоскости (x, y) следующим образом

Используя (2.4) и (2.5), получим

Из (2.1) имеем равенство ${{r}^{2}} = {{z}^{2}}{\text{t}}{{{\text{g}}}^{2}}\alpha $, подставляя которое в (2.6), получим, с учетом интеграла (2.3), соотношение

Используя последнее уравнение системы (2.5), соотношение (2.7) и равенство r² = ${{z}^{2}}{\text{t}}{{{\text{g}}}^{2}}\alpha $, из первого уравнения системы (1.2) получим

Из последнего уравнения находим для $z = z(s)$ и $s = s(z)$ соотношения:

Далее, из третьего уравнения системы (2.2) находим $\lambda = \lambda (z)$ по формуле

В последней формуле использовано (2.8) и тождество $z{\text{''}} = 0.5d{{(z{{{\text{'}}}^{2}})} \mathord{\left/ {\vphantom {{(z{{{\text{'}}}^{2}})} {dz}}} \right. \kern-0em} {dz}}$.

Найдем квадратуру для функции $\varphi = \varphi (z)$. Умножая уравнение (2.7) на второе из равенств (2.8), получим

Представим многочлен P(z) из (2.9) в виде

Многочлен $P(z)$ при $0.25z_{0}^{2} \in [{{\gamma }^{2}},\infty )$ имеет еще вещественный положительный корень ${{z}_{1}} = 0.5{{z}_{0}} - \sqrt {0.25z_{0}^{2} - {{\gamma }^{2}}} $ < z₂. Два других вещественных корня z_{3, 4} = 0.5z₀ ± $\sqrt {0.25z_{0}^{2} + {{\gamma }^{2}}} $ находятся вне (снаружи) интервала $({{z}_{1}},{{z}_{2}})$, причем ${{z}_{4}} < 0$, ${{z}_{3}} > {{z}_{2}} > 0$. При $z \in \left[ {{{z}_{1}},{{z}_{2}}} \right]$ имеем $P(z) \geqslant 0$. Нетрудно установить, что это единственный интервал изменения $z$, на котором существуют вещественные $2\pi $-периодические решения $z(\varphi )$ уравнения (2.9) для положения равновесия замкнутой нити. Этот интервал существует только тогда, когда выполнено условие $0.25z_{0}^{2} \in [{{\gamma }^{2}},\infty )$.

Отметим, что при условии $0.25z_{0}^{2} \in [0,{{\gamma }^{2}})$ уравнение $P(z) = 0$ имеет лишь два вещественных корня ${{z}_{{3,4}}} = 0.5{{z}_{0}} \pm \sqrt {0.25z_{0}^{2} + {{\gamma }^{2}}} $, один из которых (корень ${{z}_{4}}$) отрицателен. В этом случае будут соблюдаться неравенства

Тогда решения уравнения (2.9) существуют только при $z \geqslant {{z}_{3}} > 0$ и имеют асимптотический характер: нить либо “спиралью навивается” вверх на конус к уровню $z = {{z}_{3}}$ из некоторого начального положения $z = {{z}_{0}} > {{z}_{3}}$, либо же, “навиваясь спиралью”, удаляется вниз по конусу от начальной точки $z = {{z}_{0}} \geqslant {{z}_{3}}$, т.е. свойство замкнутости нити при равновесии не может быть реализовано.

Таким образом, для существования решения представленных уравнений равновесия замкнутой нити (цепочки) необходимо выполнение двух условий:

1. $0.25z_{0}^{2} \in [{{\gamma }^{2}},\infty )$; 2. При изменении z в пределах от $z = {{z}_{1}}$ до $z = {{z}_{2}}$ функция $\varphi (z)$ (решение уравнения (2.9)) изменяется ровно на $\pi $ (это условие следует из симметрии и требования замкнутости нити).

Следовательно, согласно (2.9), необходимо исследовать разрешимость уравнения

В (2.11) параметры {z₀, γ², α} изменяются в области

Исследование разрешимости уравнения (2.11) в указанной области изменения параметров проведем двумя независимыми методами.

1 метод. Использование эллиптических интегралов. Делаем в (2.11) замену

Тогда, используя (2.10), приходим к исследованию разрешимости следующего уравнения

Вводя обозначение $\mu = 4{{\gamma }^{2}}{\text{/}}z_{0}^{2} \in (0,\;1)$ и преобразуя интеграл к пределам от 0 до π/2, приходим к уравнению

Интеграл в (2.12) является полным эллиптическим интегралом 3-го рода, обозначаемым как $\Pi ({{\sigma }^{2}},k)$. Используя формулы приведения из [3, см. формулы 413.01 на стр. 228], имеем

В (2.13) фигурирует Heuman’s Lambda Function ${{\Lambda }_{0}}(\xi ,k)$, которая дается следующей формулой [3, формула 413 на стр. 228]

В (2.14) обозначены стандартным образом $K(k)$, $E(k)$ полные эллиптические интегралы, соответственно, 1-го и 2-го родов от модуля $k$, а $F(\xi ,k{\text{'}})$, $E(\xi ,k{\text{'}})$ – неполные эллиптические интегралы, соответственно, 1-го и 2-го родов с аргументом ξ от модуля $k{\text{'}} = \sqrt {1 - {{k}^{2}}} $. В нашем конкретном случае, в соответствие с обозначениями из (2.12), (2.13), имеем $\xi = \arcsin \sqrt {{{({{\sigma }^{2}} - {{k}^{2}})} \mathord{\left/ {\vphantom {{({{\sigma }^{2}} - {{k}^{2}})} {({{\sigma }^{2}}{{k}^{{'2}}})}}} \right. \kern-0em} {({{\sigma }^{2}}{{k}^{{'2}}})}}} = \arcsin (1{\text{/}}\sqrt 2 ) = \pi {\text{/}}4$. Тогда, используя обозначения из (2.12), получим из (2.13)

Подставляя полученное выражение в (2.12), приходим к уравнению

Функция ${{\Lambda }_{0}}\left( {\frac{\pi }{4},\sqrt {\frac{{1 - \mu }}{{1 + \mu }}} } \right)$, стоящая в правой части уравнения (2.15), является монотонной по μ. Это следует из формулы для производной функции ${{\Lambda }_{0}}(\varphi ,k)$ по модулю k

(см. формулу 710.11 на стр. 283 книги [3]). Кроме того, так как $k = \sqrt {\frac{{1 - \mu }}{{1 + \mu }}} $, то $\frac{{dk}}{{d\mu }} = - \sqrt {\frac{1}{{(1 - \mu ){{{(1 + \mu )}}^{3}}}}} $. Следовательно, используя (2.16), получаем

Итак, функция $I(\mu ,\alpha )$, фигурирующая в правой части уравнения (2.15), является монотонно возрастающей по параметру μ. Следовательно, для разрешимости уравнения (2.15) на интервале $0 < \mu < 1$ необходимо и достаточно выполнения двойного неравенства

Далее, имеем

Формулы (2.18) следуют из известных соотношений

(см. формулы 151.01 на стр. 36 книги [3]). Отметим, что значение $I(1,\alpha ) = \pi {\text{/}}(\sqrt 2 \sin \alpha )$ из (2.18) также может быть получено и непосредственно из (2.12) при μ = 1. Далее, используя (2.18), из (2.17) получаем неравенства

Последние неравенства эквивалентны следующим

Таким образом, для возможности равновесия замкнутой нити на конусе необходимо выполнения неравенств

В (2.19) $2\alpha $ – угол раствора конуса.

2 метод. Использование методов теории функций комплексной переменной. Вычисляем интеграл в формуле (2.11) при помощи контурного интегрирования (с использованием теоремы Коши из теории функций комплексного переменного и теории вычетов). В рассматриваемой области изменения параметров ($0 < {{z}_{0}} < \infty $, 0 < γ² < < $0.25z_{0}^{2}$, $0 < \alpha < \pi {\text{/}}2$) подкоренное выражение под знаком интеграла в (2.11) является полиномом 4-го порядка, который имеет 4 различных вещественных корня ${{z}_{1}}$, ${{z}_{2}}$, ${{z}_{3}}$, ${{z}_{4}}$, причем соблюдены следующие неравенства

Тогда интеграл из (2.11) можно записать в виде

В первой из формул (2.21) верхний знак соответствует корню ${{z}_{1}}$, а в последней формуле из (2.21) верхний знак соответствует корню ${{z}_{3}}$. Подынтегральное выражение в (2.20) будем рассматривать как функцию комплексного переменного $z = x + iy$. Выберем стандартный контур интегрирования для однозначной ветви корня в подынтегральном выражении интеграла (2.20). Этот контур состоит из окружности ${{C}_{R}}$ с центром в точке z = 0 достаточно большого радиуса $R$ ($R \to \infty $), и двух сторон трех разрезов на действительной оси ${{S}_{1}} = ( - R,{{z}_{4}}),$ ${{S}_{2}} = ({{z}_{1}},{{z}_{2}}),$ ${{S}_{3}} = ({{z}_{3}}, + R)$, ($R \to \infty $). Точки ${{z}_{1}}$, ${{z}_{2}}$, ${{z}_{3}}$, ${{z}_{4}}$ являются точками ветвления (устранимая особенность), а точка z = 0 – единственным полюсом подынтегральной функции интеграла (2.20). Однозначную ветвь корня мы выбираем так, что на верхнем береге разреза ${{S}_{2}}$ корень отрицателен (на нижнем береге – положителен), а тогда на верхних берегах разрезов ${{S}_{1}}$, ${{S}_{3}}$ корень положителен (соответственно, на нижних берегах – отрицателен). Отметим, что для этой ветви значение корня в точке z = 0 также следует выбирать со знаком минус, то есть имеет место равенство

По теореме Коши интеграл от рассматриваемой однозначной ветви подынтегральной функции по указанному замкнутому контуру равен вычету в точке $z = 0$, умноженному на $2\pi i$. Учитывая равенство (2.22), приходим к соотношению

где обозначено: ${{I}_{{{{C}_{R}}}}}$ – интеграл от рассматриваемой функции, взятый по полной окружности ${{C}_{R}}$, $I({{z}_{4}})$ – интеграл от рассматриваемой функции, взятый по действительной оси от точки $z = - R$ до точки $z = {{z}_{4}}$ (верхний берег разреза ${{S}_{1}}$), $I({{z}_{3}})$ – интеграл от рассматриваемой функции, взятый по действительной оси от $z = {{z}_{3}}$ до $z = + R$ (верхний берег разреза ${{S}_{3}}$), $I({{z}_{1}},{{z}_{2}})$ – искомый интеграл из (2.20). Устремляя в (2.23) $R \to + \infty $, несложно показать, что ${{I}_{{{{C}_{R}}}}} \to 0$, и справедливы соотношения

В результате, из (2.23) и (2.24) получаем формулу

Делаем в интегралах из (2.25) замену $z = {{z}_{0}}y$. Получим

Для упрощения выкладок введем обозначение $\varepsilon = {{\gamma }^{2}}{\text{/}}z_{0}^{2} \in (0,\;0.25)$ (так как в рассматриваемой области параметров выполнено неравенство $0 < {{\gamma }^{2}} < 0.25z_{0}^{2}$). Тогда получим

Для нижних пределов интегралов в (2.26) введены обозначения

В первом из интегралов в (2.26) делаем замену переменной $y = {{y}_{1}} + 1$. Получим

Окончательно получаем следующую формулу

Обозначим

Покажем, что функция $F(\varepsilon )$ из (2.29) является монотонной по аргументу $\varepsilon \geqslant 0$. Действительно, сделаем в интеграле из (2.29) замену переменной

Тогда получим

Из (2.30) монотонное убывание по $\varepsilon > 0$ функции $F(\varepsilon )$ (при любом фиксированном $\gamma $) становится очевидным. Следовательно, справедливы неравенства

Из (2.30) получим

Используя соотношения (2.28)–(2.33), получим неравенства

Теперь вернемся к уравнению (2.11), которое с учетом наших обозначений, имеет вид

Учитывая неравенства (2.34), можно утверждать, что разрешимость последнего уравнения эквивалентна неравенствам

В последних формулах $2\alpha $ – угол раствора конуса. Таким образом, метод 2 дал те же самые результаты, что были получены выше методом 1.

Если неравенства (2.19) выполнены, то из уравнения (2.15) мы находим то единственное значение $\mu * = \mu (\alpha ) \in (0,\;1)$, при котором возможно равновесие.

Предположим, что неравенства (2.19) выполнены, и соответствующее значение $\mu * = \mu (\alpha ) \in (0,\;1)$ найдено. Рассмотрим второе из равенств формул (2.8), которое проинтегрируем в пределах от $z = {{z}_{1}}$ до $z = {{z}_{2}}$. В силу симметрии конфигурации замкнутой нити, слева должны получить её полудлину L/2. Тогда имеем равенство

Аналогично предыдущему, делаем в интеграле формулы (2.35) замену

Тогда уравнение (2.35) приобретает вид

Интеграл, фигурирующий в (2.36), может быть сведен к полному эллиптическому интегралу 3-го рода и далее аналогично предыдущему вычислен через функцию ${{\Lambda }_{0}}\left( {\frac{\pi }{4},\frac{{1 - \mu {\text{*}}}}{{1 + \mu {\text{*}}}}} \right)$.

Из (2.36) мы находим постоянную величину ${{z}_{0}}$, которая зависит от длины нити. Далее, вспоминая обозначение для $\mu $, находим соответствующее $\gamma _{ * }^{2}$ по формуле $\gamma _{ * }^{2} = \mu {\text{*}}z_{0}^{2}{\text{/}}4$. Используя обозначение из (2.7), находим в результате константу $D$ по формуле $D = \rho g\gamma _{ * }^{2}{\text{tg}}\alpha $.

Таким образом, задача о равновесии замкнутой нити на конусе полностью разрешена. Решение этой задачи единственно, с точностью до поворотов вокруг оси симметрии $Oz$ (кроме горизонтальных положений равновесия, когда $z = {\text{const}}$).

Замечание 1. Отметим, что почти одновременно с публикацией автором результата о равновесии нити на конусе при условии (2.19) в статье [7], аналогичный результат (но другим методом) был получен также в работе [8]. Основной недостаток работы [8] состоит в следующем. При нахождении равновесной конфигурации нити-цепочки на конусе автор статьи [8] также пришел к условию разрешимости (2.11), где в правой части стоит эллиптический интеграл $I(\gamma ) = \frac{{{{\gamma }^{2}}}}{{\sin \alpha }}\int_{{{z}_{1}}}^{{{z}_{2}}} {\frac{{dz}}{{z\sqrt {P(z)} }}} $, который зависит от параметра $\gamma $. Далее, автор статьи [8] отмечает, что можно показать монотонность этого интеграла по параметру $\gamma $, однако не делает этого и даже не указывает как это можно было бы сделать.

В настоящей статье монотонность интеграла $I(\gamma )$ по параметру $\gamma $ доказана математически строго двумя независимыми методами математического анализа. Как видим, это требует немалых аналитических усилий и не является столь очевидным. Отметим, что аналогичные исследования зависимости эллиптических интегралов от параметров проводились также классиками теоретической механики при качественном анализе результатов решения задачи о сферическом маятнике (см., например, учебник [1], стр. 436–438). В статье [17] было показано (при помощи методов контурного интегрирования), что при любой (ненулевой) начальной окружной скорости сферического маятника за время его прохода от максимального до минимального значений координаты z (т.е. за четверть периода по углу отклонения от вертикали) плоскость его качаний поворачивается на угол больший прямого (π/2) и меньший развернутого (π). Из результатов статьи [17], в частности, следует, что в пределе, при нулевой начальной окружной скорости сферического маятника, он превращается в обычный (плоский) математический маятник, а плоскость его качаний (за четверть периода по углу отклонения от вертикали) поворачивается ровно на 90 градусов, хотя при наблюдении нам кажется, что она вообще не поворачивается.

2.2. Сфера. Рассмотрим в качестве поверхности сферу радиуса $a$. Для упрощения выкладок примем, что a = 1. Пусть система координат $Oxyz$ выбрана так, что точка $O$ совпадает с центром сферической поверхности, ось $Oz$ направлена вертикально вверх (т.е. против силы тяжести), а оси $Ox$ и $Oy$ лежат в горизонтальной плоскости. Тогда уравнение поверхности сферы будет таким

Пусть на эту сферу (односторонняя связь) положена нерастяжимая тяжелая однородная замкнутая нить плотности $\rho $. Исследуем возможность ее равновесия при отсутствии сил трения. В этом случае имеем $X = 0$, $Y = 0$, $Z = - \rho g$, и уравнения равновесия (1.1) принимают вид

Система (2.38) имеет следующий интеграл натяжений (“энергии”)

Следуя [1, 9], используем еще интеграл момента натяжения относительно вертикальной оси $Oz$. Вводя цилиндрические координаты ($r$, $\varphi $, $z$) по формулам

Тогда имеем соотношение

Из (2.39) и (2.41) получим равенство

Уравнение сферы (2.37) в координатах (2.40) имеет вид

Первое уравнение системы (1.2) в цилиндрических координатах (2.40) и учетом соотношения (2.43), принимает вид

Используя (2.42) и (2.44), получим дифференциальное соотношение

Ясно, что при равновесии нити на сфере с односторонней связью $h \geqslant 0$ в (2.45) должно соблюдаться условие $z \in (0,\;1)$. А из требования замкнутости и симметрии нити при равновесии должно соблюдаться следующее условие: при изменении $z$ от значения $z = {{z}_{1}}$ до значения $z = {{z}_{2}}$ угол $\varphi $ должен измениться ровно на $\pi $, где ${{z}_{1}},{{z}_{2}} \in (0,\;1)$ – различные последовательные корни уравнения $f(z,{{z}_{0}}) - {{A}^{2}} = 0$. Таким образом, задача сводится к решению уравнения

В (2.46) параметры $\{ A,{{z}_{0}}\} $ изменяются в допустимой области.

Область допустимого изменения параметров $\{ A,{{z}_{0}}\} $ находится из следующих соображений. Так как натяжение нити положительно $T = \rho g(z - {{z}_{0}}) > 0$ при $z \in (0,\;1)$, то необходимо должно соблюдаться условие ${{z}_{0}} \in \left( { - \infty ,1} \right]$. Далее, несложное исследование функции $f(z,{{z}_{0}})$ показывает, что для существования двух вещественных корней z₁, ${{z}_{2}} \in (0,1)$ уравнения $f(z,{{z}_{0}}) - {{A}^{2}} = 0$ параметр A² необходимо должен удовлетворять следующим условиям:

В (2.47) обозначено

В разделе 3 данной статьи показано, что при всех допустимых значениях параметров $\{ A,{{z}_{0}}\} $ для интеграла из (2.46) справедлива оценка $I(A,{{z}_{0}}) < \pi $. Следовательно, уравнение (2.46) не имеет решений.

Таким образом, негоризонтальные (т.е. с переменными значениями координаты z) положения равновесия замкнутой тяжелой нерастяжимой нити-цепочки на гладкой сфере невозможны.

Замечание 2. При исследовании задач равновесия, рассматриваемых в данной статье, использовались полные эллиптические интегралы Лежандра 3-го рода. Для вычисления этих интегралов автор настоящей статьи обращался к книге [3] (к сожалению, не переведенной на русский язык). Отметим, что в известном справочнике [4], для рассматриваемого в статье случая эллиптического интеграла 3-го рода, содержится ошибка. Действительно, в справочнике [4] на стр. 28, формула (22), для приведения интеграла 3-го рода в случае $ - 1 < \nu < - {{k}^{2}} < 0$, такова (цитируем, сохранив обозначения оригинала):

В (2.48) обозначено $\Delta (\theta ,k) = {{(1 - {{k}^{2}}{\text{si}}{{{\text{n}}}^{2}}\theta )}^{{1/2}}}$, $k{\text{'}} = {{(1 - {{k}^{2}})}^{{1/2}}}$, $E(k)$, $K(k)$ – полные эллиптические интегралы, соответственно, 1-го и 2-го родов, а $E(\theta ,k)$, $F(\theta ,k)$ – неполные эллиптические интегралы, соответственно, 1-го и 2-го родов (при $\theta \in (0,\pi {\text{/}}2)$, $k \in (0,\;1)$). Отметим, что в [4] для полного эллиптического интеграла 3-го рода (в отличие от обозначений данной статьи в формуле (2.12)) принято следующее обозначение

Тогда в (2.48) положено $\nu = - {{\Delta }^{2}}(\theta ,k{\text{'}}) = - (1 - {{k}^{{'2}}}{\text{si}}{{{\text{n}}}^{2}}\theta )$, ${{k}^{{'2}}} = 1 - {{k}^{2}}$, $1 > - \nu > {{k}^{2}} > 0.$

Правильная формула в (2.48) должна быть такой

Справедливость соотношения (2.49) следует из формул, приведенных в книге [3] на стр. 228, а также в классическом трактате Лежандра [6] на стр. 138. Неправильность формулы (2.48) можно установить и непосредственно, рассматривая равенство (2.48) сначала: 1) при k = 0 (так мы покажем, что в последнем слагаемом правой части равенства (2.48) обязательно должно быть $E(\theta ,k{\text{'}})$), а потом 2), полагая в (2.48) $\nu = - k$ и затем устремляя $k \to 1$ (так мы получим, что правая часть равенства (2.48) в точности равна π/4, а левая часть равенства (2.48) строго больше π/4).

Отметим, что неверное равенство (2.48) присутствует также и в источнике [5] – английском оригинале книги [4].

3. Оценка интеграла $I(A,{{z}_{0}})$ из уравнения (2.46) раздела 2. Рассмотрим функцию $I(A,{{z}_{0}})$, вычисляемую по формуле

Покажем, что для этой функции верно неравенство $I(A,{{z}_{0}}) < \pi $, которое выполняется для всех допустимых значений параметров $(A,{{z}_{0}})$, удовлетворяющих условиям (2.47) раздела 2 статьи. Мы докажем это неравенство непосредственно, не используя стандартной формулы для производной интеграла из (3.1) по параметру $A$. Эта операция некорректна, так как получаемый в результате такого дифференцирования интеграл является расходящимся.

Подынтегральная функция интеграла из (3.1) имеет два полюса в точках $z = z_{1}^{ * }$ = = +1, $z = z_{2}^{ * } = - 1$. Кроме того, точки $z = {{z}_{1}}$, $z = {{z}_{2}}$ являются точками ветвления для корня в знаменателе подынтегральной функции. Это, как было указано в разделе 2 статьи, суть положительные вещественные корни уравнения 4-го порядка

Эти корни, как следует из условий (2.47) раздела 2 статьи, при ${{z}_{0}} \in (0,\;1)$ принадлежат интервалу $({{z}_{0}},1)$, а при ${{z}_{0}} \in ( - \infty ,0)$ принадлежат интервалу (0, 1). Уравнение 4-го порядка из (3.2), конечно, имеет еще два корня (возможно, комплексных), однако, несложно показать, что эти два оставшихся корня расположены заведомо левее вертикальной прямой $z = {{z}_{0}} + iy$, $y \in ( - \infty , + \infty )$, проведенной параллельно мнимой оси в комплексной плоскости $z = x + iy$.

Вычисление интеграла из (3.1) будем производить при помощи контурного интегрирования. Контур интегрирования (см. рис. 1) состоит из трех частей и строится следующим образом. Выберем достаточно большое число $R > \max \left( {1,\left| {{{z}_{0}}} \right|} \right)$.

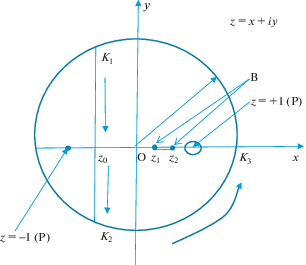
1-я часть контура – кривая ${{S}_{1}}$. Это дуга (часть) окружности радиуса $R$:

2-я часть контура – линия ${{S}_{2}}$. Это вертикальный отрезок прямой

Этот отрезок спрямляет (замыкает) дугу окружности ${{S}_{1}}$ до замкнутого контура ${{S}_{{12}}} = {{S}_{1}} \cup {{S}_{2}}$, который охватывает начало координат и точки

3-я часть контура – линия ${{S}_{3}} = S_{3}^{ + } \cup S_{3}^{ - }$. Это граница отрезка разреза вещественной оси $z = x \pm 0 \cdot i$, $x \in [{{z}_{1}},{{z}_{2}}]$, состоящая из двух берегов: верхнего $S_{3}^{ + }$ ($z = x + 0 \cdot i$, $x \in ({{z}_{1}},{{z}_{2}})$) и нижнего $S_{3}^{ - }$ ($z = x - 0 \cdot i$, $x \in ({{z}_{1}},{{z}_{2}})$).

Во внутренности области G, ограниченной указанными контурами ${{S}_{{12}}}$ и ${{S}_{3}}$, выберем однозначную ветвь квадратного корня подынтегрального выражения интеграла из (3.1) так, что на верхней границе разреза $S_{3}^{ + }$ этот корень отрицателен, а на нижней границе этого разреза $S_{3}^{ - }$ он положителен. Тогда для этой ветви в точке полюса $z_{1}^{ * } = + 1$ для корня в подынтегральном выражении в (3.1) имеем значение $( + iA)$. А в точке полюса $z_{2}^{ * } = - 1$ для этого корня при ${{z}_{0}} < - 1$ (когда, как указано было выше, два корня уравнения $(1 - {{z}^{2}}){{(z - {{z}_{0}})}^{2}} - {{A}^{2}} = 0$ лежат в комплексной плоскости заведомо левее этого полюса) имеем значение $( - iA)$.

Ясно, что в области $G$ эта однозначная ветвь подынтегральной функции является аналитической, за исключением ее полюсов $z_{{1,2}}^{ * } = \pm 1$. Если ${{z}_{0}} \in ( - 1,\;1)$, то область $G$ содержит только один полюс $z_{1}^{ * } = + 1$, а если ${{z}_{0}} < - 1$, то область $G$ содержит уже два полюса $z_{{1,2}}^{ * } = \pm 1$. В связи с этим, рассмотрим раздельно два возможных случая: 1) ${{z}_{0}} \in \left( { - 1,\;1} \right]$ и 2) ${{z}_{0}} \in \left( { - \infty , - 1} \right]$.

1 случай ${{z}_{0}} \in \left( { - 1,\;1} \right]$. Тогда полюс только один – в точке $z_{1}^{ * } = + 1$. Вычет в этой точке, умноженный на $2\pi i$, равен

Интегрируем по контуру ${{S}_{{12}}} \cup {{S}_{3}}$ так, что область $G$ при обходе контура остается все время слева по ходу движения. Применяя теорему Коши, получаем соотношение

В (3.3) $I({{S}_{1}})$ – интеграл по дуге окружности ${{S}_{1}}$, $I({{S}_{2}})$ – интеграл по вертикальному отрезку S₂, $I({{S}_{3}})$ – интеграл по двум берегам разреза ${{S}_{3}} = S_{3}^{ + } \cup S_{3}^{ - }$. Переходя в соотношении (3.3) к пределу при $R \to \infty $, получим $I({{S}_{1}}) \to 0$. Для интеграла $I({{S}_{2}})$ получим следующее предельное (когда $R \to \infty $) значение

В (3.4) обозначено

Для интеграла $I({{S}_{3}})$ имеем равенство $I({{S}_{3}}) = - 2I(A,{{z}_{0}})$. Таким образом, из (3.3) получаем соотношение

Отсюда следует равенство

Преобразуем интеграл из (3.4), используя обозначения (3.5). Получим сначала

Для корней из комплексных чисел в знаменателях подынтегрального выражения (3.7) имеем следующие формулы

Указанный выбор знаков для значений квадратных корней в (3.8) обусловлен тем, что при $a < 0$, $b \to + 0$ (нижний берег разреза $S_{3}^{ - }$ для числа $ - a - ib$) должно, как это было принято выше, получаться положительное вещественное число, а при $a < 0$, $b \to - 0$ (верхний берег разреза $S_{3}^{ + }$ для числа $ - a - ib$) должно, как это было принято выше, получаться отрицательное вещественное число. Введем обозначения

Тогда имеем из (3.8)

Используя (3.10), получим из (3.7)

Таким образом, интеграл $I({{S}_{2}})$ является вещественным.

Используя обозначения (3.5) и (3.9), из (3.11) получим

В (3.12) $a$, $b$ даются формулами

Оценим интеграл (3.12) сверху. Так как для рассматриваемого случая $z_{0}^{2} < 1$, то для всех значений $y \in (0, + \infty )$, согласно (3.13), имеем неравенства a > 0, ${{y}^{2}} + 1 - z_{0}^{2} > 0$, а из первой формулы соотношений (3.13) следует, что $A < \sqrt a $. Тогда получим оценку

А так как справедливо неравенство $\sqrt a < \sqrt {\sqrt {{{a}^{2}} + {{b}^{2}}} } $, то имеем оценку

Интеграл ${{I}_{0}}({{z}_{0}})$ из (3.14) несложно подсчитать. Воспользуемся тождеством

Тогда получим

Следовательно, устремляя $y \to \infty $, получим ${{I}_{0}}({{z}_{0}}) = \pi $. Это равенство справедливо только при ${{z}_{0}} \in ( - 1,\;1)$. Если ${{z}_{0}} = \pm 1$, то непосредственно из (3.14) получим ${{I}_{0}}( \pm 1)$ = = π/2. Отметим, что случай ${{z}_{0}} = + 1$ не реализуется физически, так как в этом случае функция $f(z,1) = (1 - {{z}^{2}}){{(z - 1)}^{2}} = {{(1 - z)}^{3}}(1 + z)$ является монотонно убывающей на отрезке $z \in [0,\;1]$, а значит, уравнение $(1 - {{z}^{2}}){{(z - 1)}^{2}} - {{A}^{2}} = 0$ имеет на этом отрезке не  более одного корня, что исключает наличие равновесных конфигураций. Случай z₀ = – 1 является особым, так как здесь построенный выше контур интегрирования проходит через точку $z = - 1$, являющейся полюсом. Тогда в правой части равенства (3.3) следует добавить еще половину вычета в точке z = –1, умноженную на $2\pi i$.

Подсчитаем полный вычет в точке z = –1, умноженный на $2\pi i$, предполагая, что ${{z}_{0}} \leqslant - 1$. В этом случае, как это было отмечено выше, два оставшихся (помимо ${{z}_{1}}$, ${{z}_{2}}$) корня уравнения $(1 - {{z}^{2}}){{(z - {{z}_{0}})}^{2}} - {{A}^{2}} = 0$ лежат левее полюса z = –1, и поэтому значение корня $\sqrt { - (z\, - \,{{z}_{1}})(z\, - \,{{z}_{2}})({{z}^{2}}\, + \,pz\, + \,q)} $ в точке z = –1 будет равно $\sqrt {{{\rho }_{1}}{{\rho }_{2}}(1\, - \,p\, + \,q){\text{exp}}(3\pi i)} $ = = –iA. Тогда получим следующее значение вычета в точке z = –1

Таким образом, в случае ${{z}_{0}} = - 1$ имеем, вместо (3.3), такое соотношение

Отсюда получаем

Выше мы доказали, что в случае z₀ = –1 справедливо строгое неравенство $I({{S}_{2}}) < {{I}_{0}}( - 1)$ = 0.5π, где ${{I}_{0}}$ определено в (3.14). Тогда из (3.16) получим $I(A,{{z}_{0}}) < \pi $. Если же ${{z}_{0}} \in ( - 1,\; + 1)$, то мы используем равенство (3.6), где, как было показано выше, должно соблюдаться строгое неравенство $I({{S}_{2}}) < \pi $. Тогда опять же получаем $I(A,{{z}_{0}}) < \pi $. Таким образом, показано, что в случае ${{z}_{0}} \in [ - 1,\;1]$ справедливо строгое неравенство $I(A,{{z}_{0}}) < \pi $.

2 случай ${{z}_{0}} \in ( - \infty , - 1]$. В этом случае все рассуждения аналогичны предыдущему пункту. Однако подынтегральная функция в интеграле из (3.1) имеет уже два полюса в точках $z = 1$, z = –1. Вычеты в этих точках, умноженные на $2\pi i$, как это было показано выше, равны ${{Q}_{1}} = {{Q}_{2}} = - \pi $. Тогда вместо (3.3) имеем такое соотношение

Отсюда, аналогично предыдущему пункту, получим следующее соотношение $I(A,{{z}_{0}}) = 0.5\left[ {2\pi + I({{S}_{2}})} \right]$, в котором $I({{S}_{2}})$ дается формулами (3.12), (3.13). Покажем, что в этом случае имеет место строгое неравенство $I({{S}_{2}}) < 0$, которое, согласно последнему соотношению, влечет строгое неравенство $I(A,{{z}_{0}}) < \pi $. Действительно, введем обозначение $\varepsilon = z_{0}^{2} - 1$, $\varepsilon \in (0, + \infty )$. Тогда из (3.12) имеем следующее неравенство

Покажем, что стоящий в правой части последнего неравенства (3.17) интеграл ${{I}_{1}}(\varepsilon )$ строго отрицателен для всех $\varepsilon > 0$. Обозначим

Преобразуем интеграл ${{I}_{1}}(\varepsilon )$ из (3.17) следующим образом:

В последнем интеграле делаем замену $z = \varepsilon {\text{/}}y$ и получаем следующую формулу

Для функции $F(y)$, даваемой формулой (3.18), справедливо неравенство

Отметим, что полное и строгое доказательство неравенства (3.20) достаточно громоздко и приводится далее в разделе 4 данной статьи.

Из (3.19) и (3.20) следует ${{I}_{1}}(\varepsilon ) < 0$. А это, согласно (3.17), означает, что $I({{S}_{2}}) < 0$. Что и требовалось доказать.

4. Доказательство неравенства (3.20) раздела 3. Покажем, что для функции $F(y)$ из (3.18) справедливо следующее утверждение.

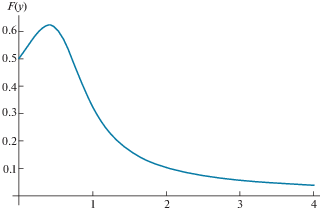
Утверждение. Функция $F(y)$ из (3.18) на интервале $y \in \left[ {0, + \infty } \right)$ ведет себя следующим образом.

1. При $y \in [0,\sqrt \varepsilon )$ $F(y)$ имеет в точности один максимум в точке, принадлежащей интервалу $y \in [0,\sqrt {0.5\varepsilon } )$. При этом выполнены неравенства $F{\text{'}}(0) > 0$, $F{\text{'}}(\sqrt \varepsilon ) < 0$, F(0) > $F(\sqrt \varepsilon )$.

2. При $y \in [\sqrt \varepsilon , + \infty {\text{)}}$ $F(y)$ монотонно убывает (вплоть до нуля при $y \to + \infty $).

Качественно, график функции $F(y)$ представлен на рис. 2. Ясно, что из приведенного утверждения будет следовать, как частный случай, неравенство (3.20). Действительно, в силу пункта 1 утверждения, справедливо неравенство $F(y) > F(\sqrt \varepsilon )$, $y \in [0,\sqrt \varepsilon )$, а в силу пункта 2 утверждения выполнено неравенство $F(\sqrt \varepsilon ) \geqslant F(\varepsilon {\text{/}}y)$, $y \in [0,\sqrt \varepsilon ]$. Объединение этих неравенств приводит к неравенству (3.20).

Доказательство утверждения. Далее, для удобства записи, рассматриваем функцию $G(y) = {{F}^{2}}(y)$, и кроме того, в качестве независимой переменной рассматриваем $u$ = y². Тогда имеем

Ясно, что достаточно доказать все свойства утверждения для функции $G(u)$, даваемой формулами (4.1). Для производной функции $G(u)$ имеем следующее выражение

Далее рассмотрим два случая: 1) ${{A}^{2}} > 0.25{{\varepsilon }^{2}}$, 2) ${{A}^{2}} < 0.25{{\varepsilon }^{2}}$.

1) ${{A}^{2}} > 0.25{{\varepsilon }^{2}}$. В этом случае имеем

Тогда из (4.2) получим

Таким образом, корень уравнения $H(u) = 0$, а, следовательно, и уравнения $G{\text{'}}(u)$ = 0, наверняка есть на интервале $u \in \left[ {0,0.5\varepsilon } \right)$. Покажем, что этот корень только один и на всем интервале $u \in \left[ {0, + \infty } \right)$. Для этого достаточно показать, что $H{\text{'}}(u) < 0$ для всех $u \in \left[ {0, + \infty } \right)$. Действительно, из (4.2) получим

Отбрасывая в правой части последнего равенства заведомо отрицательные слагаемые, получим следующую оценку

Используя неравенства $\sqrt {{{a}^{2}} + {{b}^{2}}} > b$, $a > 0$, получим из (4.3) оценку

Справедливость последнего неравенства вытекает из неравенств

Последнее неравенство следует из очевидного неравенства

Таким образом, мы показали, что $H{\text{'}}(u) < 0$ для всех $u \in \left[ {0, + \infty } \right)$. Следовательно, функция $H(u)$ является монотонной на всем интервале $u \in \left[ {0, + \infty } \right)$, а значит корень уравнения $H(u) = 0$ (а, следовательно, и уравнения $G{\text{'}}(u) = 0$) является единственным. Из доказанного свойства функции $G(u)$ следует справедливость пп. 1 и 2 утверждения. Неравенства $F{\text{'}}(0) > 0$, $F{\text{'}}(\sqrt \varepsilon ) < 0$, $F(0) > F{\text{'}}(\sqrt \varepsilon )$ устанавливаются непосредственной проверкой.

2) ${{A}^{2}} < 0.25{{\varepsilon }^{2}}$. В этом случае функция $a = {{A}^{2}} + {{u}^{2}} - \varepsilon u$ обращается в нуль в точках

Таким образом,

Здесь мы имеем следующие соотношения для функции $H(u)$

Последнее неравенство в (4.5) справедливо, так как, согласно (4.4), имеем ${{u}_{1}} < 0.5\varepsilon .$ Из (4.5) следует, что функция $H(u)$, а значит, и производная $G{\text{'}}(u)$, заведомо имеют нуль на интервале $u \in (0,{{u}_{1}}) \subset (0,0.5\varepsilon )$. Пусть ${{u}_{ * }} \in (0,{{u}_{1}})$ это первый нуль функции $G{\text{'}}(u)$. Ясно, что это точка максимума функции $G(u)$ и выполнены условия

Покажем, что этот нуль единственный. Для этого достаточно только показать, что $G{\text{'}}(u) < 0$, $u \in ({{u}_{1}},{{u}_{2}})$. Действительно, если мы это установили, то при $u \in ({{u}_{1}},{{u}_{2}})$ $G{\text{'}}(u)$ не может обратиться в нуль, а при $u \notin ({{u}_{1}},{{u}_{2}})$ мы имеем $a(u) > 0$ и можем показать (точно также, как это мы сделали в случае 1), что $H{\text{'}}(u) < 0$. Следовательно, если $G{\text{'}}(u)$ обратится в нуль еще раз (после точки $u = {{u}_{ * }}$), то это опять будет точка максимума, что явно противоречиво.

Итак, пусть $u \in ({{u}_{1}},{{u}_{2}})$. Тогда $a(u) = {{A}^{2}} + {{u}^{2}} - \varepsilon u < 0$. Обозначим a₁(u) = –a(u) = = $\varepsilon u - {{u}^{2}} - {{A}^{2}}$ > 0 и перепишем выражение для $G(u)$ из (4.1) в следующем виде

Обозначим

Из (4.6), (4.7) имеем

Из (4.8) следует, что неравенство $G{\text{'}}(u) < 0$ эквивалентно неравенству $E{\text{'}}(u) > 0$. Используя (4.8), получим

Из последнего соотношения следует, что неравенство $E{\text{'}}(u) > 0$ эквивалентно неравенству $P(u) > 0$. Введем еще обозначения

Тогда, используя (4.8) и (4.9), получим

Таким образом, неравенство $P(u) > 0$ эквивалентно неравенству $Q(u) > 0$.

Итак, надо установить справедливость неравенства $Q(u) > 0$, при $u \in ({{u}_{1}},{{u}_{2}})$, где $Q(u)$ дается формулами из (4.11), (4.10). Здесь ${{u}_{1}}$, ${{u}_{2}}$ – корни уравнения $x = \varepsilon u - {{u}^{2}} - {{A}^{2}}$ = 0, которые даются формулами (4.4), причем $x(u) > 0$, $u \in ({{u}_{1}},{{u}_{2}})$. Введем еще в рассмотрение величины ${{u}_{3}}$, ${{u}_{4}}$ – корни квадратного уравнения $y = \frac{1}{3}(\varepsilon u + {{u}^{2}}) - {{A}^{2}} = 0$, которые даются следующими формулами

Отметим, что

Из (4.4), (4.12) и неравенства ${{A}^{2}} < 0.25{{\varepsilon }^{2}}$ следуют неравенства

Исходя из неравенств (4.13), имеем три возможных случая:

Далее, рассмотрим каждый из этих случаев в отдельности.

Случай 1. Здесь $u \in ({{u}_{1}},{{u}_{4}})$. Тогда имеем

Для $Q(u)$ из (4.11) получим

т.е. неравенство $Q(u) > 0$ выполнено.

Случай 2. Здесь $u \in ({{u}_{4}},0.5\varepsilon )$. В этом случае имеем неравенства

Обозначим $\mu = x - y = \frac{{2u}}{3}(\varepsilon - 2u) > 0$. Тогда получим для Q(u) из (4.11)

Используя неравенства (34), из последнего соотношения получим оценку

Покажем, что ${{Q}_{0}} > 0$. Сначала установим справедливость неравенства

Используя обозначения для μ, y₀, получим, что последнее неравенство эквивалентно следующему

Последнее неравенство выполнено, так как квадратный трехчлен относительно $u$ не имеет вещественных корней. Далее, для доказательства неравенства ${{Q}_{0}} > 0$ достаточно показать, согласно (4.15), справедливость неравенства

Возводя в квадрат левую и правую части этого неравенства можно убедиться в его справедливости (мы не приводим подробных выкладок ввиду их громоздкости). Таким образом, в этом случае доказано, что $Q(u) > {{Q}_{0}} > 0$, т.е. неравенство $Q(u) > 0$ выполнено.

Случай 3. Здесь $u \in \left( {0.5\varepsilon ,{{u}_{2}}} \right)$. В этом случае мы имеем неравенство

Тогда, согласно (4.11) имеем следующую оценку

Покажем, что ${{Q}_{1}}(u) = {{k}^{2}}{{u}^{3}} - {{y}^{2}} - y\sqrt {{{k}^{2}}{{u}^{3}} + {{y}^{2}}} > 0$. Имеем

Вспоминая формулу для $y$, запишем последнее неравенство в следующем эквивалентном виде

Для доказательства неравенства $p(u) > 0$ при $u \in (0.5\varepsilon ,\varepsilon )$, вычисляем производные

Несложно проверить, что $p{\text{''}}(u) > 0$ при $u \in (0.5\varepsilon ,\varepsilon )$. Тогда имеем на этом участке и $p{\text{'}}(u) > 0$, так как несложно проверяется, что $p{\text{'}}(0.5\varepsilon ) > 0$. Таким образом, для справедливости неравенства $p(u) > 0$ при $u \in (0.5\varepsilon ,\varepsilon )$ достаточно установить, что $p(0.5\varepsilon ) > 0$. Вычисляем

Таким образом, установлено, что $Q(u) > {{Q}_{1}}(u) > 0$ при $u \in (0.5\varepsilon ,\varepsilon )$. Таким образом, неравенство $Q(u) > 0$ верно и в этом случае.

Утверждение полностью доказано.

5. Заключение. В статье рассмотрены задачи о поиске равновесных конфигураций тяжелой нерастяжимой нити-цепочки на гладких поверхностях: конусе и сфере. Полное исследование таких задач сводится к аналитическому исследованию эллиптических интегралов 3-го рода как функций некоторого числа параметров. Такие исследования, как показано в настоящей статье, наталкиваются на определенные математические трудности, которые в случае конической или сферической поверхностей могут быть преодолены. Для более сложных типов поверхностей, вероятно, потребуется использование численных методов.