Известия РАН. Механика твердого тела, 2021, № 4, стр. 121-141
МОДЕЛИРОВАНИЕ НОРМАЛЬНОЙ КОНТАКТНОЙ ЖЕСТКОСТИ И ДЕМПФИРОВАНИЯ АНИЗОТРОПНОГО ВЗАИМОДЕЙСТВИЯ
Чжицян Гао a, *, Вэйпин Фу a, Вэнь Ван a, Шуанци Ван a, Чжифэй Сюэ b
a Школа механики и точного приборостроения Сианьский технологический университет
Сиань, Шэньси, КНР
b Государственная лаборатория энергосистем тракторов, China YITUO Group Co., Ltd
City, КНР
* E-mail: gaozhiqiang@xaut.edu.cn
Поступила в редакцию 16.06.2020
После доработки 21.12.2020
Принята к публикации 22.12.2020
Аннотация
При контакте двух анизотропных шероховатых поверхностей их взаимодействие оказывается анизотропным или изотропным контактом, который близок к контакту азимутальных углов неровностей на микроскопическом уровне. Анизотропия / изотропия межфазного контакта будет влиять на нормальную контактную жесткость и демпфирование механических соединений. Предложена модель нормальной контактной жесткости и демпфирования между двумя анизотропными шероховатыми поверхностями, которая включает эффекты неровностей при плотном контакте и смежных неровностей. Законы влияния степени согласования контактов и анизотропии контакта на нормальную контактную жесткость и демпфирование контакта выявлены с помощью серии модельных экспериментов. Показано, что нормальной контактной жесткостью и демпфированием можно управлять, регулируя топографические особенности поверхности и ориентацию контакта между механическими частями.
1. Введение. Морфология поверхности и шероховатость деталей обуславливается режущими способами обработки материалов. При описании шероховатой поверхности часто принимается что высота, наклон и кривизна неровностей распределены случайным образом. Кроме того, поскольку поверхности деталей обрабатываются токарной обработкой, фрезерованием, строганием и т.д., ориентация механической текстуры поверхности соответствует направлению движения режущих инструментов относительно обрабатываемых деталей. Равномерность ориентации текстуры поверхности можно описать анизотропией или изотропией. При контакте двух анизотропных шероховатых поверхностей их взаимодействие может быть анизотропным или изотропным, что определяется азимутальными углами неровности контакта на микроскопическом уровне, а нормальная контактная жесткость и демпфирование различны для изотропного и анизотропного контактов. Общая контактная жесткость взаимодействий составляет более 60% от общей жесткости станка, а демпфирование контакта составляет примерно 90% от демпфирования всего станка.
Контактная нагрузка и реальная площадь контакта сильно анизотропных шероховатых поверхностей изучаются А. Бушем и др. [1], исследование показывает, что различие в режимах деформации изотропных и анизотропных поверхностей зависит от их соответствующих поверхностных характеристики. Таким образом, необходимо изучить нормальную контактную жесткость и демпфирование изотропного и анизотропного контакта. Выявление законов влияния степени согласования контакта и контактной анизотропии на нормальную контактную жесткость и демпфирование имеет большое значение. Жесткость и демпфирование всей машины можно регулировать путем изменения топографических характеристик поверхности и ориентации контакта между механическими частями в соответствии с законами влияния. Исследование контакта шероховатых поверхностей впервые было предложено в работе [2] Гринвудом и Уильямсоном, которые исследовали контакт гладких жестких плоских поверхностей, контактирующих с шероховатой поверхностью, с использованием статистического метода. Кроме того, для исследования поведения контакта между двумя шероховатыми поверхностями использовались некоторые упрощенные методы, например, модели, CEB [3], KE [4], KKE [5], JG [6, 7] и др., что в некоторой степени решало сложную проблему контактного взаимодействия. Эти модели предполагают, что контакт между двумя шероховатыми поверхностями эквивалентен контакту между шероховатой поверхностью и гладкой жесткой плоскостью. Однако при реальном контакте многие контактирующие неровности плотно прилегают друг к другу [8]. Тогда контакт двух шероховатых поверхностей не может напрямую рассматриваться как контакт между шероховатой поверхностью и гладкой жесткой плоскостью. Для плотного контакта неровностей были предложены модели поверхностного контакта, например, модель AF [9], модель SF [10, 11], модель Бина [12] и т. д. Кроме того, также были предложены некоторые модели плотного контакта неровностей со скользящей неровностью, такие как модель Ягера [13], модель Джексона [14], модель Малвихилла [15], модель Ши [16], модель Фолкнера [17] и др. И все больше и больше исследователей начинают осознавать важность плотного контакта неровностей для межфазных характеристик. В большинстве моделей плотного контакта неровностей использовалась деформация нормальной компоненты перемещения для получения касательной компоненты перемещения в соответствии с соотношением для расстояния между верхними и нижними неровностями и углом контакта неровностей с использованием метода конечных элементов. Когда пара неровностей плотно соприкасается под действием нормальной силы, происходит трение между верхними и нижними неровностями. С другой стороны, неизбежно взаимодействие смежных неровностей как деформируемого твердого тела, потому что все неровности соединены общим материалом основания. Так, были представлены многочисленные исследования взаимодействия неровностей, такие как модель ZC [18], модель CGP [19], модель CEP [20] и т. д. Однако обе эти модели основаны на предположении, что эквивалентная шероховатая поверхность контактирует с гладкой жесткой плоскостью, тогда все неровности соприкасаются вершинами. В этих моделях, основанных на предположении о единственной шероховатой поверхности, не учитывается влияние наклонной контактной силы на взаимодействие соседних неровностей. Моделирование случайной анизотропной гауссовой поверхности чрезвычайно сложно, поскольку для определения поверхности требуется по крайней мере пять параметров (дисперсия высоты поверхности m00, два главных среднеквадратичных уклона m02, m20 и две главные среднеквадратичные кривизны m04, m40) [1]. Гринвуд и Трипп [21], Уайтхаус и Арчард [22], Лонге и Хиггинс [23], Наяк [24, 25], Буш [1], Маккул [26], Уайтхаус и Филлипс [27, 28] проделали большую работу по построению модели анизотропной шероховатой поверхности. В частности, Бучковски и др. [29] была построена упруго-пластическая статистическая модель, с сильно анизотропной шероховатой поверхностью. Из модели Буша можно обнаружить, что степень анизотропии серьезно влияет на характеристики контакта. Кроме того, когда две анизотропные шероховатые поверхности контактируют, анизотропия контакта является неопределенной. Чтобы устранить недостатки существующих моделей, в этой статье представлена модель нормального контакта между двумя шероховатыми поверхностями, которая учитывает контакт плотный контакт неровностей, взаимодействие соседних неровностей и межфазную анизотропию. Сначала изучается поведение плотного контакта неровностей между парой неровностей, а затем с помощью механики упругого контакта анализируется взаимодействие соседних неровностей. По изменению азимутальных углов контакта выявлено анизотропное влияние на контактные характеристики взаимодействия. После этого могут быть рассчитаны в соответствии со статистической теорией нормальные контактные силы, нормальное рассеивание энергии контакта, нормальная контактная жесткость и нормальное демпфирование контакта между анизотропными контактными поверхностями. Наконец, область контакта, состоящую из двух анизотропных шероховатых поверхностей, можно рассматривать как систему с одной степенью свободы с вязким демпфированием. Эквивалентное демпфирование может быть получено приравниванием энергии, рассеиваемой вязким демпфированием, к энергии невязкой демпфирующей силы с предполагаемым гармоническим движением.
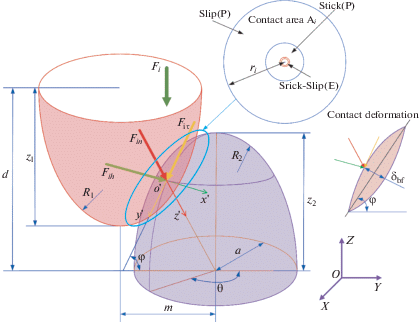
2. Плотный контакт неровностей. Графическая схема плотного соприкосновения неровностей представлена на рис. 1. Пара неровностей (высота неровностей выражается как z1 и z2) контактирует с силой ${{F}_{i}}$ (сила включает статическую силу и динамическую силу ${{F}_{i}} = {{F}_{{is}}} + {{F}_{{id}}}$), которую можно разложить на нормальную составляющую силы ${{F}_{{in}}}$, касательную нормальную составляющую силы ${{F}_{{ih}}}$ и горизонтальную составляющую силы ${{F}_{{i\tau }}}$ в направлениях $z{\kern 1pt} '$, $y{\kern 1pt} '$ и $x{\kern 1pt} '$ соответственно. Контактная деформация в направлении $z'$ обозначена как ${{\delta }_{{bf}}}$. d – среднее расстояние между двумя шероховатыми поверхностями. Радиус контактной поверхности неровностей обозначен как ${{r}_{i}}$, a – радиус области деформации основного материала на дне контактирующей неровности, $R$ – радиус неровности. Угол контакта и азимутальный угол контакта могут быть обозначены как $\varphi $ и $\theta $ соответственно, m – расстояние между верхней и нижней неровностями.
Согласно модели KE, предложенной в [4], можно выделить четыре режима деформации: упругая стадия, упруго-пластическая зона I, упруго-пластическая зона II и полная пластическая стадия. Ю. Кадин и др. [5] объединяют упруго-пластические зоны I и II в упруго-пластическую стадию, доходящую даже до полной пластической стадии. Чтобы упростить сложную задачу о контакте двух шероховатых поверхностей, деформацию неровностей можно разделить на упругую ($0 < \delta _{{bf}}^{*} \leqslant 1$) и упруго-идеально пластическую ($1 < \delta _{{bf}}^{*} < + \infty $) в соответствии с моделью Кадина [5]. Верхний индекс * обозначает безразмерную переменную, а $\delta _{{bf}}^{*}$ можно вычислить как $\delta _{{bf}}^{*} = {{{{\delta }_{{bf}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{bf}}}} {{{\delta }_{{bc}}}}}} \right. \kern-0em} {{{\delta }_{{bc}}}}}$, где ${{\delta }_{{bc}}}$ – критическая деформация в начале пластической деформации. ${{\delta }_{{bc}}}$ можно получить с помощью модели CEB [3] в виде ${{\delta }_{{bc}}} = {{\left( {{{\pi SH} \mathord{\left/ {\vphantom {{\pi SH} {2E}}} \right. \kern-0em} {2E}}} \right)}^{2}}R$ где S, H, E – максимальный коэффициент контактного давления, твердость более мягкого материала и модуль упругости Герца соответственно.
2.1.1. Упругая стадия (нагружение). Деформация неровностей находится в упругой стадии, когда безразмерная деформация неровностей $\delta _{{bf}}^{*}$ меньше единицы. Деформация $\delta _{{bf}}^{*}$ включает статическую и динамическую части $\delta _{{bf}}^{*}\, = \,\delta _{{bfs}}^{*} + \delta _{{bfd}}^{*}\, = \,\delta _{{bfs}}^{*} + \delta _{{bfdm}}^{*}{\text{sin}}(\omega t)$ на силу ${{F}_{i}}$. Неровность находится в стадии нагружения в промежутке ${{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } {(2\omega )}}} \right. \kern-0em} {(2\omega )}} \leqslant t$ ≤ ≤ π/(2ω). Согласно теории Герца, безразмерная нормальная составляющая силы на неровностях в упругой стадии может быть получена следующим образом:
(2.1)
$F_{{ine}}^{*} = {{(\delta _{{bf}}^{*})}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$(2.2)
$K_{{ine}}^{*} = \frac{{dF_{{ine}}^{*}}}{{d\delta _{{bf}}^{*}}} = \frac{3}{2}{{(\delta _{{bf}}^{*})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$2.1.2. Упругая стадия (разгрузка). Неровность находится в стадии разгрузки в интервале ${\pi \mathord{\left/ {\vphantom {\pi {(2\omega )}}} \right. \kern-0em} {(2\omega )}} \leqslant t \leqslant {{3\pi } \mathord{\left/ {\vphantom {{3\pi } {(2\omega }}} \right. \kern-0em} {(2\omega }})$. Поскольку неровность находится в стадии полной упругости, сила нормальной составляющей разгрузки равна силе нормальной составляющей нагрузки, которая также может быть выражена как
(2.3)
$F_{{ine\_un}}^{*} = {{(\delta _{{bf}}^{*})}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$(2.4)
$K_{{ine\_un}}^{*} = \frac{{dF_{{ine\_un}}^{*}}}{{d\delta _{{bf}}^{*}}} = \frac{3}{2}{{(\delta _{{bf}}^{*})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$2.1.3. Упруго-идеально пластичная стадия (нагружение). Если неровность безразмерной деформации больше единицы, неровность вызывает упруго-пластическую деформацию или полную пластическую деформацию. Упруго-пластические стадии и полная пластическая стадия могут быть скомбинированы в упруго-идеально пластическую стадию. Согласно модели Кадина [5], нормальная составляющая силы в упруго-идеально пластической стадии может быть выражена как
а контактная жесткость нормального компонента при нагрузке может быть получена согласно(2.6)
$K_{{inp}}^{*} = \frac{{dF_{{inp}}^{*}}}{{d\delta _{{bf}}^{*}}} = 1.6764{{(\delta _{{bf}}^{*} - 1)}^{{0.27}}}$2.1.4. Упруго-идеально пластичная стадия (разгрузка). Точно так же неровность находится в стадии разгрузки в интервале времени ${\pi \mathord{\left/ {\vphantom {\pi {(2\omega )}}} \right. \kern-0em} {(2\omega )}} \leqslant t \leqslant {{3\pi } \mathord{\left/ {\vphantom {{3\pi } {(2\omega }}} \right. \kern-0em} {(2\omega }})$. Согласно модели Кадина [5], нормальная составляющая силы разгрузки может быть выражена как
(2.7)
$F_{{inp\_m}}^{*} = F_{{inp\_m}}^{*}{{\left( {\frac{{\delta _{{bf}}^{*} - \delta _{r}^{*}}}{{\delta _{{bm}}^{*} - \delta _{r}^{*}}}} \right)}^{{{{n}_{p}}}}}$(2.8)
$K_{{inp\_un}}^{*} = \frac{{dF_{{inp\_un}}^{*}}}{{d\delta _{{bf}}^{*}}} = \frac{{{{n}_{p}}F_{{inp\_m}}^{*}}}{{\delta _{{bf}}^{*} - \delta _{r}^{*}}}{{\left( {\frac{{\delta _{{bf}}^{*} - \delta _{r}^{*}}}{{\delta _{{bfm}}^{*} - \delta _{r}^{*}}}} \right)}^{{{{n}_{p}}}}}$2.2. Анализ тангенциальной составляющей. Каттанео [30] и Миндлин [31] независимо исследовали проблему контакта упругих неровностей под действием касательной силы, которая показывает, что контакт имеет квазистатический переход от полного прилипания к частичному скольжению. Радиус всей площади прилипания можно выразить как
(2.9)
$c_{{i(e,p)}}^{*} = r_{{i(e,p)}}^{*}{{\left( {1 - \frac{{F_{{i\tau (e,p)}}^{*}}}{{{{\mu }_{{(e,p)}}}F_{{in(e,p)}}^{*}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}$2.2.1. Случай полного прилипания (нагружение). Как упоминалось выше, проскальзывание $\zeta _{b}^{*}$ включает статическое и динамическое проскальзывания $\zeta _{b}^{*}\, = \,\zeta _{{bs}}^{*} + \zeta _{{bd}}^{*}$ = = $\zeta _{{bs}}^{*} + \zeta _{{bdm}}^{*}{\text{sin}}(\omega t)$. Неровность находится в стадии нагружения в промежутке времени ${{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } {(2\omega )}}} \right. \kern-0em} {(2\omega )}} \leqslant t \leqslant {\pi \mathord{\left/ {\vphantom {\pi {(2\omega )}}} \right. \kern-0em} {(2\omega )}}$. Как показано на рис. 2, в упругой стадии в основном наблюдается состояние полного прилипания.
Согласно модели Эритена [32] касательная составляющая силы в состоянии прилипания может быть выражена как
и контактная жесткость касательной компоненты в состоянии полного прилипания может быть получена с помощью(2.11)
$K_{{i\tau e}}^{*} = \frac{{dF_{{i\tau e}}^{*}}}{{d\zeta _{b}^{*}}} = \frac{3}{2}r_{{ie}}^{*}$2.2.2. Случай полного прилипания (разгрузка). Неровность находится в стадии разгрузки для промежутка времени ${\pi \mathord{\left/ {\vphantom {\pi {(2\omega )}}} \right. \kern-0em} {(2\omega )}} \leqslant t \leqslant {{3\pi } \mathord{\left/ {\vphantom {{3\pi } {(2\omega }}} \right. \kern-0em} {(2\omega }})$. Касательная составляющая разгружающего усилия равна касательной составляющей нагружающего усилия, поскольку верхняя и нижняя неровности находятся в состоянии полного прилипания, тогда жесткость касательного контакта при разгрузке также равна жесткости касательного контакта нагружения.
2.2.3. Состояние частичного скольжения (нагружение). На стадии упругой идеально пластической деформации в основном присутствует состояние частичного скольжения. Согласно модели Эритена [32], тангенциальная составляющая силы в состоянии частичного скольжения может быть получена как
(2.12)
$F_{{i\tau p}}^{*} = {{\mu }_{p}}F_{{inp}}^{*}\left( {1 - {{{\left( {1 - \frac{{r_{{ip}}^{*}\zeta _{b}^{*}}}{{{{\mu }_{p}}F_{{inp}}^{*}}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right)$(2.13)
$K_{{i\tau p}}^{*} = \frac{{dF_{{i\tau p}}^{*}}}{{d\zeta _{b}^{*}}} = 1.5r_{{ip}}^{*}{{\left( {1 - \frac{{r_{{ip}}^{*}\zeta _{b}^{*}}}{{{{\mu }_{p}}F_{{inp}}^{*}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$2.2.4. Состояние частичного скольжения (разгрузка). Согласно модели Эритена [32], касательная составляющая силы разгрузки в состоянии частичного скольжения может быть выражена как
(2.14)
$F_{{i\tau p\_un}}^{*} = F_{{i\tau p\_m}}^{*} - 2\mu F_{{inp}}^{*}\left( {1 - {{{\left( {0.5\left( {\frac{{\zeta _{b}^{*}A_{{ip}}^{*}}}{{{{\mu }_{p}}F_{{inp}}^{*}}} + {{{\left( {1 - \frac{{F_{{i\tau p\_m}}^{*}}}{{{{\mu }_{p}}F_{{inp}}^{*}}}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + 1} \right)} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right)$(2.15)
$K_{{i\tau p\_un}}^{*} = \frac{{dF_{{i\tau p\_un}}^{*}}}{{d\zeta _{b}^{*}}} = 1.5{{A}_{{ip}}}{{\left( {\frac{{0.5\zeta _{b}^{*}{{A}_{{ip}}}}}{{{{\mu }_{p}}F_{{inp}}^{*}}} + 0.5{{{\left( {1 - \frac{{F_{{i\tau p\_m}}^{*}}}{{{{\mu }_{p}}F_{{inp}}^{*}}}} \right)}}^{{2/3}}} + 0.5} \right)}^{{1/2}}}$2.3. Анализ горизонтальной компоненты. Контакт неровностей имеет тот же механизм проскальзывания, что и механизм касательного проскальзывания (включая прилипание и проскальзывание) в направлении горизонтальной составляющей. Для краткости подробное описание процессов здесь опущено.
2.4. Нормальная результирующая сила и жесткость. В разделах 2.1 и 2.2 нормальная и касательная составляющие анализируются на упругой и упруго-идеально пластической стадиях соответственно. Тогда могут быть легко получены нормальные результирующие сила и жесткость в упругих и упруго-идеально пластических стадиях.
2.4.1. Упругая стадия (нагружение). Нормальная результирующая сила может быть получена как
(2.16)
$F_{{ie}}^{*} = \sqrt {{{{(\delta _{{bf}}^{*})}}^{3}} + {{{\left( {\frac{3}{2}\zeta _{b}^{*}r_{i}^{*}} \right)}}^{2}} + {{{\left( {\frac{3}{2}\xi _{b}^{*}r_{i}^{*}} \right)}}^{2}}} $Результирующую контактную жесткость можно рассчитать по формуле
2.4.2. Упругая стадия (разгрузка). Результирующие сила и жесткость при разгрузке такие же, как результирующие сила и жесткость при нагрузке, потому что в упругой стадии нет ни пластической деформации, ни частичного скольжения.
2.4.3. Упруго-идеально-пластическая стадия (нагружение). Нормальная результирующая сила в упруго-идеально пластической стадии может быть выражена как
(2.18)
$F_{{ip}}^{*}\, = \,\sqrt {{{{(1.32{{{(\delta _{{bf}}^{*}\, - \,1)}}^{{1.27}}}\, + \,1)}}^{2}}\, + \,{{{\left( {{{\mu }_{p}}F_{{inp}}^{*}\left( {1{\kern 1pt} - {\kern 1pt} {{{\left( {1\, - \,\frac{{r_{{ip}}^{*}\zeta _{b}^{*}}}{{{{\mu }_{p}}F_{{in}}^{*}}}} \right)}}^{{3/2}}}} \right)} \right)}}^{2}}\, + \,\left( {{{\mu }_{p}}F_{{inp}}^{*}\left( {1\, - \,{{{\left( {1\, - \,\frac{{r_{{ip}}^{*}\xi _{b}^{*}}}{{{{\mu }_{p}}F_{{inp}}^{*}}}} \right)}}^{{3/2}}}} \right)} \right){{}^{2}}} $Результирующую контактную жесткость можно рассчитать по формуле
(2.19)
$K_{{ip}}^{*} = \sqrt {2.81{{{(\delta _{{bf}}^{*} - 1)}}^{{0.54}}} + 2.25{{{(r_{{ip}}^{*})}}^{2}}\left( {2 - \frac{{r_{{ip}}^{*}(\zeta _{b}^{*} + \xi _{b}^{*})}}{{{{\mu }_{p}}F_{{inp}}^{*}}}} \right)} $2.4.4. Упруго-идеально пластическая стадия (разгрузка). На этапе разгрузки нормальная результирующие разгружающие усилие может быть выражена как
(2.20)
$F_{{ip\_un}}^{*} = \sqrt {{{{(F_{{inp\_un}}^{*})}}^{2}} + {{{(F_{{i\tau p\_un}}^{*})}}^{2}} + {{{(F_{{ihp\_un}}^{*})}}^{2}}} $(2.21)
$K_{{ip\_un}}^{*} = \sqrt {{{{(K_{{inp\_un}}^{*})}}^{2}} + {{{(K_{{i\tau p\_un}}^{*})}}^{2}} + {{{(K_{{ihp\_un}}^{*})}}^{2}}} $3. Анализ деформации контактной неровности. Большинство неровностей плотно контактируют, когда две шероховатые поверхности соприкасаются под действием нормальной силы, и между соседними неровностями на одной и той же шероховатой поверхности происходит взаимодействие. Предполагается, что каждая контактирующая неровность независимо деформируется в классических моделях GW [2], CEB [3], ZMC [34], KE [4], JG [6,7] и т. д. Однако взаимодействие соседних неровностей как сплошного деформируемого твердого тела неизбежно, поскольку все неровности соединены общим материалом подложки. Чжао и др. [34] и Дженг и др. [35], соответственно, изучали взаимодействие между соседними неровностями, используя принцип Сен-Венана [36] и формулу Лява [37], но эти модели основаны на предположении контакта гладкой жесткой плоскости, контактирующей с эквивалентной шероховатой поверхностью, что привело к тому, что все неровности соприкасаются на вершинах. Тогда пренебрегают влиянием наклонной контактной силы на взаимодействие соседних неровностей. Чтобы устранить этот недостаток, в этом разделе была предложена улучшенная модель взаимодействия соседних неровностей. Когда две шероховатые поверхности контактируют под действием нормальной силы, микроконтактная деформация между двумя шероховатыми поверхностями в основном включает деформацию контактирующих неровностей, деформацию основного материала и деформацию взаимодействия между соседними неровностями.
3.1. Деформация плотного контакта неровностей. Нормальная деформация, не включающая деформацию взаимодействия, может быть выражена как
(3.1)
${{\delta }_{{{v}l}}} = {{\delta }_{{{v}f}}} + {{\zeta }_{{v}}} = {{z}_{1}} + {{z}_{2}} - d - {{m}^{2}}{\text{/}}(2{{R}_{t}})$(3.2)
${{\delta }_{{{v}l}}} = {{\delta }_{{{v}f}}} + {{\zeta }_{{v}}} = {{z}_{1}} + {{z}_{2}} - d - 0.5{{R}_{t}}{\text{t}}{{{\text{g}}}^{2}}\varphi $Согласно уравнению (3.2), можно сделать выводы: деформация контактной неровности равна ${{\delta }_{{{v}l}}} = {{z}_{1}} + {{z}_{2}} - d$ когда контактный угол равен нулю, что является деформацией жесткой гладкой плоскости, контактирующей с эквивалентной шероховатой поверхностью, и совпадает с деформацией модели GW, модели CEB и модели KKE. Член $0.5{{R}_{t}}{\text{t}}{{{\text{g}}}^{2}}\varphi $ – деформация, вызванная плотным контактом неровностей. Таким образом, контакт вершины к вершине является частным случаем, когда угол контакта равен нулю.
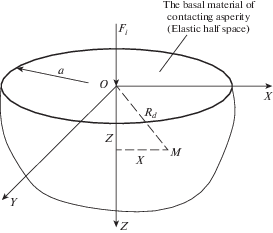
3.2. Деформация основного материала. Основной материал контактирующих неровностей можно принять как упругое полупространство под действием нормальной сосредоточенной силы, как показано на рис. 2. Здесь ${{F}_{i}}$ – сосредоточенная сила, т.е. нормальная контактная сила неровностей; a – радиус области деформации основного материала на дне контактирующей неровности; $(x,\;z)$ – координаты произвольной точки M в направлениях оси x и оси z соответственно; ${{R}_{d}}$ – расстояние между точкой M и началом координат $OXYZ$, ${{R}_{d}} = \sqrt {{{x}^{2}} + {{z}^{2}}} $.
Деформация материала основания может быть получена при z = 0 и $x = r$ согласно модели Буссинеска
где r – радиус контактной площади неровности ${{A}_{i}}$ в форме $r = \sqrt {{{{{A}_{i}}} \mathord{\left/ {\vphantom {{{{A}_{i}}} \pi }} \right. \kern-0em} \pi }} $; ${{F}_{i}}$ – нормальная контактная сила контактной неровности ${{F}_{i}} = {{P}_{i}}{{A}_{i}}$; ${{P}_{i}}$ – нормальное контактное давление на неровность. Уравнение (3.3) можно преобразовать(3.4)
${{\delta }_{s}} = \frac{{(1 - {{{v}}^{2}})}}{{\sqrt \pi }}\frac{{{{P}_{i}}\sqrt {{{A}_{i}}} }}{E}$3.3. Деформация взаимодействия между соседними неровностями. Область деформации основного материала каждой контактирующей неровности можно принять как круговую область с радиусом a. Если в области деформации двух соседних неровностей есть пересекающиеся части, то две соседние неровности взаимодействуют, в противном случае взаимодействие отсутствует. Согласно уравнению (3.4), деформация взаимодействия соседних неровностей может быть получена как
где a – радиус области деформации материала основания ${{A}_{s}}$, в форме $a = \sqrt {{{A}_{s}}{\text{/}}\pi } $;${{F}_{j}}$ – нормальные контактные силы на прилегающей части контактной неровности ${{F}_{j}} = {{P}_{j}}{{A}_{j}}$; ${{P}_{j}}$ – контактное давление на соседнюю неровность. Нижним индексом $j$ обозначена соседняя неровность. Тогда деформацию, вызванную прилегающей неровностью, можно выразить согласно(3.6)
${{\delta }_{{\operatorname{int} }}} = \frac{{(1 - {{{v}}^{2}}){{P}_{j}}}}{{\sqrt \pi E}}\frac{{{{A}_{j}}}}{{\sqrt {{{A}_{s}}} }}$Согласно принципу Сен-Венана, если силы, действующие на небольшую часть поверхности упругого тела, заменяются другой статически эквивалентной системой сил, действующих на ту же часть поверхности, это перераспределение нагрузки вызывает существенные изменения в локальном напряжении, но оказывает незначительное влияние на напряжения вдали от контакта на расстоянии, которое велико по сравнению с линейными размерами поверхности, на которой изменяются силы. Однако пока это строго не доказано. Чтобы полностью учесть взаимодействие между соседними неровностями, разумно предположить, что ${{A}_{s}} = 3{{A}_{j}}$ в соответствии с принципом Сен-Венана, тогда уравнение (3.6) можно преобразовать в
(3.7)
${{\delta }_{{\operatorname{int} }}} = \frac{{(1 - {{{v}}^{2}})}}{{\sqrt {3\pi } }}\frac{{{{P}_{j}}\sqrt {{{A}_{j}}} }}{E}$Полную деформацию контактной неровности можно получить как
(3.8)
$\begin{gathered} {{\delta }_{{v}}} = {{\delta }_{{{v}l}}} + {{\delta }_{s}} + {{\delta }_{{\operatorname{int} }}} = \\ \, = {{z}_{1}} + {{z}_{2}} - d - 0.5{{R}_{s}}{\text{t}}{{{\text{g}}}^{2}}\varphi + \frac{{(1 - {{{v}}^{2}}){{P}_{i}}\sqrt {{{A}_{i}}} }}{{\sqrt \pi E}} + \frac{{(1 - {{{v}}^{2}}){{P}_{j}}\sqrt {{{A}_{j}}} }}{{\sqrt {3\pi } E}} \\ \end{gathered} $Аналогичным образом предполагается, что, согласно принципу Сен-Венана, поверхностное давление и площадь контакта соседних неровностей равны ${{P}_{j}} = {{P}_{i}}{\text{/}}3$ и ${{A}_{j}} = {{A}_{i}}{\text{/}}3$ соответственно. Полная деформация неровностей с учетом плотного контакта и взаимодействия неровностей может быть получена согласно
(3.9)
$\begin{gathered} {{\delta }_{{v}}} = {{\delta }_{{{v}l}}} + {{\delta }_{s}} + {{\delta }_{{\operatorname{int} }}} = \\ \, = {{z}_{1}} + {{z}_{2}} - d - 0.5{{R}_{s}}{\text{t}}{{{\text{g}}}^{2}}\varphi + \frac{{10}}{9}\frac{{\left( {1 - {{{v}}^{2}}} \right){{P}_{i}}\sqrt {{{A}_{i}}} }}{{\sqrt \pi E}} \\ \end{gathered} $Согласно уравнению (3.9) можно получить, что сумма основной деформации материала и деформации взаимодействия равна ${{\delta }_{s}} + {{\delta }_{{\operatorname{int} }}} = 1.05{{P}_{i}}\sqrt {{{A}_{i}}} {\text{/}}E$ когда коэффициент Пуассона материала равен 0.23. Коэффициент 1.05 отличается от значения 0.96, данного моделью Чавареллы [19], потому что модель Чавареллы предполагает, что материал основания с контактирующими неровностями несет равномерное давление, в то время как предлагаемая модель предполагает, что материал основания находится под сосредоточенной нагрузкой.
Преобразуя уравнение (3.9) к безразмерному виду в форме
(3.10)
$\delta _{{v}}^{*} = \delta _{{{v}l}}^{*} + \delta _{s}^{*} + \delta _{{\operatorname{int} }}^{*} = z{\kern 1pt} *\; - d{\kern 1pt} * - 0.5R_{s}^{*}{\text{t}}{{{\text{g}}}^{2}}\varphi + \frac{{10(1 - {{{v}}^{2}})P_{a}^{*}\sqrt {A_{i}^{*}} }}{{9\sqrt \pi }}$4. Анализ анизотропии на границе раздела. Поверхности, обработанные токарной обработкой, обточкой или шлифованием, имеют ориентацию, соответствующую направлению движения режущих инструментов относительно заготовок, и потому необходимо использовать модель анизотропных шероховатых поверхностей. Текстура шероховатой поверхности изучалась многими учеными [1, 22–29] на основе статистического подхода для выявления контактных характеристик анизотропных шероховатых поверхностей. Однако эти методы очень сложны. Кроме того, для межфазной контактной анизотропии не определено, когда происходит контакт двух анизотропных шероховатых поверхностей. Чтобы упростить проблему анизотропии и точно выявить характеристики межфазного контакта, предлагается улучшенная анизотропная межфазная модель в соответствии с моделями Мисры [38, 39]. Высота неровностей, азимутальные углы неровностей и азимутальные углы неровностей области контакта являются основными параметрами, влияющими на контактные характеристики при взаимодействии двух шероховатых поверхностей.
4.1. Распределение высот неровностей. Согласно модели GW [2], модели GT [21], модели Буша [1], модели Наяка [24, 25] и модели Маккула [26], высота неровностей обработанной поверхности соответствует распределению Гаусса со стандартным отклонением ${{\sigma }_{z}}$, самые высокие и самые короткие неровности разделены с приблизительным расстоянием $3{{\sigma }_{z}}$. Можно предположить, что на номинальной поверхности контакта ${{A}_{n}}$ имеется неровность $N$, а среднее расстояние между двумя шероховатыми поверхностями при заданных нагрузках принимается равным d. z – высота неровностей, отсчитываемая от средней высоты неровностей. Количество контактирующих неровностей можно прогнозировать с помощью
(4.1)
${{n}_{z}} = N\int\limits_d^\infty {\Phi (z)dz} = \eta {{A}_{n}}\int\limits_d^\infty {\Phi (z)dz} $(4.2)
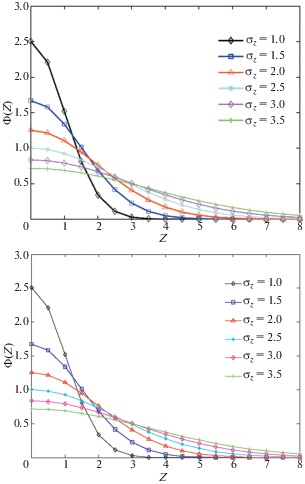
$\Phi (z) = \frac{1}{{{{\sigma }_{z}}\sqrt {2\pi } }}\exp \left( { - 0.5{{{\left( {\frac{z}{{{{\sigma }_{z}}}}} \right)}}^{2}}} \right)\quad \left( {0 \leqslant z < + \infty } \right)$На рис. 3 показано распределение вероятностей высот неровностей согласно уравнению (4.2), которое интуитивно показывает их взаимосвязь. Влияние стандартного отклонения высоты неровностей ${{\sigma }_{z}}$ на распределение вероятностей показано на рис. 4.
Рис. 4.
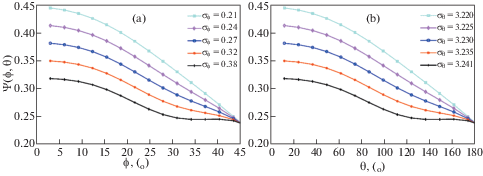
Распределение вероятности контактных (азимутальных) углов неровностей: (a) поведение ${{\sigma }_{\varphi }}$, (b) поведение ${{\sigma }_{\theta }}$.
Мы можем видеть, что поверхность с меньшим ${{\sigma }_{z}}$ имеет более концентрированные высоты неровностей в соответствии с рис. 3, что означает, что поверхность более гладкая. Поверхность становится более шероховатой с увеличением стандартного отклонения высоты неровностей ${{\sigma }_{z}}$.
4.2. Распределение контактного (азимутального) угла неровностей. Плотный контакт неровностей в основном зависит от контактного угла неровностей, в то время как однородность азимутального угла контакта определяет степень анизотропии межфазного контакта. Для описания распределения контактных (азимутальных) углов может быть использовано разложение смещенных сферических гармоник в сферических полярных координатах как функция плотности вероятности [38, 39], совместная функция плотности вероятности краевых углов и контактных азимутальных углов задается согласно
(4.3)
$\Psi (\varphi ,\theta ) = \frac{{b\sin \left( {b\varphi } \right)}}{{2\pi \sin \varphi }}\left( {1 + \frac{c}{4}\left( {3\cos (2c\varphi ) + 1} \right) + 3e{{{\sin }}^{2}}\left( {b\varphi } \right)\cos \left( {2\theta } \right)} \right)$Совместная функция плотности вероятности контактных углов неровностей и контактных азимутальных углов неровностей удовлетворяет уравнению (4.4).
(4.4)
$\int\limits_0^{2\pi } {\int\limits_0^{\pi /2a} {\sin \varphi \psi (\varphi ,\theta )d\varphi d\theta = 1} } $Тогда ${{n}_{z}}\psi (\varphi ,\theta )\sin \varphi d\varphi d\theta $ можно представить как количество неровностей контакта в течение $\sin \varphi d\varphi d\theta $, которые можно выразить как
Математическое ожидание контактных углов неровностей может быть получено с помощью
(4.6)
$E\left[ \varphi \right] = \int\limits_0^{\pi /2a} {\varphi \sin \varphi \psi (\varphi ,\theta )d\varphi d\theta } = \frac{{6 - b}}{{6a}}$Стандартная дисперсия углов контактной неровности может быть получена следующим образом:
(4.7)
$\begin{gathered} {{\sigma }_{\varphi }}{\text{ = }}E[{{\left( {\varphi - E\left[ \varphi \right]} \right)}^{2}}] = \int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi {2a}}} \right. \kern-0em} {2a}}} {{{{\left( {\varphi - E\left[ \varphi \right]} \right)}}^{2}}} \sin \varphi \psi \left( {\varphi ,\theta } \right)d\varphi = \\ \, = (36\pi - 108 + 20b - 6b\pi - {{b}^{2}}){\text{/}}36{{a}^{2}} \\ \end{gathered} $Точно так же математическое ожидание контактных азимутальных углов неровностей равно
(4.8)
$E[\theta ] = \int\limits_0^{2\pi } {\theta \sin \varphi \psi (\varphi ,\theta )d\theta = \pi } $Стандартная дисперсия контактных азимутальных углов неровностей
(4.9)
${{\sigma }_{\theta }} = E[{{\left( {\theta - E\left[ \theta \right]} \right)}^{2}}] = \int\limits_0^{2\pi } {{{{\left( {\theta - E\left[ \theta \right]} \right)}}^{2}}\sin \varphi \psi \left( {\varphi ,\theta } \right)d\theta } = c + {{\pi }^{2}}{\text{/}}3$Чтобы выявить влияние контактных углов неровностей и контактных азимутальных углов неровностей, в соответствии с уравнениями (4.3)–(4.9) были построены графики функции плотности вероятности для различных ${{\sigma }_{\varphi }}$ и ${{\sigma }_{\theta }}$, которые приведены на рис. 4. На рис. 4, а показано влияние ${{\sigma }_{\varphi }}$ на совместную функцию плотности вероятности. Можно обнаружить, что область контакта с большим ${{\sigma }_{\varphi }}$ имеет более дискретное распределение углов контакта неровностей, что означает, что степень согласования между неровностями на границе раздела хуже. Напротив, краевые углы неровностей более концентрированные, что означает, что степень согласования между двумя шероховатыми поверхностями лучше. На рис. 4, b показано влияние ${{\sigma }_{\theta }}$ на совместную функцию плотности вероятности. Мы можем обнаружить, что контактные азимутальные углы неровностей становятся более дискретными с увеличением ${{\sigma }_{\theta }}$, что означает, что контактная поверхность имеет тенденцию быть более изотропной. В противном случае область контакта имеет тенденцию быть более анизотропной.
5. Статистическая модель границы раздела. 5.1. Диссипация межфазной энергии. Нормальное контактное усилие нагружения может быть рассчитано с помощью контактного анализа неровностей в соответствии со статистической теорией следующим образом:
(5.1)
$\begin{gathered} F{\kern 1pt} * = F_{e}^{*} + F_{p}^{*} = \eta {{A}_{n}}\int\limits_{d{\kern 1pt} *}^{d{\kern 1pt} * + \delta _{{{v}c}}^{*}} {\int\limits_0^{2\pi } {\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi {2b}}} \right. \kern-0em} {2b}}} {F_{{ie}}^{*}\Psi (\varphi ,\theta )\sin \varphi d\varphi d\theta } } } \,\Phi {\kern 1pt} *(z{\kern 1pt} *)dz{\kern 1pt} * \\ \, + \eta {{A}_{n}}\int\limits_{d{\kern 1pt} * + \delta _{{{v}c}}^{*}}^{ + \infty } {\int\limits_0^{2\pi } {\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi {2b}}} \right. \kern-0em} {2b}}} {F_{{ip}}^{*}\Psi (\varphi ,\theta )\sin \varphi d\varphi d\theta } } } \,\Phi {\kern 1pt} *(z{\kern 1pt} *)dz{\kern 1pt} * \\ \end{gathered} $(5.2)
$\begin{gathered} F_{{un}}^{*} = F_{{e\_un}}^{*} + F_{{p\_un}}^{*} = \eta {{A}_{n}}\int\limits_{d{\kern 1pt} *}^{d_{{\min }}^{*} + \delta _{{{v}c}}^{*}} {\int\limits_0^{2\pi } {\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi {2b}}} \right. \kern-0em} {2b}}} {F_{{ie\_un}}^{*}\Psi (\varphi ,\theta )\sin \varphi d\varphi d\theta } } } \,\Phi {\kern 1pt} *(z{\kern 1pt} *)dz{\kern 1pt} * + \\ \, + \eta {{A}_{n}}\int\limits_{d_{{\min }}^{*} + \delta _{{{v}c}}^{*}}^{ + \infty } {\int\limits_0^{2\pi } {\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi {2b}}} \right. \kern-0em} {2b}}} {F_{{ip\_un}}^{*}{\rm H}(\delta _{{v}}^{*} - \delta _{{res}}^{*})\Psi (\varphi ,\theta )\sin \varphi d\varphi d\theta } } } \,\Phi {\kern 1pt} *(z{\kern 1pt} *)dz{\kern 1pt} * \\ \end{gathered} $Диссипация межфазной энергии во время цикла может быть выражена формулой
(5.3)
$E_{n}^{*} = \int\limits_{ - \delta _{{{v}m}}^{*}}^{\delta _{{{v}m}}^{*}} {(F{\kern 1pt} * - \,F_{{un}}^{*})d\delta _{{v}}^{*}} $5.2. Нормальная средняя динамическая контактная жесткость. Нормальную контактную жесткость на этапе нагружения можно рассчитать по формуле
(5.4)
$\begin{gathered} K{\kern 1pt} * = K_{e}^{*} + K_{p}^{*} = \eta {{A}_{n}}\int\limits_{d{\kern 1pt} *}^{d{\kern 1pt} * + \delta _{{{v}c}}^{*}} {\int\limits_0^{2\pi } {\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi {2b}}} \right. \kern-0em} {2b}}} {} K_{{ie}}^{*}\Psi (\varphi ,\theta )\sin \varphi d\varphi d\theta } } \,\Phi {\kern 1pt} *(z{\kern 1pt} *)dz + \\ \, + \eta {{A}_{n}}\int\limits_{d{\kern 1pt} * + \delta _{{{v}c}}^{*}}^{ + \infty } {\int\limits_0^{2\pi } {\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi {2b}}} \right. \kern-0em} {2b}}} {K_{{ip}}^{*}\Psi (\varphi ,\theta )\sin \varphi d\varphi d\theta } } } \,\Phi {\kern 1pt} *(z{\kern 1pt} *)dz \\ \end{gathered} $(5.5)
$\begin{gathered} K_{{un}}^{*} = K_{{e\_un}}^{*} + K_{{p\_un}}^{*} = \eta {{A}_{n}}\int\limits_{d{\kern 1pt} *}^{d_{{\min }}^{*} + \delta _{{{v}c}}^{*}} {\int\limits_0^{2\pi } {\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi {2b}}} \right. \kern-0em} {2b}}} {K_{{ie\_un}}^{*}\Psi (\varphi ,\theta )\sin \varphi d\varphi d\theta } \,} } \Phi {\kern 1pt} *(z{\kern 1pt} *)dz + \\ \, + \eta {{A}_{n}}\int\limits_{d_{{\min }}^{*} + \delta _{{{v}c}}^{*}}^{ + \infty } {\int\limits_0^{2\pi } {\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi {2b}}} \right. \kern-0em} {2b}}} {K_{{ip\_un}}^{*}{\rm H}(\delta _{{v}}^{*} - \delta _{{res}}^{*})\Psi (\varphi ,\theta )\sin \varphi d\varphi d\theta } \,} } \Phi {\kern 1pt} *(z{\kern 1pt} *)dz \\ \end{gathered} $Нормальная средняя динамическая контактная жесткость во время цикла может быть рассчитана следующим образом:
5.3. Эквивалентное демпфирование вязкого контакта. Систему стыковых поверхностей станка можно рассматривать как систему с одной степенью свободы с вязким демпфированием. Безразмерное эквивалентное демпфирование вязкого контакта $C_{n}^{*}$ можно рассчитать по формуле
6. Эксперименты по моделированию. Чтобы выявить влияние топографии поверхности и свойств материала на межфазную контактную жесткость и демпфирование контакта, было проведено моделирование со следующими параметрами.
Нормальный статический средний интервал и амплитуда динамического среднего расстояния между двумя шероховатыми поверхностями равны $d_{s}^{*} = 0.2$ и $d_{m}^{*} = 0.9$ соответственно. Частота вибрации f = 100 Гц. Модуль Юнга ${{E}_{1}} = {{E}_{2}} = 2.07 \times {{10}^{{11}}}$ Па; твердость по Бринеллю $H = 2 \times {{10}^{9}}$ Па; коэффициент Пуассона ${{{v}}_{1}} = {{{v}}_{2}} = 0.29$. Кроме того, номинальная площадь контакта принимается равной ${{A}_{n}} = 3 \times {{10}^{{ - 5}}}\;{{m}^{2}}$. Диапазон значений индекса пластичности от 0.5 до 2.5 был рассчитан из соответствующих значений $\beta $ и ${{\sigma }_{z}}{\text{/}}R$ согласно следующему определению [3]: $\psi = \left( {2E{\text{/}}1.5\pi kH} \right){{\left( {{{\sigma }_{z}}{\text{/}}R} \right)}^{{1/2}}}$(1 – ‒3.717 × 10–4/β2)1/4, а индекс пластичности в диапазоне от 0.4 до 0.7 приведен в таблице 1. Коэффициент среднего контактного давления $k$ принят равным 0.8. Из уравнения показателя пластичности видно, что показатель пластичности в первую очередь зависит от топографии поверхности и свойств материала. Более гладкие и твердые поверхности имеют более низкие показатели пластичности.
Таблица 1.
Топографические параметры поверхности и показатели пластичности
| Показатели пластичности $\psi $ | ${{{{\sigma }_{z}}} \mathord{\left/ {\vphantom {{{{\sigma }_{z}}} R}} \right. \kern-0em} R}$ | $\beta = \eta {{\sigma }_{z}}R$ |
|---|---|---|
| 0.4 | 7.4 × 10–5 | 0.0296 |
| 0.5 | 8.41 × 10–5 | 0.0336 |
| 0.6 | 9.6 × 10–5 | 0.0384 |
| 0.7 | 1.11 × 10–4 | 0.0444 |
В табл. 1 $\sigma $ – стандартное отклонение высоты поверхности, $\eta $ – поверхностная плотность неровностей и $R$ – радиус кривизны неровностей.
6.1. Эксперименты по моделированию межфазной нормальной контактной силы. На рис. 5, а показана зависимость между безразмерной нормальной контактной силой на границе раздела F* и стандартной дисперсией углов контактной неровности ${{\sigma }_{\varphi }}$. Нормальная контактная сила F* постепенно нелинейно уменьшается с увеличением ${{\sigma }_{\varphi }}$, потому что область контакта с большим ${{\sigma }_{\varphi }}$ имеет плохую степень согласования между неровностями на границе области.
Рис. 5.
Влияние стандартной дисперсии неровностей контактных (азимутальных) углов на нормальную контактную силу (а) и на ${{\sigma }_{\theta }}$ (b).
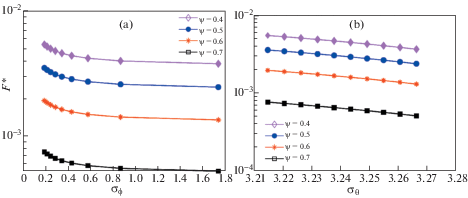
Рисунок 5, b показывает влияние стандартной дисперсии ${{\sigma }_{\theta }}$ контактных азимутальных углов неровностей на нормальную контактную силу F*, которая косвенно отражает влияние межфазной контактной анизотропии на нормальную контактную силу F*. Нормальная контактная сила F* постепенно уменьшается с увеличением ${{\sigma }_{\theta }}$, т.е. нормальная контактная сила постепенно уменьшается по мере того, как область контакта становится более изотропной. Причина в том, что контактные силы неровностей становятся более дискретными с увеличением ${{\sigma }_{\theta }}$. Нормальная контактная сила F* с более высоким показателем пластичности $\psi $ имеет меньшее значение, потому что шероховатая поверхность с более высоким показателем пластичности представляет собой более грубую или более мягкую поверхность. Следовательно, деформации неровностей имеют преимущественно пластический характер. И наоборот, более гладкие и более твердые поверхности имеют более низкие показатели пластичности $\psi $, нормальное контактное усилие между двумя шероховатыми поверхностями больше.
6.2. Эксперименты по моделированию диссипации энергии нормального контакта. На рис. 6 , а показана зависимость между диссипацией энергии нормального контакта $E_{n}^{*}$ и стандартной дисперсией углов контакта неровностей ${{\sigma }_{\varphi }}$. Диссипация нормальной контактной энергии нелинейно уменьшается с увеличением ${{\sigma }_{\varphi }}$, потому что количество контактных неровностей уменьшается с увеличением ${{\sigma }_{\varphi }}$, так что нормальная контактная диссипация энергии уменьшается.
Рис. 6.
Влияние стандартной дисперсии контактных (азимутальных) углов неровностей на нормальное рассеивание контактной энергии: влияние (a) ${{\sigma }_{\varphi }}$, (b) влияние ${{\sigma }_{\theta }}$.
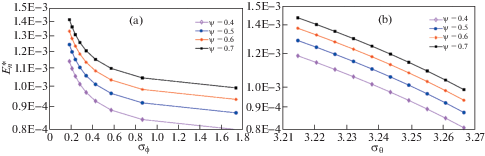
На рис. 6, b показано соотношение между нормальным рассеиванием энергии контакта $E_{n}^{*}$ и стандартными отклонениями азимутальных углов неровностей контакта ${{\sigma }_{\theta }}$. Нормальная контактная диссипация энергии $E_{n}^{*}$ уменьшается по мере того, как область контакта становится более изотропной, потому что нормальная контактная сила неровности изотропной границы раздела более дискретна по сравнению с анизотропной границей раздела, так что нормальная контактная диссипация энергии уменьшается. Диссипация контактной энергии $E_{n}^{*}$ с более высоким показателем пластичности $\psi $ имеет большее значение, потому что площадь петли гистерезиса нагрузки и разгрузки контактной силы больше с более высоким показателем пластичности $\psi $.
6.3. Эксперименты по моделированию нормальной контактной жесткости. На рис. 7, а показана зависимость между нормальной контактной жесткостью $K_{n}^{*}$ и стандартной дисперсией краевого угла неровности ${{\sigma }_{\varphi }}$. Нормальная контактная жесткость $K_{n}^{*}$ нелинейно уменьшается с увеличением ${{\sigma }_{\varphi }}$, потому что количество контактных неровностей уменьшается с увеличением ${{\sigma }_{\varphi }}$, так что нормальная контактная жесткость уменьшается.
Рис. 7.
Влияние стандартной дисперсии контактных (азимутальных) углов неровностей на нормальную контактную жесткость: влияние (a) ${{\sigma }_{\varphi }}$, (b) влияние ${{\sigma }_{\theta }}$.
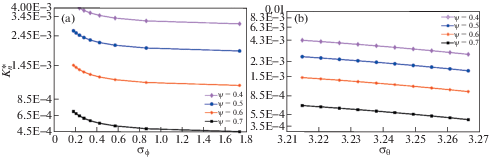
На рис. 7, b показано влияние стандартных отклонений контактных азимутальных углов неровностей ${{\sigma }_{\theta }}$ на нормальную контактную жесткость $K_{n}^{*}$. Нормальная контактная жесткость на поверхности раздела уменьшается линейно с увеличением стандартной дисперсии азимутальных углов контакта неровностей ${{\sigma }_{\theta }}$, т.е. нормальная контактная жесткость линейно уменьшается с увеличением границы раздела, как правило, более изотропной. Причина в том, что с увеличением ${{\sigma }_{\theta }}$ контактная сила неровностей становится более дискретной. Нормальная контактная жесткость $K_{n}^{*}$ с более низким показателем пластичности $\psi $ имеет большее значение, потому что более гладкие и более твердые поверхности имеют более низкие показатели пластичности $\psi $, нормальная контактная жесткость больше между двумя шероховатыми поверхностями. Следовательно, деформации неровностей в основном имеют упругий характер.
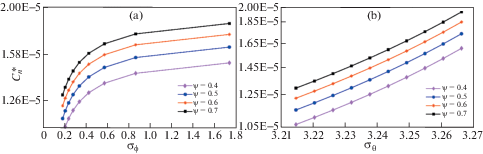
6.4. Эксперименты по моделированию нормального контактного демпфирования. На рис. 8, а показана зависимость между демпфированием нормального контакта $C_{n}^{*}$ и стандартной дисперсией углов контакта неровностей ${{\sigma }_{\varphi }}$. Демпфирование нормального контакта нелинейно увеличивается с увеличением ${{\sigma }_{\varphi }}$, потому что степень согласования между неровностями на границе раздела хуже с увеличением ${{\sigma }_{\varphi }}$. Рис. 8, b показывает влияние стандартных отклонений азимута контакта неровностей ${{\sigma }_{\theta }}$ на демпфирование нормального контакта $C_{n}^{*}$. Демпфирование нормального контакта постепенно увеличивается с увеличением ${{\sigma }_{\theta }}$, т.е. увеличение демпфирования нормального контакта с границей раздела имеет тенденцию быть более изотропным. Причина в том, что контактная сила неровностей становится более дискретной с увеличением ${{\sigma }_{\theta }}$, что вызывает уменьшение деформации неровностей, и уменьшение градиента скорости деформации неровностей больше, чем уменьшение градиента скорости диссипации энергии. Тогда эквивалентное вязкое демпфирование увеличивается с увеличением ${{\sigma }_{\theta }}$. Нормальное контактное демпфирование $C_{n}^{*}$ с более высоким показателем пластичности $\psi $ имеет большее значение, потому что шероховатая поверхность с более высоким показателем пластичности $\psi $ более мягкая и шершавая, деформации контактной шероховатости в основном имеют пластический характер.
Рис. 8.
Влияние стандартной дисперсии неровностей контактных (азимутальных) углов на нормальное контактное демпфирование: влияние (a) ${{\sigma }_{\varphi }}$, (b) влияние ${{\sigma }_{\theta }}$.
6.5. Сравнение с эквивалентными контактными моделями. При ${{\sigma }_{\varphi }} = 0.4$, ${{\sigma }_{\theta }} = 3.22$, $\psi = 0.5$, f = 100 и ${{d}_{m}} = 0.9$ были выявлены отношения между нормальной контактной силой F*, диссипацией контактной энергии $E_{n}^{*}$, контактной жесткостью $K_{n}^{*}$ и демпфированием $C_{n}^{*}$; результаты, полученные при помощи предлагаемой модели, были сравнены с традиционными контактными моделями. Следует отметить, что классические эквивалентные модели контактов не вычисляют диссипацию энергии межфазного контакта, жесткость контакта и демпфирование контакта, поэтому эти результаты рассчитываются системой с одной степенью свободы с вязким демпфированием, которые аналогичны предлагаемой модели. На рис. 9, а показано сравнение нормальных контактных сил F* между предлагаемой моделью и классическими эквивалентными моделями контакта. Нормальная контактная сила предложенной модели больше, чем контактная сила модели JG, но меньше, чем контактная сила модели Etsion [4], модели CEB и модели SF, потому что предлагаемая модель учитывает эффект контакта неровностей плечом к плечу и влияние взаимодействия неровностей. Плотный контакт неровностей приведет к уменьшению нормальной контактной силы из-за бокового контакта неровностей, а взаимодействие неровностей приведет к увеличению нормальной контактной силы в соответствии с моделью ZMC. На рис. 9 (b) приведено сравнение диссипации энергии нормального контакта между предлагаемой моделью и эквивалентными моделями контактов. Диссипация контактной энергии в предложенной модели больше, чем в других, что правдоподобно, поскольку классические модели не учитывают скольжение–прилипание и взаимодействие между неровностями.
Рис. 9.
Сравнение с эквивалентной контактной моделью: (а) нормальные контактные силы, (b) диссипации энергии нормального контакта, (c) нормальная контактная жесткость, (d) демпфирование нормального контакта.
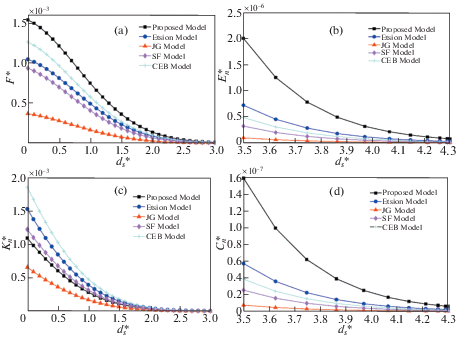
На рис. 9, c сравнивается контактная жесткость предложенной модели с жесткостью некоторых традиционных моделей. Из графиков видно, что жесткость предлагаемой модели меньше жесткости некоторых традиционных моделей, что можно объяснить эффектом плотного контакта неровностей и взаимодействием между соседними неровностями. На рис. 9, d сравнивается модель нормального контакта предложенной модели с некоторыми классическими моделями, и показано, что демпфирование нормального контакта предложенной модели больше, чем демпфирование других моделей. В предложенную модель включена диссипация энергии трения плотного контакта, которая не рассматривается в других моделях.
7. Заключение. Предложена физическая модель, описывающая контактную жесткость и демпфирование между анизотропными шероховатыми поверхностями, которая включает плотный контакт и взаимодействие соседних неровностей. С использованием статистических методов исследована нормальная контактная жесткость и демпфирование при задании параметров контакта ${{\sigma }_{\varphi }}$ и ${{\sigma }_{\theta }}$. Проанализировано влияние контактных параметров ${{\sigma }_{\varphi }}$ и ${{\sigma }_{\theta }}$ на поведение межфазного контакта. На основании проведенного исследования были сделаны следующие выводы:
(1) Межфазная контактная сила, диссипация контактной энергии и контактная жесткость в нормальном направлении нелинейно уменьшаются с увеличением стандартной дисперсии контактных углов неровностей и линейно уменьшаются с увеличением стандартной дисперсии контактных азимутальных углов неровностей. Такое поведение указывает на то, что нормальная несущая способность области контакта может быть улучшена за счет улучшения состояния контакта и увеличения анизотропии межфазного контакта.
(2) Демпфирование межфазного нормального контакта увеличивается нелинейно с увеличением стандартной дисперсии углов контакта неровностей и увеличением стандартной дисперсии контактных азимутальных углов неровностей. Можно сделать вывод, что степень согласования и анизотропия между поверхностями контакта имеет большое влияние на демпфирование нормального контакта на границе раздела, а демпфирование нормального контакта можно улучшить, отрегулировав степень согласования и анизотропию контакта. В работе решена контактная задача о взаимодействии между анизотропными шероховатыми поверхностями с использованием статистического метода в некоторой степени и выявлено влияние контактных углов неровностей и контактных азимутальных углов на нормальную контактную силу, нормальную контактную жесткость и демпфирование нормального контакта.
(3) Контактные шероховатые поверхности с более высоким показателем пластичности имеют меньшее нормальное контактное усилие и контактную жесткость, но имеют большее рассеивание нормальной контактной энергии и контактное демпфирование.
Благодарности. Авторы выражают признательность за финансовую поддержку, предоставленную Национальным фондом естественных наук Китая (№ 52005401), Китайским фондом постдокторантуры (№ 2019M663782), Проектом фундаментальных исследований естественных наук Шэньси (№ 2020JQ-629), Специальным научно-исследовательским проектом Департамента образования провинции Шэньси (№ 20JK0800), Открытым проектом Государственной ключевой лаборатории энергосистем тракторов (№ AKT2020002).
Список литературы
Bush A.W., Gibson R.D., Keogh G.P. Strongly anisotropic rough surfaces // J. Tribol. 1979. V. 101. № 1. P. 15–20.
Greenwood J.A., Williamson J.B.P. Contact of nominally flat surfaces // Proc. R. Soc. London. 1966. V. 295. № 1442. P. 300–319.
Chang W.R., Etsion I., Bogy D.B. An elastic-plastic model for the contact of rough surfaces // Asme J. Trib. 1987. V. 109. № (2). P. 257–263.
Kogut L., Etsion I. A finite element based elastic-plastic model for the contact of rough surfaces // Modell. Simul. Eng. 2011. № 3. P. 383–390.
Kadin Y., Kligerman Y., Etsion I. Unloading an elastic–plastic contact of rough surfaces // J. Mech. Phys. Solids 2006. V. 54. № 12. P. 2652–2674.
Jackson R.L., Green I. A finite element study of elastoplastic hemispherical contact against a rigid flat // J. Tribol. 2005. V. 127. № 2. P. 343–354.
Jackson R.L., Green I. A statistical model of elastoplastic asperity contact between rough surfaces // Tribol. Int. 2006. V. 39. № 9. P. 906–914.
Gorbatikh L., Popova M. Modeling of a locking mechanism between two rough surfaces under cyclic loading // Int. J. Mech. Sci. 2006. V. 48. № 9. P. 1014–1020.
Abdo J., Farhang K. Elastic–plastic contact model for rough surfaces based on plastic asperity concept // Int. J. Nonlin. Mech. 2005. V. 40. № 4. P. 495–506.
Sepehri A., Farhang K. On elastic interaction of nominally flat rough surfaces // J. Tribol. 2008. V. 130. № 1. P. 125–128.
Sepehri A., Farhang K. Closed-form equations for three dimensional elastic-plastic contact of nominally flat rough surfaces // J. Tribol. 2009. V. 131. № 4. P. 041402-1-8.
Zhao B., Zhang S., Hai Y. Loading–unloading normal stiffness model for power-law hardening surfaces considering actual surface topography // Tribol. Int. 2015. V. 90. № 2015. P. 332–342.
Jäger J. Axi-symmetric bodies of equal material in contact under torsion or shift // Arch. Appl. Mech. 1995. V. 65. № 7. P. 478–487.
Jackson R.L., Duvvuru R.S., Mahajan M. An analysis of elasto-plastic sliding spherical asperity interaction” Wear. 2007. V. 262. № 1–2. P. 210–219.
Mulvihill D.M., Kartal M.E., Hills D.A. An elastic–plastic asperity interaction model for sliding friction // Tribol. Int. 2011. V. 44. № 12. P. 1679–1694.
Shi X., Zou Y., Fang H. Numerical investigation of the three-dimensional elastic-plastic sloped contact between two hemispheric asperities // J. Appl. Mech. 2016. V. 83. № 10. P. 101004-1-8.
Faulkner A., Arnell R.D. The development of a finite element model to simulate the sliding interaction between two, three-dimensional, elastoplastic, hemispherical asperities // Wear. 2000. V. 242. № 1. P. 114–122.
Zhao Y., Chang L. A model of asperity interactions in elastic-plastic contact of rough surfaces // J. Tribol. 2001. V. 123. № 4. P. 857–864.
Ciavarella M., Greenwood J.A., Paggi M. Inclusion of “interaction” in the Greenwood and Williamson contact theory // Wear. 2008. V. 265. № 5–6. P. 729–734.
Chandrasekar S., Eriten M., Polycarpou A. An improved model of asperity interaction in normal contact of rough surfaces // J. Appl. Mech. 2013. V. 80. № 1. P. 011025-1-8.
Greenwood J.A., Tripp J.H. The contact of two nominally flat rough surfaces // P. I. Mech. Eng. 1970. V. 185. № 1970. P. 625–634.
Whitehouse D.J., Archard J.F. The properties of random surfaces of significance in their contact // P. Roy. Soc. A. 1970. V. 316. № 1524. P. 97–121.
Longuethiggins M.S. Statistical properties of an isotropic random surface // Philos. T. R. Soc. A. 1957. V. 250. № 975. P. 157–174.
Nayak P.R. Random process model of rough surfaces // J. Lubr. Technol. 1971. V. 93. № 3. P. 398–406.
Nayak P.R. Random process model of rough surfaces in plastic contact // Wear. 1973. V. 26. № 3. P. 305–333.
Mccool J.I. Predicting micro fracture in ceramics via a micro contact model // J. Tribol. 1986. V. 108. № 3. P. 380–386.
Whitehouse D.J., Phillips M.J. Two-dimensional discrete properties of random surfaces // Philos. T. R. Soc. B. 1982. V. 305. № 1490. P. 441–468.
Whitehouse D.J., Phillips M.J. Sampling in a two-dimensional plane // J. Phys. A: Gen. Phys. 1985. V. 18. № 13. P. 2465–2477.
Buczkowski R., Kleiber M. Elasto-plastic statistical model of strongly anisotropic rough surfaces for finite element 3D-contact analysis // Comput. Method. Appl. M. 2016. V. 195. № 37. P. 5141–5161.
Cattaneo C. Sul contatto di due corpi elastici: distribuzione locale degli sforzi I; II; III // Atti Accad. Naz. Lincei, Rend. VI. 1938. Ser. 27. 342–348; 434–436; 474–478.
Mindlin R.D., Deresiewicz H. Elastic spheres in contact under varying oblique forces // Trans. ASME, J. Appl. Mech. 1953. V. 20. № 3. P. 327–344.
Eriten M., Polycarpou A.A., Bergman L.A. Physics-based modeling for fretting behavior of nominally flat rough surfaces // Int. J. Solids. Struct. 2011. V. 48. № 10. P. 1436–1450.
Brizmer V., Kligerman Y., Etsion I. Elastic–plastic spherical contact under combined normal and tangential loading in full stick // Tribol. Lett. 2007. V. 25. № 1. P. 61–70.
Zhao Y., Maietta D.M., Chang L. An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow // J. Tribol. 2000. V. 122. № 1. P. 86–93.
Jeng Y.R., Peng S.R. Elastic-plastic contact behavior considering asperity interactions for surfaces with various height distributions // J. Tribol. 2006. V. 128. № 2. P. 665–697.
Knowles J.K. On Saint-Venant’s principle in the two-dimensional linear theory of elasticity // Arch. Ration. Mech. An. 1966. V. 21. № 1. P. 1–22.
Love A.E.H. The stress produced in a semi-infinite solid by pressure on part of the boundary // Philos. Trans. R. Soc. London. 1929. V. 228. № 659–669. P. 377–420.
Misra A. Mechanist model for contact between rough surfaces // J. Eng. Mech. 2011. V. 123. № 5. P. 45352–45357.
Misra A., Huang S. Effect of loading induced anisotropy on the shear behavior of rough interfaces // Tribol. Int. 2011. V. 44. № 5. P. 627–634.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела