Известия РАН. Механика твердого тела, 2021, № 4, стр. 142-150

АНАЛИТИЧЕСКАЯ АППРОКСИМАЦИЯ РЕШЕНИЯ ГЕОДЕЗИЧЕСКОЙ ЗАДАЧИ

П. А. Кучеренко^a, *, С. В. Соколов^b

^a АО “НИИАС” (Ростовский филиал)
Ростов-на-Дону, Россия

^b Московский технический университет связи и информатики
Москва, Россия

^* E-mail: pavelpost83@mail.ru

Поступила в редакцию 14.06.2020
После доработки 29.10.2020
Принята к публикации 28.12.2020

DOI: 10.31857/S0572329921040073

Полный текст (PDF)

Аннотация

Решена задача аналитического синтеза функций, аппроксимирующих зависимости длины геодезической линии от навигационных параметров ее начальной и конечной точек для сфероида и сферы Земли. Аппроксимирующие длину геодезической линии зависимости определены как для приведенной, так и для геодезической широт. Получены выражения для азимута конечной точки (при известной широте начальной точки), не требующие знания долготы конечной точки и длины геодезической линии. Найденные решения позволяют существенно сократить вычислительные затраты при решении различных классов задач навигации и геодезии.

Ключевые слова: эллипсоид, геодезическая задача, длина геодезической линии, аппроксимация функциональной зависимости

В связи с постоянным развитием высокоточных методов и систем навигации оказывается весьма актуальной проблема высокоточного описания параметров траекторий движения объектов на поверхности сфероидальной Земли. Решение этой проблемы для большинства навигационных приложений сводится к решению частного случая геодезической задачи в следующей формулировке: даны геодезические координаты – широта В и долгота L, начальной (В₀, L₀) и конечной точек (В₁, L₁) движения объекта, начальный (прямой) азимут А₀ движения, требуется найти кратчайшее расстояние S между этими точками (длину геодезической линии), а также конечный (обратный) азимут А₁ геодезической линии в конечной точке. В настоящее время данная задача решается, в основном, использованием итеративных методов при численном решении системы дифференциальных уравнений, описывающих эволюцию геодезических линий на сфероиде [1, 2]. Это приводит к значительным временным и вычислительным затратам, что для систем навигации, функционирующих в реальном времени, представляется неприемлемым.

В связи с этим, целью данной статьи является построение аналитической функциональной зависимости, аппроксимирующей с высокой точностью решение указанной геодезической задачи, т.е. связь навигационных параметров В₀, L₀, В₁, L₁, А₀ с длиной геодезической линии S и обратным азимутом А₁. Синтез данной зависимости будем рассматривать для геодезической долготы и геодезической и приведенной широт, используя следующие обозначения переменных: А – текущий азимут геодезической линии, В – геодезическая широта, u – приведенная широта, L – геодезическая долгота, E – первый эксцентриситет, е – второй эксцентриситет, а, b – большая и малая полуоси эллипсоида, ds – дифференциал линии на эллипсоиде. Для эллипсоида Красовского:

$\begin{gathered} {{E}^{2}} = 0.0066934216,\quad {{e}^{2}} = 0.0067385254,\quad с = \frac{{{{a}^{2}}}}{b} = 6399698.9018\,\,{\text{м}}, \\ M = \frac{c}{{\sqrt {{{{(1 + {{e}^{2}}{{{\cos }}^{2}}B)}}^{3}}} }},\quad N = \frac{c}{{\sqrt {1 + {{e}^{2}}{{{\cos }}^{2}}B} }} \\ \end{gathered} $

Для решения поставленной задачи используем известные уравнения связи навигационных переменных А, В, L, справедливые для любых кривых на сфероиде [1]:

(1)

$\frac{{dL}}{{ds}} = \frac{{\sin A}}{{N\cos B}}$

(2)

$\frac{{dB}}{{ds}} = \frac{{\cos A}}{M}$

и только для геодезической линии [1]:

(3)

$\frac{{dA}}{{ds}} = \frac{{{\text{tg}}B\sin A}}{N}$

Предварительно найдем зависимость текущего азимута геодезической линии А от геодезической широты В, для чего разделим уравнение (3) на уравнение (2):

$\frac{{dA}}{{dB}} = \frac{{{\text{tg}}A\,{\text{tg}}B}}{{1 + {{e}^{2}}{{{\cos }}^{2}}B}}$

Данное уравнение легко интегрируется методом разделения переменных:

(4)

$\int\limits_{{{А}_{0}}}^А {{\text{ctg}}A} dA = \int\limits_{{{В}_{0}}}^В {\frac{{{\text{tg}}B}}{{1 + {{e}^{2}}{{{\cos }}^{2}}B}}} \,dB$

где А и А₀ – текущее и начальное значения азимута, соответственно, В и В₀ – текущее и начальное значение геодезической широты.

Интеграл в левой части (4) – табличный, а в правой – находится методом замены переменных $e\cos B = Х$:

$\int {\frac{{e\sin B}}{{e\cos B(1 + {{e}^{2}}{{{\cos }}^{2}}B)}}} \,dB = - \int {\frac{{dX}}{{X(1 + {{X}^{2}})}}} = \ln \sqrt {1 + {{X}^{{ - 2}}}} = \ln \sqrt {1 + {{{[e\cos B]}}^{{ - 2}}}} $

Окончательно имеем:

$\ln \,\sin A - \ln \,\sin {{A}_{0}} = \ln \sqrt {1 + {{{[e\cos B]}}^{{ - 2}}}} - \ln \sqrt {1 + {{{[e\cos {{B}_{0}}]}}^{{ - 2}}}} $

или

$\,\,\,\,\,\ln \frac{{\sin A}}{{\sin {{A}_{0}}}} = \ln \frac{{\sqrt {1 + {{{[e\cos B]}}^{{ - 2}}}} }}{{\sqrt {1 + {{{[e\cos {{B}_{0}}]}}^{{ - 2}}}} }}$

Из последнего выражения можно получить равенство

$\sin A = \sqrt {1 + {{{[e\cos B]}}^{{ - 2}}}} {{C}_{0}},\quad {{C}_{0}} = \frac{{\sin {{A}_{0}}}}{{\sqrt {1 + {{{[e\cos {{B}_{0}}]}}^{{ - 2}}}} }}$

которое определяет зависимость текущего азимута геодезической линии от геодезической широты:

(5)

$A = \arcsin (\sqrt {1 + {{{[e\cos B]}}^{{ - 2}}}} \,\,{{C}_{0}}\,)$

Остановимся на найденной зависимости подробнее. Помимо ее дальнейшего использования для решения поставленной задачи, зависимость (5) позволяет решить задачу определения азимута А₁ конечной точки с широтой В₁ геодезической линии конечной длины без традиционного знания долготы конечной точки и длины геодезической линии (зная только параметры начальной точки А₀, В₀):

${{A}_{1}} = \arcsin (\sqrt {1 + {{{[e\cos {{B}_{1}}]}}^{{ - 2}}}} \,\,{{C}_{0}}\,)$

Интересно также сравнить полученное выражение с уравнением Клеро [1]:

$N\cos B\sin A = \frac{c}{{\sqrt {1 + {{e}^{2}}{{{\cos }}^{2}}B} }}\cos B\sin A\,\, = C$

Исходя из данного уравнения, выражение sinA может быть представлено в виде:

$\sin A\,\, = \frac{{еС\sqrt {1 + {{e}^{2}}{{{\cos }}^{2}}B} }}{{е\,\,\,\cos B\,\,\,\,с}} = \sqrt {1 + {{{[e\cos B]}}^{{ - 2}}}} \frac{{еС}}{с}$

откуда сравнением с (5) получаем:

$\frac{{еС}}{с}\, = \frac{{\,\sin {{A}_{0}}}}{{\sqrt {1 + {{{[e\cos {{B}_{0}}]}}^{{ - 2}}}} }}$

и сразу находим различные варианты выражения постоянной Клеро:

$С\, = \frac{{\,с\,\,\sin {{A}_{0}}}}{{е\sqrt {1 + {{{[e\cos {{B}_{0}}]}}^{{ - 2}}}} }} = \frac{{{{a}^{2}}\,\sin {{A}_{0}}}}{{\sqrt {{{a}^{2}} - {{b}^{2}}} \sqrt {1 + {{{[e\cos {{B}_{0}}]}}^{{ - 2}}}} }}\, = \frac{{\,\frac{{{{a}^{2}}}}{b}\,\,\sin {{A}_{0}}}}{{\sqrt {{{e}^{2}} + {{{[\cos {{B}_{0}}]}}^{{ - 2}}}} }}\,$

существенно расширяющие диапазон ее традиционного представления, приведенный в [1].

Для дальнейшего решения задачи из полученного выражения sinA найдем cosA:

$\cos A = \sqrt {1 - (1 + {{{[e\cos B]}}^{{ - 2}}})C_{0}^{2}} = \sqrt {C_{0}^{{ - 2}} - 1 - {{{[e\cos B]}}^{{ - 2}}}} \,\,\,C_{0}^{{}}$

и подставим его в уравнение (2):

$\frac{{dB}}{{ds}} = \frac{{\cos A}}{M} = \frac{{\sqrt {C_{0}^{{ - 2}} - 1 - {{{(e\cos B)}}^{{ - 2}}}} C_{0}^{{}}}}{{\frac{c}{{\sqrt {{{{(1 + {{e}^{2}}{{{\cos }}^{2}}B)}}^{3}}} }}}} = \frac{{C_{0}^{{}}\sqrt {(Р{{{[e\cos B]}}^{2}} - 1){{{(1 + {{e}^{2}}{{{\cos }}^{2}}B)}}^{3}}} }}{{(e\cos B)с}}$

$Р = C_{0}^{{ - 2}} - 1$

Полученное уравнение интегрируется методом разделения переменных

(6)

$\int\limits_0^S {ds} = \int\limits_{{{B}_{0}}}^B {\frac{{(e\cos B)с}}{{C_{0}^{{}}\sqrt {(Р{{{[e\cos B]}}^{2}} - 1){{{(1 + {{e}^{2}}{{{\cos }}^{2}}B)}}^{3}}} }}dB} $

но для возможности аналитического вычисления интеграла в левой части необходима его адекватная аппроксимация.

Для получения высокоточной аналитической аппроксимации зависимости S = f(B) проведем предварительно анализ зависимости S = f(u), где u – приведенная широта, связанная с геодезической широтой известным соотношением [1]:

(7)

$\,\sin u = \frac{{\sin В}}{{\sqrt {1 + {{e}^{2}}{{{\cos }}^{2}}B} }}$

Для приведенной широты уравнения (1)–(3) трансформируются следующим образом [1]:

$\frac{{dL}}{{ds}} = \frac{{\sin A}}{{а\cos и}}$

(8)

$\frac{{dи}}{{ds}} = \frac{{v}}{а}\cos A$

(9)

$\frac{{dA}}{{ds}} = \frac{{v}}{а}{\text{tg}}и\,\sin A$

${v} = \frac{1}{{\sqrt {1 - {{E}^{2}}{{{\cos }}^{2}}и} }}$

Предварительно найдем зависимость текущего азимута геодезической линии А от приведенной широты u. Используя уравнение Клеро для приведенной широты [1]

$\cos и \cdot \sin A = \Phi $

где $\Phi = \cos {{и}_{*}}$ или $\Phi = \sin {{A}_{*}}$, ${{и}_{*}}$ – приведенная широта наиболее удаленной от экватора точки геодезической линии, ${{A}_{*}}$ – азимут геодезической линии в точке пересечения ее с экватором, имеем:

$\sin A = \frac{\Phi }{{\cos и}} \Rightarrow A = \,\arcsin \frac{\Phi }{{\cos и}}$

откуда также вытекает соответствующее выражение для cosA:

(10)

$\cos A = \sqrt {1 - {{{\left( {\frac{\Phi }{{\cos и}}} \right)}}^{2}}} = \frac{{\sqrt {{{{\cos }}^{2}}и - {{\Phi }^{2}}} }}{{\cos и}}$

Данные соотношения могут быть получены и другим путем – делением уравнения (9) на (8) с последующим интегрированием полученного дифференциального уравнения:

$\frac{{dA}}{{du}} = {\text{tg}}A\,{\text{tg}}u \Rightarrow \int\limits_{{{A}_{0}}}^А {{\text{ctg}}AdA} = \int\limits_{{{u}_{0}}}^u {{\text{tg}}u\,du} \,\,\, \Rightarrow \,\,\,\ln \frac{{\sin A}}{{\sin {{A}_{0}}}} = \ln \frac{{\cos {{u}_{0}}}}{{\cos u}}$

где ${{и}_{0}}$ – приведенная широта начальной точки геодезической линии; ${{A}_{0}}$ – азимут геодезической линии в начальной точке, что приводит к ранее приведенному соотношению:

$\sin A = \frac{{\sin {{A}_{0}}\cos {{u}_{0}}}}{{\cos u}} = \frac{\Phi }{{\cos u}}$

в котором постоянная Клеро уже приобретает новое выражение:

$\sin {{A}_{0}}\cos {{u}_{0}}\,\, = \Phi $

Здесь необходимо отметить, что данное выражение постоянной Клеро (в отличие от приведенных выше традиционных выражений) позволяет решить задачу определения азимута А₁ конечной точки с приведенной широтой u₁, зная только параметры начальной точки А₀, u₀:

${{A}_{1}} = \arcsin \frac{{\sin {{A}_{0}}\cos {{u}_{0}}}}{{\cos {{и}_{1}}}}$

Для дальнейшего решения поставленной задачи подставим найденное выражение для cosA в уравнение (8):

$\frac{{dи}}{{ds}} = \frac{{\text{1}}}{{а\sqrt {1 - {{E}^{2}}{{{\cos }}^{2}}и} }}\frac{{\sqrt {{{{\cos }}^{2}}и - {{\Phi }^{2}}} }}{{\cos и}},\quad \frac{{ds}}{{du}} = \frac{{а\cos и\sqrt {1 - {{E}^{2}}{{{\cos }}^{2}}и} }}{{\sqrt {{{{\cos }}^{2}}и - {{\Phi }^{2}}} }}$

Данное уравнение интегрируется методом разделения переменных

(11)

$\int\limits_0^S {ds} = a\int\limits_{{{и}_{0}}}^и {\frac{{\cos и\sqrt {1 - {{E}^{2}}{{{\cos }}^{2}}и} }}{{\sqrt {{{{\cos }}^{2}}и - {{\Phi }^{2}}} }}dи} $

но для возможности аналитического вычисления интеграла в левой части необходима его соответствующая аппроксимация.

Рассмотрим с этой целью возможность упрощения его подынтегрального выражения разложением в ряд функции $\sqrt {1 - {{E}^{2}}{{{\cos }}^{2}}и} $ по аргументу ${{E}^{2}}{{\cos }^{2}}и$ (в точке ${{u}_{l}}$) с точностью до (${{E}^{2}}{{\cos }^{2}}и$)³, что, как показано далее, обеспечивает очень высокую точность аппроксимации (11) (около ${{10}^{{ - 5}}}$ метра):

(12)

$\begin{gathered} \sqrt {1 - {{E}^{2}}{{{\cos }}^{2}}и} \approx \sqrt {1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}}} - \frac{{{{E}^{2}}}}{{2\sqrt {1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}}} }}({{\cos }^{2}}и - {{\cos }^{2}}{{и}_{l}}) - \\ \, - \frac{{{{E}^{4}}}}{{8\sqrt {{{{(1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{3}}} }}{{({{\cos }^{2}}и - {{\cos }^{2}}{{и}_{l}})}^{2}} - \frac{{{{E}^{6}}}}{{16\sqrt {{{{(1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{5}}} }}{{({{\cos }^{2}}и - {{\cos }^{2}}{{и}_{l}})}^{3}} = \\ \, = {{{{\alpha }}}_{0}} + {{{{\alpha }}}_{1}}{{\cos }^{2}}и + {{{{\alpha }}}_{2}}{{\cos }^{4}}и + {{{{\alpha }}}_{3}}{{\cos }^{6}}и, \\ \end{gathered} $

где коэффициенты ${{{{\alpha }}}_{i}},i = 0,...,3$ вычисляются по следующим формулам:

${{{{\alpha }}}_{0}} = \sqrt {1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}}} + \frac{{{{E}^{2}}{{{\cos }}^{2}}{{и}_{l}}}}{{2\sqrt {1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}}} }} - \frac{{{{E}^{4}}{{{\cos }}^{4}}{{и}_{l}}}}{{8\sqrt {{{{(1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{3}}} }} + \frac{{{{E}^{6}}{{{\cos }}^{6}}{{и}_{l}}}}{{16\sqrt {{{{(1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{5}}} }}$

${{{{\alpha }}}_{1}} = - \frac{{{{E}^{2}}}}{{2\sqrt {1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}}} }} + \frac{{{{E}^{4}}{{{\cos }}^{2}}{{и}_{l}}}}{{4\sqrt {{{{(1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{3}}} }} - \frac{{3{{E}^{6}}{{{\cos }}^{4}}{{и}_{l}}}}{{16\sqrt {{{{(1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{5}}} }}$

${{{{\alpha }}}_{2}} = - \frac{{{{E}^{4}}}}{{8\sqrt {{{{(1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{3}}} }} + \frac{{3{{E}^{6}}{{{\cos }}^{2}}{{и}_{l}}}}{{16\sqrt {{{{(1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{5}}} }}$

${{{{\alpha }}}_{3}} = - \frac{{{{E}^{6}}}}{{16\sqrt {{{{(1 - {{E}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{5}}} }}$

При этом заметим, что для районов низких и высоких широт коэффициенты выражения (12) существенно упрощаются:

– для района высоких широт – ${{и}_{0}} = \frac{\pi }{2}$ (при выборе точки линеаризации в начале интервала, т.е. при ${{и}_{l}} = {{u}_{0}}$):

${{{{\alpha }}}_{0}} = 1,\quad {{{{\alpha }}}_{1}} = - \frac{{{{E}^{2}}}}{2},\quad {{{{\alpha }}}_{2}} = - \frac{{{{E}^{4}}}}{8},\quad {{{{\alpha }}}_{3}} = - \frac{{{{E}^{6}}}}{{16}}$

– для района низких широт – ${{и}_{0}} = 0$ (также при ${{и}_{l}} = {{u}_{0}}$):

${{{{\alpha }}}_{0}} = \sqrt {1 - {{E}^{2}}} + \frac{{{{E}^{2}}}}{{2\sqrt {1 - {{E}^{2}}} }} - \frac{{{{E}^{4}}}}{{8\sqrt {{{{(1 - {{E}^{2}})}}^{3}}} }} + \frac{{{{E}^{6}}}}{{16\sqrt {{{{(1 - {{E}^{2}})}}^{5}}} }} - \frac{{5{{E}^{8}}}}{{128\sqrt {{{{(1 - {{E}^{2}})}}^{7}}} }}$

${{{{\alpha }}}_{1}} = - \frac{{{{E}^{2}}}}{{2\sqrt {1 - {{E}^{2}}} }} + \frac{{{{E}^{4}}}}{{4\sqrt {{{{(1 - {{E}^{2}})}}^{3}}} }} - \frac{{3{{E}^{6}}}}{{16\sqrt {{{{(1 - {{E}^{2}})}}^{5}}} }} + \frac{{5{{E}^{8}}}}{{32\sqrt {{{{(1 - {{E}^{2}})}}^{7}}} }}$

${{{{\alpha }}}_{2}} = - \frac{{{{E}^{4}}}}{{8\sqrt {{{{(1 - {{E}^{2}})}}^{3}}} }} + \frac{{3{{E}^{6}}}}{{16\sqrt {{{{(1 - {{E}^{2}})}}^{5}}} }} - \frac{{15{{E}^{8}}}}{{64\sqrt {{{{(1 - {{E}^{2}})}}^{7}}} }}$

${{{{\alpha }}}_{3}} = - \frac{{{{E}^{6}}}}{{16\sqrt {{{{(1 - {{E}^{2}})}}^{5}}} }} + \frac{{5{{E}^{8}}}}{{32\sqrt {{{{(1 - {{E}^{2}})}}^{7}}} }}$

Тогда уравнение (11) приобретает вид:

$\int\limits_{{{и}_{0}}}^и {\,\frac{{\sum\limits_{i = 0}^3 {{{{{\alpha }}}_{i}}} {{{\cos }}^{{2i + 1}}}и}}{{\sqrt {{{{\cos }}^{2}}и - {{\Phi }^{2}}} }}} dи = \frac{S}{а}$

Первый из интегралов в левой части уравнения при замене переменных является табличным:

$\begin{gathered} \int\limits_{{{u}_{0}}}^u {\frac{{{{{{\alpha }}}_{0}}\cos и}}{{\sqrt {{{{\cos }}^{2}}и - {{\Phi }^{2}}} }}du} = {{{{\alpha }}}_{0}}\int\limits_{{{u}_{0}}}^u {\frac{{d(\sin и)}}{{\sqrt {1 - {{\Phi }^{2}} - {{{\sin }}^{2}}и} }}} = {{{{\alpha }}}_{0}}\left( {\arcsin \frac{{\sin и}}{{\sqrt {1 - {{\Phi }^{2}}} }} - \arcsin \frac{{\sin {{и}_{0}}}}{{\sqrt {1 - {{\Phi }^{2}}} }}} \right) = \\ \, = {{\alpha }_{0}}\left( {\arcsin (k\sin и) - \arcsin (k\sin {{и}_{0}})} \right),\quad k = \frac{1}{{\sqrt {1 - {{\Phi }^{2}}} }} \\ \end{gathered} $

Остальные интегралы

${{{{\alpha }}}_{i}}\int\limits_{{{u}_{0}}}^u {\frac{{{{{\cos }}^{{2i + 1}}}и}}{{\sqrt {{{{\cos }}^{2}}и - {{\Phi }^{2}}} }}} \,du = {{{{\alpha }}}_{i}}k\int\limits_{{{u}_{0}}}^u {\frac{{{{{\cos }}^{{2i + 1}}}и}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }}} \,du,\quad i = 1,2,3$

могут быть определены из [3]:

$k{{{{\alpha }}}_{1}}\int\limits_{{{u}_{0}}}^u {\frac{{{{{\cos }}^{3}}и}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }}} \,du = k{{{{\alpha }}}_{1}}\left. {\left\{ {\frac{{\sin \,u\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }}{{2{{k}^{2}}}} + \frac{{2{{k}^{2}} - 1}}{{2{{k}^{3}}}}\arcsin (k\sin u)} \right\}} \right|_{{{{u}_{0}}}}^{u}$

$\begin{gathered} k{{{{\alpha }}}_{2}}\int\limits_{{{u}_{0}}}^u {\frac{{{{{\cos }}^{5}}и}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }}} \,du = k{{{{\alpha }}}_{2}}\left\{ {\frac{{2{{k}^{2}}{{{\cos }}^{2}}и + 6{{k}^{2}} - 3}}{{8{{k}^{4}}}}\sin \,u\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} } \right. + \\ \left. {\left. {\, + \frac{{8{{k}^{4}} - 8{{k}^{2}} + 3}}{{8{{k}^{5}}}}\arcsin (k\sin u)} \right\}} \right|_{{{{u}_{0}}}}^{u} \\ \end{gathered} $

$\begin{gathered} k{{{{\alpha }}}_{3}}\int\limits_{{{u}_{0}}}^u {\frac{{{{{\cos }}^{7}}и}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }}} \,du = \\ \, = k{{{{\alpha }}}_{3}}\left\{ {\frac{{8{{k}^{4}}{{{\sin }}^{4}}и - 2{{k}^{2}}(18{{k}^{2}} - 5){{{\sin }}^{2}}и + 72{{k}^{4}} - 54{{k}^{2}} + 15}}{{48{{k}^{6}}}}} \right.\sin \,u\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} + \\ \, + \left. {\left. {\frac{{16{{k}^{6}} - 24{{k}^{4}} + 18{{k}^{2}} - 5}}{{16{{k}^{7}}}}\arcsin (k\sin u)} \right\}} \right|_{{{{u}_{0}}}}^{u} \\ \end{gathered} $

С учетом возможности представления в компактном виде суммы интегралов:

$\begin{gathered} \sum\limits_{i = 0}^3 {{{{{\alpha }}}_{i}}} \int\limits_{{{u}_{0}}}^u {\frac{{{{{\cos }}^{{2i + 1}}}и}}{{\sqrt {{{{\cos }}^{2}}и - {{\Phi }^{2}}} }}du} = \\ \, = ({{\beta }_{0}} + {{\beta }_{1}}{{\sin }^{2}}и + {{\beta }_{2}}{{\sin }^{4}}и)\sin \,u\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} + {{\beta }_{3}}\arcsin (k\sin u) + {{\beta }_{4}} \\ \end{gathered} $

где коэффициенты ${{{{\beta }}}_{i}},i = 0,...,4$ вычисляются по следующим формулам:

${{{{\beta }}}_{0}} = \,\frac{{24{{{{\alpha }}}_{1}}{{k}^{4}} + 6{{{{\alpha }}}_{2}}(8{{k}^{2}} - 3){{k}^{2}} + {{{{\alpha }}}_{3}}(72{{k}^{4}} - 54{{k}^{2}} + 15)}}{{48{{k}^{5}}}}$

${{{{\beta }}}_{1}} = - \frac{{{{{{\alpha }}}_{3}}(18{{k}^{2}} - 5) + 6{{k}^{2}}{{{{\alpha }}}_{2}}}}{{24{{k}^{3}}}},\quad {{{{\beta }}}_{2}} = \frac{{{{{{\alpha }}}_{3}}}}{{6k}}$

${{{{\beta }}}_{3}} = {{{{\alpha }}}_{0}} + \frac{{{{{{\alpha }}}_{1}}(2{{k}^{2}} - 1)8{{k}^{4}} + {{{{\alpha }}}_{2}}(8{{k}^{4}} - 8{{k}^{2}} + 3)2{{k}^{2}} + {{{{\alpha }}}_{3}}(16{{k}^{6}} - 24{{k}^{4}} + 18{{k}^{2}} - 5)}}{{16{{k}^{6}}}}$

${{{{\beta }}}_{4}} = - ({{{{\beta }}}_{0}} + {{{{\beta }}}_{1}}{{\sin }^{2}}{{и}_{0}} + {{{{\beta }}}_{2}}{{\sin }^{4}}{{и}_{0}})\sin \,{{u}_{0}}\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}{{и}_{0}}} - {{{{\beta }}}_{3}}\arcsin (k\sin {{u}_{0}})$

Окончательно аппроксимация функциональной зависимости длины геодезической линии S от приведенной широты u имеет вид:

(13)

$S = a \cdot (({{{{\beta }}}_{0}} + {{{{\beta }}}_{1}}{{\sin }^{2}}и + {{{{\beta }}}_{2}}{{\sin }^{4}}и)\sin \,u\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} + {{{{\beta }}}_{3}}\arcsin (k\sin u) + {{{{\beta }}}_{4}})$

Для оценки точности найденной аппроксимации (13) был проведен численный сравнительный анализ интеграла (11) с зависимостью (13).

На рис. 1 представлена зависимость ошибки аппроксимации δ (в метрах) функции $S = f(u)$, полученная путем сравнения значений аппроксимирующего выражения (13) и значений высокоточного численного решения уравнения (11), для параметров u₀ = 0 рад, А₀ = 0.2 рад при выборе точки линеаризации ${{u}_{l}} = 0.7$ рад.

Рис. 1.

Зависимость ошибки аппроксимации ${{\delta }}$ функции $S = f(u)$ при u₀ = 0 рад, А₀ = 0.2 рад, u_l = 0.7 рад

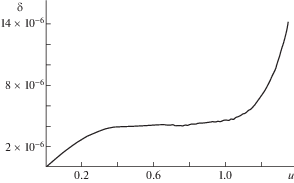
Как показали результаты моделирования, вид представленной на рис. 1 зависимости является характерным для различных начальных значений А₀, u₀ и точки линеаризации ${{u}_{l}}$ и подтверждает высокую точность полученной аналитической аппроксимации функции длины геодезической линии для земного эллипсоида.

Соответственно, для геодезической широты с учетом соотношения (7) искомая зависимость приобретает вид:

(14)

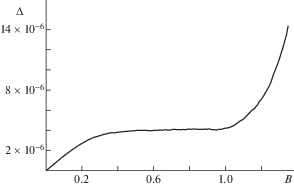
$\begin{gathered} S = a \cdot \left( {\left( {{{{{\beta }}}_{0}} + {{{{\beta }}}_{1}}\frac{{{{{\sin }}^{2}}В}}{{1 + {{e}^{2}}{{{\cos }}^{2}}B}} + {{{{\beta }}}_{2}}\frac{{{{{\sin }}^{4}}В}}{{{{{(1 + {{e}^{2}}{{{\cos }}^{2}}B)}}^{2}}}}} \right) \times } \right. \\ \, \times \frac{{\sin В\sqrt {1 + {{e}^{2}} - ({{k}^{2}} + {{e}^{2}}){{{\sin }}^{2}}В} }}{{1 + {{e}^{2}}{{{\cos }}^{2}}B}} + \\ \left. {\, + {{{{\beta }}}_{3}}\arcsin \left( {k\frac{{\sin В}}{{\sqrt {1 + {{e}^{2}}{{{\cos }}^{2}}B} }}} \right) + {{{{\beta }}}_{4}}} \right) \\ \end{gathered} $

где коэффициенты ${{{{\alpha }}}_{i}},i = 0,...,3$, ${{{{\beta }}}_{i}},i = 0,...,4$ пересчитываются также с учетом соотношения (7) и выбранной точки линеаризации для геодезической широты ${{B}_{l}}$.

Для оценки точности данной аппроксимации геодезической широты был проведен ее сравнительный численный анализ с интегралом (6) для различных начальных значений А₀, B₀ и точек линеаризации ${{B}_{l}}$, который также показал высокую точность данной аппроксимации. В качестве иллюстрирующего это примера на рис. 2 представлена зависимость ошибки аппроксимации $\Delta $ (в метрах) функции $S = f(B)$, полученная путем сравнения значений аппроксимирующего выражения (14) и значений высокоточного численного решения уравнения (6), для аналогичных параметров B₀ = 0 рад, А₀ = 0.2 рад при выборе точки линеаризации ${{B}_{l}} = 0.7$ рад.

Рис. 2.

Зависимость ошибки аппроксимации $\Delta $ функции $S = f(B)$ при B₀ = 0 рад, А₀ = 0.2 рад, B_l = 0.7 рад

Полученные выше результаты интересно далее интерпретировать для сферы и сравнить их с уже известными [1, 2].

Рассмотрим сначала выражение текущего азимута геодезической линии (ортодромии) на сфере, вытекающее из (5) при е = 0 (в данном случае в качестве переменной В выступает уже географическая широта φ ):

(15)

$A = \arcsin \left( {\sqrt {{{e}^{2}} + {{{[\cos {{\varphi }}]}}^{{ - 2}}}} \frac{{\sin {{A}_{0}}}}{{\sqrt {{{e}^{2}} + {{{[\cos {{{{\varphi }}}_{0}}]}}^{{ - 2}}}} }}} \right) = \arcsin \left( {\frac{{\cos {{{{\varphi }}}_{0}}\sin {{A}_{0}}}}{{\cos {{\varphi }}}}} \right)$

или в виде интересного соотношения:

$\frac{{\sin A}}{{\sin {{A}_{0}}}} = \frac{{\,\cos {{{{\varphi }}}_{0}}}}{{\cos {{\varphi }}}}$

Из выражения (15) легко определяется выражение для азимута конечной точки ортодромии:

${{A}_{1}} = \arcsin \left( {\frac{{\cos {{{{\varphi }}}_{0}}\sin {{A}_{0}}}}{{\cos {{{{\varphi }}}_{1}}}}} \right)$

которое может быть также получено из уравнения Клеро на сфере [1] и принципиально отличается от традиционного выражения азимута конечной точки, зависящего от значений долготы и широты как начальной, так и конечной точек (здесь требуется знание только начальных значений широты φ₀ и азимута А₀).

Аналогично, полагая е = 0, из уравнения (11) находим интегральную связь длины ортодромии S с параметрами ее начальной и конечной точек (в данном случае u = φ, a = R, R – радиус Земли):

$\int\limits_0^S {ds} = R\int\limits_{{{{{\varphi }}}_{0}}}^{{\varphi }} {\frac{{\cos {{\varphi }}}}{{\sqrt {{{{\cos }}^{2}}{{\varphi }} - {{{{\varphi }}}^{2}}} }}d{{\varphi }}} $

откуда с учетом ранее проделанных вычислений имеем:

(16)

$S = R\left( {\arcsin (k\sin {{\varphi }}) - \arcsin \,\,\,(k\sin {{{{\varphi }}}_{0}})} \right)$

Как и ранее с выражением для азимута, полученное из дифференциальных уравнений геодезической линии соотношение (16) не совпадает с традиционным выражением зависимости длины ортодромии S от широты φ, выведенной с использованием формул сферической тригонометрии [2]:

$\sin {{\varphi }} = \sin {{{{\varphi }}}_{0}}\cos S + \cos {{{{\varphi }}}_{0}}\sin S\cos {{А}_{0}}$

то есть

(17)

$S = R\left( {\arcsin \frac{{\sin {{\varphi }}}}{{\sqrt {{{{\sin }}^{2}}{{{{\varphi }}}_{0}} + {{{(\cos {{{{\varphi }}}_{0}}\cos {{А}_{0}})}}^{2}}} }} - {\text{arctg}}\frac{{{\text{tg}}{{{{\varphi }}}_{0}}}}{{\cos {{А}_{0}}}}} \right)$

Т.к. получить аналитический вывод выражения (16) из (17) (и наоборот) представляется весьма затруднительным, то для проверки их совпадения было выполнено численное моделирование выражений (16) и (17) для целого ряда значений параметров начальной точки. Результаты численного эксперимента показали полное совпадение зависимостей (16) и (17).

Таким образом, полученные выше выражения представляют собой аналитическое решение поставленной задачи и могут быть эффективно использованы в практических расчетах с минимальными вычислительными затратами.

Список литературы

Морозов В.П. Курс сфероидической геодезии. М.: Недра, 1979. 296 с.
Серапинас Б.Б. Геодезические основы карт. М.: Изд-во МГУ, 2001. 132 с.
Градштейн И.С., Рыжик И.М. Таблицы интегралов. М.: Физматлит, 1963. 1100 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал