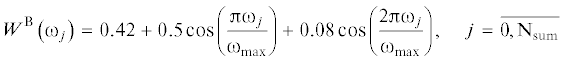Известия РАН. Механика твердого тела, 2021, № 6, стр. 139-148
РЕКОНСТРУКЦИЯ ВРЕМЕННОЙ ЗАВИСИМОСТИ НЕСТАЦИОНАРНОЙ ГРАНИЧНОЙ НАГРУЗКИ, ПРИЛОЖЕННОЙ К ТРЕХМЕРНОМУ ИЗОТРОПНОМУ ЛИНЕЙНО УПРУГОМУ ТЕЛУ
И. П. Марков a, *, Л. А. Игумнов a, **
a Национальный исследовательский Нижегородский государственный университет
им. Н.И. Лобачевского
Нижний Новгород, Россия
* E-mail: teanku@gmail.com
** E-mail: igumnov@mech.unn.ru
Поступила в редакцию 30.04.2021
После доработки 10.05.2021
Принята к публикации 22.05.2021
Аннотация
Представлена методика идентификации временной зависимости нестационарного граничного воздействия с известным пространственным распределением на трехмерное изотропное упругое тело. Реконструкция нагружения осуществляется в частотной области по зарегистрированному отклику некоторой величины, вызванному действием искомой нагрузки. При этом используются решения построенной специальным образом вспомогательной прямой задачи. Используется численное прямое и обратное преобразование Лапласа. Вспомогательная задача решается методом граничных элементов. Приведены подробные результаты демонстрационного численного примера. Установлено хорошее соответствие полученных решений результатам прямых измерений.
1. Введение. Задачи восстановления внешних воздействий на конструктивные элементы и изделия относятся к граничным обратным задачам механики [1] и имеют большое практическое значение. Во многих случаях невозможно провести прямое измерение нагрузок, действующих на элементы конструкции. Среди множества подходов [2] к определению воздействий по косвенным данным, широкое распространение получили методики в частотной области [3–6]. Кроме непосредственного восстановления внешних нагрузок, значительный интерес представляет задача отыскания некоторых других величин в заданных областях конструкции. Например, задача определения по зарегистрированным импульсам деформаций сил, действующих на образец со стороны мерных стержней в системе разрезного стержня Гопкинсона экспериментального исследования процессов динамического деформирования и разрушения материалов. В некоторых случаях (например, при использовании стержней большого диаметра), применение одномерной теории распространения упругих волн в стержнях без специализированной процедуры корректировки упругих импульсов приводит к неверному определению деформации образца.
В настоящей работе изложена оригинальная методика восстановления временной истории граничного нагружения с заданным пространственным распределением по известному отклику какой-либо величины, обусловленному действием искомого нагружения. Предложенную методику можно отнести к классу методов идентификации в частотной области. Суть комплексного подхода заключается в решении вспомогательной прямой задачи в изображениях Лапласа с априорно известными граничными условиями и использовании полученных решений для приближенного определения искомой нестационарной нагрузки. Вспомогательная задача решается методом граничных элементов. Представленная методика применима для трехмерных тел сложной формы. Для рассматриваемой изотропной линейно упругой модели материала, метод граничных элементов представляет мощное, универсальное и высокоточное средство инженерного анализа. В известных исследованиях, посвященных вопросам решения обратных задач и восстановления граничных нестационарных воздействий метод граничных элементов используется довольно редко.
2. Прямое и обратное численное преобразование Лапласа. В изложенной в следующем пункте методике восстановления временной зависимости используется как прямое, так и обратное численное преобразование Лапласа.
Для функции f(t) такой, что $f\left( t \right) = 0$ для $t < 0$, прямое преобразование Лапласа и его обращение задается следующими соотношениями
(2.1)
$\bar {f}\left( s \right) = {\text{L}}\left\{ {f\left( t \right)} \right\} = \int\limits_0^{ + \infty } {{{e}^{{ - st}}}f\left( t \right)dt} ,\quad s = {{\alpha }} + i{{\omega }}$(2.2)
$f\left( t \right) = {{{\text{L}}}^{{ - 1}}}\left\{ {\bar {f}\left( s \right)} \right\} = \frac{1}{{2{{\pi }}i}}\int\limits_{{{\alpha }} - i\infty }^{{{\alpha }} + i\infty } {{{e}^{{st}}}\bar {f}\left( s \right)ds} $Пусть известны значения fi функции f(t) в некоторых точках по времени ${{t}_{i}} \geqslant 0$, i = = $\overline {1,{\text{N}}} $. Это могут быть, например, результаты экспериментальных измерений. Тогда, подразумевая линейное изменение функции f(t) между любыми двумя соседними значениями, прямое преобразование Лапласа можно вычислить как:
(2.3)
$\bar {f}\left( s \right) \approx \frac{{{{f}_{{\text{N}}}}{{e}^{{ - s{{t}_{{\text{N}}}}}}}}}{s} + \frac{1}{{{{s}^{2}}}}\sum\limits_{i = 1}^{{\text{N - 1}}} {\left( {\left( {{{f}_{i}}s + \frac{{{{f}_{{i + 1}}} - {{f}_{i}}}}{{{{t}_{{i + 1}}} - {{t}_{i}}}}} \right){{e}^{{ - s{{t}_{i}}}}} - \left( {{{f}_{{i + 1}}}s + \frac{{{{f}_{{i + 1}}} - {{f}_{i}}}}{{{{t}_{{i + 1}}} - {{t}_{i}}}}} \right){{e}^{{ - s{{t}_{{i + 1}}}}}}} \right)} $Для численного обращение преобразования Лапласа используется метод Дурбина [7]. Выражение (2.2) можно представить в эквивалентном виде
(2.4)
$f\left( t \right) = \frac{{{{e}^{{{{\alpha }}t}}}}}{{{\pi }}}\int\limits_0^{ + \infty } {[\operatorname{Re} (\bar {f}\left( {{{\alpha }} + i{{\omega }}} \right))\cos \left( {{{\omega }}t} \right) - \operatorname{Im} (\bar {f}\left( {{{\alpha }} + i{{\omega }}} \right))\sin \left( {{{\omega }}t} \right)]d{{\omega }}} $Метод Дурбина состоит в аппроксимации (2.4) следующим образом
(2.5)
$\begin{gathered} f\left( t \right) \approx \frac{{{{e}^{{{{\alpha }}t}}}}}{T}\left[ { - \frac{1}{2}\operatorname{Re} (\bar {f}({{\alpha }})) + } \right. \\ \left. { + \;\sum\limits_{k = 0}^{{{{\text{N}}}_{{{\text{sum}}}}}} {\left\{ {\operatorname{Re} \left( {\bar {f}\left( {{{\alpha }} + i\frac{{k{{\pi }}}}{T}} \right)} \right)\cos \left( {\frac{{k{{\pi }}}}{T}t} \right) - \operatorname{Im} \left( {\bar {f}\left( {{{\alpha }} + i\frac{{k{{\pi }}}}{T}} \right)} \right)\sin \left( {\frac{{k{{\pi }}}}{T}t} \right)} \right\}} } \right] \\ \end{gathered} $3. Методика восстановления временной зависимости нестационарной нагрузки. Рассматривается трехмерное изотропное линейно упругое тело $\Omega \in {{R}^{3}}$ с граничной поверхностью $\Gamma = \partial \Omega .$ Предполагается отсутствие массовых сил. Запишем систему уравнений для перемещений при нулевых начальных условиях
(3.1)
${{C}_{{ijkl}}}{{u}_{{k,lj}}}({\mathbf{x}},t) - {{\rho }}{{\ddot {u}}_{i}}({\mathbf{x}},t) = 0,\quad {\mathbf{x}} \in \Omega ,\quad i,j,k,l = \overline {1,\;3} $Система уравнений (3.1) дополняется граничными условиями следующего вида – временные зависимости всех ненулевых компонент векторов перемещений и поверхностных усилий задаются одной и той же скалярной функцией времени $P(t)$, определяющей приложенное нестационарное воздействие:
(3.2)
${{u}_{i}}({\mathbf{x}},t) = P(t)\quad {\text{или}}\quad {{u}_{i}}({\mathbf{x}},t) = 0,\quad {\mathbf{x}} \in {{\Gamma }^{u}}$(3.3)
${{t}_{i}}({\mathbf{x}},t) = \frac{1}{2}{{C}_{{ijkl}}}\left( {{{{\bar {u}}}_{{k,l}}}({\mathbf{x}},t) + {{{\bar {u}}}_{{l,k}}}({\mathbf{x}},t)} \right){{n}_{j}}({\mathbf{x}}) = P(t)\quad {\text{или}}\quad {{t}_{i}}({\mathbf{x}},t) = 0,\quad {\mathbf{x}} \in {{\Gamma }^{t}}$Постановку задачи сформулируем следующим образом: пусть известно решение $u_{i}^{0}({{{\mathbf{x}}}^{0}},t)$ в некоторой точке ${{{\mathbf{x}}}^{0}} \in \Omega $ задачи (3.1)–(3.3) – непрерывное или дискретное на заданном наборе временных точек, и известно геометрическое распределение граничных условий вида (3.2), (3.3). Необходимо отыскать функцию P(t).
Запишем задачу (3.1)–(3.3) в изображениях Лапласа
(3.4)
${{C}_{{ijkl}}}{{\bar {u}}_{{k,lj}}}({\mathbf{x}},s) - {{\rho }}{{s}^{2}}{{\bar {u}}_{i}}({\mathbf{x}},s) = 0,\quad {\mathbf{x}} \in \Omega $(3.5)
${{\bar {u}}_{i}}({\mathbf{x}},s) = \bar {P}(s)\quad {\text{или}}\quad {{\bar {u}}_{i}}({\mathbf{x}},s) = 0,\quad {\mathbf{x}} \in {{\Gamma }^{u}}$(3.6)
${{\bar {t}}_{i}}({\mathbf{x}},s) = \frac{1}{2}{{C}_{{ijkl}}}\left( {{{{\bar {u}}}_{{k,l}}}({\mathbf{x}},s) + {{{\bar {u}}}_{{l,k}}}({\mathbf{x}},s)} \right){{n}_{j}}({\mathbf{x}}) = \bar {P}(s)\quad {\text{или}}\quad {{\bar {t}}_{i}}({\mathbf{x}},s) = 0,\quad {\mathbf{x}} \in {{\Gamma }^{t}}$Сделаем в (3.4)–(3.6) замену
(3.7)
${{\bar {u}}_{i}}({\mathbf{x}},s) = \frac{{\bar {u}_{i}^{ * }({\mathbf{x}},s)\bar {P}\left( s \right)}}{{\bar {G}\left( s \right)}}$(3.8)
${{C}_{{ijkl}}}\bar {u}_{{k,lj}}^{ * }({\mathbf{x}},s) - {{\rho }}{{s}^{2}}\bar {u}_{i}^{ * }({\mathbf{x}},s) = 0,\quad {\mathbf{x}} \in \Omega $(3.9)
$\bar {u}_{i}^{ * }({\mathbf{x}},s) = \bar {G}(s)\quad {\text{или}}\quad \bar {u}_{i}^{ * }({\mathbf{x}},s) = 0,\quad {\mathbf{x}} \in {{\Gamma }^{u}}$(3.10)
$\bar {t}_{i}^{ * }({\mathbf{x}},s) = \frac{1}{2}{{C}_{{ijkl}}}(\bar {u}_{{k,l}}^{ * }({\mathbf{x}},s) + \bar {u}_{{l,k}}^{ * }({\mathbf{x}},s)){{n}_{j}}({\mathbf{x}}) = \bar {G}(s)\quad {\text{или}}\quad \bar {t}_{i}^{ * }({\mathbf{x}},s) = 0,\quad {\mathbf{x}} \in {{\Gamma }^{t}}$После решения вспомогательной задачи (3.8)–(3.10) относительно $\bar {u}_{i}^{ * }({\mathbf{x}},s)$ из (3.7) немедленно следует
(3.11)
$\bar {P}\left( s \right) \approx \hat {\bar {P}}\left( s \right) = \frac{{\bar {u}_{i}^{0}({{{\mathbf{x}}}^{0}},s)\bar {G}\left( s \right)}}{{\bar {u}_{i}^{ * }({{{\mathbf{x}}}^{0}},s)}}$После определения $\hat {\bar {P}}\left( s \right)$, восстановление временной зависимости $P\left( t \right) \approx \hat {P}\left( t \right)$ возможно с помощью какого-либо метода численного обращения преобразования Лапласа. В данной работе используется формула (2.5) метода Дурбина.
3.1. Гранично-элементная схема. В настоящей работе для решения вспомогательной задачи (3.8)–(3.10) используется метод граничных элементов в изображениях Лапласа, подробно изложенный в монографии [8]. В основе лежат граничные интегральные уравнения (ГИУ) прямого подхода для перемещений, регуляризованные статической частью сингулярных решений:
Для пространственной дискретизации приведенных слабосингулярных ГИУ используются прямоугольные граничные элементы с квадратичными функциями формы для интерполяции геометрии границы. Применяется смешанное представление граничных полей на элементах. Перемещения аппроксимируются линейными функциями, а поверхностные усилия – постоянными. Это позволяет сохранить непрерывность перемещений и одновременно корректно моделировать разрывные поверхностные усилия. Дискретный аналог ГИУ строится с помощью метода коллокаций. В качестве точек коллокации выбираются точки аппроксимации неизвестных граничных функций. Для заданного значения комплексной частоты s формируется комплекснозначная разрешающая системы линейных алгебраических уравнений вида
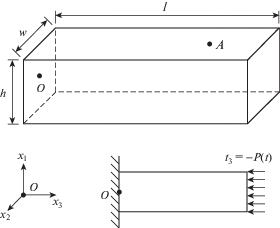
где ${\mathbf{A}}\left( s \right) \in {{{\text{C}}}^{{{{{\text{N}}}_{{{\text{dof}}}}} \cdot {{{\text{N}}}_{{{\text{dof}}}}}}}}$ – это полностью заполненная несимметричная матрица, ${\mathbf{p}} \in {{{\text{C}}}^{{{{{\text{N}}}_{{{\text{dof}}}}} \cdot 1}}}$ – это вектор неизвестных граничных функций, элементы вектора ${\mathbf{b}} \in {{{\text{C}}}^{{{{{\text{N}}}_{{{\text{dof}}}}} \cdot 1}}}$ это линейные комбинации интегралов от ядер ГИУ, соответствующие заданным граничным условиям, Ndof – это общее число степеней свободы.4. Численный пример. В качестве демонстрационного примера рассматривается задача о восстановлении нестационарной нагрузки, действующей на торец призматического тела. Схема задачи приведена на рис. 1, размеры тела заданы как $h = 0.1$ м, $w = 0.1$ м, $l = 0.5$ м, точка O находится в начале координат. На одном торце тело жестко закреплено: ${{u}_{1}}\left( t \right) = {{u}_{2}}\left( t \right) = {{u}_{3}}\left( t \right) = 0$, на противоположном торце заданы сжимающие поверхностные усилия ${{t}_{1}}\left( t \right) = {{t}_{2}}\left( t \right) = 0$, ${{t}_{3}}\left( t \right) = - P\left( t \right)$. Остальная поверхность тела свободна от усилий. Материал тела является изотропным упругим с модулем Юнга ${\text{E}} = 7 \times {{10}^{{10}}}$ Па, коэффициентом Пуассона ${{\nu }} = 0.33$ и плотностью ${{\rho }} = 2650$ кг/м3.
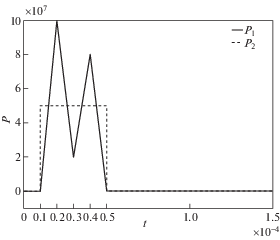
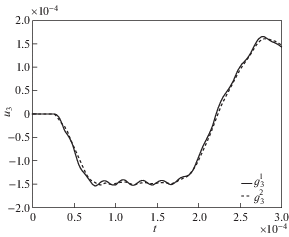
Отыскание временной зависимости $P\left( t \right)$ производится с помощью изложенной выше методики по известной функции перемещений ${{u}_{3}}\left( t \right)$ в точке ${\text{A}}\left( {0.05,\;0.0,\;0.4} \right)$ м, расположенной на боковой грани тела. Рассмотрено два варианта функции $P\left( t \right)$: ${{P}_{1}}\left( t \right)$ и ${{P}_{2}}\left( t \right)$, изображенных на рис. 2. Перемещения ${{u}_{3}}\left( t \right)$ в точке A получены численным решением задачи методом конечных элементов. Отметим, что указанные нагрузки ${{P}_{1}}\left( t \right)$ и ${{P}_{2}}\left( t \right)$ дают на заданном временном интервале $0 \leqslant t \leqslant 0.0003$ с в рассматриваемой точке очень близкие отклики перемещений, приведенные на рис. 3 и обозначенные как $g_{3}^{1}\left( t \right)$ и $g_{3}^{2}\left( t \right)$, соответственно. Конечно-элементный анализ проводился в системе ANSYS. Использовалась равномерная сетка из восьмиузловых кубических элементов SOLID185 с разбиением 10 × 10 × 50 элементов по h, w и l, соответственно. Количество шагов по времени до момента 0.0003 с составило 200.
Рис. 3.
Конечно-элементные решения для перемещений ${{u}_{3}}\left( t \right)$, обозначенные через $g_{3}^{1}\left( t \right)$ и $g_{3}^{2}\left( t \right)$ для нагрузок ${{P}_{1}}\left( t \right)$ и ${{P}_{2}}\left( t \right)$
Методом граничных элементов вспомогательная задача решалась в преобразованиях Лапласа для нагрузки ${{\bar {t}}_{3}}\left( s \right) = \bar {G}\left( s \right) \equiv - 1$, что во временной области соответствует импульсной нагрузке в виде дельта-функции Дирака ${{t}_{3}}\left( t \right) = - {{\delta }}\left( t \right)$.
Дискретный набор комплексных частот $\{ {{s}_{j}}\} $, на которых методом граничных элементов решалась вспомогательная задача и которые использовались для получения изображений $\bar {g}_{3}^{k}\left( {{{s}_{j}}} \right)$, определялся по формулам [10] для метода Дурбина численного обращения преобразования Лапласа
(4.1)
${{s}_{j}} = \frac{{{{\alpha }} + i{{{{\omega }}}_{j}}}}{{{{t}_{{\max }}}}} = \frac{{{{\alpha }} + {{ij{{\pi }}} \mathord{\left/ {\vphantom {{ij{{\pi }}} {T{\text{*}}}}} \right. \kern-0em} {T{\text{*}}}}}}{{{{t}_{{\max }}}}},\quad j = \overline {0,{{{\text{N}}}_{{{\text{sum}}}}}} ,\quad {{\alpha }} = \frac{{{{\kappa }}\ln 10}}{{T{\text{*}}}}$(4.2)
${{{{\omega }}}_{{\max }}} = 300.0,\quad {{\kappa }} = 2.0,\quad {{t}_{{\max }}} = 0.0003\,\,{\text{c}},\quad T* = 2.5,\quad {{{\text{N}}}_{{{\text{sum}}}}} = \left\lfloor {\frac{{{{{{\omega }}}_{{\max }}}T{\text{*}}}}{{{\pi }}}} \right\rfloor = 238,$После гранично-элементного решения вспомогательной задачи на заданном наборе частот $\left\{ {{{s}_{j}}} \right\}$, приближенные значения искомой функции в изображениях могут быть определены согласно выражению (3.11) как
(4.3)
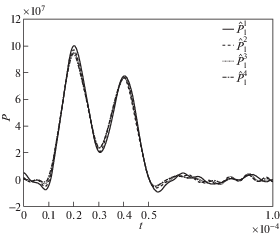
${{\hat {\bar {P}}}_{k}}\left( {{{s}_{j}}} \right) = \frac{{\bar {g}_{3}^{k}\left( {{{s}_{j}}} \right)}}{{{{{\bar {u}}}_{3}}\left( {{{s}_{j}}} \right)}},\quad k = \overline {1,\;2} ,\quad j = \overline {0,{{{\text{N}}}_{{{\text{sum}}}}}} $Временные зависимости нагрузок вычислены методом Дурбина по изображениям, полученным в (4.3). Для проверки чувствительности методики восстановления нагрузки к степени гранично-элементной дискретизации решение задачи получено на четырех гранично-элементных сетках. Сетки, обозначаемые далее надстрочными индексами “1”, “2”, “3” и “4” имеют разбиение 6 × 6 × 30, 8 × 8 × 40, 10 × 10 × 40 и 12 × 12 × 60 элементов по h, w и l, соответственно. На рис. 4 приведены восстановленные временные зависимости нагрузок $\hat {P}_{1}^{1}\left( t \right)$, $\hat {P}_{1}^{2}\left( t \right)$, $\hat {P}_{1}^{3}\left( t \right)$ и $\hat {P}_{1}^{4}\left( t \right)$ на четырех гранично-элементных сетках для нагрузки ${{P}_{1}}\left( t \right)$. Решения, полученные даже на сетке “1” с самым малым числом элементов, в достаточной степени отражают основные характеристики исходной функции.
Рис. 4.
Восстановленные временные зависимости нагрузок $\hat {P}_{1}^{1}\left( t \right)$, $\hat {P}_{1}^{2}\left( t \right)$, $\hat {P}_{1}^{3}\left( t \right)$ и $\hat {P}_{1}^{4}\left( t \right)$ на четырех гранично-элементных сетках для нагрузки ${{P}_{1}}\left( t \right)$
В частотном гранично-элементном анализе для уменьшения нежелательных колебаний, возникающих при последующем обращении во временную область из-за отсечения высокочастотной части спектра, часто используются оконные фильтры при постпроцессорной обработке результатов в изображениях. Перед численным обращением во временную область, отклик в изображениях умножается на подходящую оконную функцию в изображениях. Рассмотрено применение фильтра Блэкмана [11, 12]
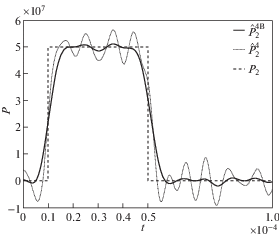
Сравнение временных зависимостей, полученных с применением оконной функции (4.4) и без нее, приведено для нагрузок ${{P}_{1}}\left( t \right)$ и ${{P}_{2}}\left( t \right)$ на рис. 5 и рис. 6, соответственно. На указанных рисунках через $\hat {P}_{k}^{{4{\text{B}}}}\left( t \right)$ обозначена восстановленная k-я нагрузка с использованием гранично-элементного решения на сетке “4” и с применением фильтра Блэкмана, через $\hat {P}_{k}^{4}\left( t \right)$ – без фильтра. По результатам подтверждается общее наблюдение: для кусочно-гладких функций с изломами применение оконных фильтров может приводить к чрезмерному сглаживанию в окрестности угловых точек и, следовательно, к некорректному определению амплитуды, но для функций с разрывами типа «скачок» этого не происходит.
Рис. 5.
Сравнение восстановленных временных зависимостей нагрузок $\hat {P}_{1}^{4}\left( t \right)$ и $\hat {P}_{1}^{{4{\text{B}}}}\left( t \right)$ с исходной функцией ${{P}_{1}}\left( t \right)$
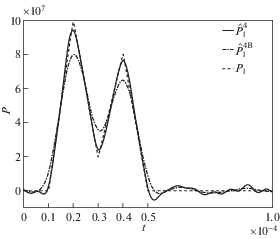
Рис. 6.
Сравнение восстановленных временных зависимостей нагрузок $\hat {P}_{2}^{4}\left( t \right)$ и $\hat {P}_{2}^{{4{\text{B}}}}\left( t \right)$ с исходной функцией ${{P}_{2}}\left( t \right)$
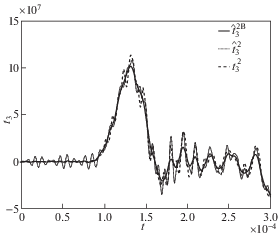
Интерес часто представляет не восстановленная нагрузка сама по себе, а отклики в других точках тела. В таких случаях изложенная методика позволяет получить результаты используя уже полученные гранично-элементные решения вспомогательной задачи. Для этого, по аналогии с формулой (3.7), гранично-элементные решения вспомогательной задачи в изображениях для искомой величины умножаются на отношение ${{\hat {\bar {P}}(s)} \mathord{\left/ {\vphantom {{\hat {\bar {P}}(s)} {\bar {G}(s)}}} \right. \kern-0em} {\bar {G}(s)}}$. После этого, временные зависимости вычисляются обращением полученных результатов в изображениях. В демонстрационном примере рассмотрено применение такой схемы для отыскания поверхностных усилий ${{t}_{3}}\left( t \right)$ в точке ${\text{O}}(0,0,0)$ м, расположенной в центре закрепленного торца. Для обоих вариантов нагрузки использовалось гранично-элементное решение, полученное на сетке “4”. На рис. 7 приведено сравнение гранично-элементного решения $\hat {t}_{3}^{1}\left( t \right)$, полученного для восстановленной нагрузки $\hat {\bar {P}}_{1}^{4}\left( s \right)$, и конечно-элементного решения $t_{3}^{1}\left( t \right)$ для исходной нагрузки ${{P}_{1}}\left( t \right)$. На рис. 8 приведены результаты для исходной нагрузки ${{P}_{2}}\left( t \right)$, а также к сравнению добавлено решение $\hat {t}_{3}^{{2{\text{B}}}}\left( t \right)$, полученное с применением фильтра Блэкмана. Полученные результаты свидетельствуют, что по одной зарегистрированной в одной точке величине $g_{3}^{k}\left( t \right)$ представленная методика позволила идентифицировать отклики другой величины в другой точке с очень хорошим соответствием прямым конечно-элементным решениям как по амплитуде, там и по характеру изменения во времени.
Рис. 7.
Сравнение гранично-элементного решения $\hat {t}_{3}^{1}\left( t \right)$, полученного для восстановленной нагрузки $\hat {\bar {P}}_{1}^{4}\left( s \right)$, и конечно-элементного решения $t_{3}^{1}\left( t \right)$ для исходной нагрузки ${{P}_{1}}\left( t \right)$
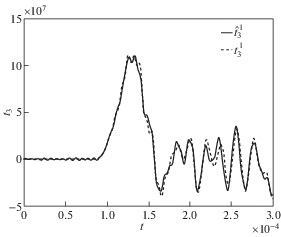
Рис. 8.
Сравнение гранично-элементных решений $\hat {t}_{3}^{{2{\text{B}}}}\left( t \right)$ и $\hat {t}_{3}^{2}\left( t \right)$, полученных для восстановленной нагрузки $\hat {\bar {P}}_{2}^{4}\left( s \right)$, и конечно-элементного решения $t_{3}^{2}\left( t \right)$ для исходной нагрузки ${{P}_{2}}\left( t \right)$
5. Заключение. В настоящей работе изложена простая методика восстановления временной зависимости поверхностной нестационарной нагрузки с заданным пространственным распределением по известным решениям или экспериментальным данным регистрируемой величины. Методика основывается на решении вспомогательной задачи с нагрузкой какого-либо известного вида методом граничных элементов в преобразованиях Лапласа и использовании полученного решения для определения отклика искомой функции в изображениях. Последующее получение зависимости во временной области проводится численным методом обращения преобразования Лапласа. Область применения представленной методики ограничена случаями, когда задаваемые граничные условия изменяются во времени по одному закону с искомыми функциями, либо являются нулевыми. К достоинствам следует отнести простоту методики и возможность использования одного и того же решения вспомогательной задачи для восстановления нагрузки по различным данным. Кроме того, изложенная методика позволяет не только восстановить нагрузку, но и немедленно получить решения задачи в изображениях в других точках тела с учетом действия восстановленной нагрузки, без необходимости обращения во временную область или повторного решения задачи.
Методика представлена для трехмерных линейных изотропных упругих тел и может быть естественным образом расширена на другие линейные теории, задачи в рамках которых можно решать методом граничных элементов: вязкоупругость, анизотропная упругость, пороупругость, электроупругость и т.д.
Работа выполнена при финансовой поддержке Министерства науки и высшего образования Российской Федерации (проект 0729-2020-0054).
Список литературы
Ватульян А.О. Обратные задачи в механике деформируемого твердого тела. М.: Физматлит, 2007. 223 с.
Martin M.T., Doyle J.F. Impact force identification from wave propagation responses // Int. J. Impact Eng. 1996. V. 18. P. 65–77.
Lee S.-K., Banerjee S., Mal A. Identification of impact force on a thick plate based on the elastodynamic and higher-order time-frequency analysis // Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2007. v. 221. № 6. P. 1249–1263.
Boukria Z., Perrotin P., Bennani A. Experimental impact force location and identification using inverse problems: Application for a circular plate // Int. J. Mech. 2011. V. 5. № 1. P. 48–55.
Gombi S.L., Ramakrishna D.S. A solution to the inverse problem of impact force determination from structural responses // Int. J. Eng. Inn. Techn. 2012. V. 1. № 3. P. 192–196.
Lage Y.E., Maia N.M.M., Neves M.M., Ribeiro A.M.R. Force identification using the concept of displacement transmissibility // J. Sound Vib. 2013. V. 332. № 7. P. 1674–1686.
Durbin F. Numerical inversion of Laplace transforms: an efficient improvement to Dubner and Abate’s method // Comput. J. 1974. V. 17. № 4. P. 371–376.
Баженов В.Г., Игумнов Л.А. Методы граничных интегральных уравнений и граничных элементов в решении задач трехмерной динамической теории упругости с сопряженными полями. М.: Физматлит, 2008. 352 с.
Gaul L., Kogl M., Wagner M. Boundary Element Methods for Engineers and Scientists. Berlin: Springer, 2003. 488 c.
Crump K.S. Numerical Inversion of Laplace Transforms Using a Fourier Series Approximation // J. ACM 1976. V. 23. № 1. P. 89–96.
Gomez Zamorano P., Uribe Campos F.A. On the Application of the numerical Laplace transform for accurate electromagnetic transient analysis // Rev. Mex. Fis. Mexico 2007. V. 53. № 3. P. 198–204.
Schanz M., Ye W., Xiao J. Comparison of the convolution quadrature method and enhanced inverse FFT with application in elastodynamic boundary element method // Comput. Mech. 2016. V. 57. № 4. P. 523–536.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела