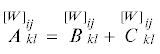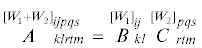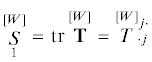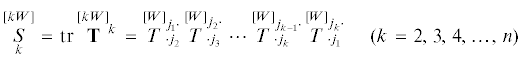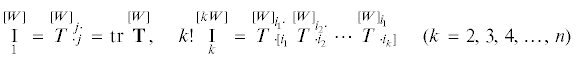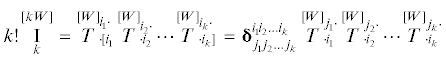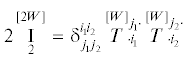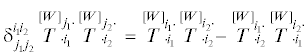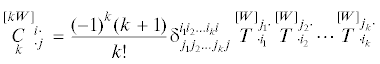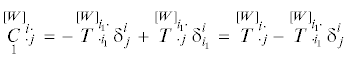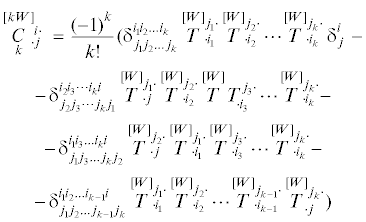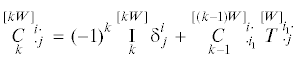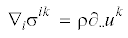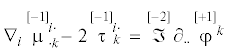Известия РАН. Механика твердого тела, 2021, № 6, стр. 130-138
ОБ ОДНОМ ОБОБЩЕНИИ АЛГЕБРАИЧЕСКОЙ ТЕОРИИ ГАМИЛЬТОНА–КЭЛИ
Е. В. Мурашкин a, *, Ю. Н. Радаев a, **
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: evmurashkin@gmail.com
** E-mail: y.radayev@gmail.com
Поступила в редакцию 21.04.2021
После доработки 24.04.2021
Принята к публикации 26.04.2021
Аннотация
В статье приводятся обобщения понятий векторного и смешанного произведения и указана их связь с фундаментальным ориентирующим скаляром, необходимых для построения алгебраической теории Гамильтона–Кэли в случае пространства произвольной заданной размерности n в псевдотензорном случае. В известных литературных источниках, касающихся механики деформируемого твердого тела, обычно рассматривается случай трехмерного пространства. Проведено доказательство теоремы Гамильтона–Кэли в псевдотензорной формулировке. Вес псевдотензора предполагается целым числом. Примерами здесь служат тензоры микрополярной теории упругости, в частности, гемитропной микрополярной упругости. Обсуждаются уравнения динамики гемитропного микрополярного континуума в терминах псевдотензоров.
Вводные замечания. Модель гемитропной микрополярной теории упругости широко используется при моделировании био-, нано- и метаметриалов, например в механике сотовых конструкций (honeycomb structures), [1–3]. Одной из особенностей гемитропных материалов является существование зеркальных мод при распространении гармонических волн, что объясняется их чувствительностью к изменению ориентации пространства (зеркальным отражениям и инверсиям пространства). Следует отметить, что подавляющее большинство работ, посвященных этим исследованиям, обходят стороной вопросы применения псевдотензоров при описании гемитропных континуумов, несмотря на достаточную проработанность аппарата алгебры псевдотензоров [4–8]. Отметим, что построение определяющего упругого потенциала для гемитропного континуума возможно исключительно при использовании псевдотензорных формулировок, и только после этого возможен корректный переход к абсолютным тензорам и вывод уравнений микрополярной теории. Еще одним существенным аспектом является необходимость согласовывать баланс весов во всех уравнениях теории, особенно при использовании символов перестановок, которые можно трактовать одновременно как псевдотензоры весов +1 и –1.
Многочисленные руководства по тензорному анализу чаще всего обходят стороной вопросы, связанные с алгеброй псевдотензоров [9]. Ранее, в работах авторов [10–12] обсуждались вопросы применения алгебры псевдотензоров в трехмерном пространстве к задачам механики растущих тел и микрополярной теории упругости. В настоящей работе рассматривается более общий случай n-мерного евклидова пространства. Введены понятия фундаментального ориентирующего псевдоскаляра, косого и векторного произведений. Приводится доказательство известной алгебраической теоремы Гамильтона–Кэли в терминах псевдотензоров в n-мерном евклидовом пространстве. Следует отметить, что указанная теорема занимает центральное место в теории определяющих уравнений механики. Рассмотрены вопросы применения алгебры псевдотензоров при построении моделей гемитропного микрополярного тела. Определены веса основных тензоров, с которыми приходится сталкиваться в механике гемитропной микрополярной среды, в том числе определяющих псевдоскаляров. Приведены уравнения динамики гемитропного микрополярного континуума в терминах перемещений и микровращений в псевдотензорной формулировке.
1. Определение и основные формулы алгебры псевдотензоров. Рассмотрим в n-мерном пространстве две системы координат xk и ${{\bar {x}}^{k}}$ ($k = 1,\;2, \ldots ,\;n$). Преобразование относительного тензора веса $W$ (псевдотензора веса $W$) от системы координат xk к новой системе координат ${{\bar {x}}^{k}}$ осуществляется по закону [13, 14]
(1.1)
$\bar {T}_{{ij \ldots k}}^{{lm \ldots n}} = {{\Delta }^{W}}({{\partial }_{p}}{{\bar {x}}^{l}})({{\partial }_{q}}{{\bar {x}}^{m}})\; \cdots \;({{\partial }_{s}}{{\bar {x}}^{n}})({{\bar {\partial }}_{i}}{{x}^{a}})({{\bar {\partial }}_{j}}{{x}^{b}})\; \cdots \;({{\bar {\partial }}_{k}}{{x}^{c}})T_{{ab \ldots c}}^{{pq \ldots s}}$Здесь черта сверху указывает на значение величины в новой системе координат ${{\bar {x}}^{k}}$ ($k = 1,2, \ldots n$), $\Delta $ – якобиан преобразования, W – вес псевдотензора. Отметим, что закон преобразования псевдотензоров отличается от закона преобразования абсолютных тензоров дополнительным множителем ${{\Delta }^{W}}$. W – целое число, так как в противном случае значение ${{\Delta }^{W}}$ не будет однозначным.
Для псевдотензоров справедливы следующие утверждения:
1. Сумма двух псевдотензоров одинаковой валентности и веса будет псевдотензором той же валентности и веса
2. Тензорное произведение псевдотензоров (возможно, различных валентностей) дает псевдотензор с итоговым весом, равным сумме весов сомножителей
3. Результатом свертки псевдотензора будет псевдотензор того же веса. В том числе, полная свертка псевдотензора веса W будет псевдоскаляром того же веса.
2. Фундаментальный ориентирующий псевдоскаляр в n-мерном пространстве. Фундаментальным понятием многомерной геометрии является относительный ковариантный n-вектор (антисимметричный псевдотензор валентности n с компонентами ${{\varepsilon }_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{n}}}}}$ [4, 15]) веса –1, с единственной существенной компонентой
Относительный контравариантный n-вектор ${{\varepsilon }^{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{n}}}}}$ задается аналогично, но имеет противоположный вес +1. Тензоры ${{\varepsilon }^{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{n}}}}}$ и ${{\varepsilon }_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{n}}}}}$ называются также символами перестановок.
Свертка антисимметричного тензора ${{e}_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{n}}}}}$ с $n$ абсолютными векторами $\mathop {\mathbf{a}}\limits_1 ,\mathop {\mathbf{a}}\limits_2 ,{\mathbf{a}},\; \ldots ,\;\mathop {\mathbf{a}}\limits_n $
(2.1)
${{e}_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{n}}}}}{{\mathop a\limits_1 }^{{{{i}_{1}}}}}{{\mathop a\limits_2 }^{{{{i}_{2}}}}}\; \ldots {{\mathop a\limits_n }^{{{{i}_{n}}}}}$(2.2)
$\lceil \mathop {\mathbf{a}}\limits_1 ,\mathop {\mathbf{a}}\limits_2 ,\; \ldots ,\;\mathop {\mathbf{a}}\limits_n \rceil $При положительном значении косого произведения (2.1) систему n векторов называют правой, а при отрицательном – левой. Косое произведение абсолютных векторов является абсолютным скаляром.
Значение косого произведения (2.1) может быть вычислено в детерминантной форме
(2.3)
$\lceil\mathop {\mathbf{a}}\limits_1 ,\mathop {\mathbf{a}}\limits_2 ,\; \ldots ,\;\mathop {\mathbf{a}}\limits_n\rceil = edet({{\mathop a\limits_c }^{i}}) = e\left| {\begin{array}{*{20}{c}} {{{{\mathop a\limits_1 }}^{1}}}&{{{{\mathop a\limits_2 }}^{1}}}& \ldots &{{{{\mathop a\limits_n }}^{1}}} \\ {{{{\mathop a\limits_1 }}^{2}}}&{{{{\mathop a\limits_2 }}^{2}}}& \ldots &{{{{\mathop a\limits_n }}^{2}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{{{\mathop a\limits_1 }}^{n}}}&{{{{\mathop a\limits_2 }}^{n}}}& \ldots &{{{{\mathop a\limits_n }}^{n}}} \end{array}} \right|$Если свернуть антисимметричный тензор ${{e}_{{{{i}_{1}}{{i}_{2}} \cdots {{i}_{n}}}}}$ с $(n - 1)$ абсолютными векторами $\mathop {\mathbf{a}}\limits_1 ,\mathop {\mathbf{a}}\limits_2 ,\; \ldots ,\;\mathop {\mathbf{a}}\limits_{n - 1} $, то получим абсолютный вектор
(2.4)
${{b}_{i}} = {{e}_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{{n - 1}}}i}}}\mathop {{{a}^{{{{i}_{1}}}}}}\limits_1 {{\mathop a\limits_2 }^{{{{i}_{2}}}}}\; \ldots \;{{\mathop a\limits_{n - 1} }^{{{{i}_{{n - 1}}}}}}$При свертке $(n - 1)$ абсолютного вектора $\mathop {\mathbf{a}}\limits_1 ,\mathop {\mathbf{a}}\limits_2 ,\; \ldots ,\;\mathop {\mathbf{a}}\limits_{n - 1} $ с антисимметричным относительным тензором ${{\varepsilon }_{{{{i}_{1}}{{i}_{2}} \cdots {{i}_{n}}}}}$ получим ковариантный псевдовектор веса –1
(2.5)
$\mathop {{{b}_{i}}}\limits^{[ - 1]} = {{\varepsilon }_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{{n - 1}}}i}}}\mathop {{{a}^{{{{i}_{1}}}}}}\limits_1 {{\mathop a\limits_2 }^{{{{i}_{2}}}}}\; \ldots ,\;{{\mathop a\limits_{n - 1} }^{{{{i}_{{n - 1}}}}}}$Косое и векторное произведения связаны соотношением
(2.6)
$\lceil\mathop {\mathbf{a}}\limits_1 ,\mathop {\mathbf{a}}\limits_2 ,\; \ldots ,\;\mathop {\mathbf{a}}\limits_n \rceil = \left[ {\mathop {\mathbf{a}}\limits_1 ,\mathop {\mathbf{a}}\limits_2 ,\; \ldots ,\;\mathop {\mathbf{a}}\limits_{n - 1} } \right] \cdot \mathop {\mathbf{a}}\limits_n $Если в качестве системы векторов $\mathop {\mathbf{a}}\limits_1 ,\mathop {\mathbf{a}}\limits_2 ,\; \ldots ,\;\mathop {\mathbf{a}}\limits_n $ принять векторы ковариантного базиса $\mathop \imath \limits_1 ,\mathop \imath \limits_2 ,\; \ldots ,\;\mathop \imath \limits_n $, в n-мерном пространстве, то на основании (4) находим
(2.7)
$\lceil\mathop \imath \limits_1 ,\mathop \imath \limits_2 ,\; \ldots ,\;\mathop \imath \limits_n \rceil= e$Учитывая формулы Лагранжа–Грамма–Шмидта, приходим к
(2.8)
${{e}^{2}} = {{\lceil\mathop \imath \limits_1 ,\mathop \imath \limits_2 ,\; \ldots ,\;\mathop \imath \limits_n \rceil}^{2}} = \left| {\begin{array}{*{20}{c}} {\mathop \imath \limits_1 \cdot \mathop \imath \limits_1 }&{\mathop \imath \limits_1 \cdot \mathop \imath \limits_2 }& \ldots &{\mathop \imath \limits_1 \cdot \mathop \imath \limits_n } \\ {\mathop \imath \limits_2 \cdot \mathop \imath \limits_1 }&{\mathop \imath \limits_2 \cdot \mathop \imath \limits_2 }& \ldots &{\mathop \imath \limits_2 \cdot \mathop \imath \limits_n } \\ \vdots & \vdots & \ddots & \vdots \\ {\mathop \imath \limits_n \cdot \mathop \imath \limits_1 }&{\mathop \imath \limits_n \cdot \mathop \imath \limits_2 }& \ldots &{\mathop \imath \limits_n \cdot \mathop \imath \limits_n } \end{array}} \right| = det({{g}_{{ij}}}) = g$Откуда следует, что g является псевдоскаляром веса +2, а также $e = \sqrt g $ для правоориентированного базиса и $e = - \sqrt g $ для левориентированного базиса.
В трехмерном пространстве e определяется смешанным произведением базисных векторов
(2.9)
$e = \mathop e\limits^{[ + 1]} = \lceil \mathop \imath \limits_1 ,\mathop \imath \limits_2 ,\mathop \imath \limits_3 \rceil = (\mathop \imath \limits_1 \cdot \mathop \imath \limits_2 ) \cdot \mathop \imath \limits_3 $(2.10)
$\frac{1}{e} = {{\mathop e\limits^{[ - 1]} }^{{ - 1}}} = \lceil \mathop \imath \limits^1 ,\mathop \imath \limits^2 ,\mathop \imath \limits^3 \rceil= (\mathop \imath \limits^1 \, \cdot \mathop \imath \limits^2 ) \cdot \mathop \imath \limits^3 $Отметим, что фундаментальный ориентирующий псевдоскаляр позволяет легко преобразовывать псевдотензоры в абсолютные тензоры. Введем тензор T согласно
Подсчитывая баланс весов, приходим к заключению о том, что T является абсолютным тензором, а соотношение (2.11) позволяет легко преобразовать полином Гамильтона–Кэли к псевдотензорной форме [11].
3. Уравнение Гамильтона–Кэли для псевдотензора второго ранга. Рассмотрим псевдотензор второй валентности (псевдоаффинор), заданный своими смешанными
компонентами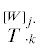 
($j,k = \overline {1,n} $), веса W в n-мерном пространстве. Простейшим псевдоинвариантом веса [W] псевдоаффинора 
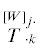является его псевдослед (имеющий вес W)
С помощью псевдоследов степеней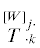 
можно определить систему псевдоинвариантов псевдоаффинора 
:
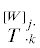Другой системой псевдоинвариантов будет
Здесь в квадратные скобки заключены индексы по которым выполняется операция альтернирования:
Абсолютный тензор ${\mathbf{\delta }}_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{k}}}}^{{{{j}_{1}}{{j}_{2}} \ldots {{j}_{k}}}}$, называемый обобщенной дельтой Кронекера, определяется в n-мерном пространстве для $k \leqslant n$ согласно правилу
(3.5)
${\mathbf{\delta }}_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{k}}}}^{{{{j}_{1}}{{j}_{2}} \ldots {{j}_{k}}}} = \left\{ {\begin{array}{*{20}{c}} { + 1,}&{{\text{если}}\;{{j}_{1}}{{j}_{2}} \ldots {{j}_{k}}\;{\text{различные}}\;{\text{натуральные}}\;{\text{числа}}\;1,2, \ldots ,n} \\ {}&{{\text{и}}\;{\text{если}}\;{{i}_{1}}{{i}_{2}} \ldots {{i}_{k}}\;{\text{является}}\;{\text{четной}}\;{\text{перестановкой}}\;{{j}_{1}}{{j}_{2}} \ldots {{j}_{k}}} \\ { - 1,}&{{\text{если}}\;{{j}_{1}}{{j}_{2}} \ldots {{j}_{k}}\;{\text{различные}}\;{\text{натуральные}}\;{\text{числа}}\;1,2, \ldots ,n} \\ {}&{{\text{и}}\;{\text{если}}\;{{i}_{1}}{{i}_{2}} \ldots {{i}_{k}}\;{\text{является}}\;{\text{нечетной}}\;{\text{перестановкой}}\;{{j}_{1}}{{j}_{2}} \ldots {{j}_{k}}} \\ {0,}&{{\text{во}}\;{\text{всех}}\;{\text{остальных}}\;{\text{случаях}}} \end{array}} \right.$Несложно заметить, что в n-мерном пространстве
(3.6)
${{\varepsilon }_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{n}}}}} = \delta _{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{n}}}}^{{12 \ldots n}},\quad {{\varepsilon }_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{n}}}}}{{\varepsilon }^{{{{j}_{1}}{{j}_{2}} \ldots {{j}_{n}}}}} = \delta _{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{n}}}}^{{{{j}_{1}}{{j}_{2}} \ldots {{j}_{n}}}},\quad \delta _{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{m}}}}^{{{{j}_{1}}{{j}_{2}} \ldots {{j}_{m}}}} = 0\quad (m > n).$Псевдоинварианты $\mathop {\text{I}}\limits_k^{[kW]} $ являются полиномами от $\mathop S\limits_1^{[W]} ,\mathop S\limits_2^{[W]} ,\; \ldots ,\;\mathop S\limits_k^{[kW]} $, причем $\mathop S\limits_k^{[kW]} $ входит в них в первой степени. Верно и обратное утверждение: псевдоинварианты $\mathop S\limits_k^{[kW]} $ определяются полиномиальной зависимостью от $\mathop S\limits_k^{[kW]} $.
Псевдоинвариант $\mathop {\text{I}}\limits_2^{[2W]} $, определенный формулой (3.4), вычисляется по формуле
и равен сумме слагаемых вида
Суммы пар слагаемых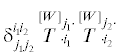 
и 
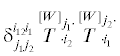равны главным минорам определителя 
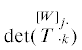, полученным вычеркиванием всех строк и столбцов кроме строк и столбцов с индексами
j1 и j2. Тогда псевдоинвариант $\mathop {\text{I}}\limits_2^{[2W]} $ равен сумме всех главных миноров второго порядка определителя 
.
Аналогично можно показать, что псевдоинвариант $\mathop {\text{I}}\limits_k^{[kW]} $ равен сумме всех главных миноров k-го порядка определителя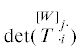 
. В частности, 
.
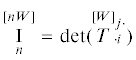Введем комитанты $\mathop {C_{{ \cdot j}}^{{ \cdot i}}}\limits_k^{[kW]} $ псевдоаффинора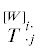 
, задающиеся согласно формуле [4]
Комитанты $\mathop {C_{{ \cdot j}}^{{i \cdot }}}\limits_k^{[kW]} $ можно выразить через степени аффинора и псевдоинварианты $\mathop I\limits_p^{[pW]} $ ($p \leqslant k$). Так например, для $\mathop {C_{{ \cdot j}}^{{i \cdot }}}\limits_1^{[W]} $ получим
Воспользуемся формулой
Заметим, что все слагаемые в правой части равенства (3.11), начиная с третьего слагаемого,
равны второму слагаемому. Поэтому, равенство (3.11) с учетом определений $\mathop {\text{I}}\limits_k^{[kW]} $ и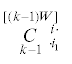 
можно записать в виде
Продолжая по индукции и вводя прямую тензорную запись, получим
(3.13)
$\mathop {\mathbf{C}}\limits_k^{[kW]} = {{\mathop {\mathbf{T}}\limits^{[W]} }^{k}}\, - \mathop {\text{I}}\limits_1^{[W]} {{\mathop {\mathbf{T}}\limits^{[W]} }^{{k - 1}}}\, + \mathop {\text{I}}\limits_2^{[2W]} {{\mathop {\mathbf{T}}\limits^{[W]} }^{{k - 2}}}\, - \cdots + {{( - 1)}^{k}}\mathop {\text{I}}\limits_k^{[kW]} \mathop {\mathbf{I}}\limits^{[0]} $При k = n правая часть равенства (3.9) содержит операцию альтернирования по n + 1 индексу и поэтому равна нулю, т.е.
(3.14)
$\mathop {\mathbf{C}}\limits_n^{[nW]} = \mathop {\mathbf{0}}\limits^{[nW]} = {{\mathop {\mathbf{T}}\limits^{[W]} }^{n}}\, - \mathop {\text{I}}\limits_1^{[W]} {{\mathop {\mathbf{T}}\limits^{[W]} }^{{n - 1}}}\, + \mathop {\text{I}}\limits_2^{[2W]} {{\mathop {\mathbf{T}}\limits^{[W]} }^{{n - 2}}}\, - \cdots + {{( - 1)}^{n}}\mathop {\text{I}}\limits_n^{[nW]} \mathop {\mathbf{I}}\limits^{[0]} $Соотношение (3.14) означает справедливость уравнения Гамильтона–Кэли для псевдотензоров в случае n-мерного пространства11. Другое доказательство, приведенное в [11] для случая трехмерного евклидова пространства, может быть также обобщено на многомерный случай.
4. Гемитропное микрополярное тело. Линейная микрополярная теория гемитропного тела корректно может быть развита только в терминах относительных тензоров. Известные из литературных источников формулировки теории гемитропного микрополярного тела в терминах абсолютных тензоров корректно получаются только из псевдотензорных формулировок [10, 12], но ни в коем случае не наоборот. Приведем в табл. 1 основные псевдотензорные величины теории микрополярной упругости с указанием их веса.
Таблица 1.
Основные псевдотензоры микрополярной теории упругости
| Терминологическое обозначение | Корневое символьное обозначение | Вес | Преобразование к абсолютному тензору |
|---|---|---|---|
| метрический тензор | gij | 0 | |
| фундаментальный тензор | gij | 0 | |
| детерминант метрического тензора | g | +2 | $\mathop g\limits^{[ + 2]} = {{e}^{2}}$ |
| тензор перестановок | ${{\varepsilon }^{{ijk}}}$ | +1 | ${{e}^{{ijk}}} = \tfrac{1}{e}{{\mathop \varepsilon \limits^{[ + 1]} }^{{ijk}}}$ |
| тензор перестановок | ${{\varepsilon }_{{ijk}}}$ | –1 | ${{e}_{{ijk}}} = e{{\mathop \varepsilon \limits^{[ - 1]} }_{{ijk}}}$ |
| фундаментальный | |||
| ориентирующий скаляр | e | +1 | $\mathop e\limits^{[ + 1]} = e$ |
| фундаментальный | |||
| ориентирующий скаляр | $\tfrac{1}{e}$ | –1 | ${{\mathop e\limits^{[ - 1]} }^{{ - 1}}} = \tfrac{1}{e}$ |
| естественный элемент объема | $d\tau $ | –1 | $dV = e\mathop {d\tau }\limits^{[ - 1]} $ |
| инвариантный элемент объема | $dV$ | 0 | |
| набла Гамильтона | ${{\nabla }_{i}}$ | 0 | |
| вектор перемещений | ${{u}^{k}}$ | 0 | |
| ассимметричный тензор деформаций | ${{\varepsilon }_{{ij}}}$ | 0 | |
| тензор малых деформаций | ${{\varepsilon }_{{(ij)}}} = {{\varepsilon }_{{ij}}}$ | 0 | |
| вектор поверхностных сил | ${{t}^{k}} = {{n}_{i}}{{\sigma }^{{ik}}}$ | 0 | |
| тензор силовых напряжений | ${{\sigma }^{{ik}}}$ | 0 | |
| объемные силы | Xk | 0 | |
| упругий потенциал | $\mathcal{U}$ | 0 | |
| плотность | ρ | 0 | |
| вектор поверхностных моментов | ${{m}_{k}} = {{n}_{i}}\mu _{{ \cdot k}}^{{i \cdot }}$ | –1 | ${{m}_{k}} = e\mathop {{{m}_{k}}}\limits^{[ - 1]} $ |
| тензор моментных напряжений | $\mu _{{ \cdot k}}^{{i \cdot }}$ | –1 |  |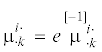
| ассоциированный вектор | |||
| моментных напряжений | μi | 0 | |
| ассоциированный вектор | |||
| силовых напряжений | ${{\tau }_{k}}$ | –1 | ${{\tau }_{k}} = e{{\mathop \tau \limits^{[ - 1]} }_{k}}$ |
| объемные моменты | Yk | –1 | ${{Y}_{k}} = e{{\mathop Y\limits^{[ - 1]} }_{k}}$ |
| коэффициент микроинерции | $\Im $ | –2 | $\Im = {{e}^{2}}\mathop \Im \limits^{[ - 2]} $ |
| тензор микроповоротов | ${{\Omega }_{{ik}}}$ | 0 | |
| вектор микровращений | ${{\phi }^{i}}$ | +1 | ${{\phi }^{i}} = \tfrac{1}{e}{{\mathop \phi \limits^{[ + 1]} }^{i}}$ |
| тензор деформации изгиба–кручения | $\kappa _{{i \cdot }}^{{ \cdot s}}$ | +1 |  |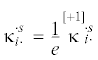
| сопутствующий вектор | |||
| деформации изгиба–кручения | ${{\kappa }_{i}}$ | 0 | |
Следуя обозначениям, принятым в работах [12, 16], уравнения динамики микрополярного тела можно принять в виде
В терминах перемещений и микровращений уравнения динамики (4.2) для гемитропного микрополярного тела в псевдотензоной формулировке можно принять в виде [12, 16]
(4.3)
$\begin{gathered} G[(1 + {{e}^{2}}{{\mathop c\limits^{[ - 2]} }_{1}}){{\nabla }^{s}}{{\nabla }_{s}}{{u}^{i}} + (1 - {{e}^{2}}{{\mathop c\limits^{[ - 2]} }_{1}}\, + 2\nu {{(1 - 2\nu )}^{{ - 1}}}){{\nabla }^{i}}{{\nabla }_{k}}{{u}^{k}} + \\ + 2{{\mathop c\limits^{[ - 2]} }_{1}}{{\varepsilon }^{{ikl}}}{{\nabla }_{k}}{{\mathop \phi \limits^{[ + 1]} }_{l}}\, + \mathop L\limits^{[ - 1]} c_{4}^{'}{{\nabla }^{i}}{{\nabla }_{k}}{{\mathop \phi \limits^{[ + 1]} }^{k}} + \mathop L\limits^{[ - 1]} c_{5}^{'}{{\nabla }^{k}}{{\nabla }_{k}}{{\mathop \phi \limits^{[ + 1]} }^{i}}] = \rho \partial _{{ \cdot \cdot }}^{2}{{u}^{i}}, \\ G\mathop L\limits^{[ - 1]} \mathop L\limits^{[ - 1]} [(1 + {{e}^{{ - 2}}}{{\mathop c\limits^{[ + 2]} }_{2}}){{\nabla }^{s}}{{\nabla }_{s}}{{\mathop \phi \limits^{[ + 1]} }^{i}}\, + (1 - {{e}^{{ - 2}}}{{\mathop c\limits^{[ + 2]} }_{2}}\, + 2{{c}_{3}}){{\nabla }^{i}}{{\nabla }_{k}}{{\mathop \phi \limits^{[ + 1]} }^{k}}\, + \\ + {{\mathop L\limits^{[ - 1]} }^{{ - 1}}}c_{4}^{'}{{\nabla }^{i}}{{\nabla }^{k}}{{u}_{k}} + {{\mathop L\limits^{[ - 1]} }^{{ - 1}}}c_{5}^{'}{{\nabla }^{k}}{{\nabla }_{k}}{{u}^{i}} + {{\mathop L\limits^{[ - 1]} }^{{ - 1}}}c_{6}^{'}{{g}^{{ik}}}{{\varepsilon }_{{ksl}}}{{\nabla }^{s}}{{\mathop \phi \limits^{[ + 1]} }^{l}}] - \\ - 2G{{\mathop c\limits^{[ - 2]} }_{1}}(2{{\mathop \phi \limits^{[ + 1]} }^{i}}\, - {{\varepsilon }^{{isr}}}{{\nabla }_{s}}{{u}_{r}}) = \rho \mathop \Im \limits^{[ - 2]} \partial _{{ \cdot \cdot }}^{2}{{\mathop \phi \limits^{[ + 1]} }^{i}} \\ \end{gathered} $Здесь $G$ – упругий модуль сдвига; $\nu $ – коэффициент Пуассона; $\mathop L\limits^{[ - 1]} $ – характерная длина микрополярной теории; $\mathop {{{c}_{1}}}\limits^{[ - 2]} $, $\mathop {{{c}_{2}}}\limits^{[ + 2]} $, c3, c4, c5, c6 – определяющие микрополярные псевдоскаляры. Во втором уравнении существенно используется формула
(4.4)
${{\varepsilon }^{{isr}}} = {{e}^{2}}{{g}^{{ij}}}{{g}^{{sk}}}{{g}^{{rl}}}{{\varepsilon }_{{jkl}}}$Заключение. В статье приведены обобщения понятий векторного и смешанного произведения и указана их связь с фундаментальным ориентирующим скаляром в случае евклидова пространства заданной размерности n.
1. Доказательство теоремы Гамильтона–Кэли проведено в терминах псевдотензоров в n-мерном пространстве.
2. Обсуждаются возможные применения алгебры псевдотензоров в механике сплошных сред.
3. Приведены веса основных псевдотензорных величин теории гемитропного микрополярного континуума.
4. Приводятся уравнения динамики гемитропного микрополярного континуума в терминах псевдотензоров.
Благодарности. Работа выполнена в рамках государственного задания (№ госрегистрации АААА-А20-120011690132-4) и при поддержке Российского фонда фундаментальных исследований проекты № 19-51-60001, № 20-01-00666.
Список литературы
Lakes R. Elastic and viscoelastic behavior of chiral materials // Int. J. Mech. Sci. 2001. V. 43, № 7. P. 1579–1589. https://doi.org/10.1016/S0020-7403(00)00100-4
Mackay T., Lakhtakia A. Negatively refracting chiral metamaterials: a review // SPIE Reviews. 2010. V. 1. № 1. P. 1–29. https://doi.org/10.1117/6.0000003
Tomar S., Khurana A. Wave propagation in thermo-chiral elastic medium // Appl. Math. Model. 2013. V. 37. № 22. P. 9409–9418. https://doi.org/10.1016/j.apm.2013.04.029
Гуревич Г.Б. Основы теории алгебраических инвариантов. М., Л.: ГИТТЛ, 1948. 408 с.
Схоутен Я.А. Тензорный анализ для физиков. М.: Наука, 1965. 456 с.
Сокольников И.С. Тензорный анализ. Теория и применения в геометрии и в механике сплошных сред. М.: Наука, 1971. 376 с.
Synge J., Schild A. Tensor calculus. Toronto: Toronto university press, 1949. V. 5. 334 p.
Truesdell C., Toupin R. The Classical Field Theories // Principles of Classical Mechanicsand Field Theory / Prinzipien der Klassischen Mechanik und Feldtheorie / Ed. by S. Flügge. Berlin, Heidelberg: Springer Berlin Heidelberg, 1960. P. 226–858.
Кочин И.Е. Векторное исчисление и начала тензорного исчисления. Москва: Изд-во Акад. наук, 1951. 427 с.
Радаев Ю.Н., Мурашкин Е.В. Псевдотензорная формулировка механики гемитропных микрополярных сред // Проблемы прочности и пластичности. 2020. Т. 82. № 4. С. 399–412.
Murashkin E.V., Radayev Yu.N. On a micropolar theory of growing solids // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2020. Т. 24. № 3. С. 424–444.
Kovalev V.A., Murashkin E.V., Radayev Yu.N. On the Neuber theory of micropolarelasticity. A pseudotensor formulation // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2020. Т. 24. № 4. С. 752–761.
Veblen O., Thomas T. Extensions of Relative Tensors // Transactions of the American Mathematical Society. 1924. V. 26. P. 373–377. URL: https://www.jstor.org/stable/1989146.
Веблен О. Инварианты дифференциальных квадратичных форм. М.: Изд-во иностранной литературы, 1948. 139 с.
Розенфельд Б.А. Многомерные пространства. М.: Наука, 1966.
Радаев Ю.Н. Правило множителей в ковариантных формулировках микрополярных теорий механики континуума // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2018. Т. 22. С. 504–517. URL: http://mi.mathnet.ru/vsgtu1635.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела
Пн.-пт.: 10.00-19.00