Известия РАН. Механика твердого тела, 2021, № 6, стр. 149-155

ОЦЕНКА УЧЕТА МОМЕНТНЫХ СВОЙСТВ СРЕДЫ НА ПРИМЕРЕ НЕСТАЦИОНАРНОЙ ОСЕСИММЕТРИЧНОЙ ЗАДАЧИ

Д. В. Тарлаковский^a, b, *, Нгуен Ван Лам^a, **

^a Московский авиационный институт (национальный исследовательский университет)
Москва, Россия

^b НИИ механики МГУ имени М.В. Ломоносова
Москва, Россия

^* E-mail: tdvhome@mail.ru
^** E-mail: nvlammai2019@gmail.com

Поступила в редакцию 28.02.2021
После доработки 28.02.2021
Принята к публикации 04.03.2021

DOI: 10.31857/S0572329921060143

Полный текст (PDF)

Аннотация

Дана оценка учета моментных свойств среды на примере нестационарной осесимметричной задачи о распространении возмущений от сферической полости в среде Коссера. С этой целью для перемещений и угла поворота выделяется упругие составляющие этих полей. Используются разложения искомых функций в ряды по полиномам Лежандра и Гегенбауэра, преобразование Лапласа по времени, а также метод малого параметра, в качестве которого используется коэффициент, характеризующий связь перемещений и угол поворота. Оригиналы регулярных составляющих решения вычисляются с помощью вычетов в линейном приближении по малому параметру. Приведены примеры расчетов для материала в виде зернистого композита из алюминиевой дроби в эпоксидной матрице. Показано, что количественные отличия практически отсутствуют, а качественно процессы в моментной и классической упругой среде существенно отличаются.

Ключевые слова: среда Коссера, сферическая полость, нестационарные осесимметричные возмущения, сравнение с упругим решением

1. Введение. C развитием современной науки и техники требуется исследование динамических процессов в композиционных материалах, которые широко применяются в различных конструкциях объектов, требуется использование моделей сплошных сред, отличных от традиционных. Таковыми являются упругие моментные среды, к которым, в том числе, относится модель Коссера [1].

Число работ, посвященных задачам нестационарной моментной теории упругости со сферической полостью, крайне ограничено. К ним относятся, например, работы [2–10]. В [2, 3] исследованы задачи о действии нестационарных осесимметричных кинематических возмущений на сферическую полость в среде Коссера. Аналогичные вопросы для упрощенной модели псевдоконтинуума Коссера рассмотрены в работах [4, 5]. В [6] дано исследование динамической связанной осесимметричной задачи микрополярной теории упругости для бесконечной в радиальном направлении изотропной среды. В статьях [7, 8] построены решения двумерных нестационарных задач для упругих моментных полупространства и полуплоскости. Осесимметричные задачи для упругих тел с несимметричным тензором напряжений со сферическими границами исследованы в работах [9, 10].

В то же время оценка учета моментных свойств среды фактически отсутствует. Этот вопрос и рассматривается в данной работе на примере задачи о распространении нестационарных осесимметричных возмущений от сферической полости в пространстве, занятом средой Коссера.

2. Постановка задачи. В пространстве, занятом средой Коссера [1], в сферической системе координат $r,\vartheta ,\theta $ ($r \geqslant 0$, $0 \leqslant \theta \leqslant \pi $, $0 \leqslant \vartheta < 2\pi $) с центром в точке O и ортонормированным базисом ${{{\mathbf{e}}}_{r}},{{{\mathbf{e}}}_{\theta }},{{{\mathbf{e}}}_{\vartheta }}$, рассматривается движение абсолютно твердого шара радиуса R вдоль оси $Oz$ прямоугольной декартовой системы координат по закону $z = Z\left( \tau \right)$, где $z = R\cos \theta $, $\tau $ – время.

В [2, 3] подробно изложена постановка более общей задачи о распространении осесимметричных кинематических возмущений от сферической полости в среде Коссера, включающая уравнения движения в потенциалах, связь перемещений с потенциалами, физические соотношения, нулевые начальные условия, требования ограниченности решения и граничные условия

(2.1)

${{\left. w \right|}_{{r = 1}}} = {{W}_{0}}\left( {\theta ,\tau } \right),\quad {{\left. {v} \right|}_{{r = 1}}} = {{V}_{0}}\left( {\theta ,\tau } \right),\quad {{\left. \omega \right|}_{{r = 1}}} = 0$

где левые части этих равенств – ненулевые компоненты векторов перемещения ${\mathbf{u}} = w\left( {r,\theta ,\tau } \right){{{\mathbf{e}}}_{r}} + {v}\left( {r,\theta ,\tau } \right){{{\mathbf{e}}}_{\theta }}$ и поворота${\mathbf{\omega }} = \omega \left( {r,\theta ,\tau } \right){{{\mathbf{e}}}_{\vartheta }}$.

Здесь и далее используются безразмерные величины со следующими единицами измерения: длина – $R$, время – ${R \mathord{\left/ {\vphantom {R {{{c}_{1}}}}} \right. \kern-0em} {{{c}_{1}}}}$, масса – $\rho {{R}^{3}}$, где c₁ – скорость распространения волн растяжения-сжатия, а $\rho $ – плотность среды.

При условии, что в рассматриваемом варианте движения шара он жестко сцеплен со средой, соответствующий вектор перемещения u и правые части первых двух равенств в (2.1) имеют вид:

(2.2)

${{\left. {\mathbf{u}} \right|}_{{r = 1}}} = Z{\mathbf{k}} = Z\left( {\cos \theta {{{\mathbf{e}}}_{r}} - \sin \theta {{{\mathbf{e}}}_{\theta }}} \right),\quad {{W}_{0}} = Z\cos \theta ,\quad {{V}_{0}}\left( {\theta ,\tau } \right) = - Z\sin \theta $

где k – единичный направляющий вектор оси $Oz$.

3. Решение задачи. В [2, 3] кинематические параметры и компоненты напряженного состояния раскладываются в ряды по полиномам Лежандра ${{P}_{n}}\left( x \right)$ и Гегенбауэра $C_{{n - 1}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}\left( x \right)$ [11, 12]. Здесь приведем эти равенства только перемещения, угла поворота, правых частей граничных условий (2.1) и физических компонент ${{\sigma }_{{r\theta }}}$ и ${{\sigma }_{{\theta r}}}$ тензора напряжений:

(3.1)

$\begin{gathered} \left( {\begin{array}{*{20}{c}} w \\ {{{W}_{0}}} \end{array}} \right) = \sum\limits_{n = 0}^\infty {\left( {\begin{array}{*{20}{c}} {{{w}_{n}}\left( {r,\tau } \right)} \\ {{{w}_{{0n}}}\left( \tau \right)} \end{array}} \right){{P}_{n}}\left( {\cos \theta } \right)} ,\quad \left( {\begin{array}{*{20}{c}} {v} \\ \omega \\ {{{V}_{0}}} \end{array}} \right) = - \sin \theta \sum\limits_{n = 1}^\infty {\left( {\begin{array}{*{20}{c}} {{{{v}}_{n}}\left( {r,\tau } \right)} \\ {{{\omega }_{n}}\left( {r,\tau } \right)} \\ {{{v}_{{0n}}}\left( \tau \right)} \end{array}} \right)C_{{n - 1}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}\left( {\cos \theta } \right)} \\ \left( {\begin{array}{*{20}{c}} {{{\sigma }_{{r\theta }}}} \\ {{{\sigma }_{{\theta r}}}} \end{array}} \right) = - \sin \theta \sum\limits_{n = 1}^\infty {\left( {\begin{array}{*{20}{c}} {{{\sigma }_{{r\theta n}}}} \\ {{{\sigma }_{{\theta rn}}}} \end{array}} \right)C_{{n - 1}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}\left( {\cos \theta } \right)} \\ \end{gathered} $

Коэффициенты этих рядов для искомых функций записываются в виде сверток (они обозначены звездочкой):

(3.2)

$\begin{gathered} {{w}_{n}}\left( {r,\tau } \right) = {{G}_{{wwn}}}\left( {r,\tau } \right) \cdot {{w}_{{0n}}}\left( \tau \right) + {{G}_{{wvn}}}\left( {r,\tau } \right) \cdot {{{v}}_{{0n}}}\left( \tau \right) \\ {{{v}}_{n}}\left( {r,\tau } \right) = {{G}_{{vwn}}}\left( {r,\tau } \right) \cdot {{w}_{{0n}}}\left( \tau \right) + {{G}_{{vvn}}}\left( {r,\tau } \right) \cdot {{{v}}_{{0n}}}\left( \tau \right) \\ {{\omega }_{n}}\left( {r,\tau } \right) = {{G}_{{\omega wn}}}\left( {r,\tau } \right) \cdot {{w}_{{0n}}}\left( \tau \right) + {{G}_{{\omega vn}}}\left( {r,\tau } \right) \cdot {{{v}}_{{0n}}}\left( \tau \right) \\ {{\sigma }_{{r\theta n}}}\left( {r,\tau } \right) = {{G}_{{\sigma r\theta wn}}}\left( {r,\tau } \right) \cdot {{w}_{{0n}}}\left( \tau \right) + {{G}_{{\sigma r\theta vn}}}\left( {r,\tau } \right) \cdot {{{v}}_{{0n}}}\left( \tau \right) \\ {{\sigma }_{{\theta rn}}}\left( {r,\tau } \right) = {{G}_{{\sigma \theta rwn}}}\left( {r,\tau } \right) \cdot {{w}_{{0n}}}\left( \tau \right) + {{G}_{{\sigma \theta rvn}}}\left( {r,\tau } \right) \cdot {{{v}}_{{0n}}}\left( \tau \right) \\ \end{gathered} $

Ядра сверток в этих равенствах есть поверхностные функции влияния, а именно, ${{G}_{{wwn}}}$, ${{G}_{{{v}wn}}}$, ${{G}_{{\omega wn}}}$, ${{G}_{{\sigma r\theta wn}}}$ и ${{G}_{{\sigma \theta rwn}}}$ – коэффициенты ${{w}_{n}}$, ${{{v}}_{n}}$, ${{\omega }_{n}}$, ${{\sigma }_{{r\theta n}}}$ и ${{\sigma }_{{\theta rn}}}$, удовлетворяющие граничным условиям

${{\left. {{{w}_{n}}} \right|}_{{r = 1}}} = \delta \left( \tau \right),\quad {{\left. {{{{v}}_{n}}} \right|}_{{r = 1}}} = {{\left. {{{\omega }_{n}}} \right|}_{{r = 1}}} = 0$

а ${{G}_{{w{v}n}}}$, ${{G}_{{{vv}n}}}$, ${{G}_{{\omega {v}n}}}$, ${{G}_{{\sigma r\theta {v}n}}}$ и ${{G}_{{\sigma \theta r{v}n}}}$ – аналогичные величины, для которых выполняются равенства

${{\left. {{{{v}}_{n}}} \right|}_{{r = 1}}} = \delta \left( \tau \right),\quad {{\left. {{{w}_{n}}} \right|}_{{r = 1}}} = {{\left. {{{\omega }_{n}}} \right|}_{{r = 1}}} = 0$

Здесь δ(τ) – дельта-функция Дирака [13].

Функции влияния определены в [2, 3] с помощью преобразования Лапласа в линейном приближении по малому параметру α, характеризующему связь поля перемещений с углом поворота. При этом показано, что две из этих функций имеют сингулярные слагаемые:

(3.3)

$\begin{gathered} {{G}_{{wwn}}}\left( {r,\tau } \right) = {{r}^{{ - 1}}}\delta \left( {\tau - r + 1} \right) + {{G}_{{wwnr}}}\left( {r,\tau } \right) \\ {{G}_{{{vv}n}}}\left( {r,\tau } \right) = {{r}^{{ - 1}}}\delta \left[ {\tau - {{\gamma }_{{1\alpha }}}\left( {r - 1} \right)} \right] + {{G}_{{{vv}nr}}}\left( {r,\tau } \right){{\gamma }_{{1\alpha }}} = {{\gamma }_{1}}\sqrt {1 - \alpha \gamma _{1}^{2}} \\ \end{gathered} $

где ${{\gamma }_{{1\alpha }}}$ и ${{\gamma }_{1}}$ – величины, обратные скоростям распространения волн свободного вращения и сдвига. При этом изображения (им соответствует индекс “$L$”) $G_{{wwnr}}^{L}\left( {r,s} \right)$, $G_{{wwn}}^{L}\left( {r,s} \right)$, $G_{{{v}wnr}}^{L}\left( {r,s} \right)$, $G_{{{vv}nr}}^{L}(r,s)$, $G_{{\omega wn}}^{L}\left( {r,s} \right)$ и $G_{{\omega {v}n}}^{L}\left( {r,s} \right)$ являются правильными рациональными функциями параметра преобразования s, что позволяет достаточно просто находить их оригиналы с помощью вычетов.

В случае прямолинейного движения шара с учетом равенств $C_{0}^{{3/2}}(x) = 1$ и ${{P}_{1}}\left( x \right) = x$ из (2.2) и (3.1) получаем

(3.4)

$\begin{gathered} {{w}_{{00}}}\left( \tau \right) = 0,\quad {{w}_{{01}}}\left( \tau \right) = Z\left( \tau \right),\quad {{{v}}_{{01}}}\left( \tau \right) = - Z\left( \tau \right), \\ {{w}_{{0n}}}\left( \tau \right) = {{{v}}_{{0n}}}\left( \tau \right) = 0\quad \left( {n \geqslant 2} \right) \\ \end{gathered} $

Следовательно, в рядах (3.1) для перемещений и угла поворота отличны от нуля только коэффициенты при n = 1:

$w = {{w}_{1}}\cos \theta ,\quad {v} = - {{{v}}_{1}}\sin \theta ,\quad \omega = - {{\omega }_{1}}\sin \theta $

При этом функции ${{w}_{1}}$, ${{{v}}_{1}}$ и ${{\omega }_{1}}$ в соответствии с (3.2) и (3.4) определяются так:

(3.5)

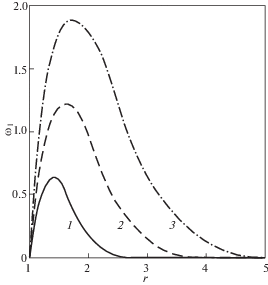
$\begin{gathered} {{w}_{1}}\left( {r,\tau } \right) = {{r}^{{ - 1}}}Z\left( {\tau - r + 1} \right) + \left[ {{{G}_{{ww1r}}}\left( {r,\tau } \right) - {{G}_{{w{v}1}}}\left( {r,\tau } \right)} \right] \cdot Z\left( \tau \right) \\ {{{v}}_{1}}\left( {r,\tau } \right) = - {{r}^{{ - 1}}}Z\left[ {\tau - {{\gamma }_{{1\alpha }}}\left( {r - 1} \right)} \right] + \left[ {{{G}_{{{v}w1}}}\left( {r,\tau } \right) - {{G}_{{{vv}1r}}}\left( {r,\tau } \right)} \right] \cdot Z\left( \tau \right) \\ {{\omega }_{1}}\left( {r,\tau } \right) = \left[ {{{G}_{{\omega w1}}}\left( {r,\tau } \right) - {{G}_{{\omega {v}1}}}\left( {r,\tau } \right)} \right] \cdot Z\left( \tau \right) \\ \end{gathered} $

На рис. 1 для примера приведены откорректированные по отношению к [3] графики распределения по радиусу функции ${{\omega }_{1}}$ в различные моменты времени. При этом полагается, что среда является зернистым композитом из алюминиевой дроби в эпоксидной матрице [14], а закон движения шара имеет вид $Z\left( \tau \right) = {{\tau }_{ + }}$.

Рис. 1.

Распределение функции ${{\omega }_{1}}\left( {r,\tau } \right)$ по радиусу в различные моменты времени: кривая 1 соответствует $\tau = 1.5$, 2 – $\tau = 2.5$, 3 – $\tau = 3.5$.

4. Оценка учета моментных свойств. Ее проведем для перемещений и угла поворота. При этом учитываем, что значение α = 0 соответствует классическому упругому решению [2, 3]. Следовательно, разность

(4.1)

${{{\mathbf{u}}}_{c}} = {\mathbf{u}} - {{{\mathbf{u}}}_{e}},\quad {{{\mathbf{u}}}_{e}} = {{\left. {\mathbf{u}} \right|}_{{\alpha = 0}}} = {{w}_{e}}\left( {r,\theta ,\tau } \right){{{\mathbf{e}}}_{r}} + {{{v}}_{e}}\left( {r,\theta ,\tau } \right){{{\mathbf{e}}}_{\theta }}$

определяет вклад в перемещения особенностей модели моментной среды.

Оценку аналогичного вклада в вектор поворота проводим с помощью следующих величин:

(4.2)

$\begin{gathered} {{{\mathbf{\omega }}}_{{ce}}} = {\mathbf{\omega }} - {{{\mathbf{\omega }}}_{e}} = {{{\mathbf{\omega }}}_{{cp}}} - {{{\mathbf{\omega }}}_{{pe}}} = {{\omega }_{{ce}}}{{{\mathbf{e}}}_{\vartheta }},\quad {{{\mathbf{\omega }}}_{{cp}}} = {\mathbf{\omega }} - {{{\mathbf{\omega }}}_{p}} = {{\omega }_{{cp}}}{{{\mathbf{e}}}_{\vartheta }} \\ {{{\mathbf{\omega }}}_{{pe}}} = {{{\mathbf{\omega }}}_{p}} - {{{\mathbf{\omega }}}_{e}} = {{\omega }_{{pe}}}{{{\mathbf{e}}}_{\vartheta }} \\ 2{{{\mathbf{\omega }}}_{e}} = {\text{rot}}{{{\mathbf{u}}}_{e}},\quad 2{{{\mathbf{\omega }}}_{p}} = {\text{rot}}{\mathbf{u}} \\ \end{gathered} $

Отметим, что векторы ${{{\mathbf{\omega }}}_{e}}$ и ${{{\mathbf{\omega }}}_{p}}$ соответствуют моделям теории упругости и псевдоконтинуума Коссера [1].

Для соответствующих функций влияния вводим подобные (4.1) и (4.2) обозначения:

(4.3)

$\begin{gathered} {{G}_{{\zeta ce}}} = {{G}_{\zeta }} - {{G}_{{\zeta e}}},\quad {{G}_{{\zeta e}}} = {{\left. {{{G}_{\zeta }}} \right|}_{{\alpha = 0}}}\quad \left( {\zeta = wwnr,w{v}n,{v}wn,{vv}nr,\omega wn,\omega {v}n} \right) \\ {{G}_{{\zeta cp}}} = {{G}_{\zeta }} - {{G}_{{\zeta p}}},\quad {{G}_{{\zeta pe}}} = {{G}_{{\zeta p}}} - {{G}_{{\zeta e}}}\quad \left( {\zeta = \omega wn,\omega {v}n} \right) \\ \end{gathered} $

Сначала рассматриваем соответствующие перемещениям функции. В силу их аналитической зависимости от малого параметра α имеют место следующие соотношения:

${{G}_{{\zeta ce}}}\left( {r,\tau } \right) = O\left( \alpha \right),\quad \alpha \to 0\quad \left( {\zeta = wwnr,w{v}n,{v}wn,{vv}nr} \right)$

Для координат векторов в (4.1)

${{w}_{{nce}}} = {{w}_{n}} - {{w}_{{ne}}},\quad {{{v}}_{{nce}}} = {{{v}}_{n}} - {{{v}}_{{ne}}},\quad {{w}_{{ne}}} = {{\left. {{{w}_{n}}} \right|}_{{\alpha = 0}}},\quad {{{v}}_{{ne}}} = {{\left. {{{{v}}_{n}}} \right|}_{{\alpha = 0}}}$

из первых двух равенств в (3.5) получаем

$\begin{gathered} {{w}_{{nce}}}\left( {r,\tau } \right) = {{G}_{{wwnrce}}}\left( {r,\tau } \right) \cdot {{w}_{{0n}}}\left( \tau \right) + {{G}_{{w{v}nce}}}\left( {r,\tau } \right) \cdot {{{v}}_{{0n}}}\left( \tau \right) \\ {{{v}}_{{nce}}}\left( {r,\tau } \right) = {{r}^{{ - 1}}}\left\{ {{{{v}}_{{0n}}}\left[ {\tau - {{\gamma }_{{1\alpha }}}\left( {r - 1} \right)} \right] - {{{v}}_{{0n}}}\left[ {\tau - {{\gamma }_{1}}\left( {r - 1} \right)} \right]} \right\} + \\ + \;{{G}_{{{v}wnce}}}\left( {r,\tau } \right) \cdot {{w}_{{0n}}}\left( \tau \right) + {{G}_{{{vv}nrce}}}\left( {r,\tau } \right) \cdot {{{v}}_{{0n}}}\left( \tau \right) \\ \end{gathered} $

Для разности в первом слагаемом во втором равенстве с учетом (3.3) при α → 0 справедливо соотношение

$\begin{gathered} {{{v}}_{{0n}}}\left[ {\tau - {{\gamma }_{{1\alpha }}}\left( {r - 1} \right)} \right] - {{{v}}_{{0n}}}\left[ {\tau - {{\gamma }_{1}}\left( {r - 1} \right)} \right] = \\ = \;\frac{{\gamma _{1}^{3}\left( {r - 1} \right)}}{2}{{{{\dot {v}}}}_{{0n}}}\left[ {\tau - {{\gamma }_{1}}\left( {r - 1} \right)} \right]\alpha + o\left( \alpha \right) = O\left( \alpha \right) \\ \end{gathered} $

Следовательно, имеют место равенства ${{w}_{{nce}}}\left( {r,\tau } \right)$, ${{{v}}_{{nce}}}\left( {r,\tau } \right) = O\left( \alpha \right)$, α → 0, т.е. поправки, вносимые в перемещение за счет учета моментных свойств, имеют порядок α.

Для оценки влияния учета моментных свойств на угол поворота, прежде всего, замечаем, что для ненулевой координаты вектора ${{{\mathbf{\omega }}}_{{pe}}}$ в (4.2) справедливо соотношение ${{\omega }_{{pe}}}\left( {r,\tau } \right) = O\left( \alpha \right)$, α → 0.

Очевидно, аналогичные оценки имеют место и для функций ${{G}_{{\omega wnpe}}}$, ${{G}_{{\omega {v}npe}}}$:

(4.4)

${{G}_{{\omega wnpe}}}\left( {r,\tau } \right),\quad {{G}_{{\omega {v}npe}}}\left( {r,\tau } \right) = O\left( \alpha \right),\quad \alpha \to 0$

Далее выражаем ненулевую координату вектора ${{{\mathbf{\omega }}}_{{cp}}}$ через перемещения:

${{\omega }_{{cp}}} = \omega - \frac{1}{{2r}}\left[ {\frac{{\partial \left( {r{v}} \right)}}{{\partial r}} - \frac{{\partial w}}{{\partial \theta }}} \right]$

При этом из формул для напряжений σ_rθ и σ_θr в [2, 3] следует равенство

${{\sigma }_{{r\theta }}} - {{\sigma }_{{\theta r}}} = 2\alpha \left[ {\frac{{\partial \left( {r{v}} \right)}}{{\partial r}} - \frac{1}{r}\frac{{\partial w}}{{\partial \theta }} - 2\omega } \right] = - 4\alpha {{\omega }_{{cp}}}$

Отсюда вытекает, что при любом n ≥ 1 равенство справедливо соотношение $4\alpha {{\omega }_{{ncp}}} = {{\sigma }_{{\theta rn}}} - {{\sigma }_{{r\theta n}}}$. Следовательно, функции ${{G}_{{\omega bncp}}}$ ($b = w,{v}$) можно вычислить так:

(4.5)

$4\alpha {{G}_{{\omega wnсp}}} = {{G}_{{\sigma \theta rwn}}} - {{G}_{{\sigma r\theta wn}}},\quad 4\alpha {{G}_{{\omega {v}nсp}}} = {{G}_{{\sigma \theta r{v}n}}} - {{G}_{{\sigma r\theta {v}n}}}$

Дальнейшие выкладки удобнее провести в пространстве преобразования Лапласа по времени. Используя построенные в [2, 3] изображения функций в правых частях равенств в (4.5), приходим к таким результатам:

$\begin{gathered} G_{{\omega bnсp}}^{L}\left( {r,s} \right) = \tilde {G}_{{\omega bnсp}}^{L}\left( {r,s} \right) + O\left( \alpha \right)\quad \left( {\alpha \to 0} \right),\quad \tilde {G}_{{\omega bnсp}}^{L}\left( {r,s} \right) = H_{{\omega bnсp}}^{L}\left( {r,s} \right){{e}^{{ - {{\gamma }_{1}}\left( {r - 1} \right)s}}} \\ H_{{\omega wnсp}}^{L}\left( {r,s} \right) = \frac{{\gamma _{1}^{2}{{R}_{{n0}}}\left( {{{\gamma }_{1}}rs} \right){{R}_{{n0}}}\left( s \right)}}{{2{{r}^{{n + 1}}}{{Q}_{n}}\left( s \right)}},\quad H_{{\omega {v}nсp}}^{L}\left( {r,s} \right) = \frac{{\gamma _{1}^{2}{{R}_{{n0}}}\left( {{{\gamma }_{1}}rs} \right){{R}_{{n1}}}\left( s \right)}}{{2{{r}^{{n + 1}}}{{Q}_{n}}\left( s \right)}} \\ \end{gathered} $

где

$\begin{gathered} {{s}^{2}}{{Q}_{n}}(s) = {{R}_{{n1}}}(x){{R}_{{n3}}}(y) - n(n + 1){{R}_{{n0}}}(x){{R}_{{n0}}}(y) \\ {{R}_{{n0}}}(z) = \sum\limits_{k = 0}^n {{{A}_{{nk}}}{{z}^{{n - k}}}} ,\quad {{A}_{{nk}}} = \frac{{\left( {n + k} \right)!}}{{{{2}^{k}}\left( {n - k} \right)!k!}}, \\ {{R}_{{n3}}}(z) = {{R}_{{n1}}}(z) - {{R}_{{n0}}}(z),\quad {{R}_{{n1}}}(z) = {{R}_{{n + 1,0}}}(z) - n{{R}_{{n0}}}(z) \\ \end{gathered} $

Таким образом, для функций ${{G}_{{\omega wnce}}}$ и ${{G}_{{\omega {v}nce}}}$ с учетом (3.4) справедливы соотношения

$\begin{gathered} {{G}_{{\omega bnсe}}}\left( {r,\tau } \right) = {{G}_{{\omega bnсp}}}\left( {r,\tau } \right) + {{G}_{{\omega bnpe}}}\left( {r,\tau } \right) = \\ = \;{{G}_{{\omega bnсp}}}\left( {r,\tau } \right) + O\left( \alpha \right) = {{{\tilde {G}}}_{{\omega bnсp}}}\left( {r,\tau } \right) + O\left( \alpha \right),\quad \alpha \to 0 \\ \end{gathered} $

С использованием их и обозначений (3.3) из третьего равенства в (2.2) с точностью до слагаемых порядка α определяем поправку, вносимую в угол поворота за счет учета моментных свойств:

$\begin{gathered} {{\omega }_{{nce}}}\left( {r,\tau } \right) = {{G}_{{\omega wnce}}}\left( {r,\tau } \right) \cdot {{w}_{{0n}}}\left( \tau \right) + {{G}_{{\omega {v}nce}}}\left( {r,\tau } \right) \cdot {{{v}}_{{0n}}}\left( \tau \right) = \\ = \;{{G}_{{\omega wncp}}}\left( {r,\tau } \right) \cdot {{w}_{{0n}}}\left( \tau \right) + {{G}_{{\omega {v}ncp}}}\left( {r,\tau } \right) \cdot {{{v}}_{{0n}}}\left( \tau \right) = \\ = \;{{\omega }_{{ncp}}}\left( {r,\tau } \right) = {{{\tilde {G}}}_{{\omega wncp}}}\left( {r,\tau } \right) \cdot {{w}_{{0n}}}\left( \tau \right) + {{{\tilde {G}}}_{{\omega {v}ncp}}}\left( {r,\tau } \right) \cdot {{{v}}_{{0n}}}\left( \tau \right) \\ \end{gathered} $

Отсюда дополнительно следует, что поправки, вносимые моделями Коссера и псевдоконтинуума Коссера, в линейном приближении совпадают.

Для определения оригиналов функций ${{\tilde {G}}_{{\omega wncp}}}$ и ${{\tilde {G}}_{{\omega {v}ncp}}}$ сначала выделяем целые части дробей $H_{{\omega wnсp}}^{L}$ и $H_{{\omega {v}nсp}}^{L}$ как функций параметра $s$:

$\begin{gathered} H_{{\omega wnсp}}^{L}\left( {r,s} \right) = \frac{{{{\gamma }_{1}}}}{{2r}} + H_{{\omega wnсpr}}^{L}\left( {r,s} \right),\quad H_{{\omega wnсpr}}^{L}\left( {r,s} \right) = H_{{\omega wnсp}}^{L}\left( {r,s} \right) - \frac{{{{\gamma }_{1}}}}{{2r}} \\ {{s}^{{ - 1}}}H_{{\omega {v}nсp}}^{L}\left( {r,s} \right) = \frac{{{{\gamma }_{1}}}}{{2r}} + H_{{\omega {v}nсpr}}^{L}\left( {r,s} \right),\quad H_{{\omega {v}nсpr}}^{L}\left( {r,s} \right) = {{s}^{{ - 1}}}H_{{\omega {v}nсp}}^{L}\left( {r,s} \right) - \frac{{{{\gamma }_{1}}}}{{2r}} \\ \end{gathered} $

Оригиналы регулярных составляющих $H_{{\omega wnсpr}}^{L}$ и $H_{{\omega {v}nсpr}}^{L}$ вычисляются с помощью вычетов. При этом оригиналы функций $\tilde {G}_{{\omega wnсp}}^{L}$ и $\tilde {G}_{{\omega {v}nсp}}^{L}$ определяются так (точка обозначает производную по времени):

$\begin{gathered} {{{\tilde {G}}}_{{\omega wnсp}}}\left( {r,\tau } \right) = \frac{{{{\gamma }_{{1\alpha }}}}}{{2r}}\delta \left[ {\tau - {{\gamma }_{1}}(r - 1)} \right] + {{G}_{{\omega wnсpr}}}, \\ {{{\tilde {G}}}_{{\omega {v}nсp}}}\left( {r,\tau } \right) = \frac{{{{\gamma }_{{1\alpha }}}}}{{2r}}\dot {\delta }\left[ {\tau - {{\gamma }_{1}}(r - 1)} \right] + {{{\dot {G}}}_{{\omega {v}nсpr}}} \\ {{G}_{{\omega wnсpr}}}\left( {r,\tau } \right) = {{H}_{{\omega wnсpr}}}\left[ {r,\tau - {{\gamma }_{1}}(r - 1)} \right]H\left[ {\tau - {{\gamma }_{1}}(r - 1)} \right] \\ {{G}_{{\omega {v}nсpr}}}\left( {r,\tau } \right) = {{H}_{{\omega {v}nсpr}}}\left[ {r,\tau - {{\gamma }_{1}}(r - 1)} \right]H\left[ {\tau - {{\gamma }_{1}}(r - 1)} \right] \\ \end{gathered} $

где H(τ) – единичная функция Хевисайда [13].

Окончательно для поправки на угол поворота получаем следующий результат:

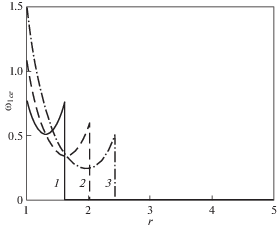
$\begin{gathered} {{\omega }_{{nce}}}\left( {r,\tau } \right) = \frac{{{{\gamma }_{1}}}}{{2r}}{{w}_{{0n}}}\left[ {\tau - {{\gamma }_{1}}(r - 1)} \right] + {{G}_{{\omega wncpr}}}\left( {r,\tau } \right) \cdot {{w}_{{0n}}}\left( \tau \right) + \\ + \;\frac{{{{\gamma }_{1}}}}{{2r}}{{{{\dot {v}}}}_{{0n}}}\left[ {\tau - {{\gamma }_{1}}(r - 1)} \right] + {{G}_{{\omega {v}ncpr}}}\left( {r,\tau } \right) \cdot {{{{\dot {v}}}}_{{0n}}}\left( \tau \right) \\ \end{gathered} $

На рис. 2 приведены графики распределения функции ${{\omega }_{{1ce}}}\left( {r,\tau } \right)$ по радиусу в различные моменты времени, соответствующие поступательному перемещению вдоль оси Oz по закону $Z\left( \tau \right) = {{\tau }_{ + }}$ жестко сцепленного с полостью абсолютно твердого шара. Они определяют поправку к результатам, изображенным на рис. 1.

Из них следует, что за исключением окрестности точки r = 1 поправка имеет порядок 10^–3, т.е. 0.1%. При этом для выбранного закона движения имеются качественные отличия, а именно, ${{\omega }_{1}}\left( {1,\tau } \right) = 0$ и ${{\omega }_{{1ce}}}\left( {1,\tau } \right) \ne 0$, а также непрерывность функции ${{\omega }_{1}}\left( {r,\tau } \right)$ и наличие разрывов первого рода в графиках ${{\omega }_{{1ce}}}\left( {r,\tau } \right)$.

5. Заключение. В линейном приближении по малому параметру найдена вносимая с учетом моментных свойств среды поправка в нестационарной осесимметричной задаче о распространении возмущений от сферической полости в пространстве. Показано, что количественные отличия практически отсутствуют. В то же время качественно процессы в моментной и классической упругой среде существенно отличаются. Эти же выводы, вероятно, можно сделать и для задач с другими геометрией и граничными условиями.

Pис. 2. Распределение поправки ${{\omega }_{{1ce}}}\left( {r,\tau } \right)$ по радиусу в различные моменты времени: кривая 1 соответствует $\tau = 1.5$, 2 – $\tau = 2.5$, 3 – $\tau = 3.5$.

Список литературы

Новацкий В. Теория упругости. М.: Мир, 1975. 872 с.
Lam V. Nguyen, Tarlakovskii D.V. Propagation of Non-stationary Axisymmetric Perturbations from a Spherical Cavity in Cosserat Medium // Advanced Structured Materials, V. 122. Nonlinear Wave Dynamics. Springer Nature Switzerland AG, 2020. P. 273–292.
Тарлаковский Д.В., Нгуен Ван Лам. Действие нестационарных осесимметричных кинематических возмущений на сферическую полость в среде Коссера // Упругость и неупругость. Матер. Междунар. научн. симпоз. по пробл. мех. деформ. тел, посвященного 110-летию со дня рождения А. А. Ильюшина. Москва 20–21 января 2021 года. М.: Изд-во Московского университета, 2021. С. 6–13.
Лай Тхань Туан, Тарлаковский Д.В. Распространение нестационарных осесимметричных возмущений от поверхности шара, заполненного псевдоупругой средой Коссера // Электронный журнал “Труды МАИ”. 2012. № 53. URL: http://trudymai.ru/published.php?ID=29267.
Лай Тхань Туан, Тарлаковский Д.В. Дифракция нестационарных волн на сферической полости в псевдоконтинууме Коссера // РЭНСИТ. 2013. Т. 5. № 1. С. 119–125.
Saxena Hirdeshwar S., Dhaliwal Ranjit S. Application of the eigen-number method to an axisymmetric coupled micropolar thermoelasticity // Bull. Pol. Acad. Sci. Techn. Sci. 1990. T. 38. № 1. P. 7–18.
Белоносов С.М. Моментная теория упругости. Владивосток: Дальнаука, 1993. 148 с.
Большаков В.И., Андрианов И.В., Данишевский В.В. Асимптотические методы расчета композитных материалов с учетом внутренней структуры. Днепропетровск: “Пороги”, 2008. 196 с.
Аэро Э.Л., Кувшинский Е.В. Континуальная теория асимметрической упругости. Равновесие изотропного тела // ФТТ. 1964. Т. 6. Вып. 9. С. 2689–2699.
Аэро Э.Л., Кувшинский Е.В. Основные уравнения теории упругости сред с вращательным взаимодействием частиц // ФТТ. 1960. Т. 2. Вып. 7. С. 1399–1409.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматгиз, 1963. 1108 с.
Справочник по специальным функциям. Под ред. М. Абрамовица, И. Стиган. М.: Наука, 1979. 832 с.
Горшков А.Г., Медведский А.Л., Рабинский Л.Н., Тарлаковский Д.В. Волны в сплошных средах: Учеб. пособ.: Для вузов. М.: Физматлит, 2004. 472 с.
Ерофеев В.И. Волновые процессы в твердых телах с микроструктурой. М.: Изд-во МГУ, 1999. 328 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал