Известия РАН. Механика твердого тела, 2022, № 1, стр. 89-102

1. Введение. Как правило, в квазистатических ситуациях прочность материала с дефектами типа трещин связывается со значением коэффициента интенсивности напряжений, измеренным в момент разрушения (вязкостью разрушения). В случае динамических задач это также позволяет успешно характеризовать и прогнозировать процесс разрыва материала при не очень быстрых и достаточно длительных воздействиях. Однако, этот подход теряет силу в случае высокоскоростных интенсивных нагрузок, а особенно в случае коротких импульсов, поскольку многие эксперименты в этих случаях показывают нестабильное и плохо предсказуемое поведение критического коэффициента интенсивности (динамической вязкости разрушения), а также его, так называемой, скоростной и/или временной зависимости, т.е. зависимости от скорости деформации (нагружения) и/или времени до разрушения [1–3]. Более того, в некоторых экспериментах наблюдается динамическое разрушение материала, возникающее тогда, когда локальное силовое поле в точке разрыва материала уже прошло свои максимальные значения и вышло на стадию заметного снижения [4–6]. Данный мало изученный, но принципиальный эффект не может быть объяснен на основе классических подходов и является основным предметом анализа данной работы.

Для удобства дальнейшего изложения введем в рассмотрение понятие задержки разрушения. Если при заданных граничных и начальных условиях разрушение в окрестности кончика трещины происходит после прохождения пика локального растягивающего силового поля, выражаемого, например, через текущий коэффициент интенсивности напряжений, то будем говорить, что разрушение происходит с задержкой. Время, прошедшее от достижения пика локального растягивающего напряжения до момента макроскопического разрыва материала будет характеризовать величину задержки разрушения. Далее будет показано, что данное явление является принципиальной особенностью процесса динамического разрушения, проявляющейся в пороговых ситуациях и связанной с наличием инкубационного подготовительного процесса, протекающего в микроструктуре материала в течение некоторого периода, предшествующего макроскопическому разрыву.

2. Критерий инкубационного времени. Применение структурно-временного подхода при кратковременных воздействиях позволяет объяснить многие наблюдаемые в опытах динамические эффекты, в частности изменение со скоростью ввода энергии (скоростью деформации) критических характеристик разрушения, определяемых растягивающим напряжением или значением коэффициента интенсивности напряжений в момент разрыва материала. Для материала имеющего макроскопический дефект в виде трещины критерий имеет форму (см., например, [1, 3]):

где $K(t)$ – значение коэффициента интенсивности напряжений (КИН) в окрестности кончика трещины, как функция времени, ${{K}_{{1c}}}$ – критическое значение КИН в статике, $\tau $ – инкубационное (структурное) время разрушения. Параметры ${{K}_{{1c}}}$ и $\tau $ являются константами материала и не зависят от формы и продолжительности воздействия. Константы ${{K}_{{1c}}}$ и $\tau $ образуют систему определяющих параметров разрушения. При этом предполагается, что моментом разрушения является то наименьшее время, при котором нарушается условие критерия.

Многочисленные исследования процесса динамического разрушения в рамках структурно-временного подхода на базе концепции инкубационного времени подтвердили его эффективность и предсказательную силу. В настоящее время он стал действенным инструментом расчета высокоскоростных динамических процессов, применяемым многими авторами в различных областях науки [7–9].

Ниже на конкретных примерах будет аналитически показано, что применение критерия инкубационного времени допускает разрушение на ниспадающих участках изменения во времени коэффициента интенсивности напряжений, т.е. через некоторое время после прохождения максимальных значений. Действительно, согласно критерию (2.1), чтобы произошло разрушение, среднее значение текущего значения коэффициента интенсивности напряжений на промежутке $\left[ {t - \tau ,t} \right]$ должно быть равным ${{K}_{{1c}}}$. Следовательно, на этом временном промежутке могут быть зоны, где $K(t) > {{K}_{{1c}}}$, и где $K(t) < {{K}_{{1c}}}$ (или на всем промежутке $\begin{array}{*{20}{c}} {\left[ {t - \tau ,t} \right]}&{K(t) = {{K}_{{1c}}}} \end{array}$). На практике это может проявляться при определенных способах импульсного воздействия, близких к пороговым, которые могут, например, отвечать минимальным предельным амплитудам при заданных длительностях или критическим длительностям при заранее установленных амплитудных характеристиках.

3. Постановка и решение динамической задачи. Рассмотрим динамическую задачу для упругой плоскости с трещиной в плоской постановке. Пусть упругая среда характеризуется модулем сдвига $\mu $ и скоростями продольных и поперечных волн ${{c}_{1}}$ и ${{c}_{2}}$ соответственно и имеет полубесконечный разрез $\begin{array}{*{20}{c}} {y = 0,}&{x \leqslant 0} \end{array}$. Тогда напряженно-деформированное состояние среды будет описываться следующей системой уравнений

Здесь φ и $\psi $ – продольный и поперечный волновые потенциалы. Компоненты вектора перемещения $u$ и ${v}$ связаны со значениями φ и $\psi $ соотношениями:

Предполагаем, что на берегах разреза $\begin{array}{*{20}{c}} {y = 0,}&{x < 0} \end{array}$ выполняются условия

т.е. к берегам разреза приложена нагрузка в виде нормального напряжения, заданного временной функцией $f(t)$. При $t < 0$ упругая среда свободна от напряжений, т.е.

Пусть приложенный в нулевой момент времени к берегам разреза импульс напряжений имеет постоянную амплитуду $P$ и описывается функцией $f(t) = P \cdot H(t)$, где $H(t)$ – функция Хевисайда. Значение коэффициента интенсивности напряжений в такой задаче известно и будет иметь вид [10, 11]

где $\alpha = 4\sqrt {\frac{2}{\pi }} \sqrt {{{c}_{1}}} \gamma \sqrt {1 - {{\gamma }^{2}}} $, $\gamma = {{{{c}_{1}}} \mathord{\left/ {\vphantom {{{{c}_{1}}} {{{c}_{2}}}}} \right. \kern-0em} {{{c}_{2}}}}$. Применяя это решение, можно найти выражение для коэффициента интенсивности напряжений при произвольном воздействии $f(t)$. Соответствующее решение можно получить, используя свертку по времени (интеграл Дюамеля) найденного решения (3.7) с соответствующей функцией: где ${{K}^{f}}\left( t \right)$ – коэффициент интенсивности напряжений для произвольного воздействия $f(t)$. Пусть, например, к берегам разреза приложен прямоугольный импульс напряжений с амплитудой $P$ и продолжительностью $T$. Таким образом, f(t) = P(H(t) – ‒ $H(t - T))$, где $H(t)$ – функция Хевисайда. Значение коэффициента интенсивности напряжений для такого воздействия будет иметь вид

Здесь и далее предполагаются значения радикалов с отрицательными аргументами равными нулю. Покажем, что аналитическое рассмотрение условия старта трещины для этого и других случаев позволяет получить и исследовать основные свойства эффекта запаздывания разрушения.

4. Анализ разрушения. При помощи структурно-временного подхода проведем анализ разрушения и выявим условия, при которых разрушение может происходить с эффектом запаздывания.

Предположим сначала, что приложенная к берегам разреза ступенчатая нагрузка действует вплоть до момента разрушения $t = t_{*}^{{}}$. Тогда, подставляя выражение (3.7) в критерий (2.1) получим

Выражение (4.1) связывает амплитуду приложенного воздействия и момент начала разрушения. На рисунке 1 сплошной линией изображена зависимость значений коэффициента интенсивности напряжений от времени. Значения времени и коэффициента интенсивности напряжений нормированы. По оси абсцисс откладывается безразмерное время t/τ, а по оси ординат отношение текущего значения КИН к критическому – ${{K(t)} \mathord{\left/ {\vphantom {{K(t)} {{{K}_{{!c}}}}}} \right. \kern-0em} {{{K}_{{!c}}}}}$. Кружками на кривой обозначены моменты времени $t_{*}^{{}}$ и $t_{*}^{{}} - \tau $. Значение КИН в этом случае растет вплоть до момента начала разрушения. При этом его величина в момент разрушения, согласно (3.7) и (4.1), будет выше статической прочности:

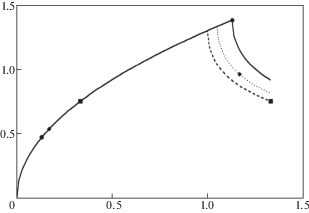
Предположим теперь, что приложенная к берегам разреза импульсная нагрузка будет снята ранее момента $t_{*}^{{}}$, определенного в (4.1), т.е. в момент времени $T < t_{*}^{{}}$. Подстановка выражения (3.9) в критерий (2.1) показывает, что для времен $t < t_{*}^{{}}$ условие критерия тоже может выполняться. В этом случае для импульса конечной длительности момент разрушения будет наступать через некоторое время после того как нагрузка будет снята. Соответствующая зависимость изображена на рисунке 1. Для времен $t \leqslant T$ значения коэффициента интенсивности не будут отличаться от посчитанных выше. При $t > T$ значения коэффициента интенсивности изображены точками. Соответствующее импульсу конечной длительности время разрушения будем по-прежнему обозначать $t_{*}^{{}}$. Моменты времени $t_{*}^{{}}$ и $t_{*}^{{}} - \tau $, отвечающие импульсу длительности $T$, изображены ромбами. Таким образом, в этом случае интенсивность локального силового поля в окрестности кончика трещины к моменту снятия нагрузки достигнет максимального значения и начнет уменьшаться вплоть до момента срабатывания условия разрушения. Интервал времени от момента снятия нагрузки до разрушения назовем задержкой разрушения. Тогда его величина определится разностью $t_{*}^{{}} - T$.

Для каждой приложенной нагрузки $P$ конечной длительности существует некий предел уменьшения времени действия нагрузки, т.е. существует наименьший момент времени T, который согласно критерию (2.1) обеспечивает разрушение. Дальнейшее уменьшение этой продолжительности уже не будет обеспечивать разрушение. В случае пороговых импульсов, имеющих наименьшую разрушающую амплитуду при заданной продолжительности (или критическую длительность при определенной амплитуде) должно выполняться условие

Здесь $K(t)$ – история коэффициента интенсивности напряжений для заданных величин $P$ и T. Продифференцировав интеграл и приравняв нулю, получим условие достижения максимума: $K(t_{*}^{{}}) = K(t_{*}^{{}} - \tau )$. Следовательно, в пороговом случае период времени, в течение которого величина коэффициента интенсивности превышает свое стартовое значение, в точности равна $\tau $. Отсюда также следует, казалось бы, парадоксальный для динамического случая вывод о том, что стартовое значение коэффициента интенсивности будет в этом случае меньше ${{K}_{{1c}}}$. Действительно на промежутке интегрирования $K\left( s \right) \geqslant K(t_{*}^{{}})$ , а среднее значение интеграла ${{K}_{{1c}}}$. Значит $K(t_{*}^{{}}) \leqslant {{K}_{{1c}}}$. Тем не менее, этот вывод не противоречит экспериментальным наблюдениям, которые проводятся, как правило, для запороговых ситуаций, когда нагрузки действуют вплоть до момента разрушения, и в этом случае, как и в (4.2), $K(t_{*}^{{}}) > {{K}_{{1c}}}$. При этом, в довольно редких случаях, когда реализуются именно интенсивные, но кратковременные, пороговые импульсы, наблюдаются значения динамической вязкости разрушения меньшие, чем статические для данного материала [12]. Примененный нами структурно временной подход позволяет качественно обосновать наблюдаемую в экспериментальных исследованиях нестабильность поведения динамической вязкости разрушения материалов.

Вычисления при помощи (2.1) дадут соотношение между моментом разрушения и продолжительностью воздействия для порогового импульса заданной длительности T:

Для такой критической (наименьшей) продолжительности T амплитуда приложенного воздействия и момент начала разрушения будут связаны соотношением

Соответствующая история для КИН изображена для времен $t > T$ на рисунке 1 пунктирной линией. Интервал интегрирования ограничен квадратами. В этом случае будет наблюдаться наибольшая для данной амплитуды воздействия задержка.

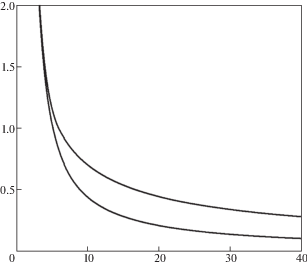
На рис. 2 представлена зависимость длительности разрушающего импульса нагрузки от его амплитуды. По оси абсцисс откладывается амплитуда приложенного импульса в МПа, а по оси ординат нормированное время действия нагрузки ${T \mathord{\left/ {\vphantom {T \tau }} \right. \kern-0em} \tau }$. Этот и последующие расчеты, если не оговорено обратное, проводились для ПММА. При этом было принято ${{c}_{1}} = $ 1970 м/с, ${{c}_{2}} = $ 1130 м/с, ${{K}_{{1c}}} = $ 1.47 МПА$\sqrt m $ и $\tau = $ 32 мкс. Нижняя кривая на рис. 2 соответствует минимально возможной продолжительности воздействия, вызывающей разрушение, а верхняя “максимально” возможной, для которой время действия нагрузки совпадает с моментом разрушения. Таким образом, область между нижней и верхней кривой можно трактовать как зону возможного разрушения на плоскости амплитуда приложенного импульса – длительность воздействия. Действительно, точки на этой плоскости, лежащие ниже нижней кривой не будут приводить к разрушению т.к. не достаточно амплитуды (или длительности воздействия), чтобы вызвать разрушение. Точки же выше верхней кривой недостижимы, поскольку разрушение начнется раньше, чем закончится действие импульса (при временах $t < T$). Следовательно, между нижней и верхней кривой находится область критических продолжительностей импульса, которые приводят к разрушению. Также стоит обратить внимание на то, что чем выше амплитуда приложенного импульса, тем шире область разрушения.

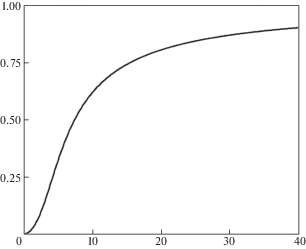
На рис. 3 изображена зависимость максимально возможной задержки разрушения от амплитуды приложенной нагрузки. По оси абсцисс откладывается амплитуда приложенного импульса в МПа, а по оси ординат задержка разрушения, отнесенная к величине инкубационного времени. Увеличение амплитуды ведет к увеличению задержки разрушения, которая не может превышать величины инкубационного времени.

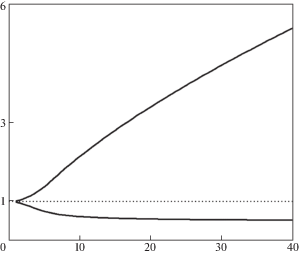
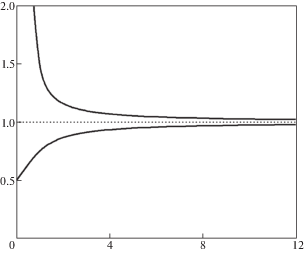
В механике квазихрупкого разрушения главной характеристикой разрушения, называемой динамической вязкостью разрушения, является значение коэффициента интенсивности напряжений в момент начала разрушения. Используя (3.9) и (4.1), (4.4) можно получить значение динамической вязкости разрушения в зависимости от амплитуды или времени воздействия. Соответствующие зависимости приведены на рис. 4 и 5. На рис. 4 по оси абсцисс откладывается амплитуда приложенного импульса в МПа, а на рис. 5 – время действия импульса, отнесенное к величине инкубационного времени ${T \mathord{\left/ {\vphantom {T \tau }} \right. \kern-0em} \tau }$. По оси ординат откладывается значение динамической вязкостью разрушения отнесенное к критическому статическому значению коэффициента интенсивности напряжений ${{K}_{{1c}}}$. При этом нижние кривые соответствуют наименьшей критической продолжительности воздействия, вызывающей разрушение, а верхние – наибольшей. Как видно из анализа, значения динамической вязкости разрушения для данного материала принципиально нестабильны и могут изменяться в довольно больших пределах при нагрузках с одинаковой амплитудой или продолжительностью. Это следует обязательно учитывать при проведении анализа разрушения и обработки опытных данных, а экспериментальное изучение пороговых ситуаций при этом будет играть важнейшую роль для выявления инкубационных характеристик разрушения и прогнозирования упомянутой нестабильности.

Можно рассмотреть исследованную выше ситуацию с другой стороны. Пусть фиксирована длительность $T$ приложенного прямоугольного импульса. Последовательно увеличивая амплитуду, можно найти ту пороговую (минимальную) для данной длительности, которая приведет к разрушению. По достижении порога разрушение произойдет в момент времени $t_{*}^{{}}$, определенный в (4.3), а пороговая амплитуда такого импульса будет определяться из (4.4). Разрушение при этом будет происходить с задержкой (т.е. сопровождаться снижением текущего КИН от момента окончания действия импульса до момента $t_{*}^{{}}$), величина которой равна $t_{*}^{{}} - T$. При дальнейшем постепенном увеличении амплитуды выше найденного порогового значения разрушение будет происходить со все меньшей задержкой. Наконец, при достижении величины амплитуды, определенной формулой (4.1), разрушение произойдет без задержки, т.е. в момент времени $t_{*}^{{}} = T$, соответствующий сбросу нагрузки. Дальнейшее увеличение амплитуды приведет к тому, что разрушение будет происходить прежде зафиксированной выше длительности воздействия $t_{*}^{{}} < T$.

Полученные выше при анализе разрушения эффекты не связаны с рассмотренным конкретным профилем нагружения. Можно взять, например, “треугольную” нагрузку с постоянной скоростью ввода импульса $f(t) = V \cdot t \cdot \left[ {H(t) - H(t - {{T}_{0}})} \right]$. Использование (3.8) позволяет получить значение коэффициента интенсивности напряжений для такого воздействия:

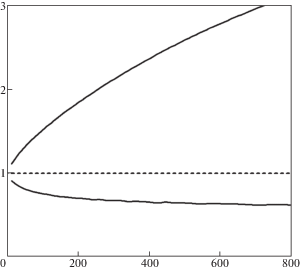
Для этого случая также можно получить формулы и расчеты, аналогичные (4.1)–(4.4). Для примера на рис. 6 приведена рассчитанная зависимость динамической вязкости разрушения от скорости приложения нагрузки. По оси абсцисс откладывается скорость приложения нагрузки в ГПа/сек, а по оси ординат значение динамической вязкости разрушения отнесенное к критическому значению коэффициента интенсивности напряжений ${{K}_{{1c}}}$.

5. Сравнение с экспериментом. Рассмотрим известную серию экспериментов по инициированию роста трещин К. Рави-Чандара и В.Г. Кнаусса [2]. Эксперименты проводились на оптически чувствительном материале Homalite – 100, который имеет ${{K}_{{{\text{I}}c}}} = 0.48\;{\text{МПа}}\sqrt {\text{м}} $, ${{c}_{1}}$ = 2150 м/с, ${{c}_{2}}$ = 1230 м/с. Образцы прямоугольной формы имели разрез. Нагружение производилось при помощи быстрого приложения к берегам разреза создаваемого магнитным полем давления, имеющего трапецеидальный временной профиль. Участок роста импульса давления имел продолжительность 25 мкс, после чего давление удерживалось постоянным. Весь эксперимент занимал не более 150 мкс, но старт трещин во всех случаях происходил до времени сброса давления на берегах. Во время эксперимента регистрировалось текущее значение коэффициента интенсивности $K(t)$. Размеры образцов были выбраны достаточно большими, таким образом, чтобы за время проведения испытания исключить взаимодействие с разрезом волн, отраженных от границ образца. Следовательно, испытуемую модель можно было рассматривать как бесконечную плоскость, имеющую полубесконечный разрез. Приложенную в опытах трапецеидальную нагрузку можно представить в виде f(t) = = $P[tH(t) - (t - {{T}_{0}})H(t - {{T}_{0}})]{\text{/}}{{T}_{0}}$, где ${{T}_{0}}$ – время роста импульса давления, $P$ – амплитуда приложенного давления на постоянном участке воздействия. Нагрузка удерживалась по крайней мере до момента разрушения ${{t}_{*}}$, который мог быть как меньше, так и больше периода нарастания давления ${{T}_{0}}$. Таким образом, в терминах предыдущих рассмотрений разрушение в данном эксперименте во всех случаях происходило в результате приложения критического максимального (запорогового) импульса. Значение коэффициента интенсивности напряжений в такой задаче находится из (3.7), (3.8):

Подставляя (5.1) в критерий (2.1) нетрудно получить выражение для величины коэффициента интенсивности напряжений в момент разрушения ${{K}_{q}} = K(t_{*}^{{}})$:

где $t_{*}^{{}}$ – момент разрушения, ${{\bar {t}}_{*}} = t_{*}^{{}}{\text{/}}\tau $, ${{\overline T }_{0}} = {{{{T}_{0}}} \mathord{\left/ {\vphantom {{{{T}_{0}}} \tau }} \right. \kern-0em} \tau }$. Теоретическая кривая и точки из [2] при τ = 10 мкс показаны на рис. 7. По оси абсцисс откладывается время действия нагрузки в микросекундах, а по оси ординат значение динамической вязкостью разрушения отнесенное к критическому статическому значению коэффициента интенсивности напряжений. Как видно из графика, проведенный расчет показывает хорошее соответствие с экспериментальными результатами.

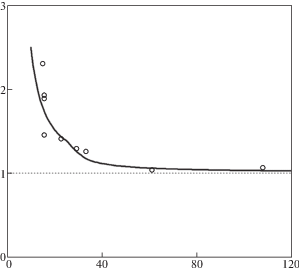
В [12] описана серия экспериментов, в которой при заданной продолжительности воздействия определялась наименьшая амплитуда, вызывающая разрушение. Эксперименты проводились на прямоугольных металлических пластинах, имеющих симметрично расположенный разрез. Нагружение проводилось волновыми импульсами растягивающего напряжения прямоугольной формы, падающими нормально на трещину. Были реализованы три серии экспериментов с продолжительностями импульсов ${{T}_{1}} = $ 18 мкс, ${{T}_{2}} = $ 40 мкс и ${{T}_{3}} = $ 80 мкс. В каждой серии определялась минимальная (пороговая) амплитуда вызывающая разрушение. С уменьшением времени воздействия пороговое значение амплитуды приобретало все большую разницу по сравнению с тем, которое должно следовать из классического критерия критического коэффициента интенсивности и оказывалось существенно большим по величине. В случае коротких импульсов описанную ситуацию можно рассматривать как воздействие на полубесконечный разрез минимального (порогового) разрушающего импульса прямоугольной формы с амплитудой $P$ и продолжительностью $T$. Критическую амплитуду, определенную по критерию критического коэффициента интенсивности, обозначим через ${{P}_{k}}$, а по критерию инкубационного времени через ${{P}_{a}}$. Тогда из (4.4) следует, что

где $\overline T = T{\text{/}}\tau $, ${{\bar {t}}_{*}} = t_{*}^{{}}{\text{/}}\tau $ – момент разрушения. Результаты расчета при $\tau $ = 10 мкс для $Q = ({{P}_{a}} - {{P}_{k}}{\text{/}}{{P}_{k}} \cdot 100\% $ приведены на рис. 8, где по оси абсцисс откладывается время действия нагрузки в мкс, а по оси ординат определенная выше безразмерная величина $Q$. При этом ${{Q}_{1}} = Q({{T}_{1}}) = $ 16%; ${{Q}_{2}} = $ 7%; ${{Q}_{2}} = $ 3%, что вполне соответствует экспериментальным наблюдениям [12], показанным точками.

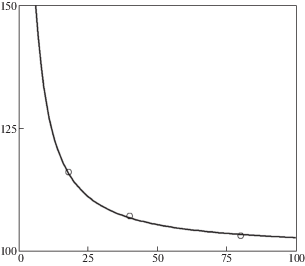
В [6] описана серия экспериментов, в которой при помощи магнитно-импульсного способа формирования нагрузки на образцах с макротрещинами из ПММА [13] проведено исследование разрушения при динамическом нагружении микросекундной длительности. Равномерно распределенное давление на берега разреза имело форму затухающих синусоид и описывалось следующей формулой

Ввиду быстрого затухания приложенного импульса в расчет принимались первые три пульсации. При этом период колебаний $T = $ 5.6 мкс, и постоянная времени затухания T₁ = 4.2 мкс не изменялись для всех реализованных испытаний. Из (5.4) следует, что в момент времени ${{t}_{m}} = {\text{arctg}}{{(2 \cdot \pi \cdot {{{{T}_{1}}} \mathord{\left/ {\vphantom {{{{T}_{1}}} T}} \right. \kern-0em} T}) \cdot T} \mathord{\left/ {\vphantom {{(2 \cdot \pi \cdot {{{{T}_{1}}} \mathord{\left/ {\vphantom {{{{T}_{1}}} T}} \right. \kern-0em} T}) \cdot T} {(2{\text{/}}\pi )}}} \right. \kern-0em} {(2{\text{/}}\pi )}}$ значение давления достигает своей максимальной величины ${{P}_{m}} = {{P}_{0}} \cdot \exp ( - {{2 \cdot {{t}_{m}}} \mathord{\left/ {\vphantom {{2 \cdot {{t}_{m}}} {{{T}_{1}}}}} \right. \kern-0em} {{{T}_{1}}}}){\text{/}}(1 + {{T}^{2}}{\text{/}}{{(2\pi {{T}_{1}})}^{2}})$, которая и принималась за амплитуду. Были проведены испытания 10 образцов. Амплитуда импульса давления ${{P}_{m}}$ варьировалась при этом от 140 до 320 МПа. В опытах фиксировалось время начала разрушения (старта трещины).

Значение коэффициента интенсивности напряжений для такой задачи согласно (3.8) имеет вид

где $\alpha = {{2 \cdot {{c}_{2}}\sqrt {c_{1}^{2} - c_{2}^{2}} } \mathord{\left/ {\vphantom {{2 \cdot {{c}_{2}}\sqrt {c_{1}^{2} - c_{2}^{2}} } {({{c}_{1}} \cdot \sqrt {\pi {\text{ }}{{c}_{1}}} )}}} \right. \kern-0em} {({{c}_{1}} \cdot \sqrt {\pi {\text{ }}{{c}_{1}}} )}}$. Поскольку при проведении экспериментов в нагрузке $P(t)$ варьировалась только величина $P{}_{{\text{0}}}$, значения коэффициентов интенсивности отличаются только множителем. Максимальное значение коэффициента интенсивности достигается в момент времени $t \approx $ 1.7 мкс после начала нагружения.

Использование критерия инкубационного времени (2.1) позволяет рассчитать наблюдаемую в эксперименте зависимость момента начала разрушения от амплитуды приложенного импульса. Для данного материала было принято $\tau $ = 32 мкс.

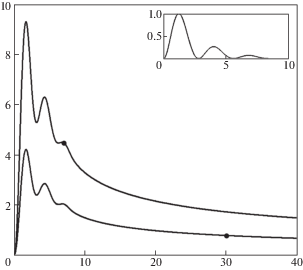
Расчет показывает, что для создаваемой в опытах нагрузки минимальная (пороговая) разрушающая амплитуда ${{P}_{m}}$ составляет 94.7 МПа. Реализованные при проведении эксперимента нагрузки превосходили минимальную до более чем в 3 раза. Значения коэффициента интенсивности напряжений от момента приложения нагрузки до начала разрушения приведены на рис. 9. Верхняя кривая соответствует наибольшей реализованной в опытах амплитуде ${{P}_{m}}$ = 320 МПа, а нижняя – наименьшей ${{P}_{m}}$ = 140 МПа. По оси абсцисс откладывается время в мкс, а по оси ординат отношение значения текущего коэффициента интенсивности напряжений к статической вязкости разрушения – ${{K(t)} \mathord{\left/ {\vphantom {{K(t)} {{{K}_{{!c}}}}}} \right. \kern-0em} {{{K}_{{!c}}}}}$. Кружками обозначены моменты начала разрушения. В верхнем правом углу представлена зависимость нормированного приложенного импульса давления на берегах от времени в мкс. Видно, что разрушение происходит с заметной задержкой, тем большей, чем меньше амплитуда, причем значение текущего коэффициента интенсивности перед стартом трещины может падать в несколько раз. При этом время, прошедшее до момента старта трещины, может на порядок превосходить как время до максимума КИН, так и время действия приложенного импульса.

Отметим также, что задержка разрушения наблюдалась и при изучении откольного разрушения [4, 5, 14].

6. Заключение. Таким образом, на основе структурно-временного подхода аналитически установлено, что разрушение материалов с трещинами может происходить в широких пределах времен и традиционных критических характеристик ударно-волнового воздействия. Так, предельное значение коэффициента интенсивности напряжений (динамическая вязкость разрушения) для данного материала при импульсном воздействии принципиально нестабильно и может изменяться в довольно больших пределах. При этом может возникать принципиальный эффект задержки разрушения, которая становится особенно заметной в случае кратковременных воздействий, близких к пороговым.

Показано, что наблюдаемая в экспериментах задержка разрушения получает отчетливое объяснение в рамках подхода, базирующегося на понятии инкубационного времени разрушения. Найдены условия ее возникновения и приведены соответствующие аналитические формулы.

Из проведенного исследования следует вывод о принципиальной необходимости изучения пороговых случаев, в которых проявляются временные эффекты, не укладывающиеся в понятия прочности и трещиностойкости, базирующиеся на локальном предельном напряжении и/или критическом КИН. Именно поэтому экспериментальное и теоретическое исследования пороговых ситуаций, до сих пор не получившие достаточного распространения и освещения, являются принципиально важными и, авторы надеются, станут одним из новых направлений исследований процессов динамического разрушения и структурных превращений в сплошных средах.

Работа выполнена при поддержке РФФИ 20-01-00291. Материал разделов 1, 2, 4 был создан Ю.В. Петровым при поддержке РФФИ-БРИКС 18-51-80008.