1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 3, 2022

Известия РАН. Механика твердого тела, 2022, № 3, стр. 40-55

УСТАНОВИВШАЯСЯ ПОЛЗУЧЕСТЬ ДЛИННОЙ УЗКОЙ ПРЯМОУГОЛЬНОЙ МЕМБРАНЫ ВНУТРИ НИЗКОЙ ЖЕСТКОЙ МАТРИЦЫ ПРИ ПРОПОРЦИОНАЛЬНОЙ ЗАВИСИМОСТИ ВЕЛИЧИНЫ ПОПЕРЕЧНОГО ДАВЛЕНИЯ ОТ ВРЕМЕНИ

А. Ф. Ахметгалеев a, *, А. М. Локощенко a, **, Л. В. Фомин a, b, ***

a Научно-исследовательский институт механики Московского государственного университета им. М.В. Ломоносова
Москва, Россия

b Самарский государственный технический университет
Самара, Россия

* E-mail: Achmet206A@yandex.ru
** E-mail: loko@imec.msu.ru
*** E-mail: fleonid1975@mail.ru

Поступила в редакцию 04.03.2021
После доработки 09.04.2021
Принята к публикации 24.05.2021

Полный текст (PDF)

Аннотация

Исследуется задача об установившейся ползучести длинной узкой прямоугольной мембраны в стесненных условиях внутри жесткой матрицы при пропорциональном возрастании величины поперечного давления от времени (с разными скоростями). Задача решается с учетом геометрической и физической нелинейности. В задаче рассматривается длинная жесткая матрица прямоугольного сечения, в которой высота не больше половины ширины. Рассматриваются два варианта условий контакта мембраны и матрицы: идеальное скольжение и прилипание. В данной работе исследованы три стадии ползучести мембраны. На первой стадии мембрана деформируется в условиях установившейся ползучести вплоть до момента касания поперечной стенки матрицы. Вторая стадия заканчивается в момент касания мембраной продольных стенок матрицы. На третьей стадии мембрана контактирует с матрицей по поперечной и продольным сторонам. Расчет проводится до времени практически полного прилегания мембраны к матрице. Представляет интерес сравнение этих времен при различных контактных условиях. В общем случае соотношение этих времен зависит от двух параметров: показателя степени в определяющем уравнении установившейся ползучести материала мембраны и величины безразмерной высоты матрицы. В данной задаче при различных скоростях возрастания величины поперечного давления и при различных степенях близости мембраны к матрице времена окончания стадий нагружения при идеальном скольжении меньше, чем при прилипании. Результаты исследований могут быть использованы при расчетах формовки мембраны в жесткой матрице.

Ключевые слова: длинная узкая мембрана, установившаяся ползучесть, низкая жесткая матрица, поперечное давление, идеальное скольжение, прилипание

1. Введение. Данная работа посвящена аналитическому исследованию установившейся ползучести в стесненных условиях длинной узкой прямоугольной мембраны, закрепленной вдоль длинных сторон и нагруженной равномерным поперечным давлением $q$, которое может изменяться во времени $t$ по заданному закону. Решение этой задачи в свободных условиях при различных физических и геометрических условиях приведено в монографиях Одквиста [1], Л.М. Качанова [2], Сторакерса [3].

В [4] проведено экспериментальное измерение деформации мембран из разных эластомеров. В [5] исследовано раздувание круглой мембраны при больших деформациях. Вязкоупругие характеристики материала мембраны описываются нелинейным интегральным определяющим уравнением. Представленный численный метод решения сочетает методы решения нелинейных интегральных уравнений Вольтерра и нелинейных обыкновенных дифференциальных уравнений.

В [6–8] приведены результаты теоретического исследования ползучести и длительной прочности мембран из анизотропных материалов. В [6] приведена математическая модель процесса изотермического свободного деформирования узкой прямоугольной мембраны из анизотропного листового материала, подчиняющегося энергетическому варианту кинетической теории ползучести и длительной прочности. Установлено, что с ростом коэффициента нормальной анизотропии предельные возможности исследованных процессов формоизменения возрастают. В [6, 7] приведена математическая модель процесса изотермического свободного деформирования узкой прямоугольной мембраны из анизотропного листового материала, подчиняющегося энергетическому варианту кинетической теории ползучести и длительной прочности. Показано влияние анизотропии механических свойств материала, геометрических размеров заготовки и накопления поврежденности на напряженное деформированное состояние заготовки, силовые режимы и предельные возможности формообразования. На основе разработанных математических моделей деформирования выполнены теоретические исследования процессов изотермического свободного деформирования узкой прямоугольной мембраны, формообразования угловых элементов многослойных конструкций, штамповки и калибровки трапециевидных элементов трехслойных листовых конструкций из анизотропных высокопрочных материалов в режиме кратковременной ползучести [8]. Выполнено сопоставление результатов расчетов при анализе изотермического свободного деформирования узкой прямоугольной мембраны в предположении переменной и постоянной толщин стенки вдоль дуги окружности.

Особый интерес представляет исследование ползучести рассматриваемой мембраны внутри жесткой матрицы. Ефимов А.Б. с соавторами [9] составили обзор основных феноменологических закономерностей, описывающих постановку задачи контактного взаимодействия общего вида.

В монографиях [10, 11] рассмотрен цикл задач о ползучести такой мембраны внутри жесткой матрицы. В [11] приведены решения задач при учете различных форм матриц: клиновидной [12], криволинейной [13] и прямоугольной при различных условиях на контакте мембраны и матрицы. Во всех приведенных решениях величина равномерного поперечного давления $q$ не зависит от времени $t$. В различных решениях использовались разные модели ползучести: установившаяся, неустановившаяся, дробно-степенная. В случае применения дробно-степенной модели ползучести [14] в зависимости от контактных условий с течением времени мембрана либо заполняет пространство внутри матрицы за конечное или бесконечное время, либо разрушается внутри матрицы [12]. В [15] приведено решение аналогичной задачи об установившейся ползучести мембраны при кусочно-постоянной зависимости скорости изменения величины поперечного давления от времени.

В [12] проведено моделирование деформирования длинной узкой прямоугольной мембраны внутри жесткой клиновидной матрицы при различных подходах и различных краевых условиях. Получены все основные соотношения, характеризующие напряженно-деформированное состояние мембраны на различных стадиях деформирования. Приведены результаты численных экспериментов, в которых исследуются особенности деформирования мембран вплоть до разрушения. Аналогичное решение для П-образной матрицы приведено в [16].

В [17] исследована деформация нелинейной вязкоупругой однородной сферической мембраны, содержащей несжимаемую жидкость между двумя жесткими параллельными пластинами. Материал мембраны моделируется нелинейным интегральным определяющим соотношением, которое в частном случае включает квазилинейную вязкоупругость.

В статье Р.А. Васина с соавторами [18] приведено экспериментально-теоретическое исследование ползучести мембран в стесненных условиях. Сформулированы особенности процедуры идентификации определяющих соотношений (нахождения материальных констант) по результатам экспериментов. Приведены методика и результаты определения материальных констант из экспериментов по формовке цилиндрических и сферических оболочек из листовых заготовок.

Методика идентификации определяющих соотношений уравнения ползучести, основанная на использовании упрощенной инженерной модели процесса сверхпластической формовки листового проката в прямоугольную матрицу, построена в рамках основных предположений безмоментной теории оболочек [19]. Применимость этой упрощенной модели обоснована путем прямого сопоставления результатов аналитических расчетов с экспериментальными данными.

Авторы [20] представили теоретическое и численное исследовани я  деформирования нелинейной вязкоупругой прямоугольной мембраны, нагруженной равномерным давлением.

Авторами [21] описаны большие контактные деформации и явление адгезии между раздутой гиперупругой мембраной и жесткой подложкой. Исходная форма мембраны – плоская, круглая, закрепленная по краю. Допустимы два условия контакта между мембраной и подложкой: контакт без трения и прилипание. Проведен анализ энергетического баланса без учета диссипации энергии.

В [22] изучается контакт длинной прямоугольной упругой мембраны с жесткой подложкой. Построенная модель основана на теории конечных деформаций. Учтены два условия контакта: идеальное скольжение и прилипание, для контакта без трения получено точное решение в замкнутой форме.

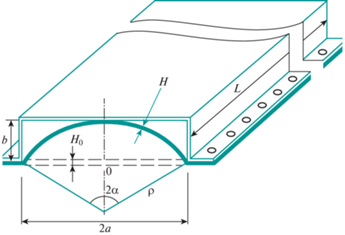
2. Постановка задачи. В данной работе исследуется установившаяся ползучесть мембраны толщины ${{Н}_{0}}$ внутри жесткой матрицы прямоугольной формы. Ширина, длина и высота матрицы равны соответственно $2a$, $L$, $b$. Отношение высоты матрицы к половине ширины удовлетворяет неравенству $\frac{b}{a} \leqslant 1$ (рис. 1). Ширина мембраны $2a$ и ее длина $L$ удовлетворяет неравенству $\frac{{2a}}{L} \ll 1$. Здесь рассматривается не постоянная величина поперечного давления $q\left( t \right) = {\text{const}}$, а пропорциональная зависимость величины $q\left( t \right)$

(2.1)
$q\left( t \right) = {{q}_{0}}k\frac{t}{{{{t}_{0}}}}$
Рис. 1.

Общий вид.

Для описания деформирования мембраны при $t > 0$ ($t$ – время) используется степенная модель установившейся ползучести материала

(2.2)
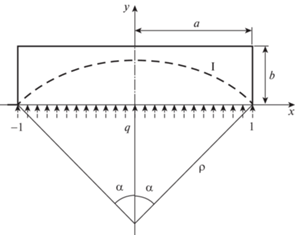
$\frac{{d{{p}_{u}}}}{{dt}} = \frac{1}{{{{t}_{0}}}}{{\left( {\frac{{{{\sigma }_{u}}}}{{{{\sigma }_{0}}}}} \right)}^{n}}$
в которой ${{\sigma }_{u}}$ и ${{\dot {p}}_{u}}$ – интенсивности напряжений и скоростей деформаций ползучести соответственно, ${{\sigma }_{0}}$, ${{t}_{0}}$ и $n$ – постоянные величины соответствующей размерности.

Координаты поперечного сечения мембраны и матрицы назовем $x$ и $y$ (рис. 2). На первой стадии мембрана, плоская в начальном состоянии, под действием давления $q$ деформируется, приобретая форму незамкнутой круговой цилиндрической оболочки с центральным углом $2\alpha $. При этом на первой стадии мембрана деформируется в условиях установившейся ползучести вплоть до касания поперечной стенки жесткой матрицы; можно показать, что угол раствора мембраны в конце этой стадии равен

$2{{\alpha }_{1}} = 2\arcsin \left( {\frac{{2ab}}{{{{a}^{2}} + {{b}^{2}}}}} \right)$
Рис. 2.

Первая стадия деформирования.

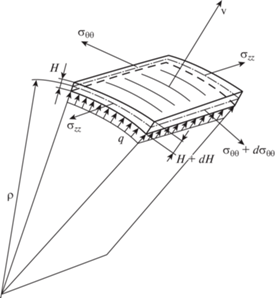
При моделировании напряженно-деформированного состояния мембраны рассматриваются главные напряжения (радиальное ${{\sigma }_{{rr}}}$, окружное ${{\sigma }_{{\theta \theta }}}$ и осевое ${{\sigma }_{{zz}}}$) и соответствующие компоненты тензора деформаций ползучести ${{p}_{{rr}}}$, ${{p}_{{\theta \theta }}}$ и ${{p}_{{zz}}}$.

Рассматривая элемент мембраны (рис. 3), принимая напряжения в элементе равномерно распределенными по толщине и записывая уравнения равновесия в проекциях на нормаль и касательную, получаем:

(2.3)
${{\sigma }_{{\theta \theta }}} = \frac{{q\rho }}{H},\,\,\,\,\,d\left( {{{\sigma }_{{\theta \theta }}}H} \right) = 0$
где $\rho $ – радиус кривизны срединной поверхности, H – толщина мембраны.

Рис. 3.

Элемент мембраны.

Следовательно,

(2.4)
${{\sigma }_{{\theta \theta }}}H = {\text{const}}$

Сопоставляя (2.3) и (2.4), заключаем, что в случае равномерного давления радиус кривизны срединной поверхности во всех ее точках один и тот же $\left( {\rho = {\text{const}}} \right)$, т.е. срединная поверхность мембраны при ее деформировании является частью поверхности кругового цилиндра с некоторым углом раствора $2\alpha $ [3]. В этом случае очевидно, что если толщина мембраны до деформации постоянна, то она постоянна и после деформации. Следовательно, согласно (2.3) окружное напряжение по длине окружности радиуса $\rho $ не изменяется.

3. Свободное деформирование мембраны в условиях ползучести (первая стадия). Введем безразмерные переменные:

(3.1)
$\begin{gathered} \bar {q} = \frac{q}{{{{\sigma }_{0}}}},\quad \bar {t} = \frac{t}{{{{t}_{0}}}},\quad \bar {H} = \frac{H}{{{{H}_{0}}}},\quad {{{\bar {H}}}_{0}} = \frac{{{{H}_{0}}}}{a},\quad \bar {b} = \frac{b}{a},\quad \bar {x} = \frac{x}{a},\quad \bar {y} = \frac{y}{a} \\ \,{{{\bar {x}}}_{0}} = {{\frac{{{{x}_{0}}}}{a}}_{{}}},\quad {{{\bar {y}}}_{0}} = \frac{{{{y}_{0}}}}{a},\quad \bar {\rho } = \frac{\rho }{a},\quad {{{\bar {\sigma }}}_{{ij}}} = \frac{{{{\sigma }_{{ij}}}}}{{{{\sigma }_{0}}}}\quad (i,\,j = 1,\;2,\;3) \\ \end{gathered} $
x и y – горизонтальная и вертикальная координаты поперечного сечения матрицы, ${{x}_{0}}$ и ${{y}_{0}}$ – координаты точек касания мембраны и матрицы.

Далее черточки над всеми безразмерными переменными (3.1) опустим. При этом под скоростями всюду понимаются производные по безразмерному времени.

В качестве связи компонент тензоров напряжений и скоростей деформаций ползучести примем гипотезу пропорциональности соответствующих девиаторов (см., например, [4]):

(3.2)
$\begin{gathered} {{{\dot {p}}}_{{ij}}} = \frac{{3f({{\sigma }_{u}})}}{{2{{\sigma }_{u}}}}({{\sigma }_{{ij}}} - \sigma ),\quad \sigma = \frac{1}{3}({{\sigma }_{{rr}}} + {{\sigma }_{{\theta \theta }}} + {{\sigma }_{{zz}}}) \\ {{\sigma }_{u}} = \frac{1}{{\sqrt 2 }}\sqrt {{{{({{\sigma }_{{rr}}} - {{\sigma }_{{\theta \theta }}})}}^{2}} + {{{({{\sigma }_{{\theta \theta }}} - {{\sigma }_{{zz}}})}}^{2}} + {{{({{\sigma }_{{zz}}} - {{\sigma }_{{rr}}})}}^{2}} + 6(\sigma _{{r\theta }}^{2} + \sigma _{{\theta z}}^{2} + \sigma _{{rz}}^{2})} \\ \end{gathered} $

В рассматриваемом плоском деформированном состоянии скорость осевой деформации ползучести ${{\dot {p}}_{{zz}}}$ принимается равной нулю:

(3.3)
${{\dot {p}}_{{zz}}} = 0$

Далее всюду будем обозначать ${{H}_{i}}(t)$ толщину мембраны на i-й стадии $\left( {i = 1 \div 3} \right)$.

Примем, как обычно, для тонкостенных цилиндрических оболочек равенство:

(3.4)
${{\sigma }_{{rr}}} = 0$
в этом случае из гипотезы пропорциональности девиаторов напряжений и скоростей деформаций ползучести (3.2) при учете (3.4) следует:

(3.5)
${{\sigma }_{{zz}}} = 0.5{{\sigma }_{{\theta \theta }}},\,\,\,\,{{\sigma }_{u}} = \frac{{\sqrt 3 }}{2}{{\sigma }_{{\theta \theta }}} = \frac{{\sqrt 3 }}{2} \cdot \frac{{q\rho }}{{{{H}_{0}}{{H}_{1}}}}$

Рассматривая два близких деформированных состояния мембраны, определим приращение окружной деформации ползучести, учитывая, что деформированное состояние однородное:

$d{{p}_{{\theta \theta }}} = \frac{{\left( {\rho + d\rho } \right)\left( {\alpha + d\alpha } \right) - \rho \alpha }}{{\rho \alpha }} = \frac{{d\rho }}{\rho } + \frac{{d\alpha }}{\alpha }$

Следовательно, скорость окружной деформации ползучести равна

(3.6)
${{\dot {p}}_{{\theta \theta }}} = \frac{{\dot {\rho }}}{\rho } + \frac{{\dot {\alpha }}}{\alpha }$

Поскольку

(3.7)
$\rho \sin \alpha = 1$
то

$\dot {\rho }\sin \alpha + \rho \dot {\alpha }\cos \alpha = 0$

Поэтому выражение (3.6) преобразуется к виду:

(3.8)
${{\dot {p}}_{{\theta \theta }}} = \left( {\frac{1}{\alpha } - {\text{ctg}}\alpha } \right)\dot {\alpha }$

Из условия несжимаемости в случае плоского деформированного состояния получаем:

(3.9)
$\begin{gathered} {{{\dot {p}}}_{{rr}}} + {{{\dot {p}}}_{{\theta \theta }}} + {{{\dot {p}}}_{{zz}}} = 0,\quad {{{\dot {p}}}_{{zz}}} = 0,\quad {{{\dot {p}}}_{{rr}}} = - {{{\dot {p}}}_{{\theta \theta }}} \\ {{{\dot {p}}}_{u}} = \frac{{\sqrt 2 }}{3}\sqrt {{{{\left( {{{{\dot {p}}}_{{rr}}} - {{{\dot {p}}}_{{\theta \theta }}}} \right)}}^{2}} + {{{\left( {{{{\dot {p}}}_{{\theta \theta }}} - {{{\dot {p}}}_{{zz}}}} \right)}}^{2}} + {{{\left( {{{{\dot {p}}}_{{zz}}} - {{{\dot {p}}}_{{rr}}}} \right)}}^{2}} + 6[{{{\left( {{{{\dot {p}}}_{{\theta r}}}} \right)}}^{2}} + {{{\left( {{{{\dot {p}}}_{{\theta z}}}} \right)}}^{2}} + {{{\left( {{{{\dot {p}}}_{{zr}}}} \right)}}^{2}}]} \\ {{{\dot {p}}}_{u}} = \frac{2}{{\sqrt 3 }}{{{\dot {p}}}_{{\theta \theta }}} \\ \end{gathered} $

Так как скорость радиальной деформации ползучести равна

${{\dot {p}}_{{rr}}} = \frac{{{{{\dot {H}}}_{1}}}}{{{{H}_{1}}}}$
то согласно равенствам (3.8)–(3.9) получаем:

(3.10)
$ - \frac{{{{{\dot {H}}}_{1}}}}{{{{H}_{1}}}} = \left( {\frac{1}{\alpha } - {\text{ctg}}\alpha } \right)\dot {\alpha }$

Проинтегрируем уравнение (3.10) при начальных условиях: $t = 0,\alpha = 0,{{H}_{1}}(0) = 1$:

(3.11)
${{H}_{1}} = \frac{{\sin \alpha }}{\alpha }$

Полученные выражения (2.1), (2.3), (3.5), (3.7), (3.9) и (3.11) позволяют представить окружное напряжение ${{\sigma }_{{\theta \theta }}}$ и интенсивность напряжений ${{\sigma }_{u}}$ в зависимости от угла раствора $\alpha $:

(3.12)
${{\sigma }_{{\theta \theta }}} = \frac{{q\rho }}{{{{H}_{1}}{{H}_{0}}}} = \frac{{{{q}_{0}}kt\alpha }}{{{{H}_{0}}{{{\sin }}^{2}}\alpha }},\quad {{\sigma }_{u}} = \frac{{\sqrt 3 }}{2}{{\sigma }_{{\theta \theta }}} = \frac{{\sqrt 3 }}{2}\frac{{{{q}_{0}}\alpha kt}}{{{{H}_{0}}{{{\sin }}^{2}}\alpha }}$

Из (2.2) при учете (3.9) и (3.12) получаем зависимость угла раствора $\alpha $ от времени t:

(3.13)
$\int\limits_0^{{{t}_{1}}} {{{t}^{n}}dt = \frac{{{{t}_{1}}^{{n + 1}}}}{{n + 1}}} = \frac{2}{{\sqrt 3 }}\int\limits_0^{\alpha _{1}^{{}}} {\left( {\frac{1}{\alpha } - {\text{ctg}}\alpha } \right){{{\left( {\frac{{2{{H}_{0}}{{{\sin }}^{2}}\alpha }}{{\sqrt 3 {{q}_{0}}k \cdot \alpha }}} \right)}}^{n}}d\alpha } $

При исследовании первой стадии деформирования мембраны угол $\alpha $ изменяется в диапазоне от $\alpha = 0$ до ${{\alpha }_{1}}$ – угла, при котором происходит касание мембраной поперечной стороны матрицы: $2\alpha \left( {{{t}_{1}}} \right) = 2{{\alpha }_{1}}$

Введем новое безразмерное время:

(3.14)
${{\tau }^{n}} = {{\left( {\frac{{{{q}_{0}}}}{{{{H}_{0}}}}} \right)}^{n}} \cdot {{t}^{{n + 1}}}$

Из (3.13)–(3.14) следует:

$\begin{gathered} \frac{{{{\tau }^{n}}}}{{\left( {n + 1} \right)}} = {{\left( {\frac{{{{q}_{0}}}}{{{{H}_{0}}}}} \right)}^{n}}\frac{{{{t}^{{n + 1}}}}}{{n + 1}} = {{\left( {\frac{2}{{\sqrt 3 }}} \right)}^{{n + 1}}} \cdot \frac{1}{{{{k}^{n}}}}\int\limits_0^\alpha {\left( {\frac{1}{\alpha } - {\text{ctg}}\alpha } \right){{{\left( {\frac{{{{{\sin }}^{2}}\alpha }}{\alpha }} \right)}}^{n}}d\alpha } \\ \tau _{1}^{0} = \tau \left( {{{\alpha }_{1}}} \right) = {{\left\{ {\left( {n + 1} \right) \cdot {{{\left( {\frac{2}{{\sqrt 3 }}} \right)}}^{{n + 1}}} \cdot \frac{1}{{{{k}^{n}}}}\int\limits_0^{\alpha _{1}^{{}}} {\left( {\frac{1}{\alpha } - {\text{ctg}}\alpha } \right){{{\left( {\frac{{{{{\sin }}^{2}}\alpha }}{\alpha }} \right)}}^{n}}d\alpha } } \right\}}^{{\frac{1}{n}}}} \\ \end{gathered} $

В конце первой стадии $(\tau = \tau _{1}^{0})$ максимальный раствор мембраны равен: $2\alpha (\tau _{1}^{0})$ = 2α1. Момент времени $\tau _{1}^{0}$, при котором происходит окончание первой стадии, и толщина мембраны $H_{{\text{1}}}^{{\text{o}}} = H(\tau _{1}^{0})$, вычисляемая с учетом зависимости (3.11), определяются согласно уравнениям:

(3.15)
$\begin{gathered} \tau _{1}^{0} = \tau \left( {\alpha = {{\alpha }_{1}} = \arcsin \left( {\frac{{2b}}{{1 + {{b}^{2}}}}} \right)} \right) \\ H_{{\text{1}}}^{{\text{o}}} = {{H}_{1}}(\tau = \tau _{1}^{0}) = \frac{{{\text{sin}}{{\alpha }_{1}}}}{{{{\alpha }_{1}}}} = \left( {\frac{{2b}}{{(1 + {{b}^{2}})\arcsin \left( {\frac{{2b}}{{1 + {{b}^{2}}}}} \right)}}} \right) \\ \end{gathered} $

Далее рассматривается ползучесть мембраны внутри жесткой матрицы при различных контактных условиях.

4. Идеальное скольжение мембраны вдоль сторон матрицы. 4.1. Вторая стадия $(0 \leqslant {{x}_{0}} \leqslant 1$ – b). Решение задачи имеет различный характер для относительно высокой матрицы ($b \geqslant 1$) и относительно низкой матрицы ($b \leqslant 1$). Для определенности в данной работе рассмотрена ползучесть мембраны внутри относительно низкой матрицы ($b \leqslant 1$).

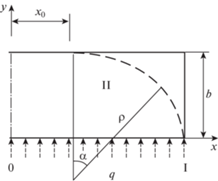
В связи с осевой симметрией мембраны и матрицы в процессе второй стадии рассматривается ползучесть правой половины мембраны в координатах $0 \leqslant x \leqslant 1 - b$, $0 \leqslant y \leqslant b$ (рис. 4).

Рис. 4.

Вторая стадия (идеальное скольжение и прилипание).

Свободное деформирование мембраны было рассмотрено в предыдущем параграфе 3. В некоторый момент времени $(t = t_{1}^{{}})$ мембрана соприкасается с поперечной стенкой матрицы. На этом свободное деформирование заканчивается, и в дальнейшем при $t > t_{1}^{{}}$ часть поверхности мембраны прилегает к поперечной поверхности матрицы.

При исследовании второй стадии ползучести мембраны выделим два близких деформированных состояния: одно характеризуется длиной участка контакта ${{x}_{0}}$, а другое – длиной участка контакта (${{x}_{0}} + d{{x}_{0}}$). С помощью геометрических соотношений (рис. 4) получим соотношение для приращения окружной деформации ползучести $d{{p}_{{\theta \theta }}}$ в виде:

(4.1)
$d{{p}_{{\theta \theta }}} = \frac{{\left( {\rho d\alpha + \alpha d\rho } \right) + d{{x}_{0}}}}{{\rho \alpha + {{x}_{0}}}}$

Каждое из слагаемых числителя (4.1) содержит множитель $d{{x}_{0}}$, следовательно, можно их сгруппировать и ввести обозначения

(4.2)
$\begin{gathered} \rho d\alpha + \alpha d\rho + d{{x}_{0}} = {{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}} \\ \rho \alpha + {{x}_{0}} = {{B}_{2}}\left( {{{x}_{0}}} \right) \\ \end{gathered} $

В этом случае

(4.3)
$d{{p}_{{\theta \theta }}} = \frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}}}}{{{{B}_{2}}\left( {{{x}_{0}}} \right)}}$

С помощью (4.3) вычислим характеристики деформированного состояния

${{\dot {p}}_{{\theta \theta }}} = \frac{{{{B}_{1}}}}{{{{B}_{2}}}}\cdot\frac{{d{{x}_{0}}}}{{dt}},\quad d{{\dot {p}}_{u}} = \frac{2}{{\sqrt 3 }}\frac{{{{B}_{1}}}}{{{{B}_{2}}}}\cdot\frac{{d{{x}_{0}}}}{{dt}}$

Проектируя наклонный радиус $\rho $ (рис. 4) на горизонталь и вертикаль, получим следующие два уравнения:

$\begin{gathered} \rho \sin \alpha = (1 - {{x}_{0}}) \hfill \\ \rho \cos \alpha = (\rho - b) \hfill \\ \end{gathered} $
в результате получаем ${{\rho }^{2}} = {{(1 - {{x}_{0}})}^{2}} + {{(\rho - b)}^{2}}$

Отсюда

$\begin{gathered} {{\left( {1 - {{x}_{0}}} \right)}^{2}} - 2\rho b + {{b}^{2}} = 0,\quad \rho = \frac{{{{{\left( {1 - {{x}_{0}}} \right)}}^{2}} + {{b}^{2}}}}{{2b}} \\ {\text{tg}}\alpha = \frac{{\left( {1 - {{x}_{0}}} \right)}}{{(\rho - b)}} = \frac{{2b\left( {1 - {{x}_{0}}} \right)}}{{[{{{(1 - {{x}_{0}})}}^{2}} - {{b}^{2}}]}} \\ \end{gathered} $

Дифференциалы $d\rho \left( {{{x}_{0}}} \right)$ и $d\alpha \left( {{{x}_{0}}} \right)$ принимают следующий вид

$d\rho = - \frac{{2(1 - {{x}_{0}})}}{{2b}}d{{x}_{0}} = - \frac{{(1 - {{x}_{0}})}}{b}d{{x}_{0}}$
$\begin{gathered} d\alpha = d\left( {\operatorname{arc} {\text{tg}}\alpha \left( {{{x}_{0}}} \right)} \right) = d\left( {\operatorname{arc} {\text{tg}}\frac{{2b(1 - {{x}_{0}})}}{{[{{{(1 - {{x}_{0}})}}^{2}} - {{b}^{2}}]}}} \right) = \\ = \frac{{\frac{{ - 2b}}{{{{{(1 - {{x}_{0}})}}^{2}} - {{b}^{2}}}} + \frac{{4b{{{(1 - {{x}_{0}})}}^{2}}}}{{{{{[{{{(1 - {{x}_{0}})}}^{2}} - {{b}^{2}}]}}^{2}}}}}}{{1 + {{{\left[ {\frac{{2b(1 - {{x}_{0}})}}{{[{{{(1 - {{x}_{0}})}}^{2}} - {{b}^{2}}]}}} \right]}}^{2}}}}d{{x}_{0}} = \frac{{ - 2b[{{{(1 - {{x}_{0}})}}^{2}} - {{b}^{2}}] + 4b{{{(1 - {{x}_{0}})}}^{2}}}}{{4{{b}^{2}}{{{(1 - {{x}_{0}})}}^{2}} + {{{[{{{(1 - {{x}_{0}})}}^{2}} - {{b}^{2}}]}}^{2}}}}d{{x}_{0}} = \\ \, = \frac{{2b}}{{[{{{(1 - {{x}_{0}})}}^{2}} + {{b}^{2}}]}}d{{x}_{0}} \\ \end{gathered} $

Подставляя $d\rho \left( {{{x}_{0}}} \right)$ и $d\alpha \left( {{{x}_{0}}} \right)$ в (4.2), получим

$\begin{gathered} \rho d\alpha = \frac{{{{{(a - {{x}_{0}})}}^{2}} + {{b}^{2}}}}{{2b}}\frac{{2b}}{{[{{{(1 - {{x}_{0}})}}^{2}} + {{b}^{2}}]}}d{{x}_{0}} = d{{x}_{0}}, \\ \alpha d\rho = \alpha \left[ { - \frac{{2(1 - {{x}_{0}})}}{{2b}}} \right]d{{x}_{0}} = - \frac{{(1 - {{x}_{0}})}}{b}\alpha d{{x}_{0}} \\ {{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}} = - \frac{{1 - {{x}_{0}}}}{b}\left( {{\text{arctg}}\left( {\frac{{2b(1 - {{x}_{0}})}}{{[{{{(1 - {{x}_{0}})}}^{2}} - {{b}^{2}}]}}} \right)} \right)d{{x}_{0}} + 2d{{x}_{0}} \\ {{B}_{2}}\left( {{{x}_{0}}} \right) = \frac{{[{{{(1 - {{x}_{0}})}}^{2}} + {{b}^{2}}]}}{{2b}}\left( {{\text{arctg}}\left( {\frac{{2b(1 - {{x}_{0}})}}{{[{{{(1 - {{x}_{0}})}}^{2}} - {{b}^{2}}]}}} \right)} \right) + {{x}_{0}} \\ \end{gathered} $

Из условия несжимаемости при учете (3.3) получаем: $d{{\dot {p}}_{{\theta \theta }}} = \, - d{{\dot {p}}_{{rr}}}$

Согласно определению ${{\dot {p}}_{{rr}}}$ имеем ${{\dot {p}}_{{rr}}} = \frac{{{{{\dot {H}}}_{2}}}}{{{{H}_{2}}}}$. Следовательно,

$\begin{gathered} {{{\dot {p}}}_{{\theta \theta }}} = - \frac{{{{{\dot {H}}}_{2}}}}{{{{H}_{2}}}},\quad d{{p}_{{\theta \theta }}} = \frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}}}}{{{{B}_{2}}\left( {{{x}_{0}}} \right)}} = - \frac{{d{{H}_{2}}}}{{{{H}_{2}}}} \\ \int\limits_{H_{1}^{0}}^{{{H}_{2}}({{x}_{0}})} {\frac{{d{{H}_{2}}}}{{{{H}_{2}}}} = - \int\limits_0^{{{x}_{0}}} {\frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}}}}{{{{B}_{2}}\left( {{{x}_{0}}} \right)}}} } ,\quad {\kern 1pt} \mathop {{{H}_{2}}}\limits^{} \left( {{{x}_{0}}} \right) = H_{1}^{0}\exp \left[ { - \int\limits_0^{{{x}_{0}}} {\frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}}}}{{{{B}_{2}}\left( {{{x}_{0}}} \right)}}} } \right] \\ H_{2}^{0} = H_{2}^{{}}({{x}_{0}} = 1 - b) = \frac{1}{{\left( {1 - b + \frac{1}{2}\pi b} \right)}} \\ \end{gathered} $

Последнее равенство следует из учета постоянства толщины $H$ мембраны вдоль всего рассматриваемого участка мембраны в конце второй стадии. Интенсивности деформаций ползучести и напряжений определяются следующими выражениями:

${{\dot {p}}_{u}} = \frac{2}{{\sqrt 3 }}{{\dot {p}}_{{\theta \theta }}},\quad {{\sigma }_{u}} = \frac{{\sqrt 3 }}{2}{{\sigma }_{{\theta \theta }}} = \frac{{\sqrt 3 }}{2}\frac{{q\left( t \right)\rho }}{{{{H}_{0}}{{H}_{2}}\left( {{{x}_{0}}} \right)}}$

Подставляя эти выражения в (2.2), получаем связь ${{x}_{0}}$ и $t$:

$\frac{2}{{\sqrt 3 }}\frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}}}}{{{{B}_{2}}\left( {{{x}_{0}}} \right)dt}} = {{\left[ {\frac{{\sqrt 3 }}{2}\frac{{q\rho }}{{{{H}_{0}}{{H}_{2}}\left( {{{x}_{0}}} \right)}}} \right]}^{n}}$
$\int\limits_{{{t}_{1}}}^{{{t}_{2}}} {{{t}^{n}}dt} = \int\limits_0^{{{x}_{0}}} {\frac{{\frac{2}{{\sqrt 3 }}\frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)}}{{{{B}_{2}}\left( {{{x}_{0}}} \right)}}}}{{{{{\left[ {\frac{{\sqrt 3 }}{2}\frac{{{{q}_{0}}k\rho }}{{{{H}_{0}}{{H}_{2}}\left( {{{x}_{0}}} \right)}}} \right]}}^{n}}}}} d{{x}_{0}} = \int\limits_0^{{{x}_{0}}} {\frac{{\frac{2}{{\sqrt 3 }}\frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)}}{{{{B}_{2}}\left( {{{x}_{0}}} \right)}}}}{{{{{\left[ {\frac{{\sqrt 3 }}{4}\frac{{{{q}_{0}}k({{{(1 - {{x}_{0}})}}^{2}} + {{b}^{2}})}}{{{{H}_{0}}{{H}_{2}}\left( {{{x}_{0}}} \right)b}}} \right]}}^{n}}}}} d{{x}_{0}},\quad {{t}_{2}} = t\left( {{{x}_{0}} = 1 - b} \right)$

Используя замену (3.14), получим:

${{\tau }_{2}}\left( {{{x}_{0}}} \right) = {{\left( {{{{(\tau _{1}^{0})}}^{n}} + \left( {n + 1} \right)\frac{1}{{{{k}^{n}}}}\int\limits_0^{{{x}_{0}}} {\frac{{\frac{2}{{\sqrt 3 }}\frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)}}{{{{B}_{2}}\left( {{{x}_{0}}} \right)}}}}{{{{{\left[ {\frac{{\sqrt 3 }}{4}\frac{{({{{(1 - {{x}_{0}})}}^{2}} + {{b}^{2}})}}{{{{H}_{2}}\left( {{{x}_{0}}} \right)b}}} \right]}}^{n}}}}} d{{x}_{0}}} \right)}^{{\frac{1}{n}}}},\quad \tau _{2}^{0} = \tau \left( {{{x}_{0}} = 1 - b} \right)$

4.2. Третья стадия $\left( {1 - b \leqslant {{x}_{0}} \leqslant 1 - \Delta } \right)$. На третьей стадии ползучести мембрана касается обеих сторон матрицы $(1\, - \,b\, \leqslant \,{{x}_{0}}\, \leqslant \,1\, - \,\Delta $, $0 \leqslant {{y}_{0}} \leqslant b)$ (рис. 5). При этом профиль мембраны представляет собой полуокружность радиуса $(1 - {{x}_{0}})$ и размеры областей контакта по продольной и поперечной осям равны $\left( {{{x}_{0}} - (1 - b)} \right) = {{y}_{0}}$. С учетом принятых допущений компоненты тензора деформаций ползучести примут вид:

$\begin{gathered} d{{p}_{{\theta \theta }}} = \frac{{\left( {2 - \frac{\pi }{2}} \right)d{{x}_{0}}}}{{\left[ {2{{x}_{0}} + \frac{\pi }{2}(1 - {{x}_{0}}) + \left( {1 - b} \right)} \right]}} = \frac{{\left( {2 - 0.5\pi } \right)d{{x}_{0}}}}{{\left[ {\left( {b + 0.5\pi - 1} \right) + \left( {2 - 0.5\pi } \right){{x}_{0}}} \right]}} \hfill \\ d{{p}_{{\theta \theta }}} = F({{x}_{0}})d{{x}_{0}},\quad F({{x}_{0}}) = \frac{{\left( {2 - 0.5\pi } \right)}}{{\left[ {\left( {b + 0.5\pi - 1} \right) + \left( {2 - 0.5\pi } \right){{x}_{0}}} \right]}} \hfill \\ \end{gathered} $
$\begin{gathered} {{p}_{{\theta \theta }}} = - \int\limits_{H_{2}^{{\text{o}}}}^{{{H}_{3}}\left( {{{x}_{0}}} \right)} {\frac{{d{{H}_{3}}}}{{{{H}_{3}}}} = \int\limits_{1 - b}^{{{x}_{0}}} {F({{x}_{0}})d{{x}_{0}}} } = \ln \frac{{H_{2}^{{\text{0}}}}}{{{{H}_{3}}\left( {{{x}_{0}}} \right)}} = \ln \left[ {\frac{{\left( {b + 0.5\pi - 1} \right) + \left( {2 - 0.5\pi } \right){{x}_{0}}}}{{1 - b + 0.5\pi b}}} \right] \\ {{H}_{3}}\left( {{{x}_{0}}} \right) = H_{2}^{{\text{0}}}\frac{{1 - b + 0.5\pi b}}{{\left[ {\left( {b + 0.5\pi - 1} \right) + \left( {2 - 0.5\pi } \right){{x}_{0}}} \right]}} = \frac{1}{{\left[ {\left( {b + 0.5\pi - 1} \right) + \left( {2 - 0.5\pi } \right){{x}_{0}}} \right]}} \\ \end{gathered} $
Рис. 5.

Третья стадия (идеальное скольжение и прилипание).

Окончание третьей стадии происходит при значении $x_{0}^{0}$, удовлетворяющем неравенству $(1 - x_{{\text{0}}}^{{\text{0}}}) = \Delta \ll 1$, где $(1 - x_{{\text{0}}}^{{\text{0}}})$ – радиус кривизны мембраны вблизи угла матрицы.

Интенсивность напряжений определяется следующим соотношением:

$\begin{gathered} {{\sigma }_{u}}(x_{0}^{{}}) = \frac{{\sqrt 3 }}{2}\frac{{q\rho }}{{{{H}_{0}}\,\cdot\,{{H}_{3}}(x_{0}^{{}})}},\quad \rho = 1 - {{x}_{0}} \\ {{\sigma }_{u}}(x_{0}^{{}}) = \frac{{\sqrt 3 }}{2}\frac{q}{{{{H}_{0}}}}\,\cdot\,\left[ {\left( {b + 0.5\pi - 1} \right) + \left( {2 - 0.5\pi } \right){{x}_{0}}} \right]\,\cdot\,\left( {1 - {{x}_{0}}} \right) \\ \end{gathered} $

Интенсивность скоростей деформаций ползучести равна:

${{\dot {p}}_{u}} = \frac{2}{{\sqrt 3 }}F\left( {{{x}_{0}}} \right)\frac{{d{{x}_{0}}}}{{dt}} = \frac{2}{{\sqrt 3 }}\,\cdot\,\frac{{\left( {2 - 0.5\pi } \right)}}{{\left[ {\left( {b + 0.5\pi - 1} \right) + \left( {2 - 0.5\pi } \right){{x}_{0}}} \right]}}\frac{{d{{x}_{0}}}}{{dt}}$

Подставляя ${{\sigma }_{u}}$ и ${{\dot {p}}_{u}}$ в (2.2), получаем:

$\begin{gathered} \frac{2}{{\sqrt 3 }}\,\cdot\,\frac{{\left( {2 - 0.5\pi } \right)}}{{\left[ {b + \left( {0.5\pi - 1} \right) + \left( {2 - 0.5\pi } \right){{x}_{0}}} \right]}}\,\cdot\,\frac{{d{{x}_{0}}}}{{dt}} = \\ \, = {{\left[ {\frac{{\sqrt 3 }}{2}\,\cdot\,\frac{q}{{{{H}_{0}}}}\left[ {\left( {b + 0.5\pi - 1} \right) + \left( {2 - 0.5\pi } \right){{x}_{0}}} \right]\,\cdot\,\left( {1 - {{x}_{0}}} \right)} \right]}^{n}} \\ \end{gathered} $

Отсюда

$t_{3}^{{n + 1}}\left( {{{x}_{0}}} \right) = t_{2}^{{n + 1}} + \left( {n + 1} \right){{\left( {\frac{2}{{\sqrt 3 }}} \right)}^{{\left( {n + 1} \right)}}}{{\left( {\frac{{{{H}_{0}}}}{{k{{q}_{0}}}}} \right)}^{n}}\int\limits_{1 - b}^{{{x}_{0}}} {\frac{{\left( {2 - 0.5\pi } \right)d{{x}_{0}}}}{{{{{\left[ {b + \left( {0.5\pi - 1} \right) + \left( {2 - 0.5\pi } \right){{x}_{0}}} \right]}}^{{\left( {n + 1} \right)}}}{{{\left( {1 - {{x}_{0}}} \right)}}^{n}}}}} $

Используя замену (3.14), получим:

(4.4)
${{\tau }_{3}}({{x}_{0}}) = {{\left[ {{{{(\tau _{2}^{0})}}^{n}}\, + \,(n\, + \,1){{{\left( {\frac{2}{{\sqrt 3 }}} \right)}}^{{\left( {n + 1} \right)}}}\,\cdot\,\left( {\frac{1}{{{{k}^{n}}}}} \right)\,\cdot\,\int\limits_{1 - b}^{{{x}_{0}}} {\frac{{\left( {2 - 0.5\pi } \right)d{{x}_{0}}}}{{{{{\left[ {b + (0.5\pi - 1) + (2 - 0.5\pi ){{x}_{0}}} \right]}}^{{\left( {n + 1} \right)}}}\,\cdot\,{{{(1 - {{x}_{0}})}}^{n}}}}} } \right]}^{{\frac{1}{n}}}}$

Время $\tau _{3}^{0}$ практически полного заполнения матрицы мембраной определяется выражением (4.11) при замене в верхнем пределе интегрирования x0 на $x_{0}^{0} = 1 - \Delta $:

${{\tau }_{3}}^{{\text{0}}} = \tau _{3}^{{}}(x_{0}^{0} = 1 - \Delta )$

5. Прилипание мембраны вдоль сторон матрицы. 5.1. Вторая стадия $(0 \leqslant {{x}_{0}} \leqslant 1 - b)$. В случае постепенного прилипания материала мембраны к матрице ее контактная часть (с переменной толщиной) не деформируется, а свободная часть (с постоянной толщиной) представляет собой часть дуги окружности. Окружная деформация в свободной части мембраны имеет вид (рис. 4):

$d{{p}_{{\theta \theta }}} = \frac{{\left( {\rho d\alpha + \alpha d\rho } \right) + d{{x}_{0}}}}{{\rho \alpha }}$

Аналогично (4.2) можно получить выражение

$\begin{gathered} {{B}_{3}}({{x}_{0}}) = \rho \alpha = \frac{{[{{{(1 - {{x}_{0}})}}^{2}} + {{b}^{2}}]}}{{2b}}\left( {\operatorname{arc} {\text{tg}}\left( {\frac{{2b(1 - {{x}_{0}})}}{{[{{{(1 - {{x}_{0}})}}^{2}} - {{b}^{2}}]}}} \right)} \right) \\ d{{p}_{{\theta \theta }}} = \frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}}}}{{{{B}_{3}}\left( {{{x}_{0}}} \right)}} \\ \end{gathered} $

Как известно, ${{\dot {p}}_{{rr}}} = \frac{{{{{\dot {H}}}_{2}}}}{{{{H}_{2}}}}$. Из условия несжимаемости $\,{{\dot {p}}_{{\theta \theta }}} = \, - {{\dot {p}}_{{rr}}}$, так что

$\begin{gathered} {{{\dot {p}}}_{{\theta \theta }}} = - \frac{{{{{\dot {H}}}_{2}}\left( {{{x}_{0}}} \right)}}{{{{H}_{2}}\left( {{{x}_{0}}} \right)}},\quad d{{p}_{{\theta \theta }}} = - \frac{{d{{H}_{2}}}}{{{{H}_{2}}}} = \frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}}}}{{{{B}_{3}}\left( {{{x}_{0}}} \right)}} \\ \int\limits_{H_{1}^{0}}^{{{H}_{2}}({{x}_{0}})} {\frac{{{{{\mathop {dH}\limits^{} }}_{2}}}}{{{{H}_{2}}}} = - \int\limits_0^{{{x}_{0}}} {\frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}}}}{{{{B}_{3}}\left( {{{x}_{0}}} \right)}}} } ,\quad {\kern 1pt} {{\mathop H\limits^{} }_{2}}\left( {{{x}_{0}}} \right) = H_{1}^{0}\exp \left[ { - \int\limits_0^{{{x}_{0}}} {\frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}}}}{{{{B}_{3}}\left( {{{x}_{0}}} \right)}}} } \right],\quad H_{2}^{0} = H_{2}^{{}}({{x}_{0}} = 1 - b) \\ \end{gathered} $

Интенсивности ${{\sigma }_{u}}$ и ${{\dot {p}}_{u}}$ равны соответственно:

${{\sigma }_{u}} = \frac{{\sqrt 3 }}{2}{{\sigma }_{{\theta \theta }}} = \frac{{\sqrt 3 }}{2}\frac{{q\rho }}{{{{H}_{0}}{{H}_{2}}\left( {{{x}_{0}}} \right)}},\quad {{\dot {p}}_{u}} = \frac{2}{{\sqrt 3 }}{{\dot {p}}_{{\theta \theta }}}$

Подставляя выражения ${{\sigma }_{u}}$ и ${{\dot {p}}_{u}}$ в (2.2), получаем:

$\begin{gathered} \frac{2}{{\sqrt 3 }}\frac{{{{B}_{1}}({{x}_{0}})d{{x}_{0}}}}{{{{B}_{3}}({{x}_{0}})dt}} = {{\left[ {\frac{{\sqrt 3 }}{2}\frac{{q\rho }}{{{{H}_{0}}{{H}_{2}}({{x}_{0}})}}} \right]}^{n}} \\ t_{2}^{{n + 1}} = t_{1}^{{n + 1}} + (n + 1)\int\limits_0^{{{x}_{0}}} {\frac{{\frac{2}{{\sqrt 3 }}\frac{{{{B}_{1}}({{x}_{0}})}}{{{{B}_{3}}({{x}_{0}})}}}}{{{{{\left[ {\frac{{\sqrt 3 }}{2}\frac{{k{{q}_{0}}\rho }}{{{{H}_{0}}{{H}_{2}}({{x}_{0}})}}} \right]}}^{n}}}}} d{{x}_{0}} = t_{1}^{{n + 1}} + (n + 1)\frac{1}{{{{k}^{n}}}}{{\left( {\frac{{{{H}_{0}}}}{{{{q}_{0}}}}} \right)}^{n}}\int\limits_0^{{{x}_{0}}} {\frac{{\frac{2}{{\sqrt 3 }}\frac{{{{B}_{1}}({{x}_{0}})}}{{{{B}_{3}}({{x}_{0}})}}}}{{{{{\left[ {\frac{{\sqrt 3 }}{4}\frac{{({{{(1 - {{x}_{0}})}}^{2}} + {{b}^{2}})}}{{{{H}_{2}}({{x}_{0}})b}}} \right]}}^{n}}}}} d{{x}_{0}} \\ \end{gathered} $

Используя замену (3.14), получим:

${{\tau }_{2}}\left( {{{x}_{0}}} \right) = {{\left[ {{{{(\tau _{1}^{0})}}^{n}} + \left( {n + 1} \right){{{\left( {\frac{4}{{\sqrt 3 }}} \right)}}^{{\left( {n + 1} \right)}}}\,\cdot\,\left( {\frac{1}{{2{{k}^{n}}}}} \right)\,\cdot\,\int\limits_0^{{{x}_{0}}} {\frac{{\frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)}}{{{{B}_{3}}\left( {{{x}_{0}}} \right)}}}}{{{{{\left[ {\frac{{({{{(1 - {{x}_{0}})}}^{2}} + {{b}^{2}})}}{{{{H}_{2}}\left( {{{x}_{0}}} \right)b}}} \right]}}^{n}}}}} d{{x}_{0}}} \right]}^{{\frac{1}{n}}}},\quad \tau _{2}^{0} = \tau \left( {{{x}_{0}} = 1 - b} \right)$

5.2. Третья стадия $\left( {1 - b \leqslant {{x}_{0}} \leqslant 1 - \Delta } \right)$. На третьей стадии ползучесть мембраны характеризуется касанием ею продольных и поперечной сторон матрицы (рис. 5):

$\begin{gathered} d{{p}_{{\theta \theta }}} = \frac{{\left[ {b - 1 + 2\left( {{{x}_{0}} + d{{x}_{0}}} \right) + 0.5\pi \left( {1 - ({{x}_{0}} + d{{x}_{0}})} \right)} \right] - \left[ {b - 1 + 2{{x}_{0}} + 0.5\pi (1 - {{x}_{0}})} \right]}}{{\left[ {0.5\pi (1 - {{x}_{0}})} \right]}} = \\ \, = \frac{{\left( {2 - 0.5\pi } \right)d{{x}_{0}}}}{{\left[ {0.5\pi (1 - {{x}_{0}})} \right]}} \\ d{{p}_{{\theta \theta }}} = F({{x}_{0}})d{{x}_{0}},\quad F({{x}_{0}}) = \frac{{2 - 0.5\pi }}{{0.5\pi (1 - {{x}_{0}})}} = \frac{{4 - \pi }}{{\pi (1 - {{x}_{0}})}} \\ {{p}_{{\theta \theta }}} = - \int\limits_{H_{2}^{{\text{o}}}}^{{{H}_{3}}\left( {{{x}_{0}}} \right)} {\frac{{d{{H}_{3}}}}{{{{H}_{3}}}} = \int\limits_{1 - b}^{{{x}_{0}}} {F({{x}_{0}})d{{x}_{0}}} } = \ln \frac{{H_{2}^{{\text{0}}}}}{{{{H}_{3}}\left( {{{x}_{0}}} \right)}} = \frac{{4 - \pi }}{\pi }\ln \left[ {\frac{b}{{(1 - {{x}_{0}})}}} \right]\;\, \\ \frac{{H_{2}^{{\text{o}}}}}{{{{H}_{3}}\left( {{{x}_{0}}} \right)}} = {{\left( {\frac{b}{{(1 - {{x}_{0}})}}} \right)}^{{\frac{{\left( {4 - \pi } \right)}}{\pi }}}},\,\,\,\,\,\,{{H}_{3}}\left( {{{x}_{0}}} \right) = H_{2}^{{\text{o}}}{{\left( {\frac{b}{{(1 - {{x}_{0}})}}} \right)}^{{ - \frac{{\left( {4 - \pi } \right)}}{\pi }}}} \\ \end{gathered} $

Окончание третьей стадии происходит при значении $x_{{\text{0}}}^{{\text{0}}}$, удовлетворяющем неравенству $(1 - x_{0}^{0}) = \Delta \ll 1$.

Интенсивность напряжений определяется следующим соотношением:

(5.1)
${{\sigma }_{u}}\left( {{{x}_{0}}} \right) = \frac{{\sqrt 3 }}{2}\frac{{q\rho }}{{{{H}_{3}}\left( {{{x}_{0}}} \right){{H}_{0}}}},\quad \rho = 1 - {{x}_{0}},\quad {{\sigma }_{u}}\left( {x_{0}^{{}}} \right) = \frac{{\sqrt 3 }}{2}\frac{q}{{{{H}_{0}}}}\cdot\frac{{\left( {1 - {{x}_{0}}} \right)}}{{{{H}_{3}}\left( {{{x}_{0}}} \right)}}$

Интенсивность скоростей деформаций ползучести равна:

(5.2)
${{\dot {p}}_{u}} = \frac{2}{{\sqrt 3 }}\frac{{\left( {4 - \pi } \right)}}{\pi }\,\cdot\,\frac{1}{{\left( {1 - {{x}_{0}}} \right)}}\frac{{d{{x}_{0}}}}{{dt}}$

Подставляя (5.1) и (5.2) в (2.2), получаем:

$\begin{gathered} t_{3}^{{n + 1}}\left( {{{x}_{0}}} \right) = t_{2}^{{n + 1}} + \frac{2}{{\sqrt 3 }}\left( {n + 1} \right)\int\limits_{1 - b}^{{{x}_{0}}} {{{{\left[ {\frac{{2{{H}_{3}}{{H}_{0}}}}{{\sqrt 3 {{q}_{0}}k(1 - {{x}_{0}})}}} \right]}}^{n}}\frac{{\left( {4 - \pi } \right)d{{x}_{0}}}}{{\pi \left( {1 - {{x}_{0}}} \right)}}} = \\ \, = t_{2}^{{n + 1}} + {{\left( {\frac{2}{{\sqrt 3 }}} \right)}^{{\left( {n + 1} \right)}}}\left( {n + 1} \right)\,\cdot\,{{\left( {\frac{{{{H}_{0}}}}{{{{q}_{0}}k}}} \right)}^{n}}\,\cdot\,\int\limits_{1 - b}^{{{x}_{0}}} {\left( {\frac{{4 - \pi }}{\pi }} \right)\,\cdot\,\frac{{{{{\left( {{{H}_{3}}\left( {{{x}_{0}}} \right)} \right)}}^{n}}}}{{{{{\left( {1 - {{x}_{0}}} \right)}}^{{\left( {n + 1} \right)}}}}}} d{{x}_{0}} \\ \end{gathered} $

Используя замену (3.14), получим:

${{\tau }_{3}}\left( {{{x}_{0}}} \right) = {{\left[ {{{{(\tau _{2}^{0})}}^{n}} + {{{\left( {\frac{2}{{\sqrt 3 }}} \right)}}^{{\left( {n + 1} \right)}}}\left( {n + 1} \right)\,\cdot\,\left( {\frac{1}{{{{k}^{n}}}}} \right)\int\limits_{1 - b}^{{{x}_{0}}} {\left( {\frac{{4 - \pi }}{\pi }} \right)\,\cdot\,\frac{{{{{\left( {{{H}_{3}}\left( {{{x}_{0}}} \right)} \right)}}^{n}}}}{{{{{\left( {1 - {{x}_{0}}} \right)}}^{{\left( {n + 1} \right)}}}}}} d{{x}_{0}}} \right]}^{{\frac{1}{n}}}}$

Время практически полного прилегания мембраны к матрице определяется выражением:

$\tau _{{\text{3}}}^{{\text{0}}} = {{\tau }_{3}}({{x}_{0}} = x_{0}^{{\text{0}}})$

6. Анализ результатов. В качестве примера рассмотрим ползучесть мембраны внутри матрицы высотой $b = 0.5$ со следующими выбранными параметрами:

$n = 3,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \;k = 0.5,\;\;1.0,\;\;1.5,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta = 0.01,\;\;0.001,\;\;0.0001$

Величина $\Delta = 1 - x_{0}^{0}$ соответствует минимальному расстоянию между поперечной стороной матрицы и мембраной.

Значения времен $\tau _{1}^{0}$, $\tau _{2}^{0}$ и $\tau _{3}^{0}$ в конце каждой стадии приведены в таблицах 1 и 2 для идеального скольжения и прилипания соответственно. На рис. 6 приведены зависимости $\alpha \left( {{{\tau }_{1}}} \right)$ в случае свободного деформирования, на рис. 7 – зависимости $x_{0}^{{}}(\tau )$ в случае идеального скольжения (сплошная кривая) и зависимости $x_{0}^{{}}(\tau )$ в случае прилипания (пунктирная кривая) при $\Delta = 0.01$.

Таблица 1.

Значения времен $\tau _{1}^{0}$, $\tau _{2}^{0}$ и $\tau _{3}^{0}$ в конце каждой стадии в случае идеального скольжения

$k$ $\tau _{1}^{0}$ $\tau _{2}^{0}$ $\begin{gathered} \Delta = 0.01 \\ \tau _{3}^{0} \\ \end{gathered} $ $\begin{gathered} \Delta = 0.001 \\ \tau _{3}^{0} \\ \end{gathered} $ $\begin{gathered} \Delta = 0.0001 \\ \tau _{3}^{0} \\ \end{gathered} $
0.5 1.14 2.23 29.1 134.2 622
1.0 0.568 1.12 14.6 67.1 311
1.5 0.379 0.745 9.70 44.7 207
Таблица 2.

Значения времен $\tau _{1}^{0}$, $\tau _{2}^{0}$ и $\tau _{3}^{0}$ в конце каждой стадии в случае прилипания

$k$ $\tau _{1}^{0}$ $\tau _{2}^{0}$ $\begin{gathered} \Delta = 0.01 \\ \tau _{3}^{0} \\ \end{gathered} $ $\begin{gathered} \Delta = 0.001 \\ \tau _{3}^{0} \\ \end{gathered} $ $\begin{gathered} \Delta = 0.0001 \\ \tau _{3}^{0} \\ \end{gathered} $
0.5 1.14 2.45 49.7 264.8 1411.0
1.0 0.568 1.22 24.8 132.4 705.7
1.5 0.379 0.816 16.6 88.2 470.5
Рис. 6.

Зависимости $\alpha ({{\tau }_{1}})$ на первой стадии деформирования.

Рис. 7.

Зависимости ${{x}_{0}}(\tau )$ в случае идеального скольжения (сплошная) и прилипания (пунктирная линия).

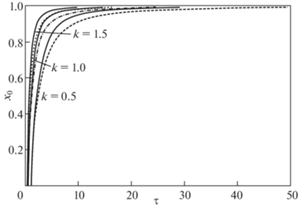
Вычисления показывают, что при заданных значениях используемых параметров длительность деформирования мембраны вплоть до практически полного прилегания мембраны к матрице при идеальном скольжении меньше, чем при прилипании. При степенях близости мембраны к матрице $\Delta = 0.01,\;\;\Delta = 0.001,\;\;\Delta = 0.0001$ отношения этих времен при различных значениях k и $\Delta $ составляют значения от 0.43 до 0.59.

7. Заключение. Приведено исследование ползучести длинной прямоугольной мембраны в стесненных условиях (внутри жесткой матрицы) под действием переменного поперечного давления, величина которого пропорциональна длительности его действия. В данной работе принимается, что высота матрицы не больше половины ее ширины. Рассматриваются два варианта условий на контакте мембраны и матрицы: идеальное скольжение и прилипание. В работе рассматриваются три последовательные стадии деформирования мембраны: ползучесть в свободных условиях, ползучесть мембраны при контакте с поперечной стороной матрицы и ползучесть мембраны при контакте со всеми сторонами матрицы. Анализ проводится до времени практически полного прилегания мембраны к матрице. Показано, что это время при условии идеального скольжения меньше, чем при условии прилипания при рассмотренных значениях $n$, $k$ и $\Delta $.

Работа выполнена при частичной финансовой поддержке Российского научного фонда (проект № 19-19-00062).

Список литературы

  1. Odqvist F.K.G. Mathematical theory of creep and creep rupture. Second edition. Oxford at the Cla-rendon Press, 1974. 200 p.

  2. Качанов Л.М. Основы механики разрушения. М.: Наука, 1974. 312 с.

  3. Storakers B. Finite creep of a circular membrane under hydrostatic pressure // Acta Polytech. Scand. Mech. Eng. Ser. 1969. № 44. 107 pp.

  4. Apratim Majumder, Chayanjit Ghosh, Mohit U. Karkhanis, Aishwaryadev Banerjee, Rugved Likhite, Carlos H. Mastrangelo, and Tridib Ghosh. Creep deformation in elastomeric membranes of liquid-filled tunable-focus lenses // Appl. Optics. 2019. V. 58. № 23. P. 6446–6454. https://doi.org/10.1364/AO.58.006446

  5. Wineman A. Nonlinear viscoelastic membranes // Comput. Math. Appl. 2007. V. 53. № 2. P 168–181. https://doi.org/10.1016/j.camwa.2006.02.017

  6. Ларин С.Н., Бессмертный А.В. Изотермическое свободное деформирование узкой прямоугольной мембраны из анизотропного листового материала при кратковременной ползучести // Известия ТулГУ. Сер. Технические науки. 2010. № 1. С. 44–51.

  7. Яковлев С.С., Ларин С.Н. Деформирование анизотропной прямоугольной мембраны в условиях ползучести // Известия ТулГУ. Сер. Технические науки. 2010. № 3. С. 37–46.

  8. Яковлев С.П., Чудин В.Н., Яковлев С.С., Соболев Я.А. Изотермическое деформирование высокопрочных анизотропных металлов. М.: Машиностроение, Изд-во ТулГУ, 2004. 427 с.

  9. Ефимов А.Б., Романюк С.Н., Чумаченко Е.Н. Об определении закономерностей трения в процессах обработки металлов давлением // Изв. РАН. МТТ. 1995. № 6. С. 82–98.

  10. Малинин Н.Н. Ползучесть в обработке металлов. М.: Машиностроение, 1986. 216 с.

  11. Локощенко А.М. Ползучесть и длительная прочность металлов М.: Физматлит, 2016. 504 с. (Lokoshchenko A.M. Creep and long-term strength of metals. Boca. Raton. London. NewYork: CRC Press. Taylor & Francis Group, 2018.)

  12. Локощенко А.М., Терауд В.В. Ползучесть длинной узкой мембраны в стесненных условиях вплоть до разрушения // ПМТФ. 2013. Т. 54. № 3. С. 126–133.

  13. Демин В.А., Локощенко А.М., Жеребцов А.А. Ползучесть длинной прямоугольной мембраны внутри криволинейной матрицы // Изв. вузов. Машиностроение. 1998. № 4–6. С. 41–46.

  14. Шестериков С.А., Юмашева М.А. Конкретизация уравнения состояния в теории ползучести // Известия АН СССР. МТТ. 1984. № 1. С. 86–91.

  15. Локощенко А.М., Абросимова Е.А. Установившаяся ползучесть длинной мембраны внутри жесткой матрицы при кусочно-постоянной зависимости скорости поперечного давления от времени // ПМТФ. 2019. № 1. С. 103–113. https://doi.org/10.15372/PMTF20190112

  16. Терауд В.В., Локощенко А.М., Шеварова Е.А. Ползучесть мембраны внутри П-образной матрицы при переменном поперечном давлении // Сборник трудов в 4 томах. XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики. Т. 3: Механика деформируемого твердого тела. – Уфа: РИЦ БашГУ. 2019. С. 382–384. https://doi.org/10.22226/2410-3535-2019-congress-v3

  17. Nhung Nguyen, Wineman A., Waas A. Contact problem of a non-linear viscoelastic spherical membrane enclosing incompressible fluid between two rigid parallel plates // Int. J. Non-Lin. Mech. 2013. V. 50. P. 97–108. https://doi.org/10.1016/j.ijnonlinmec.2012.11.009

  18. Васин Р.А., Еникеев Ф.У., Круглов А.А., Сафиуллин Р.В. Об идентификации определяющих соотношений по результатам технологических экспериментов // Изв. РАН. МТТ. 2003. № 2. С. 111–123.

  19. Сафиуллин Р.В., Еникеев Ф.У. Расчет режимов сверхпластической формовки протяженной прямоугольной мембраны // Кузнечно-штамповочное производство. Обработка материалов давлением. 2001. № 3. С. 35–40.

  20. Srivastava A., Hui C.-Y. Nonlinear viscoelastic contact mechanics of long rectangular membranes // Proc. Royal Soc. A: Math. Phys. Eng. Sci. 2014. A V. 470. P. 20140528. https://doi.org/10.1098/rspa.2014.0528

  21. Long R., Shull K., Hui C.-Y. Large deformation adhesive contact mechanics of circular membranes with a flat rigid substrate // J. Mech. Phys. Solids. 2010. V. 58. № 9. P. 1225–1242. https://doi.org/10.1016/j.jmps.2010.06.007

  22. Srivastava A., Hui C.-Y. Large deformation contact mechanics of long rectangular membranes. I. Adhesionless contact // Proc. Roy. Soc. A: Math. Phys. Eng. Sci. 2013. A 469: P. 20130424. https://doi.org/10.1098/rspa.2013.0424

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал