Известия РАН. Механика твердого тела, 2022, № 3, стр. 56-69
МОДЕЛЬ БЛОЧНЫХ СРЕД С УЧЕТОМ ВНУТРЕННЕГО ТРЕНИЯ
a Институт горного дела им. Н.А. Чинакала СО РАН
Новосибирск, Россия
* E-mail: nialex@misd.ru
Поступила в редакцию 08.06.2021
После доработки 07.08.2021
Принята к публикации 26.08.2021
- EDN: YNFEVA
- DOI: 10.31857/S0572329922020039
Аннотация
Блочная среда моделируется дискретно-периодической пространственной решеткой масс, соединенных упругими пружинами и вязкими демпферами. Для описания вязкоупругого поведения межблочных прослоек предложена реологическая модель внутреннего трения с двумя элементами Максвелла и одним элементом Фойгта с коэффициентом добротности материала, как определяющим параметром. Численные эксперименты показывают, что в рамках этой модели прослоек удается подбирать вязкость и жесткость элементов Максвелла и Фойгта так, что коэффициент добротности материала отличается от заданного постоянного значения не больше, чем на 5%. В одномерном случае в рамках предложенной модели исследовано влияние коэффициента добротности на дисперсионные свойства блочной среды и показано, что наибольшее влияние коэффициента добротности на дисперсию наблюдается в низкочастотной части спектра. В трехмерном случае в рамках предложенной модели численно исследуются некоторые геомеханические задачи для блочного полупространства, находящегося под действием поверхностной сосредоточенной вертикальной нагрузки. А именно, исследовано затухание амплитуд скоростей поверхностных блоков в зависимости от коэффициента добротности при ступенчатом воздействии и при воздействии импульса Гаусса. Кроме того, мы изучаем слой на поверхности полупространства под действием сосредоточенной вертикальной импульсной нагрузки в том случае, когда и слой, и полупространство являются блочными средами, но имеют разные свойства.
1. Введение. По современным представлениям, развитым в трудах М.А. Садовского [1] и его последователей, горные породы представляют собой иерархическую систему блоков разного масштабного уровня. Блоки одного уровня разделены между собой прослойками пород с ослабленными механическими свойствами. В [2, 3] отмечено, что размеры блоков изменяются в масштабах от фракций породного массива до гео-блоков земной коры. В экспериментальной работе [4] было показано на двумерной модели блочной среды – кирпичной стене, что для реальной геосреды можно определить размеры характерных блоков породного массива по данным сейсмического каротажа, используя обнаруженное в [5] соотношение, связывающее значение скорости распространения низкочастотной волны, частоты, ограничивающей ее спектр, и продольного размера блоков. Как показано в [2, 3, 6], движение блочной среды может быть представлено, как движение жестких блоков за счет деформации прослоек. В результате динамику блочной среды можно изучать в маятниковом приближении, когда считается, что блоки несжимаемы, а все деформации и смещения происходят за счет сжимаемости прослоек (см., например, [7–9]). В [8, 9] блочная среда моделируется как трехмерная решетка масс, соединенных элементами Фойгта в осевых и диагональных направлениях. В [9] показано качественное соответствие конечно-разностного решения по этой модели задачи Лэмба для блочной среды с результатами полевых экспериментов, проведенных на известняковом карьере. Альтернативный подход основан на математической модели блочной среды с упругими блоками, взаимодействующими через податливые прослойки [5, 10, 11]. Для описания прослоек в [10, 11] предложены различные варианты модели, в которой прослойки между упругими блоками могут быть упругими, вязкоупругими, пластическими, пористыми.
В настоящей работе модифицируется 3D модель, предложенная в [8]. В новой модели внутреннее трение в прослойках между блоками моделируется элементами Максвелла и Фойгта. Зенер [12] и Био [13] были одними из первых, кто включили элементы Максвелла и Фойгта в модели для описания неупругого поведения материалов. Модель с двумя элементами Максвелла и одним элементом Фойгта впервые была предложена Био [13], кроме того она была представлена в работе Фанг [14]. Многие исследователи затем использовали различные комбинации элементов Максвелла и Фойгта для учета неупругих потерь. При этом важной задачей в течение нескольких десятилетий в каждой модели было ограничение количества механизмов релаксации для получения удовлетворительного решения, т.е. для получения почти постоянного коэффициента добротности материала Q. В [15] исследована модель с внутренним трением для описания распространения волн в однородных неупругих средах. Эта модель включает два элемента Максвелла и один элемент Фойгта. Как показано в [15], эта модель дает возможность выбирать параметры вязкости и жесткости этих элементов, так что коэффициент добротности материала Q отличается от предписанного постоянного значения ${{Q}_{0}}$ не больше, чем на 5% на интервале частот от 3% до 100% от максимальной частоты, представляющей интерес. Важным свойством данной модели является небольшое число дополнительных переменных при максимальном охвате интересующего диапазона частот. Использование минимального количества элементов Максвелла ограничивает память и вычислительные ресурсы, необходимые в компьютерных программах для численного моделирования трехмерных задач.
Ниже для описания вязкоупругого поведения межблочных прослоек используется модель внутреннего трения с двумя элементами Максвелла и одним элементом Фойгта с коэффициентом добротности Q, как определяющим параметром. Эта модель применяется для решения геомеханических задач распространения волн.
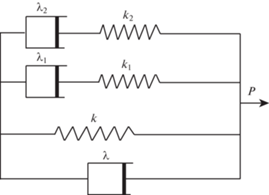
2. Одномерная модель блочной среды с учетом внутреннего трения. Продемонстрируем эту модель сначала на примере дискретно-периодической одномерной цепочки масс, соединенных вязкоупругими прослойками. Реологическая модель прослоек состоит из двух элементов Максвелла и одного элемента Фойгта (рис. 1). Все три элемента соединены параллельно. Каждый элемент Максвелла состоит из пружины и демпфера, которые соединены последовательно. Элемент Фойгта состоит также из пружины и демпфера, но соединены они параллельно. Здесь k, k1, k2 – жесткости пружин в элементе Фойгта и в двух элементах Максвелла, соответственно, $\lambda $, ${{\lambda }_{1}}$, ${{\lambda }_{2}}$ – вязкости демпферов в элементе Фойгта и в двух элементах Максвелла.
Уравнения одномерного движения блоков с данной реологической моделью прослоек имеют следующий вид:
(2.1)
$\begin{gathered} M{{{\ddot {u}}}_{j}} = K{\kern 1pt} \text{[}({{u}_{{j + 1}}} - 2{{u}_{j}} + {{u}_{{j - 1}}}) + \beta ({{{\dot {u}}}_{{j + 1}}} - 2{{{\dot {u}}}_{j}} + {{{\dot {u}}}_{{j - 1}}}) - \\ \, - {{\alpha }_{1}}{{\gamma }_{1}}({{\psi }_{{j + 1}}} - 2{{\psi }_{j}} + {{\psi }_{{j - 1}}}) - {{\alpha }_{2}}{{\gamma }_{2}}({{\varphi }_{{j + 1}}} - 2{{\varphi }_{j}} + {{\varphi }_{{j - 1}}})],\quad j = 1,2,... \\ \end{gathered} $Здесь uj – перемещения жестких блоков, $P(t)$ – действующая нагрузка, приложенная к блоку $j = 0$; K – суммарная жесткость пружин. В (2.1) введены две дополнительные переменные ${{\varphi }_{j}}$ и ${{\psi }_{j}}$, которые зависят от функции смещения uj.
Применим преобразование Фурье по времени к уравнениям движения (2.1). В частотной области ω сила, действующая на блок со стороны прослойки, может быть выражена формулой:
гдеВнутреннее затухание в среде обычно определяется коэффициентом добротности Q(ω) или его обратной величиной Q−1(ω), которая описывается формулой:
(2.2)
${{Q}^{{ - 1}}}(\omega ) = \frac{{\operatorname{Im} \tilde {F}(\omega )}}{{\operatorname{Re} \tilde {F}(\omega )}} = \frac{{\omega [\beta + {{{{\alpha }_{1}}{{\gamma }_{1}}} \mathord{\left/ {\vphantom {{{{\alpha }_{1}}{{\gamma }_{1}}} {({{\omega }^{2}} + {{\gamma }_{1}}^{2})}}} \right. \kern-0em} {({{\omega }^{2}} + {{\gamma }_{1}}^{2})}} + {{{{\alpha }_{2}}{{\gamma }_{2}}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}{{\gamma }_{2}}} {({{\omega }^{2}} + {{\gamma }_{2}}^{2})}}} \right. \kern-0em} {({{\omega }^{2}} + {{\gamma }_{2}}^{2})}}]}}{{1 - {{{{\alpha }_{1}}{{\gamma }_{1}}^{2}} \mathord{\left/ {\vphantom {{{{\alpha }_{1}}{{\gamma }_{1}}^{2}} {({{\omega }^{2}} + {{\gamma }_{1}}^{2})}}} \right. \kern-0em} {({{\omega }^{2}} + {{\gamma }_{1}}^{2})}} - {{{{\alpha }_{2}}{{\gamma }_{2}}^{2}} \mathord{\left/ {\vphantom {{{{\alpha }_{2}}{{\gamma }_{2}}^{2}} {({{\omega }^{2}} + {{\gamma }_{2}}^{2})}}} \right. \kern-0em} {({{\omega }^{2}} + {{\gamma }_{2}}^{2})}}}}$Для почв и породных материалов принято предполагать, что целевой коэффициент добротности материала остается постоянным в широком диапазоне интересующих частот, т.е. ${{Q}_{0}}(\omega ) = {{Q}_{0}}$, см. [17].
Чтобы связать параметры ${{\alpha }_{1}}$, ${{\alpha }_{2}}$, ${{\gamma }_{1}}$, ${{\gamma }_{2}}$ и $\beta $ реологической модели с Q−1(ω) с помощью простых, не зависящих от частоты приближений, введем новые безразмерные параметры ${{\hat {\alpha }}_{1}}$, ${{\hat {\alpha }}_{2}}$, ${{\hat {\gamma }}_{1}}$, ${{\hat {\gamma }}_{2}}$, $\hat {\beta }$ и частоту $\hat {\omega }$ по формулам:
(2.3)
$\begin{gathered} {{{\hat {\alpha }}}_{1}} = {{\alpha }_{1}}{{Q}_{0}},\quad {{{\hat {\alpha }}}_{2}} = {{\alpha }_{2}}{{Q}_{0}},\quad {{{\hat {\gamma }}}_{1}} = {{\gamma }_{1}}{\text{/}}{{\omega }_{{\max }}} \\ {{{\hat {\gamma }}}_{2}} = {{\gamma }_{2}}{\text{/}}{{\omega }_{{\max }}},\quad \hat {\beta } = \beta {{\omega }_{{\max }}}{{Q}_{0}},\quad \hat {\omega } = \omega {\text{/}}{{\omega }_{{\max }}} \\ \end{gathered} $В выражении (2.2) коэффициента ${{Q}^{{ - 1}}}(\omega )$ перейдем к нормированным параметрам (2.3). Тогда формула (2.2) примет вид:
Из этой формулы можно увидеть, что коэффициенты ${{\hat {\alpha }}_{1}}$, ${{\hat {\alpha }}_{2}}$, ${{\hat {\gamma }}_{1}}$, ${{\hat {\gamma }}_{2}}$, $\hat {\beta }$ не зависят от ${{\omega }_{{\max }}}$. Отсюда следует, что для заданной постоянной $Q_{0}^{{ - 1}}$, они должны вычисляться только один раз. При больших значениях целевого коэффициента добротности, то есть $Q_{0}^{{ - 1}} \to 0$, параметры становятся существенно не зависимыми от Q0.
Задача определения параметров ${{\hat {\alpha }}_{1}}$, ${{\hat {\alpha }}_{2}}$, ${{\hat {\gamma }}_{1}}$, ${{\hat {\gamma }}_{2}}$, $\hat {\beta }$ решается с допуском, так чтобы фактический коэффициент добротности оставался бы достаточно близким к целевому значению. Этот допуск, который принимается как 5% от целевого значения, выполняется в пределах от 4% до 100% от ωmax. Т.е. для заданного коэффициента добротности ${{Q}_{0}}$ параметры ${{\hat {\alpha }}_{1}}$, ${{\hat {\alpha }}_{2}}$, ${{\hat {\gamma }}_{1}}$, ${{\hat {\gamma }}_{2}}$, $\hat {\beta }$ подбираются прямой проверкой на компьютере так, чтобы условие
выполнялось для каждого $\hat {\omega }$, удовлетворяющего неравенству $0.04 \leqslant \hat {\omega } \leqslant 1$. Найденные значения параметров, соответствующие пяти значениям целевого коэффициента добротности $Q_{0}^{{ - 1}}$, представлены в табл. 1.Таблица 1.
Значения параметров, соответствующие разным значениям $Q_{0}^{{ - 1}}$
| $Q_{0}^{{ - 1}}$ | ${{\hat {\alpha }}_{1}}$ | ${{\hat {\alpha }}_{2}}$ | ${{\hat {\gamma }}_{1}}$ | ${{\hat {\gamma }}_{2}}$ | $\hat {\beta }$ |
|---|---|---|---|---|---|
| 0.2 | 0.28 | 0.28 | 0.026 | 0.23 | 0.14 |
| 0.1 | 0.14 | 0.14 | 0.03 | 0.23 | 0.07 |
| 0.05 | 0.072 | 0.072 | 0.027 | 0.22 | 0.035 |
| 0.02 | 0.029 | 0.029 | 0.026 | 0.22 | 0.014 |
| 0.01 | 0.014 | 0.014 | 0.031 | 0.222 | 0.0071 |
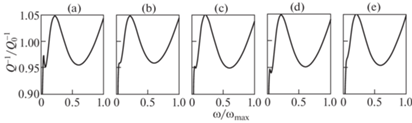
Для этих значений параметров фактические коэффициенты добротности материала, нормированные относительно $Q_{0}^{{ - 1}}$, показаны как функции частоты на рис. 2. Как видно на рис. 2, удается подобрать параметры ${{\hat {\alpha }}_{1}}$, ${{\hat {\alpha }}_{2}}$, ${{\hat {\gamma }}_{1}}$, ${{\hat {\gamma }}_{2}}$, $\hat {\beta }$ так, что допуск, который принимается как 5% от целевого значения, выполняется в пределах от 4% до 100% от ${{\omega }_{{\max }}}$.
Рис. 2.
Зависимости коэффициента добротности материала от частоты: (a) $Q_{0}^{{ - 1}} = 0.2$; (b) $Q_{0}^{{ - 1}} = 0.1$; (c) $Q_{0}^{{ - 1}} = 0.05$; (d) $Q_{0}^{{ - 1}} = 0.02$; (e) $Q_{0}^{{ - 1}} = 0.01$.
Другим важным аспектом внутренних моделей трения является дисперсия, наблюдаемая во временном отклике системы. Для дискретного уравнения (2.1) дисперсионная зависимость волнового числа q от частоты ω имеет вид:
(2.4)
${{\sin }^{2}}\left( {\frac{{ql}}{2}} \right) = \frac{{M{{\omega }^{2}}}}{{4\tilde {F}(\omega )}}$Здесь l – длина пружин, q – волновое число. Пользуясь формулой (2.4) и соотношением ${{c}_{{{\text{ph}}}}}(\omega ) = {\omega \mathord{\left/ {\vphantom {\omega q}} \right. \kern-0em} q}$, где ${{c}_{{{\text{ph}}}}}$ – фазовая скорость, можем определить зависимость фазовой скорости от частоты для одномерной модели блочной среды (2.1). Если положить $\omega \to 0$, то из (2.4) получим: ${{c}_{{{\text{ph}}}}}(0) = l\sqrt {{{K{\kern 1pt} \left( {1 - {{\alpha }_{1}} - {{\alpha }_{2}}} \right)} \mathord{\left/ {\vphantom {{K{\kern 1pt} \left( {1 - {{\alpha }_{1}} - {{\alpha }_{2}}} \right)} M}} \right. \kern-0em} M}} $. Как следует из этой формулы и таблицы 1, фазовая скорость бесконечно длинных волн падает с ростом $Q_{0}^{{ - 1}}$.
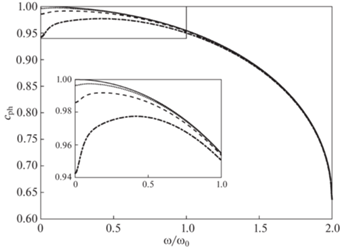
На рис. 3 представлены зависимости ${{c}_{{{\text{ph}}}}}(\omega )$ при различных значениях коэффициента добротности материала $Q_{0}^{{ - 1}}$. Здесь и далее полагаем: $l = 1$, $M = 1$, $K = 1$. В прямоугольнике представлены эти же кривые в увеличенном масштабе в низкочастотной зоне. Заметим, что в дискретном случае имеем: ${{\omega }_{{\max }}} = 2{{\omega }_{0}}$, где ${{\omega }_{0}} = \sqrt {{K \mathord{\left/ {\vphantom {K M}} \right. \kern-0em} M}} $. Видно, что наибольшее влияние коэффициента добротности на дисперсию наблюдается в низкочастотной части спектра. Кроме того, видно, что с ростом $Q_{0}^{{ - 1}}$ максимальная скорость распространения возмущений падает. В высокочастотной части спектра фазовая скорость практически не зависит от коэффициента добротности.
Рис. 3.
Зависимость фазовой скорости от частоты для одномерной модели блочной среды. Сплошные кривые – $Q_{0}^{{ - 1}} = 0$, пунктирные кривые – $Q_{0}^{{ - 1}} = 0.05$, штриховые кривые – $Q_{0}^{{ - 1}} = 0.1$, штрих-пунктирные кривые – $Q_{0}^{{ - 1}} = 0.2$.
На рис. 4 представлены результаты численных расчетов нестационарного волнового процесса в цепочке масс при действии нагрузки $P(t) = H(t)$, где $H(t)$ – ступенчатая функция Хевисайда. Расчеты проведены по одномерной модели с внутренним трением (2.1) для блока с номером $j = 10$. Сплошные кривые соответствуют $Q_{0}^{{ - 1}} = 0$, штрих-пунктирные кривые – $Q_{0}^{{ - 1}} = 0.2$. На рис. 4, a показаны деформации прослойки $\Delta {{u}_{j}} = {{u}_{{j + 1}}}$ – uj, на рис. 4, b – скорости ${{\dot {u}}_{j}}$ и на рис. 4, c – ускорения ${{\ddot {u}}_{j}}$ в зависимости от времени.
Рис. 4.
Зависимости от времени деформации прослойки (a), скорости (b) и ускорения (c) 10-го блока. Сплошные кривые – $Q_{0}^{{ - 1}} = 0$, штрих-пунктирные кривые – $Q_{0}^{{ - 1}} = 0.2$.
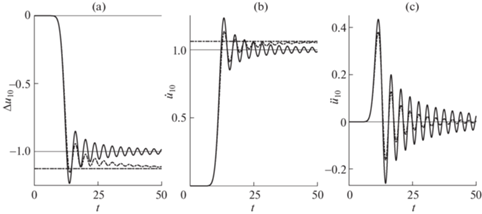
Горизонтальные линии соответствуют статическим значениям: на рис. 4, a – $\Delta {{u}_{{{\text{st}}}}} = - {1 \mathord{\left/ {\vphantom {1 {\left( {1 - {{\alpha }_{1}} - {{\alpha }_{2}}} \right)}}} \right. \kern-0em} {\left( {1 - {{\alpha }_{1}} - {{\alpha }_{2}}} \right)}}$, на рис. 4, b – ${{\dot {u}}_{{{\text{st}}}}} = {1 \mathord{\left/ {\vphantom {1 {\sqrt {1 - {{\alpha }_{1}} - {{\alpha }_{2}}} }}} \right. \kern-0em} {\sqrt {1 - {{\alpha }_{1}} - {{\alpha }_{2}}} }}$. К этим значениям стремятся амплитуды деформации прослоек и скоростей блоков при больших значениях времени. Видно, что с ростом $Q_{0}^{{ - 1}}$ увеличивается затухание максимальных амплитуд деформаций прослоек, скоростей и ускорений блоков на фронте низкочастотной волны и падает амплитуда высокочастотных осцилляций $\Delta {{u}_{j}}$ и ${{\dot {u}}_{j}}$ относительно их статических значений за фронтом волны.
3. Трехмерная модель блочной среды с учетом внутреннего трения. Блочная среда моделируется однородной трехмерной решеткой, состоящей из точечных масс, соединенных пружинами и демпферами в направлениях осей x, y, z и в диагональных направлениях плоскостей xy, xz, yz, как показано на рис. 5, a. Здесь использованы обозначения: u, ${v}$ – горизонтальные перемещения в направлениях x, y; w – вертикальные перемещения в направлении z; n, m, k – номера блоков в направлениях x, y, z. На поверхности блочного полупространства в начале координат приложена вертикальная сосредоточенная нагрузка P (рис. 5, b).
Рис. 5.
Схема соединения масс пружинами и демпферами (a) внутри полупространства и (b) на поверхности полупространства.
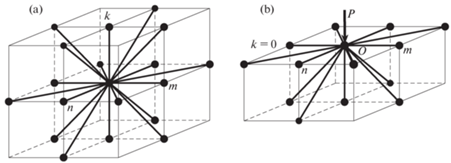
В качестве реологической модели прослоек используется модель прослоек с двумя элементами Максвелла и одним элементом Фойгта, которая только что была продемонстрирована на примере одномерной блочной среды. Далее будем полагать, что жесткости пружин и вязкости демпферов в осевых и диагональных направлениях совпадают. Кроме того, будем полагать, что параметры M, k, ${{k}_{1}}$, ${{k}_{2}}$, $\lambda $, ${{\lambda }_{1}}$, ${{\lambda }_{2}}$ имеют одни и те же значения во всех точках блочной среды.
С учетом внутреннего трения и обозначений
(3.1)
$\begin{gathered} M{{{\ddot {u}}}_{{n,m,k}}} = K\{ ({{\Lambda }_{{nn}}} + {{\Phi }_{{nk}}} + {{\Phi }_{{nm}}}){{u}_{{n,m,k}}} + {{\Psi }_{{nm}}}{{v}_{{n,m,k}}} + {{\Psi }_{{nk}}}{{w}_{{n,m,k}}} + \\ \, + \beta [({{\Lambda }_{{nn}}} + {{\Phi }_{{nk}}} + {{\Phi }_{{nm}}}){{{\dot {u}}}_{{n,m,k}}} + {{\Psi }_{{nm}}}{{{{\dot {v}}}}_{{n,m,k}}} + {{\Psi }_{{nk}}}{{{\dot {w}}}_{{n,m,k}}}] - \\ \, - {{\alpha }_{1}}{{\gamma }_{1}}[({{\Lambda }_{{nn}}} + {{\Phi }_{{nk}}} + {{\Phi }_{{nm}}})\psi _{{n,m,k}}^{u} + {{\Psi }_{{nm}}}\psi _{{n,m,k}}^{{v}} + {{\Psi }_{{nk}}}\psi _{{n,m,k}}^{w}] - \\ \, - {{\alpha }_{2}}{{\gamma }_{2}}[({{\Lambda }_{{nn}}} + {{\Phi }_{{nk}}} + {{\Phi }_{{nm}}})\varphi _{{n,m,k}}^{u} + {{\Psi }_{{nm}}}\varphi _{{n,m,k}}^{{v}} + {{\Psi }_{{nk}}}\varphi _{{n,m,k}}^{w}]\} \\ \end{gathered} $(3.2)
$\begin{gathered} M{{{\ddot {v}}}_{{n,m,k}}} = K\{ {{\Psi }_{{nm}}}{{u}_{{n,m,k}}} + ({{\Lambda }_{{mm}}} + {{\Phi }_{{mk}}} + {{\Phi }_{{nm}}}){{v}_{{n,m,k}}} + {{\Psi }_{{mk}}}{{w}_{{n,m,k}}} + \\ \, + \beta [{{\Psi }_{{nm}}}{{{\dot {u}}}_{{n,m,k}}} + ({{\Lambda }_{{mm}}} + {{\Phi }_{{mk}}} + {{\Phi }_{{nm}}}){{{{\dot {v}}}}_{{n,m,k}}} + {{\Psi }_{{mk}}}{{{\dot {w}}}_{{n,m,k}}}] - \\ \, - {{\alpha }_{1}}{{\gamma }_{1}}[{{\Psi }_{{nm}}}\psi _{{n,m,k}}^{u} + ({{\Lambda }_{{mm}}} + {{\Phi }_{{mk}}} + {{\Phi }_{{nm}}})\psi _{{n,m,k}}^{{v}} + {{\Psi }_{{mk}}}\psi _{{n,m,k}}^{w}] - \\ \, - {{\alpha }_{2}}{{\gamma }_{2}}[{{\Psi }_{{nm}}}\varphi _{{n,m,k}}^{u} + ({{\Lambda }_{{mm}}} + {{\Phi }_{{mk}}} + {{\Phi }_{{nm}}})\varphi _{{n,m,k}}^{{v}} + {{\Psi }_{{mk}}}\varphi _{{n,m,k}}^{w}]{\kern 1pt} {\kern 1pt} \} \\ \end{gathered} $(3.3)
$\begin{gathered} M{{{\ddot {w}}}_{{n,m,k}}} = K\{ {{\Psi }_{{nk}}}{{u}_{{n,m,k}}} + {{\Psi }_{{mk}}}{{v}_{{n,m,k}}} + ({{\Lambda }_{{kk}}} + {{\Phi }_{{mk}}} + {{\Phi }_{{nk}}}){{w}_{{n,m,k}}} + \\ \, + \beta [{{\Psi }_{{nk}}}{{{\dot {u}}}_{{n,m,k}}} + {{\Psi }_{{mk}}}{{{{\dot {v}}}}_{{n,m,k}}} + ({{\Lambda }_{{kk}}} + {{\Phi }_{{mk}}} + {{\Phi }_{{nk}}}){{{\dot {w}}}_{{n,m,k}}}] - \\ - {{\alpha }_{1}}{{\gamma }_{1}}[{{\Psi }_{{nk}}}\psi _{{n,m,k}}^{u} + {{\Psi }_{{mk}}}\psi _{{n,m,k}}^{{v}} + ({{\Lambda }_{{kk}}} + {{\Phi }_{{mk}}} + {{\Phi }_{{nk}}})\psi _{{n,m,k}}^{w}] - \\ \, - {{\alpha }_{2}}{{\gamma }_{2}}[{{\Psi }_{{nk}}}\varphi _{{n,m,k}}^{u} + {{\Psi }_{{mk}}}\varphi _{{n,m,k}}^{{v}} + ({{\Lambda }_{{kk}}} + {{\Phi }_{{mk}}} + {{\Phi }_{{nk}}})\varphi _{{n,m,k}}^{w}]\} \\ \end{gathered} $С учетом обозначений
(3.4)
$\begin{gathered} M{{{\ddot {u}}}_{{n,m,0}}} = K\{ ({{\Lambda }_{{nn}}} + \Phi _{{nk}}^{ - } + \Phi _{{nm}}^{{}}){{u}_{{n,m,0}}} + \Psi _{{nm}}^{{}}{{{v}}_{{n,m,0}}} + \Psi _{{nk}}^{ - }{{w}_{{n,m,0}}} + \\ \, + \beta [({{\Lambda }_{{nn}}} + \Phi _{{nk}}^{ - } + \Phi _{{nm}}^{{}}){{{\dot {u}}}_{{n,m,0}}} + \Psi _{{nm}}^{{}}{{{{\dot {v}}}}_{{n,m,0}}} + \Psi _{{nk}}^{ - }{{{\dot {w}}}_{{n,m,0}}}\,] - \\ \, - {{\alpha }_{1}}{{\gamma }_{1}}[({{\Lambda }_{{nn}}} + \Phi _{{nk}}^{ - } + \Phi _{{nm}}^{{}})\psi _{{n,m,0}}^{u} + \Psi _{{nm}}^{{}}\psi _{{n,m,0}}^{{v}} + \Psi _{{nk}}^{ - }\psi _{{n,m,0}}^{w}] - \\ \, - {{\alpha }_{2}}{{\gamma }_{2}}[({{\Lambda }_{{nn}}} + \Phi _{{nk}}^{ - } + \Phi _{{nm}}^{{}})\varphi _{{n,m,0}}^{u} + \Psi _{{nm}}^{{}}\varphi _{{n,m,0}}^{{v}} + \Psi _{{nk}}^{ - }\varphi _{{n,m,0}}^{w}{\kern 1pt} ]\} \\ \end{gathered} $(3.5)
$\begin{gathered} M{{{{\ddot {v}}}}_{{n,m,0}}} = K\{ \Psi _{{nm}}^{{}}{{u}_{{n,m,0}}} + ({{\Lambda }_{{mm}}} + \Phi _{{mk}}^{ - } + \Phi _{{nm}}^{{}}){{{v}}_{{n,m,0}}} + \Psi _{{mk}}^{ - }{{w}_{{n,m,0}}} + \\ \, + \beta [\Psi _{{nm}}^{{}}{{{\dot {u}}}_{{n,m,0}}} + ({{\Lambda }_{{mm}}} + \Phi _{{mk}}^{ - } + \Phi _{{nm}}^{{}}){{{{\dot {v}}}}_{{n,m,0}}} + \Psi _{{mk}}^{ - }{{{\dot {w}}}_{{n,m,0}}}] - \\ \, - {{\alpha }_{1}}{{\gamma }_{1}}[\Psi _{{nm}}^{{}}\psi _{{n,m,0}}^{u} + ({{\Lambda }_{{mm}}} + \Phi _{{mk}}^{ - } + \Phi _{{nm}}^{{}})\psi _{{n,m,0}}^{{v}} + \Psi _{{mk}}^{ - }\psi _{{n,m,0}}^{w}] - \\ \, - {{\alpha }_{2}}{{\gamma }_{2}}[\Psi _{{nm}}^{{}}\varphi _{{n,m,0}}^{u} + ({{\Lambda }_{{mm}}} + \Phi _{{mk}}^{ - } + \Phi _{{nm}}^{{}})\varphi _{{n,m,0}}^{{v}} + \Psi _{{mk}}^{ - }\varphi _{{n,m,0}}^{w}]\} \\ \end{gathered} $(3.6)
$\begin{gathered} M{{{\ddot {w}}}_{{n,m,0}}} = K\{ \Lambda _{k}^{ - }{{w}_{{n,m,0}}} + \Psi _{{nk}}^{ - }{{u}_{{n,m,0}}} + \Psi _{{mk}}^{ - }{{{v}}_{{n,m,0}}} + (\Phi _{{mk}}^{ - } + \Phi _{{nk}}^{ - }){{w}_{{n,m,0}}} + \\ \, + \beta [\Lambda _{k}^{ - }{{{\dot {w}}}_{{n,m,0}}} + \Psi _{{nk}}^{ - }{{{\dot {u}}}_{{n,m,0}}} + \Psi _{{mk}}^{ - }{{{{\dot {v}}}}_{{n,m,0}}} + (\Phi _{{mk}}^{ - } + \Phi _{{nk}}^{ - }){{{\dot {w}}}_{{n,m,0}}}] - \\ \, - {{\alpha }_{1}}{{\gamma }_{1}}[\Lambda _{k}^{ - }\psi _{{n,m,0}}^{w} + \Psi _{{nk}}^{ - }\psi _{{n,m,0}}^{u} + \Psi _{{mk}}^{ - }\psi _{{n,m,0}}^{{v}} + (\Phi _{{mk}}^{ - } + \Phi _{{nk}}^{ - })\psi _{{n,m,0}}^{w}] - \\ \, - {{\alpha }_{2}}{{\gamma }_{2}}[\Lambda _{k}^{ - }\varphi _{{n,m,0}}^{w} + \Psi _{{nk}}^{ - }\varphi _{{n,m,0}}^{u} + \Psi _{{mk}}^{ - }\varphi _{{n,m,0}}^{{v}} + (\Phi _{{mk}}^{ - } + \Phi _{{nk}}^{ - })\varphi _{{n,m,0}}^{w}]\} + P(t){{\delta }_{{n0}}}{{\delta }_{{m0}}} \\ \end{gathered} $Здесь ${{\delta }_{{n0}}}$ – символ Кронекера, $P(t)$ – амплитуда, действующей поверхностной нагрузки. Начальные условия нулевые.
Как показано в [8], уравнениям (3.1) – (3.6), описывающим движение блочного полупространства с упругими прослойками (${{\alpha }_{1}} = 0$, ${{\alpha }_{2}} = 0$, ${{\gamma }_{1}} = 0$, ${{\gamma }_{2}} = 0$, $\beta = 0$), соответствуют скорости продольных (${{c}_{{\text{p}}}}$), сдвиговых (${{c}_{{\text{s}}}}$) и рэлеевских (${{c}_{{\text{R}}}}$) бесконечно длинных волн:
(3.7)
${{c}_{{\text{p}}}} = l\sqrt {\frac{{3K}}{M}} ,$ ${{c}_{{\text{s}}}} = l\sqrt {\frac{K}{M}} ,$ ${{c}_{{\text{R}}}} = l\sqrt {\frac{{2K}}{M}\left( {1 - \frac{1}{{\sqrt 3 }}} \right)} $С использованием модели блочной среды (3.1) – (3.6), численно решаются две задачи о распространении волн в трехмерной блочной среде с учетом внутреннего трения при сосредоточенном вертикальном воздействии, приложенном в начале координат. В задаче 1 нагрузка действует на поверхность блочного полупространства. В задаче 2 нагрузка действует на поверхность блочного слоя, лежащего на блочном полупространстве, причем свойства слоя и полупространства различаются.
Для этих задач исследуется реакция блочной среды на два вида действующей нагрузки: (а) ступенчатое воздействие, т.е. $P(t) = {{P}_{0}}H(t)$; (б) импульс Гаусса, т.е. P(t) = = ${{P}_{0}}{\text{exp}}[ - {{{{{(t - 4\sigma )}}^{2}}} \mathord{\left/ {\vphantom {{{{{(t - 4\sigma )}}^{2}}} {(2{{\sigma }^{2}})}}} \right. \kern-0em} {(2{{\sigma }^{2}})}}]$.
4. Разностная схема. Уравнения (3.1)–(3.6) с нулевыми начальными данными решались методом конечных разностей по явной схеме. Для вторых производных по времени использовалась центрально-разностная аппроксимация второго порядка точности, для первых производных по времени применялась разность “назад” первого порядка точности:
Здесь $\tau $ – шаг разностной сетки по времени, $u_{{n,m,k}}^{s}$ – значение перемещения ${{u}_{{n,m,k}}}(t)$ в момент времени $t = s\tau $, s – номер слоя по времени в конечно-разностной схеме. Для дополнительных функций использовались аппроксимации следующего вида:
5. Результаты численных расчетов задачи 1 с учетом внутреннего трения. В этой секции представлены результаты численных расчетов возмущений в задаче Лэмба с учетом внутреннего трения, проведенных при ${{P}_{0}} = 1$ и $\tau = \pi {\text{/}}20$. Масса блоков, длина пружин и суммарная жесткость прослоек приняты за единицы: $M = 1$, $l = {\text{1}}$, $K = 1$.
На рис. 6 – 9 приведены результаты расчетов вертикальных $\dot {w} = {{\dot {w}}_{{n,m,k}}}$ и радиальных ${{\dot {u}}_{r}} = {{\left( {n\,{{{\dot {u}}}_{{n,m,k}}} + m\,{{{{\dot {v}}}}_{{n,m,k}}}} \right)} \mathord{\left/ {\vphantom {{\left( {n\,{{{\dot {u}}}_{{n,m,k}}} + m\,{{{{\dot {v}}}}_{{n,m,k}}}} \right)} {{{{({{n}^{2}} + {{m}^{2}})}}^{{1/2}}}}}} \right. \kern-0em} {{{{({{n}^{2}} + {{m}^{2}})}}^{{1/2}}}}}$ скоростей блоков в цилиндрической системе координат $r,\;\theta ,\;z$ на поверхности блочного полупространства (k = 0) на оси $m = 0$.
Рис. 6.
Зависимости от времени радиальной (a) и вертикальной (b) скоростей блоков в точке (60, 0, 0) при действии ступенчатой нагрузки. Сплошные кривые – $Q_{0}^{{ - 1}} = 0$, штриховые кривые – $Q_{0}^{{ - 1}} = 0.1$, штрих-пунктирные кривые – $Q_{0}^{{ - 1}} = 0.2$.
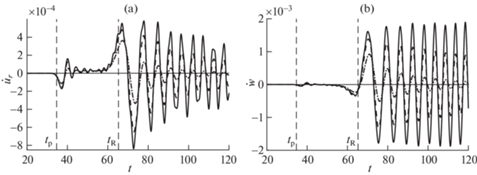
На рис. 6 приведены графики зависимости от времени радиальной ${{\dot {u}}_{r}}$ и вертикальной $\dot {w}$ скоростей блоков в точке (60, 0, 0), рассчитанные при действии ступенчатой нагрузки при различных значениях коэффициента добротности материала $Q_{0}^{{ - 1}}$. Вертикальные линии соответствуют моментам времени прихода продольных волн ${{t}_{{\text{p}}}} = {n \mathord{\left/ {\vphantom {n {{{c}_{{\text{p}}}}}}} \right. \kern-0em} {{{c}_{{\text{p}}}}}}$ и рэлеевских волн ${{t}_{{\text{R}}}} = {n \mathord{\left/ {\vphantom {n {{{c}_{{\text{R}}}}}}} \right. \kern-0em} {{{c}_{{\text{R}}}}}}$, где ${{c}_{{\text{p}}}}$ и ${{c}_{{\text{R}}}}$ определяются по формулам (3.7). Видно, что с ростом $Q_{0}^{{ - 1}}$ увеличивается затухание амплитуды скоростей блоков для всего спектра частот.
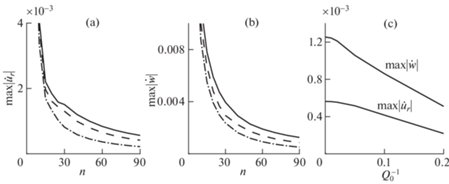
На рис. 7 приведены результаты расчетов максимальных значений абсолютных величин амплитуд радиальной и вертикальной скоростей блоков при действии ступенчатой по времени нагрузки. На рис. 7, a, b показаны зависимости этих величин от координаты n для различных значений коэффициента добротности $Q_{0}^{{ - 1}}$, на рис. 7, c – зависимости от коэффициента добротности $Q_{0}^{{ - 1}}$ в точке (90, 0, 0). Видно, что при увеличении коэффициента $Q_{0}^{{ - 1}}$ максимальные значения абсолютных величин амплитуд ${{\dot {u}}_{r}}$ и $\dot {w}$ падают быстрее с ростом n и их зависимость от коэффициента $Q_{0}^{{ - 1}}$ близка к линейной.
Рис. 7.
Зависимости от координаты n максимальных значений абсолютных величин амплитуд радиальной (a) и вертикальной (b) скоростей блоков на поверхности блочного полупространства; (c) зависимости от коэффициента добротности $Q_{0}^{{ - 1}}$ максимальных значений абсолютных величин радиальной и вертикальной скоростей блоков в точке (90, 0, 0). Сплошные кривые – $Q_{0}^{{ - 1}} = 0$, штриховые кривые – $Q_{0}^{{ - 1}} = 0.1$, штрих-пунктирные кривые – $Q_{0}^{{ - 1}} = 0.2$.
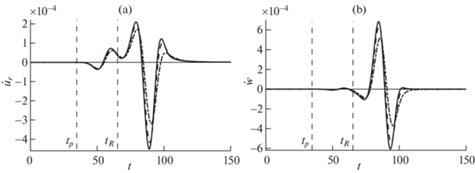
На рис. 8 приведены графики зависимости от времени радиальной и вертикальной скоростей блоков в точке (60, 0, 0), рассчитанные при различных значениях коэффициента добротности $Q_{0}^{{ - 1}}$ при действии импульса Гаусса ($\sigma = 5$). Вертикальные линии соответствуют моментам прихода продольных и рэлеевских волн. Видно, что с ростом $Q_{0}^{{ - 1}}$ уменьшаются амплитуды скоростей блоков и увеличивается время наступления максимальных амплитуд скоростей. Последнее объясняется уменьшением скорости низкочастотных волн, что можно видеть на рис. 2.
Рис. 8.
Зависимости от времени радиальной (a) и вертикальной (b) скоростей блоков в точке (60,0,0) при действии импульса Гаусса. Сплошные кривые – $Q_{0}^{{ - 1}} = 0$, штриховые кривые – $Q_{0}^{{ - 1}} = 0.1$, штрих-пунктирные кривые – $Q_{0}^{{ - 1}} = 0.2$.
На рис. 9 приведены результаты расчетов максимальных значений абсолютных величин амплитуд радиальной и вертикальной скоростей блоков на поверхности блочного полупространства при действии импульса Гаусса ($\sigma = 5$). На рис. 9, a, b показаны зависимости этих величин от координаты n для различных значений коэффициента добротности $Q_{0}^{{ - 1}}$, на рис. 9, c – зависимости от коэффициента добротности $Q_{0}^{{ - 1}}$ в точке (100, 0, 0).
Рис. 9.
Зависимости от координаты n максимальных значений абсолютных величин амплитуд радиальной (a) и вертикальной (b) скоростей блоков при различных значениях коэффициента добротности $Q_{0}^{{ - 1}}$; (c) зависимости от коэффициента добротности $Q_{0}^{{ - 1}}$ максимальных значений абсолютных величин амплитуд радиальной и вертикальной скоростей в точке (100, 0, 0). Сплошные кривые – $Q_{0}^{{ - 1}} = 0$, штриховые кривые – $Q_{0}^{{ - 1}} = 0.1$, штрих-пунктирные кривые – $Q_{0}^{{ - 1}} = 0.2$.
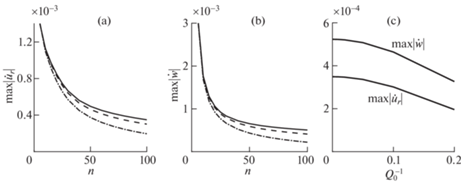
Для графиков, представленных на рис. 9, a, b получены приближенные аппроксимации степенной функцией результатов численных расчетов:
Анализ этих приближенных функций и графиков на рис. 9, a, b показывает, что с ростом коэффициента $Q_{0}^{{ - 1}}$ скорость затухания максимальных по модулю значений ${{\dot {u}}_{r}}$, $\dot {w}$ с удалением от места воздействия растет. На рис. 9, c видно, что зависимость максимальных по модулю амплитуд скоростей блоков от коэффициента $Q_{0}^{{ - 1}}$ близка к параболической.
6. Результаты численных расчетов задач 1 и 2 с учетом внутреннего трения. Ниже, на рис. 10 представлены результаты численных расчетов двух задач с учетом внутреннего трения при воздействии вертикального сосредоточенного импульса Гаусса, во-первых, на поверхность блочного полупространства (задача 1 – штриховые кривые) и, во-вторых, на поверхность блочного слоя, лежащего на блочном полупространстве, имеющем другие свойства (задача 2 – сплошные кривые).
Рис. 10.
Зависимости от времени радиальных и вертикальных скоростей блоков на поверхности блочного полупространства. Штриховые кривые – блочное полупространство, сплошные кривые – блочный слой на блочном полупространстве. Верхний ряд графиков – радиальные скорости блоков, нижний ряд – вертикальные скорости.
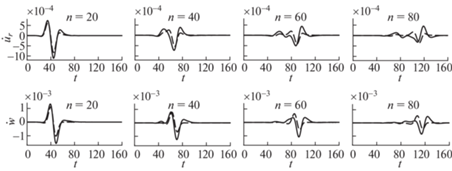
На рис. 10 показаны зависимости от времени радиальных и вертикальных скоростей блоков на поверхности блочного полупространства, находящихся на различном расстоянии от места воздействия (n = 20, 40, 60, 80). Коэффициент добротности $Q_{0}^{{ - 1}}$ = 0.1 для блочного полупространства (задача 1) и для слоя, лежащего на полупространстве (задача 2). Коэффициент добротности $Q_{0}^{{ - 1}} = 0.05$ для блочного полупространства, лежащего под слоем (задача 2). Кроме того, скорость распространения волн в блочном полупространстве и в блочном слое, лежащем на полупространстве, в два раза меньше, чем скорость распространения волн в полупространстве, лежащем под слоем.
Видно, что отражение и преломление волн на нижней границе слоя приводит к перестройке волны, бегущей по поверхности полупространства. В задаче для полупространства максимальная амплитуда скоростей блоков меньше, чем в задаче для слоя на полупространстве.
7. Заключение. Проведено математическое моделирование процесса распространения волн в блочной среде с учетом внутреннего трения при нестационарном воздействии. Предложенная модель является новой и основана на идее, что динамическое поведение блочной среды можно грубо описать как движение жестких блоков за счет сжимаемости прослоек между ними, и что деформация прослоек может быть приблизительно описана элементами Максвелла и Фойгта.
Использование реологической модели прослоек между блоками с двумя элементами Максвелла и одним элементом Фойгта позволяет подбирать параметры вязкости и жесткости этих элементов, так чтобы коэффициент добротности материала отличался от заданного постоянного значения не больше, чем на 5% на интервале частот от 4% до 100% от максимальной частоты, представляющей интерес.
С помощью этой модели численно решена задача Лэмба, а именно, изучено распространение сейсмических волн в блочной среде при нестационарном сосредоточенном вертикальном воздействии на поверхность полупространства и на поверхность слоя, лежащего на полупространстве. Для задачи Лэмба исследована степень затухания максимальных амплитуд скоростей перемещений блоков на поверхности блочного полупространства в зависимости от коэффициента добротности материала и расстояния от места воздействия. Показано, что в задаче для полупространства максимальная амплитуда скоростей блоков меньше, чем в задаче для слоя на полупространстве.
В отличие от работы [8], в которой использовалась модель Фойгта для моделирования деформации прослоек, предложенная в этой статье модель с почти постоянным коэффициентом добротности демонстрирует более равномерное затухание амплитуд возмущений для всего спектра интересующих частот.
Полученные выше результаты показывают, что наличие блочной структуры в среде приводит к следующим изменениям ее поведения по сравнению с тем, что предсказывает модель однородной упругой среды, механические свойства которой получены путем усреднения механических свойств блочной среды: (а) в отличие от однородной упругой среды, в блочной среде волны распространяются с дисперсией; (б) скорости распространения низкочастотных продольных и рэлеевских волн на поверхности блочной среды намного меньше соответствующих скоростей в однородной упругой среде; (в) основной вклад в волновой процесс на поверхности блочной среды вносят низкочастотные волны в окрестности фронта волны Рэлея; (г) за фронтом волны Рэлея в блочной среде наблюдаются высокочастотные колебания, отсутствующие в однородной упругой среде; (д) скорость распространения низкочастотных волн и степень их затухания определяются массой блоков, их размерами и свойствами прослоек; (е) диссипативные свойства прослоек приводят к дополнительному затуханию на поверхности полупространства низкочастотных возмущений вблизи фронта волны Рэлея и высокочастотных осцилляций за фронтом волны Рэлея.
Работа выполнена в рамках проекта НИР, номер государственной регистрации 121062200075-4.
Список литературы
Садовский М.А. Естественная кусковатость горной породы // ДАН СССР. 1979. Т. 247. № 4. С. 829–832.
Курленя М.В., Опарин В.Н., Востриков В.И. Волны маятникового типа. Ч. II: Методика экспериментов и основные результаты физического моделирования // ФТПРПИ. 1996. № 4. С. 3–38.
Курленя М.В., Опарин В.Н., Востриков В.И. и др. Волны маятникового типа. Ч. III: Данные натурных измерений // ФТПРПИ. 1996. № 5. С. 3–27.
Шер Е.Н., Черников А.Г. Об оценке параметров структуры блочных сред на модельном примере сейсмического зондирования кирпичной стены // ФТПРПИ. 2020. № 4. С. 11–17.
Александрова Н.И. О распространении упругих волн в блочной среде при импульсном нагружении // ФТПРПИ. 2003. № 6. С. 38–47.
Курленя М.В., Опарин В.Н., Востриков В.И. О формировании упругих волновых пакетов при импульсном возбуждении блочных сред. Волны маятникового типа Uμ // ДАН СССР. 1993. Т. 333. № 4. С. 3–13.
Александрова Н.И., Черников А.Г., Шер Е.Н. Экспериментальная проверка одномерной расчетной модели распространения волн в блочной среде // ФТПРПИ. 2005. № 3. С. 46–55.
Aleksandrova N.I. Seismic waves in a three-dimensional block medium // Proc. R. Soc. A. 2016. V. 472. № 2192. P. 20160111. https://doi.org/10.1098/rspa.2016.0111
Александрова Н.И. Волны маятникового типа на поверхности блочного породного массива при динамическом воздействии // ФТПРПИ. 2017. № 1. С. 64–69.
Sadovskii V.M., Sadovskaya O.V. Supercomputer modeling of wave propagation in blocky media accounting fractures of interlayers // Nonlinear Wave Dynamics of Materials and Structures. Advanced Structured Materials. V. 122 / Ed. by H. Altenbach, V. Eremeyev, I. Pavlov, A. Porubov. Springer, 2020. P. 379–398. https://doi.org/10.1007/978-3-030-38708-2_22.
Sadovskii V.M., Sadovskaya O.V. Numerical algorithm based on implicit finite-difference schemes for analysis of dynamic processes in blocky media // Russ. J. Num. Anal. Math. Modell. 2018. V. 33. № 2. P. 111–121. https://doi.org/10.1515/rnam-2018-0010
Zener C.M. Elasticity and anelasticity of metals. 1st. ed. Chicago: University of Chicago Press, 1948.
Biot M.A. Theory of stress-strain relations in anisotropic viscoelasticity and relaxation phenomena // J. Appl. Phys. 1954. V. 25. P. 1385–1391. https://doi.org/10.1063/1.1721573
Fung Y.C. Fundations of solid mechanics. Prentice Hall, Inc, 1965.
Bielak J., Karaoglu H., Taborda R. Memory-efficient displacement-based internal friction for wave propagation simulation // Geophys. 2011. V. 76. № 6. T131–T145. https://doi.org/10.1190/geo2011-0019.1
Toksöz M., Johnston D. Seismic wave attenuation. Tulsa, Okla.: Society of Exploration Geophysicists, 1981.
Kjartansson E. Constant Q-wave propagation and attenuation // J. Geophys. Res. 1979. V. 84. P. 4737–4748. https://doi.org/10.1029/JB084iB09p04737
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела