Известия РАН. Механика твердого тела, 2022, № 3, стр. 70-77
КОНТАКТНОЕ ВЗАИМОДЕЙСТВИЕ ОСЕСИММЕТРИЧНОГО ШТАМПА И ПОРОУПРУГОГО СЛОЯ, ЗАКРЕПЛЕННОГО НА УПРУГОМ ОСНОВАНИИ
М. И. Чебаков a, *, Е. М. Колосова a, **
a Институт математики, механики и компьютерных наук им. И.И. Воровича
Южный федеральный университет
Ростов-на-Дону, Россия
* E-mail: michebakov@yandex.ru
** E-mail: a_lena_ch@mail.ru
Поступила в редакцию 26.05.2021
После доработки 07.07.2021
Принята к публикации 08.07.2021
- EDN: NWRXCX
- DOI: 10.31857/S057232992202009X
Аннотация
В работе на основе уравнений теории пороупругих тел Ковина–Нунзиато рассматривается осесимметричная контактная задача о взаимодействии жесткого штампа с пороупругим слоем, закрепленным на упругом полупространстве. Предполагается, что основание штампа имеет плоскую форму, в зоне контакта отсутствует трение. С помощью интегрального преобразования Ханкеля поставленная задача сводится к интегральному уравнению относительно неизвестного контактного напряжения, для решения которого используется метод коллокаций. Найдены значения контактных напряжений и исследована деформация поверхности вне штампа. Исследована связь между силой, действующей на штамп, и его перемещением, которая является одной из основных характеристик при определении механических параметров материала методом индентирования. Проведен сравнительный анализ исследуемых величин для различных значений параметров пороупругого слоя и упругого основания. Численные результаты представлены в виде графиков.
Введение. Пористые материалы – это достаточно новый класс материалов с уникальными физическими, механическими, акустическими, электрическими и термическими свойствами. Благодаря оптимальному соотношению массы и прочности он широко используется в космической промышленности. Важнейшим вопросом при производстве таких материалов является контроль и оценка их механических характеристик. Существуют различные подходы.
Один из подходов моделирования пористых материалов был развит в работах Ковина–Нунзиато [1, 2]. Данная теория, называемая теорией микродилатации, была применена для исследования пористых тел с пустыми (ненасыщенными) порами. Она использует линейную теорию упругости с дополнительной кинематической переменной, которая описывает свойства изменения пористости. Таким образом, деформация и пористость являются связанными полями, имеющими общую реакцию на внешние нагрузки, прикладываемые к телу.
Линейная теория была описана в [2]. Ряд исследований был проведен в последние годы. На основе теории Ковина–Нунзиато в [3, 4] решены плоские контактные задачи для полуплоскости и полосы, соответственно. В [5–7] исследованы осесимметричные контактные задачи для пористого полупространства и слоя. В [8] рассмотрена осесимметричная задача о взаимодействии штампа и упругого слоя, закрепленного на пороупругом полупространстве.
В [9] методы композитной механики были использованы для оценки эффективных модулей упругости и параметра Био пористых сред. Новый метод анализа деформационного поведения жестких и эластичных пен с небольшим объемным содержанием твердой фазы разработан в [10]. В [11] рассмотрен несжимаемый упругий материал с периодической системой пор, представлены результаты численных расчетов модулей для материалов с порами различной конфигурации.
Целью исследований является оценка влияния параметров пороупругого слоя на контактные напряжения, приложенную нагрузку к штампу и перемещения свободной поверхности пороупругого слоя, закрепленного на упругом полупространстве, при индентировании слоя жестким штампом.
1. Постановка задач. Рассмотрим в цилиндрической системе координат (r, φ, z) осесимметричную задачу о нормальном внедрении (индентировании) на заданную глубину жесткого штампа в пороупругий слой $0 \leqslant z \leqslant h$, закрепленный на упругом полупространстве $z < 0$. Деформация пороупругого слоя описывается соотношениями Ковина и Нунзиато [2]. Будем считать, что основание штампа плоское.
Деформация слоя $0 \leqslant z \leqslant h$, состоящего из изотропного материала с пустотами, согласно теории Ковина–Нунзиато, описывается при k = 1 системой дифференциальных уравнений в частных производных [2]
(1.1)
$\left( {{{\lambda }_{k}} + {{\mu }_{k}}} \right)\frac{{\partial {{\theta }_{k}}}}{{\partial z}} + {{\mu }_{k}}\,\Delta {{w}_{k}} + \beta \frac{{\partial \phi }}{{\partial z}} = 0,\quad \alpha \,\Delta \phi - \xi \phi - \beta \,{{\theta }_{k}} = 0$Здесь $\alpha $ – коэффициент пустотной диффузии, $\beta $ – параметр связи микродилатационных и макродилатационных свойств, $\xi $ – пустотная жесткость, функция $\phi (r,z)$ описывает изменение объемной части пор, ${{\mu }_{k}}$ и ${{\lambda }_{k}}$ – коэффициенты Ламе, ${{u}_{k}}$ и ${{w}_{k}}$, соответственно, перемещения вдоль осей r и z.
Деформация упругого полупространства $z < 0$ описывается первыми двумя уравнениями из (1.1) при k = 2 и $\beta = 0$.
Компоненты тензора напряжений в пороупругом слое определяются из следующих соотношений при k = 1
(1.2)
$\sigma _{z}^{k} = {{\lambda }_{k}}{{\theta }_{k}} + 2{{\mu }_{k}}\frac{{\partial {{w}_{k}}}}{{\partial z}} + \beta \phi ,\quad \tau _{{rz}}^{k} = {{\mu }_{k}}\left( {\frac{{\partial {{w}_{k}}}}{{\partial r}} + \frac{{\partial {{u}_{k}}}}{{\partial z}}} \right)$Соотношения (1.2) определяют напряжения в упругом полупространстве при k = 2 и $\beta = 0$.
При z = h и z = 0 граничные условия примут вид
(1.3)
$\tau _{{rz}}^{1}(r,z) = \tau _{{rz}}^{2}(r,z),\quad {{w}_{1}}(r,z) = {{w}_{2}}(r,z),\quad {{u}_{1}}(r,z) = {{u}_{2}}(r,z)\quad \left( {z = 0} \right)$На бесконечности при $z \to - \infty $ напряжения и перемещения затухают.
В случае штампа с плоским основанием $\delta (r) = \delta = {\text{const}}$.
2. Вывод интегрального уравнения относительно контактных напряжений. Для определения контактных напряжений ${{\sigma }_{z}}(r,0) = q(r)$ будет построено интегральное уравнение (2.14). Предварительно, будем считать их известными. Тогда приходим к решению системы (1.1) с новыми граничными условиями
(2.1)
$\tau _{{rz}}^{1}(r,z) = \tau _{{rz}}^{2}(r,z),\quad {{w}_{1}}(r,z) = {{w}_{2}}(r,z),\quad {{u}_{1}}(r,z) = {{u}_{2}}(r,z),\quad \left( {z = 0} \right)$Неизвестные функции в системе (1.1) запишем в виде преобразования Ханкеля соответственно для пороупругого слоя (k = 1) и упругого полупространства (k = 2)
На основе граничных условий (2.1) при z = h и z = 0 получим:
(2.5)
${{B}_{1}} = {{B}_{2}},\quad {{A}_{1}} = {{A}_{2}},\quad {{\mu }_{1}}(D{{A}_{1}} - u{{B}_{1}}) = {{\mu }_{2}}(D{{A}_{2}} - u{{B}_{2}}),\quad DF = 0\,(z = 0)$Здесь использованы следующие обозначения [12]
(2.6)
$c_{k}^{2} = \frac{{{{\mu }_{k}}}}{{({{\lambda }_{k}} + 2{{\mu }_{k}})}},\quad H = \frac{\beta }{{{{\lambda }_{2}} + 2{{\mu }_{2}}}},\quad l_{1}^{2} = \frac{\alpha }{\beta },\quad l_{2}^{2} = \frac{\alpha }{\xi }$Общее решение системы (2.3) может быть представлено в виде
(2.7)
${{B}_{1}}(u,z) = ({{s}_{1}} + {{s}_{2}}z){{e}^{{uz}}} + ({{s}_{3}} + {{s}_{4}}z){{e}^{{ - uz}}} + {{s}_{5}}{{e}^{{mz}}} + {{s}_{6}}{{e}^{{ - mz}}}$(2.8)
${{s}_{3}} = {{d}_{3}} - {{d}_{4}}\frac{{c_{1}^{2} + 1 - N}}{{u(c_{1}^{2} - 1 + N)}},\quad {{s}_{4}} = {{d}_{4}},\quad {{t}_{3}} = - {{d}_{4}}\frac{{2c_{1}^{2}l_{2}^{2}}}{{l_{1}^{2}(c_{1}^{2} - 1 + N)}},\quad {{t}_{4}} = 0$Общее решение системы (2.4) может быть представлено в виде
(2.9)
${{A}_{2}}(u,z) = ({{a}_{1}} + {{a}_{2}}z){{e}^{{uz}}},\quad {{B}_{2}}(u,z) = \left( {{{b}_{1}} + {{b}_{2}}z} \right){{e}^{{uz}}}$(2.10)
${{b}_{1}} = - {{a}_{1}},\quad {{b}_{2}} = \frac{{{{a}_{2}}u(c_{2}^{2} - 1) + {{a}_{1}}(c_{2}^{2} + 1)}}{{u(1 - c_{2}^{2})}}$Для нахождения коэффициентов ${{a}_{1}}$, ${{a}_{2}}$, ${{d}_{1}}$, ${{d}_{2}}$, ${{d}_{3}}$, ${{d}_{4}}$ воспользуемся граничными условиями (2.4). В результате найдем выражение для ${{B}_{1}}(u,h),$
(2.11)
${{B}_{1}}(u,h) = \frac{{Q(u)}}{{2{{\mu }_{1}}(1 - c_{1}^{2})}}L(u),\quad L(s) = \frac{{{{L}_{1}}(s)}}{{{{L}_{2}}(s)}}\quad (s = u{{l}_{2}})$Здесь функции ${{L}_{1}}(s)$ и ${{L}_{2}}(s)$ имеют следующую структуру
(2.12)
$\begin{gathered} {{L}_{1}}(s) = {\text{ch}}\left( {Td} \right)\left[ {2{\text{ch}}(2sd){{L}_{{11}}}(s) + {{L}_{{12}}}(s)} \right] + \\ \, + {\text{sh}}(Td)\left[ {{\text{ch}}(2sd){{L}_{{13}}}(s) + {\text{sh}}(2sd){{L}_{{14}}}(s) + {{L}_{{15}}}(s)} \right] \\ \end{gathered} $Выражения для ${{L}_{{ij}}}(s)$ имеют довольно громоздкий вид и здесь не приводятся.
Используя граничное условие ${{w}_{1}}(r,0) = \delta (r)$ при $r \leqslant a$ и $z = h$ из (1.3) найдем
(2.13)
${{w}_{1}}(r,h) = \frac{1}{{2{{\mu }_{1}}(1 - c_{1}^{2})}}\int\limits_0^\infty {Q(u)L(u)u{{J}_{0}}(ur)du = \delta (r)\;(r \leqslant a)} $Подставляя в (2.13) выражение для $Q(u)$ из (2.5) и удовлетворяя граничному условию ${{w}_{1}}(r,z) = \delta (r)\,(z = h,\;r \leqslant a)$ из (1.3) после замены
получим после несложных преобразований искомое интегральное уравнение для определения контактных напряжений под штампом $q(r) = \sigma (r{\text{/}}{{l}_{2}})$(2.14)
$\int\limits_0^b {\sigma (y)yk(y,x)dy} = \frac{{{{\mu }_{1}}}}{{(1 - {{\nu }_{1}}){{l}_{2}}}}\delta (x{{l}_{2}})\quad (x \leqslant b)$Здесь $2(1 - c_{1}^{2}) = {{(1 - {{\nu }_{1}})}^{{ - 1}}}$, где ν1 – коэффициент Пуассона для упругого слоя, b = = $a{\text{/}}{{l}_{2}}$.
3. Решение интегрального уравнения. Для решения интегрального уравнения (2.14), (2.15) с символом ядра $L(s)$ из (2.11)–(2.12) применим прямой метод коллокаций [13]. Разобьем отрезок [0, b] на n частей набором точек ${{b}_{j}} = \varepsilon j$ ($\varepsilon = b{\text{/}}n$, $j\; = 0,1,...,n$) и будем считать, что на каждом отрезке $[{{b}_{{j - 1}}},\,{{b}_{j}}]$ контактные напряжения имеют постоянное значение σj. Пусть ${{x}_{k}} = ({{b}_{k}} + {{b}_{{k - 1}}}){\text{/}}2$ есть точки коллокаций, тогда интегральное уравнение дискретизируем по следующей схеме
(3.1)
$\sum\limits_{j = 1}^n {{{\sigma }_{j}}\int\limits_{{{b}_{{j - 1}}}}^{{{b}_{j}}} {k(y,{{x}_{k}})ydy} } = \frac{{{{\mu }_{1}}}}{{(1 - {{\nu }_{1}}){{l}_{2}}}}\delta \left( {{{x}_{k}}{{l}_{2}}} \right)\quad (k = \overline {1,n} )$В результате получим систему для определения ${{\sigma }_{j}}$
(3.2)
$\sum\limits_{j = 1}^n {{{\sigma }_{j}}{{a}_{{kj}}}} = \frac{{{{\mu }_{1}}}}{{1 - {{\nu }_{1}}}}\delta ({{x}_{k}}{{l}_{2}})\quad (k = \overline {1,n} )$(3.3)
${{a}_{{kj}}} = \int\limits_0^\infty {L(s){{J}_{0}}(s{{x}_{k}})\left[ {{{b}_{j}}{{J}_{1}}(s{{b}_{j}}) - {{b}_{{j - 1}}}{{J}_{1}}(s{{b}_{{j - 1}}})} \right]ds} $Для нахождения силы, действующей на штамп, получим
(3.4)
$P = 2\pi \int\limits_0^a {q(r)rdr} = 2\pi l_{2}^{2}\int\limits_0^b {\sigma (x)xdx = 2\pi \varepsilon l_{2}^{2}\sum\limits_{k = 1}^n {{{\sigma }_{k}}{{x}_{k}}} } $4. Числовые расчеты. Приведенная выше схема решения интегрального уравнения позволяет рассчитать контактные напряжения, форму поверхности вне штампа, силу, действующую на штамп при заданной величине перемещения штампа $\delta $. В расчетах основное внимание уделялось влиянию параметров N, $\mu = {{\mu }_{2}}{\text{/}}{{\mu }_{1}}$ и толщины упругого слоя $h = d\,{{l}_{2}}$ на исследуемые величины.
Безразмерные контактные напряжения $\sigma _{{}}^{*}(x) = \sigma (x)\frac{{(1 - {{\nu }_{1}})\,{{l}_{2}}}}{{{{\mu }_{1}}\delta }}$ на границе z = h показаны на рис. 1.a – 3.a, приведенная деформация $w_{{}}^{*}(x) = l_{2}^{{ - 1}}w\left( {x{{l}_{2}}} \right)$ поверхности z = h вне штампа на рис. 1b. – 3.b. Отметим, что здесь при расчетах полагалось ${{\nu }_{1}} = {{\nu }_{2}}$ = 0.3, b = 1. Вычисления проводились с погрешностью не более 0.3%, для этого было достаточно брать в системе (3.2) n = 50. При этих же параметрах вычислялась безразмерная сила $P_{{}}^{*} = \frac{{1 - {{\nu }_{1}}}}{{{{\mu }_{1}}\delta \,l_{2}^{{}}}}P$.
Рис. 1.
a) Контактные напряжения. b) Перемещения поверхности z = h. d = 0.25, N = 0.5. Линия 1 – μ = 2; линия 2 – $\mu = 1$; линия 3 – μ = 0.5.
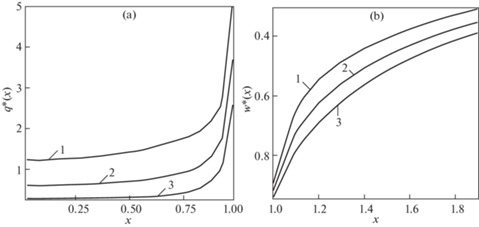
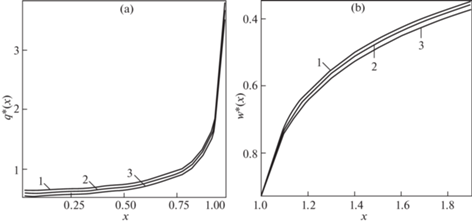
На рис. 1 приведены графики при d = 0.25, N = 0.5 и значениях $\mu = 2,\;1,\;0.5$, при этом соответствующие значения безразмерной силы $P_{{}}^{*} = 6.50,3.80$, 2.13. На рис. 2 приведены графики при d = 0.1, N = 0.5 и $\mu = 2,\;1,\;0.5$, соответствующие значения $P{\text{*}} = 7.20,\;3.89,\;2.05$. На рис. 3 приведены графики при d = 1, $\mu = 1$ и N = 0.5, 0.3, 0, соответствующие значения P* = 3.57, 3.77, 3.96.
Рис. 2.
a) Контактные напряжения. b) Перемещения поверхности z = h. d = 0.1, N = 0.5. Линия 1 – μ = 2; линия 2 – $\mu = 1$; линия 3 –μ = 0.5.
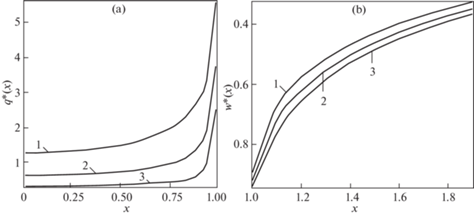
Рис. 3.
(a) Контактные напряжения. (b) Перемещения поверхности z = h. d = 1, $\mu = 1$. Линия 1 – N = 0; линия 2 – N = 0.3; линия 3 – N = 0.5.
Выводы. Расчеты показывают, что увеличение пористости слоя при постоянной величине смещения штампа, его радиуса и других параметров приводит к уменьшению контактных напряжений под штампом, величины приложенной силы и перемещений поверхности z = h. Такая же картина наблюдается при уменьшении параметра μ, характеризующего относительную жесткость пороупругого слоя.
Увеличение относительной толщины пороупругого слоя при фиксированных значениях других параметров приводит к уменьшению максимальных контактных напряжений, величины приложенной силы и перемещений свободной поверхности слоя вне штампа. Влияние этого фактора менее заметно, чем изменение относительной жесткости пороупругого слоя.
Работа финансово поддержана Южным федеральным университетом (Министерство науки и высшего образования Российской Федерации). Проект № ВнГр-07/2020-07-ИМ.
Список литературы
Nunziato G.W., Cowin S.C. A nonlinear theory of elastic materials with voids // Arch Ration Mech Anal. 1979. V. 72. P. 175–201. https://doi.org/10.1007/BF00249363
Cowin S.C., Nunziato G.W. Linear theory of elastic materials with voids // J. Elasticity. 1983. V. 13. P. 125–147. https://doi.org/10.1007/BF00041230
Scalia A., Sumbatyan M.A. Contact problem for porous elastic half-plane // J. Elasticity. 2000. V. 60. P. 91–102. https://doi.org/10.1023/A:1010880823544
Scalia A. Contact problem for porous elastic strip // Int. J. Eng. Sci. 2002. V. 40. P. 401–410. https://doi.org/10.1016/S0020-7225(01)00070-2
Chebakov M.I., Poddubnyy A.A., Kolosova E.M., Alexiev A., Datcheva M. Contact interaction of axisymmetric indenter and poroelastic foundation // Mater. Phys. Mech. 2020. V. 44. P. 423–432. https://doi.org/10.18720/MPM.4432020_13
Chebakov M.I., Poddubny A.A., Kolosova E.M., Alexiev A.R., Iankov R.Z. Contact interaction of axisymmetric indenter and poroelastic layer // Cr. Acad. Bulg. Sci. 2020. V. 73. № 6. P. 846–855. https://doi.org/10.7546/CRABS.2020.06.13
Kolosova E.M., Chebakov M.I. Analytical solution of axisymmetric contact problem for a poroelastic layer // Mech. Solids. 2020. V. 55. № 6. P. 857–864. https://doi.org/10.3103/S0025654420050118
Chebakov M.I., Kolosova E.M. Contact interaction of axisymmetric stamp and elastic layer fixed on poroelastic base // Mech. Compos. Mater. 2021. V. 56. № 6. P. 769–778. https://doi.org/10.1007/s11029-021-09922-9
Artamonova N.B., Sheshenin S.V., Frolova Yu.V., Bessonova O.Yu., Novikov P.V. Calculating components of the effective tensors of elastic moduli and biot’s parameter of porous geocomposites // Mech. Compos. Mater. 2020. V. 55. № 6. P. 715–726. https://doi.org/10.1007/s11029-020-09846-w
Pleskachevskii Yu.M., Shil’ko S.V., Chernous D.A. Structural modeling in the mechanics of porous materials // Mech. Compos. Mater. 2003. V. 39. P. 129–136. https://doi.org/10.1023/A:1023457311851
Bakhvalov N.S., Bogachev K.Yu., and Eglit M.E. Numerical calculation of effective elastic moduli for incompressible porous material // Mech. Compos. Mater. 1996. V. 32. № 5. P. 399–405. https://doi.org/10.1007/BF02313859
Iesan D., Nappa L. Axially symmetric problems for a porous elastic solid // Int. J. Solids Struct. 2003. V. 40. P. 5271–5286. https://doi.org/10.1016/S0020-7683(03)00229-4
Белоцерковский С.М., Лифанов И.К. Численные методы в сингулярных интегральных уравнениях и их применение в аэродинамике, теории упругости, электродинамике. M.: Наука, 1985. 256 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела


