Известия РАН. Механика твердого тела, 2022, № 3, стр. 16-31
ДВУХЭТАПНЫЙ МЕТОД ФОРМИРОВАНИЯ ВРАЩАЮЩЕЙСЯ ЭЛЕКТРОДИНАМИЧЕСКОЙ КОСМИЧЕСКОЙ ТРОСОВОЙ СИСТЕМЫ
Ю. М. Заболотнов a, *, П. С. Воеводин b, **, Лу Хонши a, ***
a Самарский национальный исследовательский университет
Самара, Россия
b Ракетно-космический центр “Прогресс”
Самара, Россия
* E-mail: yumz@yandex.ru
** E-mail: p.voevodin@inbox.ru
*** E-mail: 292969972@qq.com
Поступила в редакцию 29.03.2021
После доработки 15.04.2021
Принята к публикации 13.05.2021
- EDN: IAPEPZ
- DOI: 10.31857/S0572329922020210
Аннотация
Рассматривается процесс развертывания и перевода во вращение с заданной угловой скоростью электродинамической космической тросовой системы на околоземной орбите. Тросовая система представляет собой линейную группировку трех микроспутников, связанных проводящими ток изолированными тросами. Процесс формирования тросовой системы разбивается на два этапа. На первом этапе ток в тросе отсутствует и используется релейный для сил натяжения закон развертывания системы на заданную длину троса. На втором этапе с помощью управления током система переводится в заданное конечное состояние вращения с постоянной угловой скоростью. Для описания движения центров масс микроспутников используются уравнения Лагранжа. При условии медленного изменения сил натяжения получена аналитическая оценка для характеристик углового движения микроспутников относительно направления тросов. Эффективность рассматриваемого подхода к формированию вращающейся космической тросовой системы и точность аналитических решений подтверждается численными примерами.
1. Введение. Использование электродинамических тросовых систем (ЭДТС) на околоземной орбите и вблизи других небесных тел, имеющих магнитное поле, открывает новые возможности при управлении космическими аппаратами (КА) и системами. Причем, как известно [1], ЭДТС могут функционировать в двух режимах: генерации электроэнергии и создания тяги. Совместное применение этих двух режимов перспективно, так как позволяет периодически накапливать энергию в системе и затем использовать ее для управления движением КА. Следовательно, на основе ЭДТС существует возможность разработки экономичных методов управления космическими системами, в частности, тросовыми группировками КА. Данное направление использования тросовых систем неизменно присутствует в космических программах многих стран мира, что выражается в реальных тросовых экспериментах, проведенных на орбитах вблизи Земли с проводящими ток тросами, которых в настоящее время насчитывается более десятка [2–5]. С помощью проведенных экспериментов доказана возможность практического использования ЭДТС для генерации электроэнергии, для изменения параметров орбит КА, для удаления с орбит космического мусора и т. д. Реализация реальных тросовых экспериментов естественно сопровождалась многочисленными теоретическими разработками, где рассматривалась динамика и методы управления ЭДТС, например, [6–11]; исследовались процессы взаимодействия проводящих тросов с ионосферой [12, 13]. Подготовка и проведение тросовых экспериментов также стимулировали разработку конструкций ЭДТС, в частности, оборудования, обеспечивающего взаимодействие проводящих тросов с плазмой (сбор и поток в плазму электронов), например, [14, 15]. Естественно здесь упомянуты только некоторые работы из очень большого количества исследований, посвященных этому направлению.
В данной работе рассматривается метод формирования вращающейся линейной тросовой группировки из трех микроспутников, соединенных проводящими ток тросами. Предлагается использовать двухэтапный метод формирования вращающейся космической системы. На первом этапе используется известный закон “быстрого” развертывания орбитальной тросовой системы (ток в тросах отсутствует), который состоит из участков ускоренного выпуска троса и его торможения [16]. Близкий к нему закон был использован в реальном орбитальном тросовом эксперименте YES2 [17], в котором трос был развернут на длину около 30 км. После этого на втором этапе предлагается для перевода системы во вращение использовать электромагнитную силу, которая возникает в проводящих ток тросах в магнитном поле Земли. Заданная величина и направление постоянного тока в тросах обеспечивается с помощью бортовых источников энергии (режим создания тяги). Предлагаемый способ перевода тросовой системы во вращение имеет преимущества по сравнению со способом, использующим реактивные двигатели [18]. В этом случае нет необходимости размещать двигатели на крайних микроспутниках, а если они есть, то не надо расходовать топливо. Кроме того, управление ориентацией двигателей (или микроспутников) еще больше усложняет задачу. Здесь также необходимо отметить, что вращающиеся ЭДТС имеют несомненные преимущества с точки зрения устойчивости их движения, что было отмечено в [6], по сравнению с вертикальными ЭДТС, функционирование которых на орбите обеспечивается дополнительными алгоритмами стабилизации [10], [19] с помощью изменения тока в тросе.
Для описания движения линейной тросовой группировки микроспутников используются уравнения Лагранжа. Исследуются пространственные движения системы для экваториальных орбит и для орбит с не нулевым наклонением. В качестве модели магнитного поля Земли рассматривается наклонный (или косой) диполь [1], ось которого составляет некоторый угол (около 11 градусов) с осью вращения Земли. Уравнения Лагранжа, описывающие движения центров масс микроспутников, дополняются уравнениями движения спутников относительно центров масс, которые записываются в традиционной форме с помощью динамических и кинематических уравнений Эйлера. Оценивается возможность применения известного аналитического решения, описывающего угловое движение капсулы на одиночном тросе [20], для определения угла нутации (угла между направлением троса и продольной осью спутника) для микроспутников в рассматриваемой задаче, в частности, для микроспутника, расположенного в середине тросовой группировки и соединенного двумя тросами с концевыми спутниками. Использование предлагаемого способа формирования вращающейся тросовой группировки и сравнение аналитического решения для угла нутации с численным решением иллюстрируется численными примерами. В частности, показано, что применение двухэтапного способа формирования системы дает возможность в несколько раз уменьшить необходимую величину тока в тросах при переводе ЭДТС во вращение по сравнению со случаем, когда тросовая группировка переводится во вращение из вертикального состояния равновесия.
2. Уравнения движения системы. Для построения математической модели движения тросовой системы используются уравнения Лагранжа
(2.1)
$\frac{d}{{dt}}\left( {\frac{{\partial {{T}_{c}}}}{{\partial{ \dot {q}}}}} \right) - \frac{{\partial {{T}_{c}}}}{{\partial q}} = - \frac{{\partial P}}{{\partial q}} + Q$Кинетическая энергия системы определяется через скорости, определенные в абсолютной геоцентрической орбитальной системе координат $OXYZ$
(2.2)
${{T}_{c}} = \frac{1}{2}\sum\limits_{k = 1}^3 {{{m}_{k}}(\dot {x}_{k}^{2} + \dot {y}_{k}^{2} + \dot {z}_{k}^{2})} $Координаты точек в системах координат $OXYZ$ и $O{{X}_{o}}{{Y}_{o}}{{Z}_{o}}$ связаны соотношениями
(2.3)
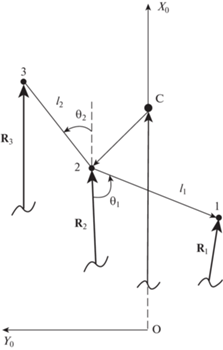
${{x}_{k}} = {{x}_{{ok}}}\cos u - {{y}_{{ok}}}\sin u,\quad {{y}_{k}} = {{x}_{{ok}}}\sin u + {{y}_{{ok}}}\cos u,\quad {{z}_{k}} = {{z}_{{ok}}}$В соответствии с рис. 1 справедливы следующие векторные соотношения
(2.4)
${{R}_{1}} = {{R}_{c}} + {{r}_{1}} + {{r}_{2}},\quad {{R}_{2}} = {{R}_{c}} + {{r}_{2}},\quad {{R}_{3}} = {{R}_{c}} + {{r}_{2}} + {{r}_{3}}$Проецируя векторные равенства на оси системы координат $O{{X}_{o}}{{Y}_{o}}{{Z}_{o}}$, получим
(2.5)
${{x}_{{o2}}} = {{R}_{c}} + \left( {{{m}_{1}}{{l}_{1}}\cos {{{{\theta }}}_{1}}\cos {{{{\varphi }}}_{1}} - {{m}_{3}}{{l}_{2}}\cos {{{{\theta }}}_{2}}\cos {{{{\varphi }}}_{2}}} \right){\text{/}}{{m}_{s}}$Потенциальная энергия соответствует центральному сферическому гравитационному полю и определяется следующим образом
Так как размеры системы много меньше расстояния до притягивающего центра ${{l}_{{1,2}}} \ll {{R}_{c}}$, то при определении обобщенных гравитационных сил потенциальная энергия представляется в виде ряда по малым параметрам с учетом членов до второго порядка. Так, например, для центрального микроспутника ${{m}_{2}}$ имеем
Подстановка выражений (2.2–2.6) в уравнения Лагранжа и проведение весьма сложных, но рутинных преобразований, в основном связанных с операцией дифференцирования функций ${{T}_{c}}$ и $P$, позволяет определить уравнения движения группировки микроспутников в виде системы 12 обыкновенных дифференциальных уравнений первого порядка с точностью до обобщенных непотенциальных сил. Эта система уравнений здесь не приводится из-за чрезвычайной громоздкости получаемых выражений. Здесь необходимо отметить, что в полученной системе уравнений движения не учитывались вторые производные $\ddot {u}$, ${{\ddot {R}}_{c}}$, то есть они были применены для орбит со сравнительно небольшим эксцентриситетом (в этой статье для $e \leqslant 0.01$).
3. Определение обобщенных непотенциальных сил. Вектор обобщенных сил $Q$ в уравнениях (2.1) определяется по-разному в соответствии с этапами формирования ВТС. На этапе развертывания системы используется способ выпуска троса, основанный только на торможении тросов в механизмах, расположенных на центральном микроспутнике. Предполагается, что механизмы не могут втягивать трос и являются практически безынерционными. Подобный метод развертывания тросовой системы использовался в реальном тросовом эксперименте [17]. Так как в построенной математической модели движения тросовой системы тросы являются невесомыми (их масса не учитывается) и инерционностью механизмов пренебрегается, то силы трения будут равны силам натяжениям в тросах. При этом силы трения будут совершать работу на возможных перемещениях ${{\delta }}{{l}_{{1,2}}}$ и соответствующие обобщенные силы будут равны ${{Q}_{{1,2}}} = - {{T}_{{1,2}}}$, причем для остальных обобщенных сил имеем ${{Q}_{k}} = 0\,\,\left( {k = 3,...6} \right)$.
На этапе развертывания системы на заданную длину тросов используется простая релейная программа изменения сил натяжения вида
(3.1)
${{T}_{{1,2}}} = \left\{ \begin{gathered} {{T}_{{\min }}},\quad {\text{если}}\quad t < {{t}_{1}} \hfill \\ {{T}_{{\min }}} + \left( {{{T}_{{\max }}} - {{T}_{{\min }}}} \right){{\sin }^{2}}\left[ {{{k}_{p}}(t - {{t}_{1}})} \right],\quad {\text{если}}\quad {{t}_{1}} \leqslant t \leqslant {{t}_{2}} \hfill \\ {{T}_{{\max }}},\quad {\text{если}}\quad t > {{t}_{2}} \hfill \\ \end{gathered} \right.$Известно, что релейная программа с одной стороны соответствует критерию быстродействия при выпуске троса на заданную длину, а другой стороны отклонение троса от вертикали по окончанию развертывания системы близко к максимально возможному [16]. Последнее обстоятельство является весьма важным в рассматриваемой здесь задаче о переводе системы во вращение, так как наличие не нулевого отклонения тросов от вертикали позволяет существенно уменьшить величину требуемого тока по сравнению со случаем, когда переход во вращение происходит из вертикального положения равновесия системы. Сглаживание релейной зависимости для силы натяжения было предложено в [20] и позволяет избежать резких скачков в силах натяжения тросов, наличие которых может повлиять на устойчивость угловых движений микроспутников относительно направления тросов. Для окончательного определения программы (3.1) решается краевая задача о выборе параметров tp, ${{T}_{{\min }}},\,{{T}_{{\max }}}$ для каждого из тросов исходя из выполнения условий по окончания их выпуска: ${{l}_{{1,2}}}({{t}_{e}}) = {{l}_{e}},{{\dot {l}}_{{1,2}}}({{t}_{e}})$ = 0, ${{{{\dot {\theta }}}}_{{1,2}}}({{t}_{e}}) = 0$, где ${{l}_{e}}$ – заданная конечная длина тросов. Дополнительными параметрами могут также рассматриваться начальные скорости разделения спутников ${{\dot {l}}_{{1,2}}}(0)$.
После окончания развертывания системы заданные длины тросов фиксируются и перевод системы во вращение осуществляется с помощью распределенных электромагнитных сил, возникающих в проводящих ток тросах при их взаимодействии с магнитным полем Земли. При определении обобщенных электромагнитных сил используется допущение о прямолинейности тросов. Это связано с тем, что, во-первых, предлагаемый способ управления будет применяться для сравнительно небольших длин тросов (несколько километров); во-вторых, предполагается, что необходимые величины токов (и соответственно интенсивность распределенной нагрузки) являются достаточно малыми (что подтверждается на численных примерах, приведенных ниже). Здесь необходимо отметить, что методика приближенного учета изгибных колебаний невесомого троса под действием распределенной нагрузки на орбите известна [1], и ранее применялась для тросовой системы с наноспутниками [11], масса которых составляла несколько килограмм. Здесь же рассматривается тросовая система с микроспутниками, массы которых по крайней мере на порядок больше, что также приводит к уменьшению изгиба тросов [11].
Обобщенные электромагнитные силы определяются по общей формуле
(3.2)
${{Q}_{k}} = \sum\limits_{i = 1}^2 {{{F}_{i}}\frac{{\partial {{\rho }_{i}}}}{{\partial {{q}_{k}}}}} \,,\,\,\,k = 3,...6$Электромагнитные силы вычисляются следующим образом [1]
где ${{I}_{{1,2}}}$ – величины тока в тросах, ${{\tau }_{{1,2}}}$ – единичные вектора, показывающие направления тока; $B$ – вектор магнитной индукции. Здесь за положительное направление токов принимаются направления, когда ток направлен от концевых спутников к центральному.Вектор магнитной индукции $B$ принимается постоянным в пределах тросовой системы и определяется в ее центре масс в соответствии с моделью наклонного диполя [1]
где ${{B}_{0}} = {{{{\mu }}}_{m}}{\text{/}}R_{c}^{3}$, ${{{{\mu }}}_{m}} = 8$ × 106 Тл км3 – магнитный момент земного диполя, ${{e}_{c}} = {{R}_{c}}{\text{/}}{{R}_{c}}$, e – единичный вектор, направленный по оси диполя; $\left( {e \cdot {{e}_{c}}} \right)$ – скалярное произведение. Вектор e составляет с осью вращения Земли угол ${{\delta }} = 11^\circ 34'$ и совершает относительно нее суточную прецессию.Вектора ${{F}_{k}}$ (3.3) приложены в средней точке тросов и их точки приложения определяются векторными равенствами ${{\rho }_{1}} = {{r}_{1}}{\text{/}}2 + {{r}_{2}},\;{{\rho }_{2}} = {{r}_{2}} + {{r}_{3}}{\text{/}}2$ (рис. 1). Следовательно, например, в орбитальной подвижной системе координат $O{{X}_{o}}{{Y}_{o}}{{Z}_{o}}$ их проекции будут равны
Тогда для вычисления скалярных произведений в формуле (3.2) вектор $B$ также должен быть преобразован в орбитальную систему координат $O{{X}_{o}}{{Y}_{o}}{{Z}_{o}}$. Это осуществляется через матрицы перехода между системами координат $OXYZ$, $O{{X}_{o}}{{Y}_{o}}{{Z}_{o}}$, $O{{X}_{m}}{{Y}_{m}}{{Z}_{m}}$, где $O{{X}_{m}}{{Y}_{m}}{{Z}_{m}}$ – геоцентрическая система координат, связанная с осью магнитного земного диполя. Матрица перехода от системы координат $OXYZ$ к системе координат $O{{X}_{m}}{{Y}_{m}}{{Z}_{m}}$ имеет вид
где ${{L}_{{{\delta }}}} = \left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos {{\delta }}}&{\sin {{\delta }}} \\ 0&{ - \sin {{\delta }}}&{\cos {{\delta }}} \end{array}} \right),$ ${{L}_{{{\lambda }}}} = \left( {\begin{array}{*{20}{c}} {\cos {{\lambda }}}&{\sin {{\lambda }}}&0 \\ { - \sin {{\lambda }}}&{\cos {{\lambda }}}&0 \\ 0&0&1 \end{array}} \right),$ ${{\lambda }}$ – угол, определяющий положение системы координат $O{{X}_{e}}{{Y}_{e}}{{Z}_{e}}$ (связанной с вращающейся Землей), относительно абсолютной геоцентрической системы координат $OXYZ$. Используя матрицу (3.5) и известную матрицу перехода между системами координат $OXYZ$ и $O{{X}_{o}}{{Y}_{o}}{{Z}_{o}}$, зависящую от углов $i,\,u$ [21], где $i$ – наклонение орбиты, u – аргумент широты, нетрудно определить проекции вектора B в орбитальной системе координат $O{{X}_{o}}{{Y}_{o}}{{Z}_{o}}$, а значит обобщенные силы (3.2). Здесь, не ограничивая общности, можно принять долготу восходящего узла орбиты равной нулю.4. Уравнения движения микроспутников относительно центра масс. Движение микроспутников относительно своих центров масс описывается с помощью классических динамических и кинематических уравнений Эйлера
(4.1)
${{\dot {\omega }}_{k}} = J_{k}^{{ - 1}}\left( {{{M}_{k}} - {{\omega }_{k}} \cdot {{J}_{k}}} \right)$(4.2)
${{{{\dot {\psi }}}}_{k}} = ({{{{\omega }}}_{{zk}}}\sin {{{{\beta }}}_{k}} - {{{{\omega }}}_{{yk}}}{\text{cos}}{{{{\beta }}}_{k}}){\text{/}}\sin {{{{\alpha }}}_{k}} + \Delta {{{{\dot {\psi }}}}_{k}}$(4.3)
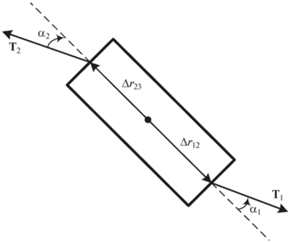
$\Delta {{{{\dot {\psi }}}}_{k}} = (\Delta {{{{\omega }}}_{{yk}}}{\text{cos}}{{{{\beta }}}_{k}} - \Delta {{{{\omega }}}_{{zk}}}\sin {{{{\beta }}}_{k}}){\text{/}}\sin {{{{\alpha }}}_{k}}$При записи уравнений (4.1) учитываются только моменты от сил натяжения тросов, которые определяются в виде
(4.4)
${{M}_{1}} = - \Delta {{r}_{1}} \cdot {{T}_{1}},\quad {{M}_{2}} = \Delta {{r}_{{12}}} \cdot {{T}_{1}} + \Delta {{r}_{{23}}} \cdot {{T}_{2}},\quad {{M}_{3}} = - \Delta {{r}_{3}} \cdot {{T}_{2}}$Начальные условия углового движения микроспутников формируются в момент их разделения. Введем обозначения для относительных скоростей при разделении спутников ${{V}_{{r1}}}$ и ${{V}_{{r3}}}$. Вектора ${{V}_{{r1}}}$ и ${{V}_{{r3}}}$ направлены в сторону отделения спутников с массами m1 и m3. В соответствии с законом сохранения импульса имеем
(4.5)
${{V}_{2}} = {{V}_{c}} - \left( {{{m}_{1}}{{V}_{{r1}}} + {{m}_{3}}{{V}_{{r3}}}} \right){\text{/}}{{m}_{s}},\quad {{V}_{{1,3}}} = {{V}_{2}} + {{V}_{{r1,3}}}$Тогда изменения кинетических моментов спутников определяются в соответствии с теоремой об изменении кинетического момента при ударном взаимодействии твердых тел
(4.6)
$\Delta {{K}_{1}} = - \Delta {{r}_{1}} \times {{S}_{1}},\quad \Delta {{K}_{2}} = \Delta {{r}_{{12}}} \cdot S_{1}^{'} + \Delta {{r}_{{23}}} \cdot S_{2}^{'},\quad \Delta {{K}_{3}} = - \Delta {{r}_{3}} \cdot {{S}_{2}}$С учетом (4.5) выражения (4.7) можно переписать в виде
(4.8)
${{S}_{{1,3}}} = \frac{{{{m}_{{1.3}}}}}{{{{m}_{s}}}}\left[ {{{V}_{{r1.3}}}\left( {{{m}_{2}} + {{m}_{{3.1}}}} \right) - {{m}_{{3.1}}}{{V}_{{r3.1}}}} \right]$Тогда угловые скорости спутников после их разделения определяются следующим образом
(4.9)
${{\omega }_{k}}\left( 0 \right) = \omega _{k}^{'}\left( 0 \right) + J_{k}^{{ - 1}}\Delta {{K}_{k}},\quad k = 1,2,3$5. Анализ движения микроспутников как материальных точек. В качестве примера рассматривается движение тросовой системы, состоящей из трех микроспутников с массами ${{m}_{{1,3}}} = 10\,\,{\text{кг,}}\,\,{{m}_{2}} = 60\,\,{\text{кг}}$. Конечная длина тросов на этапе развертывания системы составляет 3.03 км. Параметры орбиты: эксцентриситет $0.01$, высота в перигее 500 км, наклонение орбиты π/3. Начальное положение системы – перигей орбиты, причем перигей орбиты совпадает с ее линией узлов. Разделение спутников происходит в направлении, близком к местной вертикали. Относительные скорости при разделении ${{V}_{{r1,3}}} = 2.5$ м/с. После решения краевой задачи были получены следующие значения параметров программы выпуска тросов: Tmin = 0.014 H, ${{T}_{{\max }}} = 0.054\,{\text{Н,}}\,\,{{t}_{p}} = 900$ c, kp = = 0.005. При этом время развертывания системы составило $1710$ c. После окончания развертывания для перевода системы во вращение используется простая релейная программа изменения величины тока
(5.1)
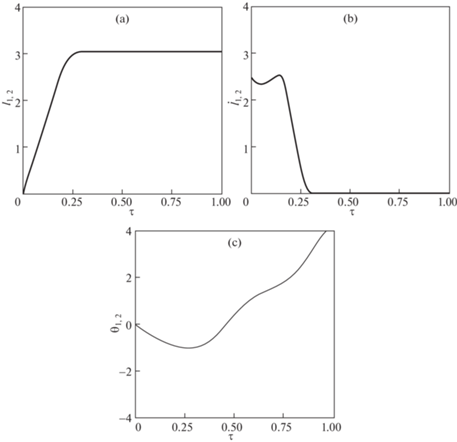
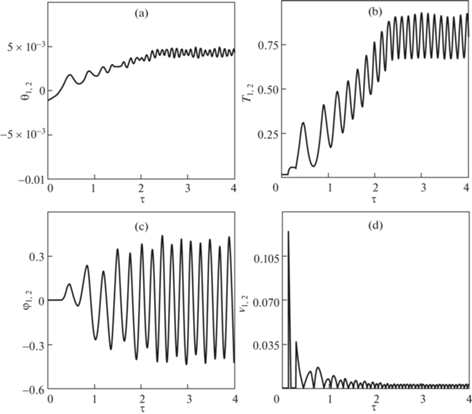
${{I}_{{1.2}}} = \left\{ \begin{gathered} {{I}_{{\max }}}\quad {\text{if}}\quad 0 \leqslant {{{{{\dot {\theta }}}}}_{{1.2}}} < {{{{{\dot {\theta }}}}}_{{\max }}} \hfill \\ 0\quad {\text{if}}\quad {{{{{\dot {\theta }}}}}_{{1.2}}} < 0 \hfill \\ \end{gathered} \right.$В случае полной симметрии системы, включая условия разделения, характерные зависимости для концевых спутников совпадают, а центр масс системы совпадает с центром масс центрального спутника. Для этого случая зависимости для основных параметров, характеризующих процесс перевода тросовой системы во вращение, приводятся на рис. 3, 4, где ${{\tau }}$ – безразмерное время (количество витков). На рис. 3 соответствует начальному этапу формирования вращающейся системы, на рис. 4 показаны параметры движения, важные для всего процесса. На втором этапе величина тока ${{I}_{{\max }}} = 0.36\,{\text{A}}$. Если ${{\tau }} \geqslant 2.4$, полагается ${{I}_{{\max }}} = 0$, и система продолжает вращаться с почти постоянной угловой скоростью. Колебания угловой скорости (рис. 2, a) объясняются тем, что для орбит с наклонением (здесь $i = {{\pi /}}3$) система совершает сложное пространственное движение, которое характеризуется колебаниями системы относительно плоскости орбиты (рис. 2, с). Наличие асимметрии в массах концевых спутников принципиального значения не имеет и лишь приводит к необходимости уточнять значения параметров программ управления (3.1) при решении краевой задачи. Ошибки в условиях разделения спутников как по скорости, так и по направлению отделения, также приводят к асимметрии движения концевых спутников, что выражается в основном в конечных длинах тросов, так как выпуск троса прекращается при выполнении условий ${{\dot {l}}_{{1.2}}}({{t}_{e}}) = 0$. Кроме того, в этом случае конечные отклонения тросов от вертикали после первого этапа формирования системы также отличаются от номинальных значений, что в итоге приводит к тому, что после достижения заданной угловой скорости вращения тросов они уже не находятся на одной прямой. Компенсация этих отклонений при необходимости может быть проведена после достижения заданных угловых скоростей вращения тросов с помощью управления токами, например, с использованием алгоритмов, описанных в [19]. Эта задача здесь не рассматривается.
Для симметричного случая нетрудно аналитически оценить необходимую величину тока для перевода системы во вращение. Для этого рассматривается более простая модель магнитного поля (прямой диполь) и не учитываются колебания системы вне плоскости орбиты (из рис. 4, с следует, что колебания по углам ${{{{\varphi }}}_{{1,2}}}$ почти симметричны), то есть полагается ${{{{\varphi }}}_{{1.2}}} = 0$ (на экваториальной орбите это условие выполняется точно, если нет начальных отклонений по углам ${{{{\varphi }}}_{{1.2}}}$). Наличие этих допущений приводит к тождественности уравнений, описывающих движения концевых спутников в плоскости орбиты, которые принимают вид
(5.2)
${{{{\ddot {\theta }}}}_{{1.2}}} + 1.5{{\dot {u}}^{2}}\sin 2{{{{\theta }}}_{{1.2}}} - {{B}_{0}}{{I}_{{1.2}}}\cos i{\text{/}}2{{m}_{{1.3}}} = 0$Уравнение (5.2) описывает движение гравитационного маятника на орбите при наличие действующего на него постоянного момента. Это уравнение имеет интеграл вида
(5.3)
${{{{\dot {\theta }}}}^{2}} - 1.5{{\dot {u}}^{2}}\cos 2{{\theta }} - {{B}_{0}}I\,{{\theta }}\cos i{\text{/}}m = C$Значения интеграла определим в момент окончания выпуска тросов (${{{{\theta }}}_{e}},\,{{{{\dot {\theta }}}}_{e}} = 0$), тогда
(5.4)
$ - 1.5{{\dot {u}}^{2}}\cos 2{{{{\theta }}}_{e}} - {{B}_{0}}I\,{{{{\theta }}}_{e}}\cos i{\text{/}}m = C$С другой стороны, нижняя оценка минимального необходимого тока соответствует отклонению системы ${{\theta }} = \pi {\text{/}}2$ (${{\dot {\theta }}} = 0$). Отсюда, приравнивая значения интеграла в двух рассмотренных положениях системы, получим
(5.5)
${{I}_{{\min }}}\left( {{{{{\theta }}}_{e}}} \right) = \frac{{3m{{{\dot {u}}}^{2}}}}{{{{B}_{0}}\cos i\left( {{{\pi }} + 2{{{{\theta }}}_{e}}} \right)}}\left( {1 + \cos 2{{{{\theta }}}_{e}}} \right)$Для круговой орбиты, так как ${{B}_{0}} = {{{{\mu }}}_{m}}{\text{/}}R_{c}^{3}$ и ${{\dot {u}}^{2}} = K{\text{/}}R_{c}^{3}$, выражение имеет наиболее простой вид
(5.6)
${{I}_{{\min }}}\left( {{{{{\theta }}}_{e}}} \right) = \frac{{3mK}}{{{{{{\mu }}}_{m}}\cos i\left( {{{\pi }} + 2{{{{\theta }}}_{e}}} \right)}}\left( {1 + \cos 2{{{{\theta }}}_{e}}} \right)$При использовании формулы, необходимо отметить, что в рассматриваемой задаче всегда ${{{{\theta }}}_{e}} < 0$. Дело в том, что в процессе развертывания системы нижний спутник ${{m}_{1}}$ отклоняется от вертикали в направлении орбитального движения центра масс системы или оси $O{{Y}_{o}}$ (рис. 1). Соответственно верхний спутник ${{m}_{3}}$ – наоборот. Это объясняется действием сил Кориолиса в подвижной орбитальной системе координат $O{{X}_{o}}{{Y}_{o}}{{Z}_{o}}$. Для формул (5.5), (5.6) очевидно выполняется ${{I}_{{\min }}}\left( {{{{{\theta }}}_{e}}} \right) \to 0$ при ${{{{\theta }}}_{e}} \to - {{\pi /}}2$. При использовании программы (3.1) удается достигнуть предельных величин порядка ${{{{\theta }}}_{e}} \approx - 1$ (рис. 3, с). В этом случае, например, получаем выигрыш в величине тока по сравнению со случаем перевода системы из положения равновесия (${{{{\theta }}}_{e}} = 0$) на круговой орбите примерно в 5.6 раза. Конечно, надо задавать ${{I}_{{\max }}} > {{I}_{{\min }}}\left( {{{{{\theta }}}_{e}}} \right)$, чтобы обеспечить необходимое натяжение тросов, которое принимает минимальное значение в окрестности особой точки ${{\theta }} = {{\pi /}}2$ (рис. 4, b). Для приведенного численного примера с помощью численных расчетов был выбран ток ${{I}_{{\max }}} = 0.36\,{\text{A}}$, при этом формула (5.6) дает ${{I}_{{\min }}}\left( { - 1} \right) = 0.34\,{\text{A}}$.
6. Анализ движения микроспутников относительно центров масс. Анализ углового движения микроспутников будем рассматривать только с учетом моментов от сил натяжения тросов, то есть гравитационные моменты и другие малые возмущения рассматриваться не будут. Предполагается, что натяжения тросов в процессе формирования системы всегда положительны (не ослабевают), что обеспечивается выбором параметров программ управления (3.1). Рассматривается два случая: 1) микроспутники статически и динамически симметричны; 2) имеется статическая и динамическая асимметрия. Статическая асимметрия характеризуется поперечными $\Delta {{y}_{k}},\,\,\Delta {{z}_{k}}$ смещениями точек крепления тросов относительно осей ${{c}_{k}}{{x}_{k}}$ (продольные оси спутников) главных центральных связанных систем координат ${{c}_{k}}{{x}_{k}}{{y}_{k}}{{z}_{k}}$, динамическая асимметрия – разностью экваториальных моментов ${{J}_{{zk}}} - {{J}_{{yk}}}\,\left( {k = 1,2,3} \right)$. Предполагается, что асимметрии являются малыми, то есть относительные величины $\left| {\Delta {{y}_{k}}{\text{/}}\Delta {{r}_{k}}} \right|$, $\left| {\Delta {{z}_{k}}{\text{/}}\Delta {{r}_{k}}} \right| \ll 1$, $\left| {\left( {{{J}_{{zk}}} - {{J}_{{yk}}}} \right){\text{/}}{{J}_{{ck}}}} \right| \ll 1$, где ${{J}_{{ck}}} = \left( {{{J}_{{yk}}} + {{J}_{{zk}}}} \right){\text{/}}2$, а за величину $\Delta {{r}_{2}}$ для центрального спутника можно принять $\Delta {{r}_{{12}}}$ или $\Delta {{r}_{{23}}}$ (4.4). С учетом этих предположений угловое движение спутника в составе тросовой системы близко к случаю Лагранжа при вращении твердого тела вокруг неподвижной точки (в данном случае вокруг его центра масс) при действии малых возмущений, связанных с наличием рассматриваемых асимметрий [22]. В симметричном случае изменение угловых характеристик движений спутников относительно своих центров масс полностью соответствует изменению сил натяжения, которые соответствуют заданной программе (3.1) и которые можно рассматривать как медленно изменяющиеся параметры. Оценку “медленности” изменения сил натяжения можно определить с помощью отношений $\omega _{{1,2}}^{{(t)}}$ = $\left| {d{{T}_{{1,2}}}{\text{/}}dt{\text{/}}{{T}_{{1,2}}}} \right|$ [22, 23], сравнивая их с характерными частотами колебаний спутников относительно центра масс ${{{{\omega }}}_{{{{\alpha k}}}}} = \sqrt {{{M}_{k}}{\text{/}}{{J}_{{ck}}}} $, где ${{{{\omega }}}_{{\alpha k}}}$ – частоты колебаний твердого тела на тросе в плоском случае при малых углах нутации [20]. Рассмотрим микроспутники со следующими параметрами: 1) концевые спутники представляют собой однородные сферы с радиусом 0.25 м; 2) центральный спутник – прямоугольный параллелепипед размерами 0.4 × 0.4 × 1 м. Для этих исходных данных изменение отношения ${{{{\nu }}}_{2}} = {{{{\omega }}}_{{{{\alpha 2}}}}}{\text{/}}\omega _{2}^{{\left( t \right)}}$, например, для центрального спутника (которое можно рассматривать как величину, пропорциональную малому параметру задачи) в процессе формирования системы приводится на рис. 4,d. Максимальное значение параметра ${{{{\nu }}}_{2}} = 0.12$ имеет место в окрестности переключения программной силы натяжения с ${{T}_{{\min }}}$ на ${{T}_{{\max }}}$ (3.1) на первом этапе формирования системы. В связи с этим для приближенной оценки зависимостей, характеризующих угловое движение микроспутников в симметричном случае, может быть использовано аналитическое решение, полученное методом усреднения в работе [20] при движении спускаемой капсулы на одиночном тросе. Это решение, записанное для центрального спутника, имеет вид
(6.1)
${{a}_{{1,2}}} = {{a}_{{1,2}}}(0){{\left( {{{\omega }_{{{{\alpha 2}}}}}(0){\text{/}}{{\omega }_{{{{\alpha 2}}}}}} \right)}^{{0.5}}}$Решение (6.1) приближенно описывает пространственный случай движения центрального спутника относительно своего центра масс и зависит от начальных угловых скоростей (4.9), которые формируются при разделении спутников, а также от начального угла нутации ${{{{\alpha }}}_{2}}\left( 0 \right)$
(6.2)
${{a}_{{1.2}}}\left( 0 \right) = \sqrt {{{\omega }}_{{z2}}^{2}\left( 0 \right) + {{{\left( {{{{{\omega }}}_{{y2}}}\left( 0 \right) + {{{{\alpha }}}_{2}}\left( 0 \right){{{{\omega }}}_{{{\text{2}}{\text{.1}}}}}\left( 0 \right)} \right)}}^{2}}} {\text{/2}}{{{{\omega }}}_{{{{\alpha 2}}}}}\left( 0 \right)$(6.3)
${{{{\alpha }}}_{{\max }}} = {{a}_{1}} + {{a}_{2}},\quad {{{{\alpha }}}_{{\min }}} = \left| {{{a}_{1}} - {{a}_{2}}} \right|$(6.4)
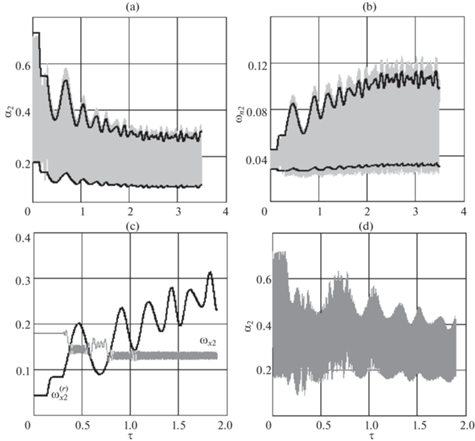
${{{{\omega }}}_{{\max }}} = {{a}_{1}}{{{{\omega }}}_{1}} - {{{{\omega }}}_{2}}{{a}_{2}},\quad {{{{\omega }}}_{{\min }}} = \left| {{{a}_{1}}{{{{\omega }}}_{1}} + {{{{\omega }}}_{2}}{{a}_{2}}} \right|$В качестве примера на рис. 5,a,b показаны зависимости ${{{{\alpha }}}_{2}}\left( {{\tau }} \right){\text{,}}\,\,{{{{\omega }}}_{{n2}}}\left( {{\tau }} \right)$, определенные по исходным уравнениям (4.1), (4.2) и соответствующие начальным условиям движения центрального спутника ${{{{\omega }}}_{{x2}}}(0) = 0.18,\,\,{{{{\omega }}}_{{y2}}}(0) = - 0.03,\,\,{{{{\omega }}}_{{z2}}}(0) = 0.03$, α2(0) = 0.3. Там же приведены кривые, построенные по аналитическим формулам (6.3), (6.4). Возникающая погрешность на рис. 5,a,b в определении предельных кривых объясняется тем, что рассмотрена орбита с ненулевым наклонением $i = {{\pi /}}3$ (и модель магнитного поля – наклонный диполь), движение по которой приводит к колебаниям системы вне орбитальной плоскости (рис. 4,с). На экваториальной орбите предельные кривые (6.3), (6.4) описывают рассматриваемые зависимости почти идеально. Приведенные зависимости (рис. 5, a, b) для симметричного центрального спутника с точки зрения теоретической механики аналогичны движению твердого тела вокруг неподвижной точки в случае Лагранжа, так как диссипация энергии (например, трение в шарнирах) здесь не учитывается, поэтому ${{{{\omega }}}_{{x2}}} = {\text{const}}$.
Наличие малой статической и динамической асимметрий спутника может привести к резонансным явлениям при его движении в составе тросовой системы [22] и, как следствие, к большим возмущениям. В этом случае угловое движение, например, центрального спутника зависит от изменения частот ${{{{\omega }}}_{{1,2}}},{{{{\omega }}}_{{x2}}}$, которые характеризуют его движение. Резонансы низшего порядка определяются при ${{{{\omega }}}_{{1,2}}} = \,\,{{{{\omega }}}_{{x2}}}$, откуда нетрудно получить резонансные значения угловой скорости ${{\omega }}_{{x2}}^{{\left( r \right)}}$ при малых углах нутации [24]
(6.5)
${{\omega }}_{{x2}}^{{\left( r \right)}} = \pm {{{{\omega }}}_{{{{\alpha 2}}}}}{\text{/}}{{(1 - {{\bar {J}}_{{x2}}})}^{{0.5}}}$Тогда окрестности резонансов характеризуются условием ${{{{\omega }}}_{{x2}}} \approx {{\omega }}_{{x2}}^{{\left( r \right)}}$. Резонансные угловые скорости (6.5) в рассматриваемой задаче не постоянны и их изменение непосредственно зависит от изменения частоты ${{\omega }_{{{{\alpha }}2}}} = {{\left( {{{M}_{2}}{\text{/}}{{J}_{{c2}}}} \right)}^{{0.5}}}$ и, следовательно, от сил натяжения тросов (3.1). В общем случае при пересечении окрестности резонанса возможны два варианта поведения угловой скорости ${{{{\omega }}}_{{x2}}}$: 1) проход через окрестность резонанса без задержки; 2) “захват” в резонанс, когда угловая скорость остается в окрестности резонансной кривой в течение достаточно длительного времени в силу действующих возмущений. В первом случае имеет место кратковременное возмущение угла нутации α2 и угловой скорости ${{{{\omega }}}_{{x2}}}$, во втором случае возмущения могут иметь “катастрофический” характер, когда, например, значения угла нутации α2 будут больше ${{\pi /}}2$, что может привести к запутыванию троса. Как показывает анализ углового движения микроспутников в рассматриваемой задаче, то здесь характерен первый вариант, то есть пересечение резонансных областей без “захвата”. Это связано с изменением резонансных значений угловой скорости (6.5), которые вследствие увеличения сил натяжения тросов (рис. 4, b) в процессе перевода системы во вращения тоже увеличиваются (в среднем). Подробно этот вопрос был рассмотрен в работе [24] при анализе резонансных движений волчка Лагранжа при малых углах нутации, где показано, что если пересечение резонансных кривых происходит при $d{{\omega }}_{{x2}}^{{\left( r \right)}}{\text{/}}dt > 0$, то вероятность “захвата”, определенная по начальным условиям движения, близка к нулю. Характерный случай изменения переменных в рассматриваемой задаче для центрального спутника при пересечении угловой скорости ${{{{\omega }}}_{{x2}}} > 0$ резонансной области приводится на рис. 5, c, d, где функция ${{{{\omega }}}_{{x2}}}\left( {{\tau }} \right)$ несколько раз пересекает резонансную кривую, не задерживаясь в окрестности резонанса. Авторам не удалось найти случаев “захвата” в резонанс в рассматриваемой задаче. Рис. 5, c, d соответствует малой асимметрии центрального спутника вида ${{(\Delta y_{2}^{2} + \Delta z_{2}^{2})}^{{0.5}}}{\text{/}}\Delta {{r}_{2}} = 0.01$. Если при разделении спутников, например, начальная угловая скорость ${{{{\omega }}}_{{x2}}}\left( 0 \right)$ принимает такое значение, что пересечения резонансных кривых (6.5) не происходит, то поведение переменных, характеризующих угловое движение спутника при наличии малой асимметрии, слабо отличается от их поведения в симметричном случае.
7. Заключение. Предложен двухэтапный способ формирования вращающейся линейной группировки микроспутников с использованием электромагнитных сил, действующих на изолированные, проводящие ток тросы в магнитном поле Земли. Рассматриваемый подход позволяет существенно (в несколько раз) уменьшить требуемую величину тока по сравнению со случаем перевода системы во вращение из положения равновесия, когда линейная группировка находится в режиме гравитационной стабилизации. Для частного случая симметричной системы получена нижняя оценка величины тока для перевода рассматриваемой системы во вращение. Проведен анализ движения микроспутников относительно своих центров масс и показана возможность использования известного аналитического решения, описывающего движение твердого тела вокруг неподвижной точки для малых углов нутации в случае Лагранжа, для оценки амплитудных характеристик углового движения микроспутников в составе рассматриваемой тросовой системы.
Исследование выполнено при финансовой поддержке РФФИ и ГФЕН Китая в рамках научного проекта № 21-51-53002.
Список литературы
Белецкий В.В., Левин Е.М. Динамика космических тросовых систем. М.: Наука, 1990. 336 с.
Zhong R., Zhu Z.H. Dynamics of nanosatellite deorbit by bare electrodynamic tether in low earth orbit // J. Spacecr. Rockets. 2013. V. 50. № 3. P. 691–700. https://doi.org/10.2514/1.A32336
Iñarrea M., Lanchares V., Pascual A., Salas J. Attitude stabilization of electrodynamic tethers in elliptic orbits by time-delay feedback control // Acta Astronaut. 2014. V. 96. P. 280–295. https://doi.org/10.1016/j.actaastro.2013.12.011
Fuhrhop K.R. Theory and Experimental Evaluation of Electrodynamic Tether Systems and Related Technologies. PhD Dissertation. University of Michigan. 2007. 307 p.
Ohkawa Y., Kawamoto S., Okumura T. et al. Review of KITE-electrodynamic tether experiment on HTV-6 // Acta Astronaut. 2020. V. 177. P. 750–758. https://doi.org/10.1016/j.actaastro.2020.03.014
Levin E.M. Dynamic analysis of space tether missions. San Diego: American Astronautical Society, 2007. 453 p.
Zhong R., Zhu Z.H. Optimal control of nanosatellite fast deorbit using electrodynamic tether // J. Guid. Contr. Dyn. 2014. V. 37. № 4. P. 1182–1194. https://doi.org/10.2514/1.62154
Iñarrea M., Lanchares V., Pascual A.I., Salas J.P. Attitude stabilization of electrodynamic tethers in elliptic orbits by time-delay feedback control // Acta Astronaut. 2014. V. 96. P. 280–295. https://doi.org/10.1016/j.actaastro.2013.12.011
Zhou X., Li J., Baoyin H., Zakirov V. Equilibrium control of electrodynamic tethered satellite systems in inclined orbits // J. Guid. Contr. Dyn. 2006. V. 29. № 6. P. 1451–1454. https://doi.org/10.2514/1.21882
Voevodin P.S., Zabolotnov Yu.M. Stabilizing the motion of a low-orbit electrodynamic tether system // J. Comput. Syst. Sci. Int. 2019. V. 58. № 2. P. 270–285. https://doi.org/10.1134/S1064230719020175
Voevodin P.S., Zabolotnov Yu.M. Analysis of the dynamics and choice of parameters of an electrodynamic space tether system in the thrust generation mode // Cosmic Res. 2020. V. 58. № 1. P. 42–52. https://doi.org/10.1134/S0010952520010062
Chen X., Sanmartín J.R. Bare-tether cathodic contact through thermionic emission by low-work-function materials // Phys. Plasmas. 2012. V. 19. P. 1–8. https://doi.org/10.1063/1.4736987
Sánchez-Arriaga G., Bombardelli C., Chen X. Impact of nonideal effects on bare electrodynamic tether performance // J. Propul. Power. 2015. V. 31. № 3. P. 951–955. https://doi.org/10.2514/1.B35393
Кульков В.М., Егоров Ю.Г., Тузиков С.А. Исследование интегральных энергетических характеристик космической электродинамической тросовой системы для орбитальных экспериментов // Изв. РАН. Энергетика. 2017. № 3. С. 114–127.
Кульков В.М., Егоров Ю.Г., Тузиков С.А. Исследование конфигурации и формирование проектного облика развернутой электродинамической тросовой системы в составе орбитальных космических аппаратов // Изв. РАН. Энергетика. 2018. № 3. С. 119–130. https://doi.org/10.7868/S0002331018030123
Ишков С.А., Наумов С.А. Управление развертыванием орбитальной тросовой системы // Вестник Самарского государственного аэрокосмического университета. 2006. Т. 9. № 1. С. 77–85.
Kruijff M. Tethers in Space. Netherlands: Delta-Utec Space Research, 2011. 432 p.
Zabolotnov Yu.M. Dynamics of the formation of a rotating orbital tether system with the help of electro-thruster // Procedia Eng. 2017. V. 185. P. 261–266. https://doi.org/10.1016/j.proeng.2017.03.339
Воеводин П.С., Заболотнов Ю.М. О стабилизации движения электродинамической тросовой системы на околоземной орбите // Изв. РАН. МТТ. 2019. № 4. С. 49–63. https://doi.org/10.1134/S057232991904010X
Заболотнов Ю.М., Наумов О.Н. Движение спускаемой капсулы относительно центра масс при развертывании орбитальной тросовой системы // Космич. исслед. 2012. Т. 50. Вып. 2. С. 177–187.
Основы теории полета космических аппаратов / Под ред. Г.С. Нариманова, М.К., Тихонравова. М.: Машиностроение, 1972. 608 с.
Заболотнов Ю.М. Применение метода интегральных многообразий для анализа пространственного движения твердого тела на тросе // Изв. РАН. МТТ. 2016. № 4. С. 3–18.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 1. Механика. М.: Наука, 1988. 216 с.
Заболотнов Ю.М. Резонансные движения статически устойчивого волчка Лагранжа при малых углах нутации // ПММ. 2016. Т. 80. № 4. С. 432–443.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела