Известия РАН. Механика твердого тела, 2022, № 3, стр. 132-141

ПАРАМЕТРИЧЕСКОЕ УПРАВЛЕНИЕ КОЛЕБАНИЯМИ ПОПЛАВКА

В. Г. Байдулов^a, *

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

Поступила в редакцию 27.09.2021
После доработки 05.12.2021
Принята к публикации 06.12.2021

EDN: RGTFUG
DOI: 10.31857/S0572329922030023

Аннотация

Исследована возможность параметрического управления характеристиками колебаний (амплитудой и частотой) симметричного тонкого протяженного плоского поплавка, колеблющегося около поверхности раздела двух тяжелых идеальных жидкостей, за счет изменения его формы (относительной высоты). Проведен анализ влияния формы тела на характеристики колебаний. Предложена численная и асимптотическая процедуры решения самосогласованной краевой задачи.

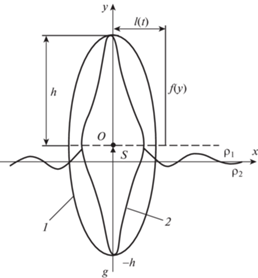
Ключевые слова: поплавок, колебания, интегродифференциальные уравнения, частота колебаний, декремент затухания, управление

1. Постановка задачи. Изучается задача управления колебаниями плоского симметричного (относительно вертикали и горизонтали) узкого поплавка, за счет изменения его формы. Поплавок совершает малые вертикальные колебания на границе раздела двух идеальных несжимаемых жидкостей разной плотности (рис. 1). Для поплавков различной формы определены зависимости локальных характеристик колебаний от времени. Исследовано влияние параметров среды на процесс колебаний. Под управлением понимается такое задание закона изменения относительной высоты поплавка ($\kappa = l{\text{/}}h$) со временем, чтобы локальные характеристики колебаний поплавка (частота и декремент затухания) в течение колебаний оставались неизменными.

Рис. 1.

Геометрия задачи. 1 – эллипсоид, 2 – поплавок Сретенского.

Задача о колебаниях поплавка – пример самосогласованной задачи [1], когда течение вокруг препятствия определяет силу гидродинамического сопротивления (по полю давления), которая вместе с силой Архимеда входит в число сил, позволяющих по второму закону Ньютона рассчитать движение центра масс поплавка. Для решения задачи требуется найти характер обтекания при произвольно заданном вертикальном набегающем потоке. В непрерывно стратифицированной жидкости ранее [2, 3] были решены задачи о свободных колебаниях сферы нейтральной плавучести в идеальной [2] и вязкой [3] жидкости. Анализ самосогласованного движения поплавка и среды, в свою очередь даст возможность для детальной проработки вопросов построения моделей вращения Земли при наличии внутренних движений, что позволит, в частности, улучшить расчеты динамики земного полюса [4]. В последнее время появился интерес к использованию поплавков в качестве базы для плавучих ветряных [5] и гидро- [6] электростанций. В этом случае актуальным оказываются вопросы стабилизации платформы поплавка относительно морского и ветрового волнения.

Известные уравнения малых колебаний поплавка “тонкого” в идеальной жидкости записываются в виде интегродифференциального уравнения, которое для поплавка переменной ширины в безразмерных переменных ($x \to lx$, $y \to hy$, $\vartheta = \Omega t$, ${{\Omega }^{2}}$ = g*/h) зависит от формы поплавка и отношения его ширины к высоте $\kappa = l{\text{/}}h \ll 1$ [7, 8]

(1.1)

$s_{{}}^{{''}} + {{\Omega }^{2}}s = - 2\kappa \left( t \right){{\Omega }^{2}}\int\limits_0^\vartheta {K\left( {\vartheta - \tau } \right)s{\kern 1pt} '\left( \tau \right)d\tau } ,\quad {{\Omega }^{2}} = \frac{4}{{\pi \left( {1 + \kappa J} \right)}}$

где $\Omega $ – частота собственных колебаний поплавка (без учета обратного влияния волнового поля). Величина J определяется формой тела и характеристиками гидродинамической системы и имеет смысл обезразмеренной присоединенной массы единицы длины поплавка

$J = \frac{4}{{{{\pi }^{2}}}}\int\limits_0^1 {\int\limits_0^1 {f{\kern 1pt} '\left( r \right)f{\kern 1pt} '\left( q \right)\ln \left| {\frac{{q + r}}{{q - r}}} \right|\,dqdr} } $

Предполагается, что относительная ширина поплавка может зависеть от времени $\kappa = \kappa \left( t \right)$. Далее для уравнения (1.1) рассматривается задача Коши, соответствующая начальному состоянию покоя $s\left( 0 \right) = 1$, $\dot {s}\left( 0 \right) = 0$. Форму поплавка описывает функция $f:\,\,x = f\left( y \right)$. Ранее [7, 8] были для некоторых форм поплавков проведены недостаточно полные расчеты.

Большое влияние на характеристики колебаний поплавка оказывает вид ядра интегральной части уравнения колебаний

(1.2)

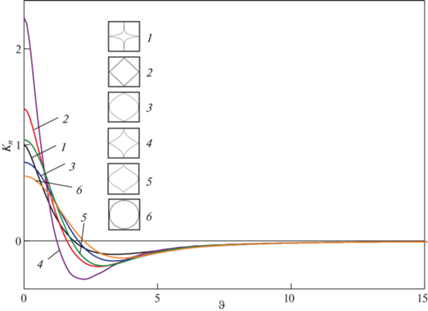
$K\left( \vartheta \right) = \int\limits_0^\infty {{{R}^{2}}\left( \xi \right)\cos \left( {\sqrt \xi \vartheta } \right)d\xi } ,\quad R\left( \xi \right) = - \int\limits_0^1 {f{\kern 1pt} '\left( y \right)\exp \left( { - \xi y} \right)dy} $

зависимость которого от аргумента (времени) имеет однотипный характер (рис. 2). Расчеты ядра интегро-дифференциального уравнения проведены для набора поплавков, с вогнутой и выгнутой относительно оси симметрии поверхности (1. f = $\exp ( - {\text{|}}y{\text{|}})$; 2. $f = 1 - \left| y \right|$; 3. $f = 1 - {{y}^{2}}$; 4. $f = {{\left( {1 - \left| y \right|} \right)}^{2}}$; 5. $f = {{(1 - {{y}^{2}})}^{2}}$; 6. f = $\sqrt {1 - {{y}^{2}}} $). Несмотря на значительные различия максимальных и минимальных значений, зависимости и положения для поплавков разных форм, причем ограничиваемые кривыми площади остаются примерно одинаковыми (равными 0.067). Как будет показано далее, ядро интегродифференциального уравнения оказывает все большее влияние на характер колебаний при увеличении относительной толщины поплавка.

Рис. 2.

Зависимость ядра интегродифференциального уравнения от времени для поплавков разной формы: 1. $f = \exp \left( { - \left| y \right|} \right)$; 2. $f = 1 - \left| y \right|$; 3. $f = 1 - {{y}^{2}}$; 4. $f = {{\left( {1 - \left| y \right|} \right)}^{2}}$; 5. $f = {{(1 - {{y}^{2}})}^{2}}$; 6. $f = \sqrt {1 - {{y}^{2}}} $.

2. Зависимость колебаний от формы поплавка по результатам численных и аналитических исследований. Рассмотрим решение задачи (1.1) при фиксированном значении параметра $\kappa $ и проанализируем зависимость решения от его величины. Для верификации используемых численных и асимптотических методов приведем решение уравнения (1.1) для поплавка с бесконечной осадкой (поплавка Сретенского [1, 4, 5], форма 1), которое может быть построено аналитически точно с использованием преобразования Лапласа

(2.1)

$s = \frac{1}{{2\pi }}\int\limits_0^\infty {[\pi \kappa ({{\xi }^{2}}P + Q)\cos \xi \vartheta - PQ - {{\pi }^{2}}{{\kappa }^{2}}{{\xi }^{2}}\sin \xi \vartheta ]\frac{{\xi d\xi }}{{{{Q}^{2}} + {{\pi }^{2}}{{\kappa }^{2}}{{\xi }^{4}}}}} $

${{f}^{2}}\left( y \right) = \exp \left( { - 2\left| y \right|} \right),\quad \left| y \right| < \infty $

$P = {{(1 + {{\xi }^{2}})}^{2}} - \kappa ({{\xi }^{2}} + 1 + 2\ln \xi ),\quad Q = (\Omega _{*}^{2} - {{\xi }^{2}}){{(1 + {{\xi }^{2}})}^{2}} - \kappa ({{\xi }^{2}}(1 + {{\xi }^{2}}) + 2{{\xi }^{2}}\ln \xi )$

В качестве численного метода использовался метод Эйлера – конечно-разностное интегрирование уравнения (1.1), когда зависимость (1.2) ядра K от времени представлялось в виде гистограммы

(2.2)

$\begin{gathered} {{s}_{{i + 1}}} = {{s}_{i}} + \delta s_{j}^{'},\quad {{s}_{0}} = 1,\quad s_{0}^{'} = 0 \hfill \\ s_{{i + 1}}^{'} = s_{j}^{'} - \delta \Omega _{{{{S}_{i}}}}^{2} - 2\kappa {{\Omega }^{2}}{{\delta }^{2}}\sum\limits_{j = 0}^i {{{K}_{{i - j}}}s_{j}^{'}} \hfill \\ \end{gathered} $

Сопоставление аналитического решения (2.1) с данными численного расчета в приближении малых времен, когда аналитическое решение может быть представлено в виде асимптотического ряда

$s = \sum {{{\vartheta }^{n}}{{s}_{n}}} $

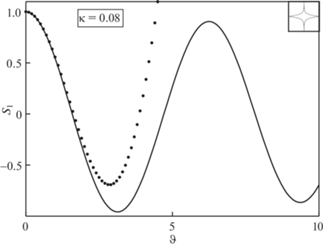
приведено на рис. 3. Сравнение показывает удовлетворительное согласие между численным и асимптотическим решениями на начальной фазе колебаний.

Рис. 3.

Зависимость смещения поплавка Сретенского от времени (начальная фаза колебаний). —— – численное решение, • • • • – асимптотика малых времен ($n = 20$).

Из результатов численного решения следует (рис. 4), что при малых значениях параметра $\kappa $ колебания происходят около положения нейтральной плавучести поплавка (нулевого уровня) и близки к гармоническим; затухание, вызванное излучением волн, мало. При увеличении относительной ширины поплавка колебания усложняются, их период меняется со временем и происходит смещение равновесного уровня, а при значениях $\kappa \geqslant 0.2$ колебания становятся ангармоническими. При значениях $\kappa > 0.3$ колебания происходят около уровня, определяемого ядром интегро-дифференциального уравнения, период колебаний заметно растет со временем.

Рис. 4.

Зависимость смещений поплавков Сретенского f = exp(–|y|) и других форм: $f = 1 - \left| y \right|$, $f\, = \,{{(1 - {{y}^{2}})}^{2}}$ и $f = \sqrt {1 - {{y}^{2}}} $ от времени (численный расчет) $\kappa = $ 0.01 (1); 0.1 (2); 0.5 (3); 0.7 (4); 0.9 (5); 1.0 (6).

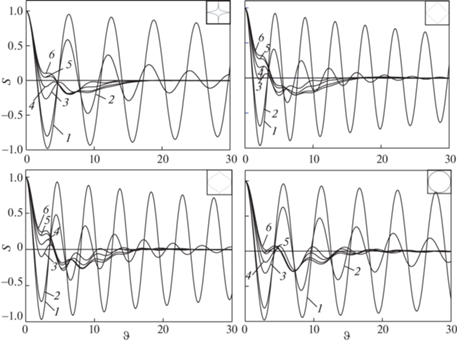
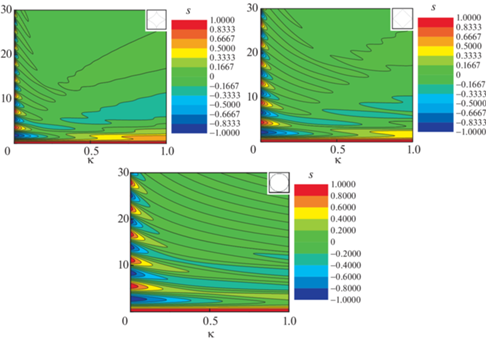
Построенные карты смещений от времени $\vartheta $ и относительной ширины $\kappa $ для поплавков вогнутой, плоской (ромбовидной) и выгнутой (эллиптической) форм показывают (рис. 5), что колебания поплавков выгнутой формы меньше подвержены затуханию, чем плоских и вогнутых поплавков. При значении параметра $\kappa > 0.3$ поплавок переходит к малым колебаниям около нулевого уровня, предварительно совершая ангармонические колебания около ненулевых уровней, величина которых со временем стремится нулю, предварительно проходя через минимальное отрицательное значение.

Рис. 5.

Карты смещений поплавков различной формы ($f = {{\left( {1 - \left| y \right|} \right)}^{2}}$; $f = 1 - \left| y \right|$; 6. $f = \sqrt {1 - {{y}^{2}}} $) в плоскости время $\vartheta $ – относительная ширина поплавка $\kappa $.

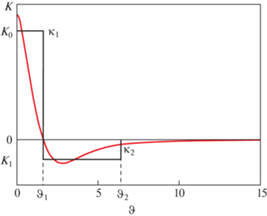
3. Локальные характеристики колебаний поплавков различной формы. Чтобы проанализировать локальные свойства колебаний и определить возможность влияния на них рассмотрим поплавок с интегродифференциальным ядром в виде трехступенчатой гистограммы (рис. 6)

(3.1)

$K\left( \vartheta \right) = \left\{ \begin{gathered} {{K}_{0}},\quad 0 \leqslant \vartheta \leqslant {{\vartheta }_{1}} \hfill \\ {{K}_{1}},\quad {{\vartheta }_{1}} \leqslant \vartheta \leqslant {{\vartheta }_{2}} \hfill \\ 0,\quad \vartheta > {{\vartheta }_{2}} \hfill \\ \end{gathered} \right.$

Рис. 6.

Преставление зависимости ядра интегродифференциального уравнения в виде трехступенчатой гистограммы.

Уравнение (1.1) при этом сведется к трем дифференциальным уравнениям с постоянными коэффициентами и сдвинутым аргументом

$\vartheta < {{\vartheta }_{1}}{\text{:}}\,\,\ddot {s} + \Omega _{0}^{2}\left( {1 + 2\kappa {{K}_{0}}} \right)s = 2\kappa \Omega _{0}^{2}{{K}_{0}}{{s}_{0}}$

(3.2)

${{\vartheta }_{1}} < \vartheta < {{\vartheta }_{2}}{\text{:}}\,\,\ddot {s} + \Omega _{0}^{2}\left( {1 + 2\kappa {{K}_{0}}} \right)s = - 2\Omega _{0}^{2}\left[ {\Delta K{{s}_{1}} - {{K}_{1}}{{s}_{0}}} \right]$

$\vartheta > {{\vartheta }_{2}}{\text{:}}\,\,\ddot {s} + \Omega _{0}^{2}\left( {1 + 2\kappa {{K}_{0}}} \right)s = - 2\Omega _{0}^{2}\left[ {\Delta K{{s}_{1}} - {{K}_{1}}{{s}_{2}}} \right]$

где $\Delta K = {{K}_{1}} - {{K}_{0}} < 0$, ${{s}_{n}} = s\left( {\vartheta - {{\vartheta }_{n}}} \right)$.

Первое уравнение (3.2) имеет вид уравнений гармонических колебаний около смещенного вверх на величину ${{S}_{0}} = \frac{{2\kappa {{K}_{0}}}}{{1 + 2\kappa {{K}_{0}}}}{{s}_{0}}$ равновесного уровня с увеличенной частотой колебаний ${{\omega }^{2}} = \Omega _{0}^{2}\left( {1 + 2\kappa {{K}_{0}}} \right)$. Учитывая значение функции ядра на втором участке гистограммы, величина равновесного уровня на втором временном интервале оказывается отрицательной. Решение однородной части второго уравнений (3.2) с помощью подстановки $s\left( \vartheta \right)\sim \exp \left( {\lambda \vartheta } \right)$ сводится к решению трансцендентного характеристического уравнения, которое оказывается не алгебраическим, а трансцендентным

${{\lambda }^{2}} + \Omega _{0}^{2}\left( {1 + 2\kappa {{K}_{0}}} \right) = - 2\kappa \Omega _{0}^{2}\Delta K{{e}^{{ - \lambda {{t}_{1}}}}}$

Наконец для третьего уравнения (3.2) величина равновесного уровня обращается в нуль, а характеристическое уравнение записывается в виде

${{\lambda }^{2}} + \Omega _{0}^{2}\left( {1 + 2\kappa {{K}_{0}}} \right) = - 2\kappa \Omega _{0}^{2}[\Delta K{{e}^{{ - \lambda {{t}_{1}}}}} + {{K}_{1}}{{e}^{{ - \lambda {{t}_{2}}}}}]$

Решение с точностью до членов первого порядка малости $\lambda \simeq {{\lambda }_{0}} + \kappa {{\lambda }_{1}}$ содержит как действительную, так и мнимую части. Действительная часть корней представляет собой локальную частоту колебаний, а мнимая – локальный декремент затухания $\lambda = i{{\Omega }_{0}} + \kappa \left( { - {{\gamma }_{1}} + i{{\omega }_{1}}} \right)$

(3.3)

${{\vartheta }_{1}} < \vartheta < {{\vartheta }_{2}}{\text{:}}\,\,{{\gamma }_{1}} = - {{\Omega }_{0}}\Delta K\sin {{\Omega }_{0}}{{\vartheta }_{1}},\quad {{\omega }_{1}} = {{K}_{0}} + \Delta K\cos {{\Omega }_{0}}{{\vartheta }_{1}}$

$\vartheta > {{\vartheta }_{2}}{\text{:}}\,\,{{\gamma }_{1}} = {{\Omega }_{0}}\left( { - \Delta K\sin {{\Omega }_{0}}{{\vartheta }_{1}} + {{K}_{1}}\sin {{\Omega }_{0}}{{\vartheta }_{2}}} \right)$

${{\omega }_{1}} = {{\Omega }_{0}}\left( {{{K}_{0}} + \Delta K\cos {{\Omega }_{0}}{{\vartheta }_{1}} - {{K}_{1}}\cos {{\Omega }_{0}}{{\vartheta }_{2}}} \right)$

на втором и третьем временном интервалах колебания становятся затухающими, частота колебаний и декремент затухания меняются в зависимости от времени и определяются собственной частотой колебаний поплавка ${{\Omega }_{0}}$ и $K$. В то же время величина равновесного уровня определяется только поведением ядра $K$.

В случае произвольной гладкой зависимости функции $K$ от времени, решение уравнения (1.1) может быть сведено к решению уравнения с ядром вида (3.1) с помощью аналитической реализации метода Эйлера, представив ядро уравнения в виде гистограммы $K = \{ {{K}_{l}},{{\vartheta }_{l}} \leqslant \vartheta \leqslant {{\vartheta }_{{l + 1}}}\,(l = \overline {0,N - 1} ,{{\vartheta }_{l}} = l\Delta \vartheta )\} $. Тогда, действуя аналогично, приходим к системе из $N$ уравнений с постоянными коэффициентами. Характеристическое уравнения в этом случае принимает вид

(3.4)

${{\lambda }^{2}} + \Omega _{0}^{2} = - 2\kappa \Omega _{0}^{2}\left[ {{{K}_{0}} - \sum\limits_{l = 0}^{m - 1} {\left( {{{K}_{l}} - {{K}_{{l + 1}}}} \right){{e}^{{ - \lambda {{\vartheta }_{{l + 1}}}}}}} } \right]$

Выделяя действительную и мнимую части корней характеристического уравнения (3.4) $\lambda = - \gamma + i\omega $ найдем по параметру $\kappa $ первое приближение к его решению.

(3.5)

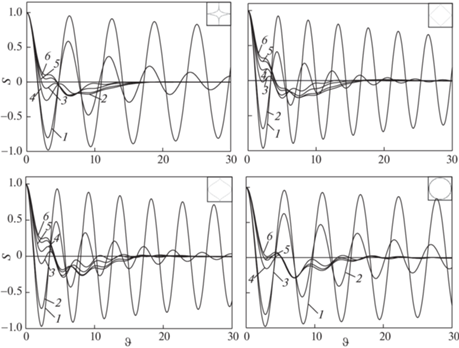
$\begin{gathered} \omega \left( \vartheta \right) = {{\Omega }_{0}}\left[ {1 + \kappa \left( {{{K}_{0}} - \sum\limits_{l = 0}^{m - 1} {\left( {{{K}_{l}} - {{K}_{{l + 1}}}} \right)\cos {{\Omega }_{0}}{{\vartheta }_{{l + 1}}}} } \right)} \right] \\ \gamma \left( \vartheta \right) = \kappa {{\Omega }_{0}}\sum\limits_{l = 0}^{m - 1} {\left( {{{K}_{l}} - {{K}_{{l + 1}}}} \right)\sin {{\Omega }_{0}}{{\vartheta }_{{l + 1}}}} \\ \end{gathered} $

Зависимости мгновенных частот и декрементов затухания от времени, приведенные на рис. 7, показывают, что для поплавков всех видов частота колебаний и декремент затухания быстро меняются в начальный период времени, затем проходит период установления, когда их величина колеблется, а затем на временах порядка пяти характерных времен становятся близкими к предельным значениям. Следует отметить, что в то время, как величина декремента затухания предсказуемо растет со временем, предельное значение частоты может как превышать частоту собственных колебаний среды, так и быть меньше ее. Величина декремента затухания в значительной степени зависит от формы поплавка, и уменьшается при переходе от поплавков вогнутой к выпуклой форме. При этом эллиптический поплавок обладает наименьшим декрементом затухания. В зависимости от параметра относительной ширины поплавка предельная частота колебаний может, как превосходить, так и быть меньше собственной частоты колебаний. Таким образом, поплавок эллиптической формы одинаковой площади и ширины (высоты различны) обладает свойством наибольшей добротности (минимального затухания), что представляет значительный интерес в теоретическом и прикладном аспектах.

Рис. 7.

Зависимости мгновенной частоты колебаний и декремента затухания для поплавков разных форм $f = {{\left( {1 - \left| y \right|} \right)}^{2}}$, $f = 1 - \left| y \right|$, $f = {{(1 - {{y}^{2}})}^{2}}$ и $f = \sqrt {1 - {{y}^{2}}} $ при $\kappa = $ 0.01 (1); 0.1 (2); 0.5 (3); 0.7 (4); 0.9 (5); 1.0 (6).

Переходя к пределу $\Delta \vartheta \to 0;m \to \infty {\text{:}}\,m\Delta \vartheta = \operatorname{const} = \vartheta $ в выражениях для мгновенной частоты и декремента затухания колебаний (3.5), получим их аналитические выражения

(3.6)

$\Omega \left( \vartheta \right){\text{/}}{{\Omega }_{0}} = 1 + \kappa \left( {{{K}_{0}} + \int\limits_0^\vartheta {\frac{{dK}}{{d\tau }}\cos {{\Omega }_{0}}\tau \,d\tau } } \right),\quad \gamma \left( \vartheta \right){\text{/}}{{\Omega }_{0}} = - \kappa \int\limits_0^\vartheta {\frac{{dK}}{{d\tau }}} \sin {{\Omega }_{0}}\tau \,d\tau $

Используя представления (3.6) можно для собственной частоты колебаний определить форму поплавка, соответствующую заданным требованиям к параметрам колебаний поплавка. Полученные выражения имеют смысл функций управления формой.

Заметим также, что характеристики поплавков могут быть изменены динамически в процессе колебаний, например, за счет изменения его ширины.

4. Управление колебаниями за счет изменения формы поплавка. Рассмотрим возможность параметрического управления динамикой движения поплавка. В качестве параметра управления выберем относительную ширину поплавка $\kappa = \kappa \left( t \right)$, которую будем менять в зависимости от требований, предъявляемых к движению. В качестве примера рассмотрим задачу фиксации значений частоты или декремента затухания на их начальном уровне. Для частоты колебаний такое требование означает, что второе слагаемое в первом выражении (3.5) или (3.6) должно оставаться неизменным в разные моменты времени, например ${{\vartheta }_{1}}$ и ${{\vartheta }_{2}}$. Тогда для представления (3.5) получаем выражения для изменения относительной ширины во времени

(4.1)

$ - \frac{{\Delta \kappa }}{{\Delta \vartheta }} = \frac{{\kappa \cos {{\Omega }_{0}}\vartheta }}{{{{K}_{0}} + \sum {\Delta {{K}_{l}}\cos {{\Omega }_{0}}{{\vartheta }_{{l + 1}}}} }}\frac{{\Delta K}}{{\Delta \vartheta }}$

где $\Delta \vartheta = {{\vartheta }_{2}} - {{\vartheta }_{1}}$, $\Delta \kappa = {{\kappa }_{2}} - {{\kappa }_{1}}$.

Переходя к пределу $\Delta \vartheta \to 0$, получаем аналитическое выражение для такого закона изменения относительной ширины, при котором частота колебаний поплавка остается неизменной

(4.2)

$ - \frac{{\dot {\kappa }}}{\kappa } = \frac{{\dot {K}\cos {{\Omega }_{0}}\vartheta \,}}{{K\left( 0 \right) + \int\limits_0^\vartheta {\dot {K}\cos {{\Omega }_{0}}\tau \,d\tau } }}$

Аналогичным образом может быть получен закон изменения относительной ширины, при котором фиксирован декремент затухания

(4.3)

$ - \frac{{\dot {\kappa }}}{\kappa } = \frac{{\dot {K}\sin {{\Omega }_{0}}\vartheta \,}}{{\int\limits_0^\vartheta {\dot {K}\sin {{\Omega }_{0}}\tau \,d\tau } }}$

Анализ выражений (4.2) и (4.3) показывает, что фиксация значений частоты и декремента затухания в зависимости от интервала времени и характеристик системы возможна не только за счет уменьшения (на первоначальном этапе колебаний), но и за счет увеличения относительной ширины поплавка.

Заключение. Проведенный анализ колебаний тонких поплавков на границе раздела двух тяжелых идеальных жидкостей показал существенную зависимость параметров колебаний от формы поплавков. Выявлено, что амплитуда колебаний поплавков выпуклой формы затухает слабее, чем у поплавков вогнутой формы, причем наименьшей степенью затухания обладает поплавок эллиптической формы. Впервые показано, что управление колебаниями поплавков может быть осуществлено за счет изменения параметра их относительной ширины. Получены выражения, описывающие закон управления, при котором частота поплавка и декремент затухания остаются неизменными в процессе колебаний. Предложенная форма управления может быть применена для управления свободно плавающими буями, которые широко используются для мониторинга физических свойств атмосферы и океана.

Исследование выполнено за счет гранта Российского научного фонда (проект № 21-11-00151).

Список литературы

Сретенский Л.Н. Теория волновых движений жидкости (2-е издание). М.: Наука, 1977. 816 с.
Larsen L.H. Oscillations of a neutrally buoyant sphere in a stratified fluid // Deep-Sea Res. 1969. V. 16. № 6. P. 587–603. https://doi.org/10.1016/0011-7471(69)90060-6
Васильев А.Ю., Чашечкин Ю.Д. Затухание свободных колебаний шара нейтральной плавучести в вязкой стратифицированной жидкости // ПММ. 2009. Т. 73. Вып. 5. С. 776–786.
Перепелкин В.В., Скоробогатых И.В., Мьо Зо Аунг Динамический анализ установившегося колебательного процесса земного полюса // Изв. РАН. МТТ. 2021. № 5. С. 141–151. https://doi.org/10.31857/S0572329921050081
Al M., Fontanella A., van der Hoek D. et al. Feedforward control for wave disturbance rejection on floating offshore wind turbines // J. Phys.: Conf. Ser. 2020. V. 1618. P. 022048. https://doi.org/10.1088/1742-6596/1618/2/022048
Kushwah S. An oscillating water column (OWC): The wave energy converter // J. Inst. Eng. India Ser. C. 2021. V. 102. P. 1311–1317. https://doi.org/10.31857/S056852812101014X
Акуленко Л.Д., Нестеров С.В. Колебания твердого тела на границе раздела двух жидкостей // Изв. АН СССР. МТТ. 1987. № 5. С. 35–40.
Акуленко Л.Д., Михайлов С.А., Нестеров С.В., Чайковский А.А. Численно-аналитическое исследование колебаний твердого тела на границе раздела двух жидкостей // Изв. АН СССР. МТТ. 1988. № 4. С. 59–66.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал