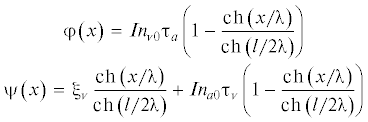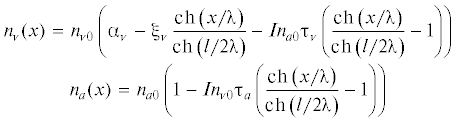Известия РАН. Механика твердого тела, 2022, № 3, стр. 122-131

1. Введение. Вопросы порообразования в кристаллических материалах занимают важное место в материаловедении как с точки зрения прочности, пластичности и долговечности изделий из таких материалов, так и с учетом широкого спектра практического применения пористых кристаллов [1–3]. Подобные материалы с заданным распределением пор используются в суперконденсаторах и батареях [4], фотонных кристаллах [5], сенсорах [6], подложках для эпитаксии [7, 8] и во многих других приложениях. Поры определяют многие свойства, начиная от способности кристаллов поглощать различные молекулы [9] до их хрупкости и прочности [10]. Так, в [11–13] было показано, что воздействие даже небольших, но постоянных нагрузок может вызвать постепенный рост пор по вакансионному механизму и привести к разрушению материала вследствие перколяции пор. В связи с этим чрезвычайно важно понимать все механизмы формирования пор под воздействием различных физических процессов для оценки долговечности материала, а также разработать методы, позволяющие контролируемо формировать кристаллы с заранее заданным распределением пор для различных приложений. В [14–16] было показано, что поры могут зарождаться при приложении механической нагрузки к кристаллу. В этом случае растягивающее напряжение вызывает образование избыточных вакансий в объеме кристалла, диффузия которых к поре приводит к её росту. Понимание этого ростового механизма, с одной стороны, позволяет предсказывать скорость разрастания пор под нагрузкой и время жизни материала (если механическая нагрузка – внешняя, неконтролируемая), а с другой – выращивать поры во всем объеме кристалла и обеспечивать желаемое распределение пор по размерам (при приложении заданной, контролируемой нагрузки). Как было показано экспериментально [17], поры могут иметь огранку, чтобы уменьшить полную свободную энергию. В связи с этим такие поры можно рассматривать как кристаллы “пустоты”, так как они имеют много общего с настоящими ограненными кристаллами. В предыдущих исследованиях [11–13] было показано, что рост подобных ограненных пор можно описать теоретически почти так же, как рост кристаллов из газовой фазы или раствора. В этих работах классические теории Бартона–Кабреры–Франка (БКФ) [18] и Чернова [19] были развиты для описания роста ограненных пор из газа вакансий в объеме кристалла. Были проанализированы все процессы, происходящие на гранях пор, а именно диффузия вакансий, испарение вакансий в объем кристалла и их осаждение на террасу, а также определены зависимости скорости роста пор от приложенной нагрузки.

Однако, как показано в серии работ А. Пимпинелли [20], Латышева и др. [21] и их коллег [22–24], поверхностные вакансии могут играть решающую роль в росте реальных кристаллов по механизму террасы-ступень-излом. Поскольку процесс роста обычного кристалла и поры подобны, то аналогично влиянию адвакансий на рост кристалла, адатомы на поверхности поры могут влиять на скорость её вакансионного роста. Настоящая работа является продолжением серии работ, посвященных росту и эволюции кристаллов [11–13, 25–28] и пор в одно- и многокомпонентных системах за счет различных механизмов, и ее основная цель – проанализировать влияние адатомов на поверхности поры на вакансионный рост поры по механизму Бартона–Кабреры–Франка, и найти выражение для зависимости скорости роста поры от приложенной механической нагрузки и свойств кристалла.

2. Формулировка проблемы. Рассмотрим кристалл, содержащий достаточно большие поры с характерным размером от десятков до сотен микрон и более. Как в работах [11–13] мы предполагаем, что поры огранены, что часто наблюдается экспериментально на поздних стадиях их роста [17] и обусловлено минимизацией поверхностной энергии. Поверхность поры, как у “кристалла пустоты”, покрыта террасами, ступенями и изломами. Мы предполагаем, что размер граней поры много больше характерного расстояния между ступенями на террасах, а расстояние между изломами, напротив, очень мало. В этом случае ступени можно рассматривать как непрерывные стоки вакансий и адатомов на поверхности. Тогда, рассматривая продвижение отдельной ступени или ее группы по террасе, можно рассматривать грань как бесконечную и пренебречь влиянием краев поры на распределение вакансий и адатомов вблизи ступеней. Расстояния между ступенями на террасах также значительно превышают длину свободного пробега вакансий и адатомов по поверхности кристалла. Рассматриваемая задача близка к задаче [11, 13] с тем ключевым отличием, что в настоящей работе мы исследуем влияние адатомов на поверхности поры, которые также могут диффундировать по террасе, рекомбинировать с вакансиями и участвовать в процессе массопереноса. Отметим, что основной целью настоящей работы является выявление общих зависимостей и закономерностей, описывающих рост ограненной поры по механизму “терраса-ступень-излом” при приложении механической нагрузки. В связи с этим, хотя мы понимаем, что в кристаллических материалах наблюдается существенная анизотропия, определяющая тензор упругих напряжений, влияние направления приложения нагрузки относительно ориентации рассматриваемой грани поры, зависимость упругих напряжений над гранью от расстояния до ребер поры и так далее, мы используем упрощенную модельную задачу с изотропным упругим напряжением. В ней, поскольку размер граней поры считается существенно большим по сравнению со всеми остальными параметрами (расстоянием между ступенями и диффузионными длинами), не учтены краевые эффекты, такие как влияние неоднородности распределения упругих напряжений возле рёбер. Поэтому величина упругих напряжений считается постоянной над всей гранью поры, и напряжения рассматриваются только как причина возникновения дополнительных вакансий в объеме кристалла, рождающихся из дефектов. Отметим, что такое приближение часто используется при рассмотрении различных задач, связанных с зарождением и перемещением вакансий в кристалле [29]. Учитывая это, рассматриваемую задачу можно представить как одномерную задачу о движении адвакансий и адатомов в полуплоскости со стоками в области ступеней, схема которой изображена на рис. 1. Влияние упомянутых выше эффектов, в частности, неоднородности распределения упругих напряжений над разными участками грани и их зависимости от размера грани, а также анизотропии приложенной нагрузки будет изучено в последующих работах.

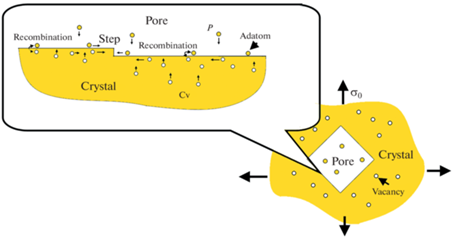
Итак, в такой модельной системе в равновесии все процессы и потоки сбалансированы. Однако, если приложить к кристаллу изотропную механическую нагрузку ${{\sigma }_{0}}$, то концентрация вакансий в объеме кристалла ${{C}_{{v}}}$ изменится и может быть описана формулой [14]:

где ${{C}_{{{v}0}}}$ – равновесная объемная концентрация вакансий без приложенной нагрузки, ${{\omega }} = {{a}^{3}}$ – объем атома в кристаллической ячейке, a – параметр решетки, ${{k}_{B}}$ – постоянная Больцмана, $T$ – температура, и, соответственно, величина ${{{{\xi }}}_{{v}}} = \frac{{{{{{\sigma }}}_{0}}{{\omega }}}}{{{{k}_{B}}T}}$ – пересыщение вакансий [14]. Отметим, что если приложенная механическая нагрузка – растягивающая, то в объеме кристалла появляется избыток вакансий, если сжимающая, то недостаток. Отметим также, что в настоящей работе мы предполагаем, что в объеме кристалла содержатся в достаточном количестве дислокации и другие дефекты, которые являются сильным источником вакансий. Это предположение означает, что концентрация вакансий в объеме всегда соответствует приложенной нагрузке и истощения вакансий в приповерхностной области не происходит. В противном случае следует использовать другой подход (механизм Чернова [19]).

Зарождающиеся в объеме вакансии диффундируют к поверхности поры и увеличивают концентрацию адвакансий на террасе. Затем адвакансии диффундируют по направлению к ступеням. Они также могут “испаряться” с террасы в объем кристалла и рекомбинировать с адатомами на поверхности поры. Адатомы ведут себя подобным образом: они могут осаждаться из газовой фазы на поверхность, испаряться, диффундировать по поверхности к ступени или от нее и рекомбинировать с адвакансиями. При растягивающих напряжениях концентрация вакансий в объеме повышается, и следует ожидать возникновения поверхностного потока адвакансий к ступеням, и вместе с тем, оттока адатомов от ступени на террасу. Оба этих потока приводят к продвижению ступени “пустоты” по террасе и увеличению объема поры. Основная цель настоящей работы состоит в анализе этих процессов и нахождении скорости продвижения ступени “пустоты”, а также скорости роста ограненной поры в зависимости от приложенной механической нагрузки.

3. Распределение адатомов и вакансий на поверхности поры. Чтобы найти скорость роста поры, мы будем использовать комбинацию подходов, предложенных в классической работе Бартона, Кабреры и Франка [18], Пимпинелли [20] и недавних работах [11, 13]. Рассмотрим одномерную задачу о движении группы эквидистантных ступеней с расстоянием l между ними. Чтобы найти решение в общем случае, введем следующие величины: ${{n}_{a}}\left( x \right)$ и ${{n}_{{v}}}(x)$ – поверхностные концентрации адатомов и адвакансий; ${{n}_{{a0}}}$ и ${{n}_{{{v}0}}}$ – их равновесные значения; ${{D}_{a}}$ и ${{D}_{{v}}}$ – их коэффициенты диффузии; ${{{{\tau }}}_{a}}$ и ${{{{\tau }}}_{{v}}}$ – время испарения адатома в объем поры и адвакансии в объем кристалла соответственно. Введем также дополнительный параметр ${{{{\alpha }}}_{{v}}} = \frac{{{{C}_{{v}}}}}{{{{C}_{{{v}0}}}}}$. Пользуясь подходами [18, 20, 28], запишем уравнение для потока вакансий из объема кристалла к поверхности ${{j}_{{{v} \uparrow }}}$ и аналогичное для адатомов, прилетающих на поверхность ${{j}_{{a \uparrow }}}$ из газовой фазы:

Первый член в правой части каждого уравнения описывает осаждение адатомов/адвакансий на террасу, второй описывает процесс “испарения”, третий – рекомбинацию адатомов и адвакансий, и последний – образование новой пары адатом-адвакансия непосредственно на террасе. K – коэффициент пропорциональности между скоростью рекомбинации и поверхностными концентрациями. Отметим, что, в отличие от работы Пимпинелли [20], мы рассматриваем возможность испарения вакансий в объем кристалла; то есть второе уравнение также содержит член, описывающий испарение. Кроме того, в модели [20] отсутствует поток к поверхности из газовой фазы, тогда как в наших исследованиях он учитывается. По сравнению с [24] система (3.1) учитывает рекомбинацию вакансий и адатомов. Вводя функции ${{\varphi }} = 1 - {{n}_{a}}{\text{/}}{{n}_{{a0}}}$ and ψ = = ${{C}_{{v}}}{\text{/}}{{C}_{{{v}0}}} - {{n}_{{v}}}{\text{/}}{{n}_{{{v}0}}}$, и переписывая систему (3.1) через них с учетом малости величины (${{\psi \varphi }}$), получим

Мы также можем записать уравнения для потоков адвакансий и адатомов по поверхности через ψ и ${{\varphi }}$ [18]:

Поскольку мы рассматриваем квазистационарный процесс, в котором движение ступени происходит очень медленно по сравнению с характерными временами других процессов, поверхностные потоки должны подчиняться уравнению неразрывности ${{j}_{ \uparrow }} = {\text{div}}~{{j}_{ \leftarrow }}$. Это позволяет нам написать окончательную систему уравнений:

При решении этой задачи мы используем следующие граничные условия: возле ступени ($x = l{\text{/}}2$), концентрации адатомов и адвакансий соответствуют их равновесным значениям (${{n}_{{v}}}\left( {l{\text{/}}2} \right) = {{n}_{{{v}0}}}$, ${{n}_{a}}\left( {l{\text{/}}2} \right) = {{n}_{{a0}}}$), из чего следует, что ${{\psi }}\left( {l{\text{/}}2} \right) = {{{{\xi }}}_{{v}}}$ and ${{\varphi }}\left( {l{\text{/}}2} \right) = 0$. В центре террасы между ступенями поток по поверхности должен быть равен нулю, так как распределение симметрично: ${{\psi }}'\left( 0 \right) = 0$, ${{\varphi }}'\left( 0 \right) = 0$. Решение системы уравнений нетрудно найти в следующем виде:

где $I = \frac{{K{{{{\xi }}}_{{v}}}}}{{1 + K{{n}_{{{v}0}}}{{{{\alpha }}}_{{v}}}{{{{\tau }}}_{a}} + K{{n}_{{a0}}}{{{{\tau }}}_{{v}}}}}$ и λ – характерная длина, которая определяется диффузионными длинами вакансий и адатомов во всех рассмотренных процессах. $\frac{1}{{{{{{\lambda }}}^{2}}}} = \frac{1}{{{{\lambda }}{{{_{a}^{e}}}^{2}}}} + \frac{1}{{{{\lambda }}{{{_{{v}}^{e}}}^{2}}}} + \frac{1}{{{{\lambda }}{{{_{a}^{r}}}^{2}}}} + \frac{1}{{{{\lambda }}{{{_{{v}}^{r}}}^{2}}}}$, где верхние индексы “e” и “r” соответствуют испарению и рекомбинации. Отметим, что λ определяется наименьшей диффузионной длиной, присутствующей в системе. Член, содержащий множитель I описывает созависимость стационарных концентраций адатомов и вакансий из-за рекомбинации в случае, если поверхностная концентрация адвакансий отклонена от равновесной. Решение (3.4) позволяет найти функции распределения адвакансий и адатомов по поверхности:

Рассмотрим некоторые частные случаи:

1) Если система находится в равновесии, то есть ${{{{\alpha }}}_{{v}}} = 1$, ${{{{\xi }}}_{{v}}} = 0$, уравнения (3.5) дают равновесные значения концентраций, как и ожидается ${{n}_{{v}}}(x) = {{n}_{{{v}0}}}$ и ${{n}_{a}}\left( x \right) = {{n}_{{a0}}}$ (рис. 2, a).

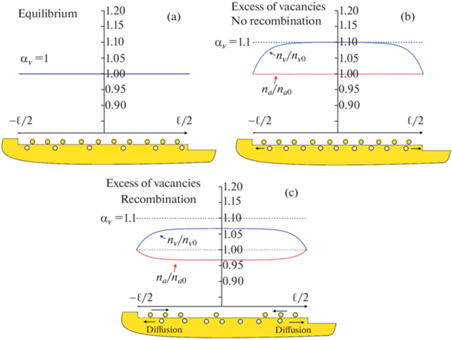
2) Если увеличить пересыщение вакансий (${{{{\alpha }}}_{{v}}} > 1$), но при этом коэффициент рекомбинации мал (ею можно пренебречь), то адвакансии не влияют на распределение адатомов на поверхности поры (рис. 2, b) и вакансионный рост поры можно описать так же, как и в работе [13]. Если же, наоборот, скорость рекомбинации достаточно высока, то концентрация как адатомов, так и вакансий уменьшается вдали от ступени относительно невозмущенных значений (без рекомбинации). При этом уменьшается приток вакансий к ступени, но возникает дополнительный диффузионный поток адатомов от ступени на террасу (Рис. 2, c), ускоряющий рост поры.

Зная функции распределения адатомов и адвакансий, нетрудно рассчитать их диффузионные потоки к ступени:

Окончательное уравнение для скорости продвижения эшелона эквидистантных ступеней имеет вид [18]:

где $\frac{1}{{{{n}_{s}}}} = {{a}^{2}}$ – площадь атома. Скорость ${v}$ считается положительной, если пора растет. Отметим, что из уравнения (3.6) следует, что основной вклад в движение ступени массоперенос может быть обусловлен как диффузией вакансий, так и адатомов, если рекомбинация достаточно эффективна. Действительно, при большем коэффициенте диффузии адатомов по поверхности по сравнению с адвакансиями $({{D}_{a}} > {{D}_{{v}}}$), что наблюдается во многих кристаллах, вклад адатомов в массоперенос становится значительным. Помимо непосредственного вклада адатомов, по сравнению с механизмом [11] при учете рекомбинации также изменяется эффективная диффузионная длина, входящая в знаменатель (3.6) и этот фактор также сильно влияет на скорость роста поры.

4. Скорость роста поры. Отметим, что пересыщение атомов в газовой фазе (в поре) в квазистационарном случае мы считаем тождественно равным нулю по следующим соображениям. Хотя приложение механической нагрузки также изменяет равновесную концентрацию адатомов на самой поверхности поры, мы рассматриваем пору как замкнутую систему ограниченного объема, не содержащую дополнительных источников газа. В первый момент после приложения нагрузки к кристаллу избыточные адатомы испаряются с поверхности в пору или, наоборот осаждаются из поры на поверхность, изменяя давление в поре. Процесс заканчивается, когда давление в поре точно соответствует равновесному при данных условиях, и потому на террасах вдали от ступени будет поддерживаться равновесная концентрация адатомов. Подставляя вместо ${{\xi }_{{v}}}$ величину $\frac{{{{\sigma }_{0}}{{\omega }}}}{{{{k}_{B}}T}}$ можно переписать (3.6) в виде:

где $I = \frac{{{{\sigma }_{0}}{{\omega }}}}{{{{k}_{B}}T}}\left( {\frac{K}{{1 + K{{n}_{{{v}0}}}{{{{\alpha }}}_{{v}}}{{{{\tau }}}_{a}} + K{{n}_{{a0}}}{{{{\tau }}}_{{v}}}}}} \right)$. Зная это выражение, найдем скорость роста поры по разным механизмам. Первый случай – это рост поры за счет перемещения группы эквидистантных параллельных ступеней “пустоты” ${{R}_{{sf}}}$ [17], который описывается формулой:

Второй механизм – спиральный рост. В работах [11, 13] авторы предположили, что по аналогии с ростом реального кристалла путем встраивания атомов в ростовые спирали, такой же процесс может иметь место и при росте поры. Если растущая пора содержит винтовую дислокацию на своей грани, то такая дислокация может стать источником ступеней “пустоты” и привести к дальнейшему спиральному росту поры за счет притока вакансий. Это вызывает образование ямок травления [30] (рис. 3) и другие явления, присущие спиральному росту обычных кристаллов.

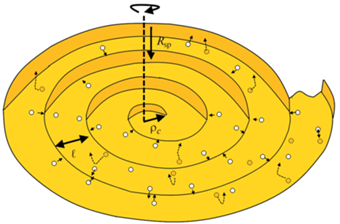
Для оценки скорости спирального роста поры воспользуемся подходом, предложенным в [11]. При спиральном росте расстояние между ступенями равно $l = 19{{{{\rho }}}_{c}}$ [20], где ${{{{\rho }}}_{c}}~$ – критический радиус двумерных зародышей вакансий [14] $({{{{\rho }}}_{c}} \approx \frac{{{\gamma }}}{{{{{{\sigma }}}_{0}}}}$, ${{\gamma }}$ – плотность поверхностной энергии кристалла). Окончательное выражение для скорости спирального роста поры ${{R}_{{sp}}}$, таким образом, можно записать как:

Отметим, что, как упоминалось в [11], упругие напряжения, вызванные наличием самой винтовой дислокации, могут существенно повлиять на расстояние между ступенями и концентрацию вакансий и даже могут привести к образованию полости вдоль ядра винтовой дислокации. В связи с этим, уравнение (4.2) следует использовать только для качественной оценки скорости, и необходим дальнейший анализ воздействия собственных упругих напряжений дислокации на рост. Отметим также, что в случае отсутствия рекомбинации уравнение (4.2) совпадает с формулой, полученной для скорости спирального роста поры в [13]. Наконец, отметим, что уравнение (4.2) справедливо, если характерные размеры поры и расстояние между точками выхода винтовых дислокаций больше расстояния между соседними ступенями и критического радиуса ${{{{\rho }}}_{c}}$. В противном случае следует использовать подходы, применяемые для описания роста маленьких ограненных кристаллов, предложенные в [31, 32].

4. Заключение. В рамках классической модели Бартона–Кабреры–Франка исследован рост ограненных пор в кристалле под воздействием механической нагрузки с учетом влияния адатомов, присутствующих на поверхности поры. Найдены функции распределения адатомов и адвакансий и показано, что в линейном приближении рекомбинация вакансий и адатомов снижает их поверхностные концентрации относительно величин, которые обусловлены приложенной механической нагрузкой. Это влияет на скорость роста пор. В случае избытка вакансий рекомбинация снижает поверхностный поток вакансий в сторону ступени, одновременно вызывая появление встречного потока адатомов от ступени на террасу. Получено аналитическое выражение, описывающее зависимость скорости продвижения ступеней по поверхности поры от приложенной механической нагрузки, а также их кинетических свойств. Показано, что при достаточно быстрой рекомбинации массоперенос в некоторых случаях может осуществляться в основном за счет диффузии адатомов, даже если сам процесс роста поры вызван пересыщением вакансий. Кроме того, характерные времена жизни адатомов и адвакансий на поверхности и характерная диффузионная длина могут определяться скоростью рекомбинации, а не испарением, как в классической теории БКФ, что также сильно влияет на скорость роста пор. Полученные результаты открывают новые возможности для анализа широкого круга экспериментальных данных по росту ограненных пор. Результаты также могут быть использованы для предсказания разрушения кристаллических материалов при низких, но постоянных механических нагрузках, при которых медленно растущие и перколирующие поры определяют долговечность материала. Показано, что рост пор по рассмотренному механизму и процесс разрушения можно замедлить за счет увеличения давления в системе пор, что снижает поверхностную концентрацию вакансий, и их поток к ступеням.

Благодарности. А.В. Редьков (постановка задачи, анализ роста поры, решение уравнений) выражает благодарность за поддержку данной работы Совету по грантам при Президенте РФ (грант № МК-201.2021.1.2). Часть работы (анализ спирального роста) поддержана государственным заданием ИПМаш РАН (№ FFNF-2021-0001).