1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 3, 2022

Известия РАН. Механика твердого тела, 2022, № 3, стр. 110-121

РЕШЕНИЕ ЗАДАЧИ О РАСШИРЕНИИ СФЕРИЧЕСКОЙ ПОЛОСТИ ПРИМЕНИТЕЛЬНО К ОЦЕНКЕ СОПРОТИВЛЕНИЯ ВНЕДРЕНИЮ ТВЕРДОГО ТЕЛА В ГРУНТ

А. М. Брагов a, *, В. В. Баландин a, **, Л. А. Игумнов a, ***, В. Л. Котов a, ****, А. К. Ломунов a, *****

a Национальный исследовательский Нижегородский государственный университет им. Н.И. Лобачевского
Н. Новгород, Россия

* E-mail: bragov@mech.unn.ru
** E-mail: balandin@mech.unn.ru
*** E-mail: igumnov@mech.unn.ru
**** E-mail: vkotov@mm.unn.ru
***** E-mail: lomunov@mech.unn.ru

Поступила в редакцию 30.04.2021
После доработки 07.10.2021
Принята к публикации 13.10.2021

Полный текст (PDF)

Аннотация

Анализируются решения задачи о расширении с постоянной скоростью сферической полости в грунтовой среде: расширение полости происходит из точки в полупространстве, занимаемом упругопластической грунтовой средой. Приводится полученное ранее линеаризованное аналитическое решение этой задачи, полученное в предположении несжимаемости среды за фронтом ударной волны. В результате сравнения с результатами численного решения задачи в полной постановке показано, что приближенное решение является хорошей аппроксимацией зависимости давления на границе полости от скорости ее расширения. Линеаризованное решение применено для расчета силы сопротивления внедрению жесткой сферы при проникании в мягкий грунт, динамическая сжимаемость и сопротивление сдвигу которого характеризуется ударной адиабатой Гюгонио и критерием текучести Мора–Кулона–Треска. Результаты аналитических и численных расчетов сравниваются с известными экспериментальными данными, представленными в виде зависимостей от скорости удара силы сопротивления внедрению сфер – ударников в водонасыщенный песок. Продемонстрировано хорошее соответствие теоретических и экспериментальных данных.

Ключевые слова: расширение полости, проникание, удар, сферический ударник, песок

1. Введение. Решения задачи о расширении сферической полости (ЗРСП) [1–5] активно применяются в механике геоматериалов [6–13]. Более общий подход, основанный на теории локального взаимодействия, развивается в работах [11–19]. Экспериментально-расчетный анализ проникания ударников с плоскими, коническими и полусферическими головными частями в грунт представлен в работах [6, 7, 12, 20–23]. Из работ за последние пять лет по решению ЗРСП в приложении к механике грунтов отметим [24–28]. В целом можно отметить [25, 26], что решение ЗРСП и его применение для расчета контактных и интегральных параметров в задачах удара и проникания достаточно развито. Учет реальных свойств материалов – нелинейной сжимаемости, зависимости предела текучести от давления и/или скорости деформаций, возможное разрушение – затрудняющих получение аналитического решения, легко осуществляется при численном решении задачи [27, 28].

Спецификой деформирования мягкого грунта является необходимость учитывать распространение как непрерывных упругопластических, так и ударных волн (УВ). Наличие сферических УВ в песчаном и глинистом грунтах, а также зависимость скорости УВ от давления на ее фронте показаны экспериментально [29–32]. Следует отметить, что существующие решения задачи о расширении полости также должны предусматривать возможность формирования УВ, распространяющейся по невозмущенному пространству.

В настоящей статье приводится постановка и решение ЗРСП применительно к определению силы сопротивления внедрению жесткого ударника в песчаный грунт. Деформационные и сдвиговые свойства грунта задаются ударной адиабатой и критерием текучести Мора–Кулона с ограничением на максимальную величину предела текучести Треска (далее – критерий Мора–Кулона–Треска). Численно получено обобщенное решение, предполагающее наличие упругого участка при дозвуковых скоростях распространения упругопластического интерфейса и формирование единой пластической УВ при сверхзвуковых скоростях. В предположении несжимаемости среды за фронтом УВ получено аналитическое решение задачи. Это решение аналогично полученному ранее жесткопластическому решению [2] задачи о расширении цилиндрической полости, где показано, что применение жесткопластического решения теоретически приводит к завышению сопротивления прониканию. Однако следует заметить, что сам подход, основанный на использовании решения задачи о расширении полости в динамике удара, является приближенным; предпочтение тому или иному решению задачи следует отдать по результатам сравнения с экспериментальными данными. В сравнении с экспериментальными и расчетными данными нами продемонстрировано, что модель проникания жесткого тела в грунт с использованием простой линеаризованной аналитической жесткопластической модели [26] обладает областью применимости, сравнимой с моделями на основе численного решения ЗРСП.

2. Решение ЗРСП в упругопластической грунтовой среде. Рассматривается одномерная задача о расширении сферической полости из точки в безграничной грунтовой среде. Упругопластические свойства грунтовой среды определяются соотношениями:

(2.1)
${{{{\sigma }}}_{r}} = {{f}_{1}}\left( {{\theta }} \right),\quad {{{{\sigma }}}_{r}} - {{{{\sigma }}}_{{{\theta }}}} = {{f}_{2}}\left( {{\theta }} \right)$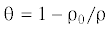
где ${{{{\sigma }}}_{r}}$ и ${{{{\sigma }}}_{{{\theta }}}}$ – компоненты тензора напряжений Коши, – относительное изменение объема, ${{{{\rho }}}_{0}}$ и ρ – начальная и текущая плотность,  f1 и f2 – заданные функции.

В работах [25, 26] приводится постановка краевой задачи для системы двух ОДУ первого порядка в результате решения которой определяются безразмерные напряжение и скорость в области пластического течения грунтовой среды

(2.2)
$U'\, + 2\frac{U}{{{\xi }}} = 0,\quad S'\, + 2\frac{{{{{\tilde {f}}}_{2}}}}{{{\xi }}} = \left( {{{\xi }} - U} \right)U',\quad {{\varepsilon }} < {{\xi }} < 1$
(2.3)
$U\left( {{{\xi }} = {{\varepsilon }}} \right) = {{\varepsilon ,}}\quad U\left( {{{\xi }} = 1} \right) = {{{{\theta }}}_{s}}$
(2.4)
$S\left( {{{\xi }} = 1} \right) = U - {{U}^{2}} = {{{{\theta }}}_{s}} - {{\theta }}_{s}^{2}$
где введены обозначения: $U = \upsilon {\text{/}}c$, $S = {{{{\sigma }}}_{r}}{\text{/}}{{{{\rho }}}_{s}}{{c}^{2}}$ – безразмерные скорость и напряжение, $\upsilon $ – размерная скорость, ${{\varepsilon }} = V{\text{/}}c$ – безразмерная координата (граница полости), $V$ – скорость расширения полости, величины ${{{{\rho }}}_{s}}$ и ${{{{\theta }}}_{s}}$ соответствуют плотности и объемной деформации на УВ, распространяющейся со скоростью c, ${{\xi }} = r{\text{/}}ct$ – безразмерная координата, штрихом обозначено дифференцирование по ξ, ${{\tilde {f}}_{2}} = {{f}_{2}}{\text{/}}({{{{\rho }}}_{s}}{{c}^{2}})$.

Принимаемое допущение о сохранении плотностью ее значения на УВ, равного ${{{{\rho }}}_{s}}$, можно иначе назвать гипотезой о несжимаемости среды за фронтом УВ.

Ударная адиабата Гюгонио грунтовых сред с достаточной для практических расчетов точностью [32, 33] может быть представлена линейным соотношением:

(2.5)
${{U}_{s}} = {{C}_{0}} + s{{u}_{p}}$
где Us и up – скорость плоской УВ и скорость частиц за фронтом УВ, ${{C}_{0}}$ и s – константы материала.

Далее при решении ЗРСП принимается [26]

(2.6)
${{U}_{s}} \equiv c$

Для определения ε получено приближение

(2.7)
${{\varepsilon }} \approx 3M{\text{/}}(1 + 3M\sqrt[3]{s})$

Используя обозначение ${{\varepsilon }} = V{\text{/}}c$, из (2.7) следует

(2.8)
$c \approx \sqrt[3]{s}V + {{C}_{0}}{\text{/}}3$

В работе [26] получено решение ЗРСП для критерия пластичности среды Мора–Кулона

${{f}_{2}} \equiv {{{{\tau }}}_{0}} + \kappa p,$
где τ0, $\kappa ~$ – константы, $p = \left( {{{{{\sigma }}}_{r}} + 2{{{{\sigma }}}_{{{\theta }}}}} \right){\text{/}}3$, в этом случае напряжение имеет вид

(2.9)
$S\left( {{\xi }} \right) = - \frac{{{{T}_{0}}}}{{{\mu }}} - 2\frac{{{{{{\varepsilon }}}^{3}}}}{{\left( {2{{\mu }} - 1} \right){{\xi }}}} + \frac{{{{{{\varepsilon }}}^{6}}}}{{\left( {{{\mu }} - 2} \right){{{{\xi }}}^{4}}}} + \left( {\frac{{{{T}_{0}}}}{{{\mu }}} + 2\frac{{{{{{\varepsilon }}}^{3}}}}{{\left( {2{{\mu }} - 1} \right)}} - \frac{{{{{{\varepsilon }}}^{6}}}}{{\left( {{{\mu }} - 2} \right)}} + {{{{\varepsilon }}}^{3}} - {{{{\varepsilon }}}^{6}}} \right){{{{\xi }}}^{{ - 2{{\mu }}}}}$

При выводе (2.9) использовалось равенство $\kappa p = {{\mu }}{{{{\sigma }}}_{r}}$, где $\mu = \kappa {\text{/}}\left( {1 + 2\kappa {\text{/}}3} \right)$, справедливое в условиях одноосной деформации.

Из (2.9) могут быть получены формулы для определения напряжения в зависимости от ξ:

(2.10)
${{{{\sigma }}}_{r}}(\xi )\, = \,{{{{\tau }}}_{0}}\left( {\frac{{{{{{\xi }}}^{{ - 2{{\mu }}}}} - 1}}{{{\mu }}}} \right)\, + \,\frac{{{{{{\rho }}}_{0}}V_{{}}^{2}{{\varepsilon }}}}{{1 - {{{{\varepsilon }}}^{3}}}}\left( {\frac{2}{{\left( {2{{\mu }} - 1} \right)}}\left( {\frac{{{{{{\xi }}}^{{ - 2{{\mu }} + 1}}} - 1}}{{{\xi }}}} \right)\, + \,\frac{{{{{{\varepsilon }}}^{3}}}}{{\left( {{{\mu }} - 2} \right)}}\left( {\frac{{1 - {{{{\xi }}}^{{ - 2{{\mu }} + 4}}}}}{{{{{{\xi }}}^{4}}}}} \right)\, + \,(1 - {{{{\varepsilon }}}^{3}}){{{{\xi }}}^{{ - 2{{\mu }}}}}} \right)$
и формула для напряжения при ξ = ε (напряжение на границе полости)

$S = \frac{{{{{{\varepsilon }}}^{{ - 2{{\mu }}}}} - 1}}{{{\mu }}}{{T}_{0}} + \frac{3}{{\left( {2{{\mu }} - 1} \right)\left( {{{\mu }} - 2} \right)}}{{{{\varepsilon }}}^{2}} + \left( {1 - {{{{\varepsilon }}}^{3}} + \frac{2}{{\left( {2{{\mu }} - 1} \right)}} - \frac{{{{{{\varepsilon }}}^{3}}}}{{\left( {{{\mu }} - 2} \right)}}} \right){{{{\varepsilon }}}^{{3 - 2{{\mu }}}}}$

Далее

(2.11)
${{{{\sigma }}}_{C}} \equiv {{{{\sigma }}}_{r}}\left( {{{\xi }}\, = \,{{\varepsilon }}} \right)\, = \,{{{{\tau }}}_{0}}\left( {\frac{{{{{{\varepsilon }}}^{{ - 2{{\mu }}}}} - 1}}{{{\mu }}}} \right) + \frac{{{{{{\rho }}}_{0}}V_{{}}^{2}}}{{1 - {{{{\varepsilon }}}^{3}}}}\left( {\frac{3}{{\left( {{{\mu }} - 2} \right)\left( {2{{\mu }} - 1} \right)}}\, + \,\frac{{2{{\mu }} + 1}}{{2{{\mu }} - 1}} \cdot {{{{\varepsilon }}}^{{1 - 2{{\mu }}}}} - \frac{{{{\mu }} - 1}}{{{{\mu }} - 2}} \cdot {{{{\varepsilon }}}^{{4 - 2{{\mu }}}}}} \right)$
(2.12)
${{{{\sigma }}}_{r}}\left( {{{\xi }} = {{\varepsilon }}} \right) = - 2{{{{\tau }}}_{0}}\ln {{\varepsilon }} + \frac{{{{{{\rho }}}_{0}}{{V}^{2}}}}{{1 - {{{{\varepsilon }}}^{3}}}}(3{\text{/}}2 - {{\varepsilon }} - {{{{\varepsilon }}}^{4}}{\text{/}}2),\quad {{\mu }} = 0$
(2.13)
${{{{\sigma }}}_{r}}\left( {{{\xi }} = {{\varepsilon }}} \right) = 2{{{{\tau }}}_{0}}({{{{\varepsilon }}}^{{ - 1}}} - 1) + \frac{{{{{{\rho }}}_{0}}{{V}^{2}}}}{{1 - {{{{\varepsilon }}}^{3}}}}(1{\text{/}}3 - 2\ln {{\varepsilon }} - {{{{\varepsilon }}}^{3}}{\text{/}}3),\quad {{\mu }} = 0.5$

В уравнениях (2.10)–(2.13) величина ${{\varepsilon }}$ определяется по линеаризованной формуле (2.7).

В работе [25] реализован алгоритм получения численного решения ЗРСП при учете образования УВ с высокой точностью. В данной работе это решение будет применяться для анализа применимости приближенного аналитического решения.

В работе [26] получено обобщение линеаризованного жесткопластического решения для среды с критерием Мора–Кулона–Треска. Аналогичный подход применялся ранее в работе [2] при решении задачи о расширении цилиндрической полости.

3. Анализ применимости жесткопластического линеаризованного решения. Приводятся результаты сравнительных расчетов, в которых динамическая сжимаемость среды характеризуется соотношением (2.5), сопротивление среды сдвигу задается линейной зависимостью Мора–Кулона. В расчетах варьируется скорость расширения полости.

Решение задачи в пластической области непрерывно при переходе в упругую область. В случае превышения значением скорости пластической волны величины скорости распространения упругой волны, формируется пластическая УВ, которая распространяется по невозмущенному пространству. Далее, в качестве иллюстрации рассматривается вариант задания параметров уравнения состояния среды с известной зависимостью напряжения от объемной деформации (ударной адиабатой) и условием пластичности Мора–Кулона, которые сведены в таблицу 1.

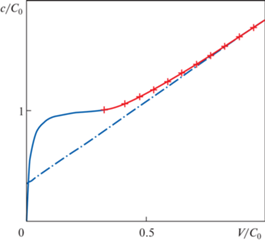
Кривые на рис. 1 соответствуют численным результатам решения задачи (2.2)–(2.4) с использованием классического метода Рунге–Кутты. Далее это решение называем точным.

Рис. 1.

Напряжение на границе полости в зависимости от скорости расширения: упругопластическое решение при $V \leqslant {{V}_{s}}$ (сплошная линия) и решение с выделением возникающей единой пластической ударной волны, распространяющейся по невозмущенной среде (сплошная линия с крестом) при $V > {{V}_{s}}$.

Обнаружено, что формирование УВ происходит при скорости расширения полости $V = {{V}_{s}}$ (отмечено пунктиром), ${{V}_{s}}$ = 550 м/с. В окрестности этого значения кривые решения имеют касание второго порядка.

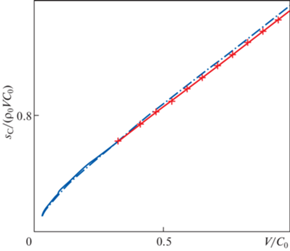
На рис. 2 скорость представлена в логарифмической шкале, пунктиром отмечено значение безразмерной скорости расширения полости ${{M}_{s}} \equiv {{V}_{s}}{\text{/}}{{C}_{0}}$, при котором происходит образование единой пластической ударной волны (${{M}_{s}}$ = 0.34).

Рис. 2.

Безразмерная зависимость $\varepsilon $ от скорости (логарифмический масштаб): точное обобщенное решение, включающее упругопластический интерфейс (сплошная синяя линия) при $M \leqslant {{M}_{s}}$ и образование пластической ударной волны (сплошная красная линия с крестом) при $M > {{M}_{s}}$, жесткопластическое линеаризованное решение (2.7) (штрихпунктирная линия).

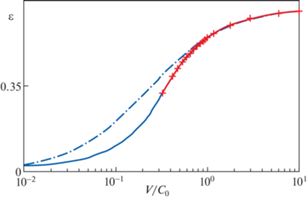
Точное решение на рис. 2 демонстрирует ограниченность параметра $\varepsilon $ при стремлении скорости расширения полости к бесконечности (${{\varepsilon }}$ < 0.663) и к нулю (${{\varepsilon }}$ > 0.023). Приближенное решение по формуле (2.7) ограничено сверху (${{\varepsilon }} < 1{\text{/}}\sqrt[3]{s}$). Ограниченным также остается величина размерного напряжения 1.13 МПа на границе полости при около нулевых скоростях. Величина ε, полученная по приближенной формуле (2.7), стремится к точному значению лишь при $M > 0.4$.

Отметим, что из решения задачи без учета возникновения пластической УВ следует ограниченность скорости упругопластического интерфейса при высоких скоростях расширения полости (сплошная линия на рис. 3). Продолжение решения с выделением единой пластической УВ (сплошная линия с крестом на рис. 3) более отвечает физической картине распространения волн.

Рис. 3.

Нормализованные зависимости c(V) (обозначения кривых как на рис. 2).

Приближенные решения на рис. 4 получены по формулам (2.7), (2.11) соответственно. Отметим хорошее соответствие приближенного линеаризованного решения и точного решения в полной постановке в достаточно широком диапазоне скоростей расширения полости вплоть до M = 0.1. Как и точное решение, безразмерное линеаризованное решение имеет нелинейный характер при $M < 0.4$, а при $M > 0.4$ может быть представлено линейной зависимостью.

Рис. 4.

Нормализованные напряжения на границе полости в зависимости от скорости расширения (обозначения кривых как на рис. 2).

Хорошее соответствие приближенного линеаризованного и точного решений может быть объяснено, если рассмотреть распределения напряжений в среде в зависимости от безразмерной координаты.

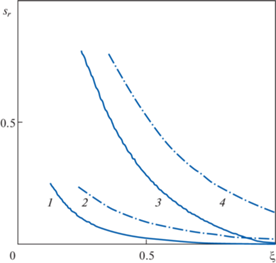
Как видно на рис. 5, значения напряжений, полученные с применением формул (2.7), (2.10), достаточно близки к точному значению только в окрестности полости. Формальное продолжение решения в область M < 0.4 приводит к погрешности в определении напряжения на границе полости в 16%. С ростом скорости расширения полости погрешности в определении напряжений с использованием формул (2.10), (2.11) существенно уменьшаются.

Рис. 5.

Распределение напряжений в среде при безразмерных скоростях расширения полости М = 0.125 (кривые 1, 2) и 0.25 (кривые 3, 4): сплошная (1, 3) и штрихпунктирная (3, 4) линии соответствуют точному обобщенному и линеаризованному жесткопластическому решениям.

Таким образом, из представленных данных сравнительных численных и аналитических расчетов следует, что соотношение (2.7) и формулы (2.11) можно использовать для аппроксимации напряжения на контактной поверхности ударников, проникающих в грунтовые среды.

4. Определение сопротивления внедрению жесткой сферы в песок. Как известно, уравнение состояния мягкого грунта включает в себя ударную адиабату, условие пластичности, а также модули упругости K и $G$ начального участка кривой деформирования. Представление ударной адиабаты в виде линейного соотношения вида (2.5) позволяет определить связь напряжения ${{{{\sigma }}}_{r}}$ и объемной деформации ${{\theta }}$ в условиях одноосной деформации:

(4.1)
${{f}_{1}}\left( {{\theta }} \right) \equiv {{{{\rho }}}_{0}}C_{0}^{2}{{\theta }}{{\left( {1 - s{{\theta }}} \right)}^{{ - 2}}}$

Сопротивление среды сдвигу определяется зависимостью предела текучести от давления

(4.2)
${{f}_{2}}\left( p \right) \equiv {{{{\sigma }}}_{0}} + kp{\text{/}}\left[ {1 + kp{\text{/}}\left( {{{{{\sigma }}}_{1}} - {{{{\sigma }}}_{0}}} \right)} \right]$
где ${{{{\sigma }}}_{0}}$, ${{{{\sigma }}}_{1}}$ и k постоянные коэффициенты.

Функция ${{f}_{3}}\left( {{\theta }} \right)$ “давление – объемная деформация” принимается в виде (4.1)

(4.3)
$p = {{f}_{1}}\left( {{\theta }} \right) \equiv {{{{\rho }}}_{0}}{{a}^{2}}{{\theta }}{{\left( {1 - b{{\theta }}} \right)}^{{ - 2}}}$
неизвестные параметры а и b в которой определяются методом наименьших квадратов.

В таблице 2 приводятся значения параметров модели водонасыщенного песка [23].

Кривая нелинейного критерия текучести (4.2) аппроксимируется билинейной зависимостью закона Мора–Кулона с ограничением Треска (таблица 3)

(4.4)
${{f}_{2}} \equiv \left\{ \begin{gathered} {{{{\tau }}}_{0}} + kp = {{{{\tau }}}_{0}} + \mu {{{{\sigma }}}_{r}},\quad 0 < {{{{\sigma }}}_{r}} \leqslant {{{{\sigma }}}_{M}} \hfill \\ {{{{\tau }}}_{M}},\quad {{{{\sigma }}}_{r}} > {{{{\sigma }}}_{M}} \hfill \\ \end{gathered} \right.$

Параметры упругого участка диаграммы деформирования и ударной адиабаты водонасыщенного песка представлены ранее в таблице 1.

Таблица 1.

Параметры уравнения состояния среды

ρ0, кг/м3 K, МПа G, МПа ${{c}_{e}}$, м/с ${{C}_{0}}$, м/с s ${{{{\sigma }}}_{0}}$, МПа k ${{\mu }}$
2080 4570 1147 1713 1700 3.4 0.021 0.5 0.375
Таблица 2.

Параметры уравнения состояния грунта [18]

w, % ρ0, кг/м3 ${{C}_{0}}$, м/с $s$ a, м/с b ${{{{\sigma }}}_{0}}$, МПа k ${{{{\sigma }}}_{1}}$, МПа
20 2080 1700 3.4 1620 3.6 0.1 0.5 50
Таблица 3.

Параметры условия пластичности Мора–Кулона–Треска (4.4)

${{{{\tau }}}_{0}}$, МПа k ${{\mu }}$ ${{{{\tau }}}_{M}}$, МПа ${{{{\sigma }}}_{M}}$, МПа
0.021 0.3 0.25 25 1000

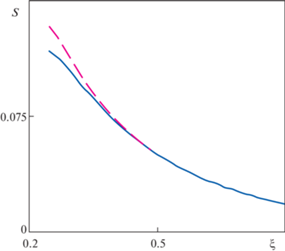
Зависимости напряжений от координаты при условии текучести Мора–Кулона–Треска [26] (сплошная линия) и Мора–Кулона (штриховая линия), полученные по формуле (2.9), изображены на рис. 6, скорость расширения полости составила 250 м/с.

Рис. 6.

Безразмерные зависимости напряжений, полученные при использовании критерия Мора–Кулона–Треска [21] и Мора–Кулона (сплошная и штриховая линии соответственно).

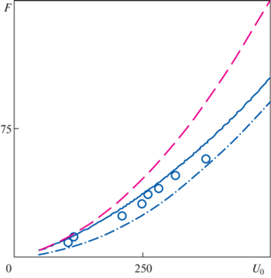
На рис. 7 сплошная линия соответствует результатам [26], штриховая линия, штрихпунктирная линия и штриховая линия с квадратом – результатам, полученным с применением уравнений (2.12), (2.13) и уравнения (2.13) при ${{{{\tau }}}_{0}} = {{{{\tau }}}_{M}}$. Можно отметить, что при малых скоростях справедливо более простое решение (2.12), а при высоких скоростях расширения полости – решение (2.13), по сравнению с более трудоемким общим решением ЗРСП с критерием Мора–Кулона–Треска [26].

Рис. 7.

Зависимости напряжений на границе полости от скорости, полученные [21] (сплошная линия) и с применением уравнений (2.12), (2.13) и (2.13) при ${{{{\tau }}}_{0}} = {{{{\tau }}}_{M}}$ штриховая линия, штрихпунктирная линии и штриховая линия с квадратом соответственно.

Сила, действующая на сферический ударник при его проникании в грунт с постоянной скоростью, может быть представлена в виде

(4.5)
$F = 2S\mathop \smallint \limits_0^{{\varphi }} \left( {{{{{\sigma }}}_{n}}\cos {{\varphi }} + {{{{\sigma }}}_{{{\tau }}}}\sin {{\varphi }}} \right)\sin {{\varphi }}d{{\varphi }}$
где $S = \pi {{R}^{2}}$ – площадь миделя поперечного сечения сферы, ${{{{\sigma }}}_{n}}$ и ${{{{\sigma }}}_{{{\tau }}}}$ – нормальное и касательное контактные напряжения, угол φ отсчитывается от вершины сферы в направлении свободной поверхности.

В соответствии с моделью расширения полости, нормальное контактное напряжение определяется давлением на стенку расширяющейся сферической полости, которое может быть представлено в виде квадратичной зависимости

(4.6)
${{{{\sigma }}}_{n}}{\text{/}}{{{{\rho }}}_{0}} = {{a}_{2}}{{u}^{2}} + {{b}_{1}}u$
где $u = - {{U}_{0}}z$ – нормальная компонента вектора скорости внедрения, ${{a}_{2}}$, ${{b}_{1}}$ – постоянные коэффициенты.

Касательные напряжения определяются законом Кулона с постоянным коэффициентом kf

(4.7)
${{{{\sigma }}}_{{{\tau }}}} = {{k}_{f}}{{{{\sigma }}}_{n}}$

Зависимость силы сопротивления внедрению сферического ударника от скорости удара имеет вид

$F = AU_{0}^{2} + B{{U}_{0}},\quad A = {{a}_{2}}\left( {{{A}_{1}} + {{k}_{f}}{{A}_{2}}} \right){{\rho }_{0}}S,\quad B = {{b}_{1}}\left( {{{B}_{1}} + {{k}_{f}}{{B}_{2}}} \right){{\rho }_{0}}S$
(4.8)
$\begin{gathered} {{A}_{1}} = \frac{{(1 - {{{\cos }}^{4}}{{\varphi }})}}{2},\quad {{A}_{2}} = \frac{{({{\varphi }} - 2\sin {{\varphi }}{{{\cos }}^{3}}{{\varphi }} + \sin {{\varphi }}\cos {{\varphi }})}}{4}, \\ {{B}_{1}} = \frac{{2(1 - {{{\cos }}^{3}}{{\varphi }})}}{3},\quad {{B}_{2}} = \frac{{2{{{\sin }}^{3}}{{\varphi }}}}{3} \\ \end{gathered} $

Угол отрыва потока принимался равным ${{\varphi }} = \pi {\text{/}}3$, коэффициент трения для водонасыщенного песка принимался вдвое меньшим, чем для сухого песка [34] ${{k}_{f}} = 0.2$.

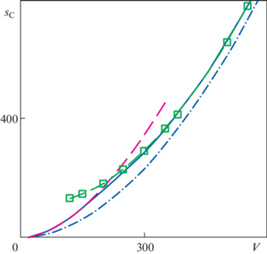
На рис. 8 отметим хорошее соответствие результатов аппроксимации и экспериментальных данных без введения подгоночных коэффициентов.

Рис. 8.

Силы сопротивления прониканию сферы в водонасыщенный песок в зависимости от скорости удара: обращенный эксперимент [18] (светлые точки) и аппроксимация на основе решения ЗРСП (обозначения кривых как на рис. 7).

Для водонасыщенного песка применение условия Мора–Кулона–Треска необходимо, так как при малых скоростях удара (до 200 м/с) существенную роль играет внутреннее трение, при более высоких скоростях сказывается ограниченность предела текучести в рамках критерия Треска.

Рассмотрим проникание ударников с высокими скоростями, когда сопротивлением сдвигу грунтовой среды можно пренебречь. Нормальное давление на поверхности, двигающейся со скоростью U0, будет выражаться уравнением (2.13) без первого слагаемого: ${{{{\sigma }}}_{r}} = {{{{\rho }}}_{0}}U_{0}^{2}(3{\text{/}}2 - {{\varepsilon }} - {{{{\varepsilon }}}^{4}}{\text{/}}2){\text{/}}(1 - {{{{\varepsilon }}}^{3}})$. Примем для напряжения на контактной поверхности форму записи ${{{{\sigma }}}_{r}} = \frac{1}{2}{{C}_{D}}{{{{\rho }}}_{0}}U_{0}^{2}$, где CD – коэффициент сопротивления. Тогда, положив величину ${{\varepsilon }} = 1{\text{/}}\sqrt[3]{s}$ (оценка сверху), получим оценку коэффициента CD в зависимости от параметра ударной адиабаты s: ${{C}_{D}} = \left( {3 - \left( {2 + \frac{1}{s}} \right){\text{/}}\sqrt[3]{s}} \right){\text{/}}\left( {1 - \frac{1}{s}} \right)$. При изменении s в диапазоне $1 < s < 4$ коэффициент сопротивления меняется в диапазоне $2 < {{C}_{D}}$ < 2.1.

5. Заключение. Применительно к задаче проникания в мягкие грунты жесткой сферы получено автомодельное аналитическое решение одномерной ЗРСП из точки в бесконечной грунтовой среде. Решение получено для модели грунта как упругопластической среды с критерием текучести Мора–Кулона–Треска при учете нелинейной сжимаемости в соответствии с известной ударной адиабатой. Численно показано, что при решении задачи о расширении полости в мягком грунте необходимо учитывать формирование пластической УВ, распространяющейся по невозмущенному пространству грунта. Проведенный параметрический анализ линеаризованного жестко-пластического решения показал, что оно является хорошей аппроксимацией зависимости давления на границе полости от скорости ее расширения применительно к широкому классу мягких грунтовых сред. Получены расчетные оценочные зависимости максимального значения силы сопротивления внедрению жесткой сферы в водонасыщенный песок при скоростях удара от 50 до 400 м/с. Сравнение аналитически и экспериментальных результатов определения сил сопротивления прониканию, показало их качественное и количественное хорошее соответствие. В этой связи при решении задач проникания в мягкие грунты может с успехом применяться простое аналитическое решение.

Благодарности. Авторы выражают признательность В.В. Баландину и Е.Ю. Линник за помощь в подготовке отдельных материалов статьи. Пункты 1–3 статьи подготовлены при финансовой поддержке Министерства науки и высшего образования Российской Федерации (проект 0729-2020-0054), пункт 4 статьи подготовлен при финансовой поддержке Российского научного фонда (грант № 21-19-00283).

Список литературы

  1. Forrestal M.J., Norwood F.R., Longcope D.B. Penetration into targets described by locked hydrostats and shear strength // Int. J. Solids Struct. 1981. V. 17. № 9. P. 915–924. https://doi.org/10.1016/0020-7683(81)90106-2

  2. Forrestal M.J., Longcope D.B. Closed-form solution for forces on conical-nosed penetrators into geological targets with constant shear strength // Mech. Materi. 1982. V. 1. № 4. P. 285–295. https://doi.org/10.1016/0167-6636(82)90028-X

  3. Forrestal M.J., Luk V.K. Penetration into soil targets // Int. J. Impact Eng. 1992. V. 12. № 3. P. 427–444. https://doi.org/10.1016/0734-743X(92)90167-R

  4. Masri R., Durban D. Cylindrical cavity expansion in compressible Mises and Tresca solids // Eur. J. Mech. A/Solids. 2007. V. 26. № 4. P. 712–727. https://doi.org/10.1016/j.euromechsol.2006.12.003

  5. Rosenberg Z., Dekel E. Analytical solution of the spherical cavity expansion process // Int. J. Impact Eng. 2009. V. 36. № 2. P. 193–198. https://doi.org/10.1016/j.ijimpeng.2007.12.014

  6. Бивин Ю.К., Викторов В.В., Коваленко Ю.Я. Определение динамических характеристик грунтов методом пенетрации // Изв. АН СССР. МТТ. 1980. № 3. С. 105–110.

  7. Бивин Ю.К., Симонов И.В. Оценки глубин проникания жестких тел в грунтовые среды при сверхзвуковых скоростях входа // Докл. РАН. 1993. Т. 328. № 4. С. 447–450.

  8. Бивин Ю.К. Внедрение твердых тел в бетон // Известия РАН. МТТ. 2018. № 1. С. 57–63.

  9. Cheng Ya., Yang H.-W., Sun D. Cavity expansion in unsaturated soils of finite radial extent // Comput. Geotech. 2018. V. 102. P. 216–228. https://doi.org/10.1016/j.compgeo.2018.06.013

  10. Su D., Yang Z.X. Drained analyses of cylindrical cavity expansion in sand incorporating a bounding-surface model with state-dependent dilatancy // Appl. Math. Modell. 2019. V. 68. P. 1–20. https://doi.org/10.1016/j.apm.2018.11.017

  11. Shi C., Wang M., Zhang K., Cheng Yi., Zhang X. Semi-analytical model for rigid and erosive long rods penetration into sand with consideration of compressibility // Int. J. Impact Eng. 2015. V. 83. P. 1–10. https://doi.org/10.1016/j.ijimpeng.2015.04.007

  12. Велданов В.А., Марков В.А., Пусев В.И. и др. Расчет проникания недеформируемых ударников в малопрочные преграды с использованием данных пьезоакселерометрии // ЖТФ. 2011. Т. 81. № 7. С. 94–104.

  13. Баженов В.Г., Баландин В.В., Григорян С.С., Котов В.Л. Анализ моделей расчета движения тел вращения минимального сопротивления в грунтовых средах // ПММ 2014. Т. 78. Вып. 1. С. 98–115.

  14. Остапенко Н.А., Якунина Г.Е. О телах наименьшего сопротивления, двигающихся в средах при наличии закона локальности // Изв. РАН. МЖГ. 1992. № 1. С. 95–106.

  15. Остапенко Н.А. Тела вращения минимального сопротивления при движении в плотных средах // Усп. мех. 2002. № 2. С. 105–149.

  16. Якунина Г.Е. Особенности высокоскоростного движения тел в плотных средах // ПММ 2012. Т. 76. Вып. 3. С. 429–449.

  17. Ben-Dor G., Dubinsky A., Elperin T. Applied High-Speed Plate Penetration Dynamics. Pt. 1. The Netherlands: Springer, 2006. 370 p.

  18. Баничук Н.В., Иванова С.Ю. Оптимизация: контактные задачи и высокоскоростное проникание. М.: Физматлит, 2016. 176 с.

  19. Баничук Н.В., Иванова С.Ю., Осипенко К.Ю. О пробивании слоистых структур твердым сферическим телом // Изв. РАН. МТТ. 2021. № 2. С. 63–71. https://doi.org/10.31857/S0572329921020033

  20. Sun Q., Sun Yu., Liu Yi., Li R., Zhao Ya. Numerical analysis of the trajectory stability and penetration ability of different lateral-abnormal projectiles for non-normal penetration into soil based on Modified Integrated Force Law method // Int. J. Impact Eng. 2017. V. 103. P. 159–168. https://doi.org/10.1016/j.ijimpeng.2017.01.010

  21. Balandin Vl.V., Balandin Vl.Vl., Bragov A.M., Kotov V.L. Experimental Study of the Dynamics of Penetration of a Solid Body into a Soil Medium // Tech. Phys. 2016. V. 61. № 6. P. 860–868. https://doi.org/10.1134/S1063784216060037

  22. Котов В.Л., Баландин Вл.В., Брагов А.М., Баландин Вл.Вл. Исследование динамических свойств водонасыщенного песка по результатам обращенных экспериментов // ЖТФ. 2018. Т. 88. № 4. С. 545–554. https://doi.org/10.21883/PJTF.2017.17.44948.16530

  23. Bragov A.M., Balandin V.V., Igumnov L.A., Kotov V.L., Krushka L., Lomunov A.K. Impact and penetration of cylindrical bodies into dry and water-saturated sand // Int. J. Impact Eng. 2018. V. 122. P. 197–208. https://doi.org/10.1016/j.ijimpeng.2018.08.012

  24. Аптуков В.Н., Хасанов А.Р. Расширение цилиндрической полости в сжимаемой упругопластической среде // Вестн. ПНИПУ. Механика. 2017. № 1. С. 5–23. https://doi.org/10.15593/perm.mech/2017.1.01

  25. Котов В.Л. Аппроксимация напряжений в окрестности полости, расширяющейся с постоянной скоростью в среде с условием пластичности Мора–Кулона // Пробл. проч. пласт. 2019. Т. 81. № 2. С. 177–190. https://doi.org/10.32326/1814-9146-2019-81-2-177-190

  26. Котов В.Л., Тимофеев Д.Б. Решение задачи о расширении сферической полости в среде с условием пластичности Мора–Кулона–Треска // Пробл. проч. пласт. 2019. Т. 81. № 3. С. 292–304. https://doi.org/10.32326/1814-9146-2019-81-3-292-304

  27. Линник Е.Ю. Оценка контактных напряжений при внедрении ударника в прочный грунт // Пробл. прочн. пласт. 2020. Т. 82. № 1. С. 52–63. https://doi.org/10.32326/1814-9146-2020-82-1-52-63

  28. Котов В.Л., Брагов А.М., Баландин В.В., Константинов А.Ю., Баландин Вл.Вл. Двусторонние оценки силы сопротивления прониканию конуса в мерзлый грунт // ПМТФ. 2021. Т. 62. № 1. С. 125–133. https://doi.org/10.15372/PMTF20210114

  29. Ляхов Г.М. Ударные волны в грунте и разжижение водонасыщенного песка // ПМТФ. 1961. Т. 2. № 1. С. 38–46.

  30. Ляхов Г.М., Нарожная З.В. Экспериментальные исследования взрывных волн в глинистом грунте // ПМТФ. 1961. Т. 2. № 2. С. 123–126.

  31. Рыков Г.В. Экспериментальное исследование поля напряжений при взрыве в песчаном грунте // ПМТФ. 1964. Т. 5. № 1. С. 85–89.

  32. Лагунов В.А., Степанов В.А. Измерение динамической сжимаемости песка при высоких давлениях // ПМТФ. 1963. Т. 4. № 1. С. 88–96.

  33. Arlery M., Gardou M., Fleureau J.M., Mariotti C. Dynamic behaviour of dry and water-saturated sand under planar shock conditions // Int. J. Impact Eng. 2010. V. 37. № 1. P. 1–10. https://doi.org/10.1016/j.ijimpeng.2009.07.009

  34. Bazhenov V.G., Kotov V.L., Kochetkov A.V., Krylov S.V., Feldgun V.R. On wave processes in soil subjected to a surface charge explosion // Mech. Solids. 2001. V. 36. № 2. P. 62–68.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал