1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 3, 2022

Известия РАН. Механика твердого тела, 2022, № 3, стр. 97-109

БОЛЬШИЕ ДЕФОРМАЦИИ И РАЗОГРЕВ УПРУГОВЯЗКОПЛАСТИЧЕСКОГО МАТЕРИАЛА В ЦИЛИНДРИЧЕСКОМ ВИСКОЗИМЕТРЕ

А. С. Бегун a, c, *, А. А. Буренин b, **, Л. В. Ковтанюк a, ***

a Институт автоматики и процессов управления ДВО РАН
Владивосток, Россия

b Хабаровский федеральный исследовательский центр ДВО РАН: Институт машиноведения и металлургии ДВО РАН
Комсомольск-на-Амуре, Россия

c Владивостокский государственный университет экономики и сервиса
Владивосток, Россия

* E-mail: asustinova@mail.ru
** E-mail: burenin@iacp.dvo.ru
*** E-mail: lk@iacp.dvo.ru

Поступила в редакцию 20.02.2021
После доработки 21.05.2021
Принята к публикации 22.05.2021

Полный текст (PDF)

Аннотация

Строится решение связной термомеханической краевой задачи теории больших деформаций одновременно учитывающей интенсивное деформирование упруговязкопластического материала и его разогрев за счет такого деформирования и пристеночного трения. Рассчитываются условия возникновения и развития вязкопластического течения в материале цилиндрического слоя, заключенного между жесткими поверхностями, одна из которых имеет возможность поворачиваться под действием меняющейся задаваемой нагрузки относительно оси вискозиметра. На всех стадиях процесса от его начала до остановки рассчитываются напряженно-деформированное состояние и распределения температуры в областях течения и обратимого деформирования, включая остановку течения, разгрузку и остывание с расчетом остаточных напряжений и деформаций. Предел текучести полагается зависимым от температуры.

Ключевые слова: упругость, вязкость, пластичность, вискозиметрическое течение, большие деформации, термопластичность

1. Введение. Для жесткопластического анализа [1] одномерная задача о вязкопластическом течении материала в цилиндрическом вискозиметре является тестовой [2, 3]. В такой постановке принципиально нелинейной математической модели деформирования упрощения в математическом аппарате достигаются допущением о недеформируемости материала жестких продвигающихся ядер и застойных зон. Такие области деформируемого тела могут изменяться только за счет изменения своих границ [4–6]. Данное допущение совершенно исключает консервативную составляющую процесса деформирования, оставляя его исключительно диссипативным. Учет же консервативной части процесса требует модельного учета упругих свойств деформируемого материала, то есть допущения упругого деформирования материла в застойных зонах и продвигающихся ядрах. В таком случае задача о вискозиметрическом вязкопластическом течении предстает в качестве одномерной задачи теории больших деформаций упруговязкопластических материалов [7–13]. В части постановок и решений краевых задач данной теории особенно удобным оказался подход, основанный на формализме неравновесной термодинамики, когда обратимые и необратимые деформации, как термодинамические параметры состояния в процессе деформирования, определяются формулированием для них дифференциальных уравнений их изменения (переноса) [11–13]. С помощью данного подхода было получено несколько решений задач теории, включая точные аналитические. Часть таких задач составили содержание [12], где рассматриваются и задачи вискозиметрического деформирования [14–17]. Так в [14] изучались особенности наложения на вискозиметрическое течение материала его осевого перемещения, в [16] влияние смазок граничных поверхностей, в [17] вязкопластическое течение усложняется наличием проскальзывания на стенках вискозиметра.

В [18–20] именно на примере решения вискозиметрических задач теории больших деформаций упруговязкопластических материалов обсуждаются особенности изменения на упругопластических границах механизмов производства необратимых деформаций. С одной стороны такой граничной поверхности необратимые деформации могут расти за счет вязких свойств деформируемого материала (ползучесть), а с другой преимущественно за счет пластических свойств (течение) [21].

Здесь обобщим решение, полученное в [17]. Будем считать, что проскальзывание тормозится трением и это приводит к разогреву деформируемого материала. Таким образом, рассмотрим связанную задачу производства тепла и необратимых деформаций за счет вискозиметрического деформирования и пристеночного трения. В качестве математической модели при постановке и решении данной задачи используем подходы [8, 22], позже последовательно изложенные в [12]. Необходимо заметить, что в рамках такой математической модели уже рассматривались [23–26] связанные термомеханические задачи, ограничиваясь при этом только прямолинейным движением упруговязкопластического материала.

2. Основные соотношения математической модели. В качестве термодинамических параметров состояния тела в процессе его деформирования наряду с температурой $T$ (или плотностью распределения энтропии $S$) принимаем обратимые (термоупругие) деформации ${\mathbf{m}}$ и необратимые деформации ${\mathbf{p}}$. Последние могут быть деформациями ползучести или деформациями пластического течения; определяться как вязкими свойствами деформируемого материала, так и пластическими. Для них принимаем важное положение о том, что существовать могут процессы деформирования, в которых необратимые деформации ${\mathbf{p}}$ неизменны. Принятие такой идеализации процесса деформирования позволяет определить необратимые и обратимые деформации следующими [11, 12] дифференциальными уравнениями их изменения (переноса)

(2.1)
$\begin{gathered} \frac{{D{\mathbf{p}}}}{{Dt}} = \frac{{d{\mathbf{p}}}}{{dt}} - {\mathbf{w}} \cdot {\mathbf{p}} + {\mathbf{p}} \cdot {\mathbf{w}} = {\mathbf{\gamma }} - {\mathbf{p}} \cdot {\mathbf{\gamma }} - {\mathbf{\gamma }} \cdot {\mathbf{p}} \\ \frac{{D{\mathbf{m}}}}{{Dt}} = {\mathbf{\varepsilon }} - {\mathbf{\gamma }} - \frac{1}{2}\left( {({\mathbf{\varepsilon }} - {\mathbf{\gamma }} + {\mathbf{z}}) \cdot {\mathbf{m}} + {\mathbf{m}} \cdot ({\mathbf{\varepsilon }} - {\mathbf{\gamma }} - {\mathbf{z}})} \right) \\ \end{gathered} $

Уравнения переноса (2.1) записаны в системе независимых пространственных переменных Эйлера и введенных обозначений

(2.2)
$\begin{gathered} {\mathbf{v}} = \frac{{\partial {\mathbf{u}}}}{{\partial t}} + {\mathbf{v}}\nabla {\mathbf{u}},\quad \nabla {\mathbf{v}} = \frac{1}{2}(\nabla {\mathbf{v}} + {{\nabla }^{T}}{\mathbf{v}}) + \frac{1}{2}(\nabla {\mathbf{v}} - {{\nabla }^{T}}{\mathbf{v}}) = {\mathbf{\varepsilon }} + {\mathbf{\omega }} \\ \,{\mathbf{w}} = - {{{\mathbf{w}}}^{T}} = {\mathbf{\omega }} + {\mathbf{z}},\quad {\mathbf{m}} = {\mathbf{e}} + \alpha {{T}_{0}}\theta {\mathbf{I}},\quad \theta = {{T}_{0}}^{{ - 1}}(T - {{T}_{0}}) \\ \,{\mathbf{z}} = - {{{\mathbf{z}}}^{T}} = {{A}^{{ - 1}}}({{B}^{2}}\left( {{\mathbf{\varepsilon }} \cdot {\mathbf{m}} - {\mathbf{m}} \cdot {\mathbf{\varepsilon }}} \right) + B({\mathbf{\varepsilon }} \cdot {{{\mathbf{m}}}^{2}} - {{{\mathbf{m}}}^{2}} \cdot {\mathbf{\varepsilon }}) + {\mathbf{m}} \cdot {\mathbf{\varepsilon }} \cdot {{{\mathbf{m}}}^{2}} - {{{\mathbf{m}}}^{2}} \cdot {\mathbf{\varepsilon }} \cdot {\mathbf{m}}) \\ A = 8 - 8{{J}_{1}} + 3J_{1}^{2} - {{J}_{2}} - \frac{1}{3}J_{1}^{3} + \frac{1}{3}{{J}_{3}},\quad B = 2 - {{J}_{1}}, \\ {{J}_{1}} = {\mathbf{I}} \cdot {\mathbf{m}},\quad {{J}_{2}} = {\mathbf{I}} \cdot {{{\mathbf{m}}}^{2}},\quad {{J}_{3}} = {\mathbf{I}} \cdot {{{\mathbf{m}}}^{3}} \\ \end{gathered} $

В (2.1) и (2.2) ${\mathbf{u}},{\mathbf{v}}$ – векторы перемещений и скорости; ${\mathbf{m}},{\mathbf{p}}$ – тензоры обратимых и необратимых деформаций; I – единичный тензор второго ранга; $T,{{T}_{0}}$ – температура и температура свободного состояния (комнатная температура) соответственно; $\alpha $ – коэффициент линейного расширения. Первое равенство в (2.1) вводит объективную производную тензора по времени, обладающую важным качеством. С ее помощью задается взаимозависимость между обратимыми и необратимыми деформациями в процессе деформирования, которая обеспечивает геометрическую непротиворечивость кинематики процесса. Когда источник ${\mathbf{\gamma }}$ в уравнении переноса необратимых деформаций p равен нулю, тогда $\frac{{D{\mathbf{p}}}}{{Dt}} = 0$ и p неизменный тензор. Следовательно при равенстве нулю скоростей необратимых деформаций ${\mathbf{\gamma }}$ деформации p неизменны, а равенство $\frac{{D{\mathbf{p}}}}{{Dt}} = 0$ служит для вычисления компонент тензора p, меняющихся также как и при жестких перемещениях тела. При равенстве нулю нелинейной добавки ${\mathbf{z}}({\mathbf{\varepsilon }},{\mathbf{m}}) = 0$, введенная объективная производная совпадает с производной Зарембо–Яумана.

Для полных деформаций Альманси из (2.1) и (2.2) следует [12]

(2.3)
${\mathbf{d}} = {\mathbf{m}} + {\mathbf{p}} - \frac{1}{2}{\mathbf{m}} \cdot {\mathbf{m}} - {\mathbf{m}} \cdot {\mathbf{p}} - {\mathbf{p}} \cdot {\mathbf{m}} + {\mathbf{m}} \cdot {\mathbf{p}} \cdot {\mathbf{m}}$

Согласно (2.3) следует, введенный тензор ${\mathbf{m}}$ является только главной линейной частью тензора ${\mathbf{m}} - 0.5{{{\mathbf{m}}}^{2}}$ обратимых деформаций.

В качестве термодинамического потенциала консервативной части процесса деформирования принимаем свободную энергию $\Psi ({\mathbf{m}},T) = \Phi ({\mathbf{d}},s) - Ts$, а термоупругий потенциал введем зависимостью $W({\mathbf{m}},\theta ) = {{\rho }_{0}}\Psi \left( {{\mathbf{m}},T} \right)$. Здесь $\Phi ({\mathbf{d}},s)$ – плотность распределения внутренней энергии. При этом принимается, что свободная энергия не зависит от необратимых деформаций. Последнее предположение является гипотетическим, но оно существенно упрощает математическую модель, разделяя консервативную и диссипативную составляющие процесса деформирования. В механике деформируемых материалов со сложными свойствами принятие данного положения является обычным [8, 10, 11, 27], принимается оно, как правило, при разработке методов численных расчетов [28]. При подобном разделении процесса деформирования на консервативную и диссипативную составляющие из закона сохранения энергии следует [12] формула Мурнагана и уравнение баланса энтропии

(2.4)
${\mathbf{\sigma }} = - p{\mathbf{I}} + {{\left( {1 + 3\alpha {{T}_{0}}\theta } \right)}^{{ - 1}}}\frac{{\partial W}}{{\partial {\mathbf{m}}}} \cdot ({\mathbf{I}} - {\mathbf{m}})$
(2.5)
$\frac{{\partial (\rho s)}}{{\partial t}} = - {\text{div}}{\mathbf{J}} - {{T}^{{ - 2}}}{\mathbf{q}} \cdot \nabla T + {{T}^{{ - 1}}}{\mathbf{\sigma }} \cdot {\mathbf{\gamma }}$

Формула Мурнагана (2.4) здесь записана для случая механически несжимаемого материала; в ней p – неизвестное гидростатическое давление. В уравнении баланса энтропии (2.5) векторы q и J являются потоками тепла и энтропии. При этом

${\mathbf{J}} = \rho s{\mathbf{v}} - {{T}^{{ - 1}}}{\mathbf{q}},\,\,\,\,\,s = - {{T}_{0}}{{\rho }^{{ - 1}}}\frac{{\partial W}}{{\partial \theta }}$

Далее деформируемый материал считаем не только механически несжимаемым, но и изотропным, для которого $W = W({{J}_{1}},{{J}_{2}},\theta )$ и ${{J}_{1}} = {\mathbf{I}} \cdot {\mathbf{c}},\,\,\,{{J}_{2}} = {\mathbf{I}} \cdot {{{\mathbf{c}}}^{2}},\,\,\,{\mathbf{c}} = {\mathbf{m}} - 0.5{{{\mathbf{m}}}^{2}}$. Для $W({{J}_{1}},{{J}_{2}},\theta )$ принимаем зависимость, следующую из разложения этой функции в ряд Тейлора относительно свободного состояния деформируемого материла при комнатной температуре ${{T}_{0}}$

(2.6)
$\begin{gathered} W({{J}_{1}},{{J}_{2}},\theta ) = - 2\mu {{J}_{1}} - \mu {{J}_{2}} + \varsigma {\text{ }}J_{1}^{2} + (\varsigma - \mu ){{J}_{1}}{{J}_{2}} - \chi J_{1}^{3} + {{\nu }_{1}}{{J}_{1}}\theta + {{\nu }_{2}}{{\theta }^{2}} - {{\nu }_{3}}{{J}_{1}}{{\theta }^{2}} - \\ \; - {{\nu }_{4}}{{J}_{1}}^{2}\theta - {{\nu }_{5}}{{J}_{2}}\theta - {{\nu }_{6}}{{\theta }^{3}} + ... \\ \end{gathered} $

В (2.6) $\mu $ – модуль сдвига, $\kappa ,\,\,\,\chi $ – упругие модули более высокого порядка, ${{\nu }_{k}}(k = 1$, 2, ..., 6) – термомеханические постоянные. Конкретные зависимости напряжений от температуры и обратимых деформаций следуют при подстановке (2.6) в (2.4).

Подстановка (2.6) в (2.5) позволяет записать уравнение теплопроводности в форме

(2.7)
$\begin{gathered} (1 + {{\beta }_{1}}\theta + {{\beta }_{2}}{{J}_{1}})\frac{{\partial \theta }}{{\partial t}} + {{\beta }_{3}}({\mathbf{\varepsilon }} - {\mathbf{\gamma }}) \cdot {\mathbf{c}} = \lambda \Delta \theta - \frac{1}{{2{{\nu }_{2}}}}{\mathbf{\sigma }} \cdot {\mathbf{\gamma }} \\ \,{{\beta }_{1}} = \frac{{(1 - 3\alpha {{T}_{0}}){{\nu }_{2}} - 3{{\nu }_{6}}}}{{{{\nu }_{2}}}},\quad {{\beta }_{2}} = - \frac{{{{\nu }_{3}}}}{{{{\nu }_{2}}}},\quad {{\beta }_{3}} = - \frac{{{{\nu }_{1}} + {{\nu }_{5}}}}{{{{\nu }_{2}}}} \\ \end{gathered} $

Здесь $\lambda $ – коэффициент температуропроводности. В области деформирования, предваряющей вязкопластическое течение, и в области разгрузки следует в (2.7) считать ${\mathbf{\gamma }} = 0$. Это означает, что производством необратимых деформаций в таких частях области деформирования в форме деформаций ползучести пренебрегаем. Тогда в них ${\mathbf{\gamma }} = 0$, а в области течения ${\mathbf{\gamma }} = {{{\mathbf{\varepsilon }}}^{{\mathbf{p}}}}$, то есть источник в уравнении переноса (2.1) совпадает с тензором скоростей пластических деформаций.

В качестве пластического потенциала принимаем следующее обобщение [29, 30] условия пластического течения Треска–Сен-Венана

(2.8)
$F({\mathbf{\sigma }}{\text{,}}{\mathbf{\gamma }},k) = max{\text{|}}{{\sigma }_{i}} - {{\sigma }_{j}}{\text{|}} - 2\eta max{\text{|}}{{\gamma }_{k}}{\text{|}} - 2k = 0$

Здесь ${{\sigma }_{i}},\,{{\gamma }_{k}}$ – главные значения тензоров, $\eta $ – коэффициент вязкого сопротивления пластическому течению, k – предел текучести, измеренный в опытах на чистый сдвиг. Зависимость предела текучести от температуры принимаем в виде [31]

(2.9)
$k = {{k}_{0}}\left( {1 - \frac{{{{\theta }^{2}}}}{{\theta _{m}^{2}}}} \right),\,\,\,\,\,{{\theta }_{m}} = ({{T}_{m}} - {{T}_{0}})T_{0}^{{ - 1}}$

В (2.9) Tm – температура плавления деформируемого материала, k0 – предел текучести материала при комнатной температуре. Скорости необратимых (пластических) деформаций связаны с напряжениями ассоциированным законом пластического течения

(2.10)
${{{\mathbf{\varepsilon }}}^{p}} = {\mathbf{\gamma }} = \phi \frac{{\partial f({\mathbf{\sigma }},{\mathbf{\gamma }},k)}}{{\partial {\mathbf{\sigma }}}},\quad \phi > 0$

Добавив к записанным здесь соотношениям уравнение равновесия $\nabla {\mathbf{\sigma }} = 0$, получаем замкнутую систему уравнений квазистационарного упруговязкопластического деформирования.

3. Постановка задачи. Обратимое деформирование начала процесса. Пусть упруговязкопластический материал заполняет область между цилиндрическими поверхностями $r = {{r}_{0}}$ и $r = R$ ($R > {{r}_{0}}$). Поверхность $r = {{r}_{0}}$ считаем закрепленной, а поверхности $r = R$ предоставим возможность поворачиваться вокруг оси цилиндра под действием внешней нагрузки. Следовательно, граничными условиями задачи будут соотношения, записанные в цилиндрических координатах $r,\varphi ,z$

(3.1)
$\begin{gathered} {\mathbf{u}}({{r}_{0}},t) = 0,\quad {\mathbf{v}}({{r}_{0}},t) = 0,\quad {{\sigma }_{{r\phi }}}(R,t) = {{R}^{{ - 2}}}f(t) \\ \end{gathered} $

Считаем, что до момента времени t = 0 начала процесса деформирования деформации в цилиндрическом слое отсутствовали, температура равнялась комнатной ${{T}_{0}}$, первоначальное обжатие равномерное ${{\sigma }_{{rr}}}(r,0) = {{\sigma }_{{\phi \phi }}}(r,0) = {{\sigma }_{{zz}}}(r,0) = {{\sigma }_{0}} = {\text{const}}.$ Рассмотрим особенности деформирования при увеличивающемся, постоянном и уменьшающемся сдвигающем напряжении на внешней поверхности $r = R$

(3.2)
$\begin{gathered} f(t) = \, \\ \end{gathered} \left\{ \begin{gathered} at,\quad 0 \leqslant t \leqslant {{t}_{1}} \hfill \\ a{{t}_{1}},\quad {{t}_{1}} \leqslant t \leqslant {{t}_{2}} \hfill \\ a{{t}_{1}} - b(t - {{t}_{2}}),\quad {{t}_{2}} \leqslant t \leqslant {{t}_{5}} \hfill \\ \end{gathered} \right.$

Первоначально, за моментом начала процесса, деформируемый материал удерживается в слое за счет сухого трения, деформируясь обратимо

(3.3)
${{\text{|}}{{\sigma }_{{r\phi }}}{\text{|}} \leqslant \delta {\text{|}}{{\sigma }_{{rr}}}{\text{|}},\quad {\text{при}}\quad r = {{r}_{0}}\quad {\text{и при}}\quad r = R}$
где $\delta $ – коэффициент трения покоя. Геометрия задачи и условие несжимаемости материала задают кинематику среды

(3.4)
$\begin{gathered} {{u}_{r}} = r(1 - cos\psi (r,t)),\quad {{u}_{\varphi }} = rsin\psi (r,t),\quad {{u}_{z}} = 0 \\ {{d}_{{rr}}} = - \frac{1}{2}{{r}^{2}}{{\left( {\frac{{\partial \psi }}{{\partial r}}} \right)}^{2}} = - 2{{g}^{2}},\quad {{d}_{{r\varphi }}} = \frac{1}{2}r{{\psi }_{{,r}}} = g,\quad {{\psi }_{{,r}}} = \frac{{\partial \psi }}{{\partial r}} \\ \end{gathered} $

Здесь $\psi = \psi (r,t)$ – неизвестная зависимая переменная, центральный угол закручивания материала при его деформировании. При подстановке (2.6) в (2.4) для рассматриваемого первоначального обратимого деформирования найдем

(3.5)
$\begin{gathered} {{\sigma }_{{rr}}} = {{\sigma }_{{zz}}} = - p - 2(\varsigma + \mu ){{g}^{2}} = - \Sigma ,\quad {{\sigma }_{{\varphi \varphi }}} = - \Sigma + 2\mu {{g}^{2}},\quad {{\sigma }_{{r\varphi }}} = 2\mu g \\ \end{gathered} $

При записи (3.5) ограничились слагаемыми до третьего порядка по обратимым (упругим) деформациям. Для метода расчетов это не принципиально, но позволяет избежать громоздкости последующих записей. Часто действительно обратимые деформации позволительно считать малыми настолько, что их третьим порядком можно пренебречь в сравнении с первым и вторым.

Если подставить (3.4) и (3.5) в уравнения равновесия (квазистатический случай)

(3.6)
$\begin{gathered} {{\sigma }_{{rr,r}}} + {{r}^{{ - 1}}}({{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}) = 0,\quad {{\sigma }_{{r\varphi ,r}}} + 2{{r}^{{ - 1}}}{{\sigma }_{{r\varphi }}} = 0 \\ \end{gathered} $
и результат проинтегрировать, то получим

(3.7)
$\begin{gathered} {{\sigma }_{{r\varphi }}} = \frac{{f(t)}}{{{{r}^{2}}}},\quad {{\sigma }_{{rr}}} = {{\sigma }_{{zz}}} = \frac{{{{f}^{2}}}}{{4\mu }}\left( {\frac{1}{{r_{0}^{4}}} - \frac{1}{{{{r}^{4}}}}} \right) + {{\sigma }_{0}} \\ {{\sigma }_{{\varphi \varphi }}} = \frac{{{{f}^{2}}}}{{4\mu }}\left( {\frac{1}{{r_{0}^{4}}} - \frac{3}{{{{r}^{4}}}}} \right) + {{\sigma }_{0}},\quad \psi = \frac{f}{{2\mu }}\left( {\frac{1}{{r_{0}^{2}}} - \frac{1}{{{{r}^{2}}}}} \right) \\ \omega = \frac{{\dot {f}}}{{2\mu }}\left( {\frac{1}{{r_{0}^{2}}} - \frac{1}{{{{r}^{2}}}}} \right),\quad \dot {f} = \frac{{df}}{{dt}} \\ \end{gathered} $

Найденное решение справедливо до некоторого момента времени $t = {{t}_{0}} < {{t}_{1}}$. В момент времени $t = {{t}_{0}}$ нарушается граничное условие (3.3) или начинается вязкопластическое течение. При $\delta {{\sigma }_{0}} < {{k}_{0}}$ проскальзывание начнется ранее начала вязкопластического течения. Тогда с момента времени $t = {{t}_{0}}$ граничное условие (3.3) при $r = {{r}_{0}}$ заменяется условием

(3.8)
$\begin{gathered} {\text{|}}{{\sigma }_{{r\varphi }}}{\text{|}} = \delta {\text{|}}{{\sigma }_{{rr}}}{\text{|}} + \xi {\text{|}}\omega {\text{|}} \\ \end{gathered} $
где $\begin{gathered} \xi \\ \end{gathered} $ – постоянная вязкого трения. При выполнении (3.8) начинается разогрев материала за счет пристеночного трения на поверхности $r = {{r}_{0}}$:

(3.9)
$\begin{gathered} \theta (r,{{t}_{0}}) = 0,\quad {{\theta }_{{,r}}}(R,t) = 0,\quad \theta ({{r}_{0}},t) = {{\alpha }_{1}}\psi ({{r}_{0}},t) \\ \end{gathered} $

Условиями (3.9) принимается, что поверхность $\begin{gathered} r = R \\ \end{gathered} $ теплоизолирована; ${{\alpha }_{1}}$ – постоянная теплопроизводства за счет трения; разогревом материала за счет термомеханической связанности обратимого деформирования с температурой пренебрегаем (коэффициент связанности считаем равным нулю). Следствием (2.4) и (2.5) в данном случае являются зависимости

(3.10)
$\begin{gathered} {{\sigma }_{{rr}}} = {{\sigma }_{{zz}}} = - p - 2(\varsigma + \mu ){{g}^{2}} + {{\xi }_{1}}\theta - {{\xi }_{2}}{{\theta }^{2}} \equiv - {{\Sigma }_{1}} \\ {{\sigma }_{{\varphi \varphi }}} = - {{\Sigma }_{1}} + 2\mu {{g}^{2}},\quad {{\sigma }_{{r\varphi }}} = 2(\mu - \theta l)g \\ {{\xi }_{1}} = {{\nu }_{1}} + 6\mu \alpha {{T}_{0}},\quad {{\xi }_{2}} = {{\nu }_{3}} + 18\mu {{\alpha }^{2}} + 3\alpha {{\nu }_{1}}{{T}_{0}},\quad l = {{\nu }_{1}} + {{\nu }_{5}} + 3\alpha \mu {{T}_{0}} \\ \end{gathered} $

Используя (3.10) вместе с интегралом второго уравнения равновесия из (2.6), получаем

(3.11)
$\begin{gathered} {{m}_{{r\varphi }}} = g,\quad {{m}_{{rr}}} = - \frac{3}{2}{{g}^{2}},\quad {{m}_{{\varphi \varphi }}} = \frac{1}{2}{{g}^{2}},\quad g = \frac{f}{{2{{r}^{2}}(\mu - l\theta )}} \\ \end{gathered} $

Эти соотношения позволяют записать уравнение теплопроводности применительно к рассматриваемому случаю

(3.12)
$\begin{gathered} \left( {1 + {{\beta }_{1}}\theta } \right)\dot {\theta } + \frac{{{{\beta }_{3}}{{a}^{2}}t}}{{2{{r}^{4}}{{{(\mu - l\theta )}}^{3}}}}(lt\dot {\theta } + \mu - l\theta ) = \lambda ({{\theta }_{{,rr}}} + {{r}^{{ - 1}}}{{\theta }_{{,r}}}) \\ \end{gathered} $

Краевыми условиями для (3.12) являются соотношения

(3.13)
$\begin{gathered} \theta ({{r}_{0}},t) = {{\alpha }_{1}}\left( {\frac{{\delta {{\sigma }_{0}}}}{\xi }({{t}_{0}} - t) + \frac{a}{{2\xi r_{0}^{2}}}({{t}^{2}} - t_{0}^{2})} \right),\quad {{\theta }_{{,r}}}(R,t) = 0 \\ \end{gathered} $

Задача (3.12)–(3.13) по расчету распределения температуры решается численно, по найденному распределению после интегрирования зависимости

${{\psi }_{{,r}}} = \frac{f}{{{{r}^{3}}(\mu - l\theta )}}$
находим перемещения и деформации. Расчеты продолжаем до тех пор, пока не выполнится условие пластического течения (2.8). Данное условие выполняется на поверхности $r = {{r}_{0}}$ в форме ${{\sigma }_{{r\varphi }}}({{r}_{0}},{{t}_{*}}) = {{k}_{0}}$ в момент времени $t = {{t}_{*}}$, для которого имеем уравнение

(3.14)
$\begin{gathered} {{t}_{*}} = \frac{{{{k}_{0}}r_{0}^{2}}}{a}\left( {1 - \frac{{{{\theta }^{2}}({{r}_{0}},{{t}_{*}})}}{{\theta _{m}^{2}}}} \right) \\ \end{gathered} $

В момент времени $t = {{t}_{*}}$ от граничной поверхности отделяется и продвигается по материалу слоя упругопластическая граница $r = {{r}_{1}}(t)$, оставляя за собой область вязкопластического течения ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$.

4. Вязкопластическое течение. В последующее за моментом $t = {{t}_{*}}$ время область деформирования разделяется на две части. В одной из них ${{r}_{1}}(t) \leqslant r \leqslant R$ продолжается обратимое деформирование (область I), в другой ${{r}_{0}} \leqslant r \leqslant {{r}_{1}}(t)$ развивается вязкопластическое течение (область II). Кинематические зависимости принятой математической модели (2.1)–(2.3) в рассматриваемом случае дают возможность записать:

(4.1)
$\begin{gathered} {{{v}}_{\varphi }} = r\omega ,\quad {{\varepsilon }_{{r\varphi }}} = \frac{{\partial {{d}_{{r\varphi }}}}}{{\partial t}} = \frac{1}{2}({{{v}}_{{\phi ,r}}} - {{r}^{{ - 1}}}{{{v}}_{r}}) = \frac{1}{2}r{{\psi }_{{,rt}}} \\ {{\varepsilon }_{{r\varphi }}} = \frac{{\partial {{e}_{{r\varphi }}}}}{{\partial t}} + {{\gamma }_{{r\varphi }}} = \frac{{\partial {{e}_{{r\varphi }}}}}{{\partial t}} + \varepsilon _{{r\varphi }}^{p} = \frac{{\partial {{e}_{{r\varphi }}}}}{{\partial t}} + \frac{{\partial {{p}_{{r\varphi }}}}}{{\partial t}} \\ \varepsilon _{{rr}}^{p} = \frac{{\partial {{p}_{{rr}}}}}{{\partial t}} + 2{{p}_{{r\varphi }}}\left( {{{w}_{{\varphi r}}} + \varepsilon _{{r\varphi }}^{p} - \frac{{\partial \psi }}{{\partial t}}} \right),\quad \varepsilon _{{\varphi \varphi }}^{p} = \frac{{\partial {{p}_{{\varphi \varphi }}}}}{{\partial t}} + 2{{p}_{{r\varphi }}}\left( {{{w}_{{r\varphi }}} + \varepsilon _{{r\varphi }}^{p} + \frac{{\partial \psi }}{{\partial t}}} \right) \\ \varepsilon _{{rr}}^{p} = - \varepsilon _{{\varphi \varphi }}^{p} = \frac{{\varepsilon _{{r\varphi }}^{p}\left( {{{e}_{{rr}}} - {{e}_{{\varphi \varphi }}}} \right)}}{{2{{e}_{{r\varphi }}}}}\quad \\ \end{gathered} $

В области вязкопластического течения напряжения в зависимости от обратимых деформаций и температуры найдутся из (2.4) и (2.6)

(4.2)
$\begin{gathered} {{\sigma }_{{rr}}} = {{\sigma }_{{zz}}} = - p - 2(\varsigma + \mu )m_{{r\varphi }}^{2} + {{\xi }_{1}}\theta - {{\xi }_{2}}{{\theta }^{2}} = - {{\Sigma }_{2}} \\ {{\sigma }_{{\varphi \varphi }}} = - {{\Sigma }_{2}} + 2\mu m_{{r\varphi }}^{2},\quad {{\sigma }_{{r\varphi }}} = 2(\mu - l\theta ){{m}_{{r\varphi }}}. \\ \end{gathered} $

Ассоциированный с поверхностью нагружения (текучести) (2.8) закон пластического течения (2.10) приводит к равенствам

(4.3)
$\begin{gathered} {{\sigma }_{{r\varphi }}} = k + \eta \varepsilon _{{r\varphi }}^{p},\quad \varphi = \varepsilon _{{r\varphi }}^{p}{{(k + \eta \varepsilon _{{r\varphi }}^{p})}^{{ - 1}}},\quad \varepsilon _{{r\varphi }}^{p} = \frac{1}{\eta }\left( {\frac{f}{{{{r}^{2}}}} - {{k}_{0}}\left( {1 - \frac{{{{\theta }^{2}}}}{{\theta _{m}^{2}}}} \right)} \right) \\ \end{gathered} $

В качестве следствия условий непрерывности напряжений на продвигающейся упругопластической границе $r = {{r}_{1}}(t)$, получаем уравнение для определения этой границы

(4.4)
$\begin{gathered} {{r}_{1}}(t) = \sqrt {\frac{{f(t)}}{{{{k}_{0}}\left( {1 - \frac{{{{\theta }^{2}}({{r}_{1}},t)}}{{\theta _{m}^{2}}}} \right)}}} \\ \end{gathered} $

В области обратимого (термоупругого) деформирования (I) уравнение теплопроводности имеет вид

(4.5)
$\begin{gathered} (1 + {{\beta }_{1}}{{\theta }^{I}}){{{\dot {\theta }}}^{I}} + \frac{{{{\beta }_{3}}{{a}^{2}}t}}{{2{{r}^{4}}{{{(\mu - l{{\theta }^{I}})}}^{2}}}}\left( {\frac{{lt{{{\dot {\theta }}}^{I}}}}{{\mu - l{{\theta }^{I}}}} + 1} \right) = \lambda ({{\theta }^{I}}_{{,rr}} + {{r}^{{ - 1}}}\theta _{{,r}}^{I}). \\ \end{gathered} $

В области вязкопластического течения уравнение (4.5) снабжается источником за счет необратимого деформирования

(4.6)
$\begin{gathered} (1 + {{\beta }_{1}}{{\theta }^{{II}}}){{{\dot {\theta }}}^{{II}}} + \frac{{{{\beta }_{3}}{{a}^{2}}t}}{{2{{r}^{4}}{{{(\mu - l{{\theta }^{{II}}})}}^{2}}}}\left( {\frac{{lt{{{\dot {\theta }}}^{{II}}}}}{{\mu - l{{\theta }^{{II}}}}} + 1} \right) = \lambda ({{\theta }^{{II}}}_{{,rr}} + {{r}^{{ - 1}}}\theta _{{,r}}^{{II}}) - \\ \, - \frac{1}{{2{{\nu }_{2}}\eta }}\frac{{at}}{{{{r}^{2}}}}\left( {\frac{{at}}{{{{r}^{2}}}} - {{k}_{0}}\left( {1 - \frac{{{{{({{\theta }^{{II}}})}}^{2}}}}{{\theta _{m}^{2}}}} \right)} \right) \\ \end{gathered} $

Таким образом, для распределения температуры по деформируемому слою имеем систему уравнений (4.5) и (4.6) с граничными и начальными условиями

(4.7)
${\theta _{{,r}}^{I}(R,t) = 0,\quad {{\theta }^{{II}}}({{r}_{0}},t) = {{\alpha }_{1}}\left( {\frac{{\delta {{\sigma }_{0}}}}{\xi }({{t}_{0}} - t) + \frac{a}{{2\xi r_{0}^{2}}}({{t}^{2}} - t_{0}^{2})} \right),\quad {{\theta }^{I}}({{r}_{1}}(t),t) = {{\theta }^{{II}}}({{r}_{1}}(t),t)}$

В качестве начального условия для ${{{\theta }^{I}}(r,t)}$ принимается распределение температуры в момент времени $t = {{t}_{*}}$ начала пластического течения, рассчитанное решением задачи обратимого деформирования с источником тепла за счет трения на поверхности $r = {{r}_{0}}$.

Для численной реализации задачи (4.5)–(4.7) вводятся две сетки по переменной r, изменяющиеся со временем: в термоупругой области r = ${{r}_{1}}_{{i + 1}}\, + \,h_{{i + 1}}^{e}j,$ $j\, = \,\overline {0,{{N}^{e}} - 1} ,$ $h_{{i + 1}}^{e}\, = \,\frac{{(1\, - \,{{r}_{1}}_{{i + 1}})}}{{{{N}^{e}}}}$, в области вязкопластического течения r = ${{r}_{0}}\, + \,h_{{i + 1}}^{p}j,$ $j\, = \,\overline {1,{{N}^{p}}} ,$ $h_{{i + 1}}^{p}\, = \,\frac{{({{r}_{1}}_{{i + 1}})\, - \,{{r}_{0}}}}{{{{N}^{p}}}}$. На каждом временном шаге $t = {{t}_{*}} + dt(i + 1),i = \overline {0,N} $ из-за движения упругопластической границы сетка меняется. Значения температуры для вновь строящейся сетки на предыдущем временном шаге находятся интерполяцией.

По найденному распределению температуры рассчитываются (4.3) скорости необратимых (пластических) деформаций, скорости полных и упругих (4.1) деформаций. Интегрированием распределения скоростей деформаций в каждый рассматриваемый момент времени определяются значения полных деформаций и их составляющих. Для функции $\psi = \psi (r,t)$ следует дифференциальное уравнение

(4.8)
$\begin{gathered} r{{\psi }^{I}}_{{,r}} = 2{{p}_{{r\phi }}} + \frac{{at}}{{{{r}^{2}}(\mu - l{{\theta }^{I}})}} \\ \end{gathered} $
с граничным условием

(4.9)
$\begin{gathered} \psi ({{r}_{0}},t) = \frac{{\delta {{\sigma }_{0}}}}{\xi }({{t}_{0}} - t) + \frac{a}{{2\xi r_{0}^{2}}}({{t}^{2}} - t_{0}^{2}) \\ \end{gathered} $

Интегрированием первого из уравнений равновесия (3.6) определяем функцию добавочного гидростатического давления $\begin{gathered} p(r,t) \\ \end{gathered} $ и следовательно диагональные компоненты тензора напряжений.

5. Деформирование при постоянной и умещающейся нагрузке. С момента времени $t = {{t}_{1}}$ сдвигающее напряжение на поверхности $r = R$ постоянно: ${{\sigma }_{{r\varphi }}}(R,t) = {\text{const}}$, $f(t) = a{{t}_{1}} = {\text{const}}$. Однако, область вязкопластического течения продолжает свое развитие. Справедливыми остаются уравнения теплопроводности (4.5) и (4.6) для областей обратимого и необратимого деформирования соответственно. Граничные условия для этих уравнений приобретают вид

(5.1)
$\begin{gathered} {{\theta }^{I}}({{r}_{0}},t)\, = \,{{\alpha }_{1}}\left( {\frac{{\delta {{\sigma }_{0}}}}{\xi }({{t}_{0}}\, - \,t)\, + \,\frac{a}{{2\xi r_{0}^{2}}}(t_{1}^{2}\, + \,t_{0}^{2}\, - \,2t{{t}_{1}})} \right),\quad {{\theta }^{I}}({{r}_{1}}(t),t)\, = \,{{\theta }^{{II}}}({{r}_{1}}(t),t),\quad \\ \end{gathered} \theta _{{,r}}^{{II}}(R,t)\, = \,0$

Скорости деформаций, обратимые и необратимые деформации находятся, как и ранее, посредством кинематических соотношений (4.1). Для распределения углового смещения $\psi (r,t)$ имеем аналог уравнения (4.8) с граничными условиями

(5.2)
${{\psi }^{I}}({{r}_{0}},t) = \frac{{\delta {{\sigma }_{0}}}}{\xi }({{t}_{0}} - t) + \frac{a}{{2\xi r_{0}^{2}}}(t_{1}^{2} + t_{0}^{2} - 2t{{t}_{1}}),\quad {{\psi }^{I}}({{r}_{1}}(t),t) = {{\psi }^{{II}}}({{r}_{1}}(t),t)$

После момента времени $t = {{t}_{2}}$ напряжение ${{\sigma }_{{r\phi }}}(R,t)$ уменьшается: f(t) = at1 – $b(t - {{t}_{2}})$. Изменения в режиме нагружения приводят к возникновению новой упругопластической границы $r = {{r}_{2}}(t)$. Эта граничная поверхность движется от стационарной поверхности $r = {{r}_{1}}({{t}_{2}})$ к центру, отделяя от уменьшающейся области ${{r}_{0}} \leqslant r \leqslant {{r}_{2}}(t)$ вязкопластического течения (III) область (II) обратимого деформирования ${{r}_{2}}(t) \leqslant r \leqslant {{r}_{1}}({{t}_{2}})$. Обратимое деформирование в этой области происходит в присутствии неизменяющегося со временем тензора необратимых деформаций. Этим данное деформирование отлично от обратимого деформирования в области (I) ${{r}_{1}}({{t}_{2}}) \leqslant r \leqslant R$, где необратимые деформации отсутствуют. В обеих областях обратимого деформирования справедливо уравнение теплопроводности (4.5) с дополнительным условием ${{\theta }^{I}}({{r}_{1}}({{t}_{2}}),t) = {{\theta }^{{II}}}({{r}_{1}}({{t}_{2}}),t)$. В области (III) вязкопластического течения, как и прежде, справедливо уравнение теплопроводности (3.6) с измененными краевыми условиями

(5.3)
$\begin{gathered} {{\theta }^{{III}}}({{r}_{0}},t) = {{\alpha }_{1}}\left( {\frac{{\delta {{\sigma }_{0}}}}{\xi }({{t}_{0}} - t) + \frac{a}{{2\xi r_{0}^{2}}}(t_{1}^{2} + t_{0}^{2} - 2t{{t}_{1}}) - \frac{b}{{2\xi r_{0}^{2}}}(t_{2}^{2} + {{t}^{2}} - 2t{{t}_{2}})} \right) \\ {{\theta }^{{III}}}({{r}_{2}}(t),t) = {{\theta }^{{II}}}({{r}_{2}}(t),t) \\ \end{gathered} $

В момент времени $t = {{t}_{3}}$ при продолжающемся уменьшении нагружающего усилия проскальзывание прекратится, и далее будет выполняться условие жесткой спайки. Момент времени $t = {{t}_{3}}$ находится из условия: $f({{t}_{3}}) = \gamma {{\sigma }_{0}}r_{0}^{2}$. Граничные условия на поверхности $r = {{r}_{0}}$ теперь следует переписать в виде

(5.4)
$\begin{gathered} {{\psi }^{{III}}}({{r}_{0}},t) = \frac{{\gamma {{\sigma }_{0}}}}{\xi }({{t}_{0}} - {{t}_{3}}) + \frac{a}{{2\xi r_{0}^{2}}}(t_{1}^{2} + t_{0}^{2} - 2{{t}_{3}}{{t}_{1}}) - \frac{b}{{2\xi r_{0}^{2}}}(t_{2}^{2} + t_{3}^{2} - 2{{t}_{3}}{{t}_{2}}) \\ \,{{\theta }^{{III}}}({{r}_{0}},t) = {{\theta }^{{III}}}({{r}_{0}},{{t}_{3}})(1 - {{\alpha }_{2}}(t - {{t}_{3}})) \\ \end{gathered} $

Область (III) вязкопластического течения исчезает из расчетной области в момент времени $t = {{t}_{4}}$, когда ее граничная поверхность $r = {{r}_{2}}(t)$ достигает жесткой стенки $r = {{r}_{0}}$. Этот момент времени находится решением уравнения

(5.5)
$\begin{gathered} r_{0}^{2}{{k}_{0}}\left( {1 - \frac{{{{\theta }^{2}}({{r}_{0}},{{t}_{4}})}}{{\theta _{m}^{2}}}} \right) = f({{t}_{4}}) \\ \end{gathered} $

Уменьшаясь, напряжение ${{\sigma }_{{r\varphi }}}(R,t)$ в некоторый момент времени $t = {{t}_{5}} = a{{b}^{{ - 1}}}{{t}_{1}} + {{t}_{2}}$ окажется равным нулю. С этого момента времени ${{\sigma }_{{r\varphi }}} = 0$ во всем цилиндрическом слое. Но процесс выравнивания температуры по материалу за счет теплопроводности будет продолжаться. Он не останавливается и после момента времени t = t6 = ${{t}_{4}} + \alpha _{2}^{{ - 1}}$, когда $\theta ({{r}_{0}},{{t}_{6}}) = 0.$

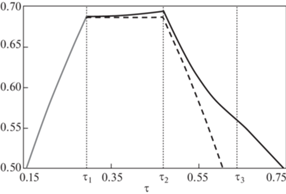
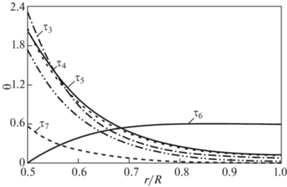
На рис. 1 показано изменение упругопластической границы (сплошная линия) в течение всего процесса деформирования, для сравнения штриховой линией показано изменение упругопластической границы без учета температурных эффектов; на рис. 2 и рис. 3 – распределение относительной температуры $\theta (r)$ и угла поворота $\psi (r)$ в различные моменты времени. Расчеты проводились в безразмерных переменных

$\begin{gathered} \tilde {r} = \frac{r}{R},\quad \tau = t\frac{a}{{\mu {{R}^{2}}}},\quad {{{\tilde {\sigma }}}_{{ij}}} = \frac{{{{\sigma }_{{ij}}}}}{\mu } \\ \end{gathered} $
результаты вычислений приведены при значениях постоянных

$\begin{gathered} \frac{{a\eta }}{{{{\mu }^{2}}{{R}^{2}}}} = 0.004,\quad \frac{{{{r}_{0}}}}{R} = 0.5,\quad \frac{k}{\mu } = 0.00621,\quad \frac{a}{b} = 1,\quad \frac{{a\xi }}{{{{\mu }^{2}}R}} = 0.005 \\ {{\beta }_{1}} = 0.5,\quad {{\beta }_{3}} = - 0.5,\quad \frac{{\delta {{\sigma }_{0}}}}{\mu } = 0.005,\quad \frac{l}{\mu } = 0.001,\quad \frac{{{{\nu }_{1}}}}{\mu } = 0.02 \\ {{\alpha }_{1}} = 1000,\quad {{\alpha }_{2}} = 100\quad \frac{q}{{{{R}^{2}}}} = 10 \\ \end{gathered} $
Рис. 1.

Граница области вязкопластического течения.

Рис. 2.

Распределение безразмерной температуры в различные моменты времени.

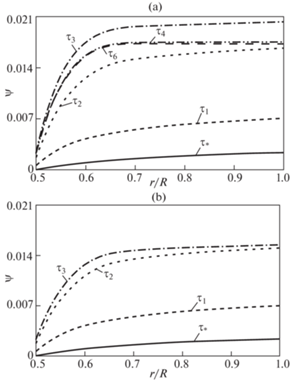
Рис. 3.

Распределение угла поворота в различные моменты времени. (а) с учетом температурных эффектов. (b) изотермический случай.

6. Заключение. Построенное численно-аналитическое решение связанной задачи больших деформаций о вискозиметрическом деформировании упруговязкопластического материала является еще одним примером полезности использования для такой цели дифференциальных уравнений переноса тензоров обратимых и необратимых деформаций. Последовательное следование формализму термодинамики таким способом помогает не только при постановке задач теории, но и в их решении.

Отметим некоторые качественные особенности процесса деформирования, определяемые учетом разогрева материала. Развитие области вязкопластического течения происходит с заметными отличиями от изотермического случая (рис. 1). Только в условиях активного процесса нагрузки такое развитие одинаково, но уже при постоянной нагрузке заметен рост области вязкопластического течения за счет связанности задачи и роста температуры в деформируемом материале за счет накопившегося тепла при трении и продолжающегося роста температуры за счет необратимого деформирования. Совершенно отличны движения разгружающихся упругопластических границ при разгрузке. В изотермическом случае данная граница достигает закрепленной поверхности (область вязкопластического течения исчезает) и только потом осуществляется прилипание материала к этой неподвижной поверхности. Когда температурные эффекты учитываются, то область вязкопластического течения уменьшается медленнее. При этом первоначально заканчивается проскальзывание и только потом вязкопластическое течение. Значения угла поворота существенно различны (рис. 3). В изотермическом случае они значительно меньше при одинаковой нагрузке.

Работа выполнена при содействии РНФ (грант 21-11-00165).

Список литературы

  1. Мосолов П.П., Мясников В.П. Механика жесткопластических сред. М.: Наука, 1981. 208 с.

  2. Сафрончик А.И. Вращение цилиндра с переменной скоростью в вязкопластичной среде // Прикл. математика и механика. 1959. Т. 23. Вып. 6. С. 998–1014.

  3. Огибалов П.М., Мирзаджанзаде А.Х. Нестационарные движения вязкопластичных сред. М.: Изд-во МГУ, 1970. 415 с.

  4. Мосолов П.П., Мясников В.П. Вариационные методы в теории течений жестковязкопластических сред. М.: Изд-во МГУ, 1971. 163 с.

  5. Быковцев Г.И., Чернышов А.Д. О вязкопластическом течении в некруговых цилиндрах при наличии перепада давления // ПМТФ. 1964. № 4. С. 94–96.

  6. Георгиевский Д.В. Жёсткие зоны в статически определимых и неопределимых задачах вязкопластического течения // Проблемы механики деформируемых твёрдых тел и горных пород. Сб. статей к 75-летию Е.И. Шемякина. М.: Физматлит, 2006. С. 135–141.

  7. Кондауров В.И. Об уравнениях упруговязкопластической среды с конечными деформациями // ПМТФ. 1982. № 4. С. 133–139.

  8. Ковтанюк Л.В., Шитиков А.В. О теории больших упругопластических деформаций при учете температурных и реологических эффектов // Вестник ДВО РАН. 2006. № 4. С. 87–93.

  9. Быковцев Г.И., Шитиков А.В. Конечные деформации упругопластических сред // Докл. АН СССР. 1990. Т. 311. № 1. С. 59–62.

  10. Роговой А.А. Определяющие соотношения для конечных упруго-неупругих деформаций // ПМТФ. 2005. Т. 46. № 45. С. 138–149.

  11. Буренин А.А., Быковцев Г.И., Ковтанюк Л.В. Об одной простой модели для упругопластической среды при конечных деформациях. // Докл. РАН. 1996. Т. 347. № 2. С. 199–201.

  12. Буренин А.А., Ковтанюк Л.В. Большие необратимые деформации и упругое последействие. Владивосток: Дальнаука, 2013. 312 с.

  13. Мясников В.П. Уравнения движения упругопластических материалов при больших деформациях // Вестн. ДВО РАН. 1996. № 4. С. 8–13.

  14. Бегун А.С., Буренин А.А., Ковтанюк Л.В. Винтовое вязкопластическое течение в зазоре между жесткими цилиндрами // Изв. РАН. Механика твердого тела. 2017. № 6. С. 55–70.

  15. Буренин А.А., Ковтанюк Л.В., Устинова А.С. Об учете упругих свойств неньютоновского материала при его вискозиметрическом течении // ПМТФ. 2008. Т. 49. № 2. С. 143–151.

  16. Буренин А.А., Ковтанюк Л.В., Устинова А.С. Вискозиметрическое течение несжимаемого упруговязкопластического материала при наличии смазки на граничных поверхностях // Сиб. журн. индустр. матем. 2012. Т. XV. № 2 (50). С. 43–55.

  17. Бегун А.С., Буренин А.А., Ковтанюк Л.В. Течение упруговязкопластического материала в зазоре между вращающимися цилиндрическими поверхностями в условиях нежесткого сцепления // ПМТФ. 2015. Т. 56. № 2. С. 146–158.

  18. Бегун А.С., Буренин А.А., Ковтанюк Л.В. Большие необратимые деформации в условиях изменяющихся механизмов их производства и проблема задания пластических потенциалов // Доклады Академии наук. 2016. Т. 470. № 3. С. 275–278.

  19. Бегун А.С., Ковтанюк Л.В., Лемза А.О. Смена механизмов накопления необратимых деформаций материалов на примере их вискозиметрического деформирования // Известия РАН. Механика твердого тела. 2018. № 1. С. 103–112.

  20. Begun A.S., Burenin A.A., Kovtanyuk L.V., Lemza A.O. On the Mechanisms of Production of Large Irreversible Strains in Materials With Elastic, Viscous and Plastic Properties // Arch. Appl. Mech. 2020. V. 90 (4). P. 829–845.

  21. Белых С.В., Буренин А.А., Ковтанюк Л.В., Прокудин А.Н. Об учете вязких свойств материалов в теории больших упругопластических деформаций // Чебышевский сб. 2017. Т. 18. № 3. С. 108–130.

  22. Ковтанюк Л.В. Моделирование больших упругопластических деформаций в неизотермическом случае // Дальневост. матем. журн. 2004. Т. 5. № 1. С. 110–120.

  23. Буренин А.А., Ковтанюк Л.В., Панченко Г.Л. Неизотермическое движение упруговязкопластической среды в трубе в условиях изменяющегося перепада давления // Доклады Академии наук. 2015. Т. 464. № 3. С. 284–287.

  24. Буренин А.А., Ковтанюк Л.В., Панченко Г.Л. Развитие и торможение вязкопластического течения в слое в условиях его нагрева за счет трения о шероховатую плоскость // Прикладная механика и техническая физика. 2015. Т. 56. № 4. С. 101–111.

  25. Ковтанюк Л.В., Панченко Г.Л. Прямолинейное течение в упруговязкопластическом цилиндрическом слое в условиях возможного двустороннего проскальзывания // Известия РАН. Механика твердого тела. 2016. № 2. С. 75–85.

  26. Буренин А.А., Ковтанюк Л.В., Панченко Г.Л. Деформирование и разогрев упруговязкопластического цилиндрического слоя при его движении за счет изменяющегося перепада давления // Известия РАН. Механика твердого тела. 2018. № 1. С. 6–18.

  27. Heng Xiao, Bruhns O.T., Meyers A. Thermodynamic laws and consistent Eulerian formulation of finite elastoplasticity with thermal effects // J. Mech. Phys. Solids. 2007. V. 55. P. 338–365.

  28. Голованов А.И., Султанов Л.У. Математические модели вычислительной нелинейной механики деформируемых сред. Казань: Казанский гос. ун-т, 2009. 464 с.

  29. Быковцев Г.И., Ивлев Д.Д. Теория пластичности. Владивосток: Дальнаука, 1998. 527 с.

  30. Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. М.: Физматлит, 2001. 704 с.

  31. Дац Е.П., Мурашкин Е.В., Ткачева А.В., Щербатюк Г.А. Температурные напряжения в упругопластической трубе в зависимости от выбора условия пластичности // Известия РAH. Механика твердого тела. 2018. № 1. С. 32–43.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал