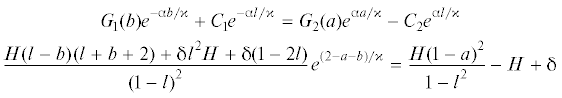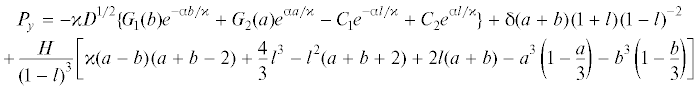Известия РАН. Механика твердого тела, 2022, № 4, стр. 90-102
ВЛИЯНИЕ ТЕКСТУРИРОВАНИЯ ПОВЕРХНОСТИ В ФОРМЕ ВЫЕМОК НА ТРЕНИЕ СКОЛЬЖЕНИЯ В КОНТАКТЕ С ВЯЗКОУПРУГИМ МАТЕРИАЛОМ
Ю. Ю. Маховская a, *, А. В. Морозов a, **
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: makhovskaya@mail.ru
** E-mail: morozovalexey@mail.ru
Поступила в редакцию 03.09.2021
После доработки 12.10.2021
Принята к публикации 13.10.2021
- EDN: KWKMXS
- DOI: 10.31857/S0572329922040080
Аннотация
Построена модель для расчета силы трения при скольжении жесткой поверхности с регулярной текстурой в форме параболических выемок по вязкоупругому материалу. Модель основана на решении контактной задачи в плоской постановке о скольжении жесткой поверхности регулярной формы по вязкоупругому основанию с учетом локального закона трения, определяемого шероховатостью и адгезией в контакте. Получены соотношения для расчета контактных характеристик и коэффициента трения в зависимости от параметров текстуры и шероховатости поверхности, скорости скольжения и приложенной внешней нагрузки. При помощи разработанной модели выполнен расчет контактного давления и коэффициента трения для случая сухого контакта между текстурированной поверхностью и вязкоупругим материалом. Исследованы вклад текстуры поверхности в общую силу трения на макроуровне и вклад шероховатости и адгезии на микроуровне. Установлено, что в исследованном диапазоне скоростей и нагрузок увеличение размера выемок текстуры приводит к уменьшению коэффициента трения. Приведен пример расчета коэффициента трения в зависимости от скорости скольжения и нагрузки для двух образцов ламинированной фанеры с различными параметрами текстуры и сходными параметрами адгезии и шероховатости на поверхности. Результаты расчета сопоставляются с экспериментальными данными, которые были получены в лабораторных испытаниях фанеры в контакте скольжения с протекторной резиной.
1. Введение. Нанесение рельефа на контактирующие поверхности широко используется в современной технике для управления их сцепными свойствами [1]. При скольжении текстурированной поверхности по вязкоупругому материалу сила трения существенно зависит от параметров рельефа, который определяет гистерезисные потери энергии в поверхностных слоях материала за счет их циклического деформирования элементами текстуры. Для моделирования этой зависимости ставятся и решаются контактные задачи в периодической постановке о скольжении индентора с заданным регулярным рельефом поверхности по вязкоупругому телу [2]. Решение задачи о скольжении штампа с регулярной поверхностью по вязкоупругой полуплоскости получено в [3]. Задача в трехмерной постановке для штампа регулярной текстуры в форме трапециевидных выступов решалась в [4] с учетом локального трения, действующего по закону Кулона. Показано, что форма поверхностного рельефа существенно влияет на распределение контактного давления, фактическую площадь контакта и силу трения. Влияние податливости элементов текстуры исследовано в [5] на примере задачи о нагружении текстурированного двухслойного упругого основания.
Помимо нанесенного макрорельефа или текстуры, трение вязкоупругих материалов определяется микрорельефом (шероховатостью) взаимодействующих поверхностей и их адгезионным притяжением. Один из подходов к изучению одновременного эффекта поверхностной шероховатости и адгезии при трении эластомеров состоит в рассмотрении контактных задач с учетом сил притяжения, действующих в зазоре между поверхностями, при этом поверхностный микрорельеф моделируется регулярной волнистостью. Метод решения таких задач для одномерного вязкоупругого основания, описываемого моделью Кельвина–Фойгта, был предложен в [6] для плоского и в [7] для пространственного случая. На основе полученного решения была построена модель для расчета силы трения и проведено сравнение с результатами трибологических тестов для резиновых образцов, обладающих различными адгезионными свойствами [8].
Задача существенно усложняется, когда необходимо учесть одновременное влияние поверхностного рельефа (текстуры) на макроуровне, а также шероховатости и адгезии на микроуровне, на гистерезисные потери и, соответственно, на силу трения при скольжении по вязкоупругому материалу. В настоящее время достаточно развитым является многомасштабный подход к моделированию трения вязкоупругих тел, в котором используется фрактальное представление поверхностной шероховатости [9–12], при этом в [10] исследованы вклады макро- и микроуровней поверхностного рельефа в возникающую силу трения, а в [12] установлен вклад двух основных масштабных уровней – наибольшего и наименьшего. Модель трения многоуровневой волнистой поверхности с учетом адгезии предложена в [13]. В этих и других работах по многомасштабной шероховатости предполагается, как правило, что форма поверхностного рельефа на всех уровнях подобна и отличается только характерным масштабом выступов.
В настоящей работе предложена модель трения жесткой поверхности по вязкоупругому материалу, включающая вклад двух существенно различных масштабных уровней – текстуру поверхности в форме параболических выемок на макроуровне и шероховатость с учетом адгезии на микроуровне. Модель использована для анализа результатов эксперимента на трение резины по поверхности ламинированной фанеры с нанесенным регулярным рельефом. Технология нанесения этого рельефа предполагает образование на изначально гладкой поверхности между выемками текстуры значительной шероховатости, в результате чего трение таких поверхностей по вязкоупругому образцу зависит от параметров рельефа на обоих масштабных уровнях.
2. Математическая модель. В этом разделе дается постановка и строится решение контактной задачи о скольжении текстурированной поверхности по вязкоупругому основанию. Предполагается, что на границе раздела действует локальный закон трения, который определяется шероховатостью и адгезией поверхностей на микроуровне.
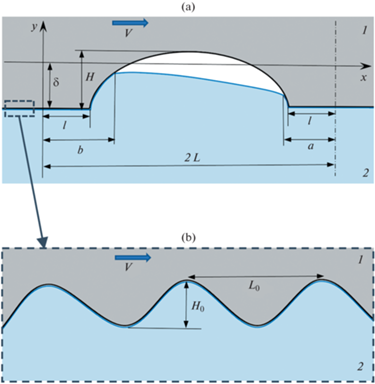
2.1. Постановка задачи на макроуровне. Рассматривается контактная задача в плоской постановке о скольжении с постоянной скоростью $V$ вдоль оси Ox жесткого штампа, поверхность которого описывается периодической функцией $f(x) = f(x + 2L)$, где L – полупериод поверхностной текстуры:
(2.1)
$f(x) = \left\{ \begin{gathered} 0,\quad 0 \leqslant x \leqslant l,\quad 2L - l \leqslant x \leqslant 2L \hfill \\ \frac{{{{{(x - L)}}^{2}}}}{{2R}} - H,\quad l \leqslant x \leqslant 2L - l \hfill \\ \end{gathered} \right.$Здесь R – радиус закругления впадины, который считается равным R = ${{(L - l)}^{2}}{\text{/}}(2H)$ (рис. 1,a). Штамп скользит по вязкоупругому основанию, механические свойства которого описываются одномерной моделью Кельвина–Фойгта с податливостью в двух направлениях:
(2.2)
${{u}_{m}} + {{T}_{{{\varepsilon }}}}\frac{{\partial {{u}_{m}}}}{{\partial t}} = \frac{1}{k}\left( {{{p}_{m}} + {{T}_{{{\sigma }}}}\frac{{\partial {{p}_{m}}}}{{\partial t}}} \right),\quad m = x,y$Рис. 1.
Схема контакта жесткого текстурированного штампа 1 с вязкоупругим основанием 2 на макроуровне на одном периоде текстуры (a) и на микроуровне (b).
Пусть неподвижная система координат (x', y') связана с вязкоупругим основанием, а система координат (x, y) связана со скользящим волнистым телом, так что:
Считаем движение установившимся по отношению к системе координат (x, y), в которой смещения и напряжения не зависят от времени t и являются функциями только координаты x. В подвижной системе координат (x, y) соотношения (2.2) принимают вид:
(2.4)
$\begin{gathered} {{u}_{x}} - VT_{{{\varepsilon }}}^{{}}\frac{{d{{u}_{x}}}}{{dx}} = \frac{1}{k}\left( {{{p}_{x}} - {{T}_{{{\sigma }}}}V\frac{{d{{p}_{x}}}}{{dx}}} \right) \hfill \\ {{u}_{y}} - VT_{{{\varepsilon }}}^{{}}\frac{{d{{u}_{y}}}}{{dx}} = \frac{1}{k}\left( {{{p}_{y}} - {{T}_{{{\sigma }}}}V\frac{{d{{p}_{y}}}}{{dx}}} \right) \hfill \\ \end{gathered} $Пусть на каждом периоде $x \in [0,2L]$ отрезок $x \in [b,2L - a]$ границы y = 0 свободен от нагружения, а на участках вне его имеет место контакт между штампом и вязкоупругим основанием (рис. 1). Тогда для вертикального давления ${{p}_{y}}$ и перемещения ${{u}_{y}}$ имеют место следующие условия контакта на периоде $x \in [0,2L]$:
(2.5)
$\begin{array}{*{20}{l}} {{{u}_{y}}(x) = - {{\delta }},}&{0 \leqslant x \leqslant l,\quad 2L - l < x < 2L} \\ {{{u}_{y}}(x) = - {{\delta }} - \frac{{{{{(L - x)}}^{2}}}}{{2R}} + H,}&{l < x < b,\quad 2L - a < x < 2L - l} \\ {{{p}_{y}}(x) = 0,}&{b \leqslant x \leqslant 2L - a,} \end{array}$(2.6)
$\begin{gathered} {{{\bar {u}}}_{m}} = \frac{{{{u}_{m}}}}{L},\quad {{{\bar {p}}}_{m}} = \frac{{{{p}_{m}}}}{{kL}},\quad \bar {m} = \frac{m}{L}\;(m = x,y),\quad {{\bar {\delta }}} = \frac{{{\delta }}}{L}, \\ \bar {a} = \frac{a}{L},\quad \bar {b} = \frac{b}{L},\quad \bar {H} = \frac{H}{L},\quad \bar {l} = \frac{l}{L},\quad {{\alpha }} = \frac{{{{T}_{{{\varepsilon }}}}}}{{{{T}_{{{\sigma }}}}}},\quad {{\kappa }} = \frac{{V{{T}_{{{\varepsilon }}}}}}{L} \\ \end{gathered} $(2.7)
${{p}_{y}}(x) = \left\{ {\begin{array}{*{20}{l}} {{{G}_{1}}(b){{e}^{{ - {{\alpha }}(b - x)/{{\kappa }}}}} - {{C}_{1}}{{e}^{{ - {{\alpha }}(l - x)/{{\kappa }}}}} + {{\delta }},}&{0 \leqslant x \leqslant l} \\ {{{G}_{1}}(b){{e}^{{ - {{\alpha }}(b - x)/{{\kappa }}}}} + {{G}_{2}}(x),}&{l \leqslant x \leqslant b} \\ {0,}&{b \leqslant x \leqslant 2 - a} \\ {{{G}_{1}}(a){{e}^{{ - {{\alpha }}(2 - a - x)/{{\kappa }}}}} + {{G}_{2}}(x),}&{2 - a \leqslant x \leqslant 2 - l} \\ {{{G}_{1}}(a){{e}^{{ - {{\alpha }}(2 - a - x)/{{\kappa }}}}} - {{C}_{2}}{{e}^{{ - {{\alpha }}(2 - l - x)/{{\kappa }}}}} + {{\delta }},}&{2 - l \leqslant x \leqslant 2} \end{array}} \right.$(2.8)
$\begin{gathered} {{G}_{{1,2}}}(x) = \{ [( \pm 2{{\kappa }}(x - 1) - {{x}^{2}} + {{l}^{2}} + 2(x - l))H - {{\delta }}{{(1 - l)}^{2}}]{{{{\alpha }}}^{2}} \mp \\ \, \mp 2H{{\kappa }}(x \mp {{\kappa }} - 1){{\alpha }} - 2{{{{\kappa }}}^{2}}H\} D \\ {{C}_{{1,2}}} = 2H{{\kappa }}({{\alpha }} - 1)\left[ {{{\kappa }} \mp {{\alpha }}(1 - l)} \right]D,\quad D = {{{{\alpha }}}^{{ - 2}}}{{(1 - l)}^{{ - 2}}} \\ \end{gathered} $Выражение (2.7) с учетом (2.8) аналитически определяет контактное давление на периоде при условии, что известны величины a и b, задающие границы областей контакта, и величина внедрения штампа ${{\delta }}$. Два алгебраических уравнения для определения величин $a$ и $b$ следуют из условий непрерывности для искомых функций и имеют вид:
Для определения величины внедрения ${{\delta }}$ при заданной внешней погонной нагрузке ${{P}_{y}}$ на период текстуры, используется условие равновесия:
где использовано безразмерное представление для погонной силы ${{\bar {P}}_{y}} = {{P}_{y}}{\text{/}}(k{{L}^{2}})$. Подставляя выражение (2.7) с учетом (2.8) в условие равновесия (2.10) и выполняя интегрирование, получим:Соотношения (2.7)–(2.9) и (2.11) позволяют определить области контакта и распределение вертикального давления ${{p}_{y}}(x)$ на периоде текстуры штампа. Далее на основании полученных соотношений будут определяться горизонтальные давления ${{p}_{x}}(x)$.
2.2. Учет шероховатости и адгезии на микроуровне. Введем локальный закон трения, определяющий напряжение $\tau (x)$, действующее по касательной к поверхности штампа:
(2.12)
${{\tau }}(x) = \left\{ {\begin{array}{*{20}{l}} {{{{{\tau }}}_{0}},}&{0 \leqslant x \leqslant b,\quad 2 - a \leqslant x \leqslant 2} \\ {0,}&{b \leqslant x \leqslant 2 - a} \end{array}} \right.$Величина ${{\tau }_{0}}$ определяется взаимодействием поверхностей на микроуровне, а именно, микрошероховатостью поверхности штампа и адгезионным притяжением между поверхностями штампа и вязкоупругого тела.
Для того, чтобы определить величину τ0, рассмотрим взаимодействие двух номинально плоских поверхностей на микроуровне – жесткого штампа и вязкоупругого основания. Пусть микрошероховатость поверхности штампа моделируется периодической функцией (рис. 1,b):
Предполагается, что между поверхностями действует адгезионное притяжение, достаточное для того, чтобы удерживать поверхности на микроуровне в состоянии насыщенного контакта во всем диапазоне рассматриваемых нагрузок и скоростей. Решение задачи в такой постановке получено в [6], где приведено следующее простое выражение для величины силы трения, действующей на период микрошероховатости:
(2.14)
${{T}_{0}} = \frac{{{{{{\pi }}}^{2}}H_{0}^{2}{{L}_{0}}kV({{T}_{\varepsilon }} - {{T}_{{{\sigma }}}})}}{{4(L_{0}^{2} + {{{{\pi }}}^{2}}T_{{{\sigma }}}^{{\text{2}}}{{V}^{2}})}}$Переходя в (2.14) к безразмерным величинам (2.6) и используя дополнительно безразмерные величины для параметров микроуровня:
(2.15)
${{\bar {H}}_{0}} = \frac{{{{H}_{0}}}}{{{{L}_{0}}}},\quad {{\bar {L}}_{0}} = \frac{{{{L}_{0}}}}{L},\quad {{\bar {\tau }}_{0}} = \frac{{{{\tau }_{0}}}}{{kL}} = \frac{{{{T}_{0}}}}{{2kL{{L}_{0}}}}$(2.16)
${{\tau }_{0}} = \frac{{{{\pi }^{2}}}}{8}\frac{{H_{0}^{2}L_{0}^{2}\kappa \alpha (\alpha - 1)}}{{L_{0}^{2}{{\alpha }^{2}} + {{\pi }^{2}}{{\kappa }^{2}}}}$Как показывает соотношение (2.16), величина силы трения на микроуровне, определяемая гистерезисными потерями в материале вследствие микрошероховатости и адгезии, в случае насыщенного контакта не зависит от величины нормального давления, но зависит от скорости скольжения штампа, вязкоупругих характеристик материала и геометрических параметров микрошероховатости. Заметим, что в выражение (2.16) не входят адгезионные характеристики поверхностей, но оно получено при условии, что силы адгезии достаточно велики, чтобы обеспечить насыщенный контакт поверхностей [6].
2.3. Расчет силы трения. Сила трения на макроуровне определяется величиной погонной силы ${{P}_{x}}$, действующей на период текстуры в горизонтальном направлении:
где использовано безразмерное представление для погонной силы ${{\bar {P}}_{x}} = {{P}_{x}}{\text{/}}(k{{L}^{2}})$. Для определения давлений ${{p}_{x}}(x)$, действующих в горизонтальном направлении, воспользуемся следующим геометрическим соотношением, связывающим напряжение ${{\tau }}$, действующее по касательной к поверхности штампа, с напряжениями ${{p}_{x}}$ и ${{p}_{y}}$, действующими в горизонтальном и вертикальном направлениях, соответственно: где $\operatorname{tg} {{\varphi }} = f_{{}}^{'}(x)$, а функция $f(x)$ определяется соотношением (2.1) на соответствующих интервалах. Из соотношения (2.18) с учетом локального закона трения (2.12) и учитывая вид функции $f(x)$ (2.1), получим для давлений, действующих в горизонтальном направлении:(2.19)
${{p}_{x}}(x) = \left\{ {\begin{array}{*{20}{l}} {{{{{\tau }}}_{{\text{0}}}}{\text{,}}}&{0 \leqslant x \leqslant l,\quad 2 - l \leqslant x \leqslant 2} \\ {{{{{\tau }}}_{{\text{0}}}}\sqrt {1 - {{t}^{2}}(x)} + t(x){{p}_{y}}(x),}&{l \leqslant x \leqslant 2 - l} \end{array}} \right.\quad $Таким образом, расчет силы трения происходит следующим образом. Считая внешнюю нормальную нагрузку ${{P}_{y}}$ заданной, из уравнения (2.11) выразим внедрение штампа ${{\delta }}$ и подставим получившееся выражение в уравнения (2.9) и выражения (2.8). Уравнения (2.9) с учетом (2.8) решаем численно относительно величин $a$ и $b$ на интервалах $l < a < 1$, $l < b < 1$. Затем определяем распределение вертикальных давлений ${{p}_{y}}(x)$ по соотношениям (2.7), (2.8). Зная функцию ${{p}_{y}}(x)$ и принимая во внимание выражение (2.16) для ${{{{\tau }}}_{{\text{0}}}}$, можно определить функцию горизонтальных давлений ${{p}_{x}}(x)$ в соответствии с (2.19). Полученная функция ${{p}_{x}}(x)$ подставляется в (2.17) и рассчитывается величина погонной силы трения на период текстуры ${{P}_{x}}$. Для получения коэффициента трения, необходимо эту величину разделить на величину нормальной нагрузки:
Коэффициент трения, рассчитанный по представленной модели, будет учитывать гистерезисные потери в вязкоупругом материале как на макроуровне (вызванные поверхностной текстурой), так и на микроуровне (связанные с шероховатостью и адгезией). Чтобы получить коэффициент трения только вследствие макротекстуры, без учета микрошероховатости и адгезии, следует при расчете положить ${{{{\tau }}}_{{\text{0}}}} = 0$ вместо соотношения (2.16). Чтобы получить коэффициент трения для поверхности, обладающей только микрошероховатостью, но без макротекстуры, необходимо в (2.20) положить ${{P}_{x}} = 2{{{{\tau }}}_{{\text{0}}}}$, где ${{{{\tau }}}_{{\text{0}}}}$ определяется выражением (2.16). В этом случае коэффициент трения имеет простой аналитический вид:
(2.21)
${{{{\mu }}}_{0}} = \frac{{{{{{\pi }}}^{2}}l}}{{8{{p}_{n}}}}\frac{{H_{0}^{2}L_{0}^{2}{{\kappa \alpha }}({{\alpha }} - 1)}}{{L_{0}^{2}{{{{\alpha }}}^{2}} + {{{{\pi }}}^{2}}{{{{\kappa }}}^{2}}}}$3. Эксперимент. В данном разделе представлены результаты измерения шероховатости и текстуры исследуемых образцов фанеры, а также результаты лабораторных испытаний на трение образцов фанеры в паре с резиновым контробразцом, который был вулканизирован в форме кольца из протекторной резины, полученной на основе комбинации бутадиенового и натурального каучуков.
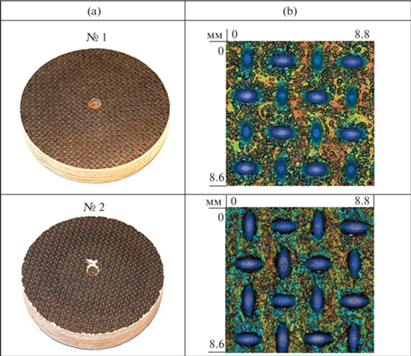
3.1. Анализ текстуры и шероховатости поверхности. Образцы для испытаний были вырезаны в форме дисков из ламинированной березовой фанеры, на поверхность которой методом термопрессования через сетку-трафарет была нанесена различная текстура. Ламинированная пленка имела плотность 122…130 г/м2. В работе исследуются лицевые поверхности двух образцов с заданным отличающимся макрорельефом, который определялся при помощи оптического 3D-профилометра S Neox (Sensofar, Испания), оснащенного моторизированным X-Y-столиком и 10Х конфокальным объективом. Область единичного сканирования составляла 1.7 × 1.4 мм с разрешением 1232 × 1028 пикселей. Сшивание 64 рядом стоящих сканирований позволило получить изображение поверхности размерами 11.7 × 9.8 мм, которое полностью охватывает повторяющиеся элементы текстуры образца. На рис. 2 представлены результаты измерения рельефа поверхности образцов, анализ которых был выполнен на типично-повторяющихся участках поверхности, при этом с целью получения надежных и повторяемых данных было проведено по три измерения в различных областях исследуемого образца. Перед определением параметров текстуры и шероховатости поверхности из полученных 3D-данных методом вычитания плоскости по трем точкам удалялся компонент формы, а для устранения “артефактов” и шумов применялся smart-фильтр из программного обеспечения профилометра. Следует отметить, что оценка параметров топографии осуществлялась после трибологических испытаний.
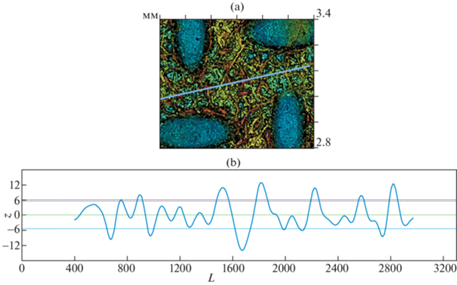
В данной работе между элементами текстуры (выемками) оцениваются высотные Sa, Sz параметры шероховатости с использованием стандартных фильтров согласно стандарту EN ISO25178-6. В результате установлено, что параметры шероховатости для двух исследуемых образцов различаются незначительно, а именно: ${{S}_{a}}$ = 4.2 мкм, ${{S}_{z}}$ = 37.2 мкм и ${{S}_{a}}$ = 4.4 мкм, ${{S}_{z}}$ = 41.5 мкм для первого и второго образца соответственно. Для оценки периода ${{L}_{0}}$ и амплитуды ${{H}_{0}}$ синусоидальной функции (2.13), используемой для моделирования шероховатости, проведен анализ 2D-профилограммы (рис. 3), полученной на шероховатом участке между элементами текстуры (выемками). Параметр ${{L}_{0}}$ был определен методом построения автокорреляционной функции.
Рис. 3.
Микрорельеф поверхности фанеры (а) и 2D-профилограмма z [мкм], L [мкм] (b), для которой ${{H}_{0}} = {{R}_{z}}{\text{/}}2$ = 13 мкм и ${{L}_{0}}$ = 350 мкм.
Геометрия текстуры измерялась при помощи инструментов, входящих в программное обеспечение прибора, при этом было зафиксировано, что шаг между выемками текстуры $2L$ одинаков для обоих изученных образцов и составляет 2.1 мм, а длина $2L - 2l$, высота $H$ и ширина ${{l}_{w}}$ выемки существенно различаются (рис. 2), а именно: для образца № 1 $2L - 2l$ = 1.4 мм, $H$ = 0.15 мм, ${{l}_{w}}$ = 0.7 мм, а для образца № 2 $2L - 2l$ = = 1.7 мм, $H$ = 0.9 мм, ${{l}_{w}}$ = 0.8 мм.
3.2. Измерение коэффициента трения. Экспериментальное изучение коэффициента трения проводилось на лабораторном трибометре UMT-2 по схеме фрикционного контакта “резиновое кольцо–диск” в условиях “сухого” трения. Методика эксперимента подробно описана в работе [14]. Испытание образцов фанер было проведено при трех уровнях нормального давления в диапазоне от 0.1 до 0.5 МПа и 11 скоростях скольжения, изменяемых в интервале 0.01 … 100 мм/с. Путь трения образца в процессе выполнения единичного теста составлял 37.7 мм, что соответствует четверти его оборота относительно неподвижного резинового контробразца. Результатом выполнения теста является зависимость коэффициента трения от времени испытания, при этом на кривой имеется участок с установившимся режимом трения, на котором определялось среднее значение коэффициента трения. Измеренные таким образом значения коэффициентов трения для всех значений скоростей скольжения и нормальных давлений представлены на рис. 4,а.
Рис. 4.
Экспериментальные (a) и расчетные (b) зависимости коэффициента трения μ от скорости V [мм/с] для двух образов фанеры: № 1 сплошные линии и № 2 пунктирные линии, где 1 – ${{p}_{n}}$ = 0.1 МПа, 2 – ${{p}_{n}}$ = = 0.3 МПа, 3 – ${{p}_{n}}$ = 0.5 МПа.
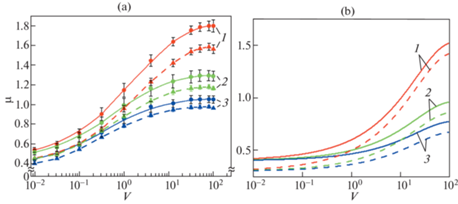
Анализ результатов эксперимента (рис. 4,а) позволяет сделать следующие основные выводы:
1) коэффициент трения увеличивается с ростом скорости скольжения для исследуемых образцов фанеры;
2) при малых скоростях влияние скорости скольжения на коэффициент трения снижается;
3) нормальная нагрузка оказывает значительное влияние на коэффициент трения скольжения: с ее увеличением коэффициент трения уменьшается;
4) коэффициент трения образца № 1 выше, чем образца № 2, во всем диапазоне исследованных скоростей и нагрузок.
4. Пример расчета. В этом разделе приведен пример расчета контактного давления и коэффициента трения по модели, представленной в п. 2. В качестве входных параметров модели приняты величины, соответствующие параметрам поверхностного рельефа для двух образцов березовой фанеры, имеющих на лицевой поверхности различную текстуру и близкие параметры шероховатости и адгезии.
4.1. Анализ контактного давления и коэффициента трения. Характеристики макро- и микрорельефа для двух образцов, полученные из испытаний (п. 3.1), а также рассчитанные на их основе безразмерные параметры рельефа, используемые в качестве входных параметров для расчета, представлены в табл. 1. На рис. 5 приведены распределения контактных давлений по одному периоду текстуры $0 \leqslant x \leqslant 2$ для двух образцов № 1 и № 2 и двух значений безразмерного параметра скорости $\kappa = 0.2$ (что соответствует скорости скольжения V = 20 мм/с при времени запаздывания Tε = 0.01 c) и $\kappa = 1$ (V = 100 мм/с, Tε = 0.01 c) и безразмерном номинальном давлении ${{p}_{n}} = 0.02$. В качестве отношения времен запаздывания и релаксации резины взята величина ${{\alpha }} = 100$.
Таблица 1.
Параметры макрорельефа (текстуры) и микрорельефа (шероховатости) двух образцов, использованные в расчетах
| № образца | Текстура | Шероховатость | |||||||
|---|---|---|---|---|---|---|---|---|---|
| $Н,$ мкм | $l,$ мкм | $L,$ мкм | $\bar {Н} = H{\text{/}}L$ | $\bar {l} = l{\text{/}}L$ | ${{Н}_{0}},$ мкм | ${{L}_{0}},$ мкм | ${{\bar {Н}}_{0}}\, = \,{{H}_{0}}{\text{/}}L$ | ${{\bar {L}}_{0}} = {{L}_{0}}{\text{/}}L$ | |
| 1 | 150 | 200 | 1050 | 0.14 | 0.19 | 13 | 350 | 0.012 | 0.33 |
| 2 | 800 | 350 | 0.76 | 0.33 | |||||
Рис. 5.
Распределения контактного давления на период текстуры для образцов 1 (кривые 1 и 1') и 2 (кривые 2 и 2') для двух значений параметра скорости ${{\kappa }} = 0.2$ (сплошные линии) и ${{\kappa }} = 1$ (штриховые линии).
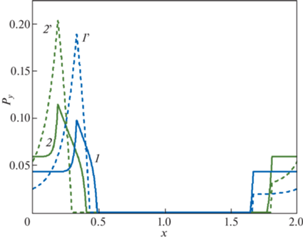
Выемка поверхностной текстуры расположена на периоде $0 \leqslant x \leqslant 2$ симметрично относительно прямой x = 1, однако, как видно из рис. 5, контактные давления расположены несимметрично относительно этой прямой. Слева от оси симметрии выемки, где текстура образует угол, “пропахивающий” вязкоупругий материал при скольжении, имеет место пик давления, и именно в окрестности этого пика происходят наиболее значительные гистерезисные потери в материале, приводящие к возникновению силы трения. Увеличение параметра скорости приводит к возрастанию этого пика. Для образца № 2 с более широкими и глубокими выемками имеют место более высокие пики давлений и их большая асимметрия, чем для образца № 1. Поэтому можно было бы ожидать, что коэффициент трения для образца № 2 должен быть выше. Однако, как показывают экспериментальные результаты, приведенные в п. 3, имеет место обратная ситуация. Это связано с тем, что помимо вклада от макротекстуры, в общей силе трения присутствует вклад микрошероховатости и адгезии.
Для сравнения этих вкладов на рис. 6 приведена зависимость коэффициента трения от безразмерной скорости скольжения для параметров рельефа, соответствующих образцу 1, остальные значения параметров те же, что и для рис. 5. Кривая 1 соответствует расчету по полной модели и соотношению (2.20) с учетом как макротекстуры, так и микрошероховатости и адгезии. Кривая 2 соответствует случаю, когда макротекстуры нет, поверхность является номинально плоской на макроуровне, а на микроуровне существует шероховатость и действует адгезионное притяжение. В этом случае коэффициент трения определяется аналитическим выражением (2.21). Кривая 3 соответствует макротекстуре без учета микрошероховатости.
Рис. 6.
Зависимость коэффициента трения от безразмерной скорости для поверхности с текстурой и шероховатостью и адгезией (1), только с шероховатостью и адгезией (2), только с текстурой (3).
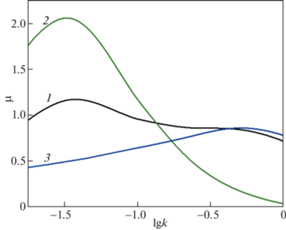
Зависимость коэффициента трения от скорости, представленная кривой 1 на рис. 6, немонотонна, что характерно для трения вязкоупругих материалов [2]. Представленная зависимость имеет два пика – один ярко выраженный при меньшей скорости и второй размытый при большей скорости. Сопоставляя эту кривую с кривыми 2 и 3 можно заключить, что левый пик связан с эффектом микрошероховатости и адгезии, а правый – с макротекстурой. Сравнение кривых 1 и 2 показывает также, что макротекстура уменьшает пиковые значения коэффициента трения по сравнению с поверхностью, на которой есть только микрошероховатость. Это происходит потому, что выемки текстуры уменьшают площадь фактического контакта поверхностей, на которой происходят гистерезисные потери и адгезия на микроуровне. С другой стороны, текстура увеличивает коэффициент трения при более высоких скоростях, когда вклад микрошероховатости и адгезии становится мал.
4.2. Сопоставление с результатами испытаний. Анализ представленных выше результатов расчета позволяет сделать вывод, что экспериментальные кривые для коэффициента трения, представленные на рис. 4, а, соответствуют условиям относительно малых скоростей, в диапазоне которых представлен только левый пик, вызванный эффектом микрошероховатости и адгезии. Для удобства сопоставления с результатами испытаний, на рис. 4, b приведены результаты расчета коэффициента трения для двух образцов в диапазоне скоростей и нагрузок, соответствующих условиям эксперимента, приведенного в п. 3.2. Результаты представлены в виде зависимости коэффициента трения от размерной скорости скольжения, при этом приняты следующие характеристики материала резины: жесткость $k = 5$ ГПа/м, время запаздывания Tε = 0.001 c, отношение времен запаздывания и релаксации ${{\alpha }} = 1000$.
Количественное сопоставление полученных результатов с экспериментальными данными невозможно, поскольку расчет проведен по модели, основанной на плоской задаче, моделирующей поведение поверхностей только в одном сечении (в данном случае рассматривалось центральное сечение для выемки, вытянутой в направлении, перпендикулярном скольжению). Однако, представленные на рис. 4, b расчетные кривые обладают перечисленными в п. 3.2 свойствами экспериментальных кривых, представленных на рис. 4, a, а именно:
1) коэффициент трения увеличивается с ростом скорости скольжения – это объясняется тем, что изученный диапазон скоростей соответствует участку возрастания немонотонной зависимости коэффициента трения от скорости;
2) влияние скорости скольжения на коэффициент трения становится менее значительным при малых скоростях – этот факт объясняется в работе [15], из которой следует, что при малых скоростях скольжения динамический коэффициент трения приближается к статическому;
3) с увеличением нормальной нагрузки коэффициент трения уменьшается; такое поведение связано с совместным проявлением гистерезисных и молекулярных свойств эластомера [16];
4) коэффициент трения для поверхности с более широкими и глубокими впадинами (образец № 2) ниже по сравнению с образцом № 1; в модели это объясняется уменьшением площади фактического контакта, которая в силу предположения о насыщенном контакте на микроуровне совпадает с номинальной.
Заметим, что хотя упрощающее предположение о насыщенном контакте на микроуровне, принятое в модели, не может полностью выполняться для реальной шероховатой поверхности, значительный вклад адгезии может приводить к зависимости площади фактического контакта от номинальной площади.
4. Заключение. Построена модель трения жесткой текстурированной поверхности по вязкоупругому материалу с учетом микрошероховатости и адгезии. Проведен расчет распределения контактного давления и коэффициента трения на примере образцов текстурированной фанеры с различными параметрами текстуры в зависимости от скорости скольжения по эластомерному образцу и номинального давления. Результаты моделирования позволили продемонстрировать тенденции изменения коэффициента трения скольжения между резиной и опорной поверхностью, на которую нанесены: только текстура, только шероховатость, а также и текстура, и шероховатость.
Проведено экспериментальное исследование по схеме контакта резиновое кольцо – диск из ламинированной березовой фанеры в диапазоне нормальных давлений характерных для контакта подошвы ботинка взрослого человека (0.1 МПа) и автомобильной легковой шины (0.5 МПа) с опорной поверхностью. Испытания были выполнены при комнатной температуре (23°С) в диапазоне скоростей скольжения от 0.01 до 100 мм/c. В работе получено, что в условиях сухого контакта коэффициент трения увеличивается с ростом скорости скольжения и снижается с увеличением нормальной нагрузки. Увеличение геометрических размеров текстуры поверхности (выемок) приводит к снижению коэффициента трения, что объясняется снижением адгезионного механизма трения из-за уменьшения площади контакта.
В результате сопоставления результатов моделирования и эксперимента установлено, что построенная математическая модель позволяет качественно описать полученные в эксперименте данные и оценить вклад в коэффициент трения скольжения двух масштабных уровней поверхностного рельефа, а также механизма трения (адгезионного и деформационного).
Работа выполнена при поддержке гранта РФФИ 19-01-00231 “Теоретико-экспериментальное исследование контактного взаимодействия деформируемых тел с нанесенным рельефом в условиях трения покоя и скольжения”.
Список литературы
Lu P., Wood R. Tribological performance of surface texturing in mechanical applications–a review // Surf. Topogr.: Metrol. Prop. 2020. V. 8. № 4. 043001. https://doi.org/10.1088/2051-672X/abb6d0
Горячева И.Г., Маховская Ю.Ю., Морозов А.В., Степанов Ф.И. Трение эластомеров. Моделирование и эксперимент. М.-Ижевск: Институт компьютерных исследований, 2017. 204 с.
Menga N., Putignano C., Carbone G., Demelio G.P. The sliding contact of a rigid wavy surface with a viscoelastic half-space // Proc. R. Soc. A. 2014. V. 470. № 2169. https://doi.org/10.1098/rspa.2014.0392
Makhovskaya Y. Effect of surface relief on sliding friction of viscoelastic bodies // Acta Mech. 2021. V. 232. P. 1933–1942. https://doi.org/10.1007/s00707-020-02864-8
Степанов Ф.И., Торская Е.В. Контакт гладкого индентора и двухслойного упругого полупространства с усложненными условиями на поверхности // Изв. РАН. МТТ. 2022. № 1. С. 59–67. https://doi.org/10.3103/S0025654422010034
Горячева И.Г., Маховская Ю.Ю. Моделирование трения на разных масштабных уровнях // Изв. РАН. МТТ. 2010. № 3. С. 100–110. https://doi.org/10.3103/S002565441003009X
Горячева И.Г., Маховская Ю.Ю. Скольжение волнистого индентора по поверхности вязкоупругого слоя при наличии адгезии // Изв. РАН. МТТ. 2015. № 4. С. 90–103. https://doi.org/10.3103/S002565441504010X
Morozov A.V., Makhovskaya Y.Y. Effect of adhesion properties of frost-resistant rubbers on sliding friction // ICIE 2018: Proceedings of the 4th International Conference on Industrial Engineering. Lecture Notes in Mechanical Engineering. Springer, 2019. P. 1029–1037. https://doi.org/10.1007/978-3-319-95630-5_108
Scaraggi M., Persson B.N.J. Friction and universal contact area law for randomly rough viscoelastic contacts // J. Phys: Condens Matter. 2015. V. 27. P. 105102–105102. https://doi.org/10.3103/S1068366615030137
Солдатенков И.А. Расчет трения индентора с фрактальной шероховатостью о вязкоупругое основание // Трение и износ. 2015. № 3. С. 257–262. https://doi.org/10.3103/S1068366616060131
Солдатенков И.А. Расчет трения индентора с фрактальной шероховатостью о вязкоупругое основание: уточненная модель // Трение и износ. 2016. № 6. С. 670–672. https://doi.org/10.3103/S1068366616060131
Popov V., Dimaki A., Psakhie S. et al. On the role of scales in contact mechanics and friction between elastomers and randomly rough self-affine surfaces // Sci. Rep. 2015. V. 5. P. 11139https://doi.org/10.1038/srep11139
Makhovskaya Y. Modeling sliding friction of a multiscale wavy surface over a viscoelastic foundation taking into account adhesion // Lubricants. 2019. V. 7. № 13. https://doi.org/10.3390/lubricants7020013
Морозов А.В., Маховкая Ю.Ю, Кравчук К.С. Влияние адгезионных свойств и текстуры поверхности ламинированной фанеры на коэффициент трения с резиной // Трение и износ. 2021. № 4. С. 437–449. https://doi.org/10.32864/0202-4977-2021-42-4-437-449
Savkoor A.R. On the friction of rubber // Wear. 1965. V. 8. № 3. P. 222–237. https://doi.org/10.1016/0043-1648(65)90161-4
Goryacheva I., Makhovskaya Y. Adhesion effect in sliding of a periodic surface and an individual indenter upon a viscoelastic base // J. Strain Anal. Eng Des. 2016. V. 51. № 4. P. 286–293. https://doi.org/10.1177/0309324715614194
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела