Известия РАН. Механика твердого тела, 2022, № 5, стр. 130-140

Введение. Явление вибрации и сопутствующая ему повышенная шумность работы оборудования различного назначения, связано, прежде всего, с возникновением колебаний тех или иных элементов самого оборудования. В большинстве отраслей, и в машиностроении, в частности, явление вибрации в основном сказывается отрицательно. Редкое исключение составляют лишь единичные технологические процессы, где используется вибрация, такие как вибрационная сварка трением. Колебания различных элементов оборудования машиностроения при их длительном воздействии вызывают усталость материала, приводящее к ухудшению его параметров и последующему разрушению, нередко являющемуся причиной серьезных аварий [1]. В рабочем цикле возникающая вибрация приводит к повышению энергозатрат, сокращению срока службы машин и станков, а также к ухудшению условий труда рабочего персонала. В этой связи для решения поставленной проблемы, прежде всего, необходима качественная и количественная оценка возникающих колебаний в тех или иных условиях, и уже только после этого принятие соответствующих решений по их устранению. Важнейшими параметрами колебательного процесса являются амплитуда и частота, определение которых относят к динамическим задачам механики. При совпадении частоты собственных и вынужденных колебаний колеблющихся элементов возникает явление резонанса, представляющего известную опасность.

Причины возникновения явления вибрации могут заключаться как в несоответствии требованиям к условиям эксплуатации оборудования, так и в различных конструкционных дефектах самого оборудования, а также в случае его неисправности. Вибрация может проявиться из-за излишнего трения движущихся частей, низкого качества сборки и различных геометрических дефектов взаимодействующих элементов конструкции машины: искривление, децентрализация, эксцентриситеты и прочее.

Задачи расчета на динамический прогиб при поперечных колебаниях реализовывались в основном для идеальных стержней с прямолинейной осью при отсутствии каких-либо посторонних внешних воздействий [2–7]. Однако, как было отмечено выше, причиной вибрации могут являться различные геометрические дефекты, требующие обязательного учета. В этом случае решение поставленной задачи усложняется. Особую важность представляет учет динамического характера продольного нагружения стержневых элементов конструкций, что приводит к дальнейшему усложнению поставленной задачи, как это было справедливо отмечено в работах [8–11].

Основную сложность решения динамических задач представляет их нелинейность. Необходимо отметить, что если рассматривать продольный удар нескольких стержней различной длины и толщины, составляющих геометрически неоднородную стержневую систему, то решение задачи известными методами [2–11] может оказаться невозможным из-за хаотичности интерференционной картины продольных волн при их переходе через границы однородных участков.

Ранее были рассмотрены задачи поперечных колебаний однородного стержня при продольном ударе о жесткую преграду с учетом собственного веса [12] и продольного удара ступенчатого стержня, имеющего начальную кривизну одного из участков [13]. Был реализован подход, заключавшийся в совместном применении метода начальных параметров [14] и волновой модели продольного удара [15–18]. В настоящей работе этот подход реализуется для расчета вибрационных характеристик геометрически неоднородной стержневой системы, имеющей начальную кривизну одного из участков, и испытывающую продольный удар об абсолютно жесткую преграду.

1. Постановка задачи. Рассматриваемая схема взаимодействия стержневых элементов довольно часто реализуется в различных машинах ударного действия, пневматических ударных механизмах, гидравлических виброударных системах, системах кузнечно-штамповочного производства и прочего. Помимо этого, такая схема возможна и в отраслях, напрямую не связанных с ударом. Это могут быть машины и механизмы самого различного назначения, где в силу тех или иных факторов возникает продольный удар стержневых элементов. Динамическое взаимодействие стержневых элементов конструкций имеет место и в строительной отрасли.

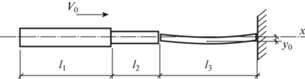
В предлагаемой работе рассматривается продольный удар ступенчатого стержня, имеющего длины однородных участков l₁ и l₂ и площади поперечных сечений А₁, А₂, о покоящийся однородный стержень длиной l₃ и площадью поперечных сечений А₃, взаимодействующий с жесткой преградой. Схема удара изображена на рис. 1. Стержень длиной l₃, взаимодействующий с жесткой преградой, имеет начальную кривизну y₀. Все стержневые элементы рассматриваемой системы предполагаются состоящими из одного материала.

Методом начальных параметров рассчитываются максимальное поперечное смещение и скорость сечений искривленного стержня, сжатого постоянной продольной силой [14]. Далее с применением волновой модели продольного удара [15–18] вычисляются продольные силы, возникающие в однородных участках стержневой системы, и рассчитывается время их действия. После прекращения действия продольных сил участки представляют из себя колебательную систему, выведенную из положения равновесия и совершающую затухающие поперечные колебания, имея вначале процесса приобретенную скорость и начальное смещение поперечных сечений [12, 13]. При известных амплитуде и частоте поперечных колебаний, а также массе колеблющегося элемента, рассчитывается среднее значение импульса, как важнейшей характеристики вибрационного процесса [19].

2. Применение метода начальных параметров. Для определения максимальной амплитуды поперечных колебаний или максимального прогиба, которые будут иметь место вначале колебательного процесса стержней после взаимодействия с жесткой преградой, можно воспользоваться дифференциальным уравнением изогнутой оси стержня постоянного поперечного сечения, несущего равномерно распределенную массу [2, 14]:

где y – прогиб оси стержня;

ξ = x/l относительная координата;

$N$ – продольная сила (положительная, если стержень сжат);

$l$ – длина стержня или его однородного участка;

$EI$ – жесткость стержня при изгибе;

m – интенсивность массы;

ω – частота свободных колебаний стержня, зависящая от условий его закрепления.

При решении поставленной задачи, уравнение (2.1) решается для каждого стержня или участка в отдельности. При продольном ударе сила $N$ будет представлять из себя кусочно-разрывную функцию, поэтому для решения поставленной задачи вычисляется среднее значение продольной силы на рассматриваемом временном интервале.

Составим характеристическое уравнение, соответствующее уравнению (2.1)

и его корни будут [14]

В зависимости от направления продольной силы (сжатие или растяжение) u⁴ и ν² принимают как положительные, так и отрицательные значения, поэтому корни (2.3) могут быть вещественными, чисто мнимыми или комплексными сопряженными числами.

Общий интеграл уравнения (2.1) при отсутствии кратных корней можно записать в виде суммы

где ${{A}_{j}}$, ${{B}_{j}}$ – постоянные интегрирования; λ_j – корни характеристического уравнения (2.2).

Выражение (2.4) для прогибов стержня дает возможность составить формулы усилий и углов поворота сечений стержней, если воспользоваться дифференциальными зависимостями [14]

Здесь $\varphi $, M – амплитуды угла поворота и изгибающего момента в сечениях; ${{Q}^{N}}$ – амплитуда поперечной силы, перпендикулярной к изогнутой оси стержня [14].

Для удобства обозначения примем

Тогда искомые зависимости запишутся в более простой форме

или в виде сумм:

В дальнейшем поставленную задачу удобнее решать методом начальных параметров, как это предлагалось В.Г. Чудновским [14]. Для получения формул метода начальных параметров необходимо постоянные интегрирования ${{A}_{j}}$ и ${{B}_{j}}$ выразить через усилия и перемещения сечения стержня, совпадающего с началом координат. Эти усилия и перемещения и будут называться начальными параметрами: ${{y}_{0}}$, ${{\varphi }_{0}}$, M₀ и Q₀. Данная методика была подробно изложена в работах [12, 13], и в соответствии с ней получено выражение для расчета величины максимального прогиба участка, имеющего начальную кривизну:

Здесь ${{\tilde {M}}_{0}}$ и $\tilde {\varphi }{}_{0}$ – относительные момент и угол поворота ударного сечения, связанные с начальной кривизной стержня. Коэффициенты $F_{\xi }^{{{\text{III}}}}$ и $F_{\xi }^{{{\text{IV}}}}$ зависят от величины возникающей продольной ударной силы и рассчитываются в соответствии с методикой, изложенной в [12, 13].

3. Определение продольной силы. Для определения продольной силы $N$ используется волновая модель продольного удара однородного стержня о жесткую преграду [15–18]. Решается волновое уравнение для трех однородных участков, составляющих стержневую систему:

где ${{u}_{1}}(x,t)$, ${{u}_{2}}(x,t)$, ${{u}_{3}}(x,t)$ – продольное перемещение поперечных сечений первого, второго и третьего участков, x − координата сечения, $t$ − время, a − скорость распространения продольной волны деформации.

Начальные условия определяют состояние стержней перед их соударением [15]: при $t = {{t}_{0}}$$ = 0$

Граничные условия определяют отсутствие силы в сечении x = 0 и равенство нулю скорости сечения, взаимодействующего с жесткой преградой x = l при взаимодействии искривленного стержня с жесткой преградой [15].

Для решения волновых уравнений (3.1)–(3.3) применяется метод Даламбера [15]:

где ${{f}_{1}}(at - x),$ ${{f}_{2}}(at - x),$ ${{f}_{3}}(at - x)$ – функции, описывающие прямые волны, распространяющиеся соответственно по однородным участкам в направлении оси $x$; ${{\varphi }_{1}}(at + x)$, ${{\varphi }_{2}}(at + x)$, ${{\varphi }_{3}}(at + x)$ – функции, описывающие обратные волны, распространяющиеся по этим же участкам в противоположном направлении; $f_{1}^{'}(at - x)$, $f_{2}^{'}(at - x)$, $f_{3}^{'}(at - x)$, $\varphi _{1}^{'}(at + x)$, $\varphi _{2}^{'}(at + x)$, $\varphi _{3}^{'}(at + x)$ − производные функций.

Целесообразно перейти к относительным величинам, определяющим прямые и обратные волны:

В дальнейшем, для удобства определения продольной силы $N$ в сечениях стержней, методом характеристик строится поле волновых состояний и диаграмма продольных сил [15–18]. Относительная продольная деформация $\bar {\varepsilon }(x,t)$, позволяющая в дальнейшем рассчитать продольную сжимающую силу N, возникающую в стержневых элементах, связана c параметрами прямых и обратных волн зависимостью (3.9). При известной величине $\bar {\varepsilon }(x,t)$ можно определить продольную силу:

где E – модуль упругости, зависящий от материала стержневой системы, А – площадь сечения соответствующего участка.

Далее, используя метод начальных параметров, можно рассчитать прогиб $y$ и скорость $y{\kern 1pt} ' = {{dy} \mathord{\left/ {\vphantom {{dy} {dt}}} \right. \kern-0em} {dt}}$ в момент прекращения действия продольной силы N. Далее сечения рассматриваемого стержня, имея приобретенную поперечную скорость $y{\kern 1pt} '$ и двигаясь по инерции до некоторого максимального отклонения ${{y}_{{\max }}}$ от положения равновесия, начинают совершать свободные поперечные колебания, что и будет являться источником вибрации.

4. Вычисление максимального прогиба и среднего импульса. Максимальное отклонение сечений стержневой системы от положения равновесия, которые и будут максимальными прогибами, легко определится по известной формуле [2]:

где y – максимальный прогиб, равный максимальной координате рассматриваемого сечения в момент прекращения действия продольной силы N, $\omega $ – циклическая частота свободных поперечных колебаний стержней при отсутствии продольной силы. Учитывая формы связей рассматриваемых стержневых элементов системы, устанавливаем для искривленного участка $\xi = 0.5$. Для первой формы поперечных колебаний (n = 1), как наиболее часто встречающейся на практике, а также с учетом зависимости (3.11) при условии, что продольная сила N не превышает критическую эйлеровскую нагрузку, имеем для каждого участка стержневой системы выражение циклической частоты поперечных колебаний:

Здесь l и d – соответственно, длина и диаметр рассматриваемого участка, $\bar {\varepsilon }$ – относительная продольная деформация. В нашем случае, когда рассматриваются поперечные колебания третьего участка, в эту формулу вместо l следует подставлять $l{}_{3}^{{}}$.

Анализируя формулу (4.2) можно заключить, что с ростом предударной скорости частота поперечных колебаний $\vartheta $ сжатого участка по первой форме будет уменьшаться и станет равной нулю при достижении продольной силы величины ${{P}_{{kr}}}$ по Эйлеру, что отмечено в [2].

В зависимости от вида связи каждого участка стержневой системы с соседними участками и с жесткой преградой, циклическую частоту свободных поперечных колебаний по первой форме $n = 1$ можно рассчитать по формуле [2]

где произведение EI является изгибной жесткостью стержня. Параметр $\wp $ выбирается с учетом сопряжения рассматриваемого искривленного участка с соседними участками и с жесткой преградой, от которого зависит частота колебаний $\omega $ [2].

Предполагая гармонический закон колебательного процесса, имеем

При малых значениях $t$ максимальная скорость сечений будет

Подставляя значения частоты свободных колебаний $\omega $ и скорости $y{\kern 1pt} '$ в формулу (4.1), получим искомый максимальный прогиб, равный максимальному перемещению поперечных сечений $y_{{\max }}^{*}$ рассматриваемого участка. В этом случае имеет место учет сил инерции, действующих на стержневую систему при динамической нагрузке, что представляло в традиционных моделях расчета довольно сложную задачу.

Если ударное взаимодействие с жесткой преградой будет многократным в течение длительного интервала времени, то возникнет вибрационный процесс. Важной его характеристикой является среднее значение создаваемого импульса колеблющимся участком стержневой системы при каждом поперечном колебании. Для расчета среднего импульса можно воспользоваться зависимостью [19]:

5. Пример и краткий анализ результатов. Рассмотрим продольный удар ступенчатой стержневой системы о жесткую преграду. Длины однородных участков: ${{l}_{1}} = {{l}_{3}} = 1.6$ м, ${{l}_{2}} = 0.8$ м, причем третий однородный участок имеет начальную кривизну ${{y}_{0}} = 2$ мм. Диаметры участков: ${{d}_{1}} = 0.12$ м, ${{d}_{2}} = 0.07$ м, ${{d}_{3}} = 0.04$ м. Предударная скорость ступенчатого стержня об искривленный однородный стержень (третий участок стержневой системы), взаимодействующий с жесткой преградой, ${{V}_{0}} = \,\,1$ м/с. Материал стержневой системы – сталь СТ-5. Циклическая частота собственных поперечных колебаний для третьего участка, имеющего начальную кривизну, $\omega = \,\,495$ р/с, при $\wp $ равном 1.

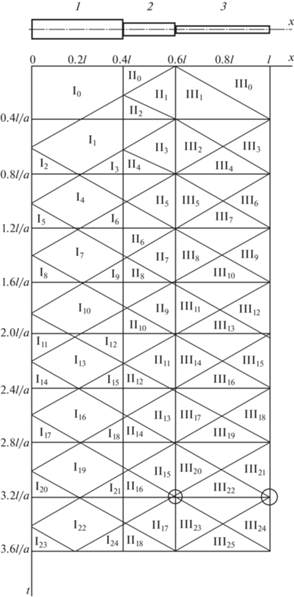
С помощью метода характеристик строим поле волновых состояний при продольном ударе для рассматриваемой стержневой системы, (рис. 2) и диаграмму продольных сил (рис. 3).

Области состояний (рис. 2) I₀– I₂₄, II₀– II₁₈, III₀– III₂₅ c соответствующими значениями $\vec {f}{\kern 1pt} '(at - x{}_{j}^{{}})$, $\bar {\varphi }{\kern 1pt} '(at + x{}_{j})$, $\bar {\varepsilon }(x,\,t)$, $\bar {\nu }(x,\,t)$ определяют параметры прямых и обратных волн деформаций, относительную продольную деформацию и скорость поперечных сечений. Длительность состояния для произвольного сечения определяется разностью ординат t, которые имеют точки наклонных линий для этого сечения.

При $t = 3.2l{\text{/}}a$ происходит отрыв однородного искривленного стержня от ступенчатого стержня и от жесткой преграды. На поле состояний (рис. 2) отрывы выделены жирными кружками.

Для вычисления среднего значения продольной силы, действующей на искривленном третьем участке стержневой системы, учитывая ее кусочно-разрывной характер, обратимся к диаграмме продольных сил (рис. 3). На интервале времени 1.2l/a ≤ ≤ $\tau \leqslant 3.2l{\text{/}}a$ продольная сила N достигает своих максимальных величин, которые оказывают основное влияние на колебательный процесс искривленного участка. Анализируя диаграмму продольных сил (рис. 3), устанавливаем среднее значение продольной силы N = 131.44 кН на рассматриваемом интервале времени, и переводя его в секунды при известных значениях общей длины l и скорости распространения продольной волны деформации а, получим значение $\tau = 9.0$ × 10^–4 сек. При учете кривизны участка, начальными параметрами являются угол поворота ${{\varphi }_{0}} = 2{{y}_{0}}{\text{/}}l{}_{3}$, и момент M₀, равный произведению ${{y}_{0}}$ на значение возникающей продольной силы N.

Далее, вычисляем коэффициенты ν² = 10.24 и u⁴ = 1002 по формулам (2.1), и используя их, вычисляем корни характеристического уравнения (2.2) по формулам (2.3): $\lambda _{1}^{2} = - 37.19$, $\lambda _{2}^{2}\, = \,26.95$. Используя полученные числовые результаты, получим значения коэффициентов $F_{\xi }^{{{\text{III}}}} = - 0.0598$ и $F_{\xi }^{{{\text{IV}}}} = - 0.461$. После подстановки этих значений в выражение (2.11) для ${{y}_{{\max }}}$, получим ${{y}_{{\max }}}$ = 0.7 мм. Такое значение прогиба возникает при постоянной продольной силе N. При кратковременном ее действии искривленный участок будет только выведен из положения равновесия и далее предоставлен самому себе. Для гармонического закона изменения координаты торцевого сечения стержня имеем (4.4):

Циклическая частота колебаний кратковременно сжатого стержня, рассчитанная по (4.2), будет равна $\vartheta = 281.09$ р/с. С учетом длительности действия продольной силы N максимальное отклонение сечения, имеющего координату $x = 0.5{{l}_{3}}$ считая от границы второго и третьего участков, в течение промежутка времени $\tau $ и, исходя из (4.7), будет равно 0.19 мм. В соответствии с (4.5) поперечная скорость рассматриваемого сечения будет равна 0.2 м/с. Тогда по формулам (4.1) и (4.6) получаем максимальное его отклонение от положения равновесия при свободных колебаниях $y_{{\max }}^{*}$ = 0.44 мм и среднее значение импульса 12.8 кг ⋅ м/c.

В работе моделировалось среднее значение вибрационного импульса для стержневых систем с различным соотношением длин однородных участков при одинаковом соотношении их толщины и одинаковой предударной скорости V₀. Как показали результаты моделирования, четкой закономерности между величиной импульса и каким-либо соотношением длин участков $l{}_{1}$, $l{}_{2}$, $l{}_{3}$ не прослеживается, что представляет немалый научный интерес.

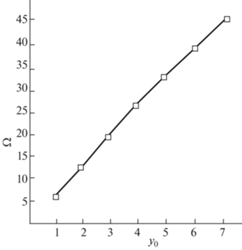
Зависимость величины ударного импульса Ω в процессе удара от начальной кривизны стержня y₀ иллюстрирована на графике (рис. 4). Как видно из графика, зависимость $\Omega \,(y{}_{0})$ близка к линейной, что подтверждается анализом выражения (2.11).

Заключение. В рассмотренной работе был представлен подход, позволяющий рассчитать амплитуду поперечных колебаний искривленного участка ступенчатой стержневой системы, испытывающей продольный удар с жесткой преградой. При многократном, периодичном характере продольного удара возникнет вибрационный процесс, являющийся известной проблемой машиностроения, надежности машин и механизмов в рабочем цикле, а также проблемой в строительной отрасли.

Рассчитан средний импульс при возникающих поперечных колебаниях искривленного участка, что дает возможность качественной и количественной оценки вибрационного воздействия возникающего колебательного процесса. С помощью предлагаемой методики можно рассчитать амплитуду колебаний и среднее значение импульса практически для любой произвольной кусочно-неоднородной стержневой системы, испытывающей динамическое воздействие, с учетом ее начального состояния.

Метод расчета величины амплитуды поперечных колебаний и среднего значения импульса искривленного участка рассматриваемой стержневой системы, описанный выше, позволил эффективно совместно применить метод начальных параметров и волновую модель продольного удара. Примененный подход позволяет учесть инерционные силы при расчете вибрационных характеристик, что представляло в традиционных методах довольно непростую задачу. Дальнейшее развитие данного подхода будет представлять интерес для решения целого ряда прикладных задач механики.

Как было отмечено выше, зависимость средней величины импульса от конфигурации стержневой системы не прослеживается. Это связано с хаотичностью интерференционной картины продольных волн деформаций при их распространении и преобразовании по длине каждого однородного участка и при переходе через границы участков. В результате, для каждой определенной конфигурации стержневой системы, образуются продольные волны разной величины и продолжительности, от которых зависит среднее значение моделируемого импульса.

Немалый научный интерес представляет изучение колебательного процесса и величины возникающего ударного импульса ступенчатой стержневой системы с учетом высших форм колебаний, что является целью дальнейшей исследовательской работы.