1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 5, 2022

Известия РАН. Механика твердого тела, 2022, № 5, стр. 120-129

О СТАЦИОНАРНЫХ ДВИЖЕНИЯХ РАВНОГРАННОГО ТЕТРАЭДРА, БЛИЗКОГО К ПРАВИЛЬНОМУ, С НЕПОДВИЖНОЙ ТОЧКОЙ В ЦЕНТРАЛЬНОМ НЬЮТОНОВСКОМ ПОЛЕ СИЛ

Е. А. Никонова a, *

a Федеральный исследовательский центр “Информатика и управление” Российской академии наук
Москва, Россия

* E-mail: nikonova.ekaterina.a@gmail.com

Поступила в редакцию 14.12.2021
После доработки 06.01.2022
Принята к публикации 07.01.2022

Полный текст (PDF)

Аннотация

Изучаются существование, устойчивость и ветвление стационарных движений тетраэдрального тела вокруг неподвижной точки в центральном ньютоновском поле сил. Рассматривается случай равногранного тетраэдра близкого к правильному.

Исследуется связь этих свойств стационарных движений со свойствами стационарных движений правильного тетраэдра.

В небесной механике гравитационное поле небесного тела неправильной формы нередко моделируется гравитационным полем некоторой совокупности массивных точек. Представления в виде совокупности двух или трёх точечных масс содержат симметрии, не присущие реальным телам. Наиболее подходящими представляются приближения гравитационных полей с помощью полей притяжения именно четырёх массивных точек.

Ключевые слова: твердое тело с неподвижной точкой, тело в центральном гравитационном поле, теория Рауса, устойчивость и ветвление стационарных движений, равногранный тетраэдр

Введение. Согласно исследованиям [1–3] в случае правильного тетраэдра, являющегося частным случаем равногранного, масса которого в равных долях сосредоточена в его вершинах, наблюдаются примечательные свойства равновесий, а именно, размерность элемента правильного тетраэдра (вершина, ребро, грань), которым он обращен в стационарном движении, в частности, и в равновесии, к притягивающему центру совпадает со степенью неустойчивости. “Чувствительность” этих свойств к геометрическим модификациям правильного тетраэдра обсуждается в работах [4–6]. Изучаются существование, устойчивость и ветвление стационарных движений равногранного тетраэдра вокруг неподвижной точки в центральном ньютоновском поле сил.

Исследование “чувствительности” динамических свойств платоновых тел восходит к публикации [7], в которой предложен оригинальный подход, опирающийся на эффективное использование симметрий в распределении масс при изучении стационарных движений в задачах динамики твердого тела (см. также [8–13]). Другое направление исследований динамики тетраэдральных тел, обусловленное потребностями механики космического полета, связано с предположением о наличии в них роторов [14–16].

Настоящее исследование инспирировано, в частности, работой [8], где рассматривается задача о движении однородного параллелепипеда, закрепленного в центре масс и находящегося в центральном ньютоновском поле сил. В работе определены все положения равновесия тела, близкого к кубу, исследованы их ветвления и устойчивость в зависимости от параметров задачи.

В небесной механике при изучении динамики малых тел со сложным распределением масс, форма которых далека от шарообразной, последние могут быть представлены в виде совокупности нескольких точечных масс, т.н. масконов. Так, например, гравитационное поле кометы (67P) Чурюмова–Герасименко может быть представлено полем притяжения образующих тетраэдр четырех массивных точек [17] (см. также [18], относительно вопроса качества приближения).

1. Постановка задачи и основные обозначения. Рассмотрим движение твердого тела $\mathcal{T}$ вокруг неподвижной точки $O$ в поле сил ньютоновского притяжения с центром в точке N. Пусть $\gamma = ({{\gamma }_{1}},{{\gamma }_{2}},{{\gamma }_{3}}{{)}^{{\text{т}}}}$ – единичный вектор, направленный от N к O, I = = ${\text{diag}}({{I}_{1}},{{I}_{2}},{{I}_{3}})$ – тензор инерции тела относительно точки $O$, $\omega = ({{\omega }_{1}},{{\omega }_{2}},{{\omega }_{3}}{{)}^{{\text{т}}}}$ – вектор угловой скорости тела. Здесь и далее все векторы и тензорные величины задаются в подвижной системе отсчета $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, оси которой направлены вдоль главных осей инерции тела, задаваемых собственными векторами тензора инерции ${\mathbf{I}}$.

Если ${{U}_{N}} = {{U}_{N}}(\gamma )$ – потенциал силового поля, то описывающие движение уравнения Эйлера–Пуассона можно записать в виде

(1.1)
${\mathbf{I}}\dot {\omega } = {\mathbf{I}}\omega \times \omega + \gamma \times \frac{{\partial {{U}_{N}}}}{{\partial \gamma }},\quad \dot {\gamma } = \gamma \times \omega $

Помимо интеграла энергии ${{\mathcal{J}}_{0}} = \frac{1}{2}({\mathbf{I}}\omega ,\omega ) + {{U}_{N}}(\gamma )$ = h и интеграла площадей ${{\mathcal{J}}_{1}} = ({\mathbf{I}}\omega ,\gamma )$ = pψ, уравнения (1.1) допускают геометрический интеграл

(1.2)
${{\mathcal{J}}_{2}} = \left( {\gamma ,\gamma } \right) - 1 = 0$
задающий в пространстве ${{R}^{3}}(\gamma )$ т.н. сферу Пуассона $\mathcal{S}$.

Как известно (см., например, [19]), система (1.1) может обладать перманентными вращениями вокруг оси NO с постоянной по величине угловой скоростью $\omega .$ Положение оси перманентного вращения в теле согласно (1.1) задаются уравнениями

$0 = \gamma \times \left( {\frac{{\partial {{U}_{N}}}}{{\partial \gamma }} - {{\omega }^{2}}{\mathbf{I}}\gamma } \right),\quad \omega = {\text{const}}$

Замечание. Согласно теории Рауса ([20, 21], см. также [22]) эти вращения могут быть найдены как критические точки приведенного (en: amended) потенциала

${{U}_{\psi }} = \frac{{p_{\psi }^{2}}}{{2I(\gamma )}} + {{U}_{N}}(\gamma )$
рассмотренного как функция на сфере (1.2). Здесь $I(\gamma ) = ({\mathbf{I}}\gamma ,\gamma )$ – момент инерции тела относительно оси вращения. При этом постоянная интеграла площадей ${{p}_{\psi }}$ и величина угловой скорости оказываются связанными соотношением ${{p}_{\psi }} = I(\gamma )\omega $.

Хорошо известно, что при описании движения твердого тела в центральном поле ньютоновского притяжения, как правило, достаточно воспользоваться разложением до слагаемых первого или второго порядка малости по параметру, характеризующему отношение размеров тела к его расстоянию до притягивающего центра. Однако, в случае, когда тензор инерции тела близок к шаровому, такие приближения, вообще говоря, оказываются недостаточными. В дальнейшем в качестве примера рассмотрим движение твердого тела $\mathcal{T}$ в виде равногранного тетраэдра с равными массами в вершинах.

2. Равногранный тетраэдр. Согласно [23], тетраэдр называется равногранным, если все грани – равные между собой треугольники. Как известно, у равногранного тетраэдра бимедианы попарно перпендикулярны и являются общими серединными перпендикулярами соответствующих скрещивающихся ребер. Пусть $\mathcal{T}$ – тело в форме равногранного тетраэдра с равными массами m в вершинах. Будем считать, что оно совершает вращение вокруг неподвижной точки O, совпадающей с точкой пересечения бимедиан. Зададим жестко связанную с тетраэдром правую систему отсчета $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ с началом в точке O и осями, направленными вдоль бимедиан. Если длины бимедиан равны $2{{a}_{1}}$, $2{{a}_{2}}$, $2{{a}_{3}}$ соответственно, то вершины $A$, $B$, $C$ и $D$ тетраэдра $\mathcal{T}$ в этой системе отсчета задаются радиус-векторами

$\begin{array}{*{20}{l}} {{{{\mathbf{r}}}_{A}} = {\mathbf{OA}} = r{{{({{a}_{1}}, - {{a}_{2}}, - {{a}_{3}})}}^{{\text{т}}}} = r{{{\mathbf{e}}}_{A}},\quad {{{\mathbf{r}}}_{B}} = {\mathbf{OB}} = r{{{( - {{a}_{1}}, - {{a}_{2}},{{a}_{3}})}}^{{\text{т}}}} = r{{{\mathbf{e}}}_{B}}} \\ {{{{\mathbf{r}}}_{C}} = {\mathbf{OC}} = r{{{( - {{a}_{1}},{{a}_{2}}, - {{a}_{3}})}}^{{\text{т}}}} = r{{{\mathbf{e}}}_{C}},\quad {{{\mathbf{r}}}_{D}} = {\mathbf{OD}} = r{{{({{a}_{1}},{{a}_{2}},{{a}_{3}})}}^{{\text{т}}}} = r{{{\mathbf{e}}}_{D}}} \end{array}$
причем длины этих векторов равны

$\left| {{\mathbf{OA}}} \right| = \left| {{\mathbf{OB}}} \right| = \left| {{\mathbf{OC}}} \right| = \left| {{\mathbf{OD}}} \right| = r,\quad a_{1}^{2} + a_{2}^{2} + a_{3}^{2} = 1$

Оси $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ являются главными центральными осями инерции тела $\mathcal{T}$, в них главные центральные моменты $\mathcal{T}$ записываются как

${{I}_{k}} = 4m{{r}^{2}}I_{k}^{'},\quad k = 1,\;2,\;3,\quad I_{1}^{'} = a_{2}^{2} + a_{3}^{2},\quad I_{2}^{'} = a_{1}^{2} + a_{3}^{2},\quad I_{3}^{'} = a_{1}^{2} + a_{2}^{2}$

3. Приближенное представление потенциала поля притяжения. Пусть N – притягивающий центр, в котором сосредоточена масса M, $\left| {{\mathbf{NO}}} \right| = d$. Пусть единицы размерности выбраны так, что гравитационная постоянная, масса M, а также величина ${{r}_{ \star }}\, = \,\sqrt {{{d}^{2}}\, + \,{{r}^{2}}} $ равны единице (ср. [24]). Тогда потенциал притяжения имеет вид

(3.1)
${{U}_{N}} = - \sum\limits_{(A,B,C,D)} \rho _{A}^{{ - 1}},\quad {{\rho }_{A}} = {{\left( {1 + \varepsilon \left( {\gamma ,{{{\mathbf{e}}}_{A}}} \right)} \right)}^{{1/2}}}$
где $(A,{\kern 1pt} B,{\kern 1pt} C,{\kern 1pt} D)$ – циклическая перестановка индексов.

Параметр разложения $\varepsilon $, предложенный в [24], удобно применять и в настоящем исследовании поскольку он позволяет одновременно описывать случаи, когда тетраэдр располагается очень далеко от притягивающего центра $N$, и когда, наоборот, центр масс тетраэдра очень близок к притягивающему центру $N$.

4. Равногранный тетраэдр, мало отличающийся от правильного. Пусть равногранный тетраэдр мало отличается от правильного, причем

(4.1)
${{a}_{1}} = \sqrt {\frac{1}{3} - \varepsilon p} ,\quad {{a}_{2}} = \frac{{\sqrt 3 }}{3},\quad {{a}_{3}} = \sqrt {\frac{1}{3} + \varepsilon p} $

Подставляя величины (4.1) в потенциал (3.1) и вновь разлагая его в ряд по параметру $\varepsilon $, имеем

(4.2)
$V = {{V}_{0}} + \varepsilon {{V}_{1}} + {{\varepsilon }^{2}}{{V}_{2}} + {{\varepsilon }^{3}}{{V}_{3}} + {{\varepsilon }^{4}}{{V}_{4}} + \; \ldots $
${{V}_{0}} = - 4,\quad {{V}_{1}} = 0,\quad {{V}_{2}} = - \frac{1}{2},\quad {{V}_{3}} = \frac{3}{2}(\gamma _{1}^{2} - \gamma _{3}^{2})p + \frac{{5\sqrt 3 }}{6}{{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}}$
${{V}_{4}} = - \frac{{35}}{{288}}(\gamma _{1}^{4} + \gamma _{2}^{4} + \gamma _{3}^{4}) - \frac{{35}}{{48}}(\gamma _{1}^{2}\gamma _{2}^{2} + \gamma _{1}^{2}\gamma _{3}^{2} + \gamma _{2}^{2}\gamma _{3}^{2})$

Предполагая, что параметр $\varepsilon $ близок к нулю, исследуем равновесия и области возможного движения (ОВД).

4.1. Равновесия. Существование. Ограничиваясь рассмотрением случая приближения третьего порядка, покажем, как число число равновесий системы зависит от значения параметра $p$. Уравнения равновесий имеют вид

$\begin{array}{*{20}{l}} {\frac{{\partial W}}{{\partial {{\gamma }_{1}}}} = \frac{{5\sqrt 3 }}{6}{{\gamma }_{2}}{{\gamma }_{3}} + \left( {\lambda + 3p} \right){{\gamma }_{1}} = 0} \\ {\frac{{\partial W}}{{\partial {{\gamma }_{2}}}} = \frac{{5\sqrt 3 }}{6}{{\gamma }_{1}}{{\gamma }_{3}} + \lambda {{\gamma }_{2}} = 0} \\ {\frac{{\partial W}}{{\partial {{\gamma }_{3}}}} = \frac{{5\sqrt 3 }}{6}{{\gamma }_{1}}{{\gamma }_{2}} + \left( {\lambda - 3p} \right){{\gamma }_{3}} = 0} \end{array}$
$W = {{V}_{3}} + \frac{\lambda }{2}\left( {\left( {\gamma ,\gamma } \right) - 1} \right) = \frac{3}{2}(\gamma _{1}^{2} - \gamma _{3}^{2})p + \frac{{5\sqrt 3 }}{6}{{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}} + \frac{\lambda }{2}(\gamma _{1}^{2} + \gamma _{2}^{2} + \gamma _{3}^{2} - 1)$

Эту систему следует рассматривать в совокупности с геометрическим интегралом (1.2). Неопределённый множитель Лагранжа λ, удовлетворяющий системе, имеет вид

$\lambda = 3(\gamma _{3}^{2} - \gamma _{1}^{2})p - \frac{{5\sqrt 3 }}{2}{{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}}$

Обозначим ${{p}_{ \star }} = \frac{{5\sqrt 6 }}{{36}}$. Тогда помимо равновесий ${{\mathcal{J}}_{1}},$ ${{\mathcal{J}}_{2}}$ и ${{\mathcal{J}}_{3}}$ вида

$\begin{array}{*{20}{l}} {{{\mathcal{J}}_{1}}{\text{:}}\quad }&{{{\gamma }_{1}} = \pm 1,}&{{{\gamma }_{2}} = 0,}&{{{\gamma }_{3}} = 0,}&{\lambda = - 3p} \\ {{{\mathcal{J}}_{2}}{\text{:}}\quad }&{{{\gamma }_{1}} = 0,}&{{{\gamma }_{2}} = \pm 1,}&{{{\gamma }_{3}} = 0,}&{\lambda = 0} \\ {{{\mathcal{J}}_{3}}{\text{:}}\quad }&{{{\gamma }_{1}} = 0,}&{{{\gamma }_{2}} = 0,}&{{{\gamma }_{3}} = \pm 1,}&{\lambda = 3p} \end{array}$
существующих при всех значениях параметра $p$, систем обладает равновесиями
$\begin{gathered} {{\mathcal{J}}_{4}}{\text{:}}\quad \gamma _{1}^{2} = \frac{1}{3} + \frac{{6p}}{{25}}\sqrt {108{{p}^{2}} + 25} + \frac{{36}}{{25}}{{p}^{2}}, \\ \gamma _{2}^{2} = \frac{1}{3} - \frac{{72}}{{25}}{{p}^{2}},\gamma _{3}^{2} = \frac{1}{3} - \frac{{6p}}{{25}}\sqrt {108{{p}^{2}} + 25} + \frac{{36}}{{25}}{{p}^{2}} \\ \end{gathered} $
такими, что
${{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}} > 0,\quad \lambda = - \frac{{\sqrt {108{{p}^{2}} + 25} }}{6},\quad p \in \left[ { - {{p}_{ \star }},{{p}_{ \star }}} \right]$
а также равновесиями
$\begin{gathered} {{\mathcal{J}}_{5}}{\text{:}}\quad \gamma _{1}^{2} = \frac{1}{3} - \frac{{6p}}{{25}}\sqrt {108{{p}^{2}} + 25} + \frac{{36}}{{25}}{{p}^{2}} \\ \gamma _{2}^{2} = \frac{1}{3} - \frac{{72}}{{25}}{{p}^{2}},\quad \gamma _{3}^{2} = \frac{1}{3} + \frac{{6p}}{{25}}\sqrt {108{{p}^{2}} + 25} + \frac{{36}}{{25}}{{p}^{2}} \\ \end{gathered} $
такими, что

${{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}} < 0,\quad \lambda = \frac{{\sqrt {108{{p}^{2}} + 25} }}{6},\quad p \in \left[ { - {{p}_{ \star }},{{p}_{ \star }}} \right]$

В случае $p \ll 1$, решения ${{\mathcal{J}}_{4}}$ порождаются равновесиями, на которых тетраэдр ориентирован на точку $N$ центром одной из своих граней. Так, например, для решения

$\begin{gathered} {{\gamma }_{1}} = \frac{{\sqrt 3 }}{3} + \frac{{3\sqrt 3 }}{5}p + \frac{{9\sqrt 3 }}{{50}}{{p}^{2}} + \; \cdots ,\quad {{\gamma }_{2}} = \frac{{\sqrt 3 }}{3} - \frac{{36\sqrt 3 }}{{25}}{{p}^{2}} + \; \cdots \\ {{\gamma }_{3}} = \frac{{\sqrt 3 }}{3} - \frac{{3\sqrt 3 }}{5}p + \frac{{9\sqrt 3 }}{{50}}{{p}^{2}} + \; \cdots \\ \end{gathered} $
порождающим является решение, на котором правильный тетраэдр “смотрит” на притягивающий центр гранью $ABC$.

Решения ${{\mathcal{J}}_{5}}$ порождаются равновесиями, на которых тетраэдр ориентирован на точку $N$ одной из своих вершин. Так, например, для решения

$\begin{gathered} {{\gamma }_{1}} = - \frac{{\sqrt 3 }}{3} + \frac{{3\sqrt 3 }}{5}p - \frac{{9\sqrt 3 }}{{50}}{{p}^{2}} + \; \cdots ,\quad {{\gamma }_{2}} = - \frac{{\sqrt 3 }}{3} + \frac{{36\sqrt 3 }}{{25}}{{p}^{2}} + \; \cdots \\ {{\gamma }_{3}} = - \frac{{\sqrt 3 }}{3} - \frac{{3\sqrt 3 }}{5}p - \frac{{9\sqrt 3 }}{{50}}{{p}^{2}} + \; \cdots \\ \end{gathered} $
порождающим является решение, на котором правильный тетраэдр “смотрит” на притягивающий центр вершиной $D$.

4.2. Равновесия. Устойчивость и ветвление. При $p \in \left( { - \infty ; - {{p}_{ \star }}} \right)$ на решении ${{\mathcal{J}}_{1}}$ функция ${{V}_{3}}$ достигает локальных минимумов, и равновесия устойчивы, степень неустойчивости $\chi = 0$. При $p \in \left( { - {{p}_{ \star }};{{p}_{ \star }}} \right)$ решению ${{\mathcal{J}}_{1}}$ отвечают седловые точки ${{V}_{3}}$, и равновесия неустойчивы, со степенью неустойчивости χ = 1. Наконец, при $p \in \left( {{{p}_{ \star }}; + \infty } \right)$ на решении ${{\mathcal{J}}_{1}}$ функция ${{V}_{3}}$ достигает локальных максимумов, равновесия неустойчивы, степень неустойчивости χ = 2. При $p = \pm {{p}_{ \star }}$ требуется дополнительное исследование устойчивости.

Для ${{\mathcal{J}}_{3}}$ имеет место, в определенном смысле, обратная ситуация. При $p \in \left( { - \infty ; - {{p}_{ \star }}} \right)$ на решении ${{\mathcal{J}}_{3}}$ функция ${{V}_{3}}$ достигает локальных максимумов, равновесия неустойчивы, степень неустойчивости χ = 2. При $p \in \left( { - {{p}_{ \star }};{{p}_{ \star }}} \right)$ решению ${{\mathcal{J}}_{3}}$ отвечают седловые точки ${{V}_{3}}$, и равновесия неустойчивы, со степенью неустойчивости χ = 1. Наконец, при $p \in \left( {{{p}_{ \star }}; + \infty } \right)$ на решении ${{\mathcal{J}}_{3}}$ функция ${{V}_{3}}$ достигает локальных минимумов, равновесия устойчивы, степень неустойчивости χ = 0. При $p = \pm {{p}_{ \star }}$ опять же требуется дополнительное исследование устойчивости.

Равновесия ${{\mathcal{J}}_{2}}$ неустойчивы и отвечают седловым точкам функции ${{V}_{3}}$.

Замечание. Имеет место следующая связь между свойствами устойчивости решений ${{\mathcal{J}}_{1}}$, ${{\mathcal{J}}_{2}}$, ${{\mathcal{J}}_{3}}$ в зависимости от параметра $p$ и значениями главных моментов инерции тетраэдра. Решение ${{\mathcal{J}}_{k}}$, $k \in 1,\;3$, устойчиво со степенью неустойчивости $\chi = 0$, если главный момент инерции тетраэдра относительно оси $O{{\gamma }_{k}}$ – наименьший. При этом, решение ${{\mathcal{J}}_{\ell }}$, $\ell \in 1,\;3$, неустойчиво со степенью неустойчивости χ = 2, если главный момент инерции тетраэдра относительно оси $O{{\gamma }_{\ell }}$ – наибольший. Наконец, если главный момент инерции тетраэдра относительно оси $O{{\gamma }_{m}}$ – средний, то решение ${{\mathcal{J}}_{m}}$ неустойчиво со степенью неустойчивости χ = 1. В рамках (4.1) индекс m = 2.

Решения ${{\mathcal{J}}_{4}}$ неустойчивы со степенью неустойчивости χ = 2. При этом, решения ${{\mathcal{J}}_{5}}$ устойчивы со степенью неустойчивости $\chi = 0$.

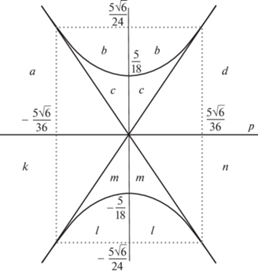
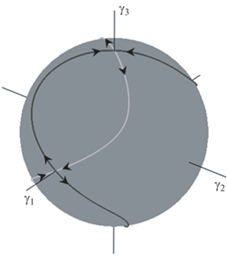
При $p = - {{p}_{ \star }}$, решения ${{\mathcal{J}}_{4}}$ рождаются из решения ${{\mathcal{J}}_{3}}$, и при $p = {{p}_{ \star }}$ сливаются с решением ${{\mathcal{J}}_{1}}$. Наоборот, при $p = - {{p}_{ \star }}$, решения ${{\mathcal{J}}_{5}}$ рождаются из решения ${{\mathcal{J}}_{1}}$, и при $p = {{p}_{ \star }}$ сливаются с решением ${{\mathcal{J}}_{3}}$, см. рис. 1, где изображены кривые на сфере Пуассона $\mathcal{S}$, определяемой геометрическим интегралом (1.2). Стрелками указаны изменения решений с ростом значения параметра $p$.

Рис. 1.

Множества равновесий ${{\mathcal{J}}_{4}}$ (светлая кривая) и ${{\mathcal{J}}_{5}}$ (темная кривая) на сфере Пуассона при изменении параметра $p$ от $ - {{p}_{ \star }}$ до ${{p}_{ \star }}$ (указано стрелками).

4.3. Области возможного движения. Для правильного тетраэдра главные центральные моменты инерции равны, слагаемое в приведенном потенциале, обусловленное центробежными силами, постоянно и не сказывается на структуре областей возможного движения. Однако, если тетраэдр отличен от правильного, это, вообще говоря, не так, и области возможного движения существенно зависят от значений постоянной интеграла площадей ${{p}_{\psi }}$. Ограничимся здесь построением ОВД лишь для нулевого уровня интеграла площадей: ${{p}_{\psi }} = 0$.

Для различных значений энергии h ОВД определяются соотношением

(4.3)
${{V}_{3}} - h \leqslant 0$

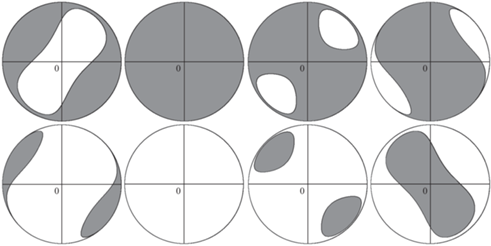
Функция ${{V}_{3}}$ непрерывна на компакте $\mathcal{S}$, и при любом значении $p$ достигает на нем своих минимального и максимального значений, обозначаемых ${{h}_{ \star }}(p)$ и ${{h}^{ \star }}(p)$. ОВД, определяемые неравенством (4.3) для различных значений постоянной $h$, задаваемой уровнем интеграла энергии, в виде проекции полусферы ${{\gamma }_{3}} > 0$ на плоскость $({{\gamma }_{1}},{{\gamma }_{2}})$ изображены на рис. 3. ОВД окрашены серым. На рис. 2 изображена диаграмма на плоскости $(p,h)$. Плоскость разбита на восемь областей $a$, $b$, $c$, $d$, $k$, $l$, $m$, $n$. Для параметров $p$, $h$ внутри каждой области ОВД топологически эквивалентны. ОВД в случае полусферы ${{\gamma }_{3}} < 0$ получается из полученных путем их отражения относительно оси ${{\gamma }_{1}} = 0$. ОВД в случае $p < 0$ получается из рассматриваемого путем отражения относительно оси ${{\gamma }_{1}} = 0$ и инверсии цветов, поэтому наличие рисунков $k$, $l$, $m$, $n$ в определенном смысле избыточно.

Рис. 2.

Бифуркационная диаграмма на плоскости параметров $(p,h)$.

Рис. 3.

Проекции областей возможного движения (закрашены серым) на плоскость $({{\gamma }_{1}},{{\gamma }_{2}})$ для различных областей $a{\kern 1pt} b{\kern 1pt} c{\kern 1pt} d{\kern 1pt} k{\kern 1pt} l{\kern 1pt} m{\kern 1pt} n$ из бифуркационной диаграммы, изображенной на рис. 2.

Замечание. Рассмотрим подробнее случай p = 0. При $h > {{h}^{ \star }}(0) = {{h}^{ \star }} = 5{\text{/}}18$ ОВД совпадает со всей сферой $\mathcal{S}$. При $h = {{h}^{ \star }}$ ОВД представляет собой $\mathcal{S}$ с четырьмя выколотыми точками $P_{1}^{ \star }$, $P_{2}^{ \star }$, $P_{3}^{ \star }$, $P_{4}^{ \star }$ вида

(4.4)
$\left( { \pm \frac{{\sqrt 3 }}{3},\; \pm \frac{{\sqrt 3 }}{3},\; \pm \frac{{\sqrt 3 }}{3}} \right)$
с положительным произведением координат. Эти точки отвечают осям $\gamma $, при которых тетраэдр ориентирован на притягивающий центр $N$ центрами граней.

При $0 < h < {{h}^{ \star }}$ окрестности точек $P_{1}^{ \star }$, $P_{2}^{ \star }$, $P_{3}^{ \star }$ и $P_{4}^{ \star }$ увеличиваются, при $h = 0$ заполняя части сферы $\mathcal{S}$, расположенные в октантах с положительным произведением координат.

При $ - 5{\text{/}}18 = {{h}_{ \star }} = {{h}_{ \star }}(0) < h < 0$ ОВД в определенном смысле “выворачиваются”, и далее представляется объединением окрестностей точек ${{P}_{{1 \star }}}$, ${{P}_{{2 \star }}}$, ${{P}_{{3 \star }}}$, ${{P}_{{4 \star }}}$ вида (4.4) с отрицательным произведением координат. Эти точки отвечают осям $\gamma $, при которых тетраэдр ориентирован на притягивающий центр $N$ вершинами.

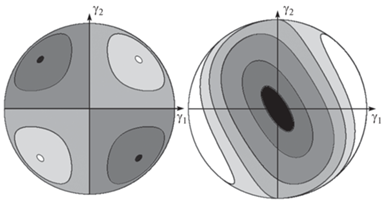
При $h = {{h}_{ \star }}$ ОВД вырождается в четыре точки, ${{P}_{{1 \star }}}$, ${{P}_{{2 \star }}}$, ${{P}_{{3 \star }}}$, ${{P}_{{4 \star }}}$. При $h < {{h}_{ \star }}$ движение невозможно. На рис. 4 (слева) для различных значений постоянной $h \in [{{h}_{ \star }}(p),{{h}^{ \star }}(p)]$ представлены ОВД, окрашенные оттенками серого цвета, изменяющимися от черного, отвечающего значению ${{h}_{ \star }}(p)$, до белого, отвечающего значению ${{h}^{ \star }}(p)$. При фиксированном значении $h$ движение возможно в тех областях, цвет которых темнее цвета, отвечающего рассматриваемому $h$. На рис. 4 (справа) представлены ОВД при $p = 5(1 + \sqrt 6 ){\text{/}}36$.

Рис. 4.

Проекции областей возможного движения (закрашены серым) на плоскость $({{\gamma }_{1}},{{\gamma }_{2}})$ при p = 0 (слева) и при $p = 5(1 + \sqrt 6 ){\text{/}}36$ (справа). ОВД окрашены оттенками серого цвета.

5. О чувствительности равновесий к степени приближения гравитационного потенциала. К отысканию равновесий можно подходить, опираясь на введение новых переменных (ср. [4, 25]). Так если в качестве таких переменных использовать величины

${{j}_{1}} = \gamma _{1}^{2} + \gamma _{2}^{2} + \gamma _{3}^{2},\quad {{j}_{2}} = \sqrt 3 (\gamma _{1}^{2} - \gamma _{3}^{2})p + \frac{5}{3}{{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}},\quad {{j}_{3}} = \gamma _{1}^{2}\gamma _{2}^{2} + \gamma _{1}^{2}\gamma _{3}^{2} + \gamma _{2}^{2}\gamma _{3}^{2}$
“обязанные” своим происхождением геометрическому интегралу и первым двум нетривиальным слагаемым в разложении потенциала, то сам потенциал (4.2) с точностью до постоянного слагаемого имеет вид

(5.1)
$V = \frac{{\sqrt 3 }}{2}{{\varepsilon }^{3}}{{j}_{2}} - \frac{{35}}{{72}}{{\varepsilon }^{4}}\left( {\frac{{j_{1}^{2}}}{4} + {{j}_{3}}} \right) + \; \ldots $

Уравнения равновесий принимают вид

$\frac{{\partial W}}{{\partial {{j}_{1}}}} = \lambda - \frac{{35}}{{72}}{{\varepsilon }^{4}}\frac{{{{j}_{1}}}}{2} + \; \ldots \; = 0,\quad \frac{{\partial W}}{{\partial {{j}_{2}}}} = \frac{{\sqrt 3 }}{2}{{\varepsilon }^{3}} + \; \ldots \; = 0,\quad \frac{{\partial W}}{{\partial {{j}_{3}}}} = - \frac{{35}}{{72}}{{\varepsilon }^{4}} + \; \ldots \; = 0$
где $W = V + \lambda ({{j}_{1}} - 1)$. Эти уравнения несовместны при достаточно малых значениях $\varepsilon \ne 0$. Таким образом, равновесия имеют место лишь там, где замена $({{\gamma }_{1}},{{\gamma }_{2}},{{\gamma }_{3}})$ $ \to $ $({{j}_{1}},{{j}_{2}},{{j}_{3}})$ вырождена, т.е. в тех точках, для которых якобиан
${{\mathcal{J}}_{p}} = \frac{{\partial ({{j}_{1}},{{j}_{2}},{{j}_{3}})}}{{\partial ({{\gamma }_{1}},{{\gamma }_{2}},{{\gamma }_{3}})}} \equiv \frac{{20}}{3}\mathcal{J}_{p}^{'}$
равен нулю, т.е. выполнено условие
(5.2)
$\mathcal{J}_{p}^{'} = \frac{{18\sqrt 3 }}{5}p \cdot {{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}}\left( {\frac{1}{3} - \gamma _{2}^{2}} \right) - (\gamma _{2}^{2} - \gamma _{3}^{2})(\gamma _{1}^{2} - \gamma _{3}^{2})(\gamma _{1}^{2} - \gamma _{2}^{2}) = 0$
Все решения, найденные в пункте 4.1, удовлетворяют равенству (5.2), определяющему однопараметрическую поверхность в пространстве ${{R}^{3}}(\gamma (p))$.

Список литературы

  1. Суликашвили Р.С. О стационарных движениях тетраэдра и октаэдра в центральном поле тяготения // Задачи исследования устойчивости и стабилизации движения. М.: ВЦ АН СССР. 1987. С. 57–66.

  2. Суликашвили Р.С. Стационарные движения тел, допускающих группу симметрии правильных многогранников в ньютоновском поле сил // ПММ. 1989. Т. 53. № 4. С. 582–586.

  3. Burov A.A., Sulikashvili R.S. On the motion of a rigid body possessing a finite group of symmetry // Prépublication du C.E.R.M.A. Ecole Nationale des Ponts et Chaussées. 1993. № 17. 8 p.

  4. Буров А.А., Никонова Е.А. Вращение равногранного тетраэдра в центральном ньютоновском поле сил: конус Штауде // Вестник Московского университета. Серия 1: Математика. Механика. 2021. № 5. С. 40–46.

  5. Буров А.А., Никонова Е.А. Установившиеся движения симметричного равногранного тетраэдра в центральном поле сил // Изв. РАН. МТТ. 2021. № 5. С. 152–164. https://doi.org/10.31857/S0572329921050032

  6. Никонова Е.А. О стационарных движениях равногранного тетраэдра с неподвижной точкой в центральном поле сил // ПММ. 2022. Т. 86. № 2. С. 153–168. http://doi.org/10.31857/S0032823522020096

  7. Карапетян А.В., Нараленкова И.И. О бифуркации равновесий механических систем с симметричным потенциалом // ПММ. 1998. Т. 62. № 1. С. 12–21.

  8. Нараленкова И.И. О ветвлении и устойчивости положений равновесия твердого тела в ньютоновском поле // Задачи исследования устойчивости и стабилизации движения. М.: ВЦ РАН. 1995. С. 53–60.

  9. Абрарова Е.В., Карапетян A.B. О стационарных движениях твердого тела в центральном гравитационном поле // ПММ. 1994. Т. 58. № 5. С. 68–73.

  10. Абрарова Е.В. Об устойчивости стационарных движений твердого тела в центральном поле // ПММ. 1995. Т. 59. № 6. С. 947–955.

  11. Буров А.А., Карапетян А.В. О движении крестообразных тел // Изв. РАН. МТТ. 1995. № 6. С. 14–18.

  12. Абрарова Е.В. Об относительных равновесиях твердого тела в центральном гравитационном поле // Задачи исследования устойчивости и стабилизации движения. М.: ВЦ РАН, 1995. С. 3–28.

  13. Абрарова Е.В., Карапетян A.B. О ветвлении и устойчивости стационарных движений и относительных равновесий твердого тела в центральном гравитационном поле // ПММ. 1996. Т. 60. № 3. С. 375–387.

  14. Буров А.А., Герман А.Д., Суликашвили Р.С. Об орбитальном движении тетраэдра-гиростата // ПММ. 2010. Т. 74. № 4. С. 594–609.

  15. Буров А.А., Герман А.Д., Суликашвили Р.С. Об установившихся движениях гиростатов с равными моментами инерции в центральном поле сил // ПММ. 2011. Т. 75. № 5. С. 738–744.

  16. Burov A.A., Guerman A.D., Sulikashvili R.S. Dynamics of a Tetrahedral Satellite-Gyrostat // AIP Conference Proceedings. 2010. V. 1281. P. 465–468. https://doi.org/10.1063/1.3498509

  17. Burov A.A., Guerman A.D., Nikonova E.A., Nikonov V.I. Approximation for attraction field of irregular celestial bodies using four massive points // Acta Astronautica. 2019. V. 157. P. 225–232. https://doi.org/10.1016/j.actaastro.2018.11.030

  18. Yang H., Li Sh., Sun J. A fast Chebyshev polynomial method for calculating asteroid gravitational fields using space partitioning and cosine sampling // Advances in Space Research. 2020. V. 65. № 4. P. 1105–1124. https://doi.org/10.1016/j.asr.2019.11.001

  19. Рубановский В.Н., Самсонов В.А. Устойчивость стационарных движений в примерах и задачах. М.: Наука. 1988. 304 с.

  20. Routh E.J. Treatise on the Stability of a Given State of Motion. Cambridge: Cambridge University press, 1877. 108 p.

  21. Routh E.J. The advanced part of a treatise on the dynamics of a system of rigid bodies. London: MacMillan, 1884. 343 p.

  22. Карапетян А.В. Устойчивость стационарных движений. М.: Эдиториал УРСС, 1998. 168 с.

  23. Шарыгин И.Ф. Задачи по геометрии. Стереометрия // “Библиотечка Квант”. Вып. 31. М.: Наука, 1984. 160 с.

  24. Vashkoviak M. A. On the stability of circular “asteroid” orbits in an N-planetary system // Celestial Mechanics. 1976. V. 13. № 3. P. 313–324.

  25. Burov A.A., Nikonov V.I. Stability and branching of stationary rotations in a planar problem of motion of mutually gravitating triangle and material point // Rus. J. Nonlin. Dyn. 2016. V. 12. № 2. P. 179–196. https://doi.org/10.20537/nd1602002

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал