Известия РАН. Механика твердого тела, 2022, № 5, стр. 114-119

СТЕРЖНЕВОЙ ПОДВЕС ИНЕРТНОЙ МАССЫ ДЛЯ БИНС МАЯТНИКОВОГО ТИПА

Ю. К. Жбанов^a, Е. А. Привалов^a, *

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

Поступила в редакцию 01.09.2021
После доработки 10.02.2022
Принята к публикации 13.02.2022

EDN: DBYKCO
DOI: 10.31857/S0572329922050154

Аннотация

В бесплатформенной инерциальной навигационной системе (БИНС) маятникового типа, предложенной академиком В.Ф. Журавлевым, в качестве чувствительного элемента используется инертная масса, которая помещена в центр изотропного упругого подвеса. При механической реализации упругого подвеса масса его элементов влияет на движение инертной массы. В работе рассмотрен стержневой подвес, не искажающий движения инертной массы, если основание подвеса неподвижно. Составлены уравнения движения подвеса на вращающемся основания, позволяющие анализировать влияние массы элементов подвеса на траекторию инертной массы.

Ключевые слова: датчик инерциальной информации, центральное поле сил, изотропный упругий подвес

Рассматривается вариант реализации новой схемы бесплатформенной инерциальной навигационной системы маятникового типа [1–6]. В схемах такого типа датчиком полной инерциальной информации о движущемся объекте является траектория материальной точки в центральном поле сил, которой придана форма эллипса. Наблюдение траектории точки в системе координат, связанной с объектом, позволяет определить ускорение поступательного перемещения объекта и его ориентацию.

Реализовать подвес инертной массы в центральном поле сил можно механическим стержневым подвесом, обеспечивающим линейную зависимость силы от смещения инертной массы. Один из возможных вариантов такого подвеса исследован в [7].

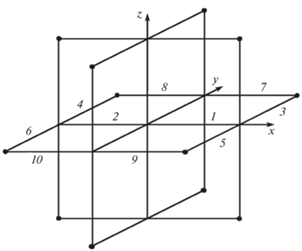
В данной работе исследуется динамика подвеса, состоящего из 30 цилиндрических стержней (рис. 1) с одинаковыми геометрическими и упруго-массовыми характеристиками.

Рис. 1.

Стержневой подвес.

Шесть центральных стержней соединены в центре $O$ подвеса и в недеформированном состоянии направлены по осям декартовой системы координат $Oxyz$, единичные векторы координатных осей которой обозначим ${{{\mathbf{e}}}_{1}}$, ${{{\mathbf{e}}}_{2}}$, ${{{\mathbf{e}}}_{3}}$. Остальные 24 боковых стержня в недеформированном состоянии образуют три одинаковых квадрата с общим центром в точке $O$ и лежат в ортогональных плоскостях системы координат $Oxyz$. В вершинах квадратов стержни скреплены с основанием подвеса.

Положение точки, принадлежащей k-му стержню, задается как функция ${{{\mathbf{r}}}_{k}}(s)$ параметра $0 \leqslant s \leqslant 1$, определяющего расстояние от начала стержня до точки. Отсчет параметра s для 6 центральных стержней ведется от центра подвеса, для остальных 24 стержней – от точек их крепления к концам центральных стержней. В табл. 1 записаны векторы ${{{\mathbf{r}}}_{{0k}}}(s)$ (k = 1–10), задающие положение точек стержней недеформированного подвеса, лежащих в плоскости $Oxy$.

Таблица 1.

Векторы ${{{\mathbf{r}}}_{{0k}}}(s)$ ($k$ = 1–10), задающие положение точек стержней недеформированного подвеса, лежащих в плоскости $Oxy$

k	${{{\mathbf{r}}}_{{0k}}}(s)$	k	${{{\mathbf{r}}}_{{0k}}}(s)$
1	$s{{{\mathbf{e}}}_{1}}$	2	$ - s{{{\mathbf{e}}}_{1}}$
3	${{{\mathbf{e}}}_{1}} + s{{{\mathbf{e}}}_{2}}$	4	$ - {{{\mathbf{e}}}_{1}} + s{{{\mathbf{e}}}_{2}}$
5	${{{\mathbf{e}}}_{1}} - s{{{\mathbf{e}}}_{2}}$	6	$ - {{{\mathbf{e}}}_{1}} - s{{{\mathbf{e}}}_{2}}$
7	${{{\mathbf{e}}}_{2}} + s{{{\mathbf{e}}}_{1}}$	8	${{{\mathbf{e}}}_{2}} - s{{{\mathbf{e}}}_{1}}$
9	$ - {{{\mathbf{e}}}_{2}} + s{{{\mathbf{e}}}_{1}}$	10	$ - {{{\mathbf{e}}}_{2}} - s{{{\mathbf{e}}}_{1}}$

Векторы ${{{\mathbf{r}}}_{{0k}}}(s)$, имеющие номера $k$ = 11–20, и векторы с номерами $k$ = 21–30 получаются циклическими перестановками векторов ${{{\mathbf{e}}}_{1}}$, ${{{\mathbf{e}}}_{2}}$, ${{{\mathbf{e}}}_{3}}$ в формулах табл. 1.

Деформации стержней при малых смещениях центра подвеса определяются методами теории сопротивления материалов [8, 9]. Используются записанные в безразмерных параметрах выражения [7] для малого угла поворота касательной к консольно-закрепленному стержню при его изгибе

(1)

$d{\text{'}} = m\xi + \left( {\xi - \frac{{{{\xi }^{2}}}}{2}} \right)f$

и для смещения точки стержня от ее положения при недеформированном состоянии стержня

(2)

$d = m\frac{{{{\xi }^{2}}}}{2} + \left( {\frac{{{{\xi }^{2}}}}{2} - \frac{{{{\xi }^{3}}}}{6}} \right)f$

Здесь $\xi $ – координата точки недеформированного стержня, отсчитываемая от точки его закрепления, $d$ – величина смещения точки, по нормали продольной оси стержня, f и $m$ – величины силы и момента силы, приложенных к свободному концу стержня. Штрихом обозначена производная $d$ по $\xi $.

На рис. 2 изображены стержни подвеса, лежащие в недеформированном состоянии в плоскости $Oxy$, при смещении центра подвеса по оси $Ox$. Смещение центра подвеса вдоль оси центрального стержня приводит к его поступательному перемещению и изгибу скрепленных с ним боковых стержней. Смещение центра подвеса по нормали к центральному стержню вызывает изгиб этого стержня и поворот касательной к нему в точке его соединения с боковыми стержнями.

Рис. 2.

Стержни подвеса, лежащие в плоскости $Oxy$ в недеформированном состоянии и деформированном состоянии при смещении центра подвеса по оси $Ox$.

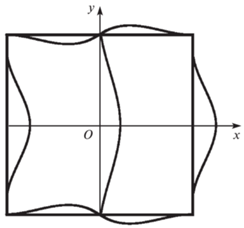
Определим форму, которую принимает боковой стержень при смещении скрепленного с ним центрального стержня вдоль своей оси. Рассмотрим деформацию консольно-закрепленного стержня под действием силы и момента силы, приложенных в его конечной точке, при условии, что касательная к стержню в этой точке не поворачивается $d{\text{'}}(1) = 0$. Из этого равенства следует

(3)

$m = - \frac{1}{2}f$

При этом смещение точки консольно-закрепленного стержня записывается в виде $d(\xi ) = d(1)(3{{\xi }^{2}} - 2{{\xi }^{3}})$. Подставив формулу (3) в (2), получим равенство $f = {{f}_{a}}{\kern 1pt} d(1)$, где ${{f}_{a}} = 12$. В результате замены переменной $\xi = 1 - s$ выражение для смещения точки бокового стержня подвеса приведем к виду $d(s) = d(0)a(s)$, где $d(0)$ – смещение центра подвеса, $a(s) = 1 - 3{{s}^{2}} + 2{{s}^{3}}$.

При определении деформации бокового стержня, вызванной изгибом центрального стержня, отметим, что точка, в которой стержни скреплены, не смещается. При условии $d(1) = 0$ из выражения (2) для смещения точки консольно-закрепленного стержня следует $f = - \frac{3}{2}m$. В результате подстановки этого равенства в (1) получим отношение

(4)

$m = 4d{\text{'}}(1)$

Смещение точки бокового стержня определяется функцией $d(\xi ) = - {{\xi }^{2}}(1 - \xi )d{\text{'}}{\kern 1pt} {\kern 1pt} (1)$.

При изгибе центрального стержня касательная к этому стержню в точке его крепления к боковым стержням и касательная к двум скрепленным с ним боковым стержням, лежащим в плоскости изгиба центрального стержня, поворачиваются на один и тот же угол. При этом два других стержня, крепящиеся к центральному стержню в этой точке, скручиваются на такой же угол.

Форму изгиба центрального стержня определим, считая его консольно-закрепленным в сместившемся на величину $d(0)$ ортогонально оси стержня в центре подвеса. Момент силы, приложенный в конечной точке стержня, пропорционален углу поворота касательной к стержню в этой точке $m = - \mu d{\text{'}}(1)$. При подстановке этого условия в выражения (1) и (2) получим равенства

$d{\text{'}}(1) = \frac{1}{{2(1 + \mu )}}f,\quad d = \left( {\frac{{{{\xi }^{2}}}}{4}\frac{{2 + \mu }}{{1 + \mu }} - \frac{{{{\xi }^{3}}}}{6}} \right)f$

Учитывая отношение (4), применимое к двум изогнутым боковым стержням, и то, что жесткость цилиндрического стержня на кручение в два раза больше жесткости на изгиб, получим μ = 12. Выражение для смещения точки центрального стержня принимает вид $d(\xi ) = d(0)\left( {\frac{{21}}{8}{{\xi }^{2}} - \frac{{13}}{8}{{\xi }^{3}}} \right)$. Из полученных отношений следует

(5)

$d{\text{'}}(1) = \frac{3}{8}d(0)$

Используя переменную $s = \xi $, форму изгиба центрального стержня подвеса запишем в виде $d(s) = d(0)b(s)$, где $b(s) = 1 - \frac{{21}}{8}{{s}^{2}} + \frac{{13}}{8}{{s}^{3}}$.

Сила, приложенная в конечной точке центрального стержня, связана со смещением центра подвеса отношением $f = {{f}_{b}}d(0)$, где ${{f}_{b}} = \frac{{39}}{4}$.

С учетом равенства (5) в результате замены переменной $\xi = 1 - s$ функция, определяющая форму бокового стержня, примет вид $d(s) = c(s)d(0)$, где $c(s) = - \frac{3}{8}s{{(1 - s)}^{2}}$.

При произвольном смещении центра подвеса форма каждого стержня представляет линейную комбинацию функций $a(s)$, $b(s)$, $c(s)$ с коэффициентами, зависящими от проекций смещения центра подвеса на оси системы координат $Oxyz$. В табл. 2 приведены формулы для векторов ${{{\mathbf{r}}}_{k}}$ (k = 1–10), которые определяют положения точек стержней, лежащих в недеформированном состоянии подвеса в плоскости $Oxy$, при смещении центра подвеса в точку ${\mathbf{R}} = x{{{\mathbf{e}}}_{1}} + y{{{\mathbf{e}}}_{2}} + z{{{\mathbf{e}}}_{3}}$.

Таблица 2.

Формулы для векторов ${{{\mathbf{r}}}_{k}}$ (k = 1–10), которые определяют положения точек стержней, лежащих в недеформированном состоянии подвеса в плоскости $\,Oxy$, при смещении центра подвеса в точку ${\mathbf{R}} = x{{{\mathbf{e}}}_{1}} + y{{{\mathbf{e}}}_{2}} + z{{{\mathbf{e}}}_{3}}$

k	${{{\mathbf{r}}}_{k}}(s)$	k	${{{\mathbf{r}}}_{k}}(s)$
1	$s{{{\mathbf{e}}}_{1}} + x{{{\mathbf{e}}}_{1}} + by{{{\mathbf{e}}}_{2}} + bz{{{\mathbf{e}}}_{3}}$	2	$ - s{{{\mathbf{e}}}_{1}} + x{{{\mathbf{e}}}_{1}} + by{{{\mathbf{e}}}_{2}} + bz{{{\mathbf{e}}}_{3}}$
3	${{{\mathbf{e}}}_{1}} + s{{{\mathbf{e}}}_{2}} + ax{{{\mathbf{e}}}_{1}} + cy{{{\mathbf{e}}}_{1}}$	4	$ - {{{\mathbf{e}}}_{1}} + s{{{\mathbf{e}}}_{2}} + ax{{{\mathbf{e}}}_{1}} - cy{{{\mathbf{e}}}_{1}}$
5	${{{\mathbf{e}}}_{1}} - s{{{\mathbf{e}}}_{2}} + ax{{{\mathbf{e}}}_{1}} - cy{{{\mathbf{e}}}_{1}}$	6	$ - {{{\mathbf{e}}}_{1}} - s{{{\mathbf{e}}}_{2}} + ax{{{\mathbf{e}}}_{1}} + cy{{{\mathbf{e}}}_{1}}$
7	${{{\mathbf{e}}}_{2}} + s{{{\mathbf{e}}}_{1}} + cx{{{\mathbf{e}}}_{2}} + ay{{{\mathbf{e}}}_{2}}$	8	${{{\mathbf{e}}}_{2}} - s{{{\mathbf{e}}}_{1}} - cx{{{\mathbf{e}}}_{2}} + ay{{{\mathbf{e}}}_{2}}$
9	$ - {{{\mathbf{e}}}_{2}} - s{{{\mathbf{e}}}_{1}} - cx{{{\mathbf{e}}}_{2}} + ay{{{\mathbf{e}}}_{2}}$	10	$ - {{{\mathbf{e}}}_{2}} - s{{{\mathbf{e}}}_{1}} + cx{{{\mathbf{e}}}_{2}} + ay{{{\mathbf{e}}}_{2}}$

Положение точек стержней с номерами $k$ = 11–20 и с номерами $k$ = 21–30 определяется формулами, получающимися в результате циклических перестановок переменных x, y, $z$ и векторов ${{{\mathbf{e}}}_{1}}$, ${{{\mathbf{e}}}_{2}}$, ${{{\mathbf{e}}}_{3}}$ в формулах табл. 2.

Уравнение движения подвеса запишем в форме Лагранжа. Жесткости подвеса по осям $Ox$, $Oy$, $Oz$ имеют одни и те же значения. Выражение для потенциальной энергии упругих деформаций элементов подвеса при смещении центра подвеса в точку R имеет вид

$U = \frac{1}{2}{{\mu }_{0}}{{{\mathbf{R}}}^{2}}$

Здесь ${{\mu }_{0}} = 8{{f}_{a}} + 4{{f}_{b}} = 135$ – приведенная жесткость стержневого подвеса.

Скорость точки подвеса, расположенного на объекте, который совершает поворот относительно инерциальной системы координат, определяется формулой

${\mathbf{V}} = {\mathbf{\dot {r}}} + {\mathbf{\omega }} \cdot {\mathbf{r}}$

где ${\mathbf{\omega }}\,$ – угловая скорость объекта, вектор r задается формулами табл. 2 и формулами, полученными в результате циклических перестановок в табл. 2.

Выражение для квадрата скорости точки представим в виде

(6)

${{{\mathbf{V}}}^{2}} = {{{\mathbf{\dot {r}}}}^{2}}{\mathbf{ + }}2{\mathbf{\omega }} \cdot ({\mathbf{r}} \cdot {\mathbf{\dot {r}}}) + {{{\mathbf{\omega }}}^{2}}{{{\mathbf{r}}}^{2}} - {{({\mathbf{\omega }} \cdot {\mathbf{r}})}^{2}}$

Для подсчета кинетической энергии $T$ стержневого подвеса выражение для квадрата скорости точки стержня следует проинтегрировать по $s$ от 0 до 1 для каждого стержня, принимая линейную плотность стержня за единичную, т.е. считая дифференциал массы стержня $dm = ds$, а затем результаты интегрирования просуммировать по всем стержням. При выполнении расчетов удобнее сначала просуммировать квадраты скоростей точек с одинаковым значением $s$ и затем проинтегрировать полученные выражения по $s$.

Расчет сумм слагаемых, входящих в формулу (6), для точек стержней подвеса с использованием выражений табл. 2 дает результаты:

$\sum {{\mathbf{\dot {r}}}_{k}^{2}} = (2 + 8{{a}^{2}} + 4{{b}^{2}} + 8{{c}^{2}}){{{\mathbf{\dot {R}}}}^{2}}$

$\sum\limits_{} {{\mathbf{r}}_{k}^{2}} = (2 + 8{{a}^{2}} + 4{{b}^{2}} + 8{{c}^{2}}){{{\mathbf{R}}}^{2}}$

$\sum\limits_{} {({{{\mathbf{r}}}_{k}} \times {{{{\mathbf{\dot {r}}}}}_{k}})} = (4b + 2{{b}^{2}}){\mathbf{R}} \cdot {\mathbf{\dot {R}}}$

$\begin{gathered} \sum\limits_{} {{{{({\mathbf{\omega }} \cdot {{{\mathbf{r}}}_{k}})}}^{2}}} = 4{{c}^{2}}{{{\mathbf{R}}}^{2}}{{{\mathbf{\omega }}}^{2}} + (4b + 2{{b}^{2}}){{({\mathbf{R}} \cdot {\mathbf{\omega }})}^{2}} + \\ + \;(2 + 8{{a}^{2}} + 2{{b}^{2}} - 4b - 4{{c}^{2}})[{{(x{{\omega }_{1}})}^{2}} + {{(y{{\omega }_{2}})}^{2}} + {{(z{{\omega }_{3}})}^{2}}] \\ \end{gathered} $

Здесь ${{\omega }_{1}}$, ${{\omega }_{2}}$, ${{\omega }_{3}}$ – проекции угловой скорости на оси системы координат $Oxyz$.

Сумма квадратов скоростей точек стержней подвеса записывается в виде:

(7)

$\begin{gathered} \sum {{\mathbf{V}}_{k}^{2} = (2 + 8{{a}^{2}} + 4{{b}^{2}} + 8{{c}^{2}})} {{{{\mathbf{\dot {R}}}}}^{2}} + (4b + 2{{b}^{2}})2{\mathbf{\omega }} \cdot {\mathbf{(R}} \cdot {\mathbf{\dot {R}}}) + \\ + \;(2 + 8{{a}^{2}} + 4{{b}^{2}} + 4{{c}^{2}}){{{\mathbf{\omega }}}^{{\mathbf{2}}}}{{{{\mathbf{\dot {R}}}}}^{{\mathbf{2}}}} - (4b + 2{{b}^{2}}){{({\mathbf{R}} \cdot {\mathbf{\omega }})}^{2}} + \\ - \;(2 + 8{{a}^{2}} + 2{{b}^{2}} - 4b - 4{{c}^{2}})[{{(x{{\omega }_{1}})}^{2}} + {{(y{{\omega }_{2}})}^{2}} + {{(z{{\omega }_{3}})}^{2}}] \\ \end{gathered} $

В результате интегрирования выражения (7) по $s$ от 0 до 1 получим:

$\begin{gathered} \int {\sum {{\mathbf{V}}_{k}^{2}} } = 6.563{{{{\mathbf{\dot {R}}}}}^{2}}{\mathbf{ + }}2.917 \cdot 2{\mathbf{\omega }} \cdot ({\mathbf{R}} \cdot {\mathbf{\dot {R}}}) + 6.557{{{\mathbf{\omega }}}^{2}} \cdot {{{\mathbf{R}}}^{2}} - 2.917{{({\mathbf{R}} \cdot {\mathbf{\omega }})}^{2}} - \\ - \;3.636({{x}^{2}}\omega _{1}^{2} + {{y}^{2}}\omega _{2}^{2} + {{z}^{2}}\omega _{3}^{2}) \\ \end{gathered} $

Запишем выражение для кинетической энергии стержней подвеса, выделив фрагмент, соответствующий кинетической энергии материальной точки, находящейся в центре подвеса

$\begin{gathered} T = \frac{1}{2}\int {\sum {{{{\mathbf{V}}}^{2}}} } = \frac{1}{2} \cdot 6.563[{{{{\mathbf{\dot {R}}}}}^{2}}{\mathbf{ + }}2{\mathbf{\omega }} \cdot ({\mathbf{R}} \cdot {\mathbf{\dot {R}}}) + {{{\mathbf{\omega }}}^{2}} \cdot {{{\mathbf{R}}}^{2}} - {{({\mathbf{R}} \cdot {\mathbf{\omega }})}^{2}}] - \\ - \;\frac{1}{2} \cdot 3.646 \cdot 2{\mathbf{\omega }} \cdot ({\mathbf{R}} \cdot {\mathbf{\dot {R}}}) + \frac{1}{2} \cdot 3.646{{({\mathbf{R}} \cdot {\mathbf{\omega }})}^{2}} - \\ - \;\frac{1}{2} \cdot 0.006{{{\mathbf{\omega }}}^{2}} \cdot {{{\mathbf{R}}}^{2}} - \frac{1}{2} \cdot 3.636[{{(x{{\omega }_{1}})}^{2}} + {{(y{{\omega }_{2}})}^{2}} + {{(z\omega _{3}^{{}})}^{2}}] \\ \end{gathered} $

Учет инертности элементов подвеса приводит к появлению коэффициента перед скобкой, определяющей кинетическую энергию инертной массы в центре подвеса, а также к появлению дополнительных слагаемых в выражении для энергии.

Уравнения Лагранжа, описывающие движение стержневого подвеса, имеют вид

$\begin{gathered} 6.563[{\mathbf{\ddot {R} + }}2{\mathbf{\omega }} \cdot {\mathbf{\dot {R}}} + {\mathbf{\dot {\omega }}} \cdot {\mathbf{R}} - {{{\mathbf{\omega }}}^{2}}{\mathbf{R}} + ({\mathbf{R}} \cdot {\mathbf{\omega }}){\mathbf{\omega }}] + 135{\mathbf{R}} = \\ = \;3.646[2{\mathbf{\omega }} \cdot {\mathbf{\dot {R}}} + {\mathbf{\dot {\omega }}} \cdot {\mathbf{R}} + ({\mathbf{R}} \cdot {\mathbf{\omega }}){\mathbf{\omega }}] - 0.006{{{\mathbf{\omega }}}^{2}}{\mathbf{R}} - 3.636{\text{||}}x\omega _{1}^{2},y\omega _{2}^{2},z\omega _{3}^{2}{\text{|}}{{{\text{|}}}^{{\text{т}}}} \\ \end{gathered} $

Слагаемые в правой части уравнения следует рассматривать как возмущающие силы. Динамика инертной массы, помещенной в механический изотропный упругий подвес, совпадает с динамикой материальной точки в центральном поле сил при условии компенсации этих сил.

Работа выполнена по госзаданию № АААА-А17-117021310382-5.

Список литературы

Журавлёв В.Ф. Бесплатформенная инерциальная система минимальной размерности (Пространственный осциллятор – датчик полной инерциальной информации) // Изв. РАН. МТТ. 2005. № 5. С. 5–10.
Журавлёв В.Ф. Бесплатформенная инерциальная навигационная система маятникового типа (БИНС МТ) // Изв. РАН. МТТ. 2014. № 1. С. 6–17.
Журавлёв В.Ф., Климов Д.М., Плотников П.К. К вопросу использования компьютерной механики в теории инерциальных навигационных систем // Изв. РАН. МТТ. 2019. № 2. С. 48–62. https://doi.org/10.1134/S0572329919020132
Журавлёв В.Ф. Пространственный осциллятор Ван-дер-Поля. Технические приложения // Изв. РАН. МТТ. 2020. № 1. С. 158–164. https://doi.org/10.31857/S0572329920010249
Бранец В.Н. Об изоморфизме математических описаний операции вращения // Изв. РАН. МТТ. 2018. № 2. С. 136–143.
Челноков Ю.Н. Уравнения и алгоритмы для нахождения инерциальной ориентации и кажущейся скорости движущегося объекта в кватернионных и бикватернионных четырехмерных ортогональных операторах // Изв. РАН. МТТ. 2016. № 2. С. 17–25.
Жбанов Ю.К., Привалов Е.А. Стержневая конструкция изотропного упругого подвеса инертной массы // Изв. РАН. МТТ. 2018. № 5. С. 19–28. https://doi.org/10.31857/S057232990002463-9
Феодосьев В.И. Сопротивление материалов. М.: МГТУ им. Н.Э. Баумана, 2007. 544 с.
Журавлёв В.Ф., Климов Д.М. Прикладные методы в теории колебаний. М.: Наука, 1988, 328 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал