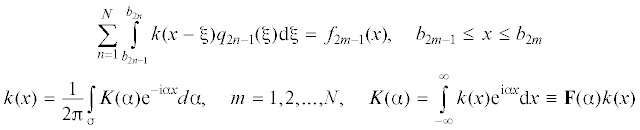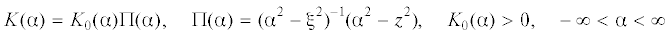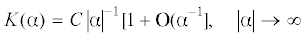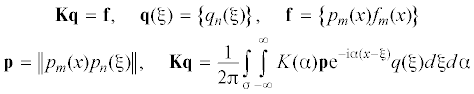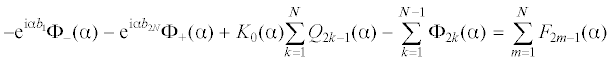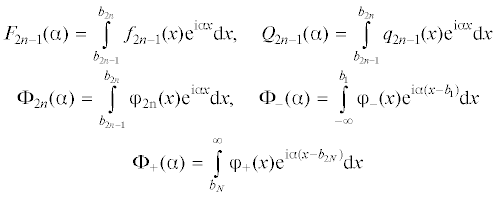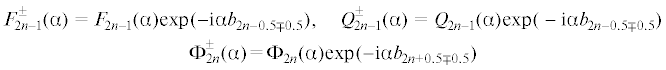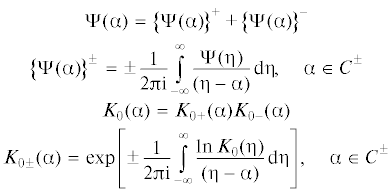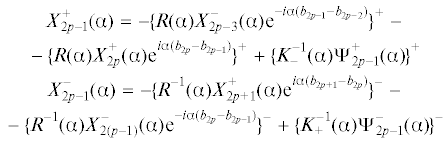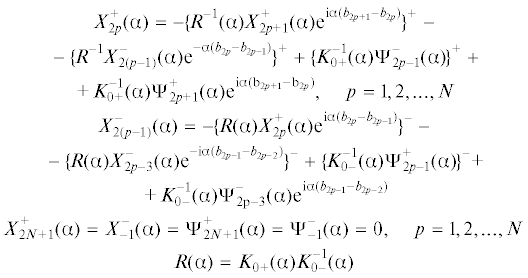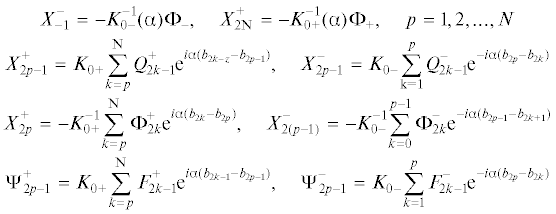Известия РАН. Механика твердого тела, 2022, № 6, стр. 72-78
ОБ ОДНОЙ МЕХАНИЧЕСКОЙ МОДЕЛИ САМООРГАНИЗАЦИИ НАНОЧАСТИЦ
В. А. Бабешко a, b, *, О. В. Евдокимова a, О. М. Бабешко b, В. С. Евдокимов a
a Южный научный центр РАН
Ростов-на-Дону, Россия
b Кубанский государственный университет
Краснодар, Россия
* E-mail: babeshko41@mail.ru
Поступила в редакцию 30.03.2022
После доработки 03.04.2022
Принята к публикации 04.04.2022
- EDN: DSLWVZ
- DOI: 10.31857/S0572329922060034
Аннотация
Опираясь на свойства блочных элементов, имитирующих наночастицы, контактирующие с многослойным основанием, строится модель самоорганизации таких объектов. Предполагается, что наночастицы контактируют без трения с находящимся в состоянии вибрации деформируемым основанием. Для построения модели в статье впервые построены аналитические соотношения, позволяющие получать параметры возникновения высокочастотного резонанса для такой механической структуры, или, что тоже самое, ловушечных мод. Благодаря этим соотношениям, на основе свойств поведения механических объектов, расположенных на поверхности деформируемого основания в условиях вибрации, строится модель их самоорганизации. Самоорганизация состоит в стремлении, при определенных механических и геометрических параметрах механической системы, к объединению поверхностных объектов. Построенная модель допускает ее перенос на наночастицы из многокомпонентных материалов.
Введение. В основе исследования лежит явление высокочастотного резонанса, свойственного слоистым структурам при наличии плоских неоднородностей, параллельных границе [1, 2]. Возможность создания такой модели продиктована полученными новыми результатами по использования в роли наночастиц математических объектов – упакованных блочных элементов. Их применение позволяет описывать в качестве наночастиц элементы из материалов различных многокомпонентных сред. Исследования с привлечением многокомпонентных материалов для моделей наночастиц важны, поскольку до конца не ясны физико-механические свойства наночастиц. Модель строится при предположениях, что деформируемое основание колеблется с частотой, при которой в среде образуется волна, уходящая от поверхностного объекта на бесконечность. Механические объекты представляют жесткие или деформируемые штампы, описываемые упакованными блочными элементами, которые без трения контактируют с основанием. Также предполагается, что самоорганизация начинается с момента, когда совокупность поверхностных объектов достигнет состояния, при котором в зоне расположения поверхностных объектов возникнет стоячая волна. В этом состоянии излучение волн на бесконечность прекратится. Система будет обладать минимальной энергией, а поверхностные объекты будут стремиться к гребню стоячей волны, при наличии внешних гармонических воздействий.
С учетом известных и достаточно детально описанных в литературе свойств наночастиц, таких как самоорганизация и самосборка, приняв во внимание возможности современной математики и механики, представлены исследования по моделированию этих явлений. В качестве моделей наночастиц принимаются математические объекты – упакованные блочные элементы граничных задач для уравнений механики и физики.
Исследование проводится на основе использования новейшего математического аппарата-метода блочного элемента [3]. Наночастицы рассматриваются как многокомпонентные физико-механические объекты, наделенные богатым набором механических и физических свойств, объединяемых между собой некоторым взаимным притяжением, в частности, вызванным высокочастотным резонансом. Построенную модель, представленную в данной статье, следует рассматривать как первое приближение при математическом описании таких наночастиц. В дальнейшем, математическое описание наночастиц может допускать различные усложнения.
В настоящее время исследования в области наноматериалов и нанотехнологии отличаются огромным разнообразием, охватывающим, как частные задачи, так и общие проблемы. Так, в работах [4–7] охватывается большой комплекс вопросов, связанных со свойствами наночастиц, производство и технологии наноматериалов, огромный объем экспериментальных данных. В том числе обсуждаются вопросы самоорганизации и самосборки наноматериалов. В [8] изучаются вопросы колебаниях однослойных углеродных нанотрубок. В [9–11] выполняется моделирование молекулярной динамики по сравнению резонансных частот перестраиваемых резонаторов из углеродных нанотрубок, с учетом нелинейной динамики резонаторов. В [12, 13] исследуется молекулярно-динамическое моделирование одностенного резонатора из углеродных нанотрубок, с учетом конечности наночастиц. В [14, 15] изучается вопрос производства электричества путем перемещения капли ионной жидкости вдоль графена и исследуется волновой его потенциал. В [16–18] обсуждается изготовление субнанометровых полупроводниковых нанолент из молибдена сверху вниз листы дисульфида, а также наномеханического датчика массы. В [19–21] исследуется средствами механики сплошной среды дефекты решетки в углеродных нанотрубках, дислокации, а также вопросы контакта с основаниями. В [22–24] исследуются вопросы влияния поверхностных нанослоев на усталостную долговечность материалов. Можно видеть огромное многообразие исследований, однако ни одно из них не связано исследованиями, выдвинутому в настоящей статье.
1. Постановка задачи. Рассматривается плоская задача теории упругости для многослойной среды, на поверхности которой находится $N$ объектов, контактирующих без трения с основанием. Объекты рассматриваются в двух вариантах: абсолютно твердые штампы и деформируемые объекты, представляющие упакованные блочные элементы, описываемые уравнением Гельмгольца. Предполагается, что в дальнейшем, учет многокомпонентных материалов будет рассматриваться с использованием нового универсального метода моделирования [25]. Он представляет решения векторных граничных задач для многокомпонентных сред посредством разложения по скалярным, используемым в настоящей работе. Предполагается, что система находится в условиях установившейся вибрации в результате гармонического вертикального воздействия на объекты зависящей от времени функцией e–iωt. Считаем, что объекты, находящиеся на поверхности, имеют носители [b2n– 1, b2n], n = 1, 2, …, N, а контактные напряжения описываются функциями q2n– 1(ξ). Расстояния между носителями имеют не нулевые отрезки [b2n, b2n+ 1].
Следуя [26] запишем систему интегральных уравнений в виде
Здесь f2m– 1 – заданные перемещения подошвы объекта в зоне контакта; K(u) – преобразование Фурье ядра системы интегральных уравнений, 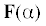 – оператор преобразования Фурье. Будем считать, что многослойная среда описывается
изотропной линейной упругостью, а в результате вибрации механической системы с частотой
${{\omega }}$ четную мероморфную функцию
– оператор преобразования Фурье. Будем считать, что многослойная среда описывается
изотропной линейной упругостью, а в результате вибрации механической системы с частотой
${{\omega }}$ четную мероморфную функцию 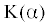 можно представить в виде [1, 2]
можно представить в виде [1, 2]
Здесь параметры ±ξ, ±z – вещественные полюсы и нули мероморфной функции K(α). Таким образом, функция K0(α) имеет только комплексные нули и полюсы. Считаем, что имеет место свойственное контактным задачам для слоистой среды асимптотическое поведение вида [26]
Контур σ обходит полюсы ${{ \pm \xi }}$ в соответствии с требованием принципа излучения волн на бесконечность [26].
Запишем систему уравнений в операторном виде в форме
Здесь pm(x), pn(ζ) проекторы на отрезки ${\text{[}}{{b}_{{{\text{2}}m - {\text{1}}}}}{\text{,}}{{b}_{{{\text{2}}m}}}{\text{],}}$ ${\text{[}}{{b}_{{{\text{2}}n - {\text{1}}}}}{\text{,}}{{b}_{{{\text{2}}n}}}{\text{],}}$ n = 1, 2, …, N.
Аналогично введем систему интегральных уравнений, в которой K(α) заменено на K0(α) вида
Для интегральных уравнений (1.2) справедлива теорема единственности и разрешимости в пространствах суммируемых функций для любых дважды непрерывно дифференцируемых правых частей [27 ] . Используя результаты работ [1, 2], представим соотношение для определения параметров высокочастотного резонанса. Справедлива для уравнения (1.1).
Теорема. Процесс, описываемый интегральным уравнением (1.1) будет являться высокочастотным резонансом тогда и только тогда, когда параметры задачи, найденные из соотношений
(1.3)
${\mathbf{F}}{\text{(}}\alpha {\text{)}}{{p}_{n}}(x){\mathbf{K}}_{{\text{0}}}^{{ - {\text{1}}}}{\mathbf{f}} = 0,\quad \alpha = \pm z,\quad n = 1,2,...,N$Здесь под физически оправданными параметрами понимаются вещественные значения, если исходные параметры были вещественными, например, параметры ${{b}_{n}}$. Они определяют носители частиц и расстояния между ними. Из соотношений (1.3) легко видеть, что они представляют целые функции, которые должны обращаться в ноль в двух точка a = ±z, а в случае четной задачи – в одной. Очевидно, чем больше частиц, тем больше возникает вариантов для организации высокочастотного резонанса для всей совокупности частиц. В случае высокочастотного резонанса в зоне, охватывающей все частицы, формируется стоячая волна резонанса. При наличии внешнего гармонического воздействия, частицы будут стремиться достичь гребня стоячей волны, демонстрируя самоорганизацию. Множество решений с физически оправданными параметрами не пусто. Действительно, в случае одного объекта, N = 1, решение приведено в [1, 2], а также в цитированиях в этих работах. При этом, рассматривался абсолютно твердый штамп с плоским основанием, то есть в правой части уравнений (1.1) принималась функция f(x) равная постоянной. Поэтому физическими параметрами высокочастотного резонанса оказались параметры носителя штампа. В случае совокупности объектов количество свободных параметров возрастает, наряду с параметрами носителей добавляются параметры расстояния между объектами. Другой вариант задачи состоит в том, что вместо абсолютно твердых штампов рассматриваются более приближенные к моделям наночастиц объекты, моделируемые упакованными блочными элементами. При составлении интегральных уравнений вида (1.1), в этом случае вместо постоянных функций fn(x) справа будут переменные по координате x функции. В этом случае количество степеней свободы в уравнении (1.3) еще больше возрастает, поскольку принимают участие параметры переменных функций fn(x).
Приняв в качестве упакованных блочных элементов решения, порождаемые граничной задачей для уравнений Гельмгольца, затем будем иметь возможность перенести эти результаты на наночастицы из многокомпонентных материалов [25].
Для применения теоремы остается открытой проблема построения обратного оператора ${\mathbf{K}}_{{\text{0}}}^{{ - {\text{1}}}}$. Ниже приводится метод, основанный на факторизационном подходе, позволяющий получать ${\mathbf{K}}_{{\text{0}}}^{{ - {\text{1}}}}$, а для достаточно протяженных носителей объектов – строить точные решения.
2. Факторизационный подход. Он заимствован из метода Винера–Хопфа [26]. Система интегральных уравнений (1.2), записанная в форме (1.1) продолжается на всю ось, введением новых неизвестных функций ${{{{\varphi }}}_{ - }}{\text{(}}x{\text{),}}\,x < {{b}_{{\text{1}}}};{{{{\varphi }}}_{ + }}{\text{(}}x{\text{),}}\,x > {{b}_{{{\text{2}}N}}}$, а также в промежутках φ2k(x), ${{b}_{{{\text{2}}k}}} < x < {{b}_{{{\text{2}}k{\text{ + 1}}}}}$. Применим к продолженному на всю ось интегральному уравнению (1.2) преобразование Фурье. В результате получим соотношение вида
Здесь введены обозначения
Введем обозначения
Для исследования и решения функционального уравнения (2.1), следуя [26], введем обозначения системы операторов факторизации вида
Здесь C+ и C– обозначают верхнюю и нижнюю комплексные полуплоскости соответственно. Функции ${{\left\{ {\Psi (\alpha )} \right\}}^{ \pm }}$, и 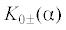 регулярны в областях C± и, кроме того, последние не имеют там нулей. Условия, налагаемые на функции для выполнения
факторизаций, оговорены в [26] и в данном случае выполняются. Применяя метод факторизации в варианте работ [26], интегральное уравнение сводим к решению системы одномерных интегральных уравнений
с вполне непрерывным оператором в пространстве непрерывных с весом функций на всей
оси
регулярны в областях C± и, кроме того, последние не имеют там нулей. Условия, налагаемые на функции для выполнения
факторизаций, оговорены в [26] и в данном случае выполняются. Применяя метод факторизации в варианте работ [26], интегральное уравнение сводим к решению системы одномерных интегральных уравнений
с вполне непрерывным оператором в пространстве непрерывных с весом функций на всей
оси
Здесь приняты обозначения
Особенностью системы интегральных уравнений (2.2) для случая, когда мероморфная функция K0(α) не имеет вещественных нулей и полюсов, являются следующие ее свойства. Система (2.2) является замкнутой, то есть число неизвестных совпадает с числом уравнений. Другой особенностью является непрерывность операторов в правой части системы уравнений в пространстве непрерывных на вещественной оси с некоторым весом функций. Норма оператора правой части системы интегральных уравнений стремится к нулю при ${{b}_{{{\text{2}}p{\text{ + 1}}}}} - {{b}_{{{\text{2}}p}}} \to \infty ,{{b}_{{{\text{2}}p}}} - {{b}_{{{\text{2}}p - {\text{1}}}}} \to \infty ,p = 1,2,...,N$. Таким образом, при достаточно больших значениях этих параметров, систему можно решать методом последовательных приближений. Построив решения интегральных уравнений (2.2), по формулам (2.3) последовательно можно найти все неизвестные и затем составить соотношения (1.3). Эти соотношения дают возможность найти условия возникновения высокочастотного резонанса, который даст возможность самоорганизоваться наночастицам.
Построив решение системы интегральных уравнений (1.2), можно оставить носители ${{b}_{{{\text{2}}p{\text{ + 1}}}}} - {{b}_{{2p}}}$ объектов неизменными и вычислить на избранной частоте ${{\omega }}$ по формуле (1.3) только параметры расстояний между объектами ${{b}_{{{\text{2}}p}}} - {{b}_{{{\text{2}}p - {\text{1}}}}}$. Внеся эти входные параметры в левую часть соотношения (1.1) и вычислив его значение на вещественной оси, получим в зоне, содержащей все объекты стоячую волну, колеблющуюся с частотой $\omega $, вовлекая на свой гребень имеющие массу поверхностные объекты.
Вывод. Свойство самоорганизации присуще наночастицам материалов самых разных физико-химических свойств. Поэтому имеется гипотеза, что в основе этого процесса находится явление, независимое от физико-химических свойств и присущее всем им. К числу такого явления, естественно, отнести обычное механическое поведение этих объектов, которое также богато различными особенностями. К ним относится явление высокочастотного резонанса в средах с неоднородностями, в рамках которого доступно данное в настоящей статье объяснение самоорганизации. В том случае, если на самоорганизацию влияют какие-нибудь физико-химические свойства, то это можно будет выявить, применяя новый универсальный метод моделирования [25], позволяющий представлять решения векторных многокомпонентных сред посредством разложения по скалярным, используемым в настоящей работе.
Работа выполнена при финансовой поддержке Российского научного фонда, проект № 22-21-00128.
Список литературы
Бабешко В.А. Некоторые соотношения для решения динамических смешанных задач на всей частотной оси // Докл. АН СССР. 1987. Т. 295. № 2. С. 312–316.
Бабешко В.А., Ворович И.И., Образцов И.Ф. Явление высокочастотного резонанса в полуограниченных телах с неоднородностями // Изв. АН СССР. МТТ. 1990. № 3. С. 74–83.
Бабешко В.А., Бабешко О.М., Евдокимова О.В. К теории блочного элемента // ДАН. 2009. Т. 427. № 2. С. 183–186 https://doi.org/10.1134/S1028335809070064
Гуткин М.Ю., Овидько И.А. Физическая механика деформируемых наноструктур. Т. 1. СПб.: Янус, 2003. 194 с.
Гусев А.И. Наноматериалы, структуры, технологии. М.: Физматлит, 2007. 416 с.
Рамбиди Н.Г. Нанотехнологии и молекулярные компьютеры. М.: Физматлит, 2007, 416 с.
Кобаяси Н. Введение в нанотехнологию. М.: Бином, 2007. 136 с.
Arghavan S., Singh A.V. On the vibrations of single-walled carbon nanotubes // J. Sound Vibr. 2011. V. 330. No. 13. P. 3102–3122. https://doi.org/10.1016/j.jsv.2011.01.032
Kang J.W., Kwon O.K. A molecular dynamics simulation study on resonance frequencies comparison of tunable carbon-nanotube resonators // Appl. Surf. Sci. 2012. V. 258. No. 6. P. 2014–2016. https://doi.org/10.1016/j.apsusc.2011.05.026
Ouakad H.M., Younis M.I. Nonlinear dynamics of electrically actuated carbon nanotube resonators // J. Computat. Nonlin. Dyn. 2009. V. 5. P. 011009. https://doi.org/10.1115/1.4000319
Poot M., Witkamp B., Otte M.A., van der Zant H.S.J. Modelling suspended carbon nanotube resonators // Phys. Status Solidi B. 2007. V. 244. No. 11. P. 4252–4256. https://doi.org/10.1002/pssb.200776130
Sapmaz S., Blanter Y.M., Gurevich L., van der Zant H.S.J. Carbon nanotubes as nanoelectromechanical systems // Phys. Rev. B. 2003. V. 67. No. 23. P. 235414. https://doi.org/10.1103/PhysRevB.67.235414
Yoon J.W., Hwang H.J. Molecular dynamics modeling and simulations of a single-walled carbon-nanotube-resonator encapsulating a finite nanoparticle // Computat. Mater. Sci. 2011. V. 50. No. 9. P. 2741–2744. https://doi.org/10.1016/j.commatsci.2011.04.033
Yin J., Zhang Z., Li X. et al. Waving potential in graphene // Nature Commun. 2014. V. 5. P. 3582. https://doi.org/10.1038/ncomms4582
Yin J., Li X., Yu J., Zhang Z., Zhou J., Guo W., Generating electricity by moving a droplet of ionic liquid along graphene // Nature Nanotech. 2014. V. 9. P. 378–383. https://doi.org/10.1038/nnano.2014.56
Liu X., Xu T., Wu X., Zhang Z., Yu J., Qiu H., Hong J., Jin C., Li J., Wang X., Sun L., Guo W. Top-down fabrication of sub-nanometre semiconducting nanoribbons derived from molybdenum disulfide sheets // Nat. Commun. 2013. V. 4. P. 1776. https://doi.org/10.1038/ncomms2803
Guo W., Liu X. 2D materials: Metallic when narrow // Nature Nanotech. 2014. V. 9. P. 413–414. https://doi.org/10.1038/nnano.2014.106
Lei X.W., Natsuki T., Shi J.X., Ni Q.Q. An atomic-resolution nanomechanical mass sensor based on circular monolayer graphene sheet: Theoretical analysis of vibrational properties // J. Appl. Phys. 2013. V. 113. P. 154313. https://doi.org/10.1063/1.4802438
Lei X.W., Nakatani A. A continuum mechanics analysis of lattice defects in carbon nanotube // 9th European Solid Mechanics Conference (ESMC). Madrid, 2015.
Ding F., Jiao K., Wu M., Yakobson B.I. Pseudoclimb and dislocation dynamics in superplastic nanotubes // Phys. Rev. Lett. 2007. V. 98. P.075503. https://doi.org/10.1103/PhysRevLett.98.075503
Lengiewicz J., Korelc J., Stupkiewicz S. Automation of finite element formulations for large deformation contact problems // Int. J. Numer. Meth. Eng. 2011. V. 85. P. 1252–1279. https://doi.org/10.1002/nme.3009
Roland T., Retraint D., Lu K., Lu J. Fatigue life improvement through surface nanostructuring of stainless steel by means of surface mechanical attrition treatment // Scripta Mater. 2006. V. 54. P. 1949–1954. https://doi.org/10.1016/j.scriptamat.2006.01.049
Tian J., Villegas J., Yuan W., Fielden D., Shaw L., Liaw P., Klarstrom D. A study of the effect of nanostructured surface layers on the fatigue behaviors of a C-2000 superalloy // Mater. Sci. Eng. A. 2007. V. 468–470. P. 164–170. https://doi.org/10.1016/j.msea.2006.10.150
Lu K., Lu J. Surface nanocrystallization (SNC) of metallic materials-presentation of the concept behind a new approach // J. Mater. Sci. Technol. 1999. V. 15. P. 193–197.
Бабешко В.А., Евдокимова О.В., Бабешко О.М. Фрактальные свойства блочных элементов и новый универсальный метод моделирования // ДАН. 2021. Т. 499. С. 21–26. https://doi.org/10.31857/S2686740021040039
Ворович И.И., Бабешко В.А. Динамические смешанные задачи теории упругости для неклассических областей. М.: Наука, 1979. 320 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела