Известия РАН. Механика твердого тела, 2022, № 6, стр. 63-71
УСТОЙЧИВОСТЬ БЕСКОНЕЧНО ДЛИННОЙ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ ПОД ДЕЙСТВИЕМ НАРУЖНОГО ДАВЛЕНИЯ, СОЗДАВАЕМОГО НАМОТКОЙ ГИБКИХ НИТЕЙ
В. В. Васильев a, *, В. А. Салов b, А. А. Склезнев b
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
b АО Центральный НИИ специального машиностроения
Хотьково, Россия
* E-mail: vvvas@dol.ru
Поступила в редакцию 15.03.2022
После доработки 16.03.2022
Принята к публикации 17.03.2022
- EDN: GLRTOS
- DOI: 10.31857/S0572329922060174
Аннотация
В статье рассматривается задача устойчивости бесконечно длинной цилиндрической оболочки, на которую наматываются с натяжением абсолютно гибкие нити, сжимающие оболочку так, что она может потерять устойчивость. С помощью уравнений нелинейной теории оболочек, получено точное решение, определяющее критическое натяжение нитей. Установлено, что критическое натяжение определяется универсальной формулой, которая включает радиус и изгибную жесткость оболочки. С помощью концепции продолжающегося нагружения полученное решение обобщается на случай упруго-пластического материала оболочки. Рассмотрена задача о давлении на упругую оболочку слоями из упругих нитей, наматываемых с натяжением. Решение сопоставляется с результатами эксперимента, проведенного на оболочках из стали, алюминия и термопласта.
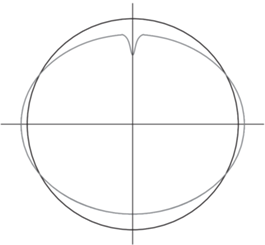
1. Введение. Задача, рассматриваемая в статье, представляет прикладной интерес в связи широким распространением композитных баллонов давления и емкостей различного назначения. Герметичность таких конструкций обеспечивается внутренней металлической или полимерной оболочкой (лейнером), на которую осуществляется намотка несущего композитного слоя [1]. При намотке с предварительным натяжением на оболочку передается наружное давление, которое может привести к потере устойчивости. На рис. 1 показаны формы потери устойчивости оболочек из стали, алюминия и термопласта. Задача устойчивости была сформулирована в нелинейной постановке В.И. Феодосьевым [2] однако ее решение не было найдено. Приближенные решения, основанные на энергетическом подходе и аппроксимации формы потери устойчивости, представлены в работах [3, 4]. Заметим, что рассматриваемая задача отличается от аналогичной задачи устойчивости оболочки в жесткой обойме [5], в которой оболочка остается круговой вне участка, на котором она потеряла устойчивость. При потере устойчивости от натяжения нитей оболочка деформируется по всей поверхности (рис. 1).
Рис. 1.
Формы потери устойчивости оболочек из стали (a), алюминия (b), термопласта (c) и исходная форма оболочки (d) в начале нагружения.

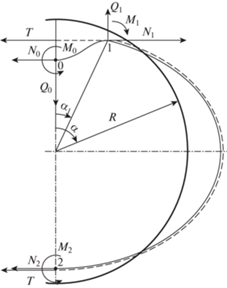
2. Исходные уравнения. Рассмотрим деформированное сечение оболочки, показанное на рис. 2 сплошной линией (штриховая линия показывает положение нити). Система нелинейных уравнений, описывающих деформацию оболочки, имеет вид [6]
(2.1)
$N{\kern 1pt} '\; + Q\left( {1 + \omega {\kern 1pt} '} \right) = 0,\quad Q_{{}}^{'} - N\left( {1 + \omega {\kern 1pt} '} \right) = {{q}_{T}},\quad M{\kern 1pt} '\; - RQ = 0.$(2.2)
$N = B{{\varepsilon }_{\alpha }},\quad M = \frac{D}{R}\omega {\kern 1pt} ',\quad B = \bar {E}h,\quad D = \frac{1}{{12}}\bar {E}{{h}^{3}},\quad \bar {E} = \frac{E}{{1 - {{{{\nu }}}^{2}}}}$(2.3)
${{\varepsilon }_{\alpha }} = \frac{1}{R}\left( {u{\kern 1pt} ' + w} \right) + \frac{1}{2}{{\omega }^{2}},\quad \omega = \frac{1}{R}\left( {u - w{\kern 1pt} '} \right),\quad ( \cdot ){\kern 1pt} ' = \frac{{d( \cdot )}}{{d{{\alpha }}}},$Здесь N, Q, M – кольцевое усилие, поперечное усилие и изгибающий момент, положительные направления которых показаны на рис. 2, u, w – кольцевое перемещение и прогиб, направленный по наружной нормали, ω – угол поворота нормали к поверхности оболочки. Уравнения (2.2) соответствуют бесконечно длинной цилиндрической оболочке. Для кольца в них следует принять ν = 0. Во второе уравнение (2.1) входит давление, создаваемое натяжением нитей T, которое изменяется по углу α следующим образом:
(2.4)
${{q}_{T}} = 0\quad {\text{при}}\quad 0 \leqslant {{\alpha }} \leqslant {{{{\alpha }}}_{1}}\quad {\text{и}}\quad {{q}_{t}} = T(1 + {{\omega }}{\kern 1pt} ')\quad {\text{при}}\quad {{{{\alpha }}}_{1}} \leqslant {{\alpha }} \leqslant {{\pi }}$3. Решение для участка 0-1. Рассмотрим участок оболочки 0-1 (рис. 2). В точке 0 в силу симметрии имеем Q0 = 0. Тогда из условия равновесия участка 0-1 в вертикальном направлении в точке 1 получим Q1 = 0. Из условия равновесия в горизонтальном направлении найдем N1 = N0. Таким образом, участок 0-1 находится в условиях чистого изгиба и осевого нагружения. Введем безразмерные величины
(3.1)
$\bar {N} = \frac{N}{Т},\quad \bar {Q} = \frac{Q}{T},\quad \bar {M} = \frac{M}{{TR}},\quad \bar {u} = \frac{u}{R},\quad \bar {w} = \frac{w}{R}$При qT = 0 уравнения (2.1) принимают вид
(3.2)
$N{\kern 1pt} '\; + \bar {Q}(1 + {{\omega }}{\kern 1pt} ') = 0,\quad \bar {Q}{\kern 1pt} '\; - \bar {N}(1 + {{\omega }}{\kern 1pt} ') = 0,\quad \bar {M}{\kern 1pt} '\; - \bar {Q} = 0$Складывая первые два уравнения, получим $\bar {N}{\kern 1pt} '\bar {N} + \bar {Q}{\kern 1pt} '\bar {Q} = 0$. Интегрируя с учетом граничных условий в точке 0 $(\bar {N} = {{\bar {N}}_{0}},\bar {Q} = 0)$, имеем
Выражая отсюда $\bar {Q}$ и подставляя в первое уравнение (3.2), получим
Интегрируя с учетом граничных условий $\bar {N}(\alpha = 0) = {{\bar {N}}_{0}},$ ω (α = 0) = 0 (рис. 2), найдем
Отсюда с учетом равенства (3.3)
(3.4)
$\bar {N} = {{\bar {N}}_{0}}\cos ({{\alpha }} + {{\omega }}),\quad \bar {Q} = {{\bar {N}}_{0}}\sin ({{\alpha }} + {{\omega }})$Поскольку $\bar {N}({{\alpha }} = {{{{\alpha }}}_{1}}) = {{\bar {N}}_{1}} = {{\bar {N}}_{0}}$ и $\bar {Q}({{\alpha }} = {{{{\alpha }}}_{1}}) = {{\bar {Q}}_{1}} = 0$ (рис. 2) имеем
Из уравнений (2.2) с учетом обозначений (3.1) получим следующее выражение для изгибающего момента:
(3.6)
$M = \frac{{{{\omega }}{\kern 1pt} '}}{{{{{{\lambda }}}^{2}}}},\quad {{{{\lambda }}}^{2}} = \frac{{T{{R}^{2}}}}{D}$Дифференцируя, выражая $\bar {M}{\kern 1pt} '$ через $\bar {Q}$ с помощью последнего уравнения (3.2) и подставляя $\bar {Q}$ из второго равенства (3.4), запишем следующее уравнение для ω:
(3.7)
${{\omega }}{\kern 1pt} '{\kern 1pt} '\; - {{{{\lambda }}}^{2}}{{\bar {N}}_{0}}\sin ({{\alpha }} + {{\omega }}) = 0$Оценим функцию φ = α + ω. Согласно граничным условиям в точках 0 и 1 (рис. 2) имеем φ (α = 0) = 0 и φ (α = α1) = 0. Таким образом, функция φ обращается в ноль на границах интервала интегрирования уравнения (3.7). Считая ее малой внутри этого интервала примем sin φ ≈ φ и упростим соответствующим образом уравнение (3.7). Учтем также, что ${{{{\lambda }}}^{2}}{{\bar {N}}_{0}} < 0$ так как усилие N0 (рис. 2) по условиям задачи является сжимающим. В результате, уравнение (3.7) принимает вид
(3.8)
${{\omega }}{\kern 1pt} '{\kern 1pt} '\; + k_{1}^{2}({{\omega }} + {{\alpha }}) = 0,\quad k_{1}^{2} = - {{{{\lambda }}}^{2}}{{\bar {N}}_{0}}$Общее решение этого уравнения
Условия ω (α = 0) = 0 дает C2 = 0, а из условия (3.5) следует sin kα1 = 0. Таким образом,
(3.9)
${{k}_{1}} = \frac{{{\pi }}}{{{{{{\alpha }}}_{1}}}},\quad {{\bar {N}}_{0}} = - \frac{{{{{{\pi }}}^{2}}}}{{{{\alpha }}_{1}^{2}{{{{\lambda }}}^{2}}}}\quad {\text{и}}\quad {{\omega }} = {{C}_{1}}\sin \frac{{{{\pi \alpha }}}}{{{{{{\alpha }}}_{1}}}} - {{\alpha }}$Преобразуем этот результат. Используя равенство (3.6), запишем изгибающий момент, действующий в точке 0 (рис. 2)
Выражая отсюда C1 и подставляя в решение (3.9), получим следующее окончательное выражение для угла поворота на участке 0-1:
(3.10)
${{{{\omega }}}_{{01}}} = \frac{{{{{{\alpha }}}_{1}}}}{{{\pi }}}(1 + {{{{\lambda }}}^{2}}{{\bar {M}}_{0}})\sin \frac{{{{\pi \alpha }}}}{{{{{{\alpha }}}_{1}}}} - {{\alpha }}$Найдем прогиб оболочки на участке 0-1. Предположим, что оболочка является недеформируемой в кольцевом направлении и примем в равенствах (2.2) B → ∞. Тогда εα = 0 и из уравнений (2.3) при учете обозначений (3.1) следует
(3.11)
$\bar {u}{\kern 1pt} ' = - \bar {w} - \frac{{{{{{\omega }}}^{2}}}}{2},\quad {{\omega }}{\kern 1pt} ' = \bar {u}{\kern 1pt} '\; - \bar {w}{\kern 1pt} '{\kern 1pt} '$Исключая u', придем к уравнению для прогиба
(3.12)
$\bar {w}{\kern 1pt} '{\kern 1pt} '\; + \bar {w} = - f({{\alpha }}),\quad f({{\alpha }}) = {{\omega }}{\kern 1pt} '\; + \frac{{{{{{\omega }}}^{2}}}}{2}$Решение этого уравнения, удовлетворяющее условию симметрии $\bar {w}{\kern 1pt} '({{\alpha }} = 0) = 0$ (рис. 2), определяет прогиб оболочки на участке 0-1
(3.13)
$\begin{gathered} {{{\bar {w}}}_{{01}}} = {{C}_{{01}}}\cos {{\alpha }} - \sin {{\alpha }}\int\limits_0^{{\alpha }} {{{f}_{{01}}}({{\alpha }})\cos {{\alpha }}d{{\alpha }} + \cos {{\alpha }}} \int\limits_0^{{\alpha }} {{{f}_{{01}}}({{\alpha }})\sin {{\alpha }}d{{\alpha }}} \\ {{f}_{{01}}}({{\alpha }}) = {{\omega }}_{{01}}^{'} + \frac{1}{2}{{\omega }}_{{01}}^{2} \\ \end{gathered} $Постоянная С01 соответствует смещению оболочки как твердого тела. Кольцевое перемещение следует из первого уравнения (3.11). Интегрируя его с учетом условия симметрии $\bar {u}({{\alpha }} = 0) = 0$, получим
(3.14)
${{\bar {u}}_{{01}}} = - \int\limits_0^{{\alpha }} {\left( {{{{\bar {w}}}_{{01}}} + \frac{{{{\omega }}_{{01}}^{2}}}{2}} \right)} d{{\alpha }}$4. Решение для участка 1-2. Для участка 1-2 (рис. 2) уравнения равновесия (2.1) с учетом равенств (2.4) и (3.1) записываются следующим образом:
(4.1)
$\bar {N}{\kern 1pt} '\; + \bar {Q}(1 + {{\omega }}{\kern 1pt} ') = 0,\quad \bar {Q}{\kern 1pt} '\; - \bar {N}(1 + {{\omega }}{\kern 1pt} ') = 1 + {{\omega }}{\kern 1pt} ',\quad \bar {M}{\kern 1pt} '\; - \bar {Q} = 0$Обозначим $\bar {N} + 1 = {{\bar {N}}_{r}}.$ Учитывая, что $\bar {N}{\kern 1pt} ' = \bar {N}_{r}^{'}$, представим первые два уравнения (4.1) в виде
(4.2)
$\bar {N}_{r}^{'} + \bar {Q}(1 + {{\omega }}{\kern 1pt} ') = 0,\quad \bar {Q}{\kern 1pt} '\; - {{\bar {N}}_{r}}(1 + {{\omega }}{\kern 1pt} ') = 0$Эти уравнения аналогичны уравнениям (3.2) и имеют решение аналогичное равенству (3.3), то есть $\bar {N}_{r}^{2} + {{\bar {Q}}^{2}} = {{C}^{2}}.$ При ${{\alpha }} = {{{{\alpha }}}_{1}}$ (рис. 2) имеем ${{\bar {N}}_{1}} = {{\bar {N}}_{0}},$ ${{\bar {N}}_{r}} = 1 + {{\bar {N}}_{0}},$ ${{\bar {Q}}_{1}}$ = 0. Таким образом, $C = {{\bar {N}}_{r}}({{\alpha }} = {{{{\alpha }}}_{1}}) = 1 + {{\bar {N}}_{0}}$ и
Выражая отсюда Q и подставляя в первое уравнение (4.1), получим
Общее решение этого уравнения
В точке 1 (рис. 2) имеем α = α1, $\bar {N} = {{\bar {N}}_{0}}$ и ω = – α1. Тогда C = π / 2 и решение принимает вид
(4.4)
$\bar {N} = (1 + {{\bar {N}}_{0}})\cos ({{\alpha }} + {{\omega }}) - 1,\quad \bar {Q} = (1 + {{\bar {N}}_{0}})\sin ({{\alpha }} + {{\omega }})$В точке 2 (рис. 2) имеем α = π, ω = 0 и ${{\bar {N}}_{2}} = - 2 - {{\bar {N}}_{0}}$, ${{\bar {Q}}_{2}} = 0.$ Уравнение равновесия половины оболочки, показанной на рис. 2 (N0 + N2 + 2T = 0), удовлетворяется при этом тождественно. Дальнейшие преобразования приводят к уравнению аналогичному уравнениям (3.7) и (3.8). Окончательно получим
(4.5)
${{\omega }}{\kern 1pt} '{\kern 1pt} '\; + k_{2}^{2}\sin ({{\alpha }} + {{\omega }}) = 0,\quad k_{2}^{2} = - {{{{\lambda }}}^{2}}(1 + {{\bar {N}}_{0}})$Предполагается и подтверждается дальнейшим расчетом, что при ${{\bar {N}}_{0}} < 0$ абсолютная величина $\left| {{{{\bar {N}}}_{0}}} \right| > 1$. В отличие от уравнения (3.7) это уравнение нельзя упростить и привести к форме (3.8). Для решения уравнения (4.5) введем новую переменную [7] y(α) = α + ω(α) и приведем уравнение (4.5) к виду $y{\kern 1pt} '{\kern 1pt} '\; + k_{2}^{2}\sin y = 0$. В этом уравнении проведем замену (y')2 = z (y), в результате которой придем к уравнению первого порядка $z{\kern 1pt} ' = - 2k_{2}^{2}y{\kern 1pt} '\sin y = 2k_{2}^{2}(\cos y){\kern 1pt} '$. Решение этого уравнения в исходных переменных имеет вид
(4.6)
${{(1 + {{\omega }}{\kern 1pt} ')}^{2}} = 2k_{2}^{2}\cos ({{\alpha }} + {{\omega }}) + {{C}_{{{\omega }}}}$Используя формулы (3.9) для ${{\bar {N}}_{0}}$ и (4.5) для $k_{2}^{2}$, найдем 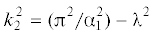 . Постоянная Cω определяется из условия непрерывности угла поворота в точке α = α1 (рис. 2). Функция ω(α1), определяемая уравнением (4.6), должна быть равна функции ω01(α1) (3.10). Окончательно, получим следующее уравнение для угла поворота на участке 1-2:
. Постоянная Cω определяется из условия непрерывности угла поворота в точке α = α1 (рис. 2). Функция ω(α1), определяемая уравнением (4.6), должна быть равна функции ω01(α1) (3.10). Окончательно, получим следующее уравнение для угла поворота на участке 1-2:
(4.7)
${{\omega }}_{{12}}^{'} = \sqrt {{{{(1 + {{{{\lambda }}}^{2}}{{{\bar {M}}}_{0}})}}^{2}} - 2\left( {\frac{{{{{{\pi }}}^{2}}}}{{{{\alpha }}_{1}^{2}}} - {{{{\lambda }}}^{2}}} \right)\left[ {1 - \cos ({{\alpha }} + {{{{\omega }}}_{{12}}})} \right]} - 1$Решение этого уравнения выражается через эллиптические интегралы. Однако при этом получается достаточно сложная неявная функция α(ω12), неудобная для расчета. В связи с этим уравнение (4.7) интегрируется численно при граничном условии ω12(α = π) = = 0 (рис. 2).
Прогиб оболочки на участке 1-2 определяется равенством аналогичным выражению (3.13), то есть
(4.8)
$\begin{gathered} {{{\bar {w}}}_{{12}}} = {{C}_{{12}}}\cos {{\alpha }} - \sin {{\alpha }}\int\limits_{{{{{\alpha }}}_{1}}}^{{\alpha }} {{{f}_{{12}}}} ({{\alpha }})\cos {{\alpha }}d{{\alpha }} + \cos {{\alpha }}\int\limits_{{{{{\alpha }}}_{1}}}^{{\alpha }} {{{f}_{{12}}}} ({{\alpha }})\sin {{\alpha }}d{{\alpha }} \\ {{f}_{{12}}}({{\alpha }}) = {{\omega }}_{{12}}^{'} + \frac{1}{2}{{\omega }}_{{12}}^{2} \\ \end{gathered} $Постоянная C12 выражается через постоянную C01 в равенстве (3.13) из условия непрерывности прогиба в точке α = α1 (рис. 2). Из этого условия получим C12 = = ${{\bar {w}}_{{01}}}({{{{\alpha }}}_{1}},{{C}_{{01}}}){\text{/}}\cos {{{{\alpha }}}_{1}}$. Постоянная C01 соответствует, как уже отмечалось, смещению оболочки как твердого тела.
Кольцевое перемещение оболочки на участке 1-2 определяется выражением аналогичным равенству (3.14). Учитывая условие непрерывности перемещения в точке α = α1 (рис. 2), получим
(4.9)
${{\bar {u}}_{{12}}} = - \int\limits_0^{{{{{\alpha }}}_{1}}} {\left( {{{{\bar {w}}}_{{01}}} + \frac{1}{2}{{\omega }}_{{01}}^{2}} \right)} d{{\alpha }} - \int\limits_{{{{{\alpha }}}_{1}}}^{{\alpha }} {\left( {{{{\bar {w}}}_{{12}}} + \frac{1}{2}{{\omega }}_{{12}}^{2}} \right)} d{{\alpha }}$При этом должно выполняться условие симметрии ${{\bar {u}}_{{12}}}({{\alpha }} = {{\pi }}) = 0$ (рис. 2).
5. Определение критического натяжения. Критическое натяжение нитей, при котором оболочка теряет устойчивость, определяется в результате расчета, состоящего из нескольких этапов. На первом этапе задается параметр λ2 (3.6), в который входит неизвестное усилие натяжения T. На втором этапе задается угол α1. Тогда для определения угла поворота ω(α) с помощью уравнений (3.10) и (4.7) необходимо знать момент ${{\bar {M}}_{0}}$. Этот момент находится в результате численного интегрирования уравнения (3.7) – он определяется методом пристрелки так, чтобы выполнялось граничное условие ω12(α = π) = 0 (рис. 2). На третьем этапе при найденном значении ${{\bar {M}}_{0}}$ и заданной величине λ2 определялся соответствующий этим параметрам угол α1. Для этого используется условие симметрии осевого перемещения (4.9) – ${{\bar {u}}_{{12}}}({{\alpha }} = {{\pi }}) = 0.$ В результате такой довольно сложной процедуры получается угол поворота ω(α), соответствующий заданному параметру λ2. На заключительном этапе расчета с помощью уравнений (3.13) и (4.8) определяется прогиб оболочки. При этом оказывается, что существует некоторое критическое значение параметра ${{\lambda }}_{{сr}}^{2}$ такое, что при ${{{{\lambda }}}^{2}} < {{\lambda }}_{{cr}}^{2}$ существует только тривиальное решение w ≡ 0, соответствующее докритическому состоянию оболочки. В результате трудоемкого параметрического анализа получено ${{\lambda }}_{{cr}}^{2} = 732.$ Прогиб оболочки при этом значении параметра и α1 = 6.39°, ${{С}_{{01}}} = \bar {w}(\alpha = 0) = 0.2$ показан на рис. 3.
Таким образом, результатом приведенного выше достаточно сложного анализа является универсальная и простая формула для критического натяжения
(5.1)
${{T}_{{cr}}} = \frac{{{{\lambda }}_{{cr}}^{2}D}}{{{{R}^{2}}}},\quad {{\lambda }}_{{cr}}^{2} = 732$Для проверки полученного результата были испытаны оболочки из алюминия, стали и термопласта (ПЭТФ), нагружавшиеся натянутыми нитями. Результаты эксперимента представлены в таблице. Среднее экспериментальное значение ${{\lambda }}_{{cr}}^{2}$ составляет 741, что отличается от расчетного результата на 1.2%. Критическое напряжение в оболочке определяется по формуле σcr = qcrR/h, где qcr = Tcr/R – контактное давление на оболочку, создаваемое нитями. С учетом равенства (5.1) получим
Как известно, при действии равномерного давления жидкости или газа на бесконечно длинную цилиндрическую оболочку критическое напряжение имеет вид σcr = = 3D/R2h. Это напряжение в 244 раза меньше напряжения (5.2).
Полученный результат справедлив для упругой оболочки при σcr ≤ σt, где σt – предел текучести материала. Величина σcr для экспериментальных оболочек приведена в таблице 1. Она значительно меньше предела текучести, который для алюминия, стали и термопласта составляет соответственно 267, 486 и 63 МПа. Если σcr > σt, оболочка теряет устойчивость за пределом упругости. Согласно концепции продолжающегося нагружения [8], в этом случае в выражении (2.2) для изгибной жесткости принимается ν = 1/2 и E = Et, где Et – касательный модуль. Таким образом, в равенстве (5.1) принимается D = Et h3/9.
Таблица 1.
Результаты экспериментальных исследований устойчивости кольцевых образцов
| Материал оболочки | R, мм | h, мм | Tcr, Н/мм | σcr, МПа | E, ГПа | ν | $\lambda _{{cr}}^{2}$ |
|---|---|---|---|---|---|---|---|
| Алюминий | 42.00 | 0.165 | 12.50 | 75.8 | 72.1 | 0.3 | 753 |
| Алюминий | 31.50 | 0.096 | 4.44 | 46.3 | 72.3 | 0.3 | 741 |
| Сталь | 50.02 | 0.183 | 37.33 | 204 | 222 | 0.3 | 736 |
| Термопласт | 40.10 | 0.242 | 3.13 | 12.9 | 5.22 | 0.4 | 739 |
| Термопласт | 40.14 | 0.232 | 2.57 | 11.1 | 5.10 | 0.4 | 739 |
| Термопласт | 40.40 | 0.260 | 3.94 | 15.2 | 5.26 | 0.4 | 737 |
6. Напряжения в оболочке, вызванные многослойной намоткой с натяжением. Рассмотрим металлическую цилиндрическую оболочку с толщиной h, на которую наматывается система композитных слоев. Предположим, что элементарный слой имеет толщину δ и предварительное напряжение s. Эффект от намотки такого слоя на оболочку моделируется приложением к оболочке наружного давления q = sδ/R. В результате намотки одного слоя в оболочке возникнет напряжение ${{{{\sigma }}}_{1}} = - qR{\text{/}}h = - s{{\delta /}}h$. Если оболочка является абсолютно жесткой, то после намотки n слоев в ней будет действовать напряжение σn = –sδn/h. Однако оболочка является податливой и при намотке каждого следующего слоя натяжение ранее уложенных слоев снижается [9].
Итак, после намотки первого слоя в нем действует напряжение s, а в металлической оболочке – напряжение ${{{{\sigma }}}_{1}} = - s{{\delta /}}h$. В результате намотки второго слоя в первом слое и в оболочке возникают дополнительные напряжения s12 и σ12, которые связаны уравнением равновесия и условием совместности деформаций
Аналогичным способом получим напряжение в оболочке после намотки третьего слоя
В общем случае после намотки слоя с номером n найдем
Заключение. В рамках нелинейной теории оболочек получено решение, определяющее критическую величину натяжения нитей, наматываемых на бесконечно длинную цилиндрическую оболочку. Установлено универсальное выражение для критического натяжения, зависящего от радиуса и изгибной жесткости оболочки. Полученное решение подтверждено экспериментально на модельных оболочках из алюминия, стали и термопласта. Исследован процесс намотки композита на упругую оболочку.
Список литературы
Васильев В.В., Мороз Н.Г. Композитные баллоны давления. Проектирование, расчет, изготовление и испытания. М.: Машиностроение, 2015. 372 с.
Феодосьев В.И. Избранные задачи и вопросы по сопротивлению материалов. М.: Наука, 1996. 368 с.
Langhaar H., Boresi A., Marcus L., Love G. Buckling of a long fiber-wound cylindrical shell due to stresses caused by winding // J. Appl. Mech. 1965. V. 32. Ser. E. № 1. P. 81–86. https://doi.org/10.1115/1.3625789
Постоев В.С. К теории устойчивости предварительно напряженной цилиндрической оболочки / Прочность гидротурбин. Труды ЦКТИ. Вып. 72. Л.: ЦКТИ, 1966. С. 3–12.
Васильев В.В., Салов В.А. Устойчивость бесконечно длинной цилиндрической оболочки, нагруженной наружным давлением, создаваемым жесткой внешней средой // Изв. РАН. МТТ. 2021. № 4. С. 134–144. https://doi.org/10.31857/S0572329921040127
Васильев В.В. Механика конструкций из композиционных материалов. М.: Машиностроение, 1988. 270 с.
Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Физматгиз, 1961, 703 с.
Вольмир А.С. Устойчивость деформируемых систем. М.: Наука, 1967, 984 с.
Васильев В.В. Упруго-пластические деформации металлических баллонов давления, усиленных однонаправленным стеклопластиком // Механика полимеров. 1969. № 6. С. 1069–1074.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела