Известия РАН. Механика твердого тела, 2022, № 6, стр. 79-96

1. Введение. Изучение упругих свойств материалов является постоянно актуальной задачей, так как величины упругих характеристик требуются во множестве инженерных и научных расчетов. Значительная часть твердых тел имеет кубическую кристаллическую структуру, в том числе кристаллы многих простых веществ и двухатомных бинарных соединений со стехиометрией АВ. Кубические кристаллы многих металлов имеют гранецентрированную структуру А1 (ГЦК структура меди) или объемно-центрированную структуру А2 (ОЦК структура вольфрама), элементы подгруппы IVA (C, Si, Ge, α-Sn) имеют структуру алмаза А4, а Po и U – примитивную кубическую структуру A_h. Бинарные соединения АВ образуют следующие кубические структуры: В1 – структуру каменной соли NaCl, состоящую из двух ГЦК подрешеток элементов А и В, с расположением атомов в единой решетке как в примитивной решетке; В2 – структуру хлорида цезия CsCl, состоящую из двух примитивных подрешеток А и В, с расположением атомов в единой решетке как в ОЦК; или В3 – структуру цинковой обманки β‑ZnS, также состоящей из двух ГЦК – подрешеток, в которой, однако, А- и В-подрешетки расположены относительно друг друга иначе, чем в структуре NaCl – ближайшими соседями каждого атома являются четыре атома противоположного типа, расположенные в вершинах правильного тетраэдра, т.е. также как в структуре алмаза.

Упругие свойства кристаллов с кубической структурой исследовали во многих работах [1–21]. В [1–3] анализировались стационарные и экстремальные значения модуля Юнга. В этих работах было продемонстрировано, что кристаллы с кубической структурой имеют три стационарных значения модуля Юнга. Два из трех значений могут являться экстремальными значениями. В [4] были проанализированы кристаллографические направления, в которых могут наблюдаться экстремальные значения модуля сдвига кубических кристаллов. Авторами работы [5] была продемонстрирована связь между экстремальными значениями модуля Юнга и модуля сдвига. В [6–21] был проведен анализ изменчивости коэффициента Пуассона для кристаллов с кубической структурой. В теории упругости анизотропного тела положительная определенность энергии деформации не накладывает каких-либо общих ограничений на коэффициенты Пуассона упругих материалов как в случае кристаллов с кубической структурой, так и кристаллов с триклинной, моноклинной, орторомбической, тетрагональной, тригональной (ромбоэдрической) и гексагональной структурой [6]. В [7–21] было продемонстрировано, что кубические кристаллы могут принимать не только положительные значения коэффициента Пуассона, но и отрицательные значения. Материалы с отрицательным коэффициентом Пуассона стали называть ауксетиками. Термин “ауксетики” был предложен профессором Кеном Эвансом [22] для материалов, которые расширяются в поперечном направлении при приложении к ним растягивающей продольной нагрузки. Все кристаллические материалы делятся на неауксетики (материалы, у которых коэффициент Пуассона принимает положительные значения при любой ориентации кристаллической решетки относительно направления растяжения), частичные ауксетики (материалы, у которых коэффициент Пуассона принимает как положительные, так и отрицательные значения в зависимости от ориентации кристаллической решетки относительно направления растяжения) и полные ауксетики (материалы, у которых коэффициент Пуассона принимает отрицательные значения при любой ориентации кристаллической решетки относительно направления растяжения) [14, 15, 18]. В [15, 18] показано, что более чем для 300 кристаллов коэффициент Пуассона может принимать отрицательные значения. Частичными ауксетиками являются кристаллы таких металлов как железо, никель, золото, серебро, литий, натрий, калий, кальций и т.д. В [12, 16] проанализированы экстремальные значения коэффициента Пуассона для кристаллов с кубической структурой. В этих работах показано, что кроме четырех основных стационарных значений, могут наблюдаться экстремально высокие значения коэффициента при растяжении в направлении близком к [111]. Такие значения коэффициента Пуассона свойственны метастабильным кристаллам, таким как кристаллы с эффектом памяти формы [16]. В [10] для ОЦК-кристаллов была предложена структурная модель, поясняющая ауксетическое поведение кристаллов. В [18] представлен обзор ауксетических материалов с кубической структурой, таких как кубические кристаллы, слоистые композиты и нано/микротрубки.

В настоящей работе будут рассматриваться одноатомные (простые вещества) и двухатомные (соединений типа АВ) кристаллы вышеуказанных структур кубической сингонии с металлической, ионной и ковалентной связью. Задачей данного исследования является установление зависимостей упругих свойств кристаллов от типа их структуры и характера межатомной связи. При анализе будет использоваться характеристическая диаграмма упругих свойств, предложенная авторами ранее [16]. Особое внимание в исследовании будет уделено структурным и физическим факторам, обуславливающим ауксетические упругие свойства кристаллов. В последнее время этим материалам уделяется большое внимание [8, 18, 23–26] потому, что это свойство материалов-ауксетиков интересно с практической точки зрения, так как оно может быть использовано при конструировании специальных устройств, а также представляет теоретический интерес, так как исходя из такого аномального упругого поведения твердых тел можно судить о природе межатомного взаимодействия.

2. Характеристические диаграммы упругих свойств кубических кристаллов. Перед тем как перейти к рассмотрению диаграмм упругих свойств кубических кристаллов определимся с обозначением используемых переменных. Упругие свойства кубических кристаллов могут быть охарактеризованы либо тремя компонентами упругих жесткостей ${{c}_{{11}}}$, ${{c}_{{12}}}$, ${{c}_{{44}}}$ либо тремя компонентами упругих податливостей ${{s}_{{11}}}$, ${{s}_{{12}}}$, ${{s}_{{44}}}$, которые связаны между собой соотношениями

где $s{\text{*}} = s_{{11}}^{2} + {{s}_{{11}}}{{s}_{{12}}} - 2s_{{12}}^{2} = \left( {{{s}_{{11}}} - {{s}_{{12}}}} \right)\left( {{{s}_{{11}}} + 2{{s}_{{12}}}} \right)$. На компоненты жесткости накладываются следующие термодинамические ограничения: ${{c}_{{11}}} > 0$, $ - 0.5 < {{c}_{{12}}}{\text{/}}{{c}_{{11}}} < 1~$ и ${{c}_{{44}}} > 0$. При этом соотношения (2.1), (2.2) и (2.3) инвариантны относительно взаимной замены переменных ${{c}_{{ij}}} \leftrightarrow {{s}_{{ij}}}$.

Упругую анизотропию кубических кристаллов будем описывать коэффициентом анизотропии A, равного комбинации упругих податливостей $s = {{s}_{{11}}} - {{s}_{{12}}} - {{s}_{{44}}}{\text{/}}2$, нормализованной на ${{s}_{{11}}}$

Для кубических кристаллов преобразование компонент тензора упругих податливостей ${{s}_{{ijkl}}}$ при изменении системы координат имеет следующий вид

где ${{s}_{{ijkl}}}$ и ${{s}_{{i'j'k'l'}}}$ – соответственно компоненты тензора упругих податливостей в базовой системе координат 〈001〉 и произвольной новой системе координат, ${{{{\Phi }}}_{{i'j'k'l'}}}$ = = $2\mathop \sum \limits_{m = 1}^3 {{l}_{{mi'}}}{{l}_{{mj'}}}{{l}_{{mk'}}}{{l}_{{ml'}}}$ – ориентационный фактор, и ${{l}_{{mi'}}}$ – направляющие косинусы между m-й и i´-й осями старой и новой систем координат. Из (2.5) видно, что кубические кристаллы упруго изотропны, т.е. ${{s}_{{i'j'k'l'}}}$ не зависит от ориентационного фактора ${{{{\Phi }}}_{{i'j'k'l'}}}$, если $s$ = 0. Из соотношения (2.5) следуют соотношения для модулей нормальной упругости ${{E}_{{\left[ {hkl} \right]}}}$

Индексы в обозначениях модуля Юнга указывают направления растяжения. В случае положительной анизотропии (A > 0) выполняется неравенство ${{E}_{{\left[ {111} \right]}}} > {{E}_{{\left[ {011} \right]}}} > {{E}_{{\left[ {001} \right]}}}$, тогда как при отрицательной анизотропии (A < 0) имеет место обратная закономерность ${{E}_{{\left[ {111} \right]}}} < {{E}_{{\left[ {011} \right]}}} < {{E}_{{\left[ {001} \right]}}}$. Следует отметить, что характеризация упругой анизотропии коэффициентом $A$ подобна характеризации известным коэффициентом Зенера ${{A}^{Z}} = 2{{c}_{{44}}}{\text{/}}\left( {{{c}_{{11}}} - {{c}_{{12}}}} \right) = 2\left( {{{s}_{{11}}} - {{s}_{{12}}}} \right){\text{/}}{{s}_{{44}}}$, поскольку они связаны между собой соотношением $A = \left( {{{s}_{{44}}}{\text{/}}2{{s}_{{11}}}} \right)({{A}^{Z}} - 1)$, где ${{s}_{{44}}}{\text{/}}2{{s}_{{11}}} > 0$. Поэтому случаи отрицательной, нулевой или положительной анизотропии, характеризуемые коэффициентом A, т.е. случаи $A > 0,{\text{\;}}A = 0,{\text{\;}}A < 0$, соответствуют случаям ${{A}^{Z}} > 1,{\text{\;}}{{A}^{Z}} = 1$, A^Z < 1.

Вторым параметром упругой анизотропии, который будет анализироваться в настоящей работе, является коэффициент Пуассона в базовой системе координат 〈001〉

Здесь и далее индексы во второй квадратной скобке указывают направления растяжения, а индексы в первой квадратной скобке – направление поперечной деформации. Использование параметров A и ν₀ в данной работе объясняется тем, что экстремальные значения коэффициента Пуассона могут быть описаны ими через простые соотношения

где ${{\nu }_{{\left[ {01\bar {1}} \right]\left[ {011} \right]}}}$, ${{\nu }_{{\left[ {100} \right]\left[ {011} \right]}}}$ и ${{\nu }_{{\left[ {001} \right]\left[ {010} \right]}}}$ – разные экстремальные значения, принимаемые коэффициентом Пуассона в зависимости от знаков A и ν₀. Подробный анализ экстремальных значений коэффициента Пуассона кубических кристаллов представлен в [16].

На рис. 1 представлены двумерные диаграммы упругих свойств кубических кристаллов. Первая (рис. 1,а), с координатными осями ${{c}_{{44}}}{\text{/}}{{c}_{{11}}}$ и ${{c}_{{12}}}{\text{/}}{{c}_{{11}}}$, была предложена Блэкманом в [27], вторая (рис. 1,b), с осями A и ν₀, – Епишиным и Лисовенко в [16]. Жирные черные линии на диаграммах – границы термодинамически допустимых значений упругих констант. Штриховые линии – границы характеристических областей коэффициента Пуассона: 1-я область – “Неауксетики” (Nonauxetics), 2-я и 3-я области – “Частичные ауксетики” (Partial auxetics) и 4-я – “Полные ауксетики” (Complete auxetics). Видно, что на обеих диаграммах нижние и верхние характеристические области разделены горизонтальными прямыми линиями, но негоризонтальные границы имеют разный вид. На диаграмме $A - {{\nu }_{0}}$-негоризонтальная граница представляет собой прямую линию, описываемую простым уравнением:

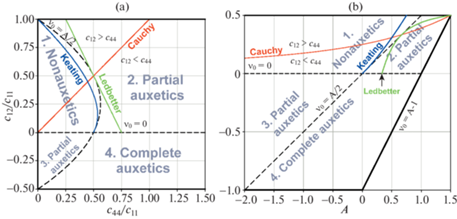
Эта линия начинается на нижней границе допустимых значений ν₀, с точки с координатами (A = –2; ν₀ = –1), проходит через начало координат (A = 0; ${{\nu }_{0}}$ = 0) и заканчивается на верхней границе допустимых значений ν₀ в точке (A = 1; ${{\nu }_{0}}$ = 0.5).

На диаграмме ${{c}_{{44}}}{\text{/}}{{c}_{{11}}} - {{c}_{{12}}}{\text{/}}{{c}_{{11}}}$ негоризонтальная граница описывается квадратичным уравнением

и имеет параболический вид.

Цветные линии на диаграммах имеют следующий смысл.

Линии Коши (красные линии) соответствуют соотношению Коши. Если все атомы расположены в узлах кристаллической решетки, а межатомные силы являются центральными силами и могут быть описаны гармоническим потенциалом, то для упругих констант должны выполнятся соотношения Коши ${{c}_{{iijk}}} = {{c}_{{ijik}}}$ ($i \ne j,~k$) [28]. Для кубических кристаллов соотношения Коши сводятся к одному соотношению:

На диаграмме ${{c}_{{44}}}{\text{/}}{{c}_{{11}}} - {{c}_{{12}}}{\text{/}}{{c}_{{11}}}$ соотношение (2.14) выполняется на исходящей из центра координат биссектрисе угла между осями ${{c}_{{44}}}{\text{/}}{{c}_{{11}}}$ и ${{c}_{{12}}}{\text{/}}{{c}_{{11}}}$. Согласно литературе, например [29], многие из кубических кристаллов следуют именно этому тренду.

На диаграмме $A - {{\nu }_{0}}$ зависимость (2.14) имеет нелинейный вид

Отсюда и далее будем называть кривую, описываемую уравнением (2.15), кривой или линией Коши. На диаграмме $A - {{\nu }_{0}}$ кривая Коши начинается в правом верхнем углу (A = 1.5; ${{\nu }_{0}}$ = 0.5) и асимптотически приближается к ν₀ = 0 при $A \to - \infty $.

Следует отметить, что разность ${{p}_{c}} = {{c}_{{12}}} - {{c}_{{44}}}$ называют давлением Коши. Поэтому линия, соответствующая соотношению Коши, разделяет диаграммы на две части: верхнюю, где давление Коши положительно (${{c}_{{12}}} > {{c}_{{44}}}$), и нижнюю, где давление Коши отрицательно (${{c}_{{12}}} < {{c}_{{44}}}$).

Линии Китинга (синие линии) теоретически предсказаны Китингом [30, 31] для алмазоподобных кристаллов с ковалентными связями методом наложения необходимых условий инвариантности на энергию деформации кристалла. В величинах упругих жесткостей c_ij оно имеет вид:

а в координатах A и ν₀:

Поэтому как на диаграмме ${{c}_{{44}}}{\text{/}}{{c}_{{11}}} - {{c}_{{12}}}{\text{/}}{{c}_{{11}}}$ так и на диаграмме $A - {{\nu }_{0}}$ зависимость Китинга имеет нелинейный вид.

Линии Ледбеттера (зеленые линии) имеют значение подобное кривым Китинга, но эта зависимость получена эмпирически Ледбеттером и соавторами [29] путем линейной аппроксимации экспериментальных точек на диаграмме ${{c}_{{44}}}{\text{/}}{{c}_{{11}}} - {{c}_{{12}}}{\text{/}}{{c}_{{11}}}$, соответствующих одноатомным и двухатомным ковалентным кубическим кристаллам. В величинах упругих жесткостей c_ij  уравнение этой линии имеет вид:

В координатах $A$ – ${{\nu }_{0}}$ зависимость Ледбеттера нелинейна:

Поэтому на диаграмме $A - {{\nu }_{0}}$ зеленая линия искривлена. Краткий вывод формул (2.13), (2.15), (2.17), (2.19) представлен в пункте 4.

Примечательно, что прямолинейная граница, разделяющая 1-ую и 2-ую характеристические области коэффициента Пуассона, и описываемая уравнением (2.12), расположена между кривыми Китинга и Ледбеттера, см. рис. 1,b. С уменьшением ν₀ кривая Китинга плавно примыкает к этой границе в начале координат (A = 0; ${{\nu }_{0}}$ = 0), т.е. для обеих линий производная $d{{\nu }_{0}}{\text{/}}dA\left( {A = 0} \right) = 1{\text{/}}2$, а кривая Ледбеттера плавно приближается к данной границе при увеличении ν₀ и касается ее в точке (A = 2/3; ${{\nu }_{0}}$ = 1/3) с идентичным же наклоном $d{{\nu }_{0}}{\text{/}}dA\left( {A = 2{\text{/}}3} \right) = 1{\text{/}}2$.

Достоинством широко известной диаграммы ${{c}_{{44}}}{\text{/}}{{c}_{{11}}} - {{c}_{{12}}}{\text{/}}{{c}_{{11}}}$ является ее простота. В то же время эта диаграмма неудобна для анализа величин коэффициента упругой анизотропии A и коэффициента Пуассона ν₀. Поскольку именно эти характеристики упругости рассматриваются в настоящей работе, ниже будет использоваться диаграмма $A - {{\nu }_{0}}$, где переменными координатных осей являются A и ν₀. Преимуществом последней диаграммы является также линейность границ, разделяющих характеристические области ауксетичности, что упрощает анализ и идентификацию типа ауксетиков.

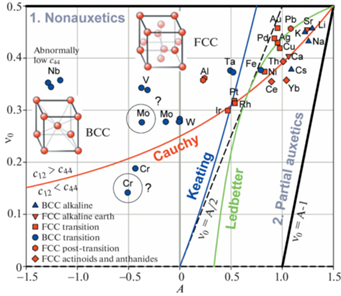
3. Анализ зависимости упругих свойств от типа структуры и межатомной связи. На рис. 2 представлена диаграмма $A - {{\nu }_{0}}$ для кубических металлов с А1 структурой меди (ГЦК) и А2 структурой вольфрама (ОЦК). Каждая точка на диаграмме имеет координаты $\left( {A,{{\nu }_{0}}} \right)$, определяемые упругими свойствами металла, название которого указано рядом. Красные символы ▼, ◼, ◆, ⬢ соответствуют ГЦК металлам, синие символы ▲, ⚫ – ОЦК металлам. Разные обозначения точек соответствуют разным типам металлов: щелочным (Li, K, Na, Cs), редкоземельным (Ca, Sr), переходным (V, Cr, Fe, Ni, Cu, Nb, Mo, Rh, Pd, Ag, Ta, W, Ir, Pt, Au), постпереходным (Al, Pb), актиноидам (Ce, Yb) и лантаноидам (Th). Как видно из рис. 2 все ГЦК металлы положительно анизотропны (A > 0), тогда так часть ОЦК металлов, V, Cr, Nb и Mo, показывает отрицательную анизотропию (A < 0). ОЦК металл W практически изотропен ($A \approx 0$). Точки большинства металлов сконцентрированы в верхней правой части диаграммы, при этом их плотность особенно высока вблизи угла диаграммы (A = 1.5; ${{\nu }_{0}}$ = 0.5) в окрестности треугольной области, ограниченной кривой Коши и прямой ${{\nu }_{0}} = A{\text{/}}2$. Эти металлы являются частичными ауксетиками, так как их точки $\left( {A,{{\nu }_{0}}} \right)$ лежат правее граничной прямой ${{\nu }_{0}} = A{\text{/}}2$, т.е. в зоне ауксетичности 2. Наиболее приближены к углу диаграммы точки щелочных ОЦК металлов Li, K, Na и щелочноземельный ГЦК металл Sr. Эти металлы имеют наименьшее значение коэффициента Пуассона среди кубических кристаллов, представленных на рис. 2: ${{\nu }_{{{\text{min}}}}} = - 0.54$ у Li, ${{\nu }_{{{\text{min}}}}} = - 0.44$ у Na, ${{\nu }_{{{\text{min}}}}}$ = –0.42 у K, ${{\nu }_{{{\text{min}}}}} = - 0.26$ у Sr [15, 18]. Их коэффициент анизотропии A и коэффициент ${{\nu }_{0}}$ близки к максимально возможным значениям и соответственно находятся в интервалах 1.22–1.29 и 0.432–0.457. Несколько далее от угла диаграммы отстоят щелочноземельный ГЦК металл Ca и щелочной ОЦК металл Cs, которые имеют большие по абсолютной величине отрицательные минимальные значения коэффициента Пуассона (${{\nu }_{{{\text{min}}}}} = - 0.27$ у Ca и ${{\nu }_{{{\text{min}}}}} = - 0.36$ у Cs). В пределах вышеуказанной треугольной области располагаются такие переходные металлы как Cu, Ag, Au, Pd, Ni (все ГЦК) и Fe (ОЦК), и постпереходной ГЦК-металл Pb. У переходных ГЦК металлов минимальное значение коэффициента Пуассона не превосходит –0.13: ${{\nu }_{{{\text{min}}}}} = - 0.13$ у Cu, ${{\nu }_{{{\text{min}}}}} = - 0.13$ у Fe, ${{\nu }_{{{\text{min}}}}} = - 0.09$ у Ag, ${{\nu }_{{{\text{min}}}}} = - 0.07$ у Ni, ${{\nu }_{{{\text{min}}}}} = - 0.04$ у Pd и ${{\nu }_{{{\text{min}}}}} = - 0.03$ у Au. Постпереходный ОЦК-металл Pb имеет ${{\nu }_{{{\text{min}}}}} = - 0.20$. Актиноиды Ce (${{\nu }_{{{\text{min}}}}}$ = –0.17) и Yb (${{\nu }_{{{\text{min}}}}} = - 0.34$) и лантаноид Th (${{\nu }_{{{\text{min}}}}} = - 0.22$) (все ГЦК) находятся несколько ниже. Pt, Rh и Ir (ГЦК переходные металлы платиновой группы) сконцентрированы у пересечения кривых Коши и Китинга и являются неауксетиками.

Характерно, что металлы из одной подгруппы периодической системы элементов, как правило, показывают подобные упругие свойства, а их точки подобным образом расположены на диаграмме $A - {{\nu }_{0}}$, например, см. конфигурации Li, K, Na, Cs (AI) и Cu, Ag, Au (BI) с одним валентным электроном, Ca, Sr (AII) с двумя валентными электронами, V, Nb, Ta (BV) и Cr, Mo, W (BVI) соответственно с пятью и шестью валентными электронами. Такое подобие упругих свойств закономерно, т.к. прочность металлической связи повышается с увеличением числа валентных электронов, участвующих в ее образовании.

Следует отметить, что после построения диаграммы на рис. 2 по данным справочника Ландольт–Берштайн [32] было обнаружено, что точки таких металлов как Ta, Al и Mo, и особенно V и Nb лежат существенно выше кривой Коши (область положительных “давлений Коши”, ${{c}_{{12}}} > {{c}_{{44}}}$), а Cr ниже, где ${{c}_{{12}}} < {{c}_{{44}}}$. Сравнение с данными из других литературных источников [33–37], см. множественные точки этих металлов, подтвердило достоверность данных для Ta, Al, V и Nb, но в то же время показало различие для Mo и Cr. Поэтому вызывающие сомнения точки Mo и Cr обозначены знаком “?”. Причиной смещения Ta, Al, V и Nb в область положительных “давлений Коши” является низкое значение их сдвиговой константы c₄₄ по сравнению с константой ${{c}_{{12}}}$. Для этих металлов отношения ${{c}_{{44}}}{\text{/}}{{c}_{{12}}}$ соответственно равны: ≈0.53, ≈0.48, ≈0.39 и ≈0.23.

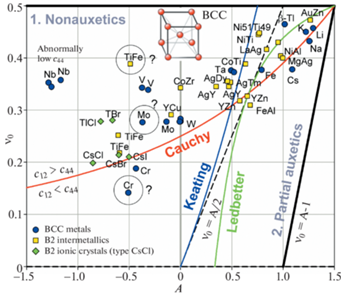
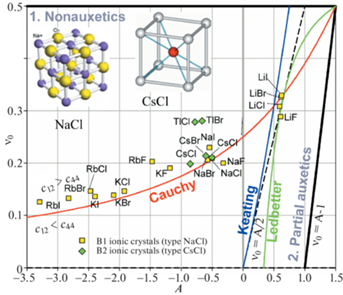
На рис. 3 сравниваются A и ${{\nu }_{0}}$ кристаллов, в которых атомы имеют ОЦК пространственное расположение в общей кристаллической решетке, но имеют разный тип межатомной связи: ОЦК-металлы – металлическая, В2 интерметаллиды – преимущественно металлическая, частично ионно-ковалентная и В2 ионные кристаллы – преимущественно ионная, частично ковалентная. Видно, что все точки, независимо от типа межатомной связи в кристаллах, имеют тенденцию располагаться вблизи кривой Коши, однако имеет место также общая закономерность смещения их вверх, где ${{c}_{{12}}} > {{c}_{{44}}}$. Это особенно явно выражено для металлов V и Nb, как отмечалось выше, а также для интерметаллида CoZr. Сильное смещение вверх одной из точек интерметаллида TiFe, помеченной знаком “?”, очевидно ошибочно, так как это не согласуется с двумя другими точками TiFe, расположенными вблизи кривой Коши, построенными по данным из двух независимых источников [32, 42]. Характерно, что В2 интерметаллиды, также как и ОЦК-металлы, могут быть положительно или отрицательно анизотропны. Большинство положительно анизотропны (A > 0), но некоторые, YCu и TiFe, отрицательно анизотропны (A < 0), а интерметаллид CoZr – изотропен ($A \approx 0$). Все представленные на рис. 3 В2 ионные кристаллы отрицательно анизотропны и являются неауксетиками, однако из этого видимо не следует делать вывод о том, что это свойство является общим для ионных кристаллов с В2 структурой, так как число представленных точек мало. Следует отметить, что число известных В2 ионных кристаллов (структура типа CsCl) весьма ограничено, например, CsCl, CsBr, TlCl, TlBr (представлены на рис. 3) и под высоким давлением RbCl, RbBr и RbI. Кристаллы со структурой типа CsCl являются соединениями одновалентных атомов металла и галогена. При этом ОЦК-расположение атомов возможно если атом металла достаточно большой, как, например, атом Cs. В противном случае отрицательные ионы галогенных атомов сойдутся на расстояние, при котором начнется их отталкивание.

На рис. 4 сравниваются A и ${{\nu }_{0}}$ ионных кристаллов со структурой В1 и В2. В обоих случаях межатомная связь ионная, но разное пространственное расположение атомов. В случае В1 (структурный тип NaCl) атомы расположены в общей примитивной кристаллической решетке, в случае В2 (структурный тип CsCl) – в общей ОЦК-решетке. Видно, что точки, соответствующие большинству кристаллов, лежат вблизи кривой Коши, хотя и несколько смещены вверх, где ${{c}_{{12}}} > {{c}_{{44}}}$. Из общей тенденции несколько выпадают точки TlCl и TlBr, однако в отличие от остальных представленных на рис. 4 ионных соединений, в данных соединениях положительный ион Tl⁺ является не щелочным металлом, а полуметаллом. Также видно, что группа LiAM (AM = F, Cl, Br или I) имеет тенденцию быть выстроенной вдоль участка локального совпадения кривой Ледберга и прямой ${{\nu }_{0}} = A{\text{/}}2$, где должны располагаться точки ковалентных кристаллов. Причина этого, видимо, заключается в том, что у соединений LiX имеется небольшая доля ковалентной связи. Отметим, что в группе LiAM (AM = F, Cl, Br или I) ауксетические свойства проявляет только LiF (${{\nu }_{{{\text{min}}}}} = - 0.02$), т.к. фтор F располагается во 2-м периоде таблицы Д.И. Менделеева, тогда как Cl, Br и I соответственно в 3-м, 4-м и 5-м.

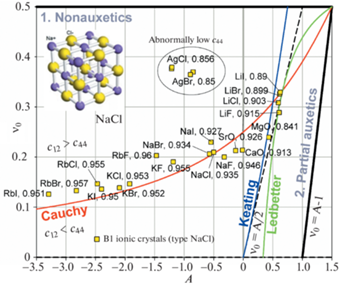
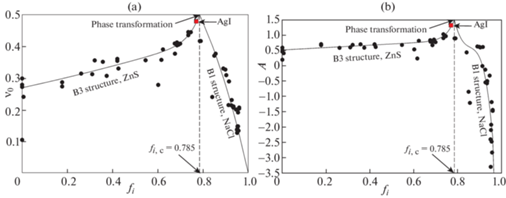
На рис. 5 представлена диаграмма $A - {{\nu }_{0}}$ отдельно для кубических кристаллов со структурой типа NaCl (В1). Такую структуру образуют бинарные соединения AIBVII т.е. галогениды (фториды, хлориды, бромиды и иодиды) таких щелочных элементов как литий (LiF, LiCl, LiBr, LiI), натрий (NaF, NaCl, NaBr, NaI), калий (KF, KCl, KBr, KI) и рубидий (RbF, RbCl, RbBr, RbI), а также хлорид и бромид серебра (AgCl, AgBr). Кроме того, структуру типа NaCl имеют некоторые окислы металлов, например, MgO и CaO (бинарные соединения типа AIIBVI). Для каждой точки на рис. 5 приведена доля ионной связи f_i, характеризующая степень поляризации межатомной связи. Данные значения f_i были рассчитаны Филлипсом [45] с использованием спектроскопической теории межатомной связи. Проведенное Филлипсом сравнение с результатами предыдущих термохимических расчетов f_i, проведенных Полингом [49], и расчетов Кулсона с соавторами [50], основанных на концепции валентных связей, показало в целом удовлетворительное совпадение. На рис. 5 видна тенденция: при смещении вверх по кривой Коши доля ионной связи f_i уменьшается. Например, RbI с f_i = 0.951 находится в нижней части кривой Коши, а LiF с f_i = 0.89 в верхней.

Точки ($A,~{{\nu }_{0}}$), соответствующие соединениям с f_i > 0.9 довольно хорошо ложатся на кривую Коши, тогда как для соединений с f_i ≈ 0.85, MgO, AgCl и AgBr имеется отклонение от этой кривой. В особенности оно велико для хлорида и бромида серебра, коэффициент Пуассона которых ${{\nu }_{0}}$ ≈ 0.37, значительно выше, чем у других ионных кристаллов, а также низкая величина сдвиговой константа ${{c}_{{44}}}$. Достоверность приведенных на рис. 5 значений для AgCl и AgBr подтверждается сравнением данных из различных источников [32, 46, 47], см. двойные точки.

Из рис. 5 видно, что наибольшая отрицательная анизотропия, –3.3 < A < –1.5, и, соответственно, наименьший коэффициент Пуассона, 0.13 < ${{\nu }_{0}}$ < 0.2, наблюдаются для галогенидов рубидия. Для этих соединений также типична высокая поляризация ионной связи,  f_i ≈ 0.95. Для галогенидов лития наблюдается положительная анизотропия, $A$ ≈ +0.6, и, соответственно, наибольший коэффициент Пуассона, ${{\nu }_{0}}$ ≈ 0.29–0.33. Для этих соединений также типична более низкая доля ионной связи, f_i ≈ 0.9. Точки для галогенидов калия и натрия занимают промежуточные значения как по величинам A и ${{\nu }_{0}}$, так и по величине f_i. В целом имеется следующая общая тенденция: при смещении щелочно-металлического компонента вниз в подгруппе АI периодической таблицы элементов Li → Na → K → Rb, т.е. с увеличением номера периода, точки ($A,~{{\nu }_{0}}$) смещаются вниз по кривой Коши. Зависимость от типа элемента-галогена не столь явная, но в первом приближении для них наблюдается обратная тенденция, с увеличением номера периода F → Cl → Br → I точки ($A,~{{\nu }_{0}}$) смещаются вверх по кривой Коши.

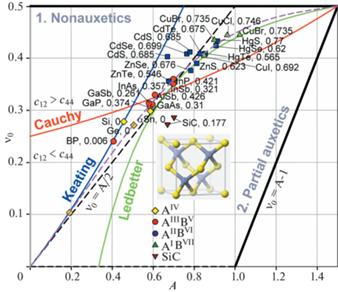
На рис. 6 представлена диаграмма $A - {{\nu }_{0}}$ для кристаллов со структурой алмаза А4, это элементы AIV группы периодической системы, C, Si, Ge и α-Sn, и кристаллов с алмазоподобной структурой цинковой обманки В3, в основном – бинарные соединения типа A^NB^8–N. Из представленных кристаллов на рис. 6 это:

– A^IIIB^V – борид фосфора BP, фосфиды, арсениды и антимониды алюминия, галия и индия, соответственно AlSb, GaP, GaAs, GaSb, и InP, InAs, InSb. Представленные материалы являются неауксетиками.

– A^IIB^VI – сульфиды, селениды и теллуриды цинка, кадмия и ртути, соответственно ZnS, ZnSe, ZnTe; CdS, CdSe, CdTe и HgS, HgSe, HgTe. Частичными ауксетиками являются ZnSe, ZnTe, CdTe и HgS, HgSe, HgTe [15, 18].

– A^IB^VII – хлориды, бориды и иодиды меди, соответственно CuCl, CuBr и CuI. Данные кристаллы являются частичными ауксетиками.

Также структуру цинковой обманки имеют кристаллы карбида кремния SiC. Кристалл SiC является частичным ауксетиком (${{\nu }_{{{\text{min}}}}} = - 0.10$).

На рис. 6 видно, что все алмазоподобные кристаллы положительно анизотропны (A > 0) и для них наблюдается зависимость: с повышением доли ионной связи f_i  упругая анизотропия, характеризуемая коэффициентом $A$, возрастает, и соответственно повышается значение ν₀. Так для алмаза с  f_i = 0, расположенного вблизи нижнего левого угла диаграммы, $A \approx $ 0.19 и ${{\nu }_{0}} \approx 0.10$, для арсенида галия GaAs с ${{f}_{i}} = $ 0.31, расположенного центральной части диаграммы, $A \approx $ 0.60 и ${{\nu }_{0}} \approx 0.31$, а для бромида меди CuBr с f_i = 0.735, расположенного в вблизи верхнего правого угла диаграммы, $A \approx $ 1.02 и ${{\nu }_{0}} \approx 0.44$.

Из рис. 6 видно, что точки, соответствующие полностью ковалентным алмазу C и кремнию Si, а также почти полностью ковалентному бориду фосфора BP (${{f}_{i}} = $ 0.006) хорошо ложатся на теоретическую кривую Китинга. Однако для двух других полностью ковалентных кристаллов, германия Ge и олова α-Sn имеется заметное отклонение от этой зависимости в сторону бóльших значений коэффициента упругой анизотропии A. По мере увеличения f_i это отклонение ΔA возрастает. Так для A^IIIB^V соединений, группы GaP, GaAs, GaSb, и InP, InAs, InSb, с f_i ≈ 0.3–0.4 отклонение ΔA составляет около 0.1–0.12, тогда как для A^IB^VII соединений, CuCl и CuBr, с f_i ≈ 0.75 отклонение ΔA достигает ≈0.3. Соединения A^IIB^VI, ZnS, ZnSe, ZnTe; CdS, CdSe, CdTe и HgS, HgSe, HgTe, с f_i ≈ 0.55–0.7 занимают промежуточное положение, для них ΔA ≈ 0.2.

Примечательным является тот факт, что точки большинства А4 и В3 кристаллов расположены вблизи прямой линии $~{{\nu }_{0}} = A{\text{/}}2$ являющейся границей, разделяющей характеристические области “1. Неауксетики” / “2. Частичные ауксетики”. Однако с повышением  f_i наблюдается отклонение и от этой граничной линии, т.е. кристаллы становятся частичными ауксетиками, как, например, HgTe (${{\nu }_{{{\text{min}}}}} = - 0.03$), HgSe (${{\nu }_{{{\text{min}}}}}$ = –0.05), HgS (${{\nu }_{{{\text{min}}}}} = - 0.04$) и CuI (${{\nu }_{{{\text{min}}}}} = - 0.03$), CuCl (${{\nu }_{{{\text{min}}}}} = - 0.07$) и CuBr (${{\nu }_{{{\text{min}}}}}$ = –0.03). Эмпирическая зависимость Ледбеттера удовлетворительно описывает отклонение точек от прямой ${{\nu }_{0}} = A{\text{/}}2$ в верхней правой части диаграммы, но дает большую ошибку в нижней левой ее части для таких полностью ковалентных кристаллов как алмаз C, борид фосфора BP и кремний Si. Поэтому для описания положения точек А4 и В3 кристаллов в настоящей работе предлагается зависимость:

Данная зависимость была получена при следующих ограничениях: исход из начала координат ($A = 0$, ν₀ = 0), также как теоретическая кривая Китинга и граничная прямая ${{\nu }_{0}} = A{\text{/}}2$, с таким же наклоном – $d{{\nu }_{0}}{\text{/}}dA\left( {A = 0} \right) = 0.5$. Окончание – в углу диаграммы ($A = 1.5$, ν₀= 0.5), также как и у кривой Ледбеттера. Последнее ограничение накладывается на подгоночные коэффициенты при A², A³ и A⁴, поэтому только два из них являются независимыми и определяют форму кривой ${{\nu }_{0}} = f\left( A \right)$. На рис. 6 зависимость (3.1) показана штриховой фиолетовой линией. Видно, что данная кривая правильно отражает характер зависимости ${{\nu }_{0}} = f\left( A \right)$ и удовлетворительно описывает положение большинства точек.

На рис. 7 представлены графики зависимостей коэффициента упругой анизотропии A и коэффициента Пуассона ${{\nu }_{0}}$ кристаллов со структурой В1 и В3 от доли ионной связи  f_i. На графиках видно, что с повышением доли ионной связи  f_i коэффициенты $A$ и ${{\nu }_{0}}$ сначала повышаются достигая максимальных значений A_max и ${{\nu }_{{0,{\text{max}}}}}$ при критическом значении ${{f}_{i}} = {{f}_{{i,c}}}$, а затем резко понижаются. Исходя из графика на рис. 5 логично предположить, что A и ${{\nu }_{0}}$ стремятся соответственно к $ - \infty $ и 0 при ${{f}_{i}} \to 1$. На основании наблюдаемых на рис. 6 экспериментальных трендов и формы кривых Коши и Ледбеттера можно также предположить, что ${{A}_{{{\text{max}}}}}$ = 1.5 и ${{\nu }_{{0,{\text{max}}}}}$ = 0.5, т.е. их значения совпадают с координатами предельной точки $\left( {A,{{\nu }_{0}}} \right)$ в верхнем правом углу диаграммы $A - {{\nu }_{0}}$. Наиболее близка к этим значениям красная точка В3 кристалла йодистого серебра AgI с $A \approx 1.3$ и ${{\nu }_{0}} \approx 0.48$. Данные величины получены используя константы c_ij, рассчитанные для В3 структуры AgI модифицированным методом Мартина в [44]. Показательно, что все точки слева от максимума соответствуют В3-кристаллам (структура ZnS), тогда как все точки справа – В1-кристаллам (структура NaCl). Из этого следует, что при достижении критической доли ионной связи ${{f}_{i}} = {{f}_{{i,c}}}$ происходит изменение кристаллической структуры В1 → В3. Согласно Филлипсу [45] это ковалентно-ионное превращение происходит при ${{f}_{{i,c}}} = 0.785$, что соответствует положению максимумов на графиках, представленных на рис. 7. Характерно, что кристаллы с f_i близким к 0.785, например, AgI, MgS и MgSe структурно нестабильны, см. [46, 47].

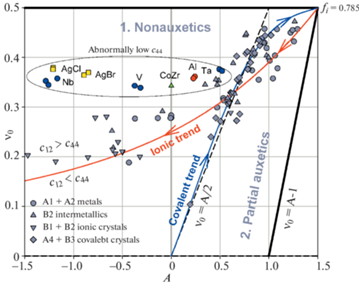
На рис. 8 представлена диаграмма $A~ - {{\nu }_{0}}$, обобщающая приведенные выше результаты для разных типов одноатомных и двухатомных кубических кристаллов. На диаграмме показаны два тренда – ковалентный (синяя линия, аппроксимация (3.1)) и ионный (красная линия, зависимость Коши (2.14, 2.15)). Исключая из рассмотрения особые точки (выделены цветом), можно сделать вывод о том, что все остальные точки (серые) в первом приближении следуют этим трендам. При этом для точек, прилегающих к линии Коши, имеется систематическое смещение вверх от этой линии, т.е. для них выполнятся неравенство ${{c}_{{12}}} > {{c}_{{44}}}$. Для некоторых кристаллов, например, Ta, Al, CoZr, V, AgBr, AgCl, Nb (см. цветные точки, заключенных в овал) это смещение особенно велико потому, что величина их сдвиговой константы c₄₄ аномально низка. Замечательным свойством диаграммы $A~ - {{\nu }_{0}}$ является то, что в отличие от диаграммы Блекмана (рис. 1,а) на ней оба тренда образуют единую непрерывную линию ${{\nu }_{0}} = f\left( A \right)$, которая исходит из начала координат $\left( {A = 0,~\,\,{{\nu }_{0}} = 0} \right)$, далее идет вверх вправо и приходит в экстремальную угловую точку диаграммы $\left( {A = 1.5,\,\,{{\nu }_{0}} = 0.5} \right)$, а затем изгибается и идет вниз влево стремясь в пределе к $\left( {A = - \infty ,\,\,{{\nu }_{0}} = 0} \right)$. Причиной этого различия в представлении кривых является то, что вся верхняя горизонтальная граница диаграммы Блекмана (${{c}_{{12}}}{\text{/}}{{c}_{{11}}} = 1$), где заканчиваются линии Коши и Ледбеттера, сводится на диаграмме $A~ - {{\nu }_{0}}$ в одну точку $\left( {A = 1.5,~\,\,{{\nu }_{0}} = 0.5} \right)$. Положение точек $\left( {A,~{{\nu }_{0}}} \right)$ ионно-ковалентных кристаллов на единой кривой ${{\nu }_{0}} = f\left( A \right)$ определяется величиной доли ионной связи f_i. При увеличении f_i от нуля до критического значения 0.785 происходит смещение точек $\left( {A,~{{\nu }_{0}}} \right)$ вдоль ковалентного тренда от начала координат к угловой точке $\left( {A = 1.5,~{{\nu }_{0}} = 0.5} \right)$. При дальнейшем увеличении f_i точки переходят на ионный тренд и смещаются в направлении предела $\left( {A = - \infty ,~{{\nu }_{0}} = 0} \right)$. Следует отметить, что перегиб единой кривой ${{\nu }_{0}} = f\left( A \right)$ в точке $\left( {A = 1.5,~\,\,{{\nu }_{0}} = 0.5} \right)$ согласуется с выводами работы [44], согласно которой ковалентно-ионный переход (изменение структуры) происходит вследствие нестабильности кристаллической решетки при приближении эффективного модуля сдвига ${{c}_{s}} = \frac{1}{2}\left( {{{c}_{{11}}} - {{c}_{{12}}}} \right)$ к нулю, что соответствует стремлению коэффициента Пуассона к пределу ${{\nu }_{0}} \to 0.5$.

4. Вывод формул (2.13), (2.15), (2.17) и (2.19). Уравнение негоризонтальной границы характеристических областей коэффициента Пуассона

Подставляя A и ν₀ соответственно из (2.4) и (2.8), и используя (2.1), (2.2) и (2.3) с заменой s_ij → c_ij, получаем

Соотношение Коши

Поставляя c₁₂ и c₄₄ соответственно из (2.2) и (2.3), и учитывая (2.4) и (2.8) получаем квадратное уравнение относительно ${{{{\nu }}}_{0}}$

Его физически корректное решение

Соотношение Китинга

Поставляя c₁₁, c₁₂ и c₄₄ соответственно из (2.1), (2.2) и (2.3), а также учитывая (2.4) и (2.8) получаем квадратное уравнение

Его физически корректное решение

Соотношение Ледбеттера

Проводя аналогичные подстановки как в предыдущем случае, получаем квадратное уравнение

Его физически корректное решение

5. Заключение. С использованием диаграммы $A~ - {{\nu }_{0}}$ проанализирована зависимость упругих свойств одноатомных и двухатомных кубических кристаллов от типов их кристаллической структуры и межатомной связи. Показано, что упругие свойства этих кристаллов следуют одному из двух трендов – ковалентному или ионному, которые на диаграмме $A~ - {{\nu }_{0}}$ образуют единую непрерывную линию ${{\nu }_{0}}\, = \,f(A)$, исходящую из начала координат $(A = 0,~{{\nu }_{0}} = 0)$, приходящую в угловую точку диаграммы $(A = 1.5,~\,\,{{\nu }_{0}} = 0.5)$ и далее изгибаясь стремящуюся к $(A = - \infty ,~\,\,{{\nu }_{0}} = 0)$. Смещение точек $(A,~{{\nu }_{0}})$ ионно-ковалентных кристаллов вдоль этой линии определяется величиной доли ионной связи f_i. При $0 \leqslant {{f}_{i}} < 0.785$ точки $(A,~{{\nu }_{0}})$ располагаются на ковалентном тренде, а при ${{f}_{i}} > 0.785$ – на ионном.

Проведенный анализ показал, что ауксетики выявляются среди одноатомных кристаллов со структурой А1 (ГЦК), относящимся к щелочноземельным (Ca, Sr), переходным (Ni, Cu, Ag, Au) и постпереходным (Pb) металлам, актиноидам (Ce, Yb) и лантаноидам (Th), и одноатомных кристаллов со структурой А2 (ОЦК), относящимся к щелочным металлам (Li, K, Na, Cs). Наибольшие отрицательные значения коэффициента Пуассона наблюдаются у щелочных металлов (${{\nu }_{{{\text{min}}}}} = - 0.54$ у Li, ${{\nu }_{{{\text{min}}}}} = - 0.44$ у Na, ${{\nu }_{{{\text{min}}}}} = - 0.42$ у K, ${{\nu }_{{{\text{min}}}}} = - 0.26$ у Sr). Большие отрицательные значения коэффициента Пуассона выявляются у щелочноземельных металлов (${{\nu }_{{{\text{min}}}}} = - 0.27$ у Ca и ${{\nu }_{{{\text{min}}}}}$ = = –0.36 у Cs), постпереходного металла Pb (${{\nu }_{{{\text{min}}}}} = - 0.20$), актиноидов Ce (${{\nu }_{{{\text{min}}}}}$ = –0.17), Yb (${{\nu }_{{{\text{min}}}}} = - 0.34$) и лантаноида Th (${{\nu }_{{{\text{min}}}}} = - 0.22$).

Среди проанализированных в этой работе бинарных двухатомных соединений наибольшее количество ауксетиков выявляется среди алмазоподобных кристаллов со структурой цинковой обманки B3, имеющих стехиометрию типа A^NB^8-N (A^IIB^VI: ZnSe, ZnTe, CdTe и HgS, HgSe, HgTe; A^IIB^VI: CuCl, CuBr и CuI). Кристаллы соединений типа A^IIIB^V, являются неауксетиками. Среди кубических В1 и В2 ионных кристаллов, структурных типов NaCl и CsCl, только один LiF, по-видимому, является ауксетиком с небольшим по абсолютной величине ${{\nu }_{{{\text{min}}}}} = - 0.02$.

Работа выполнена при поддержке гранта Российского научного фонда (проект № 22-29-01200).