Известия РАН. Механика твердого тела, 2023, № 1, стр. 47-54
ГИДРОМЕХАНИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЗАГЛУБЛЕННОГО НАЧАЛЬНОГО ИМПУЛЬСНОГО ВОЗДЕЙСТВИЯ НА ГИДРОГЕОФИЗИЧЕСКИЙ МАССИВ
К. Н. Анахаев a, b, *, В. В. Беликов b, **
a Институт прикладной математики и автоматизации Кабардино-Балкарского научного центра Российской академии наук (ИПМА КБНЦ РАН)
Нальчик, Россия
b Институт водных проблем Российской академии наук (ИВП РАН)
Москва, Россия
* E-mail: anaha13@mail.ru
** E-mail: belvv@bk.ru
Поступила в редакцию 27.10.2021
После доработки 10.12.2021
Принята к публикации 20.12.2021
- EDN: KFXNIJ
- DOI: 10.31857/S0572329922060022
Аннотация
В работе рассматривается потенциальная задача заглубленного импульсного воздействия в начальный момент времени на гидрогеофизический массив, что может иметь место при подземных (подводных) взрывах, извержениях вулканов, сейсмах и т.д. Воздействие очага импульса моделировалось источником округленной формы с единичным напором, а область стока – линией нулевого потенциала. Получено строгое гидромеханическое решение задачи с установлением аналитической взаимосвязи между физической областью течения и комплексным потенциалом на основе теории функции комплексного переменного – использования метода последовательных конформных отображений с определением всех необходимых характеристик потока. Приведены примеры расчета для частных случаев с построением криволинейных ортогональных гидродинамических сеток, очертаний семейств линий равных напоров и линий токов, профилей источников импульса, а также эпюр скоростей, напоров и расходов потенциального потока.
Введение. Импульсные воздействия на гидрогеофизические массивы могут иметь естественное (падения астероидов, извержения вулканов, сейсмические воздействия и т.д.) и искусственное (надземные, подземные и подводные взрывы) происхождения. Во многих случаях они сопровождаются крупномасштабными динамическими изменениями окружающей природной среды с возникновениями цунами, наводнений, оползней и обвалов береговых склонов [1–5] и, нередко, оказывают значительные негативно-разрушающие воздействия на населенные пункты, селитебные территории, объекты экономики, представляя значительную угрозу для безопасности жизнедеятельности людей. При научных исследованиях указанных воздействий с оценкой их мощности и прогнозом возможных последствий наиболее широкое применение получила гидродинамическая модель тяжелой идеальной жидкости [3, 5, 6]. В частности, в работах [6, 7] рассматриваются случаи падения (ударов) высокоскоростных (до 15–50 км/с) астероидов на земную и водную поверхности с проникновениями, соответственно, в грунтовую толщу и до дна водной акватории.
Особенности развития во времени подводного импульса (взрыва) рассматривается в работе [3, с. 279–281], где указано также на наличие гидродинамического парадокса – при увеличении глубины расположения источника импульса (в определенном интервале) не происходит снижение силы импульсного воздействия, то есть пробивная сила ударной волны остается постоянной. Задача о распределении импульсных давлений по ряду плавающих тел в покоящейся жидкости при ударном воздействии на одного из них в момент времени, непосредственно следующий за ударом, изложена в [6, с. 259].
Импульсные (взрывные) методы воздействия на гидрогеофизические массивы могут быть использованы также при создании искусственных островов и оградительных дамб (преимущественно в относительно мелкой воде) путем комбинированных разновременных взрывов, при которых первые (вспомогательные заряды) удаляют слой воды, а вторые (наклонные заряды с двух сторон) набрасывают (сгребают) грунт дна водоема в тело насыпи [8, с. 8].
В работе [9, с. 77] рассматривается задача о распределении давления в безграничной несжимаемой жидкости от воздействия подводного импульсного источника (взрыва мины) в начальный (весьма малый) промежуток времени в гидромеханической постановке как плоская задача осесимметричного потенциального потока без учета наличия водной поверхности.
1. Постановка задачи. В работе начальное импульсное воздействие заглубленного источника округленного профиля на гидрогеофизический массив (водный, грунтовый) рассматривается в плоской постановке как задача гидромеханического моделирования потенциального потока [1, 2, 6, 10], принимая контур источника импульса за полный (единичный) потенциал, а горизонтальную поверхность массива (линию стока) – за линию нулевого потенциала (рис. 1).
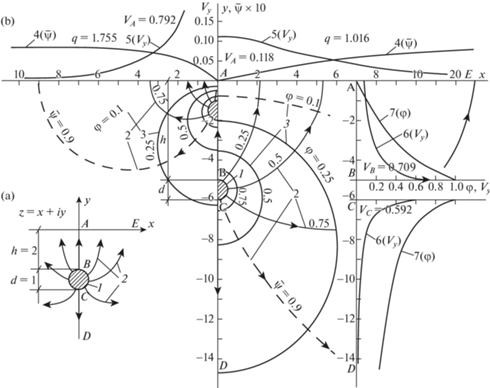
Рис. 1.
Расчетные характеристики поля потенциального потока при заглубленном начальном импульсном воздействии: a) общий симметричный характер потенциального потока; b) криволинейные ортогональные гидродинамические сетки потока при $h{\text{/}}d = 5$ (правая половина) и $h{\text{/}}d = 1$ (левая половина); 1 – очертания профилей импульсного источника $BC$; 2 – очертания семейства кривых функции тока (относительных расходов ${{\bar {\psi }}}$) – через 0.25; 3 – очертания семейства кривых линий равных напоров (потенциальной функции ${{\varphi }}$) – через 0.25; 4 – эпюры расходов (функции тока ${{\bar {\psi }}}$) вдоль границ стока; 5 – эпюры выходных скоростей потока ${{V}_{y}} = {{V}_{{out}}}$ вдоль границ стока; 6 и 7 – соответственно, эпюры действующих вертикальных скоростей ${{V}_{y}}$ и напоров ${{\varphi }}$ вдоль осевой линии области течения.
2. Метод и построение решения. Задача решается на основе теории функции комплексного переменного с использованием метода последовательных конформных отображений, отличительной особенностью от [1, 3, 6] которой является аналитическое определение в элементарных функциях характеристик потенциального потока в первоначальный момент времени импульсного воздействия.
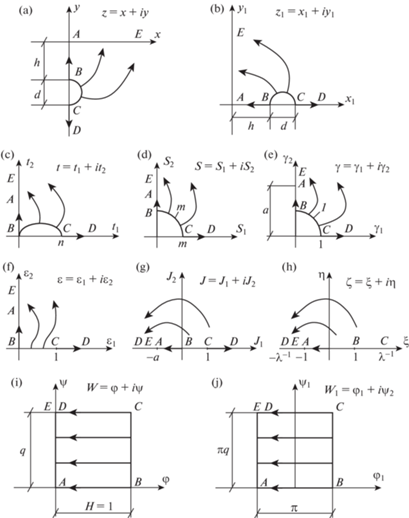
В силу симметрии физической области течения $z = x + iy$ (рис. 1, a) в качестве расчетной схемы принята правая ее половина $ABCDE$ (рис. 2, a), представленная в IV квадранте источником импульса округленного профиля (размером d по вертикальной оси), заглубленным в гидрогеофизический массив на величину $h$. Решение задачи отыскивается на основе аналитической однозначной взаимосвязи между указанной областью физической течения $z = x + iy$ (рис. 1, 2, a) и областью комплексного потенциала $W = {{\varphi }} + i{{\psi }}$, геометрический образ которого для принятой расчетной схемы представлен прямоугольником $ABCD(E)$ с точкой A в центре координат ${{\varphi }}A{{\psi }}$ (рис. 2, i), где ${{\varphi }}$ и ${{\psi }}$ – напорная (потенциальная) функция и функция тока. В указанном прямоугольнике линии равного напора $BC$ и $AE$ соответствуют значениям потенциала, равным напорам – единичному ${{\varphi }} = H = 1$ (в усл. ед.) и нулевому ${{\varphi }} = 0$, а линии тока $BA$ и $CD$ – значениям функции тока нулевого (${{\psi }} = 0$) и полного (для правой половины области течения ${{\psi }} = q$) расходов.
Рис. 2.
Схема последовательных конформных отображений, устанавливающая аналитическую взаимосвязь областей физического течения $z = x + iy$ и комплексного потенциала $W = {{\varphi }} + i{{\psi }}$ (прямоугольника).
При этом имеем следующие граничные условия (рис. 1, 2):
– по линиям осевой симметрии (непроницаемые границы) $BA$ и $CD$ функция тока ${{\psi }}$ равна, соответственно, нулевому ${{\psi }} = 0$ и полному расходу ψ = q;
– вдоль очертания импульсного источника $BC$ и линии поверхности стока $AE$ функции тока ${{\psi }}$ растут от нулевого значения ${{\psi }} = 0$ до полного расхода ψ = q;
– напорная (потенциальная) функция ${{\varphi }}$ на линии контура источника импульса $BC$ равна полному (единичному) напору $H$ (${{\varphi }} = H = 1$), а на выходном участке стока $AE$ – нулевому значению ${{\varphi }} = 0$.
Аналитическая взаимосвязь между комплексными областями физического течения $z = x + iy$ (рис. 2, a) и комплексного потенциала $W = {{\varphi }} + i{{\psi }}$ (рис. 2, i) устанавливается путем их последовательного конформного отображения на единую связующую полуплоскость ${{\zeta }} = {{\xi }} + i{{\eta }}$ (рис. 2, h) [10–12]. При этом для конформного отображения области $z = x + iy$ на полуплоскость ${{\zeta }} = {{\xi }} + i{{\eta }}$ используются промежуточные комплексные области ${{z}_{1}} = {{x}_{1}} + i{{y}_{1}}$, $t = {{t}_{1}} + i{{t}_{2}}$, $S = {{S}_{1}} + i{{S}_{2}}$, ${{\gamma }} = {{{{\gamma }}}_{1}} + i{{{{\gamma }}}_{2}}$, ${{\varepsilon }} = {{{{\varepsilon }}}_{1}} + i{{{{\varepsilon }}}_{2}}$, $J = {{J}_{1}}$ + iJ2 (рис. 2, b, c, d, e, f, g) с помощью функции [10–14]:
(2.1)
$z = - i{{z}_{1}},\quad t = \sqrt {z_{1}^{2} - {{h}^{2}}} ,\quad S = \sqrt {{{t}^{2}} - {{m}^{2}}} ,\quad {{\gamma }} = \frac{S}{m},\quad {{\varepsilon }} = \frac{1}{2}\left( {{{\gamma }} + \frac{1}{{{\gamma }}}} \right),\quad J = {{{{\varepsilon }}}^{2}}$С другой стороны, необходимо также конформно отобразить на полуплоскость ${{\zeta }} = {{\xi }} + i{{\eta }}$ область комплексного потенциала $W = {{\varphi }} + i{{\psi }}$, имеющего вид прямоугольника шириной H = 1 и длиной равной q (рис. 2, i), для точного отображения которого на полуплоскость требуется использование эллиптического синуса Якоби [10–15]. Однако, возникающие при этом математические сложности (в том числе при последующих преобразованиях эллиптических функций Якоби [15, 16]), затрудняют получение итоговых аналитических выражений в элементарных функциях для непосредственного определения гидромеханических характеристик потока в начальный момент импульсного воздействия, что имеет важное значение как для теоретического анализа, так и решения прикладных задач.
Для преодоления изложенных математических трудностей ниже приводится новая методика конформного отображения области комплексного потенциала $W = {{\varphi }} + i{{\psi }}$, представленного в виде прямоугольника, на полуплоскость ${{\zeta }} = {{\xi }} + i{{\eta }}$ [10, 17, 18]. При этом используется промежуточная комплексная область ${{W}_{1}} = {{{{\varphi }}}_{1}} + i{{{{\psi }}}_{1}}$ – прямоугольник шириной ${{\pi }}$ с осевым расположением мнимой оси $O{{{{\varphi }}}_{1}}$ ( рис. 2, j), определяемая зависимостью (при H = 1)
который (при “удлиненном” прямоугольнике $q{\text{/}}H \geqslant 1$) отображается на полуплоскость ${{\zeta }} = {{\xi }} + i{{\eta }}$ элементарными алгебраическими соотношениями (с погрешностью ≪1%) [17, 18]:(2.4)
${{\zeta }} = \frac{2}{{{{\lambda }}R}} \cdot \frac{{\sin {{W}_{1}}}}{{1 + \frac{{{{{\sin }}^{2}}{{W}_{1}}}}{{{{R}^{2}}}}}},\quad R = {\text{ch}}\left( {{{\pi }}q} \right),\quad {{\lambda }} = \frac{{2R}}{{1 + {{R}^{2}}}}$При этом комплексные области $J = {{J}_{1}} + i{{J}_{2}}$ (рис. 2, g) и ${{\zeta }} = {{\xi }} + i{{\eta }}$ (рис. 2, h) связываются между собой по соответствию трех точек: $A$ (${{J}_{A}} = - a$, ${{{{\zeta }}}_{A}} = - 1$), $B$ (${{J}_{B}} = 0$, ${{{{\zeta }}}_{B}} = 1$) и $D$ (${{J}_{D}} = - \propto $, 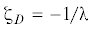 ) зависимостями:
) зависимостями:
(2.5)
$J = {{J}_{1}} + i{{J}_{2}} = \frac{{a\left( {{{\zeta }} - 1} \right)\left( {1 - {{\lambda }}} \right)}}{{2\left( {{{\lambda \zeta }} + 1} \right)}},\quad {{\zeta }} = {{\xi }} + i{{\eta }} = - \frac{{2J + a\left( {1 - {{\lambda }}} \right)}}{{2J{{\lambda }} - a\left( {1 - {{\lambda }}} \right)}}$При этом, для определения в формулах (2.4) значений параметров ${{\lambda }}$, $R$ и расхода $q$, из зависимости (2.5) для образа точки C в области ${{\zeta }} = {{\xi }} + i{{\eta }}$ (рис. 2, h)
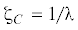 ) значение ${{\lambda }}$ в виде
подставляя которое в формулы (2.4), получим
) значение ${{\lambda }}$ в виде
подставляя которое в формулы (2.4), получим
(2.8)
$R = \frac{1}{{{\lambda }}}(1 + \sqrt {{\text{|}}1 - {{{{\lambda }}}^{2}}{\text{|}}} ),\quad q = \frac{1}{{{\pi }}}{\text{Arch}}\left( R \right)$Таким образом, устанавливаем аналитическую взаимосвязь $z = f(W)$ между областями физического течения $z = x + iy$ (рис. 2, a) и комплексного потенциала $W = {{\varphi }} + i{{\psi }}$ (рис. 2, i) с учетом значений промежуточных функций ${{z}_{1}},t,S,{{\gamma }},{{\varepsilon }},J,{{\zeta }},{{W}_{1}}$, определяемых по зависимостям (2.1)–(2.8). Разделяя в последних действительную и мнимую части и преобразовывая получим окончательные выражения в элементарных функциях для определения координат x и y области физического течения $z = x + iy$ при известных величинах $d$ и $h$ в зависимости от заданных значений напорной функции ${{\varphi }}$ и функции тока ${{\psi }}$ в виде:
(2.9)
$x = \sqrt {\frac{{\sqrt {A_{{10}}^{2} + B_{{10}}^{2}} - {{A}_{{10}}}}}{2}} ,\quad y = - \sqrt {\frac{{\sqrt {A_{{10}}^{2} + B_{{10}}^{2}} + {{A}_{{10}}}}}{2}} $(2.10)
${{A}_{7}} = {{\varepsilon }}_{1}^{2} - {{\varepsilon }}_{2}^{2} - 1,\quad {{B}_{7}} = 2{{{{\varepsilon }}}_{{\text{1}}}}{{{{\varepsilon }}}_{{\text{2}}}},\quad {{{{\varepsilon }}}_{1}} = \sqrt {\frac{{\sqrt {J_{1}^{2} + J_{2}^{2}} + {{J}_{1}}}}{2}} ,\quad {{{{\varepsilon }}}_{2}} = \sqrt {\frac{{\sqrt {J_{1}^{2} + J_{2}^{2}} - {{J}_{1}}}}{2}} $3. Анализ результатов и примеры. Полученное строгое решение рассматриваемой задачи, представленное в виде аналитической взаимосвязи $z = f(W)$, позволяет определять на основе элементарных расчетных зависимостей (2.7)–(2.10) для заданных значений параметра импульсного очага d и глубины его расположения h значения всех необходимых гидромеханических характеристик потенциального потока (поля) в области физического течения в начальный момент времени.
При этом значения скоростей потока ${{V}_{x}}$ и ${{V}_{y}}$ – горизонтальной и вертикальной составляющих полной скорости $V$, определяются по зависимостям [10, 15]:
(3.1)
${{V}_{x}} = \frac{{\Delta {{\varphi }}}}{{\Delta x}} = \frac{{\Delta {{\psi }}}}{{\Delta y}},\quad {{V}_{y}} = \pm \frac{{\Delta {{\varphi }}}}{{\Delta y}} = \pm \frac{{\Delta {{\psi }}}}{{\Delta x}},\quad V = \sqrt {V_{x}^{2} + V_{y}^{2}} $Очертание же профиля самого источника импульса определяется полуобратным методом – последовательным конформным отображением четверти дуги $BC$ единичной окружности в области ${{\gamma }} = {{{{\gamma }}}_{1}} + i{{{{\gamma }}}_{2}}$ (рис. 2, e) на область физического течения $z = x + iy$ (рис. 2, a) через промежуточные комплексные области $S = {{S}_{1}} + i{{S}_{2}}$, t = t1 + it2, ${{z}_{1}} = {{x}_{1}} + i{{y}_{1}}$ (рис. 2, d, c, b). При этом профиль источника импульса BC получает вид, описываемый параметрическими зависимостями:
(3.2)
$\begin{gathered} {{x}_{{BC}}} = \sqrt {\frac{{\sqrt {{{{(2{{m}^{2}}{{\gamma }}_{1}^{2} + {{h}^{2}})}}^{2}} + 4{{m}^{4}}{{\gamma }}_{1}^{2}(1 - {{\gamma }}_{1}^{2})} - (2{{m}^{2}}{{\gamma }}_{1}^{2} + {{h}^{2}})}}{2}} \\ {{y}_{{BC}}} = - \sqrt {\frac{{\sqrt {{{{(2{{m}^{2}}{{\gamma }}_{1}^{2} + {{h}^{2}})}}^{2}} + 4{{m}^{4}}{{\gamma }}_{1}^{2}(1 - {{\gamma }}_{1}^{2})} + (2{{m}^{2}}{{\gamma }}_{1}^{2} + {{h}^{2}})}}{2}} \\ \end{gathered} $На рис. 1, a, b приведены общая схема задачи в виде симметричного потенциального потока, а также результаты расчетов основных гидромеханических параметров для двух частных случаев при начальном импульсном воздействии (в усл. ед.):
– при $h = 5$; d = 1 (на правой половине рисунка)
– при $h = 1$; $d = 1$ (на левой половине рисунка)
При этом, для указанных случаев на рисунке также представлены:
– криволинейные ортогональные гидродинамические сетки потенциального потока;
– очертания профилей импульсного источника $BC$ в физической области течения (кривые 1);
– очертания семейств кривых функции тока (относительных расходов ${{\bar {\psi }}} = {{\psi /}}q$) – через 0.25 (кривые 2);
– очертания семейств кривых линий равных напоров (потенциальной функции ${{\varphi }}$) – через 0.25 (кривые 3);
– эпюры функции тока ${{\bar {\psi }}}$ вдоль границ стока (кривые 4);
– эпюры выходных скоростей потока ${{V}_{y}} = {{V}_{{out}}}$ вдоль границ стока (кривые 5);
– эпюры действующих вертикальных скоростей ${{V}_{y}}$ и напоров ${{\varphi }}$ вдоль осевой линии области течения при $h{\text{/}}d = 5$ (соответственно, кривые 6 и 7).
Ортогональность расчетных криволинейных ячеек гидродинамических сеток (рис. 1, b) непосредственно подтверждает потенциальность распределения гидромеханических характеристик потока импульсного источника.
Заключение. В работе дано новое гидромеханическое решение задачи заглубленного начального импульсного воздействия на гидрогеофизический массив (водный, грунтовый) с непосредственным аналитическим определением в элементарных функциях гидромеханических характеристик потенциального потока. При этом, воздействие очага импульса для начального момента времени моделировалось источником потенциального потока округленного профиля с единичным напором, а область стока – линией нулевого потенциала. Полученное строгое решение рассматриваемой задачи с установлением аналитической взаимосвязи между физической областью течения и комплексным потенциалом основано на теории функции комплексного переменного – использовании метода последовательных конформных отображений с определением полей гидромеханических характеристик потока в начальный момент времени. Приведены примеры расчета для двух частных случаев с построением: криволинейных ортогональных гидродинамических сеток, очертаний семейств линий равных напоров и линий токов, профилей источников импульса, а также эпюр скоростей потока, напоров и относительных расходов потенциального потока.
Часть работы, связанная с гидродинамикой водоемов, выполнена в рамках темы № FMWZ-2022-0001 государственного задания ИВП РАН.
Список литературы
Ильинский Н.Б., Лабуткин А.Г., Салимов Р.Б. Некоторые задачи о взрыве заглубленных зарядов // Труды семинара по краевым задачам. Вып. 12. Казань: КГУ, 1975. С. 63–75.
Меркулов В.И. Популярная гидродинамика. Киев: Технiка, 1976. 145 с.
Лаврентьев М.А., Шабат Б.В. Проблемы гидродинамики и их математические модели. М.: Наука, 1977. 407 с.
Пелиновский Е.Н. Гидродинамика волн цунами. Нижний Новгород: ИПФ РАН, 1996. 276 с.
Иванов Б.А. Распределение в пространстве энергии сейсмических волн при метеоритном ударе и взрыве // Динамические процессы в геосферах. Сб. науч. трудов ИДГ РАН. Вып. 10. М.: Графитекс, 2018. С. 46–53. https://doi.org/10.26006/IDG.2018.10.20170
Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.: Наука. 1973. 736 с.
Шувалов В.В. Выброс воды в атмосферу при падении астероидов в океан // Динамические процессы в геосферах. Сб. науч. трудов ИДГ РАН. Вып. 10. М.: Графитекс, 2018. С. 126–131. https://doi.org/10.26006/IDG.2018.10.20187
Покровский Г.И. Возведение плотин направленным взрывом. М.: Недра, 1974. 113 с.
Кочин Н.Е., Кибель И.А., Розе Н.В. Теоретическая гидромеханика. Часть 1. М.: Физматгиз, 1963. 583 с.
Анахаев К.Н. Гидромеханический расчет потенциального потока при ударе плиты о воду // Доклады Академии наук. 2012. Т. 445. № 4. С. 407–411.
Лаврик В.И., Фильчакова В.П., Яшин А.А. Конформные отображения физико-топологических моделей. Киев: Наукова думка, 1990. 374 с.
Anakhaev K.N., Ivanov P.M., Temukuev Kh.M., Chechenov M.M. The hydromechanical problem of pulse punching of a plate // Doklady Physics. 2018. V. 63. № 7. P. 288–292. https://doi.org/10.1134/S1028335818070017
Betz A. Konforme Abbildung. Berlin: Springer – Verlag, 1960. 407 s.
Лаврик В.И., Савенков В.Н. Справочник по конформным отображениям. Киев: Наукова думка, 1970. 252 с.
Павловский Н.Н. Собрание сочинений. Т. 2. Движение грунтовых вод. М.– Л.: Изд-во АН СССР, 1956. 771 с.
Милн-Томсон Л. Эллиптические функции Якоби и тета-функции // Справочник по специальным функциям. Под редакцией М. Абрамовица и И. Стиган М.: Наука. 1979. С. 380–400.
Анахаев К.Н. О расчете потенциальных потоков // Доклады Академии наук. 2005. Т. 401. № 3. С. 337–341.
Анахаев К.Н. Об определении эллиптических функций Якоби // Вестник РУДН. Серия: математика, информатика, физика. 2009. № 2. С. 90–95.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела


