Известия РАН. Механика твердого тела, 2023, № 1, стр. 55-67

ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ТЕКУЧЕСТИ МОНОКРИСТАЛЛОВ С ГЕКСАГОНАЛЬНОЙ РЕШЕТКОЙ ПРИ ЗАДАННОМ ТЕНЗОРЕ ДЕФОРМАЦИЙ И ГИДРОСТАТИЧЕСКОМ ДАВЛЕНИИ

А. Г. Кесарев^a, А. М. Власова^b, *

^a Институт физики металлов им. М.Н. Михеева УрО РАН
Екатеринбург, Россия

^b Уральский федеральный университет им. Первого президента России Б.Н. Ельцина
Екатеринбург, Россия

^* E-mail: alisa@imp.uran.ru

Поступила в редакцию 18.01.2022
После доработки 16.02.2022
Принята к публикации 17.02.2022

EDN: KFUHJA
DOI: 10.31857/S0572329922060095

Полный текст (PDF)

Аннотация

В рамках предложенного авторами обобщенного на гексагональные кристаллы критерия текучести Мизеса, решена задача определения тензора напряжений в зависимости от тензора скоростей деформаций и приложенного внешнего давления. Детально рассматриваются случаи плоской и одноосной деформации при произвольной ориентации кристаллической решетки. Для случаев плоской и одноосной деформации построены диаграммы линий уровня напряжений для начала пластического течения. Приводятся диаграммы для компонент девиатора тензора напряжений

Ключевые слова: магний, деформация, гексагональные кристаллы, прочность, пластичность, критерий текучести, критерий Мизеса, тензор напряжений, тензор скорости деформации, девиатор

1. Введение. Как хорошо известно, описание деформационного поведения металлов с гексагональной плотноупакованной кристаллической решеткой (ГПУ) представляет серьезные трудности из-за большого количества действующих деформационных мод [1, 2].

Для описания механических свойств материалов, в настоящее время используются различные физические теории пластичности, в том числе новые к ним подходы [3]. Зачастую физические модели приводят к сложным компьютерным расчетам (кроме простейшей модели Закса) на основе трудоемких экспериментов. Кроме того, они приводят к негладкой поверхности текучести, что создает значительные математические трудности. Модели, опирающиеся на закон Шмида, не всегда выполняются для ГПУ кристаллов, ввиду того, что для них двойникование – действующий и подавляющий механизм пластической деформации при комнатной температуре [2]. Проблемы, возникающие при использовании модели идеально-жесткопластических сред также известны, и в последнее время подобные определяющие соотношения редко используются исследователями. Основным их недостатком является наличие несжимаемости, из-за чего определение напряженного состояния только по изменению деформированного состояния оказывается невозможным.

Данная статья является продолжением работ [4, 5]. В работе [5] представлена феноменологическая модель для описания механических свойств ГПУ металлов, а именно нахождение простого критерия текучести монокристалла производной ориентировки. Предлагаемый критерий текучести является обобщением известного критерия Мизеса. Для различных схем деформирования монокристаллического магния при комнатной температуре определены коэффициенты этой модели, согласно экспериментальным данным для пределов текучести монокристаллов различных ориентировок. Для перехода к модели поликристаллического тела требуется подходящая процедура усреднения, чему и посвящена данная работа. Известно, что простейшими способами усреднения, оценивающими значения для верхней и нижней границ эффективных свойств композитов – являются усреднения по Рейсу и Фойгту [6]. Применительно к нашему случаю, первый способ означает предположение, что все зерна испытывают одинаковые напряжения, а второй – одни и те же деформации. При пластической деформации усреднение по Рейсу невозможно, так как в рамках жесткопластической модели без упрочнения одни и тех же напряжения при одной ориентировке зерна не вызовут никаких деформаций, при других – окажутся абсолютно недостижимыми. Усреднение по Фойгту применительно к жесткопластической модели использовали Тейлор, а также Бишоп и Хилл [7]. Его использование требует решения задачи о нахождении тензора напряжений по известному тензору скоростей деформации и приложенному гидростатическому давлению, что и является целью настоящей работы.

2. Постановка задачи и ее решение. Пусть в лабораторной системе координат задан тензор скоростей деформации ${{E}_{{ij}}}$. (Следуя нашей предыдущей работе [5], большими буквами обозначаем величины в лабораторной системе координат, маленькими – в кристаллографической системе координат. В последнем случае оси 1 и 2 лежат в базисной плоскости гексагональной ячейки, а ось 3 – ей перпендикулярна). Критерий текучести, предложенный нами в работах [4, 5], имеет вид полинома

(2.1)

$f\left( {{{p}_{{ij}}}} \right) = a + k{{I}_{2}} + {{I}_{1}} + {{\alpha }}{{\left( {{{I}_{2}}} \right)}^{2}} + {{\beta }}{{I}_{3}}$

где инварианты тензора напряжений относительно группы симметрии ГПУ–решетки

(2.2)

${{I}_{1}} = {{\left( {{{p}_{{13}}}} \right)}^{2}} + {{\left( {{{p}_{{23}}}} \right)}^{2}},\quad {{I}_{2}} = {{p}_{{33}}} - \left( {{{p}_{{11}}} + {{p}_{{22}}}} \right){\text{/}}2,\quad {{I}_{3}} = {{\left( {{{p}_{{11}}} - {{p}_{{22}}}} \right)}^{2}} + 4{{\left( {{{p}_{{12}}}} \right)}^{2}}$

Выбор полиномального вида функции текучести позволяет избежать нарушения аналитичности функции в некоторых точках.

Согласно ассоциированному закону, связь между компонентами тензоров напряжений P_ij и скоростей деформаций E_ij имеет вид [8]

(2.3)

${{E}_{{ij}}} = \dot {\Lambda }(t)\frac{{\partial f}}{{\partial {{P}^{{ij}}}}}$

Так как критерий (2.1)–(2.2) обладает цилиндрической симметрией, то для задания ориентировки зерна достаточно знать единичный вектор нормали к базисной плоскости ${\mathbf{n}}$. Так как мы используем прямоугольную систему координат, то верхние и нижние индексы не различаем, так что наличие двух повторяющихся латинских индексов означает суммирование по ним.

Выразим инварианты (2.2) через компоненты тензора напряжений и вектора нормали ${\mathbf{n}}$ к базисной плоскости. Инвариант I₁ равен разности квадратов модуля вектора напряжений, действующего на базисную плоскость и нормальной компоненты этого напряжения

(2.4)

${{I}_{1}} = {{P}_{{ij}}}{{n}_{j}}{{P}_{{ik}}}{{n}_{k}} - {{\left( {{{P}_{{ij}}}{{n}_{i}}{{n}_{j}}} \right)}^{2}}$

Второй инвариант имеет вид

(2.5)

${{I}_{2}} = \frac{{3{{p}_{{33}}} - \left( {{{p}_{{11}}} + {{p}_{{22}}} + {{p}_{{33}}}} \right)}}{2} = \frac{1}{2}\left( {3{{P}_{{ij}}}{{n}_{j}}{{n}_{i}} - {{P}_{{ii}}}} \right)$

Инвариант I₃ равен максимальной разности растягивающих напряжений, действующих в базисной плоскости (0001). Эти напряжения могут быть найдены, как экстремумы функции ${{P}_{{ij}}}{{{{\tau }}}_{i}}{{{{\tau }}}_{j}}$, где ${\mathbf{\tau }}$ – единичный вектор, перпендикулярный n, что можно записать в виде ограничений ${{{{\tau }}}_{i}}{{n}_{i}} = 0$, ${{{{\tau }}}_{i}}{{{{\tau }}}_{i}} - 1 = 0$. Задача поиска таких экстремумов, как известно, методом множителей Лагранжа сводится к задаче о поиске экстремума (без ограничений), для функции

(2.6)

${{P}_{{ij}}}{{{{\tau }}}_{i}}{{{{\tau }}}_{j}} + {{\eta }}\left( {{{{{\tau }}}_{i}}{{{{\tau }}}_{i}} - 1} \right) + {{\mu }}\left( {{{{{\tau }}}_{i}}{{n}_{i}}} \right)$

которые достигаются на векторах ${\mathbf{\tau }}$, удовлетворяющих уравнениям

(2.7)

$2{{P}_{{ij}}}{{{{\tau }}}_{j}} + 2{{\eta }}{{{{\tau }}}_{i}} + {{\mu }}{{n}_{i}} = 0,\quad \left( {i = 1,2,3} \right)$

Для решения системы уравнений (2.7) введем оператор проектирования ${\mathbf{\Pi }}$ на базисную плоскость по формуле

(2.8)

${{\Pi }_{{ij}}}{{x}_{j}} = {{{{\delta }}}_{{ij}}}{{x}_{j}} - {{n}_{i}}{{n}_{j}}{{x}_{j}}$

Подействовав оператором ${\mathbf{\Pi }}$ на уравнение (2.7), получим

(2.9)

$2{{\Pi }_{{ik}}}{{P}_{{kj}}}{{{{\tau }}}_{j}} + 2{{\eta }}{{\Pi }_{{ik}}}{{{{\tau }}}_{k}} + {{\mu }}{{\Pi }_{{ik}}}{{n}_{k}} = 2{{\Pi }_{{ik}}}{{P}_{{kj}}}{{{{\tau }}}_{j}} + 2{{\eta }}{{\Pi }_{{ik}}}{{{{\tau }}}_{k}} = 0$

Так как по определению ${\mathbf{\Pi }}\left( {\mathbf{n}} \right) = 0$, ${\mathbf{\Pi }}\left( {\mathbf{\tau }} \right) = {\mathbf{\tau }}$, это позволяет записать уравнение (2.9) в виде задачи на собственные значения и векторы для оператора проектирования ${\mathbf{A}} = {\mathbf{\Pi P}}$

(2.10)

${\mathbf{A}}{{\tau }} = {{\lambda \tau }}$

где ${{\lambda }} = - {{\eta }}$. Заметим, что оператор A – симметрический, как произведение симметрических операторов. Так как ${\mathbf{\Pi }}\left( {\mathbf{n}} \right) = 0$, то оператор A вырожден и среди его собственных значений имеется нулевое. Следовательно, характеристический полином оператора A имеет вид [9]

(2.11)

$ - \left( {{{{{\lambda }}}_{1}} - {{\lambda }}} \right)\left( {{{{{\lambda }}}_{2}} - {{\lambda }}} \right){{\lambda }} = - {{{{\lambda }}}^{3}} + {{I}_{A}}{{{{\lambda }}}^{2}} - I{{I}_{A}}{{\lambda }} + II{{I}_{A}}$

где

(2.12)

${{I}_{A}} = {{a}_{{11}}} + {{a}_{{22}}} + {{a}_{{33}}} = {{{{\lambda }}}_{1}} + {{{{\lambda }}}_{2}} = {\text{tr}}A$

(2.13)

$I{{I}_{A}} = \frac{1}{2}[{{\left( {{\text{tr}}A} \right)}^{2}} - {\text{tr}}{{A}^{2}}] = {{a}_{{ii}}}{{a}_{{jj}}} - {{a}_{{ij}}}{{a}_{{ji}}} = {{{{\lambda }}}_{1}}{{{{\lambda }}}_{2}},\quad II{{I}_{A}} = \det A$

где $A = \left( {{{a}_{{ij}}}} \right)$ – матрица оператора A, ${\text{tr}}A = {{a}_{{ii}}}$ – шпур матрицы. Тогда, используя определение третьего инварианта, выражения (2.12)–(2.13) и определение оператора A получим

(2.14)

$\begin{gathered} {{I}_{3}} = {{\left( {{{{{\lambda }}}_{1}} - {{{{\lambda }}}_{2}}} \right)}^{2}} = {{I}_{A}}^{2} - 4I{{I}_{A}} = 2{\text{tr}}{{A}^{2}} - {{\left( {{\text{tr}}A} \right)}^{2}} = \hfill \\ = 2\left( {{{P}_{{il}}} - {{n}_{i}}{{n}_{k}}{{P}_{{kl}}}} \right)\left( {{{P}_{{li}}} - {{n}_{l}}{{n}_{s}}{{P}_{{si}}}} \right) - {{\left( {{{P}_{{ii}}} - {{n}_{i}}{{n}_{s}}{{P}_{{si}}}} \right)}^{2}} \hfill \\ \end{gathered} $

Теперь, используя выражения для инвариантов (2.4), (2.5) и (2.14), запишем критерий текучести $f\left( {{{P}_{{ij}}}} \right)$ (2.1) через компоненты тензора напряжений в лабораторной системе координат при произвольной ориентировке кристалла

(2.15)

$\begin{gathered} f\left( {{{P}_{{ij}}}} \right) = a + k\frac{{3{{P}_{{ij}}}{{n}_{i}}{{n}_{j}} - {{P}_{{ii}}}}}{2} + {{P}_{{ij}}}{{P}_{{ik}}}{{n}_{j}}{{n}_{k}} - {{\left( {{{P}_{{ij}}}{{n}_{i}}{{n}_{j}}} \right)}^{2}} + \frac{{{\alpha }}}{4}{{\left( {3{{P}_{{ij}}}{{n}_{i}}{{n}_{j}} - {{P}_{{ii}}}} \right)}^{2}} + \\ \, + {{\beta }}[2\left( {{{P}_{{il}}} - {{n}_{i}}{{n}_{k}}{{P}_{{kl}}}} \right)\left( {{{P}_{{li}}} - {{n}_{l}}{{n}_{s}}{{P}_{{si}}}} \right) - {{\left( {{{P}_{{ii}}} - {{n}_{i}}{{n}_{s}}{{P}_{{si}}}} \right)}^{2}}] \\ \end{gathered} $

Это выражение позволяет, с использованием ассоциированного закона (2.3) установить связь между компонентами тензоров напряжений и скоростей деформации в лабораторной системе координат. Дифференцирование необходимо проводить с учетом симметрии тензора P_ij. Следуя [9], находим

(2.16)

$d\left( {{{P}_{{rs}}}{{n}_{r}}{{n}_{s}}} \right) = \frac{d}{{d\xi }}\left( {{{P}_{{rs}}} + \xi \delta {{P}_{{rs}}}} \right){{n}_{r}}{{n}_{s}} = {{n}_{r}}{{n}_{s}}\delta {{P}_{{rs}}}$

где

(2.17)

$\delta {{P}_{{rs}}} = \delta {{P}_{{ij}}}\left[ {{{\delta }_{{ir}}}{{\delta }_{{js}}} + {{\delta }_{{is}}}{{\delta }_{{jr}}}} \right]{\text{/}}2$

Подставляя выражение (2.17) в (2.16), получаем

(2.18)

$\frac{{\partial {{P}_{{rs}}}{{n}_{r}}{{n}_{s}}}}{{\partial {{P}_{{ij}}}}} = {{n}_{i}}{{n}_{j}}$

Аналогично находим

(2.19)

$\frac{{\partial {{P}_{{lr}}}{{P}_{{rl}}}}}{{\partial {{P}_{{ij}}}}} = {{P}_{{ji}}} + {{P}_{{ij}}},\quad \frac{{\partial \left( {{{P}_{{rs}}}{{P}_{{rk}}}{{n}_{s}}{{n}_{k}}} \right)}}{{\partial {{P}_{{ij}}}}} = \left( {{{n}_{s}}{{n}_{j}}{{P}_{{is}}} + {{n}_{i}}{{n}_{s}}{{P}_{{js}}}} \right)$

(2.20)

$\frac{{\partial {{{\left( {{{P}_{{rs}}}{{n}_{r}}{{n}_{s}}} \right)}}^{2}}}}{{\partial {{P}_{{ij}}}}} = 2\left( {{{P}_{{rs}}}{{n}_{r}}{{n}_{s}}} \right){{n}_{i}}{{n}_{j}}$

Кроме того, заметим, что

(2.21)

$2\left( {{{P}_{{rl}}} - {{n}_{r}}{{n}_{k}}{{P}_{{kl}}}} \right)\left( {{{P}_{{lr}}} - {{n}_{l}}{{n}_{s}}{{P}_{{sr}}}} \right) = 2[{{P}_{{rl}}}{{P}_{{lr}}} - {{n}_{r}}{{n}_{k}}{{P}_{{kl}}}{{P}_{{lr}}} - {{n}_{l}}{{n}_{s}}{{P}_{{rl}}}{{P}_{{sr}}} + {{\left( {{{n}_{r}}{{n}_{l}}{{P}_{{kl}}}} \right)}^{2}}]$

Используя ассоциированный закон (2.3), дифференцируя функцию текучести (2.15), с использованием выражений (2.18)–(2.20) получаем связь тензора напряжений и тензора деформаций

(2.22)

$\begin{gathered} {{E}_{{ij}}} = \dot {\Lambda }\left\{ {k\frac{{3{{n}_{i}}{{n}_{j}} - {{{{\delta }}}_{{ij}}}}}{2} + {{P}_{{ik}}}{{n}_{k}}{{n}_{j}} + {{P}_{{jk}}}{{n}_{k}}{{n}_{i}} - 2\left( {{{P}_{{kl}}}{{n}_{k}}{{n}_{l}}} \right){{n}_{i}}{{n}_{j}} + \frac{{{\alpha }}}{2}\left( {3{{P}_{{kl}}}{{n}_{k}}{{n}_{l}} - {{P}_{{kk}}}} \right)} \right. \times \\ \, \times \left. {(3{{n}_{i}}{{n}_{j}} - {{{{\delta }}}_{{ij}}})\, + \,{{\beta }}[4({{P}_{{ij}}} - {{P}_{{kj}}}{{n}_{i}}{{n}_{k}} - {{P}_{{ki}}}{{n}_{j}}{{n}_{k}} + {{P}_{{kl}}}{{n}_{k}}{{n}_{l}}{{n}_{i}}{{n}_{j}}) - \mathop {2({{P}_{{ll}}} - {{n}_{l}}{{n}_{k}}{{P}_{{lk}}})({{{{\delta }}}_{{ij}}} - {{n}_{i}}{{n}_{j}})}\limits^{} ]} \right\} \\ i,j = 1,2,3 \\ \end{gathered} $

Заметим, что шпур тензора напряжений равен взятому с обратным знаком утроенному гидростатическому давлению ${{P}_{{kk}}} = - 3p$. Эту величину нельзя найти, зная только тензор скоростей деформации – она задается внешними условиями. Гидростатическое давление не зависит от выбора системы координат. Для нахождения тензора напряжений при известном тензоре деформации и гидростатическом давлении, разрешив систему уравнений (2.16) относительно компонент тензора напряжений P_ij. Учитывая ${{n}_{j}}{{n}_{j}} = 1$ и ${{\delta }_{{ij}}}{{n}_{j}} = {{n}_{i}}$, умножим обе части уравнения (2.22) на компоненты вектор нормали к базисной плоскости n_j и проведем свертку по индексу j

(2.23)

${{E}_{{ij}}}{{n}_{j}} = \dot {\Lambda }\left\{ {k{{n}_{i}} + {{P}_{{is}}}{{n}_{s}} - \left( {{{P}_{{rs}}}{{n}_{r}}{{n}_{s}}} \right){{n}_{i}} + \left. {{{\alpha }}\left( {3{{P}_{{rs}}}{{n}_{r}}{{n}_{s}} - {{P}_{{ss}}}} \right){{n}_{i}}} \right\}} \right.$

Теперь уравнение (2.23) еще раз умножим на ${{n}_{i}}$ и свернем по индексу i

(2.24)

${{E}_{{ij}}}{{n}_{j}}{{n}_{i}} = \dot {\Lambda }\left\{ {k + \left. {{{\alpha }}\left( {3{{P}_{{kl}}}{{n}_{k}}{{n}_{l}} - {{P}_{{kk}}}} \right)} \right\}} \right.$

Из выражения (2.24) найдем

(2.25)

${{P}_{{rs}}}{{n}_{r}}{{n}_{s}} = \frac{{{{E}_{{rs}}}{{n}_{r}}{{n}_{s}} - \dot {\Lambda }k}}{{3{{\alpha }}\dot {\Lambda }}} - p$

а из выражений (2.23), (2.25) –

(2.26)

${{P}_{{ik}}}{{n}_{k}} = - \left[ {p + \frac{k}{{3{{\alpha }}}}} \right]{{n}_{i}} + \frac{1}{{\dot {\Lambda }}}\left[ {{{E}_{{ij}}}{{n}_{j}} + \left( {\frac{1}{{3{{\alpha }}}} - 1} \right){{E}_{{rs}}}{{n}_{r}}{{n}_{s}}{{n}_{i}}} \right]$

Заменив в (2.26) i на j и j на i, сложим с (2.26)

(2.27)

${{P}_{{ik}}}{{n}_{k}}{{n}_{j}} + {{P}_{{jk}}}{{n}_{k}}{{n}_{i}} = \frac{{{{E}_{{ir}}}{{n}_{r}}{{n}_{i}} + {{E}_{{rj}}}{{n}_{r}}{{n}_{j}}}}{{\dot {\Lambda }}} - 2\left[ {p + \frac{k}{{3{{\alpha }}}}} \right]{{n}_{i}}{{n}_{j}} + \frac{2}{{\dot {\Lambda }}}\left( {\frac{1}{{3{{\alpha }}}} - 1} \right){{E}_{{rs}}}{{n}_{r}}{{n}_{s}}{{n}_{i}}{{n}_{j}}$

Подставив выражения (2.25), (2.26) в уравнение (2.22) и разрешив его относительно ${{P}_{{ij}}}$, получим выражение

(2.28)

${{P}_{{ij}}} = \frac{{{{E}_{{ij}}}}}{{4{{\beta }}\dot {\Lambda }}} + \frac{{{{E}_{{ir}}}{{n}_{r}}{{n}_{j}} + {{E}_{{rj}}}{{n}_{r}}{{n}_{i}}}}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right) + A{{n}_{i}}{{n}_{j}} + B{{{{\delta }}}_{{ij}}}$

где

(2.29)

$A = - \frac{k}{{2{{\alpha }}}} + \frac{{{{E}_{{rs}}}{{n}_{r}}{{n}_{s}}}}{{\dot {\Lambda }}}\left( {\frac{1}{{8{{\beta }}}} + \frac{1}{{2{{\alpha }}}} - 2} \right),\quad B = - p + \frac{k}{{6{{\alpha }}}} + \left( {\frac{1}{{8{{\beta }}}} - \frac{1}{{6{{\alpha }}}}} \right)\frac{{{{E}_{{rs}}}{{n}_{r}}{{n}_{s}}}}{{\dot {\Lambda }}}$

Для нахождения $\dot {\Lambda }$ сначала выразим инварианты ${{I}_{1}}$ – ${{I}_{3}}$ через компоненты тензора скоростей деформации ${{E}_{{ij}}}$. Первые два инварианта находятся по формулам (2.4), (2.5)

(2.30)

$\begin{gathered} {{I}_{1}} = {{P}_{{ij}}}{{n}_{j}}{{P}_{{ik}}}{{n}_{k}} - {{\left( {{{P}_{{ij}}}{{n}_{i}}{{n}_{j}}} \right)}^{2}} = {{\left( {p + \frac{k}{{3{{\alpha }}}}} \right)}^{2}} + \frac{1}{{{{{\dot {\Lambda }}}^{2}}}}\left\{ {{{E}_{{ri}}}{{n}_{r}}{{E}_{{si}}}{{n}_{s}} + \left( {\frac{1}{{9{{{{\alpha }}}^{2}}}} - 1} \right){{{\left( {{{E}_{{rs}}}{{n}_{r}}{{n}_{s}}} \right)}}^{2}}} \right\} - \\ \, - \frac{2}{{3{{\alpha }}\dot {\Lambda }}}\left[ {p + \frac{k}{{3{{\alpha }}}}} \right]{{E}_{{rs}}}{{n}_{r}}{{n}_{s}} - {{\left( {\frac{{{{E}_{{rs}}}{{n}_{r}}{{n}_{s}}}}{{3{{\alpha }}\dot {\Lambda }}} - \frac{k}{{3{{\alpha }}}} - p} \right)}^{2}} = \frac{1}{{{{{\dot {\Lambda }}}^{2}}}}[{{E}_{{ri}}}{{n}_{r}}{{E}_{{si}}}{{n}_{s}} + {{\left( {{{E}_{{rs}}}{{n}_{r}}{{n}_{s}}} \right)}^{2}}] \\ \end{gathered} $

(2.31)

${{I}_{2}} = \frac{1}{2}\left( {3{{P}_{{ij}}}{{n}_{j}}{{n}_{i}} - {{P}_{{ii}}}} \right) = \frac{{{{E}_{{rs}}}{{n}_{r}}{{n}_{s}}}}{{2{{\alpha }}\dot {\Lambda }}} - \frac{k}{{2{{\alpha }}}}$

Для нахождения инварианта ${{I}_{3}}$ заметим, что

(2.32)

${{P}_{{il}}} - {{n}_{i}}{{n}_{k}}{{P}_{{kl}}} = \frac{{{{E}_{{il}}}}}{{4{{\beta }}\dot {\Lambda }}} + \left( {1 - \frac{1}{{4{{\beta }}}}} \right)\frac{{{{E}_{{ir}}}{{n}_{r}}{{n}_{l}} - {{E}_{{kr}}}{{n}_{r}}{{n}_{l}}{{n}_{i}}{{n}_{k}}}}{{\dot {\Lambda }}} - \frac{{{{E}_{{kl}}}{{n}_{i}}{{n}_{k}}}}{{4{{\beta }}\dot {\Lambda }}} + B\left( {{{{{\delta }}}_{{il}}} - {{n}_{i}}{{n}_{l}}} \right)$

Используя соотношения

(2.33)

$\begin{gathered} \left( {{{E}_{{ir}}}{{n}_{r}}{{n}_{l}} - {{E}_{{kr}}}{{n}_{k}}{{n}_{r}}{{n}_{l}}{{n}_{i}}} \right)\left( {{{E}_{{ls}}}{{n}_{s}}{{n}_{i}} - {{E}_{{st}}}{{n}_{s}}{{n}_{t}}{{n}_{i}}{{n}_{l}}} \right) = \\ \, = \left( {{{E}_{{ir}}}{{n}_{r}}{{n}_{l}} - {{E}_{{kr}}}{{n}_{k}}{{n}_{r}}{{n}_{l}}{{n}_{i}}} \right)\left( {{{{{\delta }}}_{{il}}} - {{n}_{i}}{{n}_{l}}} \right) = 0 \\ \end{gathered} $

(2.34)

$\left( {{{{{\delta }}}_{{il}}} - {{n}_{i}}{{n}_{l}}} \right)\left( {{{{{\delta }}}_{{il}}} - {{n}_{i}}{{n}_{l}}} \right) = {{{{\delta }}}_{{il}}}{{{{\delta }}}_{{il}}} - {{n}_{i}}{{n}_{l}}{{{{\delta }}}_{{il}}} - {{{{\delta }}}_{{il}}}{{n}_{i}}{{n}_{l}} + {{n}_{i}}{{n}_{l}}{{n}_{i}}{{n}_{l}} = 2$

находим

$\begin{gathered} \left( {{{P}_{{il}}} - {{n}_{i}}{{n}_{k}}{{P}_{{kl}}}} \right)\left( {{{P}_{{li}}} - {{n}_{l}}{{n}_{s}}{{P}_{{si}}}} \right) = \\ \, = \frac{{{{E}_{{il}}}{{E}_{{li}}}}}{{16{{{{\beta }}}^{2}}{{{\dot {\Lambda }}}^{2}}}} + \frac{{{{E}_{{il}}}}}{{4{{\beta }}\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right)\frac{{{{E}_{{lt}}}{{n}_{t}}{{n}_{i}} - {{E}_{{st}}}{{n}_{t}}{{n}_{s}}{{n}_{i}}{{n}_{l}}}}{{\dot {\Lambda }}} - \frac{{{{E}_{{il}}}{{E}_{{is}}}{{n}_{s}}{{n}_{l}}}}{{16{{{{\beta }}}^{2}}{{{\dot {\Lambda }}}^{2}}}} + \frac{{{{E}_{{il}}}B}}{{4\beta \dot {\Lambda }}}\left( {{{\delta }_{{il}}} - {{n}_{i}}{{n}_{l}}} \right) + \\ \, + \left( {1 - \frac{1}{{4\beta }}} \right)\frac{{{{E}_{{ir}}}{{n}_{r}}{{n}_{l}} - {{E}_{{kr}}}{{n}_{r}}{{n}_{l}}{{n}_{i}}{{n}_{k}}}}{{\dot {\Lambda }}}\frac{{{{E}_{{li}}}}}{{4\beta \dot {\Lambda }}} + {{\left( {1 - \frac{1}{{4\beta }}} \right)}^{2}}\frac{{{{E}_{{ir}}}{{n}_{r}}{{n}_{l}} - {{E}_{{kr}}}{{n}_{r}}{{n}_{l}}{{n}_{i}}{{n}_{k}}}}{{\dot {\Lambda }}} \times \\ \, \times \frac{{{{E}_{{lr}}}{{n}_{r}}{{n}_{i}} - {{E}_{{sr}}}{{n}_{r}}{{n}_{s}}{{n}_{i}}{{n}_{l}}}}{{\dot {\Lambda }}} - \left( {1 - \frac{1}{{4\beta }}} \right)\frac{{{{E}_{{lr}}}{{n}_{r}}{{n}_{l}} - {{E}_{{kr}}}{{n}_{r}}{{n}_{l}}{{n}_{i}}{{n}_{k}}}}{{\dot {\Lambda }}}\frac{{{{E}_{{is}}}{{n}_{s}}{{n}_{l}}}}{{4\beta \dot {\Lambda }}} + \\ \end{gathered} $

(2.35)

$\begin{gathered} + \left( {1 - \frac{1}{{4{{\beta }}}}} \right)\frac{{{{E}_{{ir}}}{{n}_{r}}{{n}_{i}} - {{E}_{{kr}}}{{n}_{r}}{{n}_{l}}{{n}_{i}}{{n}_{k}}}}{{\dot {\Lambda }}}B\left( {{{\delta }_{{il}}} - {{n}_{i}}{{n}_{l}}} \right) - \frac{{{{E}_{{kl}}}{{n}_{i}}{{n}_{k}}}}{{4{{\beta }}\dot {\Lambda }}}\frac{{{{E}_{{li}}}}}{{4{{\beta }}\dot {\Lambda }}} - \frac{{{{E}_{{kl}}}{{n}_{i}}{{n}_{k}}}}{{4{{\beta }}\dot {\Lambda }}} \times \\ \, \times \left( {1 - \frac{1}{{4{{\beta }}}}} \right)\frac{{{{E}_{{lr}}}{{n}_{r}}{{n}_{i}} - {{E}_{{sr}}}{{n}_{r}}{{n}_{s}}{{n}_{i}}{{n}_{l}}}}{{\dot {\Lambda }}} + \frac{{{{E}_{{kl}}}{{n}_{i}}{{n}_{k}}}}{{4\beta \dot {\Lambda }}}\frac{{{{E}_{{is}}}{{n}_{s}}{{n}_{l}}}}{{4\beta \dot {\Lambda }}} - \frac{{{{E}_{{kl}}}{{n}_{i}}{{n}_{k}}}}{{4\beta \dot {\Lambda }}}B\left( {{{\delta }_{{il}}} - {{n}_{i}}{{n}_{l}}} \right) + \\ \, + B\left( {{{\delta }_{{il}}} - {{n}_{i}}{{n}_{l}}} \right)\frac{{{{E}_{{li}}}}}{{4{{\beta }}\dot {\Lambda }}} + B\left( {{{\delta }_{{il}}} - {{n}_{i}}{{n}_{l}}} \right)\frac{{{{E}_{{il}}}}}{{4{{\beta }}\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right)\frac{{{{E}_{{lt}}}{{n}_{t}}{{n}_{i}} - {{E}_{{st}}}{{n}_{t}}{{n}_{s}}{{n}_{i}}{{n}_{l}}}}{{\dot {\Lambda }}} - \\ \left. {\, - B\left( {{{\delta }_{{il}}} - {{n}_{i}}{{n}_{l}}} \right)\frac{{{{E}_{{is}}}{{n}_{s}}{{n}_{l}}}}{{4{{\beta }}\dot {\Lambda }}} + {{B}^{2}}\left( {{{\delta }_{{il}}} - {{n}_{i}}{{n}_{l}}} \right)\left( {{{\delta }_{{il}}} - {{n}_{i}}{{n}_{l}}} \right)} \right] = \\ \end{gathered} $

$ = \frac{{{{E}_{{il}}}{{E}_{{li}}}}}{{16{{{{\beta }}}^{2}}{{{\dot {\Lambda }}}^{2}}}} - \frac{{{{E}_{{il}}}{{E}_{{is}}}{{n}_{s}}{{n}_{l}}}}{{8{{{{\beta }}}^{2}}{{{\dot {\Lambda }}}^{2}}}} - \frac{{B{{E}_{{il}}}{{n}_{i}}{{n}_{l}}}}{{2{{\beta }}\dot {\Lambda }}} + \frac{{{{{\left( {{{E}_{{lr}}}{{n}_{r}}{{n}_{i}}} \right)}}^{2}}}}{{16{{{{\beta }}}^{2}}{{{\dot {\Lambda }}}^{2}}}} + 2{{B}^{2}}$

Используя (2.25), получаем

(2.36)

$3{{P}_{{rs}}}{{n}_{r}}{{n}_{s}} - 3{{P}_{{rr}}} = \frac{{{{E}_{{rs}}}{{n}_{r}}{{n}_{s}}}}{{{{\alpha }}\dot {\Lambda }}} - \frac{k}{{{\alpha }}} - 2{{P}_{{rr}}}$

а используя (2.29) –

(2.37)

$2B + \left( {\frac{{{{E}_{{rs}}}{{n}_{r}}{{n}_{s}}}}{{3{{\alpha }}\dot {\Lambda }}} - \frac{k}{{3{{\alpha }}}} + 2p} \right) = \frac{{{{E}_{{rs}}}{{n}_{r}}{{n}_{s}}}}{{4{{\beta }}\dot {\Lambda }}}$

(2.38)

$ - \frac{{B{{E}_{{il}}}{{n}_{i}}{{n}_{l}}}}{{{{\beta }}\dot {\Lambda }}} + 4{{B}^{2}} - {{\left( {\frac{{{{E}_{{rs}}}{{n}_{r}}{{n}_{s}}}}{{3{{\alpha }}\dot {\Lambda }}} - \frac{k}{{3{{\alpha }}}} + 2p} \right)}^{2}} = \frac{{{{E}_{{rs}}}{{n}_{r}}{{n}_{s}}}}{{\dot {\Lambda }{{\beta }}}}\left( {\frac{k}{{12{{\alpha }}}} - \frac{{{{E}_{{kl}}}{{n}_{k}}{{n}_{l}}}}{{12{{\alpha }}\dot {\Lambda }}} - \frac{p}{2} - \frac{B}{2}} \right)$

(2.39)

$ - \frac{{B{{E}_{{il}}}{{n}_{i}}{{n}_{l}}}}{{{{\beta }}\dot {\Lambda }}} + \frac{{{{{\left( {{{E}_{{lr}}}{{n}_{r}}{{n}_{l}}} \right)}}^{2}}}}{{8{{{{\beta }}}^{2}}{{{\dot {\Lambda }}}^{2}}}} + 4{{B}^{2}} - {{\left( {\frac{{{{E}_{{rs}}}{{n}_{r}}{{n}_{s}}}}{{3{{\alpha }}\dot {\Lambda }}} - \frac{k}{{3{{\alpha }}}} + 2p} \right)}^{2}} = \frac{{{{{\left( {{{E}_{{lr}}}{{n}_{r}}{{n}_{l}}} \right)}}^{2}}}}{{16{{{{\beta }}}^{2}}{{{\dot {\Lambda }}}^{2}}}}$

Подставляя (2.35)–(2.39) в выражение для 3-го инварианта (2.14), находим его выражение через компоненты тензора скоростей деформации.

(2.40)

${{I}_{3}} = \frac{{{{E}_{{il}}}{{E}_{{li}}}}}{{8{{{{\beta }}}^{2}}{{{\dot {\Lambda }}}^{2}}}} - \frac{{{{E}_{{il}}}{{E}_{{is}}}{{n}_{s}}{{n}_{l}}}}{{4{{{{\beta }}}^{2}}{{{\dot {\Lambda }}}^{2}}}} + \frac{{{{{\left( {{{E}_{{lr}}}{{n}_{r}}{{n}_{l}}} \right)}}^{2}}}}{{16{{{{\beta }}}^{2}}{{{\dot {\Lambda }}}^{2}}}}$

Подставляя выражения для инвариантов (2.28), (2.29), (2.41) в критерий текучести (2.1), группируя члены при одинаковых степенях $\dot {\Lambda }$ и умножая на ${{\dot {\Lambda }}^{2}}$, находим уравнение для нахождения $\dot {\Lambda }$, которое имеет единственное положительное решение

(2.41)

$\dot {\Lambda } = \sqrt {\left[ {\frac{{{{E}_{{il}}}{{E}_{{li}}}}}{{8{{\beta }}}} + \left( {1 - \frac{1}{{4{{\beta }}}}} \right){{E}_{{ir}}}{{E}_{{is}}}{{n}_{r}}{{n}_{s}} + \left( { - 1 + \frac{1}{{4{{\alpha }}}} + \frac{1}{{16{{\beta }}}}} \right){{{\left( {{{E}_{{lr}}}{{n}_{r}}{{n}_{l}}} \right)}}^{2}}} \right]{\text{/}}\left( {\frac{{{{k}^{2}}}}{{4{{\alpha }}}} - a} \right)} $

Уравнения (2.28), (2.29) и (2.41) решают поставленную задачу исследования – определить тензор напряжений при известном тензоре пластической деформации. Далее за оси координат примем главные оси тензора скоростей деформации. В этой системе координат, с учетом условия несжимаемости, тензор скоростей будет иметь вид

(2.42)

${\mathbf{E}} = \left( {\begin{array}{*{20}{c}} {{{E}_{x}}}&0&0 \\ 0&{{{E}_{y}}}&0 \\ 0&0&{ - {{E}_{x}} - {{E}_{y}}} \end{array}} \right)$

Тогда выражения (2.29) принимают вид

(2.43)

$A = - \frac{k}{{2{{\alpha }}}} + \frac{{[{{E}_{x}}(n_{x}^{2} - n_{z}^{2}) + {{E}_{y}}(n_{y}^{2} - n_{z}^{2})]}}{{\dot {\Lambda }}}\left( {\frac{1}{{8{{\beta }}}} + \frac{1}{{2{{\alpha }}}} - 2} \right)$

(2.44)

$B = - p + \frac{k}{{6{{\alpha }}}} + \left( {\frac{1}{{8{{\beta }}}} - \frac{1}{{6{{\alpha }}}}} \right)\frac{{[{{E}_{x}}(n_{x}^{2} - n_{z}^{2}) + {{E}_{y}}(n_{y}^{2} - n_{z}^{2})]}}{{\dot {\Lambda }}}$

а выражение (2.41) – вид

(2.45)

$\begin{gathered} \dot {\Lambda } = \left\{ {\frac{{{{{\left( {{{E}_{x}} + {{E}_{y}}} \right)}}^{2}} - {{E}_{x}}{{E}_{y}}}}{{4{{\beta }}}} + \left( {1 - \frac{1}{{4{{\beta }}}}} \right)[E_{x}^{2}n_{x}^{2} + E_{y}^{2}n_{y}^{2} + {{{\left( {{{E}_{x}} + {{E}_{y}}} \right)}}^{2}}n_{z}^{2}]} \right. + \\ {{\left. {\, + \left( { - 1 + \frac{1}{{4{{\alpha }}}} + \frac{1}{{16{{\beta }}}}} \right){{{[{{E}_{x}}(n_{x}^{2} - n_{z}^{2}) + {{E}_{y}}(n_{y}^{2} - n_{z}^{2})]}}^{2}}} \right\}}^{{1{\text{/}}2}}}{\text{/}}\sqrt {\left( {\frac{{{{k}^{2}}}}{{4{{\alpha }}}} - a} \right)} \\ \end{gathered} $

Используя (2.28), находим компоненты тензора напряжений

(2.46)

${{P}_{{xx}}} = \frac{{{{E}_{x}}}}{{4{{\beta }}\dot {\Lambda }}} + \frac{{2{{E}_{x}}n_{x}^{2}}}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right) + An_{x}^{2} + B$

(2.47)

${{P}_{{yy}}} = \frac{{{{E}_{y}}}}{{4{{\beta }}\dot {\Lambda }}} + \frac{{2{{E}_{y}}n_{y}^{2}}}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right) + An_{y}^{2} + B$

(2.48)

${{P}_{{zz}}} = - \frac{{\left( {{{E}_{x}} + {{E}_{y}}} \right)}}{{4{{\beta }}\dot {\Lambda }}} - \frac{{2\left( {{{E}_{x}} + {{E}_{y}}} \right)n_{z}^{2}}}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right) + An_{z}^{2} + B$

(2.49)

${{P}_{{xy}}} = \left[ {\frac{{{{E}_{x}} + {{E}_{y}}}}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right) + A} \right]{{n}_{x}}{{n}_{y}}$

(2.50)

${{P}_{{xz}}} = \left[ {A - \frac{{{{E}_{y}}}}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4\beta }}} \right)} \right]{{n}_{x}}{{n}_{z}},\quad {{P}_{{yz}}} = \left[ {A - \frac{{{{E}_{x}}}}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right)} \right]{{n}_{y}}{{n}_{z}}$

3. Случай плоской деформации. Рассмотрим теперь в главных осях случай плоской деформации

(3.1)

${{E}_{x}} = - {{E}_{z}} = E,\quad {{E}_{y}} = 0$

Этот случай представляет большой практический интерес, поскольку в некоторых экспериментальных работах [1, 2], по изучению механических свойств монокристаллов магния, исследуется именно плоская деформация. Уравнение (2.45) с учетом (3.1) принимает вид

(3.2)

$\dot {\Lambda } = E\sqrt {\left[ {1 - n_{y}^{2} + \frac{{n_{y}^{2}}}{{4{{\beta }}}} + {{{(n_{x}^{2} - n_{z}^{2})}}^{2}}\left( { - 1 + \frac{1}{{4{{\alpha }}}} + \frac{1}{{16{{\beta }}}}} \right)} \right]{\text{/}}\left( {\frac{{{{k}^{2}}}}{{4{{\alpha }}}} - a} \right)} $

а уравнения для компонент тензора напряжений (2.46)–(2.50) вид –

${{P}_{{xx}}} = \frac{E}{{4{{\beta }}\dot {\Lambda }}} + \frac{{2En_{x}^{2}}}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right) + An_{x}^{2} + B,\quad {{P}_{{yy}}} = An_{y}^{2} + B$

(3.3)

${{P}_{{zz}}} = - \frac{E}{{4{{\beta }}\dot {\Lambda }}} - \frac{{2En_{z}^{2}}}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right) + An_{z}^{2} + B,\quad {{P}_{{xy}}} = \left[ {\frac{E}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4\beta }}} \right) + A} \right]{{n}_{x}}{{n}_{y}}$

${{P}_{{xz}}} = A{{n}_{x}}{{n}_{z}},\quad {{P}_{{yz}}} = \left[ { - \frac{E}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right) + A} \right]{{n}_{y}}{{n}_{z}},$

(3.4)

$A = - \frac{k}{{2{{\alpha }}}} + \frac{{E(n_{x}^{2} - n_{z}^{2})}}{{\dot {\Lambda }}}\left( {\frac{1}{{8{{\beta }}}} + \frac{1}{{2{{\alpha }}}} - 2} \right),\quad B = - p + \frac{k}{{6{{\alpha }}}} + \frac{{E(n_{x}^{2} - n_{z}^{2})}}{{\dot {\Lambda }}}\left( {\frac{1}{{8{{\beta }}}} - \frac{1}{{6{{\alpha }}}}} \right)$

Ориентировка кристалла задается углами Эйлера способом, используемым в кристаллографии [11]. Кристалл, кристаллографические оси которого первоначально совпадают с осями лабораторной системы координат X, Y, Z, (ось Z совпадает с кристаллографической осью c) последовательно поворачивается на угол ${{{{\varphi }}}_{1}}$ вокруг оси Z, затем на угол $\Phi $ вокруг оси X' (которое принимает ось X после первого поворота), затем вокруг оси Z'' (новое положение оси Z после двух предыдущих поворотов) на угол ${{{{\varphi }}}_{2}}$. Поскольку критерий (1) обладает цилиндрической симметрией вращения вокруг кристаллографической оси ${\mathbf{c}}$, то последнее вращение на угол ${{{{\varphi }}}_{2}}$ и сам этот угол можно не рассматривать, и задавать ориентировку кристалла парой углов $\left( {\begin{array}{*{20}{c}} {{{{{\varphi }}}_{1}}}&\Phi \end{array}} \right)$. Единичный, нормальный к базисной плоскости) вектор n имеет вид

(3.5)

${\mathbf{n}} = - \sin {{{{\varphi }}}_{1}}\sin \Phi {{{\mathbf{e}}}_{{\mathbf{1}}}} + \cos {{{{\varphi }}}_{1}}\sin \Phi {{{\mathbf{e}}}_{{\mathbf{2}}}} + \cos \Phi {{{\mathbf{e}}}_{{\mathbf{3}}}},\quad {{{{\varphi }}}_{1}} \in \left[ {0,2{{\pi }}} \right],\quad \Phi \in \left[ {0,{{\pi }}} \right]$

Особый интерес представляет случай, когда недиагональные компоненты равны нулю и таким образом, главные компоненты тензоров напряжений и деформаций совпадают. Согласно формулам (3.3), (3.5) таким случаям соответствуют значения углов $\Phi = 0^\circ ,\,\,180^\circ $. Кроме того, из уравнения (3.3) легко увидеть, что недиагональные члены обращаются в ноль, когда

(3.6)

${{n}_{y}} = 0\quad {\text{и}}\quad A = 0$

Тогда из уравнения (3.4), (3.8) следует

(3.7)

$\cos {{{{\varphi }}}_{1}} = 0,\quad \sin {{{{\varphi }}}_{1}} = \pm 1$,

(3.8)

$n_{x}^{2} - n_{z}^{2} = {{\sin }^{2}}\Phi - {{\cos }^{2}}\Phi = - \cos 2\Phi $

Тогда из уравнений (3.3), (3.4) находим уравнение для определения $\Phi $

(3.9)

$A = - \frac{k}{{2{{\alpha }}}} - \frac{{E\cos 2\Phi }}{{\dot {\Lambda }}}\left( {\frac{1}{{8{{\beta }}}} + \frac{1}{{2{{\alpha }}}} - 2} \right)$

где

(3.10)

$\dot {\Lambda } = E\sqrt {\left[ {1 + {{{\cos }}^{2}}2\Phi \left( { - 1 + \frac{1}{{4{{\alpha }}}} + \frac{1}{{16{{\beta }}}}} \right)} \right]{\text{/}}\left( {\frac{{{{k}^{2}}}}{{4{{\alpha }}}} - a} \right)} $

соответственно, а из второго условия (3.6) следует

(3.11)

$\frac{k}{{2{{\alpha }}}} = - \frac{{\left( {\frac{1}{{8{{\beta }}}} + \frac{1}{{2{{\alpha }}}} - 2} \right)\sqrt {\left( {\frac{{{{k}^{2}}}}{{4{{\alpha }}}} - a} \right)} \cos 2\Phi }}{{\sqrt {\left[ {1 + {{{\cos }}^{2}}2\Phi \left( { - 1 + \frac{1}{{4{{\alpha }}}} + \frac{1}{{16{{\beta }}}}} \right)} \right]} }}$

причем $\cos 2\Phi < 0$. Разрешая уравнение (3.11) относительно $\cos 2\Phi $, находим

(3.12)

$\cos 2\Phi = - {{\left[ {\sqrt {{{{\left( {\frac{1}{{8{{\beta }}}} + \frac{1}{{2{{\alpha }}}} - 2} \right)}}^{2}}\left( {{{\alpha }} - \frac{{4{{{{\alpha }}}^{2}}}}{{{{k}^{2}}}}a} \right) - \left( { - 1 + \frac{1}{{4{{\alpha }}}} + \frac{1}{{16{{\beta }}}}} \right)} } \right]}^{{ - 1}}}$

Для дальнейшего анализа рассмотрим линии уровня для каждой из компонент, используя значения коэффициентов модели, полученных в нашей предыдущей работе [5] $a = - 0.28$ МПа², ${{\alpha }} = 7.07 \times {{10}^{{ - 4}}}$, ${{\beta }} = 5.36 \times {{10}^{{ - 4}}}$, $k = 6.37 \times {{10}^{{ - 2}}}$ МПа. Поскольку для определения диагональных компонент тензора деформаций необходимо знание приложенного гидростатического давления, ограничимся построением графиков для компонент девиаторов напряжений, которые совпадают с соответствующими компонентами тензора напряжений в случае недиагональных компонент. Диагональные компоненты отличаются от компонент девиаторов на величину гидростатического давления.

(3.13)

${{S}_{{ij}}} = {{P}_{{ij}}} - \frac{1}{3}{{\delta }_{{ij}}}{{P}_{{kk}}} = {{P}_{{ij}}} + {{\delta }_{{ij}}}p$

Линии уровней диагональных компонент ${{S}_{{xx}}},{{S}_{{yy}}},{{S}_{{zz}}}$ представлены на рис 1, a–c соответственно, и линии уровней недиагональных компонент ${{S}_{{xy}}},{{S}_{{xz}}},{{S}_{{yz}}}$ на рис 2, a–c соответственно.

Рис. 1.

Линии уровней диагональных компонент (a) ${{S}_{{xx}}},$ (b) ${{S}_{{yy}}},$ (c) ${{S}_{{zz}}}$. $\Phi ,{{\varphi }}$ измеряются в градусах.

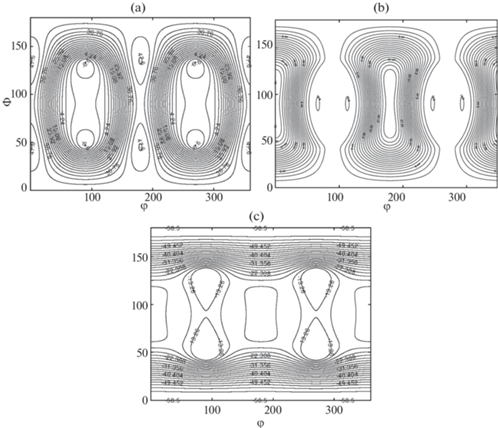
Рис. 2.

Линии уровней недиагональных компонент (a) ${{S}_{{xy}}},$ (b) ${{S}_{{xz}}},$ (c) ${{S}_{{yz}}}$. $\Phi ,{{\varphi }}$ измеряются в градусах.

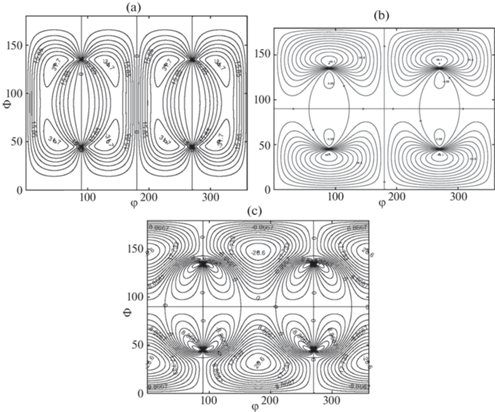
Зависимости компонент от углов ${{{{\varphi }}}_{1}}$ и $\Phi $ являются достаточно сложными, имеют большое количество локальных максимумов и минимумов и нулевые изолинии достаточно сложного вида, особенно ${{S}_{{yz}}}$ и ${{S}_{{xz}}}$, за исключением компоненты ${{S}_{{zz}}}$, которая всегда отрицательна. Компонента ${{S}_{{xx}}}$ достигает максимальных значений при углах $\Phi = 45^\circ $ и $\Phi = 135^\circ $, а также ${{{{\varphi }}}_{1}} = 0^\circ $ и ${{{{\varphi }}}_{1}} = 180^\circ $. Эти ориентировки для свободного зерна являются наиболее легкими для пластической деформации, но здесь направление легкого скольжения заблокировано приложенной ограничивающей силой, обеспечивающей плоскую геометрию деформации. Наибольшее по абсолютной величине значение компоненты ${{S}_{{zz}}}$ возникает при $\Phi = 0^\circ ,\,\,180^\circ $ и соответствуют сжатию в направлении нормали к базисной плоскости. Из внешнего вида кривых изолиний недиагональных компонент (рис. 2) и согласно формулам (3.3) и (3.5), видно, что недиагональные компоненты обращаются в нуль при углах $\Phi = 0^\circ ,\;180^\circ $, а также при четырех ориентировках, соответствующих всем возможным комбинациям углов ${{{{\varphi }}}_{1}} = 90^\circ ,\;{{{{\varphi }}}_{1}} = 270^\circ $; $\Phi \approx 46^\circ ,\;\Phi \approx 134^\circ $.

4. Случай одноосной деформации. Рассмотрим теперь случай одноосной деформации, определяемый условием

(4.1)

${{E}_{x}} = {{E}_{y}} = E,\quad {{E}_{z}} = - {{E}_{x}} - {{E}_{y}}$

Фактически имеем два случая. Случай E > 0 (сжатие вдоль оси z и растяжение вдоль осей x, y) и E < 0 (сжатие вдоль осей x и y, растяжение вдоль оси z). Аналогичные два случая можно рассмотреть и для плоской деформации, при этом второй случай получается из первого заменой координатных осей.

Для одноосной деформации, формулы (2.46)–(2.50) для компонент тензора напряжений, соответствующих пределу текучести, с учетом (3.5) принимают вид

(4.2)

${{P}_{{xx}}} = {{S}_{0}} - 2{{P}_{{xyM}}}{{\sin }^{2}}{{{{\varphi }}}_{1}} - p,\quad {{P}_{{yy}}} = {{S}_{0}} - 2{{P}_{{xyM}}}{{\cos }^{2}}{{{{\varphi }}}_{1}} - p,\quad {{P}_{{zz}}} = {{S}_{{zz}}} - p$

(4.3)

${{P}_{{xy}}} = {{P}_{{xyM}}}\sin 2{{{{\varphi }}}_{1}},\quad {{P}_{{yz}}} = {{P}_{{yzM}}}\cos {{{{\varphi }}}_{1}},\quad {{P}_{{xz}}} = - {{P}_{{yzM}}}\sin {{{{\varphi }}}_{1}}$

где $p$ – это гидростатическое давление,

(4.4)

${{S}_{0}} = \frac{E}{{4{{\beta }}\dot {\Lambda }}} + {{B}_{0}}$

${{S}_{0}}$ – это составляющая девиатора диагональных компонент тензора напряжений, не зависящая от угла ${{{{\varphi }}}_{1}}$;

(4.5)

${{S}_{{xyM}}} = - \frac{{{{{\sin }}^{2}}\Phi }}{2}\left[ {\frac{{2E}}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right) + A} \right]$

${{S}_{{xyM}}}$ – значение ${{P}_{{xy}}}$, соответствующее углу ${{{{\varphi }}}_{1}} = 45^\circ $, при котором эта абсолютная величина этой компоненты достигает максимального по ${{{{\varphi }}}_{1}}$ значения;

(4.6)

${{S}_{{yzM}}} = \frac{{\sin 2\Phi }}{2}\left[ {A - \frac{E}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4{{\beta }}}}} \right)} \right]$

${{S}_{{yzM}}}$ – значение компоненты ${{P}_{{yzM}}}$, соответствующее углу ${{{{\varphi }}}_{1}} = 0^\circ $,

(4.7)

${{S}_{{zz}}} = - \frac{E}{{2\beta \dot {\Lambda }}} - \frac{{4E{{{\cos }}^{2}}\left( \Phi \right)}}{{\dot {\Lambda }}}\left( {1 - \frac{1}{{4\beta }}} \right) + A{{\cos }^{2}}\left( \Phi \right) + {{B}_{0}}$

${{S}_{{zz}}}$ – девиатор компоненты ${{P}_{{zz}}}$ тензора напряжений;

(4.8)

$A = - \frac{k}{{2{{\alpha }}}} + E\frac{{1 - 3{{{\cos }}^{2}}\Phi }}{{\dot {\Lambda }}}\left( {\frac{1}{{8{{\beta }}}} + \frac{1}{{2{{\alpha }}}} - 2} \right)$

(4.9)

${{B}_{0}} = \frac{k}{{6{{\alpha }}}} + E\left( {\frac{1}{{8{{\beta }}}} - \frac{1}{{6{{\alpha }}}}} \right)\frac{{1 - 3{{{\cos }}^{2}}\Phi }}{{\dot {\Lambda }}}$

(4.10)

$\dot {\Lambda } = \sqrt {\left[ {\frac{{3{{E}^{2}}}}{{4{{\beta }}}} + \left( {1 - \frac{1}{{4{{\beta }}}}} \right){{E}^{2}}(1 + 3n_{z}^{2}) + \left( { - 1 + \frac{1}{{4{{\alpha }}}} + \frac{1}{{16{{\beta }}}}} \right){{E}^{2}}{{{(1 - 3n_{z}^{2})}}^{2}}} \right]{\text{/}}\left( {\frac{{{{k}^{2}}}}{{4{{\alpha }}}} - a} \right)} $

где ${{n}_{z}}$ находится из формулы (3.5). Данный случай затруднительно реализовать практически при произвольной ориентировке монокристалла, но он, по-видимому, играет важную роль при одноосевой деформации поликристаллического образца со случайной ориентировкой кристаллитов. Из формул (4.4)–(4.10) видно, что коэффициенты ${{S}_{0}}$, ${{S}_{{xyM}}}$, ${{S}_{{yzM}}}$, как и компонента девиатора тензора напряжений ${{S}_{{zz}}}$, зависят только от угла $\Phi $ между направлением приложения внешней силы и нормалью к плоскости базиса (0001). Эти зависимости для сжатия (рис. 3,а) и растяжения (рис. 3,b).

Рис. 3.

(а) Зависимость ${{S}_{0}}$, ${{S}_{{xyM}}}$, ${{S}_{{yzM}}}$, ${{S}_{{zz}}}$ угла Ф в случае сжатия, (b) Зависимость ${{S}_{0}}$, ${{S}_{{xyM}}}$, ${{S}_{{yzM}}}$, ${{S}_{{zz}}}$ угла Ф в случае растяжения. $\Phi $ измеряется в градусах, S – в МПа.

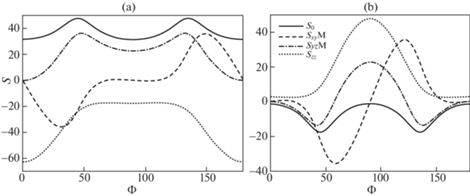
5. Осреднение. Осреднение в физических теориях пластичности применяется в приближении Фойгта. В механической теории пластичности этот метод впервые применен Тейлором и развит Бишопом и Хиллом [7]. Данный подход предполагает, что все зерна деформируются одинаково, т.е. макроскопический тензор скоростей деформации ${{E}_{{ij}}}$ задан и совпадает с микроскопическим. Тогда с использованием критерия текучести (в подходе Тейлора – это закон Шмида с явным учетом работающих систем скольжения) вычисляется тензор напряжений для каждого зерна и проводится осреднение. В данной работе в качестве критерия текучести используется феноменологический критерий [4]. При этом кроме тензора скоростей деформации должно быть известно гидростатическое давление, которое задается независимо и связано с внешними условиями. Исходя только из компонент тензора ${{E}_{{ij}}}$ можно определить только девиатор тензора напряжений.

Зная тензор напряжений для каждой ориентировки ${{P}_{{ij}}}\left( {{{{{\varphi }}}_{1}},\Phi } \right)$, умножим его на функцию распределения ориентировок [7], где ${{\rho }}\left( {{{{{\varphi }}}_{1}},\Phi } \right)$ – плотность распределения зерен по различным ориентировкам, затем проинтегрируем по всем возможным ориентировкам и окончательно получим

(5.1)

$\left\langle {{{P}_{{ij}}}} \right\rangle = \int\limits_{{{S}_{1}}} {{{\rho }}\left( {\mathbf{n}} \right){{P}_{{ij}}}\left( {\mathbf{n}} \right)} d{\mathbf{n}} = \int\limits_0^{{\pi }} {\int\limits_0^{2{{\pi }}} {{{\rho }}\left( {\Phi ,{{{{\varphi }}}_{1}}} \right)} } {{P}_{{ij}}}\left( \Phi \right)\sin \Phi d{{{{\varphi }}}_{1}}d\Phi $

Здесь ${{S}_{1}}$ – единичная сфера с центром в начале координат. Одним из очевидных преимуществ такого подхода является возможность рассмотрения различной геометрии деформации. Ограничимся здесь, как и ранее, случаем свободного растяжения и сжатия при равномерном распределении зерен по ориентировкам, т.е. ${{\rho }}\left( {\mathbf{n}} \right) = {\text{const}}$ и текстура отсутствует. Образец – прямоугольный параллелепипед, ориентированный вдоль оси Oz, квадратного поперечного сечения. С торцов приложены силы растяжения или сжатия вдоль оси Oz, причем касательные составляющие предполагаем равными нулю. На боковых сторонах образца напряжения отсутствуют.

(5.2)

${{P}_{{xx}}} = {{P}_{{yy}}} = 0$

Из симметрии задачи следует, что деформация должна быть одноосной и в лабораторной системе координат имеет вид (4.1). Гидростатическое давление p находится из условий на свободных поверхностях (5.2). Из определения девиатора тензора напряжений (4.3), и гидростатического давления имеем

(5.3)

$p = - \frac{1}{3}{{P}_{{ii}}}$

Из условия (5.2) следует, что

(5.4)

${{P}_{{zz}}} = 1.5{{S}_{{zz}}}$

Выражение для девиатора тензора напряжения получается из (4.2)–(4.10), если принять p = 0. При отсутствии текстуры ${{\rho }}\left( {\Phi ,{{{{\varphi }}}_{1}}} \right) = 1{\text{/}}4{{\pi }}$ и соответствующие критические напряжения растяжения ${{P}_{{{\text{tr}}}}}$ и сжатия ${{P}_{{{\text{cr}}}}}$ с учетом (3.20) принимают вид

(5.5)

${{P}_{{tr}}} = \frac{3}{4}\int\limits_0^{{\pi }} {{{S}_{{zz}}}\left( \Phi \right)} \sin \Phi d\Phi = {\text{37}}\,\,{\text{МПа}}$

(5.6)

${{P}_{{cr}}} = - \frac{3}{4}\int\limits_0^{{\pi }} {{{S}_{{zz}}}\left( \Phi \right)} \sin \Phi d\Phi = {\text{37}}\,\,{\text{МПа}}$

Заметим, что случай (5.5) соответствует $E < 0$, а случай (5.6) –$E > 0$. Видно, что критические напряжения для сжатия и растяжения равны между собой. Полученные расчетные значения критических напряжений для сжатия и растяжения примерно в 1.5 раза превышают экспериментальные значения для литого поликристаллического магния ${{{{\sigma }}}_{{0.2}}}$ [12].

6. Заключение. В рамках обобщенного на гексагональные кристаллы критерия текучести Мизеса, решена задача определения напряжения при заданном тензоре скоростей пластической деформации и известном значении приложенного внешнего давления.

Применен метод осреднения по Фойгту значений предела текучести по различным ориентировкам гексагональных монокристаллитов, с целью получения оценочных значений пределов текучести для поликристаллических образцов при одноосной деформации, в рамках предложенной модели. Данный подход дает правильный порядок условного предела текучести и, таким образом, значительно точнее описывает свойства поликристаллического гексагонального материала, в частности магния, чем классический подход Закса. Тем не менее, вычисленный предел текучести остается сильно завышенным.

Подробно исследован случай плоской деформации, найдены условия, когда главные оси тензора напряжений и деформаций совпадают.

Построены диаграммы линий уровня напряжений для начала пластического течения, рассчитаны компоненты девиатора тензора напряжений.

Работа выполнена в рамках государственного задания по теме “Давление” Г.р. № 122021000032-5.

Список литературы

Kelley E.W., Hosford W.F. Plane–strain compression of magnesium and magnesium alloy crystals // Trans. Metall. Soc. AIME. 1968. V. 242. P. 5–13.
Wonsiewicz B.C., Backofen W.A. Plasticity of magnesium crystals // Trans. Metall. Soc. AIME. 1967. V. 239. P. 1422–1431.
Трусов П.В. Классические и многоуровневые конститутивные модели для описания поведения металлов и сплавов: проблемы и перспективы (в порядке обсуждения) // Изв. РАН. МТТ. 2021. № 1. С. 69–82. https://doi.org/10.31857/S0572329921010128
Vlasov A.M., Kesarev A.G. Deformation model of magnesium single crystals // Russ. Phys. J. 2018. V. 61. P. 1258–1269. https://doi.org/10.1007/s11182-018-1527-y
Власова А.М., Кесарев А.Г. Обобщение критерия Мизеса на монокристаллы с гексагональной решеткой // Изв. РАН. МТТ. 2019. № 6. С. 86–98.
Победря Б.Е. Механика композиционных материалов. М.: МГУ, 1984. 336 с.
Трусов П.В., Волегов П.С., Кондратьев Н.С. Физические теории пластичности. Пермь: ПНИПУ, 2013. 244 с.
Седов Л.И. Механика сплошной среды. Т. 2. М.: Наука, 1994. 560 с.
Седов Л.И. Механика сплошной среды. Т. 1. М.: Наука, 1994. 528 с.
Победря Б.Е. Лекции по тензорному анализу. М.: МГУ, 1986. 264 с.
Уманский Я.С., Скаков Ю.А., Иванов А.Н., Расторгуев Л.Н. Кристаллография, рентгенография и электронная микроскопия. М.: Металлургия, 1982. 631 с.
Лахтин Ю.М., Леонтьева В.П. Материаловедение, М.: Машиностроение, 1990. 528 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал