Известия РАН. Механика твердого тела, 2023, № 1, стр. 129-141
ПРИМЕНЕНИЕ МЕТОДОВ ТЕОРИИ КРИТИЧЕСКИХ РАССТОЯНИЙ ДЛЯ ОЦЕНКИ РАЗРУШЕНИЯ КВАЗИХРУПКИХ МАТЕРИАЛОВ С ВЫРЕЗАМИ
a Институт горного дела Севера им. Н.В. Черского СО РАН
Якутск, Россия
* E-mail: suknyov@igds.ysn.ru
Поступила в редакцию 25.02.2022
После доработки 04.04.2022
Принята к публикации 05.04.2022
- EDN: KLQBAS
- DOI: 10.31857/S0572329922100191
Аннотация
Рассмотрено применение различных методов теории критических расстояний для оценки разрушения отрывом квазихрупкой пластины с вырезом в виде кругового отверстия, подверженной одноосному растяжению, одноосному сжатию, а также совместному действию растягивающих и сжимающих напряжений. Расчеты критических напряжений выполнены на основе предложенного ранее подхода, в соответствии с которым структурный параметр нелокального критерия разрушения представляется в виде суммы двух слагаемых. Первое из них характеризует собственно структуру материала и является константой, а второе отражает образование неупругих деформаций и зависит от пластических свойств материала, геометрии образца и краевых условий. Проведено сопоставление результатов расчетов с известными экспериментальными данными.
1. Введение. Подходы механики сплошной среды и механики разрушения имеют различные области практического применения в расчетах конструкций на прочность. Первый подход используется при проектировании конструкции, когда ставится задача оптимизации ее формы с целью максимально возможного снижения концентрации напряжений, а второй подход используется на стадии эксплуатации конструкции, когда ставится задача оценки ее остаточного ресурса с учетом влияния имеющихся в конструкции дефектов, наибольшую опасность из которых представляют дефекты типа трещин. Проблема состоит в том, что большая часть конструктивных, технологических и эксплуатационных дефектов и концентраторов напряжений, имеющих высокое, но конечное значение коэффициента концентрации напряжений, оказывается вне области применения этих подходов [1]. Поэтому актуальной является задача разработки новых подходов к расчетам конструкций на прочность, позволяющих охватить весь спектр концентраторов напряжений и с единых позиций подходить к расчету конструкции с тупым вырезом и с трещиной.
Этим требованиям отвечают нелокальные критерии разрушения, которые основаны на представлении о формировании в материале возле наиболее напряженной точки зоны предразрушения, в которой происходит локальное перераспределение упругих напряжений. За пределами этой малой по сравнению с размерами деформируемого тела области материал деформируется упруго вплоть до разрушения. Основы нелокальных критериев разрушения были заложены в работах [2–5]. Перераспределение напряжений в зоне предразрушения учитывается в неявном виде путем применения условия разрушения не в точке максимума, а на некотором расстоянии от нее, либо путем использования процедуры осреднения напряжений.
В дальнейшем эти подходы были развиты в работах [6–14] и других, причем развитие критериев идет по разным направлениям. Одно направление связано с уточнением функции эквивалентного напряжения (например, использование вместо максимального тангенциального напряжения максимального касательного напряжения [10], интенсивности напряжений [13], максимальной тангенциальной деформации [8] или плотности энергии деформации [7, 14]). Другое направление связано с изменением процедуры применения критерия (например, выполнение осреднения напряжений не по линии, а в некоторой области вблизи выреза [9]).
Другой подход к расчетам на прочность состоит в применении методов механики разрушения. Для трещины в твердом теле составляется энергетический баланс при ее виртуальном приращении на бесконечно малую величину и записывается условие роста трещины, которое и является критерием разрушения. Процедура применения критериев механики разрушения обычно сводится к расчету соответствующего коэффициента интенсивности напряжений и приравнивания его к критическому значению, которое также полагается константой материала. Для того чтобы критерий линейной упругой механики разрушения (LEFM) применить к описанию разрушения у тупого выреза поступают следующим образом. Предполагают, что в вершине выреза в зоне концентрации напряжений изначально существует воображаемая (фиктивная) трещина, длина которой является константой материала, характеризующей его структуру. Для трещины, находящейся в неоднородном поле напряжений, рассчитывается коэффициент интенсивности напряжений и применяется критерий LEFM. Одними из первых этот подход применили Waddoups, Eisenmann и Kaminski [15] для оценки прочности композитных пластин с круговым отверстием, подверженных растяжению.
Еще один критерий предложен в работах [16, 17]. Он основан на концепции механики конечных трещин (finite fracture mechanics), получившей в последнее время широкое распространение [18–22]. В этом критерии постулируется, что рост трещины, включая момент ее возникновения у выреза, происходит скачкообразно. Разрушение происходит, если энергия, высвобождаемая при скачкообразном изменении длины трещины, достигнет критического значения. Конечный размер приращения длины трещины рассматривается в качестве константы материала.
В настоящее время нелокальные критерии получили развитие в рамках теории критических расстояний (theory of critical distances). Хотя критерии основаны на различных подходах, Тейлор (Taylor) [23] обратил внимание, что предсказания, сделанные на этих методах расчетов, дают очень близкие результаты, и предложил рассматривать их как частные выражения некой общей теории, которую он назвал теорией критических расстояний (TCD). В рамках теории рассматриваются четыре критерия (метода расчетов).
1. Точечный метод (point method). В этом методе предполагается, что разрушение происходит тогда, когда упругое напряжение достигнет предела прочности материала ${{\sigma }_{0}}$ на некотором расстоянии d0 от вершины выреза. Следуя [6], этот метод будем также называть критерием напряжений в точке (point stress criterion).
2. Линейный метод (line method). В этом методе предполагается, что разрушение происходит тогда, когда усредненное на некотором расстоянии d0 упругое напряжение достигнет предела прочности материала ${{\sigma }_{0}}$. Осреднение выполняется вдоль линии, исходящей от вершины выреза. Следуя [6], этот метод будем также называть критерием средних напряжений (average stress criterion).
3. Метод воображаемой трещины (imaginary crack method). В этом методе предполагается, что в вершине выреза имеется воображаемая трещина длиной d0, а разрушение происходит тогда, когда коэффициент интенсивности напряжений в вершине трещины достигнет критического значения ${{K}_{c}}$. Этот метод будем также называть критерием фиктивной трещины (fictitious crack criterion).
4. Последний, четвертый метод реализует концепцию механики конечных трещин. Этот метод будем также называть критерием конечной трещины (finite crack criterion).
Общим свойством этих критериев является введение дополнительного параметра – внутреннего размера материала (intrinsic material length) d0, характеризующего его структуру, что позволяет описать масштабный эффект в условиях концентрации напряжений и тем самым расширить область применения по сравнению с традиционными критериями, не учитывающими масштабный эффект. В последнее время появилось большое количество работ (например, [24–28]), посвященных развитию TCD и ее применению для оценки прочности материалов и элементов конструкций с вырезами.
В квазихрупких материалах, таких как геоматериалы (бетон, гипс, горные породы), композиты, керамика, чугун, графит, формирование зоны предразрушения обычно связывают с локальным повреждением материала в результате микрорастрескивания или появления микропор. Зона поврежденности или, как ее часто называют, зона процесса разрушения (fracture process zone) не только предшествует образованию макротрещины, но и сопровождает ее в процессе распространения, окружая вершину трещины.
Вместе с тем, перераспределение напряжений в пределах размера d0 вызвано, прежде всего, дискретностью структуры, а не поврежденностью материала и связанными с ней неупругими деформациями. Поэтому область применения нелокальных критериев ограничена хрупким, либо квазихрупким разрушением с малой зоной предразрушения d, когда ее размер не сильно отличается от d0, т.е. при выполнении условия $d \approx {{d}_{0}}$ = const. При этом неупругие (пластические) свойства материала проявляются слабо. В то же время, если материал обладает достаточно сильно выраженными пластическими свойствами, образование неупругих деформаций приводит к увеличению зоны предразрушения и нарушению условия $d = const$. В работе рассматривается возможность применения методов теории критических расстояний в случае квазихрупкого разрушения с развитой зоной предразрушения $d > {{d}_{0}}$, когда перераспределение напряжений в зоне предразрушения определяется не только дискретностью структуры материала, но и его пластическими свойствами.
2. Размер зоны предразрушения. Ранее предпринимались попытки модернизировать нелокальные критерии за счет корректировки параметра d0 с целью более точного описания результатов конкретного эксперимента. Так, в работе [29] для описания экспериментальных данных о разрушении пластин из композитного материала с круговым отверстием радиуса R параметр d0 представляется в виде ${{d}_{0}} = \frac{{{{{(R{\text{/}}{{R}_{0}})}}^{m}}}}{C}$, а затем путем подгонки определяются феноменологические константы m и C (${{R}_{0}}$ – вспомогательный параметр, введенный, чтобы обезразмерить R). Подобным образом поступают в работе [30] для описания аналогичных экспериментальных данных, полученных на образцах с отверстиями эллиптической формы.
Другой подход предложен в работе [31]. На основе анализа диаграмм хрупкого, квазихрупкого и вязкого разрушения размер зоны предразрушения d представляется в следующем виде:
где ${{L}_{e}}$ – размер зоны концентрации напряжений, β – безразмерный параметр, характеризующий пластичность материала. Для хрупких материалов $\beta = 0$, для пластичных материалов $\beta \gg 1$. При β ~ 1 материал характеризуется умеренными пластическими свойствами. Первое слагаемое в выражении (2.1) характеризует собственно структуру материала, а второе отражает вклад неупругих деформаций. Таким образом, пластические свойства материала начинают проявляться при $d > {{d}_{0}}$ и проявляются тем сильнее, чем больше d по отношению к d0. Если $d = {{d}_{0}}$ будем говорить о хрупком разрушении, если $d > {{d}_{0}}$ – о квазихрупком разрушении, которое в пределе $d \gg {{d}_{0}}$ переходит в вязкое разрушение. При вязком разрушении критическое напряжение не зависит от размера концентратора напряжений, поэтому размер зоны предразрушения пропорционален размеру концентратора и, соответственно, размеру ${{L}_{e}}$ (при неизменных граничных условиях). При хрупком разрушении, напротив, размер зоны предразрушения не зависит от размера концентратора напряжений и определяется структурой материала.Таким образом, условие малости зоны предразрушения, ограничивающее область применения нелокальных критериев в рамках теории критических расстояний, принимает вид $\beta {{L}_{e}} \ll {{d}_{0}}$. В этом случае можно принять $d \approx {{d}_{0}} = const$. Для развитой зоны предразрушения второе слагаемое в выражении (2.1) не является малым по отношению к ${{d}_{0}}$, оно может быть сопоставимым или даже превышать характерный размер структуры материала, при этом $d \ne const$. Этот случай является предметом настоящего рассмотрения. При этом будем считать, что зона предразрушения остается малой по отношению к размерам деформируемого тела, и за пределами этой области материал деформируется упруго.
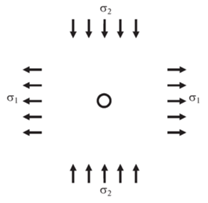
Рассмотрим возможность применения нелокальных критериев разрушения в задаче об образовании трещин отрыва в пластине с круговым отверстием, подверженной пропорциональному нагружению равномерно распределенными на бесконечности растягивающими ${{\sigma }_{1}} \equiv {{k}_{1}}p$ и сжимающими ${{\sigma }_{2}} \equiv {{k}_{2}}p$ напряжениями (рис. 1), с учетом изложенных выше представлений о формировании зоны предразрушения.
3. Критерии квазихрупкого разрушения. Применение первых трех методов теории критических расстояний для оценки разрушения квазихрупкого материала с круговым отверстием, подверженного двухосному нагружению, рассмотрено в работах [32, 33]. Приведем формулы для критического напряжения ${{p}_{c}}$ в момент образования трещин отрыва на контуре отверстия с учетом принятых обозначений.
Критерий средних напряжений (ASC) или линейный метод в теории критических расстояний:
(3.1)
${{p}_{c}} = 2\chi {{C}_{0}}{{[{{k}_{1}}(1 + {{\gamma }^{{ - 1}}})(2 + {{\gamma }^{{ - 2}}}) + {{k}_{2}}\left( {1 + \gamma } \right){{\gamma }^{{ - 3}}}]}^{{ - 1}}}$Критерий напряжений в точке (PSC) или точечный метод в теории критических расстояний:
(3.2)
${{p}_{c}} = 2\chi {{C}_{0}}{{[{{k}_{1}}(2 + {{\gamma }^{{ - 2}}} + 3{{\gamma }^{{ - 4}}}) + {{k}_{2}}( - {{\gamma }^{{ - 2}}} + 3{{\gamma }^{{ - 4}}})]}^{{ - 1}}}$Критерий фиктивной трещины (FCC) или метод воображаемой трещины в теории критических расстояний:
(3.3)
$\begin{gathered} {{p}_{c}} = 2\chi {{C}_{0}}[{{k}_{1}}(2 + {{\gamma }^{{ - 1.5}}} + 0.375{{\gamma }^{{ - 3.5}}}(5 + 2\gamma + {{\gamma }^{2}})) + \\ \; + {{k}_{2}}( - {{\gamma }^{{ - 1.5}}} + 0.375{{\gamma }^{{ - 3.5}}}(5 + 2\gamma + {{\gamma }^{2}}))] \\ \end{gathered} $Здесь $\chi = {{\sigma }_{0}}{\text{/}}{{C}_{0}}$; ${{\sigma }_{0}}$ – предел прочности при растяжении; ${{C}_{0}}$ – предел прочности при сжатии; $\gamma = 1 + d{\text{/}}a$; a – радиус отверстия. Размер d определяется выражением (2.1), в котором размер зоны концентрации напряжений ${{L}_{e}} = a{{\left( {3{{k}_{1}} + {{k}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {3{{k}_{1}} + {{k}_{2}}} \right)} {\left( {7{{k}_{1}} + 5{{k}_{2}}} \right)}}} \right. \kern-0em} {\left( {7{{k}_{1}} + 5{{k}_{2}}} \right)}}$. В случае квазихрупкого разрушения, выражение для γ принимает вид:
Применяя критерий фиктивной трещины к материалам, содержащим вырезы, необходимо помнить о проблеме сшивки критерия с традиционным критерием хрупкого разрушения сплошной среды при больших размерах выреза [34]. В этом случае критерий FCC дает заниженное на 12% значение разрушающей нагрузки. Проблема может быть преодолена путем приближенного расчета коэффициента интенсивности напряжений в вершине фиктивной трещины способом, изложенным в [34]. Если этого не сделать, то ошибка в определении асимптотического значения разрушающей нагрузки может привести к ошибке в определении параметра β и неправильной оценке характера разрушения материала.
В соответствии с формулами (3.1)–(3.3) критическое напряжение с ростом диаметра отверстия уменьшается, асимптотически приближаясь к некоторому напряжению ${{T}_{0}}$ в случае хрупкого разрушения и к напряжению ${{T}_{s}}$ (${{C}_{0}} > {{T}_{s}} > {{T}_{0}}$) в случае квазихрупкого или вязкого разрушения. Отношение напряжений ${{T}_{s}}$ и ${{T}_{0}}$ связано с величиной параметра пластичности β в выражении (2.1). Приведем формулы для асимптотического значения критического напряжения:
(3.4)
${{T}_{s}} = {{T}_{0}}\frac{{2(3{{k}_{1}} + {{k}_{2}})}}{{{{k}_{1}}(1 + \gamma _{s}^{{ - 1}})(2 + \gamma _{s}^{{ - 2}}) + {{k}_{2}}\left( {1 + {{\gamma }_{s}}} \right)\gamma _{s}^{{ - 3}}}}\;\;{\text{для ASC}}$(3.5)
${{T}_{s}} = {{T}_{0}}\frac{{2(3{{k}_{1}} + {{k}_{2}})}}{{{{k}_{1}}(2 + \gamma _{s}^{{ - 2}} + 3\gamma _{s}^{{ - 4}}) + {{k}_{2}}( - \gamma _{s}^{{ - 2}} + 3\gamma _{s}^{{ - 4}})}}\;\;{\text{для}}\;{\text{PSC}}$(3.6)
$\begin{gathered} {{T}_{s}}\, = \,{{T}_{0}}\frac{{2(3{{k}_{1}} + {{k}_{2}})}}{{{{k}_{1}}(2\, + \,\gamma _{s}^{{ - 1.5}}\, + \,0.375\gamma _{s}^{{ - 3.5}}(5\, + \,2{{\gamma }_{s}}\, + \,\gamma _{s}^{2}))\, + \,{{k}_{2}}( - \gamma _{s}^{{ - 1.5}}\, + \,0.375\gamma _{s}^{{ - 3.5}}(5\, + \,2{{\gamma }_{s}}\, + \,\gamma _{s}^{2}))}} \\ {\text{для}}\;{\text{FCC}} \\ \end{gathered} $Здесь ${{\gamma }_{s}} = 1 + \beta \frac{{3{{k}_{1}} + {{k}_{2}}}}{{7{{k}_{1}} + 5{{k}_{2}}}}$, ${{T}_{0}} = \frac{{\chi {{C}_{0}}}}{{3{{k}_{1}} + {{k}_{2}}}}$ – асимптотическое значение критического напряжения для хрупкого материала. Для квазихрупких материалов, характеризующихся умеренными пластическими свойствами, ${{T}_{s}} \approx {{T}_{0}}\left( {1 + \beta {\text{/}}2} \right)$ для ASC, ${{T}_{s}}\, \approx \,{{T}_{0}}(1\, + \,\beta )$ для PSC и ${{T}_{s}} \approx {{T}_{0}}\left( {1 + 3\beta {\text{/}}4} \right)$ для FCC.
Необходимо сделать еще одно важное замечание относительно критерия FCC. Чтобы принять справедливость допущения $d = const$ в хрупком материале, содержащем вырез произвольного размера (в том числе, при его отсутствии), мы должны допустить изначальное существование в теле микродефектов, играющих роль фиктивных трещин. На первый взгляд, модель твердого тела с распределенными в нем микротрещинами (трещинами Гриффитса) выглядит вполне реалистичной и согласующейся с общепринятыми представлениями о реальном твердом теле, обладающем изначальной, присущей ему дефектностью (роль микротрещин могут, к примеру, выполнять границы зерен). Но в действительности такая модель может быть использована только для оценки прочности твердого тела, содержащего большой ансамбль гладких дефектов, например, пор. Чтобы применить модель для оценки прочности однородного тела, содержащего одиночный дефект произвольного размера, трещины Гриффитса должны заполнять объем всего тела, что физически абсурдно. Поэтому в рамках модели твердого тела с распределенными микротрещинами могут рассматриваться только достаточно большие отверстия, вырезы или полости, размер которых намного превышает размер микротрещин, а также расстояние между ними.
Применение четвертого метода теории критических расстояний для оценки разрушения квазихрупкого материала с круговым отверстием, подверженного двухосному нагружению, рассмотрено в работах [33, 35]. Метод основан на концепции механики конечных трещин (FFM), согласно которой рост трещины, включая момент ее возникновения у выреза, происходит скачкообразно. Конечное приращение длины трещины рассматривается в качестве константы материала: $\delta l = d = {\text{const}}$. Условие разрушения имеет вид [23]:
Важным преимуществом инкрементального условия разрушения (3.7) перед обычным дифференциальным условием $K = {{K}_{c}}$ является то, что оно может быть применено не только в качестве условия роста уже существующей в теле трещины, но и для предсказания появления трещин у концентраторов напряжений в теле, не содержащем начальных трещин. Для этого в уравнении (3.7) достаточно принять $l = 0$. При этом не требуется делать никаких дополнительных допущений о существовании в теле неких фиктивных или воображаемых трещин, представление о которых лежит в основе критерия FCC и приводит к определенным физическим противоречиям. Формула для расчета критического напряжения имеет следующий вид:
(3.8)
${{p}_{c}} = \chi {{C}_{0}}\frac{{16\left( {\gamma - 1} \right)}}{{\sqrt {k_{1}^{2}{{J}_{1}} + 2{{k}_{1}}{{k}_{2}}{{J}_{{12}}} + k_{2}^{2}{{J}_{2}}} }}$Асимптотическое (при $a \to \infty $) значение критического напряжения:
(3.9)
${{T}_{s}} = {{T}_{0}}\frac{{16\left( {{{\gamma }_{s}} - 1} \right)(3{{k}_{1}} + {{k}_{2}})}}{{\sqrt {k_{1}^{2}{{J}_{1}}\left( {{{\gamma }_{s}}} \right) + 2{{k}_{1}}{{k}_{2}}{{J}_{{12}}}\left( {{{\gamma }_{s}}} \right) + k_{2}^{2}{{J}_{2}}\left( {{{\gamma }_{s}}} \right)} }}$Для квазихрупких материалов, характеризующихся умеренными пластическими свойствами, ${{T}_{s}} \approx {{T}_{0}}\left( {1 + \beta {\text{/}}2} \right)$.
4. Сопоставление с экспериментальными данными и обсуждение результатов расчетов. 4.1. Одноосное растяжение. В работе [30] приведены результаты испытаний на растяжение пластин из эпоксидного углепластика с квазиизотропной укладкой слоев с круговыми отверстиями. На рис. 2 представлены экспериментальные данные (точки) о величине разрушающей нагрузки в зависимости от диаметра отверстия 2a [мм] и результаты расчета критического напряжения согласно критерию ASC по формуле (3.1) при $\beta = 0$ (кривая 1) и $\beta = 0.4$ (кривая 2). Размер d0 составил 1.6 мм. Штриховая и сплошная прямые, рассчитанные по формуле (3.4), показывают асимптотические значения кривых 1 и 2, соответственно.
Рис. 2.
Зависимость критического напряжения от диаметра отверстия для эпоксидного углепластика при растяжении. Расчет – по критерию ASC.
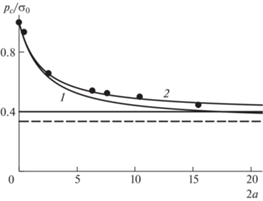
Параметры d0 и β подбирали исходя из наилучшего соответствия результатов расчета (кривая 2) и экспериментальных данных. Кривая 1 проведена для того, чтобы сравнить модифицированный и общепринятый критерии ASC и показать роль параметра β для предсказания разрушающей нагрузки. Модифицированный критерий ASC хорошо описывает экспериментальные данные во всем исследованном диапазоне диаметров отверстий (кривая 2). Неучет пластичности материала приводит к тому, что предсказания разрушающей нагрузки дают хорошие результаты только для малых диаметров отверстия, когда область неупругих деформаций также мала (кривая 1).
Расчеты критического напряжения по критериям ASC, PSC, FCC и FFM, выполненные по формулам (3.1), (3.2), (3.3) и (3.8) дают близкие результаты (рис. 3). Параметры материала, использованные в расчетах, приведены в табл. 1. При этом асимптотические значения критического напряжения, вычисленные по формулам (3.4), (3.5), (3.6) и (3.9), для всех критериев совпадают (табл. 1).
Рис. 3.
Зависимость критического напряжения от диаметра отверстия для эпоксидного углепластика при растяжении. Кривые 1, 2, 3, 4 – расчет по критериям ASC, PSC, FCC и FFM.
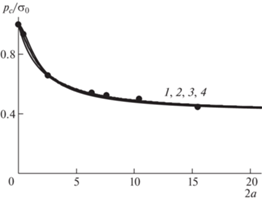
Таблица 1.
Параметры материала (эпоксидный углепластик)
| Критерий | d0, мм | $\beta $ | ${{T}_{s}}{\text{/}}{{T}_{0}}$ |
|---|---|---|---|
| ASC | 1.6 | 0.4 | 1.2 |
| PSC | 0.55 | 0.2 | 1.2 |
| FCC | 0.82 | 0.267 | 1.2 |
| FFM | 1.6 | 0.4 | 1.2 |
4.2. Неравнораспределенное сжатие. В работе [32] приведены экспериментальные данные о разрушении гипсовых плит с отверстием, подверженных неравномерно распределенному сжатию. Образцы изготавливали из гипсового материала с высоким (более 80%) содержанием полуводного гипса в исходном составе (гипс 1). Нагрузка прикладывалась к образцу через жесткие вставки, помещенные между образцом и нагружающими плитами. При этом, как было показано в работе [36], в центральной части образца (вне зоны влияния отверстия) реализуется достаточно однородное двухосное напряженное состояние: растяжение по горизонтальной оси и сжатие по вертикальной оси образца (рис. 1). Напряжения ${{\sigma }_{1}} \equiv {{k}_{1}}p$ и ${{\sigma }_{2}} \equiv {{k}_{2}}p$ рассчитывались методом конечных элементов в центре образцов без отверстия, нагруженных через вставки заданного размера. В первой серии экспериментов использовались вставки фиксированного размера, для них были определены ${{k}_{1}} = 0.143$ и ${{k}_{2}} = 0.764$.
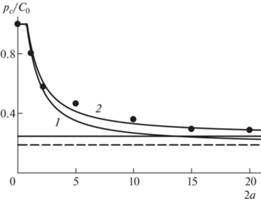
На рис. 4 представлены экспериментальные данные (точки) о критической нагрузке в момент образования трещин отрыва у отверстия в зависимости от его диаметра 2a [мм] и результаты расчета критического напряжения согласно критерия ASC по формуле (3.1) при $\beta = 0$ (кривая 1) и $\beta = 0.6$ (кривая 2). Размер d0 составил 1.0 мм. Штриховая и сплошная прямые, рассчитанные по формуле (3.4), показывают асимптотические значения кривых 1 и 2 соответственно. Модифицированный критерий ASC хорошо описывает экспериментальные данные во всем исследованном диапазоне диаметров отверстий (кривая 2). Так же, как в случае разрушения пластин из эпоксидного углепластика при растяжении, неучет пластичности гипсового материала приводит к тому, что предсказания критической нагрузки дают хорошие результаты только для малых диаметров отверстия (кривая 1).
Рис. 4.
Зависимость критического напряжения от диаметра отверстия для гипса 1 при неравнораспределенном сжатии. Расчет – по критерию ASC.
Результаты расчетов критического напряжения по критериям ASC, PSC, FCC и FFM показаны для сравнения на рис. 5. Параметры материала, использованные в расчетах, приведены в табл. 2.
Рис. 5.
Зависимость критического напряжения от диаметра отверстия для гипса 1 при неравнораспределенном сжатии. Кривые 1, 2, 3, 4 – расчет по критериям ASC, PSC, FCC и FFM.
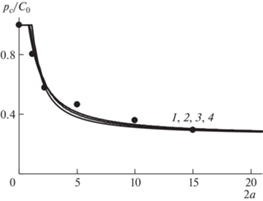
Таблица 2.
Параметры материала (гипс 1)
| Критерий | d0, мм | $\beta $ | ${{T}_{s}}{\text{/}}{{T}_{0}}$ |
|---|---|---|---|
| ASC | 1.0 | 0.6 | 1.3 |
| PSC | 0.3 | 0.3 | 1.3 |
| FCC | 0.5 | 0.4 | 1.3 |
| FFM | 1.0 | 0.6 | 1.3 |
Для малых отверстий критическое напряжение ограничено пределом прочности материала на сжатие, откуда следует, что существует критическое значение диаметра отверстия $2a = 2{{a}_{c}}$, ниже которого трещины отрыва на контуре отверстия не образуются. Другими словами, при $2a \leqslant 2{{a}_{c}}$ материал не чувствует присутствия концентратора напряжений. Это согласуется с современными представлениями о реальном твердом теле, обладающем изначальной, присущей ему дефектностью. Согласно им малые искусственные дефекты, размеры которых сопоставимы с размерами структурных составляющих материала, не оказывают влияния на его прочность до тех пор, пока их размеры не достигнут определенного (критического) значения.
4.3. Одноосное сжатие. В работе [37] приведены экспериментальные данные о разрушении гипсовых плит с отверстием, подверженных одноосному сжатию. Формирование трещин отрыва на контуре кругового отверстия диаметром 10 мм и более в образцах с низким (60–70%) содержанием полуводного гипса в исходном составе (гипс 2) происходило постепенно, что характерно для вязкого разрушения. Это связано с тем, что содержащиеся в исходном составе кристаллы двухводного гипса не участвуют в реакции гидратации при затворении гипсового вяжущего водой и фактически играют роль заполнителя, препятствуя формированию жесткого скелета материала.
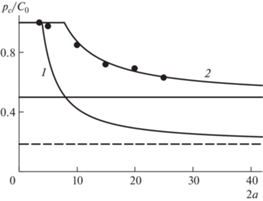
На рис. 6 представлены экспериментальные данные (точки) о критической нагрузке в момент образования трещин отрыва у отверстия в зависимости от его диаметра 2a [мм] и результаты расчета критического напряжения согласно критерию ASC по формуле (3.1) при $\beta = 0$ (кривая 1) и $\beta = 2.5$ (кривая 2). Размер d0 составил 2.0 мм. Модифицированный критерий ASC хорошо описывает экспериментальные данные во всем исследованном диапазоне диаметров отверстий (кривая 2). Расчет по общепринятому критерию ASC, не учитывающему пластичность материала, не позволяет получить приемлемые оценки критической нагрузки (кривая 1).
Рис. 6.
Зависимость критического напряжения от диаметра отверстия для гипса 2 при одноосном сжатии. Расчет – по критерию ASC.
Сравнительные результаты расчетов критического напряжения по критериям ASC, PSC, FCC и FFM показаны на рис. 7. Параметры материала, использованные в расчетах, приведены в табл. 3.
Рис. 7.
Зависимость критического напряжения от диаметра отверстия для гипса 2 при одноосном сжатии. Кривые 1, 2, 3, 4 – расчет по критериям ASC, PSC, FCC и FFM.
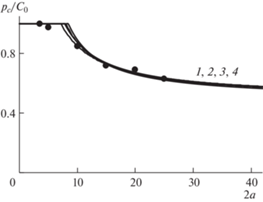
Таблица 3.
Параметры материала (гипс 2)
| Критерий | d0, мм | $\beta $ | ${{T}_{s}}{\text{/}}{{T}_{0}}$ |
|---|---|---|---|
| ASC | 2.0 | 2.5 | 2.7 |
| PSC | 0.6 | 1.0 | 2.7 |
| FCC | 0.9 | 1.45 | 2.7 |
| FFM | 2.2 | 2.6 | 2.7 |
Строго говоря, случай вязкого разрушения выходит за рамки применимости теории критических расстояний. Тем не менее, рассмотренный выше пример показывает, что предложенный подход, расширяющий область применения TCD на квазихрупкие материалы, может быть успешно применен для оценки критических напряжений и в этом случае.
Полученные результаты свидетельствуют о том, что модифицированные нелокальные критерии хорошо предсказывают влияние размера выреза на разрушение казихрупких материалов при различных условиях нагружения. Следует обратить внимание на то, что, хотя модифицированные критерии ASC и FFM несколько лучше описывают данные эксперимента, чем критерии PSC и FCC, отличие в расчетах по этим четырем критериям незначительно. Гораздо большее значение для расчетов имеет корректная оценка размера d, учитывающая образование неупругих деформаций. Другими словами, в рассмотренных задачах принципиальное значение имеет не вид используемого критерия разрушения, а корректное определение его параметров, прежде всего, размера зоны предразрушения.
5. Заключение. Область применения известных, основанных на теории критических расстояний нелокальных критериев разрушения, отличительной особенностью которых является введение дополнительного параметра материала размерности длины, характеризующего его структуру, ограничена хрупким, либо квазихрупким разрушением с малой зоной предразрушения. Для расширения области применения критериев на квазихрупкое разрушение с развитой зоной предразрушения ранее было предложено отказаться от гипотезы о размере зоны предразрушения, как о константе материала, связанной только с его структурой. Структурный параметр, лежащий в основе нелокальных критериев, должен рассматриваться в качестве константы материала только в одном частном случае – при хрупком разрушении. Для квазихрупких материалов этот параметр представляется в виде суммы двух слагаемых. Первое их них характеризует собственно структуру материала и является константой, а второе отражает образование неупругих деформаций и зависит от пластических свойств материала, геометрии образца и краевых условий. Предложенный подход использован при разработке модифицированных критериев средних напряжений, напряжений в точке, фиктивной трещины и конечной трещины. Проведена верификация разработанных критериев в задачах о разрушении квазихрупких материалов с круговым отверстием, подверженных одноосному растяжению, одноосному сжатию, а также совместному действию растягивающих и сжимающих напряжений. Показано хорошее соответствие результатов расчета критической нагрузки и экспериментальных данных.
Список литературы
Сукнев С.В. Критерий локальной прочности // Пробл. прочности. 2004. № 4. С. 108–124.
Wieghardt K. Über das Spalten und Zerreisen elastischer Körper // Z. Math. Phys. 1907. V. 55. № 1–2. P. 60–103.
Neuber H. Kerbspannungslehre, Grundlagen für eine genaue Spannungsrechnung. Berlin: Springer-Verlag, 1937. 160 p.
Peterson R.E. Notch sensitivity // Metal fatigue. New York: McGraw Hill, 1959. P. 293–306.
Новожилов В.В. О необходимом и достаточном критерии хрупкой прочности // ПММ. 1969. Т. 33. № 2. С. 212–222.
Whitney J.M., Nuismer R.J. Stress fracture criteria for laminated composites containing stress concentrations // J. Compos. Mater. 1974. V. 8. № 4. P. 253–265.
Kipp M.E., Sih G.C. The strain energy density failure criterion applied to notched elastic solids // Int. J. Solids Struct. 1975. V. 11. № 2. P. 153–173.
Wu H.-C., Chang K.-J. Angled elliptic notch problem in compression and tension // Trans. ASME. J. Appl. Mech. 1978. V. 45. № 2. P. 258–262.
Carter B.J., Lajtai E.Z., Yuan Y. Tensile fracture from circular cavities loaded in compression // Int. J. Fract. 1992. V. 57. № 3. P. 221–236.
Radaj D., Zhang S. Process zone fracture criteria for crack tips // Eng. Fract. Mech. 1995. V. 50. № 1. P. 111–120.
Seweryn A., Mroz Z. A non-local stress failure condition for structural elements under multiaxial loading // Eng. Fract. Mech. 1995. V. 51. № 6. P. 955–973.
Mikhailov S.E. A functional approach to non-local strength condition and fracture criteria // Eng. Fract. Mech. 1995. V. 52. № 4. P. 731–754.
Toribio J. A fracture criterion for high-strength steel notched bars // Eng. Fract. Mech. 1997. V. 57. № 4. P. 391–404.
Yosibash Z., Bussiba A., Gilad I. Failure criteria for brittle elastic materials // Int. J. Fract. 2004. V. 125. № 3–4. P. 307–333. https://doi.org/10.1023/B:FRAC.0000022244.31825.3b
Waddoups M.E., Eisenmann J.R., Kaminski B.E. Macroscopic fracture mechanics of advanced composite materials // J. Compos. Mater. 1971. V. 5. № 4. P. 446–454.
Pugno N.M., Ruoff R.S. Quantized fracture mechanics // Philos. Mag. 2004. V. 84. № 27. P. 2829–2845. https://doi.org/10.1080/14786430412331280382
Taylor D., Cornetti P., Pugno N. The fracture mechanics of finite crack extension // Eng. Fract. Mech. 2005. V. 72. № 7. P. 1021–1038. https://doi.org/10.1016/j.engfracmech.2004.07.001
Hebel J., Dieringer R., Becker W. Modelling brittle crack formation at geometrical and material discontinuities using a finite fracture mechanics approach // Eng. Fract. Mech. 2010. V. 77. № 18. P. 3558–3572. https://doi.org/10.1016/j.engfracmech.2010.07.005
Carpinteri A., Cornetti P., Sapora A. Brittle failures at rounded V-notches: a finite fracture mechanics approach // Int. J. Fract. 2011. V. 172. № 1. P. 1–8. https://doi.org/10.1007/s10704-011-9640-8
Weißgraeber P., Leguillon D., Becker W. A review of Finite Fracture Mechanics: crack initiation at singular and non-singular stress raisers // Arch. Appl. Mech. 2016. V. 86. № 1–2. P. 375–401. https://doi.org/10.1007/s00419-015-1091-7
Strobl M., Dowgiałło P., Seelig T. Analysis of Hertzian indentation fracture in the framework of finite fracture mechanics // Int. J. Fract. 2017. V. 206. № 1. P. 67–79. https://doi.org/10.1007/s10704-017-0201-7
Sapora A., Torabi A.R., Etesam S., Cornetti P. Finite Fracture Mechanics crack initiation from a circular hole // Fatigue Fract. Eng. Mater. Struct. 2018. V. 41. № 7. P. 1627–1636. https://doi.org/10.1111/ffe.12801
Taylor D. The theory of critical distances: a new perspective in fracture mechanics. Oxford: Elsevier, 2007. 284 p.
Li W., Susmel L., Askes H., Liao F., Zhou T. Assessing the integrity of steel structural components with stress raisers using the Theory of Critical Distances // Eng. Fail. Anal. 2016. V. 70. P. 73–89. https://doi.org/10.1016/j.engfailanal.2016.07.007
Fuentes J.D., Cicero S., Procopio I. Some default values to estimate the critical distance and their effect on structural integrity assessments // Theor. Appl. Fract. Mech. 2017. V. 90. P. 204–212. https://doi.org/10.1016/j.tafmec.2017.04.015
Taylor D. The Theory of Critical Distances: A link to micromechanisms // Theor. Appl. Fract. Mech. 2017. V. 90. P. 228–233. https://doi.org/10.1016/j.tafmec.2017.05.018
Vedernikova A., Kostina A., Plekhov O., Bragov A. On the use of the critical distance concept to estimate tensile strength of notched components under dynamic loading and physical explanation theory // Theor. Appl. Fract. Mech. 2019. V. 103. P. 102280. https://doi.org/10.1016/j.tafmec.2019.102280
Justo J., Castro J., Cicero S. Notch effect and fracture load predictions of rock beams at different temperatures using the Theory of Critical Distances // Int. J. Rock Mech. Min. Sci. 2020. V. 125. P. 104161. https://doi.org/10.1016/j.ijrmms.2019.104161
Pipes R.B., Wetherhold R.C., Gillespie J.W. (Jr.) Notched strength of composite materials // J. Compos. Mater. 1979. V. 13. P. 148–160.
Tan S.C. Laminated composites containing an elliptical opening. II. Experiment and model modification // J. Compos. Mater. 1987. V. 21. № 10. P. 949–968.
Сукнев С.В. Нелокальные и градиентные критерии разрушения квазихрупких материалов при сжатии // Физ. мезомех. 2018. Т. 21. № 4. С. 22–32. https://doi.org/10.24411/1683-805X-2018-14003
Сукнев С.В. Разрушение квазихрупкого геоматериала с круговым отверстием при неравномерно распределенном сжатии // ПМТФ. 2019. Т. 60. № 6. С. 162–172. https://doi.org/10.15372/PMTF20190617
Suknev S.V. Extending the theory of critical distances to quasi-brittle fracture // Theor. Appl. Fract. Mech. 2021. V. 114. P. 102996. https://doi.org/10.1016/j.tafmec.2021.102996
Сукнев С.В. Применение нелокальных и градиентных критериев для оценки разрушения геоматериалов в зонах концентрации растягивающих напряжений // Физ. мезомех. 2011. Т. 14. № 2. С. 67–75.
Сукнев С.В. Применение подхода механики конечных трещин для оценки разрушения квазихрупкого материала с круговым отверстием // Изв. РАН. МТТ. 2021. № 3. С. 13–25. https://doi.org/10.31857/S0572329921020161
Сукнев С.В. Разрушение хрупкого геоматериала с круговым отверстием при двухосном нагружении // ПМТФ. 2015. Т. 56. № 6. С. 166–172. https://doi.org/10.15372/PMTF20150618
Сукнев С.В. Образование трещин отрыва в зонах концентрации растягивающих напряжений в гипсе // ФТПРПИ. 2008. № 1. С. 47–55.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела