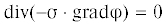Известия РАН. Механика твердого тела, 2023, № 1, стр. 142-155
ВЫЧИСЛЕНИЕ ПАРАМЕТРОВ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ПОЛИМЕРНОГО КОМПОЗИТА В ПОЛЕ ПОСТОЯННОГО ЭЛЕКТРИЧЕСКОГО ТОКА
П. А. Люкшин a, *, Б. А. Люкшин a, b, c, **, С. В. Панин a, d, ***, С. А. Бочкарева a, b, ****
a Институт физики прочности и материаловедения СО РАН
г. Томск, Россия
b Томский государственный университет систем управления и радиоэлектроники
г. Томск, Россия
c Национальный исследовательский Томский государственный университет
г. Томск, Россия
d Национальный исследовательский Томский политехнический университет
г. Томск, Россия
* E-mail: petrljuk@ispms.tsc.ru
** E-mail: lba2008@yandex.ru
*** E-mail: svp@ispms.tsc.ru
**** E-mail: bochkarevas@ispms.ru
Поступила в редакцию 27.04.2022
После доработки 03.06.2022
Принята к публикации 20.06.2022
- EDN: KLQDXU
- DOI: 10.31857/S0572329922600232
Аннотация
В электропроводящих композитах, помещенных в электрическое поле, происходит выделение тепла и формируются неоднородные температурные поля. Это, в свою очередь, индуцирует деформации и напряжении в таких композитах. В работе решается последовательность несвязанных краевых задач: электропроводности в поле постоянного электрического тока, теплопроводности, термоупругости. Показано, что при протекании электрического тока в медно-графитовом и наполненном порошком меди полимерном композите возникают перемещения, деформации и напряжения даже в том случае, когда компоненты композита не обладают пьезоэффектом.
1. Введение. Полимерные композиционные материалы (ПКМ) получают все более широкое распространение при решении практических задач. Это обусловлено как расширением номенклатуры ПКМ, так и возможностью придания им уникальных функциональных свойств. Используются разнообразные по составу, размеру и свойствам наполнители, описания и рекомендации по применению которых достаточно широко представлены на страницах научной и справочной литературы [1, 2]. Полимерные матрицы в силу своего строения не обладают свойством электропроводности, и традиционно применяются в качестве электрических изоляторов. Однако контролируемое введение в их состав токопроводящих включений, в том числе нанонаполнителей, способно превратить их в композиты, обладающие рядом ценных физических и функциональных свойств.
Одним из наиболее популярных нанонаполнителей для придания полимерным матрицам свойства электропроводности являются углеродные нанотрубки (УНТ). Так, в работе [3] анализирован ряд полимерных нанокомпозитов, формируемых различными технологическими методами. Вводились привитые к полимеру и чистые УНТ, а в качестве матрицы использовались латекс и полистирол. Оценивались как электрические, так и механические свойства нанокомпозитов. Показано, что одинаковые параметры микроструктуры не обязательно обеспечивают идентичные механические и электрофизические свойства композитов.
Функциональным наполнителем является, например, порошок алюминия, который в работе [4] добавляли в акрило-нитрильную бутадиеновую резину. Подобное наполнение сопровождалось снижением предела текучести и удлинения при разрыве. Показано существование известного перколяционного перехода (порога). Обсуждается известный механизм проводимости Пула–Френкеля (Poole–Frenkel conduction mechanism – перенос электронов с помощью ловушек в электрическом изоляторе), преобладающий при комнатной температуре. Использование модели C. Цангариса (S. Tsangaris) позволило получить хорошее согласие между расcчитанными и экспериментально измеренными значениями диэлектрической постоянной.
Однако, помимо придания полимерам электропроводности как таковой, возникает вопрос, как возникающее электрическое поле влияет на формирование механических напряжений. Обычно проявление механических эффектов в поле электрического тока наблюдается в пьезоматериалах. Однако эта задача актуальна, в частности, и в приложении к твердотельным полимерным электролитам, а именно литий-ионным твердотельным аккумуляторам [5]. В цитируемой работе с помощью конечно-элементного анализа показано, что в силу связности развивающихся при разряде процессов формируются неоднородные профили концентрации ионов, обусловливающие появление напряжений и деформаций, которые могут приводить к механическому разрушению полимера и выходу батарей из строя.
В другой работе на эту тему [6] показано, что низкая электрическая эффективность трехмерных твердотельных литий-ионных батарей обусловлена не только их неоднородной 3D-структурой, но и низкой ионной проводимостью электролита, а также интенсивностью диффузии на катоде. Это приводило к крайне неоднородному распределению плотности тока и неэффективному использованию катода.
Помимо “батарейных” приложений вопросы взаимосвязи механических и электрических полей изучали в приложении к электропроводящим полимерным покрытиям [7]. При этом анализировали взаимосвязь микроструктуры и деформационного отклика. Исследованы процессы, индуцированные термомеханическим нагружением, с позиции их влияния на развитие вязко-хрупкого перехода, а также растрескивание покрытия в областях наиболее крупных дефектов макромолекул.
Интерес к электропроводящим полимерам вызван не только возможностью обеспечения “настраиваемых” электрических свойств, но и простотой синтеза и изготовления, а также устойчивостью ко многим факторам окружающей среды [8]. В цитируемом обзоре рассмотрены модели транспорта электрического тока, объясняющие механизм проводимости, а также достигаемые физические свойства, включая оптические и механические.
В развитие аспектов накопителей энергии (energy storage) в работе [9] рассмотрены аспекты создания проводящих полимеров, обладающих требуемыми упругими свойствами, а также способностью к генерации/запасанию энергии. На примере эластичного проводящего полимера поли(3,4-этилендиокситиофен) показана возможность его применения для создания деформируемых органических термоэлектрических модулей. Данную тему продолжает работа [10], в которой исследованы характеристики токопроводящих полимеров с позиции механических (деформация, скорость деформации, напряжения, силы, модуль упругости) и электрических (емкость) свойств. Указанные параметры анализируются с позиции (электрофизической) активации полимера, а также оптимизации условий его синтеза.
В работе [11] проведен обзор моделей электропроводности проводящих полимеров и полимерных композитов как потенциальных материалов для изготовления полимерных электролитических мембран для топливных ячеек. Показано, что путем управления ориентацией наполнителя в токопроводящих полимерных композитах можно одновременно повысить их механические свойства и электропроводность.
Еще одним перспективным направлением использования токопроводящих полимеров являются актуаторы [12]. Для придания данного функционального свойства необходимо формировать проводящую взаимопроникающую полимерную сеть. С этой целью формировали сеть из полиэтилоксида и полибутадиена, в которую был диспергирован проводящий полимер поли(3,4-этилендиокситиофен). Исследования его свойств проведены с помощью динамического механического анализа (ДМА).
Таким образом, создание токопроводящих полимеров имеет некоторую практику и несомненную перспективу. Традиционно реакция на электрическое поле в виде появления напряжений и деформаций связывается с пьезоэлектрическими свойствами материала [13–16]. Электропроводность композита порождает ряд эффектов в виде выделения тепла и появления неоднородных температурных полей, что, в свою очередь, вызывает наличие деформаций и напряжений в структурно неоднородном материале, не связанных с пьезоэффектами. По этой причине исследование поведения армированных/наполненных пластиков в электрических полях представляет научный и практический интерес.
Для изучения этой проблемы в настоящей работе решается последовательность несвязанных краевых задач электропроводности, теплопроводности, термоупругости для структурно-неоднородного тела. В результате определяется напряженно-деформированное состояние в композитах, по которым протекает постоянный электрический ток. Задачи решались применительно к наполненному полимерному композиту “поли(3,4-этилендиокситиофен) – медный порошок” и композиту медь–графит. В расчете использовались свойства для измельченного графита.
Свойства материалов, используемые для расчета свойств композитов, приведены в табл. 1.
Таблица 1.
Свойства материалов
| Свойства | Поли(3,4-этилендиокситиофен) | Графит измельченный | Медный порошок |
|---|---|---|---|
| Модуль упругости Е, Па | 1.0 × 109 | 5.8 × 109 | 1.23 × 1011 |
| Коэффициент Пуассона ν | 0.35 | 0.25 | 0.3 |
| Коэффициент линейного расширения α, К–1 | 11.0 × 10–5 | 6.0 × 10–6 | 16.5 × 10–6 |
| Удельная теплоемкость С, Дж/(кг · К) | 2300 | 750 | 380 |
| Плотность ρ, кг/м3 | 1333 | 1750 | 8900 |
| Коэффициент теплопроводности К, Вт/(м · К) | 0.4 | 1.2 | 385 |
| Удельная электрическая проводимость, Ом–1 ⋅ м–1 | 800 | 1.25 × 106 | 5.9 × 107 |
2. Решение задачи электропроводности для композита. Электрическое поле постоянного тока в ячейке композиционного материала (КМ) описывается следующими уравнениями [17, 18]:
где ${{\bar {\delta }\;}}$ – плотность тока, ${{\bar {\sigma }}}~$ – удельная электрическая проводимость, ${{\bar {E}}}~$ – напряженность электрического поля.Введем новую переменную φ – потенциал электрического поля. Напряженность электрического поля связана с потенциалом следующим соотношением:
Подставляя ее в (2.1), получим уравнение Лапласа:
Для определения потенциала электрического поля постоянного тока в рассматриваемой области ABCD (рис. 1, a) необходимо решить уравнение Лапласа (2.2) с граничными условиями, например, Неймана и Дирихле ${{\varphi }}$.
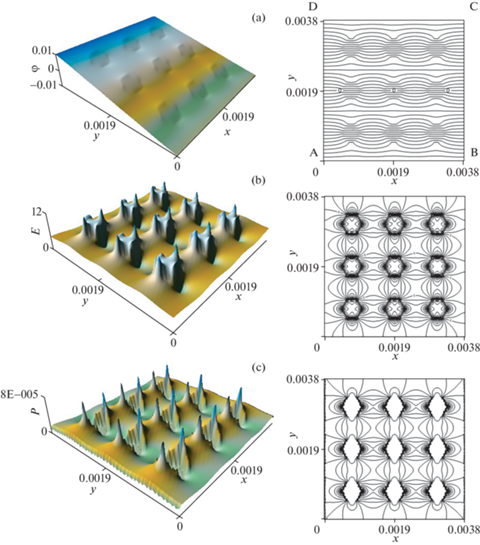
Рис. 1.
Поверхности и изолинии для композита “медь–графит” в плоскости xy (м): (а) – скалярный электрический потенциал (φ, в); (b) – напряженность электрического поля (Е, в/м); (с) – мощность тепловых потерь электрического поля постоянного тока (Р, Вт).
Электрический потенциал на границах АВ и DC принимался равным 0.01 В. Для электрического потенциала φ на границе двух сред (матрицы и включений) с различными проводимостями σ1, σ2 выполняются условия равенства потенциалов и нормальных компонент плотности тока [17, 18]
Решение уравнения Лапласа (2.2) эквивалентно отысканию минимума функционала χ [19]
Минимизация функционала позволяет получить систему алгебраических уравнений
[k(e)] – матрица “жесткости” одного элемента,
{φ} – вектор неизвестных значений потенциала,
{F} – вектор “нагрузки” в задаче электропроводности.
Система алгебраических уравнений (2.3) решается методом Гаусса [20].
Матрица “жесткости” конечного элемента в задачах электропроводности по форме совпадает с матрицей “жесткости” в задачах электростатики и теплопроводности
(2.4)
$[{{{\text{k}}}^{{\left( {\text{e}} \right)}}}] = \mathop \smallint \limits_{{{{\text{V}}}^{{\left( {\text{e}} \right)}}}} {{[{{{\text{B}}}^{{\left( {\text{e}} \right)}}}]}^{{\text{T}}}}[{{{\text{D}}}^{{\left( {\text{e}} \right)}}}] \cdot [{{{\text{B}}}^{{\left( {\text{e}} \right)}}}]{\text{dV}}$Матрица [D(е)], входящая в (2.4), характеризует физические свойства элемента, в случае задачи электропроводности равна
Матрица [B(e)] (содержащая производные от функции формы), входящая в (2.4), может быть записана как:
Коэффициенты bj, bk, cj, ck получаются круговой перестановкой индексов.
Мощность тепловых потерь в проводнике объемом V вычисляется по интегральной формуле Джоуля–Ленца [18]
На рис. 1, 2 приведены результаты решения задачи электропроводности для композитов “медь–графит” и “поли(3,4-этилендиокситиофен) – медный порошок”.
Рис. 2.
Поверхности и изолинии для композита “поли(3,4-этилендиокситиофен)–медный порошок” в плоскости xy (м): (а) – скалярный электрический потенциал (φ, в); (b) – напряженность электрического поля (Е, в/м); (с) – мощность тепловых потерь электрического поля постоянного тока (Р, Вт).
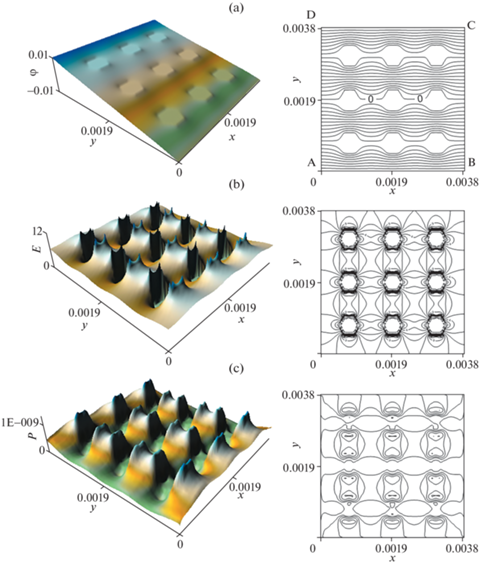
Следует отметить, что в случае композита “медь–графит” проводимость матрицы на порядок превышает проводимость включений, в случае композита “поли(3,4-этилендиокситиофен) – медный порошок” проводимость матрицы меньше проводимости включений на 4 порядка. Поэтому интегральная мощность тепловых потерь в ячейке композите “медь–графит” равна РABCD = 0.563 Вт (рис. 1, с), а в композите “поли (3,4-этилендиокситиофен) – медный порошок” РABCD = 0.143 × 10–4 Вт (рис. 2, с), т.е. различие составляет 4 порядка. На рис. 1, b и 2, b в разных композитах напряженность практически одинакова, но по изолиниям видно, что детальное распределение напряженности по ячейке отличается, в связи с разным соотношением проводимостей матрицы и включений. По этой же причине отличаются и изолинии электрического потенциала разных композитов (рис. 1, а и 2, а).
Далее предполагается, что вся мощность тепловых потерь, которая выделяется при прохождении электрического тока в композите, расходуется на повышение температуры. Для вычисления поля температуры в композите, обусловленной нагревом вследствие прохождения электрического тока, решается нестационарная задача теплопроводности.
3. Решение краевой задачи теплопроводности для композита. Уравнение теплопроводности для двумерного случая имеет вид [19, 20]:
На кромках АВ и DC задавалась температура (условия Дирихле)
На кромках AD и BC задавались условия симметрии (условия Неймана)
Начальная температура в расчетной области ABCD равна нулю, Т|t = 0 = 0.
На границе двух фаз с различными теплофизическими характеристиками выполняются условия идеального контакта: равенство температур и тепловых потоков [19]:
Решение нестационарной двумерной задачи теплопроводности эквивалентно минимизации функционала
На рис. 3 приведены результаты решения нестационарной задачи теплопроводности в композитах “медь–графит” и “поли(3,4-этилендиокситиофен)–медный порошок”.
Рис. 3.
Поверхности и изолинии распределения температуры (Т, °С) в композитах в плоскости xy (м): a) “медь–графит”; b) “поли(3,4-этилендиокситиофен)–медный порошок”.
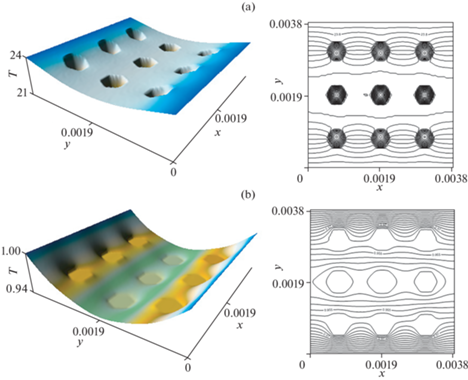
Ячейке композита “медь–графит” сообщено количество теплоты ΔQ = 0.034 Дж, соответствующее полученной выше мощности тепловых потерь при прохождении электрического тока P = 0.562 Вт за время Δt = 0.06 с (рис. 3, a), а композиту “поли(3,4-этилендиокситиофен) – медный порошок” сообщено количество теплоты ΔQ = 0.00136 Дж за время Δt = 96 с (рис. 3, b).
Температура в композите “медь–графит” при прохождении электрического тока повышается до 24°С за 0.06 секунды, а температура в композите “поли(3,4-этилендиокситиофен) – медный порошок” повышается на 1°С за 96 секунд.
В композите “медь–графит” коэффициент теплопроводности включений графита на два порядка меньше проводимости матрицы (медь), а в полимерном композите “поли(3,4-этилендиокситиофен)–медный порошок” теплопроводность включений выше на 3 порядка. Вследствие большей проводимости матрицы температура при прохождении электрического тока в композите “медь–графит” повышается на порядок больше, чем в композите с полимерной матрицей “поли(3,4-этилендиокситиофен)–медный порошок”.
4. Решение задачи термоупругости для структурно-неоднородного тела. Для расчета напряженно-деформированного состояния композита при изменении поля температуры используется метод конечных элементов [21, 22]. Для этого записывается функционал энергии упругого тела при наличии в нем начальных деформаций ε0. Из условия минимума функционала энергии П [19]
получается система линейных алгебраических уравнений где {U} – вектор перемещений, [K] – глобальная матрица жесткости механической системы, {F} – вектор нагрузок.Глобальная матрица жесткости сетки конечных элементов равна сумме матриц жесткости отдельных элементов:
Матрица упругих характеристик [D] для изотропного материала равна:
В предыдущем выражении величины ${{d}_{{11}}},{{d}_{{12}}}$ равны, соответственно:
где Е – модуль упругости, ν – коэффициент Пуассона.Глобальный вектор сил {F} равен сумме векторов сил отдельных элементов {f(e)}
Вектор температурной деформации в случае плоского напряженного состояния равен
где ΔT – изменение температуры,
α – коэффициент линейного теплового расширения.
Закон Гука запишется в виде
На границах двух фаз выполняются условия идеального контакта, а именно равенство векторов перемещений и нормальных напряжений.
Граничные условия при решении задачи термоупругости следующие (см. рис. 4, a): на линии O3O4 перемещение вдоль оси у равно нулю, на линии О1О2 перемещение вдоль оси х равно нулю. Кромки расчетной области ABCD свободны от напряжений.
Рис. 4.
Поверхности и изолинии в ячейке композита “медь–графит”: (а) – перемещения вдоль оси у (V, м); (b) – интенсивность напряжений (σi, МПа) в плоскости xy (м), (c) – интенсивность деформаций (εi).
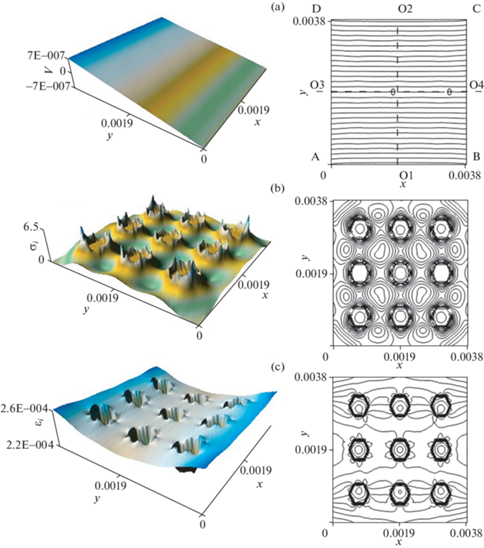
На рис. 4, 5 приведены результаты решения задачи термоупругости для композита “медь–графит” и композита “поли(3,4-этилендиокситиофен)–медный порошок” при температурном поле приведенном на рис. 3.
Рис. 5.
Поверхности и изолинии в ячейке композита “поли(3,4-этилендиокситиофен)–медный порошок”: (а) – перемещения вдоль оси у (V, м); (b) – интенсивность напряжений (σi, МПа), (c) – интенсивность деформаций (εi).
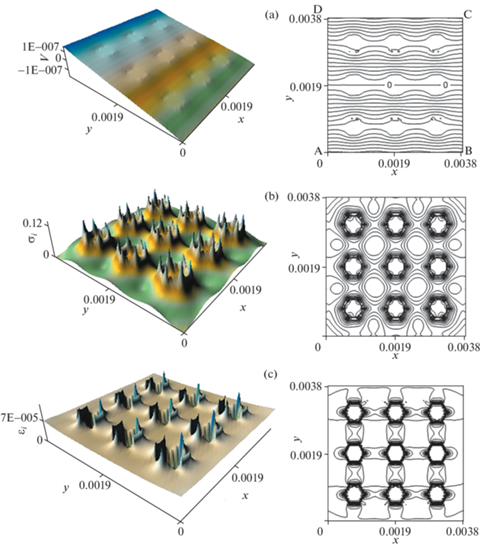
На рис. 4, а поле перемещений для композита “медь–графит” однородно, в отличии от поля перемещений для композита “поли(3,4-этилендиокситиофен)–медный порошок” (рис. 5, а), вследствие небольшого отличия в коэффициентах температурного расширения матрицы и включений. Из рис. 4, b и 5, b видно, что интенсивность напряжений в композите “медь–графит” превышает интенсивность напряжений в композите “поли(3,4-этилендиокситиофен)–медный порошок” примерно в 50 раз.
Результаты параметрических исследований влияния напряженности электрического поля на интенсивность деформаций и интенсивность напряжений в композите “медь–графит” приведены на рис. 6.
Рис. 6.
Зависимости средней интенсивности деформаций (εiср) (а) и максимальной интенсивности напряжений (σimax, МПа) (b) в композите “медь–графит” от напряженности электрического поля постоянного тока (Е, В/м5).
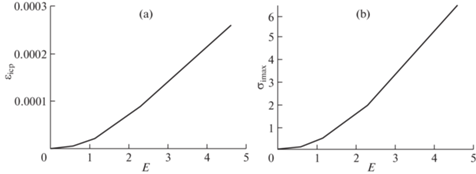
При изменении напряженности поля в 10 раз, с 0.46 до 4.6 В/м, интенсивность деформаций в композите “медь–графит” изменяется от 4.3 × 10–6 до 2.6 × 10–4, интенсивность напряжений изменяется от 0.1 до 6.5 МПа, т.е. примерно в 60 раз. В проводнике количество теплоты определяется законом Джоуля–Ленца, в соответствии с которым это количество пропорционально квадрату протекающего тока, а сила тока определяется напряженностью электрического поля. При увеличении напряженности в 10 раз количество выделяемого тепла увеличивается в 100 раз, что объясняет нелинейность связи между параметрами напряженно-деформированного состояния и напряженностью электрического поля.
5. Заключение. Развитый подход, заключающийся в последовательном решении задач электропроводности, теплопроводности и термоупругости, позволяет определить поля электрического потенциала и напряженности, поле температуры, поля перемещений, деформаций и напряжений в композитах при протекании через них постоянного электрического тока. Учет в явном виде включений (их свойств, размеров, формы) позволяет оценить их влияние на параметры напряженно-деформированное состояние композита при прохождении через него электрического тока.
Анализ композитов двух видов с разными электрофизическими характеристиками фаз показывает, что значения напряжений и деформаций много выше в случае, когда обе фазы материала – матрица и включения – обладают проводимостью, т.е. не являются электроизоляторами. Это объясняется увеличением силы тока в этом случае и количеством выделенного тепла.
Показано, что если компоненты композита не обладают пьезоэффектом, то вследствие нагрева при протекании электрического тока в таком неоднородном материале с различными теплофизическими свойствами фаз возникают поля перемещений, деформаций и напряжений. В то же время, в пьезоматериалах, испытывающих воздействие электрического поля, возникают напряжения и деформации, не связанные с выделением тепла.
Показано, что параметры напряженно-деформированного состояния внутри композита растут быстрее, с увеличением напряженности электрического поля, т.е. для рассмотренных композитов эта связь является нелинейной.
Предложенная методика позволяет вычислить численные значения напряжений в композите при протекании через него электрического тока, и, при использовании соответствующего критерия прочности, оценить, насколько напряженное состояние композита близко к предельному (разрушению).
Моделирование композита при прохождении электрического тока позволяет вычислить параметры напряженно-деформированного состояния композита и оценить возможность потери прочности композита в результате электрического разогрева. Если в качественном плане можно определить характер влияния обсуждаемых факторов на параметры НДС в композите, то предложенный и реализованный в работе подход позволяет сделать количественные оценки.
Благодарности. The work was performed according to the government research assignment for ISPMS SB RAS, project FWRW-2021-0010.
Список литературы
Skelhorn D. Particulate fillers in elastomers. In: Rothon RN (ed) Particulate-filled polymer composites. 2nd ed. Shrewsbury, UK: Rapra Tec. Lim., 2003. 324 p.
Hohenberger W. Fillers and reinforcements/coupling agents // Plastics Additives Handbook. 5th ed. Ed. by H. Zweifel, R. D. Maier, M. Schiller. Munich: Carl Fanser Verlag, 2001. P. 919–966.
Masenelli-Varlot K., Chazeau L., Gauthier C., Bogner A., Cavaillé J.Y. The relationship between the electrical and mechanical properties of polymer–nanotube nanocomposites and their microstructure // Compos. Sci. Technol. 2009. V. 69. P. 1533–1539. https://doi.org/10.1016/j.compscitech.2009.01.035
Hassan H.H., Nasr G.M. and El-Waily M.A. Electrical and mechanical properties of aluminum-loaded NBR composites // J. Elastomers Plastics. 2013. V. 45. P. 121–141. https://doi.org/10.1177/0095244312462160
Grazioli D., Zadin V., Brandell D., Simone A. Electrochemical-mechanical modeling of solid polymer electrolytes: Stress development and non-uniform electric current density in trench geometry microbatteries // Electrochimica Acta. 2019. V. 296. P. 1142–1162. https://doi.org/10.1016/j.electacta.2018.07.146
Talin A.A., Ruzmetov D., Kolmakov A., McKelvey K., Ware N., Gabaly F. El, Dunn B., White H.S. Fabrication, testing, and simulation of all-solid-state three-dimensional Li-Ion batteries // ACS Appl. Mater. Interfaces. 2016. V. 8. P. 32385–32391. https://doi.org/10.1021/acsami.6b12244
Wang X.-S., Tang H.-P., Li X.-D., Hua X. Investigations on the mechanical properties of conducting polymer coating-substrate structures and their influencing factors. Review // Int. J. Mol. Sci. 2009. V. 10. P. 5257–5284. https://doi.org/10.3390/ijms10125257
Namsheer K., Rout C.S. Conducting polymers: a comprehensive review on recent advances in synthesis, properties and applications // RSC Adv. 2021. V. 11. P. 5659–5697. https://doi.org/10.1039/d0ra07800j
Kim N., Lienemann S., Petsagkourakis I., Mengistie D.A., Kee S., Ederth T., Gueskine V., Leclère P., Lazzaroni R., Crispin X., Tybrandt K. Elastic conducting polymer composites in thermoelectric modules // Nat. Commun. 2020. V. 11 (1). № 1424. P. 1–10. https://doi.org/10.1038/s41467-020-15135-w
Melling D., Jager E.W.H. Conducting polymers as EAPs: characterization methods and metrics // Electromechanically Active Polymers. Polymers and Polymeric. Composites: A Reference Series. Springer, 2016. P. 319–351. https://doi.org/10.1007/978-3-319-31530-0_14
Mohd Radzuan N.A., Sulong A.B., Sahari J. A review of high-temperature proton exchange membrane fuel cell (HT-PEMFC) system // Int. J. Hydrogen Energy. 2017. V. 42 (14). № 6. P. 9262–9273. https://doi.org/10.1016/j.ijhydene.2016.03.045
Plesse C., Vidal F., Randriamahazaka H., Teyssié D., Chevrot C. Synthesis and characterization of conducting interpenetrating polymer networks for new actuators // Polymer. 2005. V. 46. P. 7771–7778. https://doi.org/10.1016/j.polymer.2005.03.103
Fu P., Liu H., Chu X. An efficient multiscale computational formulation for geometric nonlinear analysis of heterogeneous piezoelectric composite // Compos. Struct. 2017. 167. P. 191–206. https://doi.org/10.1016/j.compstruct.2017.02.005
Yaghmaie R., Ghosh S. Computational modeling of finite deformation piezoelectric material behavior coupling transient electrical and mechanical fields // J. Computat. Phys. 2018. V. 373. P. 148–170. https://doi.org/10.1016/j.jcp.2018.06.070
Koh S.J.A., Zhou T., Li J., Zhao X., Hong W., Zhu J., Suo Z. Mechanisms of large actuation strain in dielectric elastomers // J. Polym. Sci. Part B. Polym. Phys. 2011. V. 49. P. 504–515.
Mota A., Zimmerman J.A. A variational, finite-deformation constitutive model for piezoelectric materials // Int. J. Numer. Methods Eng. 2011. V. 85 (6). P. 752–767.
Атабеков Г.И., Купалян С.Д., Тимофеев А.Б. и др. Теоретические основы электротехники: Учебник для студентов втузов. В 3-х частях. М.: Энергия, 1979. Ч. 2, 3. 432 с.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Л.: Энергия, 1975. Т. 2. 407 с.
Дульнев Г.Н., Заричняк Ю.П. Теплопроводность смесей и композиционных материалов. Справочная книга. Л.: Энергия, 1974. 246 с.
Segerlind L. Applied Finite Element Analysis. N.Y.: John Willey & Sons, 1976. = Сегерлинд Л. Применение метода конечных элементов. М.: Мир, 1979. 392 с.
Neto E.A.S., Peri’c D., Owen D.R.J. Computational methods for plasticity theory and applications. John Wiley & Sons Ltd., 2008. 816 p.
Zienkiewicz O.C., Taylor R.L., Zhu J.Z. The Finite Element Method: Its Basis and Fundamentals, 7th Ed. Butterworth-Heinemann, 2013. 752 p.
Гришаева Н.Ю., Люкшин П.А., Люкшин Б.А., Панин С.В., Бочкарева С.А., Реутов Ю.А., Матолыгина Н.Ю. Модификация теплофизических характеристик полимеров введением микронаполнителей // Мех. композиц. матер. констр. 2016. Т. 22. № 3. С. 342–361.
Bochkareva S.A., Grishaeva N.Yu., Lyukshin B.A., Lyukshin P.A., Matolygina N.Yu., Panin S.V., Reutov Yu.A. A unified approach to determining the effective physicomechanical characteristics of filled polymer composites based on variational principles // Mech. Compos. Mater. 2019. V. 54. № 6. P. 775–788. https://doi.org/10.1007/s11029-019-9782-8
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела