Известия РАН. Механика твердого тела, 2023, № 1, стр. 115-128
ИССЛЕДОВАНИЕ ПОГРЕШНОСТИ БЫСТРОЙ ТРИГОНОМЕТРИЧЕСКОЙ ИНТЕРПОЛЯЦИИ ПРИ РЕШЕНИИ ЗАДАЧИ О НАПРЯЖЕНИЯХ В БРУСЕ
А. Д. Чернышов a, *, В. В. Горяйнов b, **, М. И. Попов a, ***
a Воронежский государственный университет инженерных технологий
Воронеж, Россия
b Воронежский государственный технический университет
Воронеж, Россия
* E-mail: chernyshovad@mail.ru
** E-mail: gorvit77@mail.ru
*** E-mail: mihail_semilov@mail.ru
Поступила в редакцию 27.03.2022
После доработки 24.04.2022
Принята к публикации 25.04.2022
- EDN: KIQKNY
- DOI: 10.31857/S0572329922100142
Аннотация
С помощью быстрой тригонометрической интерполяции решена задача о напряжениях в брусе прямоугольного сечения. Проведено сравнение полученного приближенного аналитического решения с точным, в ходе которого исследована относительная погрешность компонент перемещений, компонент тензора напряжений, невязка уравнений равновесия Ламе и невязка граничных условий. Установлено, что при использовании в быстрых разложениях граничной функции второго порядка и небольшом количестве членов в рядах Фурье (от двух до шести) максимальная относительная погрешность δmax компонент перемещений и компонент тензора напряжений составляет менее одного процента. С увеличением порядка граничной функции и/или количества членов N в рядах Фурье δmax быстро уменьшается. Увеличение порядка граничной функции является более эффективным способом уменьшения погрешности вычислений δmax, чем увеличение количества членов в рядах Фурье. При исследовании интенсивности напряжений $\tilde {\sigma }$ в брусе с различными габаритными размерами прямоугольного сечения, но одинаковой площадью всех сечений выяснилось, что наименьшее значение ${{\tilde {\sigma }}_{{\max }}}$ среди всех сечений наблюдается в брусе с квадратным сечением.
1. Введение. Среди аналитических методов, применяемых для решения задач теории упругости, можно выделить такие как метод угловых суперпозиций [1, 2], метод расширения границ [3], метод возмущений [4–6], лучевой метод [7–9], разложения в ряды [10–14] и по функциям Фадля–Папковича [15, 16], двухшаговый метод последовательного возмущения параметров [17], метод быстрых разложений [18–20]. Последний, из перечисленных методов, имеет следующие положительные качества, которыми в совокупности не обладает ни один из известных методов:
1. Доказана сходимость и получена оценка погрешности метода [21].
2. Показана быстрая сходимость используемых рядов Фурье, что позволяет ограничиваться в расчетах небольшим количеством членов ряда и, как следствие, проводить расчет на ЭВМ с высокой точностью при большой экономии времени [22].
3. Метод быстрых разложений применим для решения как линейных [18–20], так и нелинейных задач [23–25], а также задач для криволинейных областей [24, 25], с подвижными границами [25] и фазовыми превращениями [25].
Классическую тригонометрическую интерполяцию чаще всего используют для улучшения качества обработки изображений [26] и восстановления периодических дискретных сигналов конечной длительности [27]. Для решения инженерных задач интегро-дифференциального типа применение классической тригонометрической интерполяции на конечном отрезке проблематично из-за невозможности ее дифференцирования в общем случае и большой ошибки между интерполяционными точками. Устранение подобных недостатков можно осуществить при использовании быстрой тригонометрической интерполяции. Быстрая тригонометрическая интерполяция использовалась при исследовании напряжений в клине [20], расчете траектории космических кораблей [23], решении нелинейного уравнения теплопроводности для криволинейной области с условиями Дирихле [24] и решении двухфазной задачи Стефана с внутренним источником [25]. В данной работе будет исследована погрешность быстрой тригонометрической интерполяции в зависимости от порядка граничной функции и количества членов в рядах Фурье на примере решения задачи о напряжениях в брусе.
2. Постановка задачи. В условиях плоской деформации проекции вектора перемещений материальных точек бруса зависят только от координат x, y:
Компоненты тензора напряжения будут иметь вид:
(2.2)
$\begin{gathered} {{\sigma }_{{xx}}} = \left( {\lambda + 2\mu } \right)\frac{{\partial U}}{{\partial x}} + \lambda \frac{{\partial V}}{{\partial y}}{\text{,}}\quad {{\sigma }_{{yy}}} = \left( {\lambda + 2\mu } \right)\frac{{\partial V}}{{\partial y}} + \lambda \frac{{\partial U}}{{\partial x}} \\ {{\sigma }_{{xy}}} = \mu \left( {\frac{{\partial U}}{{\partial y}} + \frac{{\partial V}}{{\partial x}}} \right){\text{,}}\quad {{\sigma }_{{zz}}} = \lambda \left( {\frac{{\partial U}}{{\partial x}} + \frac{{\partial V}}{{\partial y}}} \right){\text{,}}\quad {{\sigma }_{{xz}}} = {{\sigma }_{{yz}}} = 0 \\ \end{gathered} $Запишем уравнения равновесия Ламе для перемещений с учетом массовых сил $X\left( {x,y} \right),$ $Y\left( {x,y} \right)$
(2.3)
$\left( {\lambda + 2\mu } \right)\frac{{{{\partial }^{2}}U}}{{\partial {{x}^{2}}}} + \left( {\lambda + \mu } \right)\frac{{{{\partial }^{2}}V}}{{\partial x\partial y}} + \mu \frac{{{{\partial }^{2}}U}}{{\partial {{y}^{2}}}} + X\left( {x,y} \right) = 0$(2.4)
$\left( {\lambda + 2\mu } \right)\frac{{{{\partial }^{2}}V}}{{\partial {{y}^{2}}}} + \left( {\lambda + \mu } \right)\frac{{{{\partial }^{2}}U}}{{\partial x\partial y}} + \mu \frac{{{{\partial }^{2}}V}}{{\partial {{x}^{2}}}} + Y\left( {x,y} \right) = 0$К уравнениям (2.3), (2.4) необходимо добавить граничные условия. Будем считать, что упругий брус имеет прямоугольное сечение $\Omega = (0 \leqslant x \leqslant a,\;0 \leqslant y \leqslant b)$. На сторонах бруса зададим условия Дирихле в общем виде
(2.5)
${{\left. U \right|}_{{x = 0}}} = {{f}_{1}}\left( y \right),\quad {{\left. U \right|}_{{x = a}}} = {{f}_{3}}\left( y \right),\quad {{\left. V \right|}_{{x = 0}}} = {{\varphi }_{1}}\left( y \right),\quad {{\left. V \right|}_{{x = a}}} = {{\varphi }_{3}}\left( y \right)$(2.6)
${{\left. U \right|}_{{y = 0}}} = {{f}_{2}}\left( x \right),\quad {{\left. U \right|}_{{y = b}}} = {{f}_{4}}\left( x \right),\quad {{\left. V \right|}_{{y = 0}}} = {{\varphi }_{2}}\left( x \right),\quad {{\left. V \right|}_{{y = b}}} = {{\varphi }_{4}}\left( x \right)$Функции, входящие в граничные условия (2.5) и (2.6), следует подбирать с учетом условий их согласования
(2.7)
$\begin{gathered} {{f}_{1}}\left( 0 \right) = {{f}_{2}}\left( 0 \right),\quad {{f}_{3}}\left( 0 \right) = {{f}_{2}}\left( a \right),\quad {{f}_{3}}\left( b \right) = {{f}_{4}}\left( a \right),\quad {{f}_{4}}\left( 0 \right) = {{f}_{1}}\left( b \right) \\ {{\varphi }_{1}}\left( 0 \right) = {{\varphi }_{2}}\left( 0 \right),\quad {{\varphi }_{3}}\left( 0 \right) = {{\varphi }_{2}}\left( a \right),\quad {{\varphi }_{3}}\left( b \right) = {{\varphi }_{4}}\left( a \right),\quad {{\varphi }_{4}}\left( 0 \right) = {{\varphi }_{1}}\left( b \right) \\ \end{gathered} $В качестве примера функции из (2.5), (2.6) зададим следующим образом
(2.8)
$\begin{gathered} {{f}_{1}}\left( y \right) = 0,\quad {{f}_{2}}\left( x \right) = 0,\quad {{f}_{3}}\left( y \right) = K\sin 1.2\pi ay,\quad {{f}_{4}}\left( x \right) = K\sin 1.2\pi bx \\ {{\varphi }_{1}}\left( y \right) = 0,\quad {{\varphi }_{2}}\left( x \right) = 0,\quad {{\varphi }_{3}}\left( x \right) = - K\sin a\sin y,\quad {{\varphi }_{4}}\left( x \right) = - K\sin x\sin b \\ \end{gathered} $Массовые силы в (2.3), (2.4) запишем выражениями
(2.9)
$\begin{gathered} \, + \left( {\lambda + \mu } \right)K\cos x\cos y + {{\left( {1.2\pi x} \right)}^{2}}\mu K\sin 1.2\pi xy \\ Y\left( {x,y} \right) = - \left( {\lambda + 2\mu } \right)K\sin x\sin y - \mu K\sin x\sin y + \\ \end{gathered} $Зависимости (8) и (9) подобраны так, что задача (3)–(6) имеет точное решение
где K – константа, регулирующая величину перемещений.Точное решение (2.10) позволит провести исследование погрешности решения краевой задачи (2.3)–(2.6) путем сравнения с приближенным аналитическим решением, полученным методом быстрых разложений. При сравнении будут вычислены: относительная погрешность компонент перемещений (2.1), компонент тензора напряжений (2.2), невязка уравнений равновесия Ламе (2.3), (2.4) и невязка граничных условий (2.5), (2.6).
3. Метод и построение решения. Для решения используем приближенный метод быстрых разложений [21], в соответствии с которым представим $U = U(x,y)$ и V = V(x, y) в виде суммы граничных функции $M_{{2p}}^{U}\left( {x;y} \right),$ $M_{{2p}}^{V}\left( {x;y} \right)$ и ряда Фурье по синусам
(3.1)
$\begin{gathered} U = M_{{2p}}^{U}\left( {x;y} \right) + \sum\limits_{m = 1}^{{{N}_{1}}} {{{u}_{m}}\left( x \right)\sin m\pi \frac{y}{b}} ,\quad V = M_{{2p}}^{V}\left( {x;y} \right) + \sum\limits_{m = 1}^{{{N}_{1}}} {{{{v}}_{m}}\left( x \right)\sin m\pi \frac{y}{b}} \\ x \in \left[ {0;a} \right],\quad y \in \left[ {0;b} \right] \\ \end{gathered} $Здесь N1 – число учитываемых членов в рядах Фурье. Граничные функции $M_{{2p}}^{U}(x;y)$ и $M_{{2p}}^{V}\left( {x;y} \right)$ порядка 2p определяются равенствами
(3.2)
$M_{{2p}}^{U}\left( {x;y} \right) = \sum\limits_{i = 1}^{2p + 2} {{{A}_{i}}\left( x \right){{P}_{i}}\left( y \right)} ,\quad M_{{2p}}^{V}\left( {x;y} \right) = \sum\limits_{i = 1}^{2p + 2} {{{B}_{i}}\left( x \right){{P}_{i}}\left( y \right)} $Для исследования влияния порядка граничной функции на точность решения краевой задачи (2.3)–(2.6) в быстрых разложениях (3.1) будем использовать граничные функции второго, четвертого и шестого порядков, которые получаются из (3.2) при p = 1, p = 2 и p = 3 соответственно, т.е.
(3.3)
$\begin{gathered} M_{2}^{U}\left( {x;y} \right) = \sum\limits_{i = 1}^4 {{{A}_{i}}\left( x \right){{P}_{i}}\left( y \right)} ,\quad M_{2}^{V}\left( {x;y} \right) = \sum\limits_{i = 1}^4 {{{B}_{i}}\left( x \right){{P}_{i}}\left( y \right)} \\ M_{4}^{U}\left( {x;y} \right) = M_{2}^{U}\left( {x;y} \right) + \sum\limits_{i = 5}^6 {{{A}_{i}}\left( x \right){{P}_{i}}\left( y \right)} ,\quad M_{4}^{V}\left( {x;y} \right) = M_{2}^{V}\left( {x;y} \right) + \sum\limits_{i = 5}^6 {{{B}_{i}}\left( x \right){{P}_{i}}\left( y \right)} \\ M_{6}^{U}\left( {x;y} \right) = M_{4}^{U}\left( {x;y} \right) + \sum\limits_{i = 7}^8 {{{A}_{i}}\left( x \right){{P}_{i}}\left( y \right)} ,\quad M_{6}^{V}\left( {x;y} \right) = M_{4}^{V}\left( {x;y} \right) + \sum\limits_{i = 7}^8 {{{B}_{i}}\left( x \right){{P}_{i}}\left( y \right)} \\ \end{gathered} $Быстрые полиномы ${{P}_{i}}\left( y \right)$ и коэффициенты ${{A}_{i}}\left( x \right),$ ${{B}_{i}}\left( x \right)$ определяются равенствами
(3.4)
$\begin{gathered} {{P}_{8}}\left( y \right) = \left( {\frac{{{{y}^{7}}}}{{5040b}} - \frac{{b{{y}^{5}}}}{{720}} + \frac{{7{{b}^{3}}{{y}^{3}}}}{{2160}} - \frac{{31{{b}^{5}}y}}{{15120}}} \right) \\ {{A}_{1}}\left( x \right) = {{\left. U \right|}_{{y = 0}}},\quad {{A}_{2}}\left( x \right) = {{\left. U \right|}_{{y = a}}},\quad {{A}_{3}}\left( x \right) = {{\left. {\frac{{{{\partial }^{2}}U}}{{\partial {{y}^{2}}}}} \right|}_{{y = 0}}},\quad {{A}_{4}}\left( x \right) = {{\left. {\frac{{{{\partial }^{2}}U}}{{\partial {{y}^{2}}}}} \right|}_{{y = a}}} \\ \end{gathered} $Для возможности выполнения выражений (3.4) необходимо потребовать, чтобы U = U(x, y) и V = V(x, y) удовлетворяли условию гладкости $\left( {U,V} \right) \in {{C}^{{\left( 6 \right)}}}\left( \Omega \right)$.
Неизвестными в (3.1) являются функции, зависящие только от одной переменной х
(3.5)
${{A}_{1}}\left( x \right) - {{A}_{{2p + 2}}}\left( x \right),\quad {{B}_{1}}\left( x \right) - {{B}_{{2p + 2}}}\left( x \right),\quad p = 1...3,\;{{u}_{m}}\left( x \right),\;{{{v}}_{m}}\left( x \right),\quad m = 1...{{N}_{1}}$Функции из (3.5) представим быстрыми разложениями по переменной х. Причем в повторных разложениях будут использованы граничные функции тех же порядков, что и в быстрых разложениях (3.1) по переменной у:
(3.6)
$\begin{gathered} {{A}_{i}}\left( x \right) = M_{{2p}}^{{A\left( i \right)}}\left( x \right) + \sum\limits_{n = 1}^{{{N}_{2}}} {a_{{n + 2p + 2}}^{{\left( i \right)}}\sin n\pi \frac{x}{a}} ,\quad {{B}_{i}}\left( x \right) = M_{{2p}}^{{B\left( i \right)}}\left( x \right) + \sum\limits_{n = 1}^{{{N}_{2}}} {b_{{n + 2p + 2}}^{{\left( i \right)}}\sin n\pi \frac{x}{a}} \\ {{u}_{m}}\left( x \right) = M_{{2p}}^{{u\left( m \right)}}\left( x \right) + \sum\limits_{n = 1}^{{{N}_{2}}} {u_{{n + 2p + 2}}^{{\left( m \right)}}\sin n\pi \frac{x}{a}} ,\quad {{{v}}_{m}}\left( x \right) = M_{{2p}}^{{{v}\left( m \right)}}\left( x \right) + \sum\limits_{n = 1}^{{{N}_{2}}} {{v}_{{n + 2p + 2}}^{{\left( m \right)}}\sin n\pi \frac{x}{a}} \\ i = 1...2p + 2,\quad p = 1...3,\quad m = 1...{{N}_{1}} \\ \end{gathered} $В (3.6) обозначено через ${{N}_{2}}$ – число учитываемых членов в рядах Фурье. Граничные функции $M_{{2p}}^{{A\left( i \right)}}\left( x \right),$ $M_{{2p}}^{{B\left( i \right)}}\left( x \right),$ $M_{{2p}}^{{u\left( m \right)}}\left( x \right),$ $M_{{2p}}^{{{v}\left( m \right)}}\left( x \right)$ определяем равенствами
(3.7)
$\begin{gathered} M_{{2p}}^{{A\left( i \right)}}\left( x \right) = \sum\limits_{k = 1}^{2p + 2} {a_{k}^{{\left( i \right)}}{{P}_{k}}\left( x \right)} ,\quad M_{{2p}}^{{B\left( i \right)}}\left( x \right) = \sum\limits_{k = 1}^{2p + 2} {b_{k}^{{\left( i \right)}}{{P}_{k}}\left( x \right)} \\ M_{{2p}}^{{u\left( m \right)}}\left( x \right) = \sum\limits_{k = 1}^{2p + 2} {u_{k}^{{\left( m \right)}}{{P}_{k}}\left( x \right)} ,\quad M_{{2p}}^{{{v}\left( m \right)}}\left( x \right) = \sum\limits_{k = 1}^{2p + 2} {{v}_{k}^{{\left( m \right)}}{{P}_{k}}\left( x \right)} \\ \end{gathered} $При p = 3 выражения для коэффициентов граничных функций $a_{k}^{{\left( i \right)}}$, $b_{k}^{{\left( i \right)}}$, $u_{k}^{{\left( m \right)}}$, ${v}_{k}^{{\left( m \right)}}$ и быстрых полиномов ${{P}_{k}}\left( x \right)$ имеют вид
(3.8)
$\begin{gathered} {{P}_{5}}\left( x \right) = \left( {\frac{{{{x}^{4}}}}{{24}} - \frac{{{{x}^{5}}}}{{120a}} - \frac{{a{{x}^{3}}}}{{18}} + \frac{{{{a}^{3}}x}}{{45}}} \right),\quad {{P}_{6}}\left( x \right) = \left( {\frac{{{{x}^{5}}}}{{120a}} - \frac{{a{{x}^{3}}}}{{36}} + \frac{{7{{a}^{3}}x}}{{360}}} \right) \\ {{P}_{7}}\left( x \right) = \left( {\frac{{{{x}^{6}}}}{{720}} - \frac{{{{x}^{7}}}}{{5040a}} - \frac{{a{{x}^{5}}}}{{360}} + \frac{{{{a}^{3}}{{x}^{3}}}}{{270}} - \frac{{2{{a}^{5}}x}}{{945}}} \right) \\ \end{gathered} $(3.9)
$\begin{gathered} a_{1}^{{\left( i \right)}} = {{\left. {{{A}_{i}}} \right|}_{{х = 0}}},\quad a_{2}^{{\left( i \right)}} = {{\left. {{{A}_{i}}} \right|}_{{х = а}}},\quad a_{3}^{{\left( i \right)}} = {{\left. {A_{i}^{{''}}} \right|}_{{х = 0}}},\quad a_{4}^{{\left( i \right)}} = {{\left. {A_{i}^{{''}}} \right|}_{{х = а}}},\quad a_{5}^{{\left( i \right)}} = {{\left. {A_{i}^{{(4)}}} \right|}_{{х = 0}}} \\ a_{6}^{{\left( i \right)}} = {{\left. {A_{i}^{{(4)}}} \right|}_{{х = а}}},\quad a_{7}^{{\left( i \right)}} = {{\left. {A_{i}^{{(6)}}} \right|}_{{х = 0}}},\quad a_{8}^{{\left( i \right)}} = {{\left. {A_{i}^{{(6)}}} \right|}_{{х = а}}},\quad i = 1..8 \\ \end{gathered} $(3.10)
$\begin{gathered} b_{1}^{{\left( i \right)}} = {{\left. {{{B}_{i}}} \right|}_{{х = 0}}},\quad b_{2}^{{\left( i \right)}} = {{\left. {{{B}_{i}}} \right|}_{{х = а}}},\quad b_{3}^{{\left( i \right)}} = {{\left. {B_{i}^{{''}}} \right|}_{{х = 0}}},\quad b_{4}^{{\left( i \right)}} = {{\left. {B_{i}^{{''}}} \right|}_{{х = а}}},\quad b_{5}^{{\left( i \right)}} = {{\left. {B_{i}^{{(4)}}} \right|}_{{х = 0}}} \\ b_{6}^{{\left( i \right)}} = {{\left. {B_{i}^{{(4)}}} \right|}_{{х = а}}},\quad b_{7}^{{\left( i \right)}} = {{\left. {B_{i}^{{(6)}}} \right|}_{{х = 0}}},\quad b_{8}^{{\left( i \right)}} = {{\left. {B_{i}^{{(6)}}} \right|}_{{х = а}}},\quad i = 1..8 \\ \end{gathered} $(3.11)
$\begin{gathered} u_{1}^{{\left( m \right)}} = {{\left. {{{u}_{m}}} \right|}_{{x = 0}}},\quad u_{2}^{{\left( m \right)}} = {{\left. {{{u}_{m}}} \right|}_{{x = a}}},\quad u_{3}^{{\left( m \right)}} = {{\left. {u_{m}^{{''}}} \right|}_{{x = 0}}},\quad u_{4}^{{\left( m \right)}} = {{\left. {u_{m}^{{''}}} \right|}_{{x = a}}},\quad u_{5}^{{\left( m \right)}} = {{\left. {u_{m}^{{(4)}}} \right|}_{{x = 0}}} \\ u_{6}^{{\left( m \right)}} = {{\left. {u_{m}^{{(4)}}} \right|}_{{x = a}}},\quad u_{7}^{{\left( m \right)}} = {{\left. {u_{m}^{{(6)}}} \right|}_{{x = 0}}},\quad u_{8}^{{\left( m \right)}} = {{\left. {u_{m}^{{(6)}}} \right|}_{{x = a}}},\quad m = 1...{{N}_{1}} \\ \end{gathered} $(3.12)
$\begin{gathered} {v}_{1}^{{\left( m \right)}} = {{\left. {{{{v}}_{m}}} \right|}_{{x = 0}}},\quad {v}_{2}^{{\left( m \right)}} = {{\left. {{{{v}}_{m}}} \right|}_{{x = a}}},\quad {v}_{3}^{{\left( m \right)}} = {{\left. {{v}_{m}^{{''}}} \right|}_{{x = 0}}},\quad {v}_{4}^{{\left( m \right)}} = {{\left. {{v}_{m}^{{''}}} \right|}_{{x = a}}},\quad {v}_{5}^{{\left( m \right)}} = {{\left. {{v}_{m}^{{(4)}}} \right|}_{{x = 0}}} \\ {v}_{6}^{{\left( m \right)}} = {{\left. {{v}_{m}^{{(4)}}} \right|}_{{x = a}}},\quad {v}_{7}^{{\left( m \right)}} = {{\left. {{v}_{m}^{{(6)}}} \right|}_{{x = 0}}},\quad {v}_{8}^{{\left( m \right)}} = {{\left. {{v}_{m}^{{(6)}}} \right|}_{{x = a}}},\quad m = 1...{{N}_{1}} \\ \end{gathered} $Если p = 2, то для описания граничных функций (3.7) из (3.8) следует взять первые шесть полиномов, а в (3.9)–(3.12) учесть первые шесть коэффициентов. При p = 1 граничные функции (3.7) будут содержать первые четыре полинома из (3.8) и первые четыре коэффициента из (3.9)–(3.12).
Таким образом, краевая задача (2.3)–(2.6) сведена к определению 2(2p + 2 + + N1)$(2p + 2 + {{N}_{2}})$ неизвестных коэффициентов
(3.13)
$\begin{gathered} a_{k}^{{\left( i \right)}},\;b_{k}^{{\left( i \right)}},\;u_{k}^{{\left( m \right)}},\;{v}_{k}^{{\left( m \right)}},\quad i = 1...2p + 2,\quad k = 1...2p + 2,\quad p = 1...3,\quad m = 1...{{N}_{1}} \\ a_{{n + 2p + 2}}^{{\left( i \right)}},\quad b_{{n + 2p + 2}}^{{\left( i \right)}},\quad u_{{n + 2p + 2}}^{{\left( m \right)}},\quad {v}_{{n + 2p + 2}}^{{\left( m \right)}},\quad n = 1...{{N}_{2}} \\ \end{gathered} $Значения восьми коэффициентов
(3.14)
$a_{1}^{{\left( 1 \right)}},\;b_{1}^{{\left( 1 \right)}},\;a_{2}^{{\left( 1 \right)}},\;b_{2}^{{\left( 1 \right)}},\;a_{1}^{{\left( 2 \right)}},\;b_{1}^{{\left( 2 \right)}},\;a_{2}^{{\left( 2 \right)}},\;b_{2}^{{\left( 2 \right)}}$Для нахождения остальных $2\left( {2p + 2 + {{N}_{1}}} \right)\left( {2p + 2 + {{N}_{2}}} \right) - 8$ коэффициентов из (3.13) используем быструю тригонометрическую интерполяцию, апробированную в работах [20, 22–25]. Для этого подставим $U = U(x,y)$ и $V = V(x,y)$ из (3.1) в дифференциальные уравнения (2.3), (2.4) и граничные условия (2.5), (2.6). Полученные таким образом выражения в статье не приводим из-за их громоздкости.
Из граничных условий (2.5), (2.6) линейные алгебраические уравнения получим следующим образом. Промежуток [0, b] равномерно разобьем точками y = ys = = ${{sb} \mathord{\left/ {\vphantom {{sb} {\left( {{{N}_{1}} + 2p + 1} \right)}}} \right. \kern-0em} {\left( {{{N}_{1}} + 2p + 1} \right)}},$ $s = 0,1,..,{{N}_{1}} + 2p + 1$ на ${{N}_{1}} + 2p + 1$ отрезков и запишем уравнения, полученные из граничных условий (2.5) при подстановке $U = U(x,y)$ и $V = V(x,y)$ из (3.1), в каждой внутренней расчетной точке $y = {{y}_{s}},$ $s = 1,..,{{N}_{1}} + 2p$. Будем иметь $4\left( {{{N}_{1}} + 2p} \right)$ линейных алгебраических уравнений. Аналогично, промежуток [0, a] равномерно разобьем точками $x = {{x}_{s}} = {{sa} \mathord{\left/ {\vphantom {{sa} {\left( {{{N}_{2}} + 2p + 1} \right)}}} \right. \kern-0em} {\left( {{{N}_{2}} + 2p + 1} \right)}},$ $s = 0,1,...,{{N}_{2}} + 2p + 1$ на ${{N}_{2}} + 2p + 1$ отрезков и запишем уравнения, полученные из граничных условий (2.6) при подстановке $U = U(x,y)$ и $V = V(x,y)$ из (3.1), в каждой внутренней расчетной точке $x = {{x}_{s}},$ $s = 1,...,{{N}_{2}} + 2p$. Тем самым, будем иметь еще $4\left( {{{N}_{2}} + 2p} \right)$ линейных алгебраических уравнений.
Из дифференциальных уравнений (2.3), (2.4) линейные алгебраические уравнения запишем следующим образом. На область прямоугольника $x \in \left[ {0;a} \right],$ $y \in \left[ {0;b} \right]$ равномерно нанесем сетку в ${{N}_{2}} + 2p + 2$ точках $x = {{x}_{s}} = {{sa} \mathord{\left/ {\vphantom {{sa} {\left( {{{N}_{2}} + 2p + 1} \right)}}} \right. \kern-0em} {\left( {{{N}_{2}} + 2p + 1} \right)}},$ $s = 0,1$, ..., N2 + + 2p + 1 и в ${{N}_{1}} + 2p + 2$ точках $y = {{y}_{s}} = {{sb} \mathord{\left/ {\vphantom {{sb} {\left( {{{N}_{1}} + 2p + 1} \right)}}} \right. \kern-0em} {\left( {{{N}_{1}} + 2p + 1} \right)}},$ $s = 0,1,...,{{N}_{1}} + 2p + 1$. Для составления системы линейных алгебраических уравнений используются только внутренние точки, образующие сетку из $\left( {{{N}_{1}} + 2p} \right)\left( {{{N}_{2}} + 2p} \right)$ внутренних точек $\left( {{{x}_{s}},{{y}_{s}}} \right)$. Затем, уравнения (2.3), (2.4) при подстановке в них $U = U(x,y)$ и $V = V(x,y)$ из (3.1) запишем в каждой расчетной точке $\left( {{{x}_{s}},{{y}_{s}}} \right)$. В итоге, получаем $2\left( {{{N}_{1}} + 2p} \right)\left( {{{N}_{2}} + 2p} \right)$ линейных алгебраических уравнений. В результате приходим к замкнутой системе $2\left( {{{N}_{1}} + 2p} \right)\left( {{{N}_{2}} + 2p} \right) + 4\left( {{{N}_{1}} + 2p} \right) + 4\left( {{{N}_{2}} + 2p} \right)$ линейных алгебраических уравнений относительно оставшихся $\left( {2\left( {2p + 2 + {{N}_{1}}} \right)\left( {2p + 2 + {{N}_{2}}} \right) - 8} \right)$ неизвестных из (3.13). Данная система уравнений решена в среде Maple. После чего, найденные неизвестные (3.13) подставлены в быстрые разложения (3.1). Тем самым, построено приближенное аналитическое решение краевой задачи (2.3)–(2.6).
4. Полученные результаты и их анализ. В вычислительных экспериментах будем использовать граничные функции (3.3) второго, четвертого и шестого порядков. Количество членов в рядах Фурье первого (3.1) и второго (3.6) быстрых разложений примем одинаковыми, т.е. ${{N}_{1}} = {{N}_{2}} = N$, и выполним расчеты при N = 2…6. В качестве материала бруса выберем тяжелый бетон B30 с характеристиками [28] $E = 32.5$ × 109 Па, ${v} = 0.2$. Тогда коэффициенты Ламе будут равны $\lambda = 9.03$ × 109 Па, $\mu = 1.35$ × 1010 Па. Величину параметра K и размеры сечения примем равными $K = {{10}^{{ - 6}}},$ $a = 1$ м, $b = 1$ м.
Приближенное аналитическое решение (3.1) сравнивается с точным (2.10). Относительная погрешность перемещений (2.1), тензора напряжений (2.2), невязка уравнений равновесия Ламе (2.3), (2.4) и граничных условий (2.5), (2.6) вычислялась по формуле
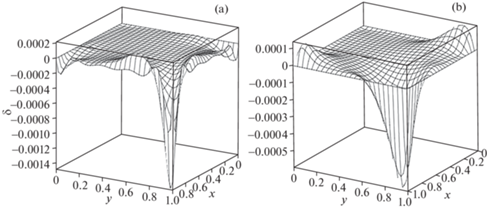
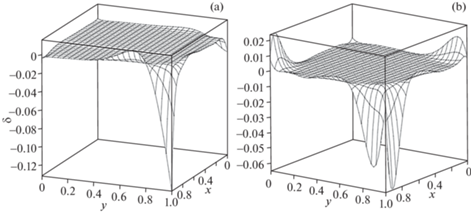
Покажем на рис. 1–4 относительную погрешность расчетов, выполненных при использовании граничной функции четвертого порядка ${{M}_{4}}$ ($p = 2$) для $N = 4$. Из рисунков видно, что максимальная относительная погрешность ${{\delta }_{{\max }}}$ у компонент тензора напряжений ${{\sigma }_{{xx}}}$, ${{\sigma }_{{zz}}}$, ${{\sigma }_{{xy}}}$ и невязки дифференциального уравнения (2.3) достигается в точке (1; 1), а у компонент перемещений U и V, компоненты тензора напряжений ${{\sigma }_{{yy}}}$ и невязки дифференциального уравнения (2.4) – в ее окрестности. Поэтому в табл. 1–3 приведены значения ${{\delta }_{{\max }}}$ всех исследуемых объектов в этих точках для граничных функций второго ${{M}_{2}}$ (p = 1), четвертого ${{M}_{4}}$ (p = 2) и шестого ${{M}_{6}}$ (p = 3) порядков при $N = 2...6$.
Рис. 2.
Относительная погрешность δ компонент тензора напряжений: (а) ${{\sigma }_{{xx}}}$, (b) ${{\sigma }_{{yy}}}$, (c) ${{\sigma }_{{zz}}}$, (d) ${{\sigma }_{{xy}}}$.
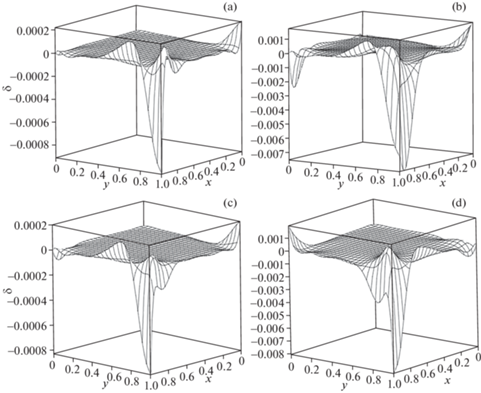
Рис. 4.
Невязка граничных условий: (а) ${{\left. U \right|}_{{x = a}}}$, ${{\left. U \right|}_{{y = b}}}$, (b) ${{\left. V \right|}_{{x = a}}}$, $V{{{\text{|}}}_{{y = b}}}$.

Таблица 1.
Относительная погрешность ${{\delta }_{{\max }}}$, % при использовании ${{M}_{2}}$
| Исследуемый объект | N | |||||
|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | ||
| Компоненты перемещений | U | 0.32 | 0.13 | 7.28 × 10–2 | 4.21 × 10–2 | 2.70 × 10–2 |
| V | 0.12 | 5.80 × 10–2 | 3.00 × 10–2 | 1.67 × 10–2 | 9.80 × 10–3 | |
| Компоненты тензора напряжений | ${{\sigma }_{{x\,x}}}$ | 1.59 | 0.73 | 0.41 | 0.25 | 0.17 |
| ${{\sigma }_{{yy}}}$ | 1.16 | 0.53 | 0.30 | 0.18 | 0.12 | |
| ${{\sigma }_{{zz}}}$ | 1.42 | 0.65 | 0.36 | 0.22 | 0.15 | |
| ${{\sigma }_{{x\,y}}}$ | 1.46 | 0.67 | 0.37 | 0.23 | 0.15 | |
| Невязка ДУ | (3) | 11.12 | 6.36 | 4.25 | 3.08 | 2.35 |
| (4) | 12.66 | 4.87 | 2.19 | 1.15 | 0.86 | |
| Невязка ГУ | ${{\left. U \right|}_{{x = a}}}$, ${{\left. U \right|}_{{y = b}}}$ | 0.27 | 0.11 | 4.70 × 10–2 | 2.52 × 10–2 | 1.47 × 10–2 |
| ${{\left. V \right|}_{{x = a}}}$, $V{{{\text{|}}}_{{y = b}}}$ | 1.11 × 10–3 | 4.51 × 10–4 | 2.18 × 10–4 | 1.18 × 10–4 | 7.10 × 10–5 | |
| ${{\left. U \right|}_{{x = 0}}}$, ${{\left. U \right|}_{{y = 0}}}$, ${{\left. V \right|}_{{x = 0}}}$, $V{{{\text{|}}}_{{y = 0}}}$ | 0 | 0 | 0 | 0 | 0 | |
Из табл. 1–3 можно увидеть, что точнее всего определяются компоненты перемещений U и V (искомая функция). По сравнению с компонентами перемещений точность нахождения компонент тензора напряжений ${{\sigma }_{{xx}}}$, ${{\sigma }_{{yy}}}$, ${{\sigma }_{{zz}}}$, ${{\sigma }_{{xy}}}$ (первые производные искомой функции) падает на порядок, а точность вычисления невязки уравнений равновесия Ламе (2.3), (2.4) (вторые производные искомой функции) падает на два порядка. Подобная тенденция наблюдается при выборе любого порядка граничной функции и для любого N, а также согласуется с многочисленными вычислительными экспериментами авторов, например [15].
Табл. 1 показывает, что даже при использовании граничной функции второго порядка ${{M}_{2}}$ и небольшом количестве членов в рядах Фурье $N = 3$ достигается точность вычислений компонент перемещений и компонент тензора напряжений (${{\delta }_{{\max }}} < 1\% $) выше, чем точность входных данных из справочников. С увеличением порядка граничной функции и/или количества членов в рядах Фурье (см. табл. 2 и 3) эта точность быстро возрастает. Так, если в быстрых разложениях (3.1) и (3.6) использовать граничную функцию второго порядка ${{M}_{2}}$, то увеличение N количества членов в рядах Фурье на четыре (с двух до шести) ведет к увеличению точности вычислений компонент перемещений, компонент тензора напряжений и невязки дифференциальных уравнений (2.3), (2.4) примерно на один порядок (см. табл. 1). Такое же увеличение точности вычислений можно достичь, используя граничную функцию четвертого порядка ${{M}_{4}}$ (см. табл. 2) и увеличивая N в рядах Фурье на три (с двух до пяти). Если же применить граничную функцию шестого порядка ${{M}_{6}}$ (см. табл. 3), то повышение точности вычислений на порядок можно достичь увеличением N в рядах Фурье на два (с двух до четырех).
Таблица 2.
Относительная погрешность δmax, % при использовании ${{M}_{4}}$
| Исследуемый объект | N | |||||
|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | ||
| Компоненты перемещений | U | 1.50 × 10–2 | 3.50 × 10–3 | 1.49 × 10–3 | 7.25 × 10–4 | 3.80 × 10–4 |
| V | 4.80 × 10–3 | 1.52 × 10–3 | 5.90 × 10–4 | 2.70 × 10–4 | 1.35 × 10–4 | |
| Компоненты тензора напряжений |
${{\sigma }_{{x\,x}}}$ | 6.15 × 10–2 | 2.10 × 10–2 | 9.10 × 10–3 | 4.79 × 10–3 | 2.82 × 10–3 |
| ${{\sigma }_{{yy}}}$ | 5.32 × 10–2 | 1.81 × 10–2 | 7.50 × 10–3 | 3.61 × 10–3 | 2.06 × 10–3 | |
| ${{\sigma }_{{zz}}}$ | 5.46 × 10–2 | 1.87 × 10–2 | 8.10 × 10–3 | 4.31 × 10–3 | 2.59 × 10–3 | |
| ${{\sigma }_{{x\,y}}}$ | 5.61 × 10–2 | 1.92 × 10–2 | 8.29 × 10–3 | 4.33 × 10–3 | 2.60 × 10–3 | |
| Невязка ДУ | (3) | 0.64 | 0.26 | 0.13 | 7.53 × 10–2 | 4.67 × 10–2 |
| (4) | 0.38 | 0.13 | 6.52 × 10–2 | 3.51 × 10–2 | 2.10 × 10–2 | |
| Невязка ГУ | ${{\left. U \right|}_{{x = a}}}$, ${{\left. U \right|}_{{y = b}}}$ | 6.81 × 10–3 | 2.00 × 10–3 | 7.50 × 10–4 | 3.32 × 10–4 | 1.65 × 10–4 |
| ${{\left. V \right|}_{{x = a}}}$, $V{{{\text{|}}}_{{y = b}}}$ | 1.92 × 10–6 | 6.10 × 10–7 | 2.40 × 10–7 | 1.10 × 10–7 | 5.50 × 10–8 | |
| ${{\left. U \right|}_{{x = 0}}}$, ${{\left. U \right|}_{{y = 0}}}$, ${{\left. V \right|}_{{x = 0}}}$, $V{{{\text{|}}}_{{y = 0}}}$ | 0 | 0 | 0 | 0 | 0 | |
Таблица 3.
Относительная погрешность ${{\delta }_{{\max }}}$, % при использовании ${{M}_{6}}$
| Исследуемый объект | N | |||||
|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | ||
| Компоненты перемещений | U | 2.22 × 10–4 | 6.00 × 10–5 | 2.09 × 10–5 | 8.52 × 10–6 | 3.90 × 10–6 |
| V | 1.05 × 10–4 | 2.59 × 10–5 | 8.45 × 10–6 | 3.27 × 10–6 | 1.37 × 10–6 | |
| Компоненты тензора напряжений |
${{\sigma }_{{x\,x}}}$ | 1.44 × 10–3 | 4.14 × 10–4 | 1.60 × 10–4 | 7.50 × 10–5 | 3.77 × 10–5 |
| ${{\sigma }_{{yy}}}$ | 1.55 × 10–3 | 4.18 × 10–4 | 1.42 × 10–4 | 5.65 × 10–5 | 2.78 × 10–5 | |
| ${{\sigma }_{{zz}}}$ | 1.28 × 10–3 | 3.67 × 10–4 | 1.46 × 10–4 | 6.70 × 10–5 | 3.50 × 10–5 | |
| ${{\sigma }_{{x\,y}}}$ | 1.31 × 10–3 | 3.37 × 10–4 | 1.45 × 10–4 | 6.68 × 10–5 | 3.50 × 10–5 | |
| Невязка ДУ | (3) | 2.00 × 10–2 | 6.34 × 10–3 | 2.57 × 10–3 | 1.21 × 10–3 | 6.32 × 10–4 |
| (4) | 1.29 × 10–2 | 3.82 × 10–3 | 1.50 × 10–3 | 6.49 × 10–4 | 3.37 × 10–4 | |
| Невязка ГУ | ${{\left. U \right|}_{{x = a}}}$, ${{\left. U \right|}_{{y = b}}}$ | 1.14 × 10–4 | 2.58 × 10–5 | 8.80 × 10–6 | 3.40 × 10–6 | 1.44 × 10–6 |
| ${{\left. V \right|}_{{x = a}}}$, $V{{{\text{|}}}_{{y = b}}}$ | 2.24 × 10–9 | 5.59 × 10–10 | 1.95 × 10–10 | 7.60 × 10–11 | 3.35 × 10–11 | |
| ${{\left. U \right|}_{{x = 0}}}$, ${{\left. U \right|}_{{y = 0}}}$, ${{\left. V \right|}_{{x = 0}}}$, $V{{{\text{|}}}_{{y = 0}}}$ | 0 | 0 | 0 | 0 | 0 | |
Из табл. 1–3 видно, что граничные условия ${{\left. U \right|}_{{x = 0}}}$, ${{\left. U \right|}_{{y = 0}}}$, ${{\left. V \right|}_{{x = 0}}}$, ${{V}_{{y = 0}}}$ выполняются точно при выборе любого порядка граничной функции и при любом количестве учитываемых членов в рядах Фурье. Точность выполнения граничных условий ${{\left. U \right|}_{{x = a}}}$, ${{\left. U \right|}_{{y = b}}}$, ${{\left. V \right|}_{{x = a}}}$, $V{{{\text{|}}}_{{y = b}}}$, а также дифференциальных уравнений (2.3), (2.4), и точность вычисления компонент перемещений и компонент тензора напряжений зависят от выбора порядка граничной функции и количества членов в рядах Фурье. Если увеличить порядок граничной функции (со второго до четвертого или с четвертого до шестого), а N во всех расчетах взять одинаковым, то относительная погрешность ${{\delta }_{{\max }}}$ у компонент перемещений и компонент тензора напряжений уменьшится на два порядка. Также на два порядка уменьшится невязка граничных условий ${{\left. U \right|}_{{x = a}}}$, ${{\left. U \right|}_{{y = b}}}$. Для граничных условий ${{\left. V \right|}_{{x = a}}}$, $V{{{\text{|}}}_{{y = b}}}$ невязка уменьшается на три порядка.
Анализируя поведение максимальной невязки дифференциальных уравнений (2.3), (2.4) можно сделать следующий вывод: увеличение порядка граничной функции со второго до четвертого ведет к уменьшению невязки на один порядок, а при увеличении порядка граничной функции с четвертого до шестого на возрастание точности еще влияет число N. Так, при $N = 2$ уменьшение невязки будет составлять один порядок, при $N = 6$ уже два порядка.
С помощью табл. 4 и 5 можно ответить на вопрос, что более эффективно для уменьшения погрешности вычислений – увеличение порядка граничной функции или увеличение количества членов в ряде Фурье. В табл. 4 представлено количество линейных алгебраических уравнений в системах, которые необходимо решить для расчета данных, указанных в табл. 1–3. В табл. 5 записано время расчета программы в секундах на персональном компьютере с процессором Intel Core i3-4160 и ОЗУ 8 ГБ. Из табл. 4 видно, что одинаковая трудоемкость вычислений получается при выборе следующих комбинаций параметров p и N:
Таблица 4.
Количество линейных алгебраических уравнений
| Граничная функция | N | ||||
|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | |
| ${{M}_{2}}$ (p = 1) | 64 | 90 | 120 | 154 | 192 |
| ${{M}_{4}}$ (p = 2) | 120 | 154 | 192 | 234 | 280 |
| ${{M}_{6}}$ (p = 3) | 192 | 234 | 280 | 330 | 384 |
Таблица 5.
Время расчета
| Граничная функция | N | ||||
|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | |
| ${{M}_{2}}$ (p = 1) | 6.98 с | 10.42 с | 14.42 с | 19.37 с | 25.40 с |
| ${{M}_{4}}$ (p = 2) | 12.20 с | 16.85 с | 24.28 с | 37.75 с | 49.73 с |
| ${{M}_{6}}$ (p = 3) | 23.68 с | 34.07 с | 47.65 с | 67.57 с | 96.62 с |
1) p = 1 и $N = 4$ или p = 2 и $N = 2$–120 линейных алгебраических уравнений;
2) p = 1 и $N = 5$ или p = 2 и $N = 3$–154 линейных алгебраических уравнения;
3) p = 1 и $N = 6$ или p = 2 и $N = 4$ или p = 3 и $N = 2$–192 линейных алгебраических уравнения;
4) p = 2 и $N = 5$ или p = 3 и $N = 3$–234 линейных алгебраических уравнения;
5) p = 2 и $N = 6$ или p = 3 и $N = 4$–280 линейных алгебраических уравнений.
Учитывая данные табл. 1–3 можно сделать вывод, что в каждом из пяти указанных вариантов комбинаций параметров p и N точность расчетов выше (значение ${{\delta }_{{\max }}}$ в среднем падает на порядок) в случаях, соответствующих более высокому значению параметра p, т.е. более высокому порядку граничной функции. Принимая во внимание данные табл. 5, отметим, что повышение порядка граничной функции приводит и к сокращению времени расчета. Для пяти комбинаций параметров p и N, соответствующих одинаковой трудоемкости расчетов, уменьшение времени расчета при большем значении параметра p составляет от 2.5% (третья комбинация) до 15% (первая комбинация).
При изучении свойств поля напряжений в брусе наибольший интерес представляет исследование влияния геометрических размеров его сечения на величину интенсивности напряжений $\tilde {\sigma }$ [29]
Размеры сечения в расчетах подобраны таким образом, чтобы площадь сечения бруса оставалась постоянной. Вычислительные эксперименты показали, что качественный вид профилей интенсивности напряжений $\tilde {\sigma }$ квадратного и прямоугольного сечений бруса будут различны. Виды подобных профилей для случаев $a = b = 1$ и $a = 2$, $b = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ изображены на рис. 5, из которого видно, что точка с максимальной интенсивностью напряжений ${{\tilde {\sigma }}_{{\max }}}$ для квадратного сечения расположена на стороне y = 1, а для прямоугольного – находится в угловой точке (2; 0). Значения ${{\tilde {\sigma }}_{{\max }}}$ для различных значений a и b, и координаты точки, в которой достигается ${{\tilde {\sigma }}_{{\max }}}$ записаны в табл. 6. Анализируя данные этой таблицы, можно сделать вывод, что для прямоугольного сечения наибольшая интенсивность напряжений ${{\tilde {\sigma }}_{{\max }}}$ всегда расположена в крайней точке длинной жестко защемленной стороны при x = a. Также из табл. 6 видно, что напряжения в брусе тем выше, чем больше превосходство длины одной стороны над длиной другой стороны прямоугольного сечения. Наименьшая интенсивность напряжений среди всех сечений наблюдается в брусе с квадратным сечением.
Рис. 5.
Интенсивность напряжений $\tilde {\sigma }$: (а) $a = b = 1$, (b) $a = 2$, $b = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$.
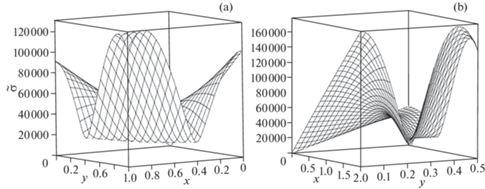
Таблица 6.
Значения ${{\tilde {\sigma }}_{{\max }}}$ и ее координаты
| Размеры сечения | $a = b = 1$ | $a = 2$, b = 1/2 | $a = 3$, b = 1/3 | $a = 4$, b = 1/4 | $a = 5$, b = 1/5 |
|---|---|---|---|---|---|
| Значение ${{\tilde {\sigma }}_{{\max }}}$ | 1.31 × 105 Па | 1.79 × 105 Па | 2.65 × 105 Па | 3.54 × 105 Па | 4.43 × 105 Па |
| Координаты точки | (0.86; 1) | (2; 0) | (3; 0) | (4; 0) | (5; 0) |
5. Заключение. В статье показана эффективность быстрой тригонометрической интерполяции при решении задач теории упругости на примере задачи о напряжениях в брусе прямоугольного сечения. При использовании в быстрых разложениях граничной функции второго порядка и небольшом количестве членов в рядах Фурье (от двух до шести) максимальная относительная погрешность δmax компонент перемещений и компонент тензора напряжений составляет менее 1% , что является приемлемой погрешностью для большинства технических расчетов. С увеличением порядка граничной функции и/или количества членов N в рядах Фурье погрешность δmax быстро уменьшается. Увеличение порядка граничной функции является более эффективным способом уменьшения погрешности δmax по сравнению с увеличением количества членов в рядах Фурье.
При исследовании интенсивности напряжений $\tilde {\sigma }$ в брусе с различными габаритными размерами прямоугольного сечения, но одинаковой площадью всех сечений выяснилось, что наименьшее значение ${{\tilde {\sigma }}_{{\max }}}$ среди всех сечений наблюдается в брусе с квадратным сечением. В этом случае точка с ${{\tilde {\sigma }}_{{\max }}}$ расположена на стороне $у = b$ не далеко от угловой точки $\left( {a;b} \right)$. Для прямоугольного сечения точка с максимальной интенсивностью напряжений ${{\tilde {\sigma }}_{{\max }}}$ будет расположена на длинной стороне в точке $\left( {a;0} \right)$. При этом, чем больше превосходство длины одной стороны прямоугольного сечения над длиной его другой стороны, тем выше ${{\tilde {\sigma }}_{{\max }}}$.
Список литературы
Савичев И.С., Чернышов А.Д. Применение метода угловых суперпозиций для решения контактной задачи о сжатии упругого цилиндра // Изв. РАН. МТТ. 2009. № 3. С. 151–162.
Чернышов А.Д. Метод угловых суперпозиций для краевых задач. LAP LAMBERT Academic Publishing, 2012. 350 c.
Чернышов А.Д. Решение задачи о кручении упругого стержня – угольного сечения методом расширения границ // ПМТФ. 2009. Т. 50. № 6 (298). С. 193–200.
Гоцев Д.В., Ковалев А.В., Спорыхин А.Н. Локальная неустойчивость пластин с запрессованными кольцевыми включениями при упругопластическом поведении материалов // ПМТФ. 2001. Т. 42. № 3 (247). С. 146–151.
Минаева Н.В. О применении метода возмущений в механике деформируемых тел // Изв. РАН. МТТ. 2008. № 1. С. 37–39.
Шашкин А.И., Минаева Н.В., Гриценко А.В. Квазистатическое деформирование упругого стержня при продольном изгибе // Изв. высш. уч. зав. Машиностр. 2008. № 12. С. 21–25.
Вервейко Н.Д., Егоров М.В. Математическое моделирование динамического деформирования упруговязкопластических оболочек конечной длины лучевым методом // Вестн. Самарск. гос. тех. ун-та. Сер.: Физ.-мат. науки. 2018. Т. 22. № 2. С. 325–343. https://doi.org/10.14498/vsgtu1610
Севастьянов Г.М., Штука В.И., Буренин А.А. Лучевой метод в приближенном решении задачи об ударном нагружении несжимаемого цилиндрического слоя // Вестн. Чувашск. гос. пед. ун-та им. И.Я. Яковлева. Сер.: Мех. пред. сост. 2015. № 4 (26). С. 50–62.
Буренин А.А., Рагозина В.Е. К построению приближенных решений краевых задач ударного деформирования // Изв. РАН. МТТ. 2008. № 2. С. 106–113.
Вестяк А.В., Земсков А.В. Модель нестационарных упруго-диффузионных колебаний шарнирно опертой балки Тимошенко // Изв. РАН. МТТ. 2020. № 5. С. 107–119. https://doi.org/10.31857/S0572329920030174
Гандилян Д.В., Устинов К.Б. Влияние поверхностных эффектов в задачах теории упругости для областей, ограниченных неконцентрическими окружностями // Изв. РАН. МТТ. 2020. № 5. С. 95–106. https://doi.org/10.31857/S0572329920050062
Тарлаковский Д.В., Федотенков Г.В. Пространственное нестационарное движение упругой сферической оболочки // Изв. РАН. МТТ. 2015. № 2. С. 118–128.
Буренин А.А., Ковтанюк Л.В., Мурашкин Е.В. Об остаточных напряжениях в окрестности цилиндрического дефекта сплошности вязкоупругопластического материала // ПМТФ. 2006. Т. 47. № 2 (276). С. 110–119.
Timoshenko S.P., Goodier J.N. Theory of elasticity. 3rd ed. McGraw-Hill Inc., 1970. 567 p. = Тимошенко С.П., Гудьер Дж. Теория упругости. М.: Наука, 1979. 560 с.
Меньшова И.В. Разложения по функциям Фадля–Папковича. Основные формулы // Вестн. Чувашск. гос. пед. ун-та им. И.Я. Яковлева. Сер.: Мех. пред. сост. 2012. № 4 (14). С. 133–139.
Себряков Г.Г., Коваленко М.Д., Меньшова И.В., Шуляковская Т.Д. Разложения Лагранжа по функциям Фадля–Папковича в краевой задаче теории упругости для полуполосы // Доклады aкадемии наук. 2015. Т. 460. № 5. С. 540. https://doi.org/10.7868/S0869565215050126
Петров В.В. Двухшаговый метод последовательного возмущения параметров и его применение к решению нелинейных задач механики твердого деформируемого тела // Проблемы прочности элементов конструкций под действием нагрузок и рабочих сред. Саратов: Сарат. гос. техн. ун-т, 2001. С. 6–12.
Горяйнов В.В., Попов М.И., Чернышов А.Д. Решение задачи о напряжениях в остром клиновидном режущем инструменте методом быстрых разложений и проблема согласования граничных условий // Изв. РАН. МТТ. 2019. № 5. С. 113–130. https://doi.org/10.1134/S0572329919050088
Чернышов А.Д., Горяйнов В.В., Кузнецов С.Ф., Никифорова О.Ю. Применение быстрых разложений для построения точных решений задачи о прогибе прямоугольной мембраны под действием переменной нагрузки // Вестн. Томск. гос. ун-та. Мат. мех. 2021. № 70. С. 127–142. https://doi.org/10.17223/19988621/70/11
Chernyshov A.D., Goryainov V.V., Danshin A.A. Analysis of the stress field in a wedge using the fast expansions with pointwise determined coefficients // IOP Conf. Ser.: J. Phys: Conf. Ser. 2018. V. 973. P. 012002. https://doi.org/10.1088/174265.
Чернышов А.Д. Метод быстрых разложений для решения нелинейных дифференциальных уравнений // Ж. выч. мат. физ. Т. 54. № 1. 2014. С. 13–24. https://doi.org/10.7868/S0044466914010062
Чернышов А.Д., Горяйнов В.В., Лешонков О.В., Соболева Е.А., Никифорова О.Ю. Сравнение скорости сходимости быстрых разложений с разложениями в классический ряд Фурье // Вестн. Воронеж. гос. ун-та. Сер.: Сист. анализ инф. технол. 2019. № 1. С. 27–34. https://doi.org/10.17308/sait.2019.1/1273
Чернышов А.Д., Горяйнов В.В., Чернышов О.А. Применение метода быстрых разложений для расчета траекторий космических кораблей // Изв. вузов. Авиац. техн. 2015. № 2. С. 41–47.
Чернышов А.Д. Решение нелинейного уравнения теплопроводности для криволинейной области с условиями Дирихле методом быстрых разложений // Инж.-физ. ж. 2018. Т. 91. № 2. С. 456–468.
Чернышов А.Д. Решение двухфазной задачи Стефана с внутренним источником и задач теплопроводности методом быстрых разложений // Инж.-физ. ж. 2021. Т. 94. № 1. С. 101–120.
Briand T. Trigonometric polynomial interpolation of images // Image Processing on Line. 2019. V. 9. P. 291– 316. https://doi.org/10.5201/ipol.2019.273
Поршнев С.В., Кусайкин Д.В. Восстановление периодических дискретных сигналов конечной длительности с помощью тригонометрической интерполяции // Изв. высш. учебн. завед. Приборостр. 2017. Т. 60. № 6. С. 504–512. https://doi.org/10.17586/0021-3454-2017-60-6-504-512
URL: https://docs.cntd.ru/document/554403082?marker=A840NF (дата обращения: 18.03.2022).
Писаренко Г.С., Можаровский Н.С. Уравнения и краевые задачи пластичности и ползучести. Киев: Наук. думка, 1981. 496 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела