Микроэлектроника, 2019, T. 48, № 6, стр. 430-438
Моделирование влияния структуры межзеренной границы на эффективные заряды ионов в процессах электромиграции
Т. М. Махвиладзе 1, М. Е. Сарычев 1, *
1 Физико-технологический институт имени К.А. Валиева Российской академии наук
117218 Москва, Нахимовский проспект, 36/1, Россия
* E-mail: sarych@yandex.ru
Поступила в редакцию 27.02.2019
После доработки 02.03.2019
Принята к публикации 15.03.2019
Аннотация
Впервые предложена модель, позволяющая рассчитывать эффективный заряд собственных и примесных ионов при электромиграции в наклонной межзеренной границе металла. В модели считается, что основным фактором, приводящим к отличию в значениях эффективного заряда при электромиграции в границе и в объеме монокристалла, является различие их атомных плотностей. Это влияет на силу электронного ветра, определяющего величину эффективного заряда иона. С целью проведения конкретных расчетов в работе улучшена методика вычисления форм-факторов ионов, а также развиты модельные представления, позволяющие связать атомную плотность в наклонной межзеренной границе с параметрами ее структуры. В рамках модели рассчитаны эффективные заряды ионов алюминия и меди в межзеренной границе алюминия, как функции угла разориентировки границы, текстуры образующих ее зерен и температуры.
1. ВВЕДЕНИЕ
Понятие эффективного заряда иона (или вакансии) в проводнике возникает при рассмотрении прохождения через него электрического тока [1]. В этом случае на ион (собственный или примесный) действует как непосредственно электрическое поле, так и сила электронного ветра, обусловленного движением электронов проводимости. Проблема вычисления эффективных зарядов в поликристаллических проводниках является одной из важнейших при моделировании электромиграционных отказов микро- и наноэлектронной металлизации [2]. Величины эффективных зарядов сильно влияют на характерные времена подобных отказов, а также на возможность блокирования электромиграции ионов проводника за счет добавления примесей.
Ранее, в работе [3], был развит подход для расчета из первых принципов эффективных зарядов ионов и вакансий в объеме монокристаллических металлов и сплавов. Подход основан на вычислении силы электронного ветра, действующей на соответствующий дефект, путем нахождения системы форм-факторов, т.е. матричных элементов псевдопотенциала взаимодействия электронов проводимости с ионами, взятых по электронным волновым функциям состояний плоских волн с различными импульсами. Подученные таким образом величины эффективных зарядов обычно и используются в расчетах электромиграционных процессов [2, 4[. Однако на практике микроэлектронная металлизация являются поликристаллической. В ней, как известно, ионная электромиграция происходит в основном либо по межзеренным границам (алюминиевая металлизация), либо по границе между проводником и барьерным слоем (медная металлизация) [2], и, следовательно, величины эффективных зарядов, полученные для объемов монокристаллических металлов, не являются корректными для описания процессов в реальных микропроводниках. Это делает актуальной разработку адекватной модели для расчета эффективных зарядов ионов в межзеренных границах (или в границах различных материалов).
В настоящей работе предложена микроскопическая модель для расчета эффективных зарядов ионов в наклонной межзеренной границе. Она позволяет рассчитать зависимость их величин от угла разориентировки границы, текстуры образующих ее зерен и температуры. В модели межзеренная граница рассматривается как монокристаллический слой и получено, что плотность атомов в ней (удельный атомный объем) зависит от угла разориентировки границы и текстуры смежных зерен. Считается также, что рассматриваемый ион находится в объеме этого слоя и его эффективный заряд определяется соотношениями работы [3]. Однако, поскольку входящие в эти соотношения величины силы электронного ветра и удельного сопротивления зависят от атомной плотности и температуры, то возникает зависимость эффективного заряда от указанных характеристик межзеренной границы и температуры.
Сформулированная модель применена для расчета эффективного заряда ионов алюминия и меди (Сu) в наклонной межзеренной границе алюминия (Al) при различных температурах, углах наклона границы и текстурах образующих ее зерен.
2. ФОРМУЛИРОВКА МОДЕЛИ; ОБЩИЕ СООТНОШЕНИЯ
В соответствии со сказанным выше, основные положения предлагаемой модели для расчета эффективного заряда иона в межзеренной границе состоят в следующем. Во-первых, граница рассматривается как монокристаллический слой, а ион считается находящимся в объеме этого слоя (влиянием границ слоя пренебрегается). Во-вторых, полагается, что можно использовать соотношения [3], полученные для эффективного заряда иона в монокристаллическом объеме, но при этом в качестве входящей в них атомной плотности брать плотность межзеренной границы, которая определяется ее структурой.
Таким образом, исходя из данных модельных представлений требуется, прежде всего, выявить те величины в соотношениях работы [3], которые зависят от атомной плотности (или удельного атомного объема). Необходимо также развить модель, позволяющую рассчитывать атомную плотность в наклонной межзеренной границе как функцию угла ее разориентировки θ ($\theta = 0$ отвечает монокристаллу) и текстуры смежных зерен. Это дает возможность расчета зависимостей эффективных зарядов ионов в межзеренной границе от ее характеристик.
В соответствии со сформулированным подходом и согласно результатам работы [3], эффективный заряд $Z_{{{\text{GB}}}}^{ * }$ иона (примесного или собственного) в наклонной межзеренной границе (в единицах модуля заряда электрона $e = 1.6 \times {{10}^{{ - 19}}}$ Кл) может быть задан следующим выражением:
(1)
$Z_{{{\text{GB}}}}^{ * } = {{Z}_{{{\text{dir}}}}} - \frac{{{{F}_{{{\text{NN}}}}}\left( \theta \right)}}{{j{{\rho }_{{{\text{GB}}}}}\left( {T,\theta } \right)e}},$Рассматривая далее, как и в [3], случай вакансионного механизма дрейфа иона, для вектора силы электронного ветра, действующего на ион в объеме монокристаллического металла, имеем выражение [3]
(2)
${\mathbf{F}}_{{{\text{NN}}}}^{0} = \frac{{\Omega _{0}^{2}m{\text{*}}{{k}_{{{\text{F}}0}}}}}{{{\text{4}}{{\pi }^{{\text{3}}}}{{\hbar }^{2}}}}\left( {\frac{{{{{\mathbf{v}}}_{{\text{d}}}}}}{{{{v}_{{\text{F}}}}}}} \right)\int\limits_0^{2{{k}_{{F0}}}} {w\left( q \right){{w}_{0}}\left( q \right)j_{1}^{'}\left( {q{{R}_{{{\text{NN}}}}}} \right){{q}^{3}}{\text{d}}q} ,$В интересующем нас для расчетов случае иона меди в алюминиевой межзеренной границе из (2) (с учетом записи (1)) приходим к следующему выражению для модуля действующей на него силы электронного ветра
(3)
$\frac{{{{F}_{{{\text{NN}}}}}(\theta )}}{j} = \frac{{{{\Omega }^{2}}{{{(m*)}}^{2}}k_{{\text{F}}}^{{\text{4}}}}}{{{\text{4}}{{\pi }^{{\text{3}}}}{{\hbar }^{3}}en}}\int\limits_0^2 {{{w}^{{{\text{Cu}}}}}\left( {x,\theta } \right){{w}^{{{\text{Al}}}}}\left( {x,\theta } \right)j_{1}^{'}\left( {x{{k}_{{{\text{F0}}}}}{{{\left( {\frac{{{{\Omega }_{0}}}}{\Omega }} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{{R}_{{{\text{NN}}}}}} \right){{x}^{3}}{\text{d}}x} ,$Отметим, что, если в (3) заменить wCu на wAl и подставить (3) в (1), то получим выражение для эффективного заряда иона алюминия в алюминиевой межзеренной границе [3], которое также использовалось в расчетах (разд. 6).
В приближении свободных электронов величина ${{k}_{{\text{F}}}} = {{k}_{{\text{F}}}}(\theta )$ дается следующим выражением [5]
(4)
${{k}_{{\text{F}}}} = {{k}_{{\text{F}}}}(\theta ) = {{\left( {\frac{{3{{\pi }^{2}}Z}}{\Omega }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} \equiv {{k}_{{{\text{F}}0}}}{{\left( {\frac{{{{\Omega }_{0}}}}{{\Omega (\theta )}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$Выражения (1) и (3) позволяют рассчитывать эффективный заряд ионов $Z_{{{\text{GB}}}}^{ * }$ в алюминиевой межзеренной границе. Для проведения таких расчетов необходимо конкретизировать зависимости удельного сопротивления ${{\rho }_{{{\text{GB}}}}}\left( {T,\theta } \right),$ форм-факторов wCu и wAl и плотности атомов ${{n}_{{\text{a}}}} = {{\Omega }^{{ - 1}}}$ в межзеренной границе от угла ее разориентировки $\theta $ (см. Разд. 3–5).
3. ЛОКАЛЬНОЕ УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ В МЕЖЗЕРЕННОЙ ГРАНИЦЕ
Получим теперь, каким образом локальное удельное сопротивление ${{\rho }_{{{\text{GB}}}}}\left( {T,\theta } \right)$ в межзеренной границе которое входит в (1), зависит от плотности атомов ${{n}_{{\text{a}}}} = {{\Omega }^{{ - 1}}}$ в ней.
Величина ${{\rho }_{{{\text{GB}}}}}\left( {T,\theta } \right),$ вообще говоря, включает три вклада, описывающих рассеяние на фононах, рассеяние на примесях и влияние дислокаций. Однако в обычных условиях и при не слишком больших концентрациях примеси два последних малы по сравнению с первым, который, используя метод псевдопотенциала, можно записать в виде [5]
(5)
${{\rho }_{{{\text{ph}}}}}\left( {T,\theta } \right) = {{\rho }_{{{\text{GB}}}}}\left( {T,\theta } \right) = \tilde {\rho }\left( {T,\theta } \right) + {\text{const,}}$и $C = {{3\pi m{\text{*}}\Omega } \mathord{\left/ {\vphantom {{3\pi m{\text{*}}\Omega } {8\hbar {{e}^{2}}{{E}_{{\text{F}}}}}}} \right. \kern-0em} {8\hbar {{e}^{2}}{{E}_{{\text{F}}}}}},$ ${{E}_{{\text{F}}}} = {{{{\hbar }^{2}}k_{{\text{F}}}^{2}} \mathord{\left/ {\vphantom {{{{\hbar }^{2}}k_{{\text{F}}}^{2}} {2m{\text{*}}}}} \right. \kern-0em} {2m{\text{*}}}}$ − энергия Ферми в границе, W(T, θ) − фактор Дебая–Уоллера [5], связанный с колебаниями атомов решетки в межзеренной границе, $w\left( {q,\theta } \right)$ – форм-фактор ионов, образующих межзеренную границу. В (5) специально выделена константа, связанная с вкладом нулевых колебаний решетки. Такое представление оказывается удобным для привязки к конкретным экспериментальным данным по удельному сопротивлению при расчетах эффективных зарядов ионов (см. Разд. 6).
Далее для фактора Дебая–Уоллера будем использовать его выражение ${{W}_{{\text{D}}}}$ в дебаевском приближении [5], т.е.
(6)
$W = {{W}_{{\text{D}}}} = \frac{3}{2}\frac{{{{\hbar }^{2}}g_{n}^{2}}}{{Mk\Theta _{{\text{D}}}^{2}}}T,$Запишем теперь для температуры Дебая выражение, позволяющее проследить ее зависимость от температуры и от угла разориентировки межзеренной границы. Для этого используем известное приближенное выражение [6]
(7)
${{\Theta }_{{\text{D}}}} \approx \frac{{\hbar {{\omega }_{{\text{p}}}}}}{{k\sqrt {3\varepsilon \left( {{{q}_{{\text{D}}}}} \right)} }},$(8)
${{\omega }_{{\text{p}}}} = {{\left[ {\frac{{4\pi {{{\left( {Ze} \right)}}^{2}}{{n}_{{\text{a}}}}}}{M}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,\,\,{{q}_{{\text{D}}}} = {{\left( {6{{\pi }^{2}}{{n}_{{\text{a}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$Таким образом, в межзеренной границе ωр и qD, а вместе с ними ε(qD) и ΘD, через атомную плотность ${{n}_{{\text{a}}}}(\theta ) = {1 \mathord{\left/ {\vphantom {1 \Omega }} \right. \kern-0em} \Omega }$ будут зависеть от угла ее разориентировки θ. Ниже для конкретных расчетов дебаевской температуры использовалась диэлектрическая проницаемость $\varepsilon ({{q}_{{\text{D}}}}) = {{\varepsilon }_{0}}({{q}_{{\text{D}}}})$ в приближении Хартри [5, 6] (см. также выражение (11)). Используя (8), удобно переписать дебаевскую температуру (7) в виде
(9)
${{\Theta }_{{\text{D}}}}\left( {T,\theta } \right) = {{\Theta }_{{\text{D}}}}\left( {T,0} \right){{\left[ {\frac{{{{n}_{{\text{a}}}}\left( \theta \right)}}{{{{n}_{{\text{a}}}}\left( 0 \right)}}\frac{{\varepsilon \left( {{{q}_{{\text{D}}}}\left( 0 \right)} \right)}}{{\varepsilon \left( {{{q}_{{\text{D}}}}\left( \theta \right)} \right)}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$Кроме того, при расчетах фактора $W = {{W}_{{\text{D}}}}$ в межзеренной границе в (6) следует также учитывать, что
(в частности, для монокристалла алюминия gn0 = = $2\pi {{\sqrt 3 } \mathord{\left/ {\vphantom {{\sqrt 3 } {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}},$ a0 = 4.05 Å – постоянная решетки Al [7]).
Формулы (5)–(9) при наличии соответствующей системы форм-факторов $w\left( {q,\theta } \right)$ и зависимости ${{n}_{{\text{a}}}}(\theta ) = {{\Omega }^{{ - 1}}}$ позволяют вычислять удельное сопротивление в межзеренной границы как функцию угла ее разориентировки и температуры.
4. СИСТЕМЫ ФОРМ-ФАКТОРОВ ИОНОВ В МЕЖЗЕРЕННОЙ ГРАНИЦЕ
Согласно выражениям (1) и (3)–(5) для расчетов эффективных зарядов $Z_{{{\text{GB}}}}^{ * }$ в межзеренной границе необходимо найти, как зависят от плотности атомов (т.е. угла разориентировки границы θ) форм-факторы собственных или примесных ионов, т.е. матричные элементы вида
Здесь через w обозначен модельный псевдопотенциал взаимодействия соответствующих ионов с электронами проводимости, ${\mathbf{k}}$ и ${\mathbf{q}}$ – волновые векторы электронов в зоне проводимости.
Вычисление форм-факторов ионов в объеме монокристаллических металлов проводилось в ряде работ (см., например [8]). Модельное выражение для форм-факторов в этом случае учитывает конечные размеры ионов и использует выражение для диэлектрической проницаемости в локальном приближении, но с учетом многочастичных эффектов. Основными параметрами модели являются радиус иона rc и постоянная β [8, 9], введенная для учета силы взаимодействия электронов с остовом иона. Тогда выражение для форм-факторов имеет вид [8]
(10)
$w\left( q \right) \equiv \left\langle {{\mathbf{k}} + {\mathbf{q}}} \right|w\left| {\mathbf{k}} \right\rangle = \left[ { - \frac{{4\pi Z{{e}^{2}}}}{{{{q}^{2}}}} + \frac{\beta }{{{{{\left[ {1 + {{{\left( {q{{r}_{c}}} \right)}}^{2}}} \right]}}^{2}}}}} \right]\frac{1}{{\Omega {{\varepsilon }_{0}}\left( q \right)}},$где
(11)
${{\varepsilon }_{0}}\left( q \right) = 1 + \frac{{m{\text{*}}{{e}^{2}}}}{{2\pi {{k}_{{\text{F}}}}{{\hbar }^{2}}{{\eta }^{2}}}}\left( {\frac{{1 - {{\eta }^{2}}}}{{2\eta }}{\text{ln}}\left| {\frac{{1 + \eta }}{{1 - \eta }}} \right| + 1} \right),\,\,\,\,\eta = {q \mathord{\left/ {\vphantom {q {\left( {2{{k}_{{\text{F}}}}} \right)}}} \right. \kern-0em} {\left( {2{{k}_{{\text{F}}}}} \right)}},$Проведенный нами анализ показал, что выражение (10) достаточно хорошо описывает поведение форм-факторов ионов простых металлов (например, иона Al в алюминии), но плохо соотносится с наилучшими из известных данных по форм-факторам ионов переходных металлов, к которым относится медь [10]. Оказалось, что более корректные выражения получаются, если заменить экспоненциальное распределение отталкивания остова иона более реалистичным гауссовым ехр[–(r/rcore)2/2] и учесть конечность размера остова иона rcore и в первом слагаемом в квадратных скобках в (10), описывающем притяжение (аналогично модельному потенциалу в [11, 12]). В итоге вместо (10) получаем
(12)
$w\left( q \right) = \left\{ { - \frac{{4\pi Z{{e}^{2}}}}{{{{r}_{{{\text{core}}}}}{{q}^{3}}}}{\text{sin}}\left( {q{{r}_{{{\text{core}}}}}} \right)} \right. + \left. {\beta {\text{exp}}\left[ { - \frac{1}{2}{{{\left( {{{r}_{{{\text{core}}}}}q} \right)}}^{{{{2}^{{^{{^{{}}}}}}}}}}} \right]} \right\}\frac{1}{{\Omega \varepsilon \left( q \right)}}.$Помимо этого, с целью улучшения расчетов форм-факторов ионов меди в (12) для ε(q) будем использовать выражение, учитывающее, в отличие от приближение Хартри (11), многочастичный характер взаимодействия электронов [13]:
(13)
$\varepsilon \left( {\mathbf{q}} \right) = {{\varepsilon }_{0}}\left( {\mathbf{q}} \right) - G\left( {\mathbf{q}} \right)\left( {{{\varepsilon }_{0}}\left( {\mathbf{q}} \right) - 1} \right),$с функцией Грина G(q), найденной в [14]:
Проведенные расчеты показали, что выражения (12) и (13) позволяют с помощью двух подгоночных параметров rcore и β достаточно точно интерполировать лучшие из полученных систем форм-факторов иона Al в объеме алюминия [15] и иона Cu в объеме меди [10].
Учтем еще следующее обстоятельство. Как известно, d – состояния электронов остова иона Cu сильно делокализованы [16], что ведет к отличию свойств примесного иона меди в алюминии от его свойств в объеме чистой меди. В работах [16] с помощью теории возмущений показано, что этими различиями можно пренебречь, но важно учитывать изменение экранирования иона из-за различия валентностей ионов меди и алюминия. Учитывая разницу валентностей ионов, для оценки волнового числа Ферми-электронов Al в окрестности иона меди необходимо ввести поправку ΔkF, связанную с контактной разностью потенциалов [17]. Для случая, когда ион меди окружен ионами алюминия, перераспределение заряда было оценено в [17] в приближение Томаса–Ферми и оказалось равным e/3, и для ${{k}_{{\text{F}}}}$ вместо (4) надо записать
(14)
${{k}_{{\text{F}}}} = {{\left( {\frac{{{{\Omega }_{0}}}}{\Omega }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{{k}_{{{\text{F0}}}}} - \Delta {{k}_{{\text{F}}}} = {{k}_{{{\text{F0}}}}}{{\left( {\frac{{{{\Omega }_{0}}}}{\Omega }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}\left( {1 - \Delta {{k}_{{\text{F}}}}{{{\left( {\frac{{{{\Omega }_{0}}}}{\Omega }} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{{k}_{{{\text{F0}}}}}} \right),$где
Таким образом, при вычислении эффективного заряда иона меди в межзеренной границе алюминия форм-факторы рассчитываются по формулам (12), (13) с учетом поправки (14) и зависимости $\Omega \equiv \Omega \left( \theta \right) = {{\left[ {{{n}_{{\text{a}}}}\left( \theta \right)} \right]}^{{ - 1}}}$ от угла разориентировки границы.
5. МОДЕЛИРОВАНИЕ АТОМНОЙ ПЛОТНОСТИ В МЕЖЗЕРЕННОЙ ГРАНИЦЕ
Развитые выше модельные представления, позволили выразить все основные величины, входящие в выражение (1) для эффективного заряда иона в наклонной межзеренной границе через ее атомную плотность ${{n}_{{\text{a}}}}\left( \theta \right).$ Получим теперь соотношения для расчета зависимости ${{n}_{{\text{a}}}}\left( \theta \right).$
С этой целью воспользуемся моделью структуры наклонной межзеренной границы, развитой в работе [18]. Согласно модели, такая граница представляет собой последовательность дислокаций, каждая из которых, будучи изолированной, имеет ядро радиуса r0, а расстояние между соседними одинаково и равно
(15)
$h = \frac{b}{{2{\text{sin}}{\theta \mathord{\left/ {\vphantom {\theta {\text{2}}}} \right. \kern-0em} {\text{2}}}}},$В [18] показано, что изменение объема межзеренной границы при изменении угла ее наклона почти полностью связано с изменением объема ядер дислокаций, и приближенно в качестве объемного расширения (“пористости”) границы может быть взят объем ядер входящих в нее дислокаций. В модели считается, что при θ < θс ядра имеют почти эллипсоидальную форму. Тогда при θ < θc удельная пористость ΔVGB (т.е. приходящаяся на единицу поверхности границы) равна отношению площади эллипса в сечении ядра к расстоянию (15) между соседними ядрами и дается выражением [18]:
(16)
$\Delta {{V}_{{{\text{GB}}}}}(\theta ) = \frac{{{\text{arcsin }}{{\alpha }_{0}}}}{{{{\alpha }_{0}}}}\alpha {\text{*}}{{r}_{0}},$(17)
${\text{sin}}\left( {\frac{{{{\theta }_{{\text{c}}}}}}{2}} \right) = \frac{b}{{2\pi {{r}_{0}}}}.$В [18] считается также, что эффективная ширина формирующегося при θ > θс волнообразного слоя может быть рассчитана как среднее арифметическое ее минимальной и максимальной величины. Тогда удельная пористость ΔVGB при θ > θс дается выражением
(18)
$\Delta {{V}_{{{\text{GB}}}}}(\theta ) = \frac{{{{r}_{0}}}}{{{{\alpha }_{0}}}}\left( {\alpha {\text{*}} + \alpha _{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{*}} \right)\,,$Отметим, что критический угол (см. (17)) и величина пористости (16), (18) зависят от выбора величины радиуса ядра изолированной дислокации r0. В работе [18] путем сравнения полей напряжения дислокации в модели с ядром конечного радиуса и дислокации в модели Пайерлса–Набарро показано, что наиболее близкие результаты получаются, если принять r0 = b/2. В настоящей работе также используем это соотношение, и тогда расчет по уравнению (17) дает θс = 37.1°.
Другой особенностью модели является то, что описание удельной пористости выражениями (16), (18) нарушается в непосредственной окрестности угла θс, т.к. слой не образуется сразу при θ = θс. Однако, угловой интервал, в котором это происходит составляет лишь несколько градусов, что позволяет при расчетах (см. Разд. 6) дополнить зависимость $\Delta {{V}_{{{\text{GB}}}}}(\theta )$ в данном интервале графической аппроксимацией.
Используя эти представления, получим угловую зависимость плотности атомов в межзеренной границе. Поскольку (16) и (18) дают изменение объема границы на единицу ее площади, то для полного изменения ее объема (относительно монокристалла с тем же количеством атомов) имеем соотношение:
(19)
${{N}_{{{\text{GB}}}}}\left( {\Omega - {{\Omega }_{0}}} \right) = \Delta {{V}_{{{\text{GB}}}}}{{A}_{{{\text{GB}}}}},$(20)
${{n}_{{{\text{GB}}}}}\left( \theta \right) = {{n}_{0}}{{\left( {1 + \frac{{\Delta {{V}_{{{\text{GB}}}}}}}{b}} \right)}^{{ - 1}}},$На самом деле, величина ${{n}_{{{\text{GB}}}}}\left( \theta \right),$ полученная в (20), еще не является истинной атомной плотностью межзеренной границы ${{n}_{{\text{a}}}}\left( \theta \right),$ введенной выше, поскольку ${{n}_{{{\text{GB}}}}}\left( \theta \right)$ не обладает определенными свойствами, связанными с симметрией кристаллической решетки смежных зерен. Например, для границ, образованных зернами с текстурой (100) или (111), корректная угловая зависимость атомной плотности должна удовлетворять соотношениям ${{n}_{{\text{a}}}}(0) = {{n}_{{\text{a}}}}(\pi {\text{/}}2)$ в первом случае и ${{n}_{{\text{a}}}}(0) = {{n}_{{\text{a}}}}(\pi {\text{/}}3)$ – во втором. Чтобы учесть это обстоятельство, воспользуемся способом, предложенным в работе [19] для расчета энергии наклонных границ. Будем считать, что в первом приближении корректная угловая зависимость ${{n}_{{\text{a}}}}(\theta )$ может быть получена следующей симметризацией выражения (20):
(21)
${{n}_{{\text{a}}}}\left( \theta \right) = {{n}_{{{\text{GB}}}}}\left( \theta \right) + {{n}_{{{\text{GB}}}}}\left( {\frac{\pi }{2} - \theta } \right) - {{n}_{{{\text{GB}}}}}\left( {\frac{\pi }{2}} \right)$для текстуры (100) и
(22)
${{n}_{a}}\left( \theta \right) = {{n}_{{{\text{GB}}}}}\left( \theta \right) + {{n}_{{{\text{GB}}}}}\left( {\frac{\pi }{3} - \theta } \right) - {{n}_{{{\text{GB}}}}}\left( {\frac{\pi }{3}} \right)$для текстуры (111), где зависимости nGB(θ) берутся в соответствии с (20).
Именно зависимости (21) и (22) с учетом соотношения $\Omega = \Omega (\theta ) = {{[{{n}_{{\text{a}}}}(\theta )]}^{{ - 1}}}$ использованы ниже в расчетах удельного сопротивления, форм-факторов и эффективных зарядов в межзеренной границе как функций угла ее наклона и текстуры смежных зерен.
6. РЕЗУЛЬТАТЫ РАСЧЕТОВ
С помощью развитых выше модельных представлений были выполнены расчеты эффективных зарядов ионов Al и Cu в наклонной межзеренной границе алюминия. Для этого были взяты следующие значения величин, относящихся к монокристаллическому Al: волновое число Ферми-электронов kF0 = 1.7523 × 1010 м–1; плотность электронов проводимости при Т = 273.15 K – n0 = = 0.181 × 1030 м–3: атомный объем при Т = 273.15 К: Ω0 = 0.16508 × 10–28 м3: удельное сопротивление при Т = 273.15 К: ρ0 = 2.5 μОм ⋅ м [7].
Температура Дебая при температуре T = 273.15 K бралась равной ${{\Theta }_{{\text{D}}}}\left( {T = 273.15\,\,{\text{K;}}\,\,0} \right) = 433$ K [7], а температурная зависимость ${{\Theta }_{{\text{D}}}}\left( {T,0} \right)$ находилась путем расчета удельного сопротивления в монокристалле Al по выражению (5) при θ = 0 и подгонки результатов этого расчета к экспериментальным данным [7], хорошо описываемым аппроксимацией
Эти вычисления показали также, что постоянное слагаемое const в (5) должно быть равно const = –0.01033 μОм ⋅ м. Полученное значение использовалось затем в (5) при расчетах удельного сопротивления межзеренной границе (небольшими изменениями этой величины при изменении удельного атомного объема Ω(θ) пренебрегалось).
Для расчета форм-факторов ионов в межзеренной границе алюминия (см. Разд. 4) было принято, что в соотношениях (12), (13) m*/m = 1.001 (m = 9.1095 × 10–31 кг – масса свободного электрона), а параметры псевдопотенциала β ≅ ≅ 42.354 Ry ⋅ (a.е.)3 и rcore ≅ 0.202 a.е. С этими значениями расчет форм-факторов по выражению (12) дает с точностью около 5% результаты [15] для монокристалла Al. Выбранные величины β и rcore, как и следовало ожидать, близки, к значениям 41.1 Ry ⋅ (a.е.)3 и 0.2 a.е., полученным в [8, 20] для иона Al в алюминии.
В настоящей работе приведенные выше значения были использованы в соотношениях Разд. 2–5 при расчетах зависимости эффективных зарядов соответственно ионов меди и алюминия в алюминиевой межзеренной границе от температуры при некоторых углах ее наклона для текстур (100) и (111) образующих ее зерен. Результаты этих расчетов приведены соответственно на рис. 1 и рис. 2.
Рис. 1.
Зависимость эффективного заряда иона меди от температуры в межзеренной границе поликристаллического алюминия. Угол наклона межзеренной границы: θ = 0° (монокристалл) – штрих-пунктир; θ = 30° (текстура (111)) – пунктир, θ = 45° (текстура (100)) – сплошная линия.
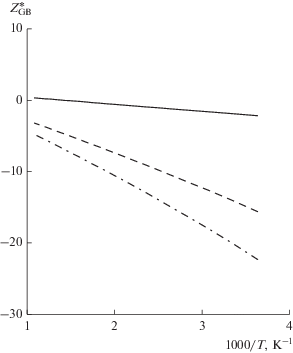
Рис. 2.
Зависимость эффективного заряда иона алюминия от температуры в межзеренной границе поликристаллического алюминия. Угол наклона межзеренной границы: θ = 0° (монокристалл) штрих-пунктир; θ = 30° (текстура (111)) – пунктир, θ = 45° (текстура (100)) – сплошная линия.
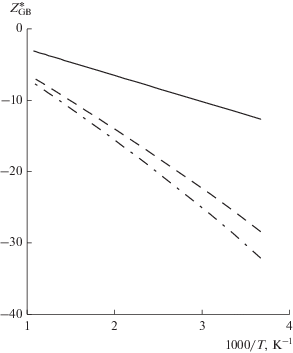
Все рассчитанные зависимости показывают заметное отличие величин эффективных зарядов в межзеренной границе ($\theta \ne 0$) от их значений в монокристаллическом объеме (θ = 0). При этом значительное влияние оказывает также и текстура смежных зерен.
Как и в объеме, величины эффективных зарядов ионов в границе уменьшаются с уменьшением температуры. Однако для межзеренной границы этот рост происходит медленнее, что ожидалось и на основании феноменологических соображений [21]. Таким образом результаты рис. 1 и 2 показывают, что отличие в величинах эффективных зарядов в случаях монокристалла и межзеренной границы растет с уменьшением температуры.
В связи с полученными результатами отметим, что анализ экспериментальных данных по электромиграции, проведенный в [22], и результаты [22] по моделированию экспериментов, выполненных в [23], также свидетельствуют, что абсолютные значения эффективных зарядов в границах должны быть значительно меньше, чем в монокристаллических объемах. Укажем еще, что результаты рис. 1, 2 при θ = 0 хорошо согласуются с теоретическими исследованиями [24] по эффективным зарядам ионов в монокристаллических сплавах.
Отметим также интересную особенность, следующую из результатов расчетов в случае примесных ионов меди в межзеренной границе алюминия. Как видно из рис. 1, их эффективный заряд при текстуре зерен (100), угле наклона границы 45° и при температуре Т ≈ 770 K проходит через нуль. Этот эффект может оказаться полезным в микроэлектронной технологии, поскольку примесь меди давно пытаются использовать для торможения приводящей к отказам электромиграции ионов алюминиевой металлизации [2]. Однако эффективность этого метода ограничивается тем, что ионы меди сами подвержены электромиграции в межзеренных границах алюминия. Согласно же полученным результатам (рис. 1) за счет подбором углов наклона и текстур зерен в границах можно было бы попытаться замедлить электромиграцию ионов медной примеси при рабочих температурах и тем самым усилить ее влияние.
ЗАКЛЮЧЕНИЕ
В настоящей работе впервые развита модель, позволяющая рассчитывать эффективный заряд собственных и примесных ионов в наклонной межзеренной границе поликристаллического металла как функцию параметров границы. Величина ионного эффективного заряда играет большую роль в процессах электромиграции, приводящим к отказам микро- и наноэлектронной металлизации.
В модели считается, что основной фактор, приводящий к различным значениям эффективного заряда иона в границе и в монокристалле, связан с отличием их атомных плотностей, от которых зависят сила электронного ветра и локального удельного сопротивления, определяющие величину эффективного заряда. С целью проведения конкретных расчетов в работе улучшена методика вычисления форм-факторов ионов, а также развит подход, позволяющий связать атомную плотность в наклонной межзеренной границе с углом ее разориентировки и текстурой смежных зерен. Это, в свою очередь, дает возможность рассчитывать зависимости эффективных зарядов ионов от параметров межзеренной границы.
В рамках развитой модели в работе рассчитаны эффективные заряды ионов алюминия и меди в наклонной межзеренной границе алюминия, как функции угла разориентировки границы, текстуры образующих ее зерен и температуры.
Расчеты, как в случае ионов меди, так и алюминия, показали, что в межзеренной границе абсолютные значения эффективных зарядов меньше, чем обычно используемые при моделировании электромиграционных процессов. Эти результаты согласуются с высказанными ранее феноменологическими соображениями относительно соотношения величин эффективных зарядов в границах и монокристаллическом объеме. Полученные температурные зависимости эффективных зарядов показали уменьшение их величины в границе с уменьшением температуры при различных углах разориентировки границы и текстурах образующих ее зерен. В частности, получено, что в определенных условиях эффективный заряд примесного иона меди в алюминиевой межзеренной границе может обратиться в нуль.
Результаты работы могут оказаться полезными для улучшения технологии изготовления и повышения надежности функционирования элементов микро- и наноэлектронных схем.
Работа выполнена в рамках Государственного задания Физико-технологического института имени К.А. Валиева Российской академии наук Минобрнауки РФ по теме № 0066-2019-0004.
Список литературы
Фикс В.Б. Ионная проводимость в металлах и полупроводниках. М.: Наука, 1969. 295 с.
Валиев К.А., Гольдштейн Р.В., Житников Ю.В., Махвиладзе Т.М., Сарычев М.Е. Теория и моделирование нано- и микропроцессов разрушения тонкопленочных проводников и долговечность металлизации интегральных микросхем. Часть 1. Общая теория переноса вакансий, генерации механических напряжений и зарождения микрополостей при электромиграции. Деградация и разрушение многоуровневой металлизации // Микроэлектроника. 2009. Т. 38. № 6. С. 404–427.
Sorbello R.S. A pseudopotential based theory of the driving forces for electromigration in metals. The J. Physics and Chemistry of Solids. 1973. V. 34. № 3. P. 937–950.
Ceric H., Selberherr S. Electromigration in submicron interconnect features of integrated circuits // Materials Science and Engineering: R: Reports. 2011. V. 71(5–6). P. 53–86.
Займан Дж. Принципы теории твердого тела. М.: Мир, 1974. 416 с.
Animalu A.O.E. Intermediate quantum theory of crystalline solids. New Jersey: Englewood Cliffs. 1977. 325 p.
Бабичев А.П., Бабушкина Н.А., Братковский А.М. и др. Физические величины: Справочник / Под ред. Григорьева И.С. и Мелихова Е.З. М.: Энергоатомиздат, 1991.
Harrison W.A. Pseudopotentials in the theory of metals. New York–Amsterdam: W.A. Benjamin. Inc. 1966. 425 p.
Harrison W.A. Model pseudopotential and Kohn effect in lead. Physical Review. 1965. V. 139. № 1A. P. A179–A185.
Dagens L. The resonant model, potential form factor: general theory and application to copper, silver and calcium. J. Physics F: Metal Physics. 1976. V. 6. № 10. P. 1801–1817.
Heine V., Abarenkov I. A new method for the electronic structure of metals. The Philosophical Magazine. 1964. V. 9. № 99. P. 451–465.
Abarenkov I.V., Heine V. The model potential for positive ions. The Philosophical Magazine. 1965. V. 12. № 117. P. 529–537.
Hubbard J. Description of the collective movements in the many particle system by disturbance theory methods. II. The correlation energy of the free electron gas. Proceeding of Royal Society. 1958. V. A243. № 1. P. 336.
Singwi K.S., Tosi M.P., Land R.H. Electron correlations at metallic densities. Physical Review. 1968. V. 176. № 2. P. 589–599.
Animalu A.O.E., Heine V. The screened model potential for 25 elements. The Philosophical Magazine. 1965. V. 12. № 120. P. 1249–1270.
Taut M., Paasch G. The charge of model potentials in alloying. Physica Status Solidi (b). 1972. V. 51. № 1. P. 295–306.
Heine V., Weaire D. Pseudopotential theory of cohesion and structure. Solid State Physics. V. 24, eds., Ehrenreich H., Seitz F., Turnbull D. New York: Academic Press. 1970. P. 295–543.
Li J.C.H. High-angle tilt boundary – a dislocation model // J. Appl. Phys. 1961. V. 32. № 3. P. 525–542.
Van der Merve J.H. On the stress and energies associated with intercrystalline boundaries // Proc. Phys. Soc. 1950. Sec. A. V. 3. № 3. P. 616–637.
Harrison W.A. Electron structure of a series of metals. Physical Review. 1963. V. 131. № 6. P. 2433–2442.
Tu K.N., Gupta T. Defect and diffusion forum. 1993. V. 95–97. P. 257–262.
Sarychev M.E., Zhitnikov Yu.V., Borucki L., Liu C.-L. Makhviladze T.M. A new, general model for mechanical stress evolution during electromigration // Thin Solid Films. 2000. V. 365. P. 211–218.
Wang P.C., Cargill III G.S., Noyan L.C., Hu C.-K. Electromigration-induced stress in aluminum conductor lines measured by X-ray microdiffraction // Appl. Phys. Lett. 1998. V. 72(11). P. 1296–1298.
Dekker J.P., Lodder A. Theory electromigration wind force in dilute alloys. Phys. Review B. 1997. V. 56. № 19. P. 12167–12177.
Дополнительные материалы отсутствуют.
Инструменты
Микроэлектроника


