1. На главную
  2. Электронные версии
  3. Микроэлектроника
  4. T. 49, № 1, 2020

Микроэлектроника, 2020, T. 49, № 1, стр. 18-26

Массивы углеродных нанотрубок в поле непрерывного лазерного излучения

С. А. Афанасьев a, *, И. О. Золотовский a,  c, А. С. Кадочкин a,  c, С. Г. Моисеев a,  c, В. В. Светухин b, А. А. Павлов c, С. В. Булярский c

a Ульяновский государственный университет, НОЦ “Кремний-углеродные нанотехнологии”
432017 Ульяновск, ул. Льва Толстого, 42, Россия

b НПК “Технологический центр”
124498 Зеленоград, Москва, пл. Шокина, 1, Россия

c Институт нанотехнологий микроэлектроники РАН Ленинский проспект
119991 Москва, 32А, Россия

* E-mail: asa_rpe@mail.ru

Поступила в редакцию 27.05.2019
После доработки 26.07.2019
Принята к публикации 26.07.2019

Полный текст (PDF)

Аннотация

Проведен численный анализ условий фазового синхронизма при падении одного или двух встречных лазерных пучков на упорядоченный массив одностенных углеродных нанотрубок. Определены условия генерации медленных поверхностных плазмонных волн терагерцевого и дальнего ИК диапазона, распространяющихся вдоль нанотрубок облучаемого массива. Показано, что частотой плазмонов можно управлять за счет изменения угла падения лазерного излучения на исследуемую структуру. Таким образом можно добиться выполнения условия продольного резонанса, при котором каждая нанотрубка массива представляет собой дипольную антенну, излучающую на частоте плазмона. При этом массив образует систему большого числа синфазных излучателей, что позволяет существенно повысить эффективность преобразования лазерного излучения в терагерцевое по сравнению с одиночной наноантенной.

ВВЕДЕНИЕ

В настоящее время актуальной задачей является разработка компактных генераторов терагерцового (ТГц) излучения, работающих при комнатной температуре. Такие генераторы могли бы найти практические применения в спектроскопии, системах безопасности, медицинской диагностике и других областях науки и техники [1, 2].

В современных твердотельных источниках ТГц излучения обычно осуществляется параметрическое взаимодействие импульса лазерного излучения с полупроводниковой структурой [1–5]. Полупроводниковые квантовые каскадные лазеры в ТГц диапазоне работают только при криогенных температурах и не обладают возможностью существенной перестройки частоты. Газовые лазеры, хотя и работают при комнатной температуре, также не способны заметно перестраивать длину волны излучения. Источники ТГц излучения, созданные на основе фемтосекундных лазеров, обладают чрезвычайно широким спектром излучения (порядка 1 THz), в результате чего в ТГц излучение преобразуется лишь малая часть энергии, обычно эффективность преобразования не превышает 10–3 [3–5].

Повысить эффективность преобразования лазерного излучения в ТГц можно, переходя к преобразованию в непрерывном режиме. Также для повышения эффективности мишень может содержать плазмонные структуры различного рода. Одним из перспективных направлений создания генераторов ТГц излучения представляется использование массивов углеродных нанотрубок (УНТ) и нанокомпозитов на их основе, облучаемых непрерывным лазерным излучением. Совокупность большого числа уникальных свойств УНТ в сочетании с их геометрическими размерами делает их перспективными при рассмотрении задачи генерации ТГц (и СВЧ) излучения [6–16]. Предлагаемые применения УНТ как излучателей электромагнитных волн опираются на тот факт, что УНТ может выступать в качестве линии передачи (волновода), поддерживающей распространение поверхностной электромагнитной волны [7, 11–13, 17–22]. Важной особенностью генерации субмиллиметровых волн массивом УНТ является необходимость значительного (более чем в сто раз) замедления поверхностных волн по сравнению со скоростью света в вакууме.

В данной работе рассматривается механизм генерации под воздействием лазерного излучения медленных поверхностных плазмон-поляритонов (ПП) в массивах одностенных УНТ. Плазмонные волны, генерируемые в массиве УНТ одним или двумя лазерными пучками, могут рассматриваться как антенны, обеспечивающие генерацию излучения в субмиллиметровом диапазоне. Получены условия генерации ПП в подобного рода структурах при использовании лазерного излучения на длине волны 1.06 мкм, на которой работают наиболее распространенные и доступные волоконные и твердотельные лазерные источники с большой средней и пиковой мощностями.

В работе будут рассмотрены две схемы генерации.

1. Использование для возбуждения медленных ПП в УНТ массива двух лазерных источников со слабо различающимися частотами. При этом генерация соответствующего медленного ПП осуществляется на разностной частоте.

2. Медленные ПП возбуждаются в массиве УНТ в условиях взаимодействия узкополосного лазерного излучения (падающей и дифрагированной волны) с периодически расположенными УНТ. В этом случае рассматривается самораспад (типа параметрического трехфотонного взаимодействия в периодической структуре) исходной лазерной волны на дифрагированную волну и ПП на поверхности нанотрубок.

Как в первом, так и во втором случаях должны быть реализованы условия фазового синхронизма соответствующих волновых процессов.

УСЛОВИЯ ФАЗОВОГО СИНХРОНИЗМА

Будем рассматривать двумерный упорядоченный массив из одинаковых одностенных УНТ радиуса a, расположенных параллельно друг другу (рис. 1). На структуру под углом ${{\theta }_{1}}$ к оси $x$ (нормаль к осям симметрии трубок) падает лазерный пучок частоты ${{\omega }_{1}}$ с волновым числом ${{k}_{1}} = {{{{\omega }_{1}}} \mathord{\left/ {\vphantom {{{{\omega }_{1}}} c}} \right. \kern-0em} c}$ (c – скорость света в вакууме). Лазерное поле будем аппроксимировать плоской волной ТМ поляризации. При данной поляризации падающей волны имеется составляющая ее электрического поля, направленная вдоль осей трубок (ось $z$). Ее наличие является необходимым условием возникновения продольной составляющей вектора плотности тока, текущего по поверхности трубки и возбуждения замедленной поверхностной волны, направляемой трубкой, выступающей в качестве волновода [7, 11, 17–22].

Рис. 1.

Геометрия задачи: генерация ПП в массиве УНТ при облучении двумя (а) и одним (б) лазерными пучками.

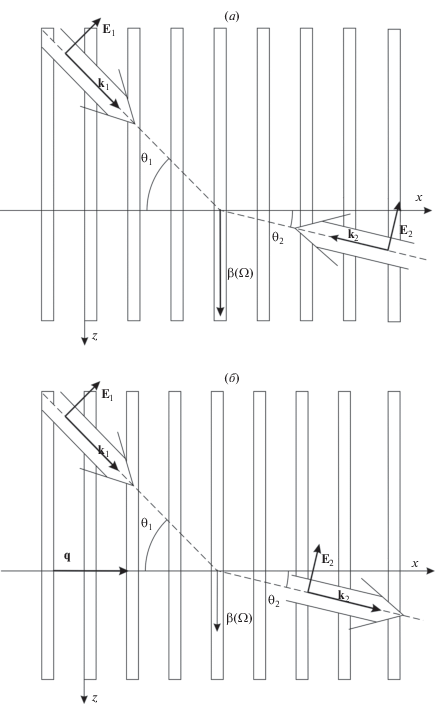
В первом варианте данная схема будет рассмотрена в условиях двухпучкового возбуждения, когда на массив УНТ падает под углом ${{\theta }_{2}}$ второй (встречный) лазерный пучок с отличной от ${{\omega }_{1}}$, но близкой к ней частотой ${{\omega }_{2}}$ (рис. 1а). Генерация ПП в нанотрубках при этом происходит на разностной частоте $\Omega = {{\omega }_{1}} - {{\omega }_{2}}.$ В этом случае условие фазового синхронизма запишется в виде

(1)
${{k}_{1}}\sin {{\theta }_{1}} - {{k}_{2}}\sin {{\theta }_{2}} = \beta (\Omega ),$
где ${{k}_{2}} = {{{{\omega }_{2}}} \mathord{\left/ {\vphantom {{{{\omega }_{2}}} c}} \right. \kern-0em} c},$ а $\beta $ – волновое число возбуждаемого в нанотрубках ПП. Обеспечить выполнение условия (1) можно, например, подбирая необходимое значение угла ${{\theta }_{2}}$ при фиксированном значении угла падения опорного пучка ${{\theta }_{1}}.$

Вторая (менеее сложная технически) схема может быть реализована при наличии только одного лазерного пучка (рис. 1б), однако она требует строгой периодичности массива параллельных УНТ. Массив представляет собой в данном случае дифракционную решетку с периодом $d$ ($d$ – расстояние между соседними нанотрубками). Дифрагированный пучок уменьшенной частоты ${{\omega }_{2}} = {{\omega }_{1}} - \Omega $ имеет волновой вектор величины ${{k}_{2}} = {{{{\omega }_{2}}} \mathord{\left/ {\vphantom {{{{\omega }_{2}}} c}} \right. \kern-0em} c},$ направленный под углом ${{\theta }_{2}}$ к оси $x$. Условие дифракции Брэгга с учетом генерации ПП, возбуждаемого на разностной частоте Ω и распространяющегося вдоль трубок (ось $z$) с волновым вектором ${\mathbf{\beta }}$ имеет вид:

(2)
${{{\mathbf{k}}}_{{\text{1}}}} = {{{\mathbf{k}}}_{{\text{2}}}} + {\mathbf{\beta }}(\Omega ) \pm {\mathbf{q}},$
где ${\mathbf{q}}$ – волновой вектор периодической структуры ($q = {{2\pi p} \mathord{\left/ {\vphantom {{2\pi p} d}} \right. \kern-0em} d},$ $p$ – порядок дифракции). Далее будем учитывать только дифракционные пучки 1 порядка с $p = \pm 1.$

В проекциях на оси $x,\;z$введенной системы координат (2) запишется как

(3)
$\left\{ \begin{gathered} {{k}_{1}}\cos {{\theta }_{1}} - {{k}_{2}}\cos {{\theta }_{2}} = q, \hfill \\ {{k}_{1}}\sin {{\theta }_{1}} - {{k}_{2}}\sin {{\theta }_{2}} = \beta (\Omega ). \hfill \\ \end{gathered} \right.$

Для реального массива УНТ обеспечить периодичность облучаемой структуры достаточно сложно. Однако в случае неупорядоченного, но достаточно плотного массива условие фазового синхрогнизма будет выполняться для некоторого числа трубок, расположение которых удовлетворяет (3).

ДИСПЕРСИОННОЕ СООТНОШЕНИЕ

Для решения и анализа фазовых соотношений (1) и (3) необходимо иметь дисперсионное соотношение, т.е. зависимость β(Ω) для волнового вектора ПП, распространяющегося вдоль трубок. Существуют различные подходы к решению электродинамической задачи о распространении поверхностной волны в волноводе, образованном УНТ [7, 18–24], но получаемые при этом дисперсионные зависимости достаточно хорошо согласуются друг с другом. В данной работе мы используем дисперсионное соотношение для поверхностной ТМ волны в металлической одностенной УНТ без учета потерь, приведенное в [19]:

(4)
$i\Omega {{\varepsilon }_{0}} = {{\sigma }_{{zz}}}{{\beta }^{2}}aI(\beta a)K(\beta a),$
где ${{\varepsilon }_{0}}$ – диэлектрическая постоянная, $I(\beta a)$ и $K(\beta a)$ – модифицированные функции Бесселя 1 и 2 рода, а ${{\sigma }_{{zz}}}$ – продольная компонента тензора проводимости металлической одностенной УНТ:

(5)
${{\sigma }_{{zz}}} = \frac{{i{{n}_{0}}{{e}^{2}}}}{{{{m}_{{\text{e}}}}\Omega }}$

(${{n}_{0}}$ – равновесная поверхностная плотность $\pi $‑электронов в УНТ, $e$ – элементарный заряд, ${{m}_{{\text{e}}}}$– эффективная масса электрона).

Для входящего в (5) отношения ${{{{n}_{0}}} \mathord{\left/ {\vphantom {{{{n}_{0}}} {{{m}_{{\text{e}}}}}}} \right. \kern-0em} {{{m}_{{\text{e}}}}}}$ в [25] получена следующая оценка:

$\frac{{{{n}_{0}}}}{{{{m}_{{\text{e}}}}}} = \frac{{2{{V}_{{\text{F}}}}}}{{{{\pi }^{2}}a}}$
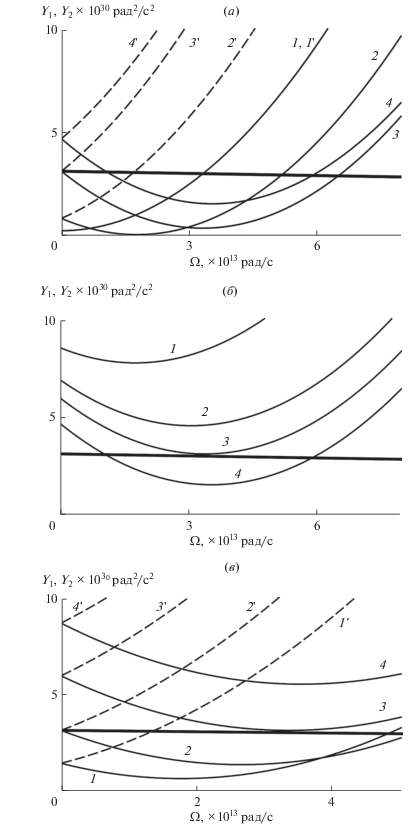
где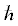 – постоянная Планка, ${{V}_{{\text{F}}}}$ – скорость Ферми, значение которой для металлических одностенных УНТ оценивается как ${{V}_{{\text{F}}}} \approx (0.9 - 1) \times {{10}^{6}}$ м/с [20].

Далее анализируются условия существования решений уравнений (1) и (3) и проводится их численный анализ с учетом соотношения (4) при различных значениях угла падения опорного лазерного пучка в интервале его значений $0 \leqslant {{\theta }_{1}} \leqslant 90^\circ .$

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

А) Двухпучковая схема

Результаты численного анализа условия (1) для двухпучковой схемы представлены на рис. 2, где изображены зависимости угла падения ${{\theta }_{2}}$ второго пучка от частоты $\Omega $ ПП, возбуждаемых в нанотрубках массива. Расчеты проводились при фиксированных значениях угла падения ${{\theta }_{1}}$ с учетом соотношения (4).

Рис. 2.

Зависимости угла падения второго лазерного пучка от разностной частоты: а – при $a$ = 1 нм, ${{\theta }_{1}}$ = 15, 30, 45, 60, 75 и 90° (1–6); б – при ${{\theta }_{1}} = 45^\circ ,$ $a$ = 0.5, 1.5, 2.5 нм (1–3).

На рис. 2а изображены зависимости ${{\theta }_{2}}(\Omega )$ для различных значений угла падения ${{\theta }_{1}}$ при фиксированном значении радиуса нанотрубки a = 1 нм. Видно, что угол ${{\theta }_{2}}$ уменьшается с ростом частоты $\Omega $ и при не слишком больших значениях угла ${{\theta }_{1}}$ может сменить знак (положительным считается направление отсчета угла ${{\theta }_{2}}$, показанное на рис. 1а). Следует отметить линейный характер представленных зависимостей, который нарушается только при достаточно больших углах падения ${{\theta }_{1}}$ (начиная примерно с 60°) для небольших частот $\Omega $ из исследуемого диапазона.

На рис. 2б даны зависимости ${{\theta }_{2}}(\Omega )$ для различных значений радиуса нанотрубки $a$ при фиксированном значении угла ${{\theta }_{1}} = 45^\circ .$ Можно отметить, что значение $a$ слабо влияет на ход зависимости, а с уменьшением частоты $\Omega $ его влияние становится несущественным. Таким образом, данная схема может быть практически нечувствительной к возможным вариациям поперечных размеров отдельных нанотрубок массива.

Б) Самораспад лазерного пучка

Будем искать корни ${{\theta }_{2}}$ и $\Omega $ системы (3) в зависимости от угла падения ${{\theta }_{1}}$ лазерного пучка на структуру при фиксированном значении периода решетки $d$. Из первого и второго уравнений системы (3) получаем выражения для косинуса и синуса искомого угла ${{\theta }_{2}}$:

(6)
$\cos {{\theta }_{2}} = \frac{{{{k}_{1}}\cos {{\theta }_{1}} \mp q}}{{{{k}_{2}}}} = \frac{{{{\omega }_{1}}\cos {{\theta }_{1}} \mp qc}}{{{{\omega }_{1}} - \Omega }},$
(7)
$\sin {{\theta }_{2}} = \frac{{{{k}_{1}}\sin {{\theta }_{1}} - \beta (\Omega )}}{{{{k}_{2}}}} = \frac{{{{\omega }_{1}}\sin {{\theta }_{1}} - \beta (\Omega )c}}{{{{\omega }_{1}} - \Omega }},$

откуда следует соотношение

(8)
${{({{\omega }_{1}} - \Omega )}^{2}} = {{({{\omega }_{1}}\cos {{\theta }_{1}} \mp qc)}^{2}} + {{({{\omega }_{1}}\sin {{\theta }_{1}} - \beta (\Omega )c)}^{2}}.$

Численно решая (8), находим $\Omega $, а затем из (6), (7) – угол ${{\theta }_{2}}$.

Некоторые важные закономерности процесса самораспада лазерного пучка можно получить аналитически, используя приближение $\Omega \ll {{\omega }_{1}}.$ Тогда уравнение (6) принимает вид

(9)
$\cos {{\theta }_{2}} = \cos {{\theta }_{1}} - {q \mathord{\left/ {\vphantom {q {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}} = \cos {{\theta }_{1}} \mp {{{{\lambda }_{1}}} \mathord{\left/ {\vphantom {{{{\lambda }_{1}}} d}} \right. \kern-0em} d},$
где ${{\lambda }_{1}}$ – длина волны падающего излучения. В случае $q > 0$ из (9) вытекает условие $d \geqslant {{{{\lambda }_{1}}} \mathord{\left/ {\vphantom {{{{\lambda }_{1}}} 2}} \right. \kern-0em} 2},$ ограничивающее снизу величину периода решетки. Также видно, что ситуация с $q < 0$ возможна только при $d \geqslant {{\lambda }_{1}}.$

Теперь, переписывая (7) в приближении Ω $ \ll $ ω1 как

$\sin {{\theta }_{2}} = \sin {{\theta }_{1}} - {{\beta (\Omega )} \mathord{\left/ {\vphantom {{\beta (\Omega )} {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}}$

можно получить с учетом (9) величину волнового вектора ПП $\beta $:

(10)
${\beta \mathord{\left/ {\vphantom {\beta {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}} = \sin {{\theta }_{1}} \pm \sqrt {1 - {{{\left( {\cos {{\theta }_{1}} \mp {{{{\lambda }_{1}}} \mathord{\left/ {\vphantom {{{{\lambda }_{1}}} d}} \right. \kern-0em} d}} \right)}}^{2}}} .$

На рис. 3 представлены результаты графического решения уравнения (8) относительно переменной $\Omega $ в нескольких частных случаях для массива из нанотрубок радиусом a = 1 нм. Вначале рассмотрим ситуацию $d \geqslant {{\lambda }_{1}},$ которая допускает два частных случая, отличающиеся знаком параметра $q$. Также необходимо учесть, что соотношение (10) допускает возможность двух знаков волнового числа $\beta $, т.е. распространения ПП вдоль трубок как в положительном, так и в отрицательном направлениях оси $z$. Именно, величина $\beta $ меняет знак при “критическом” значении угла падения

(11)
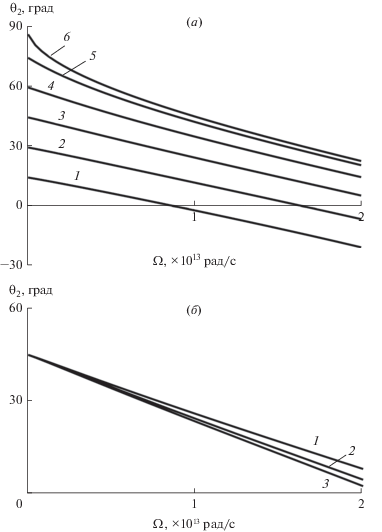
$\theta _{1}^{{\operatorname{cr} }} = \arccos \left( {{{{{\lambda }_{1}}} \mathord{\left/ {\vphantom {{{{\lambda }_{1}}} {2d}}} \right. \kern-0em} {2d}}} \right).$
Рис. 3.

Графическое решение уравнения (8) относительно частоты ПП: а – при $d$ = 1.5 мкм (случай $q > 0$), ${{\theta }_{1}} = 0,30,69$ и 90° (1–4); б – при $d$ = 1,5 мкм ($q < 0$), ${{\theta }_{1}} = 30,60,73$ и 90° (1–4); в – при $d$ = 0.8 мкм, ${{\theta }_{1}} = 0,49,71$ и 90° (1–4). Жирная линия – левая часть ${{Y}_{1}}$, тонкие – правая часть ${{Y}_{2}}$: сплошные линии – случай $\beta > 0,$ штриховые – $\beta < 0.$

При $d \geqslant {{\lambda }_{1}}$ величина $\theta _{1}^{{\operatorname{cr} }}$ лежит в интервале от 60 до 90°.

На рис. 3а, 3б представлены результаты для решетки с периодом $d$ = 1.5 мкм при различных значениях угла падения ${{\theta }_{1}}$ для случаев $q > 0$ (а) и $q < 0$ (б). Сплошной жирной линией изображена частотная зависимость ${{Y}_{1}}(\Omega )$ левой части уравнения (8), не зависящей от ${{\theta }_{1}}$. Тонкие линии соответствуют зависимостям ${{Y}_{2}}(\Omega )$ правой части, причем сплошные линии относятся к положительным, а штриховые – к отрицательным значениям волнового вектора $\beta $. Точки пересечения жирной и тонких линий дают частоты ПП, распространяющихся в нанотрубках.

В случае $q > 0$ (рис. 3а) в интервале углов $0 \leqslant {{\theta }_{1}} < \theta _{1}^{{{\text{cr}}}}$ существует два корня, соответствующие двум ПП с различными частотами и отличающимся направлением распространения (пример – кривые 2, 2 ' для ${{\theta }_{1}} = 30^\circ $). При ${{\theta }_{1}} = 0$ сплошная кривая 1 сливается со штриховой 1', что соответствует двум ПП одинаковой частоты. При “критическом” угле падения ${{\theta }_{1}} = \theta _{1}^{{\operatorname{cr} }} \approx 69^\circ $ (кривые 3, 3') пропадает корень, отвечающей плазмону с $\beta < 0$, и при ${{\theta }_{1}} > \theta _{1}^{{\operatorname{cr} }}$ имеем два корня, отвечающих плазмонам одного (положительного) направления распространения (кривые 4, 4 ').

Решения с $q < 0$ возможны, если угол падения θ1 превышает значение

$\theta _{1}^{{\min }} = \arccos \left( {{{1 - {{\lambda }_{1}}} \mathord{\left/ {\vphantom {{1 - {{\lambda }_{1}}} d}} \right. \kern-0em} d}} \right).$

В условиях рис. 3б $\theta _{1}^{{\min }} \approx 73^\circ ;$ при этом угле падения решение только одно (кривая 3), при ${{\theta }_{1}} < \theta _{1}^{{\min }}$ решений нет (кривые 1 и 2), а при ${{\theta }_{1}} > \theta _{1}^{{\min }}$ (кривая 4) их два, причем оба отвечают плазмонам с $\beta > 0.$

Значения углов ${{\theta }_{2}}$, отвечающие двум корням уравнения (8) (при их наличии), отличаются только знаком, т.е. направления двух дифрагированных пучков симметричны относительно оси $x$. Это схематично показано на рис. 4, где, помимо волновых векторов падающего и дифрагированных пучков, изображены волновые векторы $\beta $ ПП, генерируемых в массиве УНТ. Рис. 4а отображает ситуацию, характерную для интервала углов падения ${{\theta }_{1}} < \theta _{1}^{{{\text{cr}}}} < \theta _{1}^{{{\text{min}}}},$ где имеется два дифрагированных пучка с волновыми векторами ${{{\mathbf{k}}}_{{21}}}$ и ${{{\mathbf{k}}}_{{22}}}.$ Для углов падения из интервала ${{\theta }_{1}} > \theta _{1}^{{{\text{min}}}} > \theta _{1}^{{{\text{cr}}}}$ (рис. 4б) помимо двух пучков (${\mathbf{k}}_{{21}}^{ + }$ и ${\mathbf{k}}_{{22}}^{ + }$), возникающих в случае $q > 0,$ появляются еще два пучка (${\mathbf{k}}_{{21}}^{ - }$ и ${\mathbf{k}}_{{22}}^{ - }$), отвечающие условию $q < 0.$ При этом для $q > 0$ минимальное значение угла дифракции $\theta _{{2\min }}^{ + } = \arccos \left( {{{1 - {{\lambda }_{1}}} \mathord{\left/ {\vphantom {{1 - {{\lambda }_{1}}} d}} \right. \kern-0em} d}} \right)$ соответствует углу падения ${{\theta }_{1}} = 0$, а максимальное $\theta _{{2\max }}^{ + } = \arccos \left( {{{ - {{\lambda }_{1}}} \mathord{\left/ {\vphantom {{ - {{\lambda }_{1}}} d}} \right. \kern-0em} d}} \right)$ реализуется при ${{\theta }_{1}} \to 90^\circ .$ Таким образом, углы $\theta _{2}^{ + }$ могут быть как острыми, так и тупыми, т.е. имеет место либо прохождение излучения через структуру, либо его отражение. При $q < 0$ угол дифракции $\theta _{2}^{ - }$ может быть только острым, не превышающим по модулю величины $\arccos \left( {{{{{\lambda }_{1}}} \mathord{\left/ {\vphantom {{{{\lambda }_{1}}} d}} \right. \kern-0em} d}} \right).$ При ${{\theta }_{1}} = \theta _{1}^{{\min }}$ дополнительный дифрагированный пучок лишь один, направленный по оси $x$.

Рис. 4.

Схема волновых векторов падающего и дифрагированных лазерных пучков, а также ПП, возбуждаемых в массиве УНТ: а – $d > {{\lambda }_{1}},$ ${{\theta }_{1}} < \theta _{1}^{{{\text{cr}}}} < \theta _{1}^{{{\text{min}}}};$ б – $d > {{\lambda }_{1}},$ ${{\theta }_{1}} > \theta _{1}^{{{\text{min}}}} > \theta _{1}^{{{\text{cr}}}};$ в – ${{{{\lambda }_{1}}} \mathord{\left/ {\vphantom {{{{\lambda }_{1}}} 2}} \right. \kern-0em} 2} < d < {{\lambda }_{1}},$ ${{\theta }_{1}} < \theta _{1}^{{{\text{cr}}}} < \theta _{1}^{{{\text{max}}}}.$

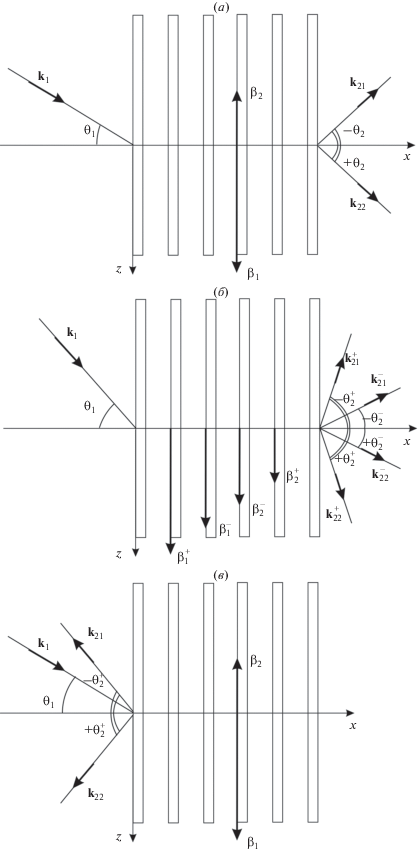
Результаты численного решения уравнения (8) для случая ${{{{\lambda }_{1}}} \mathord{\left/ {\vphantom {{{{\lambda }_{1}}} 2}} \right. \kern-0em} 2} < d < {{\lambda }_{1}}$ представлены на рис. 3в (для расчетов было выбрано значения периода решетки $d$ = 0.8 мкм). Решения с $q < 0$ в этом случае отсутствуют. При $q > 0$ здесь, как и в предыдущем случае, существует “критический” угол, определяемый той же формулой (11) и имеющий тот же смысл, но теперь его значения попадают в интервал от 0 до 60°. Имеется еще одно существенное отличие: решения отсутствуют, если угол падения превышает максимально допустимое значение

(12)
$\theta _{1}^{{\max }} = \arccos \left( {{{{{\lambda }_{1}}} \mathord{\left/ {\vphantom {{{{\lambda }_{1}}} d}} \right. \kern-0em} d} - 1} \right).$

В условиях рис. 3в характерные углы падения, согласно формулам формулам (11) и (12), имеют значения $\theta _{1}^{{\operatorname{cr} }} \approx 49^\circ $ и $\theta _{1}^{{\max }} \approx 71^\circ .$

Углы дифракции в случае ${{{{\lambda }_{1}}} \mathord{\left/ {\vphantom {{{{\lambda }_{1}}} 2}} \right. \kern-0em} 2} < d < {{\lambda }_{1}}$ могут быть только тупыми, т.е. падающее излучение полностью отражается от структуры. Это схематично показано на рис. 4в для угла падения из интервала ${{\theta }_{1}} < \theta _{1}^{{{\text{cr}}}} < \theta _{1}^{{{\text{max}}}}.$ При $\theta _{1}^{{}} = \theta _{1}^{{\max }}$ два корня сливаются в один при ${{\theta }_{2}} = 180^\circ ,$ т.е. имеется один дифрагированный (отраженный) пучок и возбуждается только один ПП в каждой нанотрубке. Такая ситуация представляется отптимальной для повышения эффективности данной структуры, используемой в качестве антенны ТГц диапазона.

ЗАКЛЮЧЕНИЕ

Облучаемые лазером УНТ можно рассматривать как генерирующие антенны, излучающие в ТГц и дальнем ИК диапазонах излучения. В результате последовательных переотражений бегущей поверхностной волны от торцов плазмонного волновода, формируемого нанотрубкой, формируются стоячие волны тока и напряжения. При заданной длине нанотрубки $L$ существует дискретный набор частот, для которых выполняется условие формирования стоячих волн $\beta (\Omega )L = m\pi $ ($m$ – целое число). Отдельно следует подчеркнуть, что в нашем случае резонансы должны наблюдаться для длин волн, которые в свободном пространстве могут существенно (на порядки) превышать размеры соответствующей антенны, что объясняется сильным замедлением ПП.

Таким образом, показано, что лазерное излучение ближнего ИК диапазона может быть использовано для эффективной генерации ТГц и дальнего ИК излучения в условиях двухпучкового лазерного облучения непериодического массива параллельных УНТ и однопучкового облучения массива периодически расположенных УНТ. Важно, что частота излучения массива УНТ может управляться изменением угла падения лазерного излучения. Такая подстройка необходима для выполнения условия геометрического резонанса, в результате чего эффективность излучающей системы может быть резко повышена.

Работа поддержана Российским фондом фундаментальных исследований (проект № 18-29-19101), Министерством науки и высшего образования (проект № 0004-2019-0002).

Список литературы

  1. Lee Y.S. Principles of Terahertz Science and Technology. N.Y.: Springer, 2009. P. 340.

  2. Братман В.Л., Литвак А.Г., Суворов Е.В. Освоение терагерцевого диапазона: источники и приложения // УФН. 2011. Т. 161. № 8. С. 867–874.

  3. Bugay A.N., Sazonov S.V. The generation of terahertz radiation via optical rectification in the self-induced transparency regime // Phys. Lett. A. 2010. V. 374. № 8. P. 1093–1096.

  4. Fülöp J.A., Pálfalvi L., Klingebiel S., Almási G., Krausz F., Karsch S., Hebling J. Generation of sub-mJ terahertz pulses by optical rectification // Optics Letters. 2012. V. 37. № 4. P. 557–559.

  5. Nagai M., Matsubara E., Ashida M. High-efficiency terahertz pulse generation via optical rectification by suppressing stimulated Raman scattering process // Optics Express. 2012. V. 20. № 6. P. 6509–6514.

  6. Sharma S., Vijay A. Terahertz generation via laser coupling to anharmonic carbon nanotube array // Phys. of Plasmas. 2018. V. 25. № 2. P. 023114.

  7. Slepyan G.Ya., Maksimenko S.A., Lakhtakia A., Yevtushenko O.M., Gusakov A.V. Electrodynamics of carbon nanotubes: Dynamic conductivity, impedance boundary conditions, and surface wave propagation // Phys. Rev. B. 1999. V. 60. № 24. P. 17136.

  8. Садыков Н.Р., Скоркин Н.А. Квантовый подход для описания процесса усиления излучения на основе массива нанотрубок // ЖТФ. 2013. Т. 83. № 5. С. 1–5.

  9. Batrakov K.G., Kibis O.V., Kuzhir P.P., da Costa M.R., Portnoi M.E. Teraherz processes in carbon nanotubes // J. of Nanophotonics. 2010. V. 4. № 1. P. 041665.

  10. Batrakov K.G., Maksimenko S.A., Kuzhir P.P., Thomsen C. Carbon nanotube as a Cherenkov-type light emitter and free electron laser // Phys. Rev. B. 2009. V. 79. № 12. P. 125408.

  11. Shuba M.V., Slepyan G.Ya., Maksimenko S.A., Thomsen C., Lakhtakia A. Theory of multiwall carbon nanotubes as waveguides and antennas in the infrared and the visible regimes // Phys. Rev. B. 2009. V. 79. № 15. P. 155403.

  12. Hanson G.W. Fundamental transmitting properties of carbon nanotube antennas // IEEE Transactions on Antennas and Propagation. 2005. V. 53. № 11. P. 3426–3435.

  13. Hao J., Hanson G.W. Electromagnetic scattering from finite-length metallic carbon nanotubes in the lower IR bands // Phys. Rev. B. 2006. V. 74. № 3. P. 035119.

  14. Булярский С.В., Дудин А.А., Орлов А.П., Павлов А.А., Леонтьев В.Л. Вынужденные колебания углеродной нанотрубки с током эмиссии в электромагнитном поле // ЖТФ. 2017. Т. 87. № 11. С. 1624–1627.

  15. Chepurnov A.S., Ionidi V.Y., Kirsanov M.A., Kitsyuk E.P., Klenin A.A., Kubankin A.S., Oleinik A.N., Pavlov A.A., Shchagin A.V. Nanotubes based neutron generator for calibration of neutrino and dark matter detectors // J. Physics: Conference Series. 2017. V. 934. Conf. 1. P. 012013.

  16. Атдаев А., Данилюк А.Л., Лабунов В.А., Прищепа С.Л., Павлов А.А., Басаев А.С., Шаман Ю.П. Взаимодействие электромагнитного излучения с магнитно-функционализированным УНТ-нанокомпозитом в субтерагерцовом диапазоне частот // Известия высших учебных заведений. Электроника. 2015. Т. 20. № 4. С. 357–364.

  17. Kadochkin A.S., Moiseev S.G., Dadoenkova Y.S., Svetukhin V.V., Zolotovskii I.O. Surface plasmon polariton amplification in a single-walled carbon nanotube // Optics Express. 2017. V. 25. № 22. P. 27165–27171.

  18. Wei L., Wang Y.N. Electromagnetic wave propagation in single-wall carbon nanotubes // Phys. Lett. A. 2004. V. 333. № 3–4. P. 303–309.

  19. Moradi A. Surface plasmon-polariton modes of metallic single-walled carbon nanotubes // Photonics and Nanostructures. 2013. V. 11. № 1. P. 85–88.

  20. Moradi A. Theory of Carbon Nanotubes as Optical Nano Waveguides // J. Electromagnetic Analysis & Applications. 2010. V. 2. № 12. P. 672–676.

  21. Martin-Moreno L., Garcia de Abajo F.J., Garcia-Vidal F.J. Ultraefficient Coupling of a Quantum Emitter to the Tunable Guided Plasmons of a Carbon Nanotube // Phys. Rev. Lett. 2015. V. 115. № 17. P. 173601.

  22. Attiya A.M. Lower Frequency Limit of Carbon Nanotube Antenna // Progress in Electromagnetics Research. 2009. V. 94. P. 419–433.

  23. Nakanishi T., Ando T. Optical Response of Finite-Length Carbon Nanotubes // J. the Physical Society of Japan. 2009. V. 78. № 11. P. 114708.

  24. Sasaki K., Murakami Sh., Yamamoto H. Theory of intraband plasmons in doped carbon nanotubes: Rolled surface-plasmons of graphene // Appl. Phys. Lett. 2016. V. 108. № 16. P. 163109.

  25. Miano G., Villone F. An Integral Formulation for the Electrodynamics of Metallic Carbon Nanotubes Based on a Fluid Model // IEEE Transactions on Antennas and Propagation. 2006. V. 54. № 10. P. 2713–2724.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Микроэлектроника

Архивы выпусков Информация о журнале Отправить рукопись в журнал