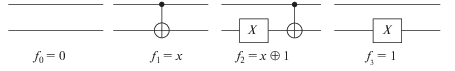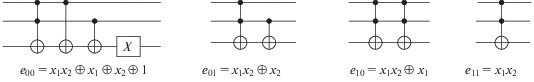Микроэлектроника, 2020, T. 49, № 1, стр. 3-17
О связи булевой алгебры с квантовой информатикой
Ю. И. Богданов a, b, c, *, Н. А. Богданова a, b, Д. В. Фастовец a, b, **, В. Ф. Лукичев a
a Нахимовский проспект, 36, корп. 1
117218 Москва,, Россия
b Национальный исследовательский университет МИЭТ
124498 Зеленоград, Москва, пл. Шокина, 1, Россия
c Национальный исследовательский ядерный университет МИФИ
115409 Москва, Каширское ш., 31, Россия
* E-mail: bogdanov_yurii@inbox.ru
** E-mail: fast93@mail.ru
Поступила в редакцию 14.06.2019
После доработки 25.07.2019
Принята к публикации 25.07.2019
Аннотация
Рассматривается фундаментальная взаимосвязь между квантовой физикой и дискретной математикой. Описан метод представления булевых функций в виде унитарных преобразований. Рассмотрен вопрос о связи полиномов Жегалкина, определяющих алгебраическую нормальную форму булевой функции, с квантовыми схемами. Показано, что квантово-информационный язык предоставляет простой алгоритм построения полинома Жегалкина на основе таблицы истинности. Разработанные методы и алгоритмы обобщены на случай произвольной булевой функции с многобитовой областью определения и многобитовым множеством значений, а также на случай многозначных (k-значных) логик, когда $k = p$-простое число. Разработанный подход имеет существенное значение для реализации квантовых компьютерных технологий и является основой для перехода от классической машинной логики к квантовому аппаратному обеспечению.
1. ВВЕДЕНИЕ
Дискретная математика – важный раздел математики, который исследует свойства различных дискретных объектов: графы [1], булевы функции [2, 3], конечные автоматы и т.д. Методы дискретной математики успешно применяются в различных областях, включая реализацию логических элементов электронных устройств, оптимизацию транспортных путей сообщения, построение бизнес-моделей и т.д.
Свойства булевых функций находят широкое применение в вопросах информационной безопасности [4–6]. Все аппаратно-программные средства, предназначенные для обеспечения безопасности передаваемой информации, должны обладать рядом криптографических свойств. Особенности используемых средств защиты находят свое отражение в булевых математических моделях в виде ряда специфических свойств используемых булевых функций (или систем булевых функций).
В настоящее время все большее внимание исследователей привлекают перспективы применения квантовых методов обработки информации к задачам криптографии [7–12].
Дискретные системы также активно исследуются в рамках квантовой механики и квантовой теории информации. Понятия дискретизации и квантования аналогичны по содержанию. Однако, долгие годы, дискретная математика развивалась без видимой связи с квантовой теорией – истинной наукой о дискретных объектах.
Такой важный объект дискретной математики, как полином Жегалкина [13] находит интересное и важное применение при построении квантовых схем. Оказывается, что множество всех полиномов Жегалкина и набор квантовых схем, состоящих из гейта X и его условных аналогов, связаны посредством инъективного отображения. Другими словами, любому полиному Жегалкина можно поставить в соответствие квантовую схему. Этот факт подробно описан ниже в тексте данной статьи. Важной особенностью является простота построения схемы. Кроме того, нами продемонстрирован эффективный метод построения полинома Жегалкина по таблице истинности исходной функции.
Наличие гейтов X, CNOT, CCNOT и т.д. в схемах, построенных по полиномам Жегалкина, объясняется тем фактом, что в классической логике существуют аналогичные преобразования [14]. Квантовая механика предоставляет, кроме того, ресурсы в виде унитарных операций, которые не только позволяют построить квантовые аналоги классических схем, но и обобщить их, например, введя обратное преобразование, соответствующее булевой функции, а также рассматривая квантовые суперпозиции базисных состояний. Таким образом, квантовые булевы функции являются более совершенными объектами по сравнения с классическими битовыми функциями. Заметим также, что сами квантовые булевы функции являются только подмножеством гораздо более широкого класса квантовых преобразований.
Основная современная инфраструктура информационного сообщества основана на принципах булевой алгебры и методах дискретной математики. Информационные технологии являются основным драйвером мировой экономики, начиная с середины 20-го столетия по сей день. В настоящее время становится все более очевидным, что в ближайшие годы и десятилетия драйвером развития самих информационных технологий должны стать квантовые информационные технологии. Таким образом, необходима интеграция методов дискретной математики и квантовой информатики.
2. ПРЕДСТАВЛЕНИЕ БУЛЕВОЙ ФУНКЦИИ НА ЯЗЫКЕ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ
В теории квантовой информации доказано, что любую булеву функцию $f\left( x \right)$ можно представить в виде квантового преобразования [15, 16]:
Здесь символом $x$ обозначен регистр из $n$ кубитов–регистр области определения булевой функции (еще его называют регистром данных или регистром запроса). Символом$y$ обозначен регистр множества значений, который может быть как однокубитовым, так и многокубитовым. Символ $ \oplus $ означает сложение по модулю 2.
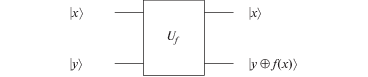
Графическое представление формулы (1) показано на рис. 1. Многокубитовый гейт ${{U}_{f}}$ осуществляет преобразование, задаваемое булевой функцией $f\left( x \right).$
Следует заметить, что, если на вход квантовой схемы подается регистр $\left| y \right\rangle $ в нулевом состоянии, то на выходе мы получим регистр значений, содержащий значения функции $f\left( x \right).$ Данное преобразование представляет собой частный случай (1):
В настоящем разделе мы будем считать что регистр запроса состоит из $n$ кубитов, а регистр значений – из одного кубита. В этом случае матрица, соответствующая гейту ${{U}_{f}},$ будет иметь размер ${{2}^{{n + 1}}} \times {{2}^{{n + 1}}}.$ В разделе 4 мы представим обобщение на булевы функции с многобитовым множеством значений.
Рассмотрим вначале простейший случай – булеву функцию $f\left( x \right)$ с однобитовыми областью определения и множеством значений. Всего существует 4 таких функции, и все они представлены в табл. 1.
В булевой алгебре приняты следующие обозначения: ${{f}_{0}} = 0,$ ${{f}_{3}} = 1$ – постоянные функции, а ${{f}_{1}} = x,$ ${{f}_{2}} = x \oplus 1$ – переменные функции. На основе определения (1) легко построить четыре унитарных матрицы, реализующие квантовые аналоги этих четырех функций:
(2)
${{U}_{0}} = \left( {\begin{array}{*{20}{c}} I&0 \\ 0&I \end{array}} \right),\,\,{{U}_{1}} = \left( {\begin{array}{*{20}{c}} I&0 \\ 0&X \end{array}} \right),\,\,{{U}_{2}} = \left( {\begin{array}{*{20}{c}} X&0 \\ 0&I \end{array}} \right),\,\,{{U}_{3}} = \left( {\begin{array}{*{20}{c}} X&0 \\ 0&X \end{array}} \right),$Аналогичный принцип построения булевых функций сохраняется и для многобитовых булевых функций. При этом матрица преобразования ${{U}_{f}}$ для $n$-битовой булевой функции будет состоять из ${{2}^{n}}$ блоков, каждый из которых есть либо $I$, либо $X$. Сформулируем данный принцип построения в виде общего утверждения:
Утверждение 1 (о блочно-диагональном характере булевых преобразований)
Унитарная матрица, отвечающая булевой функции, имеет блочно-диагональный вид, причем, значениям функции $f\left( x \right) = 0$ соответствует матрица $I$, а значениям функции $f\left( x \right) = 1$ соответствует матрица $X$. Предполагается, что значения аргумента $x$ для $n$-битовой функции упорядочены в порядке возрастания от 0 до ${{2}^{n}} - 1.$
Из булевой алгебры известно, что всего существует ${{2}^{{{{2}^{n}}}}}$ $n$-битовых булевых функций. Этот факт также напрямую следует из Утверждения 1. Следует заметить, что формула (3), введенная для однобитовых функций, также справедлива и для $n$‑битовых функций. Таким образом, формула (3) – есть математическое описание Утверждения 1.
Квантовые преобразования удобно представлять в виде графических схем. Квантовые схемы для четырех рассмотренных выше однобитовых булевых функций представлены на рис. 2.
Функции ${{f}_{0}} = 0$, соответствующей тождественному преобразованию, отвечают просто два “голых” квантовых провода. Функции ${{f}_{3}} = 1$ соответствует действие на нижний кубит (регистр результатов) безусловного оператора отрицания $X$ (NOT). Функции ${{f}_{1}} = x$ отвечает очень важный для квантовых вычислений логический элемент условного отрицания CNOT – так называемое управляемое (условное) – НЕ (Controlled-Not) преобразование. Наконец, функции ${{f}_{2}} = x \oplus 1$ отвечает последовательное действие операторов CNOT и $X$ (NOT).
Сложение (по модулю два) двух булевых функций-столбцов, в соответствии с Утверждением 1, сводится к умножению двух блочно-диагональных унитарных матриц. При этом матричное тождество $I \cdot I = {{I}^{2}} = I$ соответствует булеву тождеству 0 + 0 = 0; матричное соотношение $I \cdot X = X \cdot I = X$ соответствует булеву соотношению 0 + 1 = 1 + 0 = 1; наконец матричное тождество $X \cdot X = {{X}^{2}} = I$ соответствует булеву тождеству 1 + 1 = 0. Здесь и далее в тексте, под знаком суммы мы подразумеваем сложение по модулю 2.
Обозначим область определения $x$ однобитовой булевой функции через одноименный вектор-столбец $x = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right).$ Этот вектор будем рассматривать в качестве базисного вектора ${{e}_{1}}$ двумерного векторного пространства ${{e}_{1}} = x = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right).$ В качестве второго базисного вектора будет выступать вектор-столбец ${{e}_{0}} = x + 1 = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right).$ Булевой функции, соответствующей вектору ${{e}_{0}},$ отвечает полином $1 + x = 1 \cdot {{x}^{0}} + 1 \cdot {{x}^{1}},$ коэффициенты которого образуют вектор-столбец ${{p}_{0}} = \left( {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right).$ Здесь ${{x}^{0}} = \left( {\begin{array}{*{20}{c}} 1 \\ 1 \end{array}} \right),$ ${{x}^{1}} = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)$ – нулевая и первая степени вектора $x = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right).$ А булевой функции, соответствующей вектору ${{e}_{1}},$ отвечает полином $x = 0 \cdot {{x}^{0}} + 1 \cdot {{x}^{1}},$ коэффициенты которого образуют вектор-столбец ${{p}_{1}} = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right).$ Выражение для базисных функций ${{e}_{0}}$ и ${{e}_{1}}$ мы трактуем, прежде всего, как функции-столбцы, отвечающие некоторым полиномам от векторного аргумента $x = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right).$ Само выражение ${{e}_{0}} = x + 1$ можно трактовать, одновременно, и традиционно, как числовую функцию: ${{e}_{0}} = 1$ при $x = 0$ и ${{e}_{0}} = 0$ при $x = 1.$ Удобство векторной записи в том, что она представляет рассматриваемую логическую функцию целиком, как единый объект. Удобство векторов-столбцов ${{p}_{0}}$ и ${{p}_{1}}$ в том, что они представляют в качестве единых объектов коэффициенты рассматриваемых полиномов. Как мы увидим ниже, представленные элементарные соображения для однобитовых логических функций позволят нам легко получать нетривиальные результаты в многобитовом случае, фактически обеспечив автоматизацию соответствующих вычислений.
Базисные векторы-столбцы ${{e}_{0}}$ и ${{e}_{1}},$ объединенные вместе, образуют единичную матрицу
Аналогично, векторы-столбцы ${{p}_{0}}$ и ${{p}_{1}},$ объединенные вместе, образуют следующую матрицу:
Базисные векторы ${{e}_{0}}$ и ${{e}_{1}}$, так же как и векторы-столбцы ${{p}_{0}}$ и ${{p}_{1}}$, введенные нами для описания однобитовых функций, составляют основу и для представления многобитовых функций. Такое рассмотрение мы проведем с использованием полиномов Жегалкина и соответствующих им квантовых схем. Мы увидим, что использование базисных векторов ${{e}_{0}}$ и ${{e}_{1}}$ позволяет нам просто и наглядно выписать полином Жегалкина в аналитическом виде. В свою очередь, использование векторов-столбцов ${{p}_{0}}$ и ${{p}_{1}}$ позволяет очевидным образом автоматизировать весь процесс нахождения коэффициентов полинома Жегалкина, избавив нас от громоздкой процедуры раскрытия скобок и приведения подобных слагаемых.
3. ПРЕДСТАВЛЕНИЕ ПОЛИНОМА ЖЕГАЛКИНА В ВИДЕ КВАНТОВОЙ СХЕМЫ
Перейдем к рассмотрению двухбитовых булевых функций ($n = 2$). Развивая описание на языке вектор-столбцов, логично определить двухбитовые базисные векторы через тензорное произведение однобитовых векторов, например:
С другой стороны ${{e}_{0}} = 1 + {{x}_{1}}$ для первого бита и ${{e}_{0}} = 1 + {{x}_{2}}$ для второго бита, поэтому получаем сразу следующий полином Жегалкина:
Справа мы представили полином Жегалкина в лексикографическом порядке по показателям степени (00, 01, 10, 11).
Используя, введенные ранее, вектор-столбцы коэффициентов получаем тот же результат для коэффициентов полинома Жегалкина:
Таким образом, вектору ${{e}_{{00}}}$ соответствует столбец
в таблице истинности и, одновременно, полином Жегалкина
коэффициенты которого есть
Трехкубитовая квантовая схема, отвечающая данному полиному, представлена на рис. 3 слева. Два верхних кубита отвечают области определения функции, третий кубит – множеству значений. Слагаемому ${{x}_{1}}{{x}_{2}}$ отвечает гейт CCNOT (два верхних кубита управляют нижним); слагаемому ${{x}_{1}}$ отвечает гейт CNOT, в котором верхний кубит управляет нижним; слагаемому ${{x}_{2}}$ отвечает гейт CNOT, в котором средний кубит управляет нижним; наконец слагаемому $1$ отвечает однокубитовый гейт $X$ (NOT), который действует на нижний кубит. Аналогично, для трех оставшихся базисных векторов получаем следующие выражения:
Мы видим, что векторы-столбцы ${{p}_{{00}}},$ ${{p}_{{01}}},$${{p}_{{10}}}$ и ${{p}_{{11}}}$ в точности задают коэффициенты полиномов Жегалкина, которые отвечают базисным двухбитовым функциям ${{e}_{{00}}},$ ${{e}_{{01}}},$ ${{e}_{{10}}}$ и ${{e}_{{11}}}$ соответственно. При этом, столбец ${{p}_{{00}}}$ задает полином ${{e}_{{00}}}$, столбец ${{p}_{{01}}}$ определяет полином ${{e}_{{01}}}$ и т.д. Все рассматриваемые функции представлены графически на рис. 3.
Всего существует 16 двухбитовых булевых функций (табл. 2). Мы описали 4 функции, которые являются базисными. Все остальные 12 функций могут быть представлены как суперпозиции четырех базисных, например:
Таблица 2.
Таблица истинности для 16 возможных двухбитовых булевых функций
| ${{x}_{1}}$ | ${{x}_{2}}$ | ${{e}_{{00}}}$ | ${{e}_{{01}}}$ | ${{e}_{{10}}}$ | ${{e}_{{11}}}$ | ${{e}_{{00}}} + {{e}_{{01}}}$ | ${{e}_{{00}}} + {{e}_{{10}}}$ | ${{e}_{{00}}} + {{e}_{{11}}}$ | ${{e}_{{01}}} + {{e}_{{10}}}$ |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| ${{x}_{1}}$ | ${{x}_{2}}$ | ${{e}_{{01}}} + {{e}_{{11}}}$ | ${{e}_{{10}}} + {{e}_{{11}}}$ | ${{e}_{{00}}} + 1$ | ${{e}_{{01}}} + 1$ | ${{e}_{{10}}} + 1$ | ${{e}_{{11}}} + 1$ | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
Проводя то же самое вычисление на языке $p$-векторов, сразу получаем правильный результат для столбца коэффициентов полинома Жегалкина:
Заметим, что гейт, соответствующий полиному ${{e}_{{00}}} + {{e}_{{01}}} = 1 + {{x}_{1}},$ сводится к действию двухкубитового оператора CNOT (первый кубит управляет третьим) и действию однокубитового гейта $X$ (NOT), который действует на нижний кубит.
Полученные в настоящем разделе результаты можно сформулировать в виде следующих двух утверждений.
Утверждение 2 (алгоритм построения булевой функции в виде полинома Жегалкина)
Произвольная булева функция является суперпозицией базисных функций ${{e}_{{{{j}_{1}}{{j}_{2}}...{{j}_{n}}}}}$ = = ${{e}_{{{{j}_{1}}}}} \otimes {{e}_{{{{j}_{2}}}}} \otimes ... \otimes {{e}_{{{{j}_{n}}}}}.$ Индексу ${{j}_{k}}$ отвечает множитель $\left( {{{x}_{k}} + 1} \right)$ при ${{j}_{k}} = 0$ и множитель ${{x}_{k}}$ при ${{j}_{k}} = 1$. Столбец коэффициентов полинома Жегалкина задается при этом суммой тензорных произведений $p$-столбцов базисных функций ${{p}_{{{{j}_{1}}{{j}_{2}}...{{j}_{n}}}}}$ = ${{p}_{{{{j}_{1}}}}} \otimes {{p}_{{{{j}_{2}}}}} \otimes ... \otimes {{p}_{{{{j}_{n}}}}}$. Индексу ${{j}_{k}}$ отвечает столбец ${{p}_{0}}$ при ${{j}_{k}} = 0$ и столбец ${{p}_{1}}$ при ${{j}_{k}} = 1$.
Утверждение 3 (о преобразовании полиномов Жегалкина в квантовые схемы)
Каждому полиному Жегалкина соответствует некоторая квантовая схема. Слагаемому 1 соответствует оператор $X$, действующий на кубит результатов $y$; слагаемому ${{x}_{{{{j}_{k}}}}}$отвечает оператор CNOT с соответствующим управляющим кубитом; произведению из $m$ булевых аргументов ${{x}_{{{{j}_{1}}}}}{{x}_{{{{j}_{2}}}}}...{{x}_{{{{j}_{m}}}}}$ отвечает соответствующий оператор C(m)NOT, где $m = 1,...,n,$ $n$ – число битов в области определения.
Из Утверждения 3 следует, что каждому слагаемому в полиноме Жегалкина сопоставляется некоторый гейт (вентиль). Перечислим все возможные вентили такого рода. Имеется $C_{n}^{0} = 1$ гейт X, действующий непосредственно на кубит результатов, имеется $C_{n}^{1} = n$ различных гейтов $CNOT,$ $C_{n}^{2}$ гейтов ${{C}^{{(2)}}}NOT$ и т.д. Таким образом, полный набор базовых вентилей содержит $\sum\nolimits_{k = 0}^n {C_{n}^{k}} = {{2}^{n}}$ элементов. Каждый из элементов-вентилей может либо входить, либо не входить в квантовую схему, следовательно всего имеется ${{2}^{{{{2}^{n}}}}}$ различных булевых квантовых схем в полном соответствии с числом возможных булевых функций.
4. БУЛЕВЫ ФУНКЦИИ С МНОГОБИТОВЫМ МНОЖЕСТВОМ ЗНАЧЕНИЙ
До сих пор мы предполагали, что регистр множества значений $y$ содержит только один кубит. Рассмотрение можно легко обобщить на произвольный случай, когда регистр множества значений $y$ содержит произвольное число $m$ кубитов.
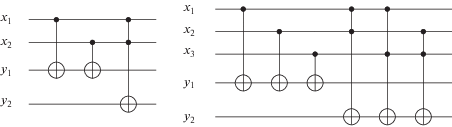
В качестве примеров таких более сложных логических элементов (гейтов) рассмотрим полусумматор (half-adder) и сумматор (adder). Рассматриваемые элементы используются для реализации устройств, производящих операцию сложения. Оба гейта имеют двухкубитовый регистр множества значений ($m = 2$); при этом область определения полусумматора имеет два кубита ($n = 2$), а область определения сумматора содержит три кубита ($n = 3$).
Состояние кубитов ${{y}_{1}}$ и ${{y}_{2}}$ множества значений полусумматора в зависимости от состояния кубитов ${{x}_{1}}$ и ${{x}_{2}}$ области определения задается следующими соотношениями:
Для сумматора аналогичные соотношения имеют вид:
На рис. 4 представлены квантовые схемы полусумматора и сумматора.
Утверждение 1 о блочно-диагональном характере булевых преобразований может быть обобщено на случай многобитового множества значений. Как было показано выше, в случае однобитового множества значений в качестве блочных матриц выступают следующие две матрицы размерности $2 \times 2$: ${{u}_{0}} = I,$ ${{u}_{1}} = X.$ В общем случае m‑битового множества значений, в качестве блочных матриц будут выступать уже матрицы размерности ${{2}^{m}} \times {{2}^{m}}.$ Например, в случае двухбитового множества значений в качестве блочных матриц выступают следующие четыре матрицы размерности $4 \times 4$:
Здесь нижние индексы матриц идентифицируют значения битов множества значений булевой функции. Сказанное делает очевидным построение блочных матриц и в более сложных случаях.
Представленные выше рассуждения совместно со знанием таблиц истинности (табл. 3, 4) позволяют легко построить унитарные матрицы преобразований для произвольных булевых функций с n-битовой областью определения и m-битовым множеством значений.
Таблица 3.
Таблица истинности для полусумматора
| ${{x}_{1}}$ | ${{x}_{2}}$ | ${{y}_{1}} = {{x}_{1}} + {{x}_{2}}$ | ${{y}_{2}} = {{x}_{1}}{{x}_{2}}$ |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Таблица 4.
Таблица истинности для сумматора
| ${{x}_{1}}$ | ${{x}_{2}}$ | ${{x}_{3}}$ | ${{y}_{1}} = {{x}_{1}} + {{x}_{2}} + {{x}_{3}}$ | ${{y}_{2}} = {{x}_{1}}{{x}_{2}} + {{x}_{1}}{{x}_{3}} + {{x}_{2}}{{x}_{3}}$ |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
В общем случае булевой функции с n-битовой областью определения и m-битовым множеством значений унитарная матрица преобразования ${{U}_{f}}$ действует на состояния регистра из $n + m$ кубит и имеет размерность соответственно ${{2}^{{n + m}}} \times {{2}^{{n + m}}}.$
Представленное выше Утверждение 1 можно обобщить следующим образом.
Утверждение 1А (о блочно-диагональном характере булевых преобразований с n-битовой областью определения и m-битовым множеством значений)
Унитарная матрица, отвечающая булевой функции, имеет блочно-диагональный вид, причем значениям функции $f\left( x \right) = {{j}_{1}}...{{j}_{m}}$ соответствует матрица ${{u}_{{{{j}_{1}}...{{j}_{m}}}}} = {{u}_{{{{j}_{1}}}}} \otimes ... \otimes {{u}_{{{{j}_{m}}}}},$ где ${{u}_{0}} = I,$ ${{u}_{1}} = X.$ Предполагается, как и раньше, что значения аргумента $x$ для n-битовой области определения упорядочены в порядке возрастания от 0 до ${{2}^{n}} - 1.$
Заметим также, что в случае, когда регистр множества значений $y$ содержит произвольное число m кубитов, в таблице истинности возникает m булевых столбцов значений функции. К каждому такому столбцу непосредственно применимы Утверждения 2 и 3. Это свойство уже фактически было использовано нами в изображениях квантовых схем для полусумматора и сумматора.
Для Утверждения 1А можно получить аналог формулы (3). Если булева функция имеет m-битовую область значений (${{y}_{1}},{{y}_{2}},...,{{y}_{m}}$), то легко видеть, что итоговое квантовое преобразование ${{U}_{f}}$ основано на преобразованиях, полученных из составляющих исходной функции ${{U}_{{{{y}_{1}}}}},{{U}_{{{{y}_{2}}}}},...,{{U}_{{{{y}_{m}}}}}.$ Первые элементы тензорных произведений на главной диагонали матрицы ${{U}_{f}}$ представляют собой диагональ матрицы ${{U}_{{{{y}_{1}}}}},$ вторые элементы в тензорном произведении – диагональ матрицы ${{U}_{{{{y}_{2}}}}}$ и т.д. Данный факт может быть описан математически следующим образом:
где $A * B = {{\left( {{{A}_{{ij}}} \otimes {{B}_{{ij}}}} \right)}_{{ij}}}$ – операция умножения Хатри-Рао [17], которая по сути является поэлементным тензорным умножение для блочных матриц. То есть формула (4) является произведением (в смысле Хатри-Рао) формул (3) для каждой из функций ${{y}_{1}},{{y}_{2}},...,{{y}_{m}}.$ Следовательно, формула (4) может быть переписана в следующем виде:Проведя несложные вычисления, получим итоговую формулу:
Или в более сокращенном виде:
(5)
${{U}_{f}} = \operatorname{diag} \left( {\sum\limits_{{{i}_{1}},{{i}_{2}},...,{{i}_{m}} = 0}^1 {\prod\limits_{j = 1}^m {\left( {{{i}_{j}} \cdot {{y}_{j}} + {{{\bar {i}}}_{j}} \cdot {{{\bar {y}}}_{j}}} \right) \cdot \mathop \otimes \limits_{j = 1}^m {{X}^{{{{i}_{j}}}}}} } } \right).$В случае если мы имеем дело с однобитовой функцией ($m = 1$), данная формула сводится к формуле (3).
5. ОБОБЩЕНИЕ НА СЛУЧАЙ МНОГОЗНАЧНОЙ ЛОГИКИ
Перед рассмотрением общего случая многозначной логики, подробно рассмотрим трехзначную логику. Вместо битов/кубитов используются триты/кутриты. Если мы рассматриваем функции с n-тритной областью определения, то всего можно составить ${{3}^{{{{3}^{n}}}}}$ различных функции.
В случае битовых функций мы имели дело с операцией инвертирования. Для функций многозначной логики вводятся операции сдвига. Для трехзначной логики – операции сдвига соответственно на 0, 1 и 2 представляются в виде матриц:
Матрица ${{T}_{1}}$ обеспечивает сдвиг на 1
В обозначениях Дирака эти переходы можно записать следующим образом:
Аналогично, матрица ${{T}_{2}}$ обеспечивает сдвиг на 2
В этом случае имеем:
Нетрудно проверить справедливость следующих тождеств:
Можно заметить, что действие оператора ${{T}_{1}}$ оказывается аналогичным повороту плоскости на 120 градусов. Три таких поворота, осуществленные последовательно, приводят к тождественному преобразованию.
Оказывается, что такое наглядное качественное геометрическое представление можно строго формализовать. Введем для этого посредством матричной экспоненты следующее унитарное преобразование: $T = \exp \left( { - iS\theta } \right).$ Здесь $\theta $ – угол поворота, а $S$ – эрмитов оператор, который нужно подобрать таким образом, чтобы при $\theta = \frac{{2\pi }}{3}$ (120 градусов) преобразование превращалось в ${{T}_{1}}$, поэтому:
Вычисление главного матричного логарифма от ${{T}_{1}}$ приводит к следующему результату для оператора $S$:
Замечательно, что полученная в результате матрица $S$ есть эрмитов оператор, задающий проекцию спина 1 на некоторое выделенное направление. Путем явного вычисления матричной экспоненты $T = \exp \left( { - iS\theta } \right)$ можно показать, что для угла поворота в 120 градусов $\left( {\theta = \frac{{2\pi }}{3}} \right)$ действительно получаем оператор ${{T}_{1}}$ :
Аналогично, для угла поворота в 240 градусов получаем оператор ${{T}_{2}}$, а для углов в 0 и 360 градусов – тождественное преобразование.
Собственные значения оператора $S$ есть m = = –1,0,1. Эти числа соответствуют возможным значениям проекции спина и, таким образом, нумеруют возможные состояния, в которых может находиться частица со спином 1 (в нашем случае- это трехуровневый логический элемент). Традиционный номер логического состояния отличается от спиновой проекции на единицу: $x = m + 1 = 0,1,2.$
Заметим наконец, что представленная матричная экспонента имеет смысл для произвольного угла поворота $\theta $. В этом общем случае, в результате преобразования, система оказывается в суперпозиции всех трех базисных состояний. Пусть, например, система первоначально находилась в состоянии $\left| 0 \right\rangle .$ Рассмотрим преобразование, отвечающее углу $\theta = \frac{\pi }{3}$ (60 градусов). Это преобразование условно можно назвать “сдвигом на 1/2”, поскольку отвечает половине от угла, задающего сдвиг на 1. Можно показать, что в результате данного преобразования возникнет следующее состояние, которое является суперпозицией всех трех возможных состояний:
Полученные коэффициенты разложения задают амплитуды вероятности. Понятно, что рассматриваемый общий случай преобразования соответствует переходу от традиционной классической дискретной математики к квантовой информатике.
Зная таблицу истинности для заданной функции, можно легко построить ее унитарное представление, которое, как и в случае обычной двоичной логики, будет блочно-диагональным (только теперь элементарные блоки – это матрицы $3 \times 3$).
Утверждение 1Б (о блочно-диагональном характере булевых преобразований в приложении к троичной логике)
Унитарная матрица, отвечающая булевой функции, имеет блочно-диагональный вид, причем значениям функции $f\left( x \right) = 0$ соответствует матрица ${{T}_{0}} = I,$ значениям функции $f\left( x \right) = 1$ соответствует матрица ${{T}_{1}}$, а значениям функции $f\left( x \right) = 2$ соответствует матрица ${{T}_{2}}$. Предполагается, что значения аргумента $x$ для функции от $n$ аргументов упорядочены в порядке возрастания от 0 до ${{3}^{n}} - 1.$
Для данного утверждения легко построить формулу, аналогичную формуле (3) для Утверждения 1:
(6)
${{U}_{f}} = \operatorname{diag} \left( {{{m}_{0}}(f) \cdot {{T}_{0}} + {{m}_{1}}(f) \cdot {{T}_{1}} + {{m}_{2}}(f) \cdot {{T}_{2}}} \right),$Для формирования базисных функций следует рассмотреть степени вектора $x$ от 0 до 2 (рассматриваем арифметические операции по модулю 3).
Векторы-столбцы ${{x}^{0}},$ ${{x}^{1}}$и ${{x}^{2}}$ объединим в единую матрицу:
Стандартные базисные функции можно представить в виде суперпозиции столбцов ${{x}^{0}},$ ${{x}^{1}}$и ${{x}^{2}}$:
В полной аналогией с рассмотренной выше двузначной логикой, введем векторы-столбцы ${{p}_{0}},$ ${{p}_{1}}$ и ${{p}_{2}},$ содержащие коэффициенты полиномов Жегалкина для функций ${{e}_{0}},$ ${{e}_{1}}$ и ${{e}_{2}}$ соответственно.
Объединим рассматриваемые столбцы в единую матрицу:
Рассматриваемая матрица $P$ является обратной по отношению к матрице Q, т.е. $QP = PQ = I$ (результат матричного умножения рассматривается по модулю 3). Это условие справедливо и для двухзначной логики (в этом случае матрицы $P$ и $Q$ совпадают).
Теперь перейдем к общему случаю – рассмотрим k-значную логику. В этом случае, для формирования базисных функций следует рассмотреть степени вектор а$x$ от 0 до $k - 1.$ Соответствующий набор будет полным в том и только том случае, когда $k = p$ – простое число [2]. В остальном, рассмотрение аналогично представленному выше случаю $k = 3.$
В k-значной логике рассматриваются функции от произвольного числа переменных ($n$) с количеством логических уровней k, где $k$ – простое число. Пусть логическая функция $f$представляет собой столбец из ${{k}^{n}}$ чисел, заданных в лексикографическом порядке. При этом каждое из ${{k}^{n}}$ логических значений функции есть целое число от 0 до $k - 1.$
Пусть столбец логических значений есть
На основе степеней $x$ от 0 до $k - 1$ строится матрица $Q$ размерности $k \times k$: $Q = \left[ {\begin{array}{*{20}{c}} {{{x}^{0}}}&{...}&{{{x}^{{k - 1}}}} \end{array}} \right].$ Для матрицы $Q$ строится обратная к ней матрица $P$. Таким образом, при вычислениях по модулю $k$, справедливо тождество: $QP = PQ = I$ (результат матричного умножения рассматривается по модулю k). При нахождении коэффициентов полинома Жегалкина ключевую роль играют столбцы матрицы $P$: $P = \left[ {\begin{array}{*{20}{c}} {{{p}_{0}}}&{...}&{{{p}_{{k - 1}}}} \end{array}} \right].$ Заметим, что для того, чтобы матрица $Q$ была неособенной и соответственно существовала обратная матрица, необходимо и достаточно, чтобы число k, определяющее размерность логики, было простым.
Утверждение 1 в общем случае (о блочно-диагональном характере булевых преобразований в приложении к k-уровневой логике)
Унитарная матрица, отвечающая булевой функции, имеет блочно-диагональный вид, причем значениям функции $f\left( x \right) = 0$ соответствует матрица ${{T}_{0}} = I,$ значениям функции $f\left( x \right) = 1$ соответствует матрица ${{T}_{1}}$, значениям функции $f\left( x \right) = 2$ соответствует матрица ${{T}_{2}}$ и т.д., где ${{T}_{i}}$ – описанный выше оператор сдвига на $i$. Предполагается, что значения аргумента $x$ для функции от $n$ аргументов упорядочены в порядке возрастания от 0 до ${{k}^{n}} - 1.$
Математически данное утверждение выглядит следующим образом (по аналогии с (6)):
(7)
${{U}_{f}} = \operatorname{diag} \left( {\sum\limits_{i = 0}^{k - 1} {{{m}_{i}}(f) \cdot {{T}_{i}}} } \right).$Утверждение 2 в общем случае (алгоритм построения булевой функции в виде полинома Жегалкина)
Столбец $a$ размерности ${{k}^{n}},$ определяющий коэффициенты полинома Жегалкина, задается суммой тензорных произведений $p$-столбцов ${{p}_{{{{j}_{1}}{{j}_{2}}...{{j}_{n}}}}} = {{p}_{{{{j}_{1}}}}} \otimes {{p}_{{{{j}_{2}}}}} \otimes ... \otimes {{p}_{{{{j}_{n}}}}}$ по всем строкам таблицы истинности с весами, равными значениям логической функции $f$ в рассматриваемых строках. Логическому индексу ${{j}_{m}}$ (${{j}_{m}} = 0,1,..,k - 1$) отвечает столбец ${{p}_{{{{j}_{m}}}}}$, т.е. получаем столбец ${{p}_{0}}$ при ${{j}_{m}} = 0$, ${{p}_{1}}$ при ${{j}_{m}} = 1$, …, ${{p}_{{k - 1}}}$ при ${{j}_{m}} = k - 1.$
Возникающий в результате столбец a, определяющий коэффициенты полинома Жегалкина, также оказывается представленным в лексикографическом порядке в отношении показателей степени переменных ${{x}_{1}},...,{{x}_{n}}.$
Представленное Утверждение 2 задает алгоритм преобразования столбца логической функции f в столбец a коэффициентов полинома Жегалкина. При этом используются столбцы матрицы P, а в качестве весов фигурируют значения логической функции f.
Можно показать, что обратному преобразованию, которое осуществляет переход от столбца a коэффициентов полинома Жегалкина к значениям логической функции f, соответствует использование столбцов матрицы $Q$ совместно с элементами столбца a в качестве весов. Последовательное применение рассматриваемых преобразований (прямого и обратного) приводит к тождественному преобразованию.
Таким образом, между функциями-столбцами f и $a$ имеет место дуализм – своеобразное отношение двойственности, которое можно представить в следующем символьном виде:
Либо:
Будем говорить, что первое из представленных выражений задает $P$ – преобразование, второе – $Q$-преобразование. $P$ – преобразование позволяет найти столбец коэффициентов полинома Жегалкина $a$ по известной булевой функции $f$. $Q$-преобразование, напротив, позволяет найти булеву функцию $f$ по известному столбцу коэффициентов полинома Жегалкина $a$.
В случае обычной двухуровневой логики $P = Q,$ поэтому
В этом случае в результате многократного применения $Q$-преобразования столбцы $f$ и $a$ поочередно переходят друг в друга. Таким образом, в случае двухуровневой логики столбец истинности $f$ сам может рассматриваться как столбец коэффициентов полинома Жегалкина для функции $a$.
Представленные здесь методы и алгоритмы были апробированы нами для логик с размерностями, задаваемыми следующими простыми числами: $k = 2,3,5,7,11,13,17,19,23$ и $29$. Соответствующие им матрицы $P$ представлены в приложении. Программный код на языке Matlab для расчета этих матриц может быть найден на репозитории https://github.com/PQCLab/DiscreteMath.
6. ВЫВОДЫ
Представленные методы и алгоритмы наглядно демонстрируют глубокую связь между классической дискретной математикой и квантовой информатикой. Разработанные нами методы и алгоритмы позволяют рассмотреть унитарные квантовые представления для произвольных булевых функции с многобитовыми областями определения и многобитовыми множествами значений. Подробно описана связь полиномов Жегалкина и схем квантовой логики. Выполнено обобщение разработанной теории на случай многозначных ($k$-значных) логик, когда $k = p$-простое число
Разработанные методы и алгоритмы имеют существенное значение для перехода от классической машинной логики к квантовым компьютерам. Автоматизация построения квантовых схем является важной проблемой при реализации полноценных квантовых вычислительных устройств. Наш подход, позволяет существенно упростить эту процедуру для квантовых преобразований, основанных на использовании классических булевых функций.
Список литературы
Панюкова Т.А. Комбинаторика и теория графов. М.: Ленанд. 2014, 216 с.
Яблонский С.В. Введение в дискретную математику. М.: Высшая школа, 2003. 386 с.
Зарипова Э.Р., Кокотчикова М.Г., Севастьянов Л.А. Дискретная математика. Часть II. Математическая логика // М.: РУДН. 2013.
Зуев Ю.А. По океану дискретной математики. От перечислительной комбинаторики до современной криптографии. В 2 томах. Т. 2. Графы. Алгоритмы. Коды, блок-схемы, шифры. М.: Либроком. 2012, 370 с.
Гордеев Э.Н., Леонтьев В.К., Медведев Н.В. О свойствах булевых полиномов, актуальных для криптосистем // Вопросы кибербезопасности. 2017. № 3(21). С. 63–69.
Токарева Н.Н. Симметричная криптография. Краткий курс: учебное пособие. Новосибирск. Новосиб. гос. ун-т. 2012, 234 с.
Quantum Computing: Progress and Prospects. 2019 Edition. Washington DC, National Academies of Sciences, Engineering, and Medicine. The National Academies Press.
Panjin Kim, Daewan Han, Kyung Chul Jeong Time–space complexity of quantum search algorithms in symmetric cryptanalysis: applying to AES and SHA-2 // Quantum Information Processing. 2018. 17:339.
Markus Grassl, Brandon Langenberg, Martin Roetteler, Rainer Steinwandt. Applying Grover’s Algorithm to AES: Quantum Resource Estimates // PQCrypto 2016: Post-Quantum Cryptography. 2016. P. 29–43.
Денисенко Д.В., Никитенкова М.В. Применение квантового алгоритма Гровера в задаче поиска ключа блочного шифра SDES // ЖЭТФ. 2019. Т. 155. № 1. С. 32.
Денисенко Д.В., Маршалко Г.Б., Никитенкова М.В., Рудской В.И., Шишкин В.А. Оценка сложности реализации алгоритма Гровера для перебора ключей алгоритмов блочного шифрования ГОСТ Р 34.12-2015 // ЖЭТФ. 2019. Т. 155. № 4. С. 645.
Денисенко Д.В. О реализации подстановок в виде квантовых схем без использования дополнительных кубитов // ЖЭТФ. 2019. Т. 155. № 6. С. 999.
Жегалкин И.И. О технике вычислений предложений в символической логике // Матем. сб. 1927. Т. 34. № 1. С. 9–28.
Новиков Ф. А. Дискретная математика для программистов // Издательство: Питер. 2008, 384 с.
Нильсен М., Чанг И. Квантовые вычисления и квантовая информация // М.: Мир. 2006, 824 с.
Валиев К. А., Кокин А.А. Квантовые компьютеры: надежда и реальность // Ижевск: НИЦ “Регулярная и хаотическая динамика”. 2001, 352 с.
Liu S., Trenkler G. Hadamard, Khatri-Rao, Kronecker and other matrix products // International Journal of Information and Systems Sciences. 2007. V. 4. № 1. P. 160–177.
Дополнительные материалы отсутствуют.
Инструменты
Микроэлектроника