Микроэлектроника, 2020, T. 49, № 2, стр. 83-100
Квантовый чип с оптимизированной туннельной структурой для измерения зарядового кубита на двойной квантовой точке
А. В. Цуканов a, *, И. Ю. Катеев a, **
a Физико-технологический институт им. К.А. Валиева Российской АН
117218 Москва, Нахимовский просп., 34, корп. 1, Россия
* E-mail: tsukanov@ftian.ru
** E-mail: ikateyev@mail.ru
Поступила в редакцию 16.10.2019
После доработки 16.10.2019
Принята к публикации 21.10.2019
Аннотация
Предложена схема измерительного чипа для определения произвольного чистого состояния зарядового кубита. Сила тока, протекающего через одноэлектронный транзистор в стационарном режиме, зависит от состояния кубита. Для повышения чувствительности транзистора его рабочая часть формируется из трех квантовых точек, энергетические уровни которых образуют симметричную конфигурацию. Параметры системы рассчитываются в рамках микроскопической модели двумерных квантовых точек. Получены зависимости заселенностей состояний структуры от времени, а также определены сила тока, чувствительность и измерительный контраст как функции геометрических параметров системы. Изучено влияние диссипативных процессов, связанных с акустическими фононами, на процесс измерения и рассчитаны скорости релаксации и дефазировки электрона в двухуровневой системе.
1. ВВЕДЕНИЕ
В квантовой информатике особый интерес вызывают наноструктуры, сформированные на основе квантовых точек (КТ) [1]. В частности, структура, состоящая из двух КТ (ДКТ) и содержащая один электрон, неоднократно предлагалась в качестве твердотельного масштабируемого зарядового кубита [2, 3]. Орбитальные состояния электрона, локализованные в разных КТ, служат в качестве логических состояний такого кубита. Возможность надежного измерения состояний кубитов является одним из ключевых требований к выполнению квантовых алгоритмов. Как правило, измерение состояния зарядового кубита производится с помощью одноэлектронного транзистора (ОЭТ) – квантового детектора, работающего в режиме кулоновской блокады [4]. Поле, создаваемое электроном кубита, смещает энергию транспортного уровня КТ за счет эффекта Штарка. При этом величина тока через ОЭТ будет зависеть от пространственного положения электрона в ДКТ. Следовательно, измеряя ток через детектор, можно определить, в каком состоянии находится кубит.
В нашей работе рассматривается новый подход к дизайну ОЭТ с целью улучшения его измерительных свойств. Мы предлагаем заменить одиночную КТ линейной структурой – “молекулой” из трех туннельно-связанных одноуровневых КТ. Как будет показано, в этом случае ток оказывается более чувствительным к изменению электрического поля, связанного с перемещением электрона внутри кубита. Для этого следует использовать режим нерезонансного туннелирования, смещая энергию уровня в центральной КТ на величину, существенно превышающую энергию туннелирования, при соблюдении равенства энергий уровней в крайних КТ.
В качестве конкретного примера рассматривается чип с планарной архитектурой на основе КТ, формируемых затворами в двумерном электронном газе. Именно на таких системах в 2003–2005 гг. впервые был продемонстрирован принцип измерения зарядового кубита [5–7]. Используя экспоненциально-степенное приближение для формы электростатического потенциала двумерной КТ, мы вычислили энергию ее основного состояния, а также энергии туннелирования и кулоновского взаимодействия электронов, находящихся в ОЭТ и кубите. Скорости диссипативных процессов, связанных с фононами, также были найдены в рамках данной модели. С помощью численного моделирования динамики электронов получены зависимости заселенностей состояний КТ от времени. Показано, что ток через ОЭТ в стационарном режиме демонстрирует устойчивость по отношению к флуктуациям некоторых величин (размеров и ориентации КТ), которые обычно приводят к нарушению электронного когерентного транспорта в замкнутой структуре. Оптимизация измерительных свойств ОЭТ (чувствительности, контраста, силы тока) возможна по каждому из параметров системы. Электронная релаксация и в особенности дефазировка начинает заметно влиять на протекание тока, если их характерные времена оказываются порядка сотен пикосекунд и меньше.
2. ДИССИПАТИВНЫЙ ТРАНСПОРТ ЭЛЕКТРОНОВ, ВЗАИМОДЕЙСТВУЮЩИХ С КУБИТОМ, ЧЕРЕЗ ОЭТ
Мы используем модель зарядового кубита на основе одноэлектронной ДКТ, состоящей из двух КТ A и B, которые для простоты будем считать одинаковыми [2]. Будем предполагать наличие двух основных орбитальных состояний электрона, $\left| A \right\rangle $ и $\left| B \right\rangle ,$ с волновыми функциями ${{\psi }_{A}}\left( {\mathbf{r}} \right) = \left\langle {{\mathbf{r}}} \mathrel{\left | {\vphantom {{\mathbf{r}} A}} \right. \kern-0em} {A} \right\rangle $ и ${{\psi }_{B}}\left( {\mathbf{r}} \right) = \left\langle {{\mathbf{r}}} \mathrel{\left | {\vphantom {{\mathbf{r}} B}} \right. \kern-0em} {B} \right\rangle ,$ локализованными в КТ A и КТ B, соответственно. Если энергия размерного квантования электрона в изолированной КТ существенно больше, чем матричный элемент туннелирования V0 между основными состояниями соседних КТ, то можно воспользоваться приближением сильной связи для гамильтониана электрона, находящегося в одном из этих состояний (или же в их суперпозиции):
(1)
${{H}_{{{\text{qubit}}}}} = {{\varepsilon }_{A}}\left( t \right)\left| A \right\rangle \left\langle A \right| + {{\varepsilon }_{B}}\left( t \right)\left| B \right\rangle \left\langle B \right| - {{V}_{0}}\left( t \right)\left( {\left| A \right\rangle \left\langle B \right| + \left| B \right\rangle \left\langle A \right|} \right),$${{\varepsilon }_{A}}$ и ${{\varepsilon }_{B}}$ – энергии основных состояний $\left| A \right\rangle $ и $\left| B \right\rangle $ изолированных КТ. Выберем в качестве логических состояний “нуль” и “единица” кубита основные состояния $\left| A \right\rangle $ и $\left| B \right\rangle $ электрона в КТ A и КТ B, соответственно. Вектор состояния электрона $\left| {\Psi \left( t \right)} \right\rangle $ в момент времени t может быть представлен в виде разложения по состояниям $\left| A \right\rangle $ и $\left| B \right\rangle $:
(2)
$\left| {\Psi \left( t \right)} \right\rangle = {{c}_{A}}\left( t \right)\left| A \right\rangle + {{c}_{B}}\left( t \right)\left| B \right\rangle .$Квантовые операции, приводящие к требуемому набору амплитуд вероятности, реализуются посредством внешних электрических полей, которые влияют на параметры гамильтониана (1). Измерение кубита производится при выключенном управляющем поле, когда ${{\varepsilon }_{{A,B}}} = {\text{const}}$ и ${{V}_{0}} = 0.$
Рассмотрим квазиодномерную наноструктуру ОЭТ, состоящую из двух металлических контактов, которые представляют собой электронные резервуары (источник S и сток D), и цепочки из трех КТ (L, C и R). Благодаря конфигурации уровней Ферми εS(D) контактов и уровней КТ, показанной на рис. 1, возможно движение электронов через структуру слева направо. Для описания процесса попадания электрона из источника в левую КТ L и из правой КТ R в сток мы воспользуемся реалистичной и общепринятой моделью некогерентного (одностороннего) туннелирования [8]. Внутри наноструктуры электрон туннелирует между КТ когерентным образом. Будем предполагать наличие связанных состояний $\left| L \right\rangle $ в левой КТ, $\left| R \right\rangle $ в правой КТ, и $\left| C \right\rangle $ в центральной КТ, с энергиями ${{\varepsilon }_{L}},$ ${{\varepsilon }_{R}},$ и ${{\varepsilon }_{C}},$ соответственно. Удобно ввести разности энергий (отстройки) основных состояний в крайних КТ и в центральной КТ, ${{\delta }_{L}} = {{\varepsilon }_{L}} - {{\varepsilon }_{C}}$ и ${{\delta }_{R}} = {{\varepsilon }_{R}} - {{\varepsilon }_{C}}.$ Они задаются формой и химическим составом КТ в ходе формирования структуры и могут контролироваться с помощью внешних полей управляющих затворов [4, 5]. Состояния $\left| {L(R)} \right\rangle $ и $\left| C \right\rangle $ связаны между собой за счет одноэлектронного туннелирования с энергией ${{V}_{{L(R)}}}.$ Для неглубоких КТ инжекция второго электрона приводит к выталкиванию уровня в непрерывный спектр и, как следствие, к прекращению электронного транспорта. Поэтому при рассмотрении двухчастичных эффектов мы ограничимся зарядовыми конфигурациями, в которых электроны занимают уровни в разных КТ. Обозначим энергию кулоновского взаимодействия двух электронов в состоянии $\left| {j,k} \right\rangle $ ОЭТ ${{U}_{{j,k}}},$ где $j,k = L,C,R.$ Гамильтониан линейной структуры из трех КТ имеет вид
где(4)
${{H}_{0}} = {{\varepsilon }_{L}}\left| L \right\rangle \left\langle L \right| + {{\varepsilon }_{R}}\left| R \right\rangle \left\langle R \right| + {{\varepsilon }_{C}}\left| C \right\rangle \left\langle C \right|,$(5)
${{H}_{V}} = - {{V}_{L}}\left( {\left| C \right\rangle \left\langle L \right| + \left| L \right\rangle \left\langle C \right|} \right) - {{V}_{R}}\left( {\left| C \right\rangle \left\langle R \right| + \left| R \right\rangle \left\langle C \right|} \right),$(6)
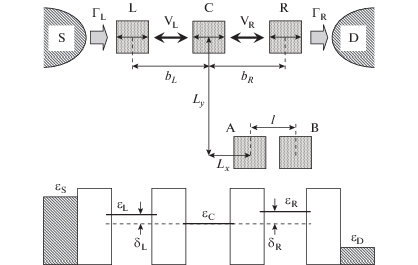
${{H}_{{{\text{coul}}}}} = {{U}_{{L,R}}}\left| {L,R} \right\rangle \left\langle {L,R} \right| + {{U}_{{L,C}}}\left| {L,C} \right\rangle \left\langle {L,C} \right| + {{U}_{{R,C}}}\left| {R,C} \right\rangle \left\langle {R,C} \right|.$Рис. 1.
Вверху: принципиальная схема измерительного устройства, состоящего из ДКТ (зарядовый кубит) и ОЭТ с центральной частью, представленной тремя туннельно-связанными КТ. Внизу: потенциальный профиль ОЭТ и энергетические уровни КТ. Пунктиром отмечено положение энергии состояния $\left| C \right\rangle $ в центральной КТ.
Выбирая за начало отсчета энергию ${{\varepsilon }_{C}}$ состояния $\left| C \right\rangle ,$ можно переписать гамильтониан (4) в виде: ${{H}_{0}} = {{\delta }_{L}}\left| L \right\rangle \left\langle L \right| + {{\delta }_{R}}\left| R \right\rangle \left\langle R \right|.$ Кулоновское взаимодействие электрона зарядового кубита и электронов, туннелирующих через ОЭТ, приводит к сдвигам энергий состояний системы:
(7)
$\begin{gathered} {{H}_{{{\text{qubit}} - {\text{SET}}}}} = {{W}_{{A,L}}}\left| {A,L} \right\rangle \left\langle {A,L} \right| + {{W}_{{A,C}}}\left| {A,C} \right\rangle \left\langle {A,C} \right| + {{W}_{{A,R}}}\left| {A,R} \right\rangle \left\langle {A,R} \right| + \\ + \,\,{{W}_{{B,L}}}\left| {B,L} \right\rangle \left\langle {B,L} \right| + {{W}_{{B,C}}}\left| {B,C} \right\rangle \left\langle {B,C} \right| + {{W}_{{B,R}}}\left| {B,R} \right\rangle \left\langle {B,R} \right|, \\ \end{gathered} $Чтобы изучить эволюцию состояния нашей системы, представленной матрицей плотности ρ, мы воспользуемся уравнением Линдблада, которое включает в себя диссипативные компоненты:
(8)
$\begin{gathered} \frac{{d\rho }}{{dt}} = - i\left[ {{{H}_{{{\text{qubit}}}}} + {{H}_{{{\text{SET}}}}} + {{H}_{{{\text{qubit}} - {\text{SET}}}}},\rho } \right] + {{\Gamma }_{L}}D\left( {\left| L \right\rangle \left\langle {va{{c}_{L}}} \right|} \right) + {{\Gamma }_{R}}D\left( {\left| {va{{c}_{R}}} \right\rangle \left\langle R \right|} \right) + \\ + \,\,{{\gamma }_{{{\text{rel}},L}}}D\left( {\left| C \right\rangle \left\langle L \right|} \right) + {{\gamma }_{{{\text{rel}},R}}}D\left( {\left| C \right\rangle \left\langle R \right|} \right) + {{\gamma }_{{{\text{deph}},L}}}D\left( {\left| L \right\rangle \left\langle L \right| - \left| C \right\rangle \left\langle C \right|} \right) + \\ + \,\,{{\gamma }_{{{\text{deph}},R}}}D\left( {\left| R \right\rangle \left\langle R \right| - \left| C \right\rangle \left\langle C \right|} \right) + {{\gamma }_{{{\text{deph}},q}}}D\left( {\left| A \right\rangle \left\langle A \right| - \left| B \right\rangle \left\langle B \right|} \right). \\ \end{gathered} $Такой подход дает возможность рассматривать открытую структуру в токовом режиме. Электроны попадают в левую КТ из источника S со скоростью ΓL (при условии, что состояние $\left| L \right\rangle $ не заселено) и уходят из правой КТ в сток D со скоростью ΓR. Эти процессы являются необратимыми и моделируются операторами Линдблада $D\left( O \right) = O\rho {{O}^{\dag }}$ – ${{\left[ {{{O}^{\dag }}O,\rho } \right]} \mathord{\left/ {\vphantom {{\left[ {{{O}^{\dag }}O,\rho } \right]} 2}} \right. \kern-0em} 2}.$ Состояние $\left| {va{{c}_{{L(R)}}}} \right\rangle $ описывает КТ L(R) без электронов. Аналогично вводятся диссипативные процессы, оказывающие влияние на динамику носителей заряда – релаксация и дефазировка электронов ОЭТ со скоростями ${{\gamma }_{{{\text{rel}},L(R)}}}$ и ${{\gamma }_{{{\text{deph}},L(R)}}},$ а также дефазировка кубита со скоростью ${{\gamma }_{{{\text{deph}},q}}}.$ Поскольку скорость некогерентной накачки ОЭТ ΓL значительно превышает скорости фононной релаксации и дефазировки, то уширение уровней будет в основном определяться ее величиной. Влияние диссипации на когерентную эволюцию КТ-кубитов препятствует выполнению квантовых операций. В установившемся режиме, напротив, она может повышать скорость измерения [10].
Уравнение (8) интегрируется на достаточно длительном отрезке времени t s.s. ≈ 1/ΓL(R), по истечении которого система переходит в стационарный режим. В качестве начального состояния ОЭТ мы выбираем вакуумное состояние $\left| {vac} \right\rangle $, когда в структуре нет электронов. Матрица плотности начального состояния системы “кубит + ОЭТ” имеет вид $\rho \left( 0 \right) = \left| {vac} \right\rangle \left\langle {vac} \right| \otimes \left| \Psi \right\rangle \left\langle \Psi \right|.$ Конечным результатом расчетов является заселенность ${{\tilde {\rho }}_{{RR}}}\left( t \right)$ состояния $\left| R \right\rangle $ правой КТ в ОЭТ. Матрица $\tilde {\rho }\left( t \right) = T{{r}_{{{\text{qubit}}}}}\rho \left( t \right)$ представляет собой приведенную матрицу ОЭТ, которая получается путем взятия частичного следа от матрицы $\rho \left( t \right)$, являющейся решением уравнения (8) с указанным начальным условием, по состояниям кубита. Ток на выходе ОЭТ в установившемся режиме
(9)
$I = {{2\pi e{{\Gamma }_{R}}\tilde {\rho }_{{RR}}^{{s.s.}}} \mathord{\left/ {\vphantom {{2\pi e{{\Gamma }_{R}}\tilde {\rho }_{{RR}}^{{s.s.}}} \hbar }} \right. \kern-0em} \hbar }$пропорционален величине $\tilde {\rho }_{{RR}}^{{s.s.}} = {{\tilde {\rho }}_{{RR}}}\left( {{{t}^{{s.s.}}}} \right).$ Как мы увидим, она зависит от различных факторов и, в первую очередь, от состояния кубита. В качестве единиц измерения примем эффективные атомные единицы, полагая 1 ат. ед. = Ry* = = m*Ry/meε2 для энергии и 1 ат. ед. = $a_{B}^{*} = {{{{a}_{B}}{{m}_{e}}\varepsilon } \mathord{\left/ {\vphantom {{{{a}_{B}}{{m}_{e}}\varepsilon } {m{\text{*}}}}} \right. \kern-0em} {m{\text{*}}}}$ для длины, где Ry =13.6 эВ – энергия Ридберга, aB = 0.52 × 10–10 м – радиус Бора, me – масса свободного электрона, m* – эффективная масса электрона, ε – диэлектрическая проницаемость полупроводника. Для арсенида галлия (ε = 12 и m* = 0.067me) имеем Ry* = 6 мэВ и $a_{B}^{*}$ = 10 нм.
3. ИЗМЕРЕНИЕ КУБИТА
Принцип измерения зарядового кубита с помощью ОЭТ основывается на том, что каждому состоянию (2) отвечает определенная величина стационарного тока, протекающего через ОЭТ. Каноническое проективное измерение, переводящее кубит в базисное состояние $\left| A \right\rangle $ предполагает проведение серии идентичных экспериментов для определения вероятности ${{P}_{A}} = {{\left| {{{c}_{A}}} \right|}^{2}}$ обнаружить кубит в данном состоянии. В нашем случае мы имеем дело с т.н. слабым постоянным измерением (weak continuous measurement), в ходе которого может быть получена вся возможная информация о состоянии кубита. При этом его матрица плотности приобретает диагональный вид, сохраняющий распределение амплитудных вероятностей, однако, при полной потере фазовой когерентности. Тем не менее, такой тип измерения относят к классу “неразрушающих”.
Взаимодействие кубита и ОЭТ приводит к запутыванию их квантовых степеней свободы. Матрица плотности системы в установившемся режиме является диагональной:
(10)
${{\rho }^{{s.s.}}} = {{\tilde {\rho }}^{{s.s.}}}\left( A \right) \otimes \rho _{{AA}}^{'}\left| A \right\rangle \left\langle A \right| + {{\tilde {\rho }}^{{s.s.}}}\left( B \right) \otimes \rho _{{BB}}^{'}\left| B \right\rangle \left\langle B \right|,$(11)
${{\tilde {\rho }}^{{s.s.}}} = T{{r}_{{{\text{qubit}}}}}{{\rho }^{{s.s.}}} = {{\tilde {\rho }}^{{s.s.}}}\left( A \right)\rho _{{AA}}^{'} + {{\tilde {\rho }}^{{s.s.}}}\left( B \right)\rho _{{BB}}^{'}.$Если кубит на момент начала измерений находился в произвольном чистом состоянии $\left| \Psi \right\rangle $ = = ${{c}_{A}}\left| A \right\rangle + {{c}_{B}}\left| B \right\rangle ,$ то при условии, что релаксацией кубита можно пренебречь и положить в (11) $\rho _{{AA}}^{'} = {{\left| {{{c}_{A}}} \right|}^{2}}$ и $\rho _{{BB}}^{'} = {{\left| {{{c}_{B}}} \right|}^{2}},$ выражение (9) для стационарного тока через ОЭТ приобретает простой вид:
(12)
$I\left( \Psi \right) = {{\left| {{{c}_{A}}} \right|}^{2}}{{I}_{A}} + \left( {1 - {{{\left| {{{c}_{A}}} \right|}}^{2}}} \right){{I}_{B}},$(13)
$\left| {{{c}_{A}}} \right| = \sqrt {\frac{{I\left( \Psi \right) - {{I}_{B}}}}{{{{I}_{A}} - {{I}_{B}}}}} ,\,\,\,\,\left| {{{c}_{B}}} \right| = \sqrt {1 - {{{\left| {{{c}_{A}}} \right|}}^{2}}} .$Чтобы определить разность фаз Δϕ = argcA – argcB базисных состояний кубита, необходимо применить к исходному состоянию преобразование Адамара ${\text{Had}} = {{\left( {\left| A \right\rangle \left\langle A \right| + \left| A \right\rangle \left\langle B \right| + \left| B \right\rangle \left\langle A \right| - \left| B \right\rangle \left\langle B \right|} \right)} \mathord{\left/ {\vphantom {{\left( {\left| A \right\rangle \left\langle A \right| + \left| A \right\rangle \left\langle B \right| + \left| B \right\rangle \left\langle A \right| - \left| B \right\rangle \left\langle B \right|} \right)} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }},$ которое конвертирует фазу исходного состояния в амплитуду, и измерить ток $I\left( {{{\Psi }_{H}}} \right)$ с кубитом в состоянии $\left| {{{\Psi }_{H}}} \right\rangle = {\text{Had}}\left| \Psi \right\rangle $. Нетрудно показать, что тогда разность фаз вычисляется по формуле
(14)
$\Delta \phi = \arccos \left\{ {\frac{1}{2}\frac{{\left[ {2I\left( {{{\Psi }_{H}}} \right) - {{I}_{A}} - {{I}_{B}}} \right]\left[ {{{I}_{A}} - {{I}_{B}}} \right]}}{{\sqrt {\left[ {I\left( \Psi \right) - {{I}_{B}}} \right]\left[ {{{I}_{A}} - I\left( \Psi \right)} \right]} }}} \right\}.$Таким образом, для определения состояния кубита достаточно трех операций – двух измерений тока через ОЭТ и вентиля Адамара, примененного к кубиту.
Важной характеристикой любого измерительного устройства является способность различать два близких по физическим свойствам состояния измеряемого объекта. Применительно к нашей задаче это означает, что разность величин тока через ОЭТ для этих состояний, то есть производная ${{dI} \mathord{\left/ {\vphantom {{dI} {d\left| {{{c}_{A}}} \right|}}} \right. \kern-0em} {d\left| {{{c}_{A}}} \right|}},$ иногда называемая чувствительностью, должна быть достаточно большой. Количественно данное свойство связано с измерительным контрастом (видностью):
(15)
${{C}_{I}} = \left| {{{\left( {{{I}_{A}} - {{I}_{B}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{I}_{A}} - {{I}_{B}}} \right)} {\left( {{{I}_{A}} + {{I}_{B}}} \right)}}} \right. \kern-0em} {\left( {{{I}_{A}} + {{I}_{B}}} \right)}}} \right|,$поскольку ${{dI} \mathord{\left/ {\vphantom {{dI} {d\left| {{{c}_{A}}} \right|}}} \right. \kern-0em} {d\left| {{{c}_{A}}} \right|}}$ = $2{{C}_{I}}\left( {{{I}_{A}} + {{I}_{B}}} \right)\left| {{{c}_{A}}} \right|.$ Если инструментальная погрешность при измерении тока амперметром составляет $\Delta I,$ то интервал амплитуд вероятностей с центром $\left| {{{c}_{A}}} \right|,$ которые будут ошибочно отождествляться с этим состоянием, равен
(16)
$\Delta \left| {{{c}_{A}}} \right| \approx \frac{{\Delta I}}{{2{{C}_{I}}\left( {{{I}_{A}} + {{I}_{B}}} \right)\left| {{{c}_{A}}} \right|}}.$Следовательно, при фиксированном $\Delta I,$ для успешной процедуры детектирования с помощью ОЭТ необходимо подобрать системные параметры, при которых величина (15) будет максимальной. Кроме того, необходимо поддерживать высокий уровень тока. В данной работе мы представим анализ некоторых геометрических параметров и укажем условия, обеспечивающие высокую надежность измерения состояния кубита.
4. РАСЧЕТ ПАРАМЕТРОВ ГАМИЛЬТОНИАНА СИСТЕМЫ В МОДЕЛИ ДВУМЕРНЫХ КТ
Параметры, входящие в уравнение Линдблада, могут быть найдены в некотором приближении, конкретизирующем вид удерживающего потенциала КТ. Координатная зависимость потенциальной энергии электрона в двумерной КТ хорошо аппроксимируется экспоненциально-степенной функцией [11]:
(17)
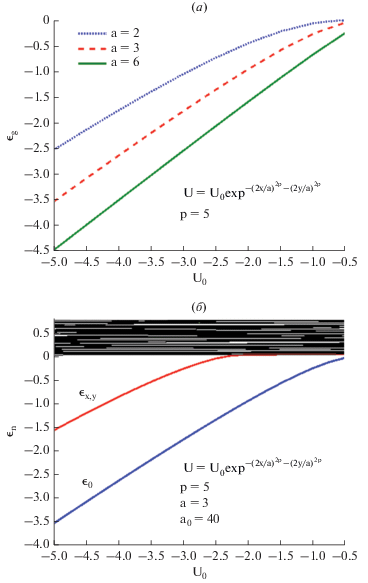
$U\left( {x,y} \right) = {{U}_{0}}\exp \left[ { - {{{\left( {{{2x} \mathord{\left/ {\vphantom {{2x} {{{a}_{x}}}}} \right. \kern-0em} {{{a}_{x}}}}} \right)}}^{{2p}}} - {{{\left( {{{2y} \mathord{\left/ {\vphantom {{2y} {{{a}_{y}}}}} \right. \kern-0em} {{{a}_{y}}}}} \right)}}^{{2p}}}} \right].$Здесь ${{U}_{0}}$ – глубина потенциальной ямы, ${{a}_{{x\left( y \right)}}}$ – характерная длина локализации волновой функции электрона вдоль направления x(y), а p – параметр, определяющий гладкость потенциала $U\left( {x,y} \right).$ Мы ограничимся рассмотрением симметричной КТ, для которой ${{a}_{x}} = {{a}_{y}} = a$. Собственные энергии и волновые функции потенциала (17) рассчитываются конечно-разностным методом второго порядка. Область вычислений, на границах которой волновые функции полагаются равными нулю, представляет собой прямоугольник с размерами, значительно превосходящими размеры КТ. На рис. 2 приведены примеры потенциала КТ (17) и волновой функции электрона в основном состоянии данной КТ. График энергии основного состояния ${{\varepsilon }_{g}}$ КТ в зависимости от глубины ${{U}_{0}}$ для нескольких значений ее ширины a показан на рис. 3а. Энергии ${{\varepsilon }_{n}}$ (n = 200) низколежащих одноэлектронных уровней приведены на рис. 3б как функции глубины потенциала ${{U}_{0}}$ квантовой точки с параметрами a = 3 и p = 5. С уменьшением глубины КТ из нее вначале “выталкивается” дублет ${{\varepsilon }_{{x,y}}}$ вырожденных p-состояний, а затем и основное s‑состояние. Энергии ${{\varepsilon }_{n}} > 0$ воспроизводят (квази)континуум, волновые функции которого делокализованы по всему вычислительному пространству (квадрат со стороной ${{a}_{0}} = 40$).
Рис. 2.
Энергетический профиль двумерной КТ, аппроксимируемый экспоненциально-степенной функцией (а), и волновая функция электрона в основном состоянии (б). Белая линия отмечает эффективную границу потенциала КТ.
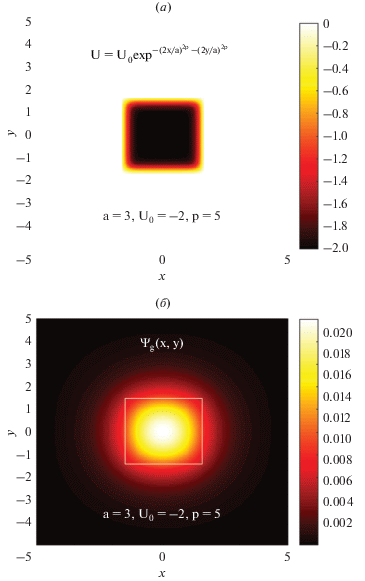
Рис. 3.
Графики зависимостей энергии основного состояния для трех значений ширины КТ (а) и энергий локализованных и низколежащих делокализованных состояний КТ (б) от глубины КТ.
Для расчета энергии V туннельного взаимодействия двух КТ в рамках двумерного приближения (17) необходимо выбирать энергии уровней соседних КТ одинаковыми. В этом случае энергия расщепления гибридизированных уровней ДКТ равна удвоенной энергии туннелирования или
(18)
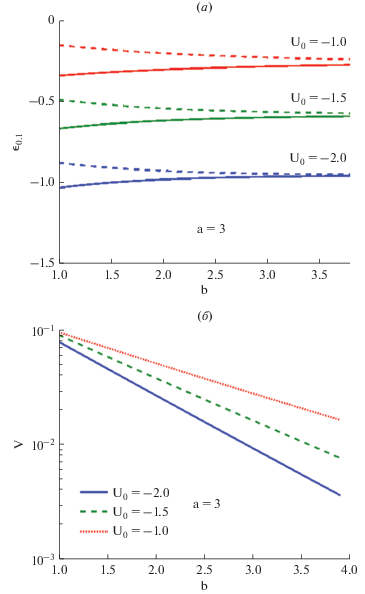
$V = {{\left( {{{\varepsilon }_{1}} - {{\varepsilon }_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\varepsilon }_{1}} - {{\varepsilon }_{0}}} \right)} 2}} \right. \kern-0em} 2}.$Данный параметр (как и коэффициент прозрачности барьера) демонстрирует экспоненциальную зависимость от толщины барьера и от положения энергии изолированных КТ относительно его вершины. Чем шире и глубже КТ, тем ниже расположена энергия ${{\varepsilon }_{g}}$ основного состояния, а значит, тем слабее будет связь между двумя такими КТ. Перекрытие волновых функций соседних КТ, характеризующее их туннельную связь, происходит в области барьера, где они экспоненциально затухают при удалении от центров КТ. Возможность представить гамильтонианы в форме (1) и (5) предполагает, что энергия V существенно меньше, чем энергия размерного квантования КТ (приближение сильной связи). Приведем графики энергий ${{\varepsilon }_{0}}$ и ${{\varepsilon }_{1}}$ как функций толщины барьера b для фиксированной ширины КТ a = 3 и нескольких значений глубины КТ U0, с помощью которых найдем величину V (рис. 4). Как и ожидалось, она зависит экспоненциально от b. Поэтому, чтобы рассчитать энергию туннелирования в выражении (5) для произвольных значений b, мы будем использовать аппроксимацию
(19)
$V\left( x \right) = V\left( {{{x}_{1}}} \right)\exp \left\{ { - \left[ {\ln \frac{{V\left( {{{x}_{1}}} \right)}}{{V\left( {{{x}_{2}}} \right)}}} \right]\frac{{x - {{x}_{1}}}}{{{{x}_{2}} - {{x}_{1}}}}} \right\},$Рис. 4.
Графики зависимостей энергий основного и первого возбужденного гибридизированных состояний ДКТ, состоящей из двух одинаковых КТ (а), и энергии туннелирования электрона (б) от толщины барьера и глубины КТ.
построенную по двум известным значениям, которые были найдены в ходе расчетов. Здесь $x = a + b$ – расстояние между центрами соседних КТ, которое складывается из ширины барьера и половины суммы ширин КТ.
Энергии кулоновского взаимодействия двух электронов в КТ j и k с известными волновыми функциями ${{\psi }_{j}}\left( {\mathbf{r}} \right)$ и ${{\psi }_{k}}\left( {\mathbf{r}} \right)$ вычисляются по формуле
(20)
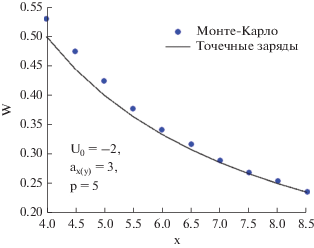
$U{{\left( W \right)}_{{j,k}}} = 2\iint {\frac{{{{{\left| {{{\psi }_{j}}\left( {{{{\mathbf{r}}}_{1}}} \right)} \right|}}^{2}}{{{\left| {{{\psi }_{k}}\left( {{{{\mathbf{r}}}_{2}}} \right)} \right|}}^{2}}{\mathbf{d}}{{{\mathbf{r}}}_{1}}{\mathbf{d}}{{{\mathbf{r}}}_{2}}}}{{\left| {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right|}}}.$Как правило, если требуемая относительная точность не превышает 10–3, то интеграл (20) оценивается посредством метода Монте-Карло. Более того, если предположить, что электронная плотность в основном состоянии КТ сосредоточена в ее центральной области, то можно рассматривать электроны как точечные заряды. В этом случае энергии парного взаимодействия в (6) и (7) вычисляются как
(21)
$U{{\left( W \right)}_{{j,k}}} = {2 \mathord{\left/ {\vphantom {2 {{{r}_{{j,k}}}}}} \right. \kern-0em} {{{r}_{{j,k}}}}},$5. ОЦЕНКА ВЛИЯНИЯ ДИССИПАТИВНЫХ ПРОЦЕССОВ
В ходе измерения логические состояния кубита $\left| A \right\rangle $ и $\left| B \right\rangle $ изолированы друг от друга, и электронная релаксация оказывается подавленной. Однако взаимодействие ДКТ с тепловыми фононами кристаллической решетки вызывает стохастические флуктуации энергий логических состояний, приводящие к дефазировке кубита со скоростью ${{\gamma }_{{{\text{deph}},q}}}.$ Кроме того, взаимодействие ОЭТ и кубита за промежуток времени ${{\tau }_{{{\text{SET}}}}}\sim {1 \mathord{\left/ {\vphantom {1 {\max \left( {{{\Gamma }_{L}},{{\Gamma }_{R}}} \right)}}} \right. \kern-0em} {\max \left( {{{\Gamma }_{L}},{{\Gamma }_{R}}} \right)}}$ приводит к дефазировке последнего.
Геометрия ОЭТ, рассматриваемого в нашей работе, такова, что энергии состояний в крайних КТ примерно одинаковы, а энергия состояния в центральной КТ меньше на величину, превосходящую энергии туннелирования VL(R). Тогда электрон может релаксировать из состояния $\left| {L\left( R \right)} \right\rangle $ в состояние $\left| C \right\rangle $ со скоростью ${{\gamma }_{{{\text{rel}},L(R)}}},$ испустив фонон с частотой ${{\delta }_{{L\left( R \right)}}},$ причем механизм релаксации зависит от частоты перехода. В GaAs-соединениях при частотах, меньших 1 мэВ, релаксация связана с акустическими фононами, а выше 10–15 мэВ она обусловлена двухфононными процессами распада полярона, представляющего собой коррелированное (запутанное) состояние электрона и оптического фонона [9]. При конечной температуре Т возможен и обратный процесс (некогерентное поглощение фонона). Мы будем полагать $T \ll {{\delta }_{{L(R)}}},$ что делает поглощение фонона маловероятным. Как и для кубита, тепловые флуктуации фононного поля вызывают дефазировку крайних состояний ОЭТ относительно центрального состояния со скоростями ${{\gamma }_{{{\text{deph}},L}}}$ и ${{\gamma }_{{{\text{deph}},R}}}.$
Для расчета скоростей диссипативных процессов будем использовать волновые функции, найденные выше. Рассмотрим две одиночных GaAs-КТ 1 и 2 с почти одинаковыми размерами, расстояние между центрами которых равно d. Предположим, что изолированная КТ 1 (2) имеет только одно электронное состояние $\left| {1(2)} \right\rangle $ с энергией ${{\varepsilon }_{{1(2)}}},$ описываемое волновой функцией ${{\Psi }_{{1(2)}}}({\mathbf{r}}).$ В нашей модели разность $\left| {{{\varepsilon }_{1}} - {{\varepsilon }_{2}}} \right|$ не превышает нескольких миллиэлектронвольт, поэтому основной вклад в диссипацию вносит взаимодействие электрона с продольными акустическими (LA) фононами кристалла через так называемый деформационный потенциал. Этот процесс описывается гамильтонианом
(22)
${{H}_{{e - ph}}} = \sum\limits_{\mathbf{q}} {\sqrt {\frac{{\hbar qE_{a}^{2}}}{{2{{\rho }_{{{\text{GaAs}}}}}\Omega {{c}_{l}}}}} \left( {{{b}_{{\mathbf{q}}}} + b_{{ - {\mathbf{q}}}}^{\dag }} \right){{e}^{{i{\mathbf{qr}}}}}} = \sum\limits_{\mathbf{q}} {{{H}_{{\mathbf{q}}}}} ,$(23)
$g_{{\mathbf{q}}}^{{({\text{rel}})}} = \left\langle 2 \right|{{H}_{{\mathbf{q}}}}\left| 1 \right\rangle = \sqrt {\frac{{\hbar qE_{a}^{2}}}{{2{{\rho }_{{{\text{GaAs}}}}}\Omega {{c}_{l}}}}} M_{{\mathbf{q}}}^{{({\text{rel}})}},$(24)
$M_{{\mathbf{q}}}^{{({\text{rel}})}} = \int {d{\mathbf{r}}\Psi _{2}^{*}({\mathbf{r}}){{e}^{{i{\mathbf{qr}}}}}{{\Psi }_{1}}({\mathbf{r}})} .$Скорость релаксации электрона вычисляется с помощью золотого правила Ферми:
(25)
${{\gamma }_{{{\text{rel}}}}} = \frac{{2\pi }}{\hbar }\sum\limits_{\mathbf{q}} {{{{\left| {g_{{\mathbf{q}}}^{{({\text{rel}})}}} \right|}}^{2}}\left( {{{n}_{q}} + \frac{1}{2} \pm \frac{1}{2}} \right)\delta \left( {\Delta \varepsilon - \hbar {{\omega }_{q}}} \right)} .$Здесь ${{n}_{q}} = {{\left[ {\exp \left( {{{\hbar {{\omega }_{q}}} \mathord{\left/ {\vphantom {{\hbar {{\omega }_{q}}} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right) - 1} \right]}^{{ - 1}}}$ – функция распределения числа фононов с частотой ${{\omega }_{q}} = {{c}_{l}}q$ при температуре T, kB – постоянная Больцмана, $\Delta \varepsilon = {{\varepsilon }_{1}} - {{\varepsilon }_{2}} = \hbar \omega .$ Знак “+” (“–”) соответствует испусканию (поглощению) фонона при электронном переходе $\left| 1 \right\rangle \to \left| 2 \right\rangle $ ($\left| 2 \right\rangle \to \left| 1 \right\rangle $). Дальнейший расчет был произведен для следующих параметров GaAs-кристалла: ${{\rho }_{{{\text{GaAs}}}}}$ = 5.3 г/см3, ${{c}_{l}}$ = 5.2 × × 105 см/с, ${{E}_{a}}$ = 6.8 эВ.
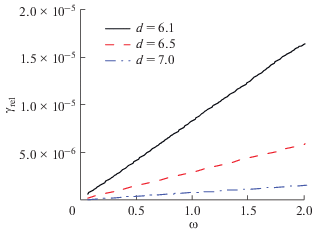
Мы вычисляем скорость релаксации γrel электрона для процесса $\left| 1 \right\rangle \to \left| 2 \right\rangle $ при T = 0 для КТ, волновая функция которых была получена в п. 4 путем численного решения двумерного уравнения Шредингера с экспоненциально-степенным потенциалом (17), в зависимости от частоты при различных расстояниях d между центрами КТ. Как можно видеть, зависимость скорости релаксации γrel от частоты близка к линейной, а увеличение расстояния d ожидаемо приводит к резкому уменьшению величины γrel (рис. 6). Монотонный рост зависимости ${{\gamma }_{{{\text{rel}}}}}(\omega )$ не согласуется с полученным в работе [12] результатом для системы из двух туннельно-связанных трехмерных КТ. Там волновая функция электрона имеет гауссов вид ${{\Psi }_{1}}({\mathbf{r}}) \sim \exp \left( {{{ - {{r}^{2}}} \mathord{\left/ {\vphantom {{ - {{r}^{2}}} {2{{a}^{2}}}}} \right. \kern-0em} {2{{a}^{2}}}}} \right),$ и при больших частотах γrel падает с ростом ω. Для того, чтобы проверить корректность наших расчетов, мы исследовали частотную зависимость скорости релаксации для трехмерных гауссовых КТ, один из поперечных размеров которых существенно отличается остальных двух.
Рис. 6.
Зависимость скорости релаксации γrel от частоты ω при различном расстоянии d для КТ с экспоненциально-степенным потенциалом (17).
Предположим, что волновая функция КТ имеет следующий вид
(26)
${{\Psi }_{1}}({\mathbf{r}}) = \frac{1}{{\sqrt {\pi \sqrt \pi c{{a}^{2}}} }}\exp \left( { - \frac{{{{x}^{2}} + {{y}^{2}}}}{{2{{a}^{2}}}} - \frac{{{{z}^{2}}}}{{2{{c}^{2}}}}} \right),$(27)
${{\gamma }_{{{\text{rel}}}}} = \frac{{E_{a}^{2}{{\omega }^{2}}{{\omega }_{0}}}}{{2\sqrt {2\pi } \hbar {{\rho }_{{{\text{GaAs}}}}}c_{l}^{5}}}{{e}^{{ - \frac{{{{d}^{2}}}}{{2{{a}^{2}}}}}}}\operatorname{erf} \left( {\frac{\omega }{{\sqrt 2 {{\omega }_{0}}}}} \right),\,\,\,\,\frac{1}{{\omega _{0}^{2}}} = \frac{1}{{\omega _{a}^{2}}} - \frac{1}{{\omega _{c}^{2}}},$(28)
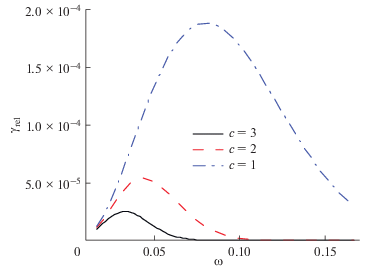
${{\gamma }_{{{\text{rel}}}}}\left( \omega \right) = \frac{{E_{a}^{2}{{\omega }^{3}}}}{{2\pi \hbar {{\rho }_{{{\text{GaAs}}}}}c_{l}^{5}}}\exp \left( { - \frac{{{{\omega }^{2}}}}{{2\omega _{a}^{2}}} - \frac{{{{d}^{2}}}}{{2{{a}^{2}}}}} \right).$Сначала с ростом частоты γrel увеличивается, достигая максимума при значении ${{\omega }_{m}} = \sqrt 3 {{\omega }_{a}},$ которое линейно убывает с ростом размера a. Затем при дальнейшем росте ω скорость релаксации быстро уменьшается. Для несимметричных КТ (a > c) наблюдается несколько иная картина. При уменьшении их аксиального размера c значение ${{\omega }_{m}}$ увеличивается, причем скорость релаксации резко возрастает, значительно превышая величину γrel для симметричных КТ (рис. 7). В итоге при c = 0, когда волновая функция КТ становится двумерной, зависимость ${{\gamma }_{{{\text{rel}}}}}(\omega )$ оказывается монотонно возрастающей во всем диапазоне частот акустических фононов. При этом очевидно (см. (28)), что как для КТ с экспоненциально-степенным потенциалом, так и для КТ с гауссовой волновой функцией рост расстояния d между центрами КТ приводит к резкому падению γrel из-за уменьшения интеграла (24).
Рис. 7.
Зависимость скорости релаксации γrel электрона от частоты ω при различном аксиальном размере c при a = 3, d = 7 для КТ с гауссовой волновой функцией (26).
Помимо релаксации электрон-фононное взаимодействие вызывает дефазировку состояний $\left| 1 \right\rangle $ и $\left| 2 \right\rangle $ с матричным элементом
(29)
$g_{{\mathbf{q}}}^{{{\text{(deph)}}}} = \frac{1}{2}\left( {\left\langle 1 \right|{{H}_{{\mathbf{q}}}}\left| 1 \right\rangle - \left\langle 2 \right|{{H}_{{\mathbf{q}}}}\left| 2 \right\rangle } \right) = \sqrt {\frac{{\hbar qE_{a}^{2}}}{{2{{\rho }_{{{\text{GaAs}}}}}\Omega {{c}_{l}}}}} M_{{\mathbf{q}}}^{{{\text{(deph)}}}},$(30)
$M_{{\mathbf{q}}}^{{{\text{(deph)}}}} = \frac{1}{2}\int {d{\mathbf{r}}\left( {{{{\left| {{{\Psi }_{1}}({\mathbf{r}})} \right|}}^{2}} - {{{\left| {{{\Psi }_{2}}({\mathbf{r}})} \right|}}^{2}}} \right)} {{e}^{{i{\mathbf{qr}}}}}.$Дефазировка приводит к экспоненциальному уменьшению со временем недиагональных элементов матрицы плотности системы, то есть ${{\rho }_{{{\text{off}} - {\text{diag}}}}} \sim {{e}^{{ - {{B}^{2}}(t)}}}.$ Спектральная функция ${{B}^{2}}(t),$ характеризующая дефазировку двухуровневой КТ-системы в фононном резервуаре, вычисляется согласно формуле [14–16]
(31)
${{B}^{2}}(t) = 8\sum\limits_{\mathbf{q}} {\frac{{{{{\left| {g_{{\mathbf{q}}}^{{{\text{(deph)}}}}} \right|}}^{2}}}}{{{{\hbar }^{2}}\omega _{q}^{2}}}{{{\sin }}^{2}}\frac{{{{\omega }_{q}}t}}{2}{{{\operatorname{th} }}^{{ - 1}}}\frac{{\hbar {{\omega }_{q}}}}{{2{{k}_{B}}T}}} .$В стационарном режиме удобно ввести скорость дефазировки, усредненную на большом промежутке времени Δt
(32)
${{\gamma }_{{{\text{deph}}}}} = \frac{1}{{\Delta t}}\int\limits_0^{{\Delta }t} {{{\gamma }_{{{\text{deph}}}}}(t)dt} = \frac{{{{B}^{2}}\left( {\Delta t} \right)}}{{\Delta t}}.$Для двумерных КТ с экспоненциально-степенным потенциалом (см. п. 4) функция B2 при T = 0 быстро увеличивается со временем (рис. 8), однако затем при t > 0.2 пс ее рост замедляется. Расчет скорости дефазировки, произведенный нами на быстрорастущем участке кривых ${{B}^{2}}(t)$, дает значение γdeph ~ 0.04, что существенно превосходит скорость релаксации γrel (рис. 6). Это обусловлено тем, что интеграл $M_{{\mathbf{q}}}^{{{\text{(rel)}}}}$ (24) определяется малым перекрытием волновых функций разных КТ, в отличие от интеграла $M_{{\mathbf{q}}}^{{{\text{(deph)}}}}$ (30). В частности, это приводит к тому, что B2 и γdeph практически не зависят от расстояния d между центрами КТ, в то время как величина γrel быстро уменьшается с ростом d (рис. 6).
Рис. 8.
Зависимость спектральной функции от времени при различном расстоянии d для КТ с экспоненциально-степенным потенциалом (17).
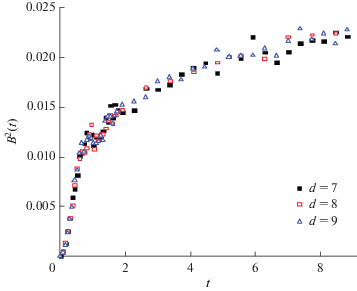
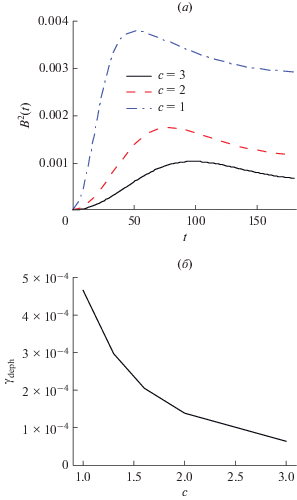
Чтобы изучить влияние формы КТ на дефазировку, мы снова рассчитали кривые ${{B}^{2}}(t)$ и вычислили значения γdeph при T = 0 для КТ, имеющих различные поперечные размеры, с гауссовой электронной волновой функцией (26). Оказалось, что уменьшение аксиального размера КТ вызывает существенное увеличение функции B2 и экспоненциальный рост величины γdeph (рис. 9), аналогично поведению скорости релаксации (рис. 7).
Рис. 9.
Зависимость спектральной функции от времени (а) и скорость дефазировки γdeph как функция аксиального размера c (б) при a = 3 и d = 7 для КТ с гауссовой волновой функцией (26).
Таким образом, изучение процессов релаксации и дефазировки при взаимодействии электронов с акустическими фононами в двухуровневой КТ-системе продемонстрировало, что скорость релаксации γrel электронов, определяемая перекрытием волновых функций соседних КТ, которое крайне мало, на несколько порядков меньше скорости дефазировки γdeph. Оценка этих скоростей для исследованных нами двумерных КТ с экспоненциально-степенным потенциалом дает значения γrel < 2 × 10–5Ry* = 1.2 × 10–7 эВ и γdeph ~ ~ 0.04Ry* = 2.4 × 10–4 эВ. Расчет, выполненный нами для КТ различной формы с гауссовой волновой функцией, показывает, что в реальных трехмерных КТ скорость дефазировки, вызванной акустическими фононами, значительно меньше. Следует также отметить, что в двумерных КТ зависимость скорости релаксации от частоты монотонно возрастает, в отличие от трехмерного случая.
Как мы увидели, геометрия системы (размеры КТ, их форма и ориентация друг относительно друга) оказывает большое влияние на ее динамические свойства. Поэтому оптимизация измерительной процедуры должна состоять в поиске такого взаимного расположения кубита и ОЭТ, при котором разность силы тока для базисных состояний кубита будет максимальной. Ниже мы представим результаты моделирования динамики ОЭТ и кубита, иллюстрирующие данный алгоритм на частных примерах, связанных с варьированием некоторых геометрических параметров.
6. МОДЕЛИРОВАНИЕ ИЗМЕРЕНИЯ ЗАРЯДОВОГО КУБИТА
Заселенность КТ R (и, следовательно, ток через ОЭТ) зависит от большого числа параметров, входящих в уравнение (8), которые, в свою очередь, зависят от геометрии и материала чипа. При достаточном сближении КТ L, С и R, размеры и форма которых выбираются примерно одинаковыми, ${{\delta }_{{L(R)}}} \ll {{V}_{{L(R)}}}$ и туннельная связь между КТ оказывается резонансной. Это выражается в гибридизации состояний отдельных КТ и формировании триплета состояний, делокализованнных по всей структуре. В этом случае электронный транспорт через ОЭТ оказывается устойчивым по отношению к небольшим штарковским сдвигам ${{W}_{{j,k}}} \leqslant {{V}_{{L(R)}}}$ энергий КТ, вызываемых кубитом. Это закономерно приводит к резкому уменьшению контраста, если кубит находится на значительном удалении от ОЭТ. Для повышения чувствительности устройства можно перейти в режим нерезонансного туннелирования, отстраивая энергию состояния в центральной КТ от энергий состояний в крайних КТ на величину, превышающую энергию туннелирования: ${{\delta }_{{L(R)}}} \geqslant {{V}_{{L(R)}}}.$ Тогда ток будет течь через ОЭТ только при соблюдении равенства ${{\delta }_{L}} = {{\delta }_{R}},$ причем даже небольшие отклонения от условия симметрии отстроек будут вызывать блокировку тока. Оптимизация функции CI может проводиться как за счет увеличения отстройки, так и путем уменьшения энергии туннелирования. Однако необходимо помнить, что выполнения одного только условия CI ≈ 1 оказывается недостаточно для качественного измерения. Сам по себе уровень стационарного тока должен быть высоким.
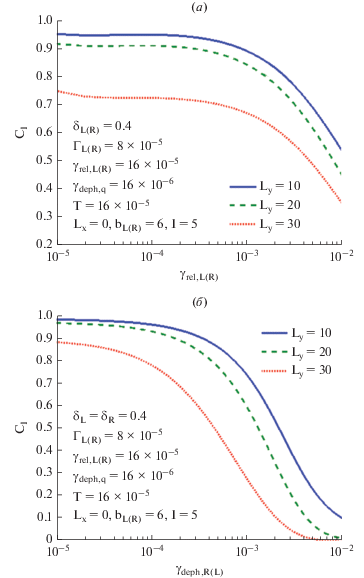
Ниже мы представим результаты численного анализа уравнения (8) в установившемся режиме. В качестве основных характеристик измерительной процедуры мы используем безразмерный ток $\tilde {\rho }_{{RR}}^{{s.s.}}\left( k \right)$ на выходе из ОЭТ, зависящий от состояния кубита k = A, B, и контраст CI. Нас будет интересовать поведение данных величин как функций геометрических параметров чипа, а также скоростей диссипативных процессов. Принцип измерения основывается на том, что разность значений тока через ОЭТ для разных логических состояний кубита должна быть как можно больше. В нерезонансном режиме этот подход усиливается вследствие повышенной чувствительности электронного транспорта к симметрии параметров гамильтониана (отстроек, энергий туннелирования и кулоновского взаимодействия). В работе [17] было подробно исследовано влияние отстроек на измерительные свойства ОЭТ. Ниже мы рассмотрим туннельные свойства структуры, от которых зависит и контраст, и уровень тока. Кроме того, будут проанализированы вопросы, связанные с нарушением пространственной симметрии и диссипативными процессами.
В резонансно-туннельных структурах важную роль играет прозрачность потенциального барьера, разделяющего соседние КТ. С одной стороны, она должна быть достаточно высокой, чтобы поддерживать ток через структуру на уровне, допускающем его надежное детектирование с помощью измерительного прибора (амперметра). С другой стороны, чем слабее туннельная связь, тем она чувствительнее к изменениям внешнего поля, что способствует увеличению контраста. Как следует ее выбирать, чтобы чувствительность измерения была оптимальной? Для ответа на этот вопрос получим графики зависимостей тока и контраста от расстояния bR между центрами КТ C и R, варьируемого на некотором интервале, при фиксированном расстоянии bL между центрами КТ C и L. Данные приводятся для трех значений расстояния Ly от ОЭТ до кубита (рис. 10). Другие параметры системы приводятся на рис. 11.
Рис. 10.
Графики зависимостей тока (а) и контраста (б) от расстояния между центрами КТ C и КТ R (толщины барьера при заданном диаметре КТ) для фиксированного расстояния между КТ C и КТ L и трех расстояний от ОЭТ до кубита.
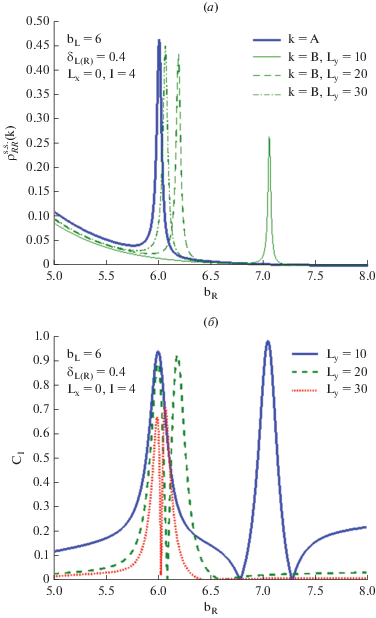
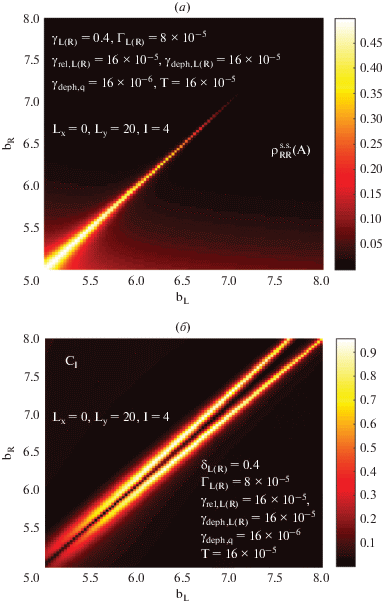
Рис. 11.
Графики зависимостей тока (а) и контраста (б) от расстояния между центрами КТ C и КТ L(R) для фиксированного расстояния от кубита до ОЭТ.
Как можно видеть, помимо пика CI при bR = bL, связанного с симметрией относительно центра ОЭТ и не зависящего от расстояния Ly от ОЭТ до кубита, существует еще один пик при bR ≠ bL, положение которого зависит от расстояния примерно как 1/Ly. С увеличением Ly оба пика сближаются и сливаются при Ly $ \gg $ l, что сопровождается спадом контраста до нуля. Сопоставляя графики, нетрудно понять, что второй пик соответствует нахождению электрона кубита в КТ В.
Природу его возникновения можно объяснить, если принять во внимание связь данного пика с асимметрией барьеров и, как следствие, несовпадения энергий туннелирования VL и VR. Уже небольшой дисбаланс этих энергий ΔV = VL – VR приводит к полной блокировке тока для кубита с электроном в КТ А. Вместе с тем, для состояния кубита с электроном в КТ B происходит эффективное “восстановление” энергетической симметрии при определенном соотношении bR и bL, т.е. сохранении структурной асимметрии. Поскольку это соотношение связано с расстоянием Ly, то можно заключить, что именно кулоновское взаимодействие электронов кубита и ОЭТ компенсирует дисбаланс для данной геометрии чипа. На контурных графиках (рис. 11) показаны зависимости этих же характеристик от расстояний bR и bL для кубита, умеренно удаленного от ОЭТ (Ly = 20). Видно, что смещение в 0.2 ед. одного пика относительно другого остается практически постоянным, поскольку интервал изменения bL(R) значительно меньше Ly. Полученные результаты указывают на существование максимального расстояния, на котором может располагаться кубит, чтобы точность измерения его состояния с помощью ОЭТ была приемлемой. На больших расстояниях ОЭТ не различает распределение электронной плотности внутри кубита, воспринимая его как точечный заряд. Резкий рост максимального значения тока при уменьшении толщины барьера до bL(R) = 5 для обоих состояний кубита и ослабление контраста свидетельствуют о начале перехода в резонансный режим. Напротив, быстрое убывание силы тока с ростом толщины барьеров обусловлено экспоненциальной зависимостью энергий VL(R) от bL(R). Сопоставляя оба графика, можно указать область 5.5 < bL(R) < 6.5, при которых и ток, и контраст одновременно сохраняют высокие значения. Ширина пика зависит и от толщины барьера, и от расстояния до кубита, являясь, по-видимому, сложной функцией входящих в уравнение (8) энергий.
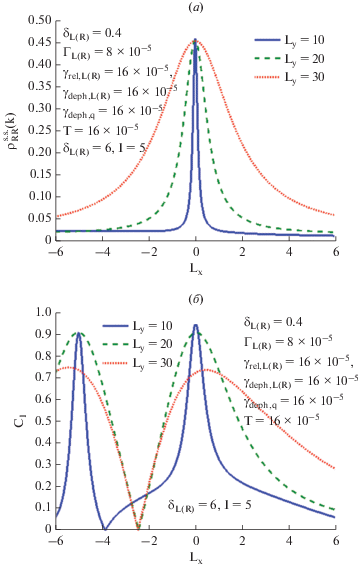
Другим параметром, влияние которого на характеристики измерения мы рассмотрим, будет горизонтальное смещение кубита Lx вдоль оси ОЭТ (см. схему чипа на рис. 1). Равноудаленное положение КТ А кубита от КТ L и КТ R ОЭТ, обеспечивающее симметричную конфигурацию отстроек, отвечает значению Lx = 0, для которого были получены все перечисленные выше результаты. Смещение КТ А влево в точку Lx = –l/2 приводит к конфигурации с равноудаленными КТ А и В от центральной КТ С, причем конфигурации отстроек ОЭТ для базисных состояний кубита будут зеркально-симметричными относительно КТ С. В данном случае CI = 0 для расстояний Ly > 15, а на меньших расстояниях контраст отличен от нуля из-за асимметрии, связанной с направлением протекания тока через ОЭТ (рис. 12). При Lx = –l роли КТ А и В меняются на противоположные: симметричная конфигурация отстроек теперь отождествляется с КТ В, а не с КТ А. С увеличением расстояния между кубитом и ОЭТ пик контраста уменьшается, а уровень тока сохраняется.
Рис. 12.
Графики зависимостей тока (а) и контраста (б) от горизонтального смещения кубита Lx вдоль оси ОЭТ для фиксированного расстояния между КТ C и КТ L (R) и трех расстояний от ОЭТ до кубита.
Роль диссипативных процессов, как правило, всегда заключается в подавлении когерентного транспорта и ускорении перехода системы в равновесное состояние. Как было показано выше, скорость электронной релаксации экспоненциальным образом зависит от расстояния между КТ, а скорость дефазировки определяется формой и размерностью КТ. Усиление релаксации в тройной КТ с более широкой центральной КТ будет ускорять (подавлять) туннельный переход электрона из левой (центральной) КТ в центральную (правую) КТ, что приведет к ослаблению и даже блокировке тока через структуру. Увеличение скорости дефазировки до значений порядка VL(R) и выше может “замораживать” электронный переход между КТ вследствие быстрых случайных относительных смещений энергий их уровней (эффект Зенона). Таким образом, для данной конфигурации уровней декогерентность оказывает отрицательное влияние на установившуюся динамику электронов в ОЭТ, переводя систему в равновесное состояние, которое характеризуется слабым током и низким контрастом, что подтверждается расчетами (рис. 13). Инженерия фононного спектра и коэффициентов электрон-фононного взаимодействия за счет подбора материала и формы КТ может существенно замедлить оба паразитных процесса.
ЗАКЛЮЧЕНИЕ
Квантовые вычислительные схемы, использующие кодирование квантовой информации в орбитальные степени свободы электрона в квазиодномерном бистабильном потенциале, характеризующем твердотельную наноструктуру, представляют на сегодняшний день большой интерес как с экспериментальной, так и с теоретической точек зрения. Высокая скорость выполнения квантовых операций (от нескольких пикосекунд до нескольких наносекунд), эффективная и уже апробированная процедура измерения квантового состояния и, разумеется, масштабируемость, делают данные схемы весьма привлекательными для изготовления и изучения прототипов квантовых компьютеров.
Рассмотренная в данной работе GaAs-структура из трех КТ, представляющая собой “сенсорную” часть ОЭТ, может работать как в резонансном, так и в нерезонансном туннельных режимах. Как было показано, последний обладает явными преимуществами, обеспечивая высокий измерительный контраст даже для кубитов, находящихся на большом расстоянии (более ста нанометров) от ОЭТ. Чтобы использовать эту особенность нерезонансного режима, нужно соблюдать требования, обусловленные сохранением симметрии параметров гамильтониана (отстройки, энергии туннелирования и кулоновского взаимодействия электронов). В противном случае ток через ОЭТ оказывается заблокированным. Анализ динамики в установившемся режиме выявил также возможность восстановления тока при наличии асимметрии за счет компенсации естественного (технологического) дисбаланса одних параметров путем искусственно вводимого отклонения других параметров.
Оценка скоростей релаксации и дефазировки при взаимодействии электрона с акустическими фононами в системе, состоящей из двух двумерных КТ, которые могут играть роль как ДКТ-кубита, так и элементов ОЭТ, показало, что скорость релаксации оказалась менее 1.2 × 10–7 эВ, а скорость дефазировки составила около 2.4 × 10–4 эВ. Такая большая дефазировка приводит к уменьшению измерительного контраста при измерении состояния ДКТ-кубита. Однако расчет, выполненный нами для КТ различной формы с гауссовой волновой функцией, показывает, что в реальных трехмерных КТ скорости данных диссипативных процессов, вызванных акустическими фононами, значительно меньше. Без ограничения общности, результаты, полученные в предположении, что ДКТ относится к типу электрически формируемых, могут быть применены и к кристаллической ДКТ, образованной по методу Странского–Крастанова.
Работа выполнена в рамках Государственного задания ФТИАН им. К.А. Валиева РАН Минобрнауки РФ по теме № 0066-2019-0005 “Фундаментальные исследования в области квантовых вычислений и прикладные разработки твердотельной элементной базы квантовых компьютеров 2019”.
Список литературы
Joyce B.A., Kelires P.C., Naumovets A.G., Vvedensky D.D. Quantum Dots: Fundamentals, Applications, and Frontiers (NATO Science Series, 2003).
Fedichkin L., Yanchenko M., Valiev K.A. Coherent charge qubit based on GaAs quantum dots with a built-in barrier // Nanotechnology. 2000. V. 11. P. 387–391.
Tanamoto T. Quantum gates by coupled asymmetric quantum dots and controlled-NOT-gate operation // Phys. Rev. A. 2000. V. 61. P. 022305.
Kastner M.A. The single-electron transistor // Rev. Mod. Phys. 1992. V. 64. P. 849.
Hayashi T., Fujisawa T., Cheong H.D., Jeong Y.H., Hirayama Y. Coherent Manipulation of Electronic States in a Double Quantum Dot // Phys. Rev. Lett. 2003. V. 91. P. 226804. 4 p.
Gorman J., Hasko D.G., Williams D.A. Charge-Qubit Operation of an Isolated Double Quantum Dot // Phys. Rev. Lett. 2005. V. 95. P. 090502.
Petta J.R., Johnson A.C., Marcus C.M., Hanson M.P., Gossard A.C. Manipulation of a Single Charge in a Double Quantum Dot // Phys. Rev. Lett. 2004. V. 93. P. 186802.
Kulkarni M., Cotlet O., Türeci H.E. Cavity-coupled double-quantum dot at finite bias: Analogy with lasers and beyond // Phys. Rev. B. 2014. V. 90. P. 125402.
Zibik E.A., Grange T., Carpenter B.A., Porter N.E., Ferreira R., Bastard G., Stehr D., Winnerl S., Helm M., Liu H.Y., Skolnick M.S., Wilson L.R. Long lifetimes of quantum-dot intersublevel transitions in the terahertz range // Nature Mat. 2009. V. 8. P. 803.
Majumdar A., Bajcsy M., Rundquist A., Kim E., Vučković J. Phonon-mediated coupling between quantum dots through an off-resonant microcavity // Phys. Rev. B. 2012. V. 85. P. 195301.
Ciurla M., Adamowski J., Szafran B., Bednarek S. Mo-delling of confinement potentials in quantum dots // Physica E. 2002. V. 15. P. 261.
Calarco T., Datta A., Fedichev P., Pazy E., Zoller P. Spin-based all-optical quantum computation with quantum dots: Understanding and suppressing decoherence // Phys. Rev. A. 2003. V. 68. P. 012310.
Brandes T., Vorrath T. Adiabatic transfer of electrons in coupled quantum dots // Phys. Rev. B. 2002. V. 66. P. 075341.
Fedichkin L., Fedorov A. Error rate of a charge qubit coupled to an acoustic phonon reservoir // Phys. Rev. A. 2004. V. 69. P. 032311.
Stavrou V.N., Hu X. Charge decoherence in laterally coupled quantum dots due to electron-phonon interactions // Phys. Rev. B. 2005. V. 72. P. 075362.
Hohenester U. Quantum control of polaron states in semiconductor quantum dots // J. Phys. B. 2007. V. 40. P. S315.
Tsukanov A.V. Measurement of a charge qubit using a single-electron transistor based on a triple quantum dot // Phys. Rev. A. 2019. Принято к печати.
Дополнительные материалы отсутствуют.
Инструменты
Микроэлектроника