Российские нанотехнологии, 2020, T. 15, № 2, стр. 171-175
РАЗМЕРНЫЙ ЭФФЕКТ В АДСОРБЦИОННЫХ СВОЙСТВАХ УЛЬТРАМАЛЫХ ЧАСТИЦ ЗОЛОТА
Ф. И. Далидчик 1, Е. М. Балашов 1, *, С. А. Ковалевский 1
1 Федеральный исследовательский центр химической физики им. Н.Н. Семенова РАН
Москва, Россия
* E-mail: embalashov@yandex.ru
Поступила в редакцию 23.01.2020
После доработки 27.03.2020
Принята к публикации 06.04.2020
Аннотация
В рамках теории туннельной резонансной электронно-колебательной спектроскопии с учетом межэлектронного (кулоновского) взаимодействия, существенного для ультрамалых металлических наночастиц (≤5 нм), построена модель, количественно объясняющая результаты литературных спектроскопических экспериментов, проведенных с помощью сканирующей туннельной микроскопии, в которых для наночастиц золота (Au-НЧ), осажденных на пиролитический графит, ранее наблюдались эквидистантные серии отрицательных дифференциальных сопротивлений с периодами 0.1–0.5 В. Установлено, что серии с достаточно большими периодами (~0.3–0.5 В), имеющие растущие (по мере повышения напряжения на наноконтакте) огибающие, коррелируют с размерами Au-НЧ и формируются по механизму кулоновской блокады. Серии с малыми периодами (~0.1 В) соответствуют колебательным переходам атомных частиц, адсорбированных на поверхности Au-НЧ. Впервые обнаружен новый размерный эффект, состоящий в повышенной адсорбционной способности ультрамалых наночастиц золота, имеющих те же размеры (≈3.2 нм), что и частицы, обладающие повышенной каталитической активностью. Новый адсорбционный эффект дает прямой и утвердительный ответ на часто обсуждаемый вопрос о “собственной” суперактивности Au-НЧ, которая не связана со свойствами носителей.
ВВЕДЕНИЕ
В основе современных нанотехнологий лежат размерные эффекты, т.е. зависимости физических, химических и биохимических свойств наночастиц (НЧ) от их геометрических параметров. Чаще всего эти эффекты становятся доступными для наблюдения по мере уменьшения средних размеров изучаемых НЧ. Известны случаи, когда уникальными свойствами, не характерными для массивных тел, обладают НЧ определенных размеров. В качестве хорошо известного примера можно привести нанокатализаторы на основе ультрамалых наночастиц (УМНЧ) благородных металлов [1]. Прежде всего нанозолота, суперактивность, т.е. повышенная активность которого наблюдается для частиц размером R в диапазоне от 2 до 5 нм [2–4]. Для поисков и изучения размерных эффектов, которые проявляются в узких диапазонах изменений геометрических параметров, как правило, используются монодисперсные ансамбли с варьируемыми средними размерами и малыми, не более 1–2 нм, отклонениями размеров частиц от средних. Синтез таких ансамблей, несмотря на значительный прогресс, достигнутый в последние годы [5], все еще остается трудной задачей.
Альтернативный вариант организации экспериментов, нацеленных на поиски размерных эффектов, требующих высокой степени монодисперсности изучаемых НЧ, может быть связан с применением методов сканирующей туннельной микроскопии (СТМ) и спектроскопии [6]. В частности, метода туннельной резонансной электронно-колебательной спектроскопии [7–10], который позволяет проводить химический анализ вещества на уровне единичных поверхностных комплексов. В том числе адсорбционных комплексов (АК) на поверхности УМНЧ металлов11.
В настоящей работе такой подход реализован на примере размерного эффекта в адсорбционных свойствах нанозолота. Корректный анализ туннельных спектров, измеренных в [12–18] для Au-НЧ с адсорбционными комплексами газовых реагентов, который стал возможным после публикации [19], приводит к выводу о повышенной адсорбционной активности частиц, имеющих размеры, близкие к размерам, для которых наблюдается свойство низкотемпературной каталитической суперактивности [2–4]. Существование этого важного для “золотого” нанокатализа размерного эффекта предполагалось ранее в [20, 21], но никогда это предположение не подтверждалось результатами прямых физических (спектроскопических) измерений. Полученные результаты прямо указывают на определяющую роль адсорбции в формировании уникальных каталитических свойств нанозолота в реакциях низкотемпературного гидрирования и окисления [2–4], что может быть полезным при оптимизации состава и строения Au-нанокатализаторов этих процессов.
РАЗМЕРНЫЙ ЭФФЕКТ В АДСОРБЦИОННЫХ СВОЙСТВАХ Au-УМНЧ
Адсорбция – фундаментальное гетерогенное явление, влияющее на все свойства реальных и модельных поверхностей [22]. Строение и свойства единичных АК активно изучаются в экспериментах СТМ-методами резонансной туннельной электронно-колебательной спектроскопии, базовые представления которых сложились в основном при описании экспериментов по зондированию точечных дефектов твердых тел [7–10]. На первый взгляд, такой подход возможен и для точечных поверхностных дефектов УМНЧ (R < 7–10 нм), которые сегодня вызывают наибольший научный и практический интерес. Это предположение использовалось, в частности, в обширной серии работ по изучению в СТМ-экспериментах адсорбции газовых реагентов (Н2, О2, СО) на поверхности металлических УМНЧ (Au, Pt, Ni, Cu, 2–7 нм) [12–18]. Здесь наблюдались серии эквидистантных резонансных особенностей отрицательных дифференциальных сопротивлений (ОДС), которые отождествлялись с колебательными спектрами и поэтому анализировались в рамках известных представлений туннельной резонансной электронно-колебательной спектроскопии [7–10]. Для УМНЧ, однако, этих представлений недостаточно.
К такому выводу можно прийти, если заметить, что периоды всех серий ОДС, наблюдавшихся в туннельных спектрах УМНЧ после адсорбции газовых реагентов [12–18], лежат в диапазоне изменений напряжений, который в равной мере соответствует и колебательным квантам АК (ħω = 0.1–0.5 эВ) и энергиям одноэлектронного заряда металлических УМНЧ (2–6 нм), находившихся под острием СТМ. Эти энергии ΔV, никак не связанные с колебательными переходами, зависят только от размеров УМНЧ, которые определяют их электростатические емкости С:
Для близких по составу и строению квазисферических НЧ, которые могут заметно различаться только характерными размерами D, естественно принять
Здесь β – постоянная, значение которой нетрудно оценить по результатам топографических и спектроскопических СТМ-измерений, определяющих значения ΔV и D.Энергии ΔV(D) определяют характерные периоды “кулоновских осцилляций” туннельных проводимостей наноконтактов, содержащих малые металлические островки [11]. При ΔV(D) ≈ ω установить природу серий равноотстоящих ОДС, используя только критерий их эквидистантности, невозможно. Здесь требуется дополнительная информация, которая, согласно результатам [19], содержится в огибающих линиях ОДС. В зависимости от полярности приложенного напряжения и постоянной электронно-колебательного взаимодействия (α) огибающие могут быть быстро спадающими (или, напротив, быстро растущими и обрывающимися) в случае колебательных спектров или монотонно растущими (с ростом модуля напряжения) в случае кулоновских серий.
Аналитическое выражение для тока резонансных электронов ${{I}^{r}}$, описывающее туннельные спектры УМНЧ с учетом и колебательных переходов, и эффектов одноэлектронного туннелирования, приведено в [19] (формула (16)):
(3)
$\begin{gathered} {{I}^{r}}(\nu ,\eta ) = const\sum\limits_k {{{W}_{k}}(V)} \,\, \times \\ \times \,\,\sum\limits_\nu {\frac{{{{\Gamma }_{1}}(\eta ){{\Gamma }_{2}}(\nu ,\eta ){{\Gamma }_{{12}}}(\nu ,\eta )}}{{{{{(E_{1}^{0}(\eta ) - E_{2}^{0}(\eta ) \pm \omega (\nu + 1{\text{/}}2) + k\Delta V)}}^{2}} + \Gamma _{{12}}^{2}(\nu ,\eta )}}} . \\ \end{gathered} $(4)
${{W}_{k}}(V) = \left\{ \begin{gathered} 1,\quad при\quad (k - 1)\Delta V < V < k\Delta V \hfill \\ 0,\quad при\quad V < (k - 1)\Delta V,\quad V > k\Delta V \hfill \\ \end{gathered} \right..$При надлежащем выборе электронных и колебательных параметров, в число которых входят распадные ширины ${{\Gamma }_{1}}$ и ${{\Gamma }_{2}}$, колебательные кванты ω, постоянные электронно-колебательного взаимодействия α, и энергии одноэлектронного заряжения УМНЧ ΔV, расчеты по этой формуле с хорошей точностью воспроизводят все характерные особенности туннельных спектров частиц с диаметрами D < 5 нм (рис. 1; рис. 2 в [19]).
Рис. 1.
Зависимость для наночастицы золота на пиролитическом графите после трех последовательных экспозиций в водороде и кислороде: 1 – эксперимент [12]; 2 и 3 – фоновый и резонансный токи соответственно при значении параметра “пик-долина”, ξ = 4; 4 – (пунктирная кривая) результаты вычислений резонансного тока по формуле (3) при значениях параметров: α = 0.95, ΔV = 0.4 В, ħω = 0.12 В, ${{\Gamma }_{1}}({v})$ = 0.01 эВ, ${{\Gamma }_{2}}(\nu = 0,{v})$ = 0.032 эВ, ${{\Gamma }_{2}}(\nu = 1,{v})$ = = 0.029 эВ, ${{\Gamma }_{2}}(\nu = 2,{v})$ = 0.007 эВ.

В спектрах, приведенных на рис. 1, отчетливо выделяются короткие колебательные серии, имеющие “малые” периоды (порядка 0.1–0.2 В), которым можно сопоставить колебательные переходы АК, и кулоновские серии с периодами от 0.3 до 0.6 В, простирающиеся на весь диапазон используемых напряжений. Любой подобный спектр можно использовать для количественной оценки коэффициента $\beta $ в формуле (2). При ΔV ≈ 0.4 В, что соответствует спектру, приведенному на рис. 1 настоящей работы, используя результаты соответствующего топографического сканирования, D ≈ 0.3 нм, (рис. 1 [12]), находим $\beta $ ≈ 1.2 В нм. Заметим, что это значение, которое будет использоваться при статистическом анализе результатов спектроскопических измерений, приведенных в [12], хорошо согласуется с данными [11].
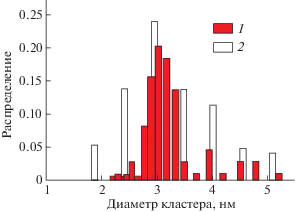
Решение вопроса о физической природе серий равноотстоящих ОДС [19], о наблюдении которых сообщалось в работах по СТМ-зондированию Au-УМНЧ, содержащих [12–18] и не содержащих [23] АК, позволяет получить ответы на некоторые принципиально важные вопросы “золотого” нанокатализа. Прежде всего найдем ответ на вопрос о достоверности предположения о размерном эффекте в адсорбционных свойствах Au-УМНЧ [20]. Воспользуемся с этой целью установленным выше значением постоянной β и по распределению периодов кулоновских осцилляций спектров УМНЧ, содержащих АК, Nа = = Nа(ΔV) (рис. 5 а [12]), найдем распределение “адсорбционно активных” частиц по основному геометрическому параметру D: Nа = Nа(D). Сравнив это распределение с распределением частиц до их взаимодействий с реагентами N = N(D) (рис. 2), приходим к выводу, что в процессах адсорбции газовых реагентов (Н2 и О2) наибольшей активностью обладают частицы с размерами, лежащими в узком диапазоне изменений размеров, от 2.5 до 3.5 нм. Сравнив распределение Nа = = Nа(D) с зависимостями каталитической активности Au-УМНЧ от D, известными из [2–4], приходим к выводу, что именно эти, наиболее активные в процессах адсорбции, УМНЧ определяют свойства каталитической суперактивности нанозолота (рис. 3, 4), как это ранее предполагали авторы [21].
Рис. 3.
Размерные эффекты в адсорбционных и окислительно-каталитических свойствах УМНЧ золота: 1 и 2 – каталитические активности Au/TiO2 катализаторов в реакции низкотемпературного окисления СО кислородом, согласно данным, приведенным на рис. 1 и рис. 3а в [21] соответственно; 3 – распределение “адсорбционно активных” частиц.
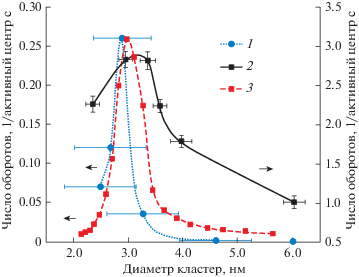
Рис. 4.
Адсорбционная активность УМНЧ золота в сравнении с низкотемпературной активностью Au/Al2O3 катализатора в реакции гидрирования ацетилена: 1 – распределение “адсорбционно активных” частиц; 2 – каталитическая активность Au/Al2O3 катализатора в реакции гидрирования ацетилена, приведенная на рис. 7 в [3].

ЗАКЛЮЧЕНИЕ
Вопрос о роли всех возможных, допускаемых или предполагаемых, этапов сложного поверхностного превращения относится к числу первостепенных в физике и химии гетерогенного катализа. Адсорбция по крайней мере одного из реагентов – необходимый акт многоступенчатого каталитического процесса [22]. В конкретных частных случаях “золотого” нанокатализа – в низкотепературном окислении СО и гидрировании ацетилена, именно этот акт оказывается максимально ускоренным. Причина этого ускорения, которая может быть связана с атомно-структурными [20] или электронными [21] особенностями Au-УМНЧ, нуждается в отдельном рассмотрении.
Работа выполнена в рамках государственного задания по теме “Фундаментальные основы создания наноструктурированных систем нового поколения с уникальными эксплуатационными электрическими и магнитными свойствами” № 0082-2018-0003 (регистрационный номер АААА-А18-118012390045-2) и при финансовой поддержке Российского фонда фундаментальных исследований (грант № 18-03-00453).
Список литературы
Jin R. // Nanotechnol. Rev. 2012. V. 1. P. 31. https://doi.org/10.1515/ntrev-2011-0003
Haruta M., Kobayashi T., Sano H. et al. // Chem. Lett. 1987. V. 16. P. 405. https://doi.org/10.1246/cl.1987.405
Haruta M., Daté M. // Appl. Catal. A. 2001. V. 222. P. 427.
Takei T., Akita T., Nakamura I. et al. // Adv. Catal. 2012. V. 55. P. 1. https://doi.org/10.1016/b978-0-12-385516-9.00001-6
Li G., Jin R. // Nanotechnol. Rev. 2013. V. 2. № 5. P. 529. https://doi.org/10.1515/ntrev-2013-0020
Scanning Tunneling Microscopy I. General Principles and Applications to Clean and Absorbate-Covered Surfaces / Eds. Guntherodt H.-J., Wiesendanger R. Berlin; Heidelberg; New-York: Springer-Verlag, 1994. P. 242.
Далидчик Ф.И., Шуб Б.Р. // Российские нанотехнологии. 2006. Т. 1. № 1–2. С. 82.
Далидчик Ф.И., Буданов Б.А., Колченко Н.Н. и др. // ЖЭТФ. 2012. Т. 142. № 6. С. 1218. https://doi.org/10.1134/S106377611213002
Далидчик Ф.И., Ковалевский С.А., Балашов Е.М. и др. // Кинетика и катализ. 2012. Т. 53. № 5. С. 649. https://doi.org/10.1134/S002315841205004
Dalidchik F., Kovalevskii S., Balashov E. // J. Chem. Phys. 2017. V. 146. P. 194308. https://doi.org/10.1063/1.4983486
Likharev K.K. // Proc. IEEE. 1999. V. 87. № 4. P. 606. https://doi.org/10.1109/5.752518
Гатин А.К., Гришин М.В., Гуревич и др. // Изв. РАН. Серю хим. 2014. Т. 8. С. 1696.
Гришин М.В., Гатин А.К., Дохликова Н.В. и др. // Российские нанотехнологии. 2016. Т. 11. № 11–12. С. 49. https://doi.org/10.1134/S1995078016060112
Гришин М.В., Гатин А.К., Дохликова Н.В. и др. // Кинетика и катализ. 2015. Т. 56. № 4. С. 539. https://doi.org/10.7868/S0453881115040085
Гришин М.В., Гатин А.К., Дохликова Н.В. и др. // Изв. РАН. Сер. хим. 2013. Т. 7. С. 1525. https://doi.org/10.1007/s11172-013-0219-6
Гатин А.К., Гришин М.В., Кирсанкин А.А. и др. // Российские нанотехнологии. 2013. Т. 8. № 1–2. С. 39. https://doi.org/10.1134/S1995078013010059
Гатин А.К., Гришин М.В., Сарвадий С.Ю., Шуб Б.Р. // Синтез, строение и свойства металл/полупроводник содержащих наноструктурированных композитов / Под ред. Трахтенберга Л.И., Мельникова М.Я. М.: Техносфера, 2016. С. 622
Гатин А.К., Гришин М.В., Сарвадий С.Ю. и др. // Химическая физика. 2018. Т. 37. № 3. С. 48. https://doi.org/10.7868/S0207401X18030081
Далидчик Ф.И., Балашов Е.М., Ковалевский С.А. // Письма в ЖЭТФ. 2018. Т. 108. № 7. С. 504. https://doi.org/10.1134/S0370274X18190098
Hvolbæk B., Janssens T.V.W., Clausen B.S. et al. // NanoToday. 2007. V. 2. P. 14. https://doi.org/10.1016/s1748-0132(07)70113-5
Valden M., Lai X., Goodman D.W. // Science. 1998. V. 281. P. 1647. https://doi.org/10.1126/science.281.5383.1647
Крылов О.В. // Гетерогенный катализ. М.: ИКЦ “Академкнига”, 2004. 679 с.
Houbertz R., Weber U., Hartmann U. // Appl. Phys. A. 1998. V. 66. P. S149. https://doi.org/10.1007/s003390051119
Дополнительные материалы отсутствуют.
Инструменты
Российские нанотехнологии