Российские нанотехнологии, 2024, T. 19, № 2, стр. 178-182
Анизотропия диффузии вакансий азота в кристаллическом нитриде алюминия со структурой вюрцита
М. А. Даниляк 1, И. В. Белов 1, В. Г. Валеев 1, *
1 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия
* E-mail: valeev_vg@nrcki.ru
Поступила в редакцию 12.12.2023
После доработки 12.12.2023
Принята к публикации 14.12.2023
Аннотация
Рассчитаны компоненты тензора диффузии вакансий азота в кристаллическом нитриде алюминия со структурой вюрцита, изучен характер их зависимости от концентрации вакансий и температуры системы. Полученные результаты необходимы для разработки замкнутого гидродинамического описания процессов формирования и эволюции вакансионных филаментов в нитридных мемристивных структурах с резистивным переключением.
ВВЕДЕНИЕ
Физический механизм резистивного переключения в нитридных мемристорах (НМ) – эволюция проводящих филаментов в их рабочей зоне – представляет собой процесс диффузии вакансий азота в AlN под действием электрического поля и градиента температуры в системе [1]. Согласно [2] оптимальные условия функционирования НM достигаются в результате сложного компромисса между составом, структурой и геометрией гетероструктуры и ограничениями на диапазоны внешних условий. Исчерпывающие реальные исследования подобных многопараметрических задач по понятным причинам не только весьма затратны, но и невыполнимы практически. Поэтому единственным продуктивным сценарием является их сочетание с численным экспериментом, основанным на понимании физических процессов в системе, формализованных в математическую модель, которая алгоритмизована и воплощена в соответствующей программе. В рассматриваемом случае такой инструмент должен обеспечить самосогласованное описание процессов эволюции распределения в системе электростатического потенциала, температуры и плотности вакансий под действием переменного внешнего смещения и при определенных граничных условиях на все эти поля. Для процессов переноса, как известно, оптимальным по соотношению качества результатов, скорости счета и требований к вычислительным ресурсам, является гидродинамическое приближение. Но для того чтобы применить его к описанию исследуемой системы, необходимо знать тензор диффузии вакансий азота в AlN.
В [3] из первых принципов рассчитаны высоты активационных барьеров при перескоках вакансий азота на соседние узлы кристаллической решетки AlN в зависимости от их заряда и направления движения в рабочей области рассматриваемых здесь НМ – слое кристаллического нитрида алюминия со структурой вюрцита. В табл. 1 приведены величины активационных барьеров при диффузии вакансий азота в кристаллическом AlN со структурой вюрцита в зависимости от их заряда и направления перескока.
Таблица 1.
Величины активационных барьеров при диффузии вакансий азота в кристаллическом AlN со структурой вюрцита в зависимости от их заряда и направления перескока
| Заряд вакансии N в AlN | Активационный барьер при диф-фузии вакансии в плоскости $\alpha \left( {a \cap b} \right)$, эВ | Активационный барьер при диф-фузии вакансии в плоскости $\beta \left( {a \cap c} \right)$, эВ |
|---|---|---|
| –3е | 2.01 | 2.53 |
| –2e | 1.77 | 2.63 |
| –1e | 1.43 | 2.54 |
| 0 | 2.73 | 3.69 |
| 1e | 4.31 | 4.58 |
| 2e | 5.31 | 3.50 |
| 3e | 3.35 | 2.72 |
В настоящей работе на основе полученных данных рассчитан тензор диффузии $\hat {D}$ вакансий азота в этой системе в отсутствие внешнего электрического поля. Для анализа зависимости его компонент от локальной температуры среды расчеты проведены для трех температур – 300, 500 и 1000 К. Как будет видно из результатов, этого массива данных вполне достаточно для ее характеризации. При этом рассмотрен лишь случай вакансий $V_{{\text{N}}}^{q}$ с зарядом $q = - 1$e, которые, согласно табл. 1, в основном определяют кинетику филаментов в НМ.
МЕТОД ИССЛЕДОВАНИЯ
Рассмотрим диффузию заряженных вакансий азота в кристаллическом AlN со структурой вюрцита как термически активированное скачкообразное движение по узлам N кристаллической решетки. Если все ближайшие узлы решетки заполнены, возможны 12 направлений прыжков заряженных вакансий азота: шесть из них расположены в плоскости (0001) кристалла, еще по три направления ориентированы вверх и вниз относительности плоскости (0001) попарно симметрично относительно нее. Хотя рассматриваемая система имеет объемную симметрию $C_{{6{v}}}^{4}$, возможные пути диффузии заряженных вакансий $V_{{\text{N}}}^{q}$ (рис. 1) характеризуются тригональной симметрией ${{C}_{{3{v}}}}$.
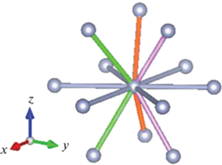
Рис. 1.
Возможные пути диффузии вакансий азота в кристаллическом AlN со структурой вюрцита. Траектории движения, попарно симметричные относительно плоскости (0001), окрашены одним цветом.
В предположении, что перенос вакансий в системе обусловлен только градиентом их концентрации n(r, t), компоненты соответствующей плотности потока частиц j(r, t) подчиняются закону Фика:
(1)
${{j}_{\alpha }}({\mathbf{r}},t) = - {{D}_{{\alpha \beta }}}{{\nabla }_{\beta }}n({\mathbf{r}},t),$(2)
${{\partial n({\mathbf{r}},t)} \mathord{\left/ {\vphantom {{\partial n({\mathbf{r}},t)} {\partial t}}} \right. \kern-0em} {\partial t}} = {{\nabla }_{\alpha }}{{D}_{{\alpha \alpha }}}{{\nabla }_{\alpha }}n({\mathbf{r}},t),$Предположим, что тензор диффузии в (2) зависит явно только от концентрации диффузанта: ${{D}_{{\alpha \alpha }}} = {{D}_{{\alpha \alpha }}}\left( {n({\mathbf{r}},t)} \right)$, а профиль концентрации диффундирующих частиц в начальный момент времени зависит лишь от координаты вдоль одного из его главных направлений – пусть для определенности ${{\left. {n({\mathbf{r}},t)} \right|}_{{t = o}}} = n(x,0)$. Тогда уравнение (2) становится одномерным, а подстановка Больцмана ${{\left( {x - {{X}_{M}}} \right)} \mathord{\left/ {\vphantom {{\left( {x - {{X}_{M}}} \right)} {2\sqrt t }}} \right. \kern-0em} {2\sqrt t }} = \xi $, где ${{X}_{M}}$ – координата некой фиксированной точки оси $Ox$, позволяет свести его к обыкновенному нелинейному дифференциальному уравнению вида
(3)
$2\xi \frac{{dn}}{{d\xi }} = \frac{d}{{d\xi }}\left( {{{D}_{{xx}}}\left( n \right)\frac{{dn}}{{d\xi }}} \right).$На этом свойстве уравнения (2) основан классический метод Матано–Больцмана [4], который позволяет решить обратную задачу и определить неизвестную компоненту тензора диффузии по известным из эксперимента значениям $n(x,t)$ для так называемой диффузионной пары – пространственно-однородной системы толщиной ${{L}_{ \prec }} + {{L}_{ \succ }}$ с одномерным начальным распределением концентрации диффундирующих частиц вида $n(x,0)$ = = $n{}_{ \prec }\theta \left( {{{L}_{ \prec }} - x} \right)$ + $n{}_{ \succ }\theta \left( {x - {{L}_{ \succ }}} \right)$ и при условии, что в ходе эксперимента они не успевают достичь ее внешних границ, т.е. что ${{\left. {{{\partial n(x,t)} \mathord{\left/ {\vphantom {{\partial n(x,t)} {\partial x}}} \right. \kern-0em} {\partial x}}} \right|}_{{{{L}_{ \pm }}}}} = 0.$ В этом случае любая плоскость заданной концентрации перемещается в эксперименте со скоростью ~$\sqrt t $. При этом параметр ${{X}_{M}}$ выбирается из условия, чтобы поток диффундирующих частиц через плоскость $x = {{X}_{M}}$ (называемую плоскостью Матано) был равен нулю: ${{\left. {{\mathbf{j}}({\mathbf{r}},{{t}_{0}})} \right|}_{{x = {{X}_{M}}}}}$ ≡ ${{j}_{x}}(x,{{t}_{0}}){{{\mathbf{e}}}_{x}}$ = 0, где ${{t}_{0}}$ – момент измерения, ${{{\mathbf{e}}}_{x}}$ – единичный вектор оси $Ox$.
Соответствующее дискретизированное решение обратной задачи диффузии имеет вид, например, [5]:
(4)
$\begin{gathered} {{D}_{{xx}}}\left( {n({{x}_{i}})} \right) = \frac{1}{{2{{t}_{0}}}}\left[ {\frac{{{{x}_{{i + 1}}} + {{x}_{{i - 1}}}}}{{n({{x}_{{i + 1}}}) - n({{x}_{{i - 1}}})}}} \right] \times \\ \times \;\sum\limits_{i = 2}^N {\left[ {\left( {{{X}_{M}} - \frac{{{{x}_{{i + 1}}} + {{x}_{{i - 1}}}}}{2}} \right)\left( {n({{x}_{{i + 1}}}) - n({{x}_{{i - 1}}})} \right)} \right]} , \\ \end{gathered} $(5)
${{X}_{M}} = \frac{1}{{{{n}_{{\max }}} - {{n}_{{\min }}}}}\sum\limits_{1 = 1}^{N - 1} {\left[ {\left( {\frac{{n({{x}_{{i + 1}}}) - n({{x}_{i}})}}{2}} \right)\left( {{{x}_{{i + 1}}} + {{x}_{i}}} \right)} \right]} ,$Отметим, что последнее условие ставит под сомнение саму возможность осуществления реального эксперимента в такой постановке, но не представляет трудности для его численного моделирования, пусть и сопряженного с определенными методическими ограничениями. Действительно, нахождение массива концентраций $\left\{ {n({{x}_{i}},{{t}_{0}})} \right\}$ заряженных вакансий методом молекулярной динамики затруднено, так как временной шаг молекулярной динамики ~10–15 c, тогда как в исследуемой системе имеют место высокобарьерные события с характерными временами ~10–9 c и более (табл. 1). Поэтому для ее моделирования существенно более эффективен кинетический метод Монте-Карло [6], который численно описывает процесс хаотического движения системы через последовательность квазиравновесных состояний, отвечающих реализации наименьших энергетических барьеров вдоль траектории конфигурационного пространства, ведущей к состоянию термодинамического равновесия. Здесь рассмотрены процессы диффузии вакансий азота при фиксированных температурах в сверхъячейке кристаллического нитрида алюминия со структурой вюрцита, состоящей из 50 × 50 × 200 элементарных ячеек со структурой вюрцита, и реализован алгоритм моделирования канонического ансамбля атомов, подробно описанный, к примеру, в [6].
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Некоторые результаты моделирования процесса диффузии вакансий в главных направлениях тензора диффузии при температуре 1000 К представлены на рис. 2. Начальная высота концентрационной ступеньки в этих расчетах составляла от 1 до 100% вакансий азота на элементарную ячейку нитрида алюминия с шагом 9%. При этом 100% начальной высоты концентрационной ступеньки вакансий соответствует структуре, состоящей из 175 × 104 атомов и 25 × 104 вакансий с зарядом –1е.
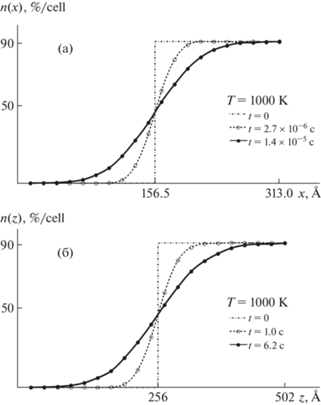
Рис. 2.
Зависимости концентрации вакансий от координат по мере расплывания концентрационной ступеньки высотой 91% на элементарную ячейку AlN (пунктир с точкой) в расчетах коэффициента диффузии методом Матано–Больцмана при Т = 1000 К: a – ось Oz ориентирована вдоль направления [0001], б – ось Ox лежит в плоскости (0001).
Результаты расчета концентрационной зависимости главных компонент тензора диффузии на основе формул (4), (5) приведены на рис. 3, где сплошной линией изображен результат подгонки зависимостью
(6)
${{D}_{{\alpha \alpha }}}\left( {n({{x}_{\alpha }})} \right) = D_{{\alpha \alpha }}^{{(0)}}\exp \left( { - {{n({{x}_{\alpha }})} \mathord{\left/ {\vphantom {{n({{x}_{\alpha }})} {n_{\alpha }^{{(0)}}}}} \right. \kern-0em} {n_{\alpha }^{{(0)}}}}} \right),$Рис. 3.
Концентрационные зависимости главных значений тензора диффузии вакансий азота в кристаллическом нитриде алюминия при Т = 300, 500 и 1000 К: a – ось Oz ориентирована вдоль направления [0001], б – ось Ox лежит в плоскости (0001). Сплошная линия – результат подгонки полученных данных зависимостью, ${{D}_{{\alpha \alpha }}}\left( {n({{x}_{\alpha }})} \right)$ = = $D_{{\alpha \alpha }}^{{(0)}}\exp \left( { - {{n({{x}_{\alpha }})} \mathord{\left/ {\vphantom {{n({{x}_{\alpha }})} {n_{\alpha }^{{(0)}}}}} \right. \kern-0em} {n_{\alpha }^{{(0)}}}}} \right)$, где $\alpha = x,z$, а параметры подгонки даны в табл. 2, 3 соответственно.
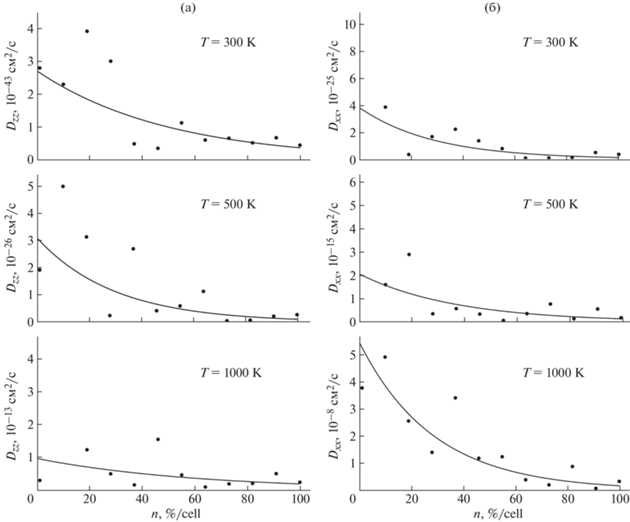
Таблица 2.
Величины параметров подгонки для концентрационной зависимости главного значения ${{D}_{{zz}}}$ тензора диффузии вакансий азота в кристаллическом AlN со структурой вюрцита при Т = 300, 500 и 1000 К
| Т, К | $D_{{zz}}^{{(0)}}$, см2/c | $n_{z}^{{(0)}}$, см–3 |
|---|---|---|
| 300 | 2.7 × 10–43 | 50.1 |
| 500 | 3.1 × 10–26 | 29.8 |
| 1000 | 9.6 × 10–14 | 61.4 |
Таблица 3.
Величины параметров подгонки для концентрационной зависимости главного значения ${{D}_{{xx}}}$ тензора диффузии вакансий азота в кристаллическом AlN со структурой вюрцита при Т = 300, 500 и 1000 К
| Т, К | $D_{{xx}}^{{(0)}}$, см2/c | $n_{x}^{{(0)}}$, см–3 |
|---|---|---|
| 300 | 3.8 × 10–25 | 28.7 |
| 500 | 2.1 × 10–15 | 36.9 |
| 1000 | 5.5 × 10–8 | 28.6 |
Как видно, параметры подгонки существенным образом зависят от температуры, и дальнейшее применение рассмотренного метода расчета компонент тензора диффузии к решению конкретных задач потребует более детального анализа этих зависимостей.
Согласно результатам выполненного расчета диффузия вакансий азота в кристаллическом нитриде алюминия со структурой вюрцита имеет существенно анизотропный характер, так что в отсутствие внешнего электрического поля перенос вакансий в исследованном здесь интервале температур 300–1000 К происходит преимущественно в плоскости (0001). Нетрудно видеть, что в данном интервале температур вклад в диффузию перескоков, не лежащих в этой плоскости, ничтожен, так что ${{D}_{{xx}}} = {{D}_{{yy}}}$ ~ $\exp ({{ - \hbar {{\omega }_{{{\text{jamp}}}}}} \mathord{\left/ {\vphantom {{ - \hbar {{\omega }_{{{\text{jamp}}}}}} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}})$, где частота перескоков ${{\omega }_{{{\text{jamp}}}}} \approx 1.43$ эВ (табл. 1).
ЗАКЛЮЧЕНИЕ
В контексте мемристивных применений указанный выше факт означает, что в рабочем режиме НМ перенос вакансий через границы пленки AlN, выращенной вдоль плоскости (0001), практически отсутствует, но может иметь место под действием импульса формовки. Кинетика происходящих при этом процессов требует специального рассмотрения, однако априори ясно, что оптимальная степень нестехиометричности рабочей области мемристора по азоту является существенным параметром, выбор которого зависит, в частности, и от меры участия электродов в ее вакансионном балансе.
Отметим, что полученные результаты позволяют восстановить и зависимости компонент тензора диффузии вакансий от градиента потенциала, что дает возможность применить их для моделирования процессов формирования и эволюции вакансионных филаментов в исследуемой системе в рамках самосогласованного гидродинамического приближения.
Работа выполнена при финансовой поддержке Российского научного фонда, проект № 22-29-00535.
Численное моделирование выполнено на ресурсах Федерального центра коллективного пользования научным оборудованием “Комплекс моделирования и обработки данных исследовательских установок мега-класса” НИЦ “Курчатовский институт”.
Список литературы
Chen C., Yang Y.C., Zeng F. et al. // Appl. Phys. Lett. 2010. V. 97. № 8. P. 083502. https://doi.org/10.1063/1.3483158
Kim H.D., An H.M., Lee E.B. et al. // IEEE Trans. Electron Dev. 2011. V. 58. № 10. P. 3566. https://doi.org/10.1109/TED.2011.2162518
Даниляк М.А., Белов И.В., Чумаков Н.К., Валеев В.Г. // Российские нанотехнологии. 2023. Т. 18. № 6. С. 761. https://doi.org/10.56304/S1992722323060055
Glicksman M.E. Diffusion in Solids: Field Theory, Solid-State Principles, and Applications. Wiley, 2000. 481 p.
Лобанов М.Л., Зорина М.А. Методы определения коэффициентов диффузии. Екатеринбург. Изд-во Урал. ун-та, 2017. 100 с.
Kolesnikov S.V., Saletsky A.M., Dokukin S.A. et al. // Math. Models Comput. Simul. 2018. V. 10. P. 564. https://doi.org/10.1134/S2070048218050071
Дополнительные материалы отсутствуют.
Инструменты
Российские нанотехнологии


