Неорганические материалы, 2019, T. 55, № 10, стр. 1101-1107

Исследование кристаллизационной устойчивости оптически активных стекол GeS_x〈Bi〉

А. М. Кутьин¹, А. Д. Плехович^1, *, М. В. Суханов¹, К. В. Балуева¹

¹ Институт химии высокочистых веществ им. Г.Г. Девятых Российской академии наук
603951 Нижний Новгород, Тропинина ул., 49, Россия

^* E-mail: plehovich@gmail.com

Поступила в редакцию 28.12.2018
После доработки 12.02.2019
Принята к публикации 28.02.2019

DOI: 10.1134/S0002337X19080050

Полный текст (PDF)

Аннотация

Методом дифференциальной сканирующей калориметрии (ДСК) в области 320−1000 К изучена кинетика кристаллизации особочистых стекол системы Ge–S, легированных висмутом GeS_x〈nBi〉 (1.25 ≤ х ≤ 1.6, n = 1 ат. %). Развитая методика обработки кристаллизационных пиков дает возможность их описания, не уступающего полуэмпирической модели Ерофеева при аналитической форме степени кристаллизации α (t, Т), развивающей упрощенный вариант теории Колмогорова–Мейла–Джонсона. Найденные по методике кинетические характеристики кристаллизации стекла в зависимости α (t, Т) и ее графическом представлении в виде ТТТ (Time–Temperature–Transition)-диаграммы позволяют определить оптимальные температурно-временные условия изготовления волоконных световодов.

Ключевые слова: кинетика кристаллизации, дифференциальная сканирующая калориметрия, халькогенидное стекло

ВВЕДЕНИЕ

Халькогенидные германийсодержащие стекла, легированные висмутом, рассматриваются как перспективные материалы для нелинейной оптики, оптоэлектроники и высококонтрастной фотолитографии благодаря наличию ультраширокой полосы люминесценции [1, 2]. Они прозрачны в спектральном диапазоне от 0.6 до 8.0 мкм, имеют высокие температуры стеклования, низкие энергии фононов, характеризуются высокой растворимостью редкоземельных элементов [3].

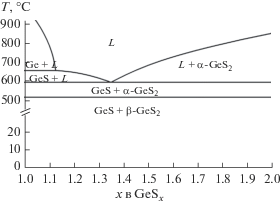
На фазовой диаграмме базовой стеклообразующей системы Ge–S [4] (ее часть представлена на рис. 1) отмечены эвтектика при х = 1.35 как фактор, сопутствующий стеклообразованию, и две стеклообразующие области [5–7] при х = 2−9 и х = 1.31−1.5. Определены области стеклообразования указанных стекол с добавками висмута. По данным работы [8], такая область расположена вдоль линии Ge₂₀S₈₀ _– x−Bi_x до 15 ат. % Bi, а в работе [9] – вдоль линии GeS₂−Bi₂S₃ до 25 ат. % Bi.

Рис. 1.

Часть диаграммы состояния системы Ge–S [4–6].

Изучение кристаллизации в температурной области переохлажденного расплава Ge–S [10, 11] показало, что кинетика кристаллизации хорошо описывается моделью Шестака–Берггрена, в основе которой полуэмпирическая модель Ерофеева. Однако отсутствие аналитически выраженной температурно-временной зависимости степени кристаллизации затрудняет ее практическое использование, в том числе учет неизотермичности измерений методом дифференциальной сканирующей калориметрии (ДСК).

Введение редкоземельных элементов или Bi в качестве оптически активных добавок в бинарную основу GeS_x ставит перед производителями оптических элементов дополнительные задачи, связанные с исследованием кристаллизационной устойчивости новых по составу стекол для получения волоконных и планарных устройств с необходимой фазовой чистотой.

В статье [12] в связи с природой люминесценции висмута изучено его межфазное распределение. Было показано, что легирующая примесь Bi не включается в решетку кристаллов сульфида германия, а в стекле находится в растворенном виде. Содержание висмута более 1 ат. % повышает вероятность образования индивидуальной металлической фазы. Кинетика кристаллизации легированных висмутом стекол GeS_x в настоящее время не изучена.

Целью настоящей работы явилось исследование кристаллизационных процессов в синтезированных высокочистых образцах стекол, легированных висмутом GeS_x〈nBi〉 (1.25 ≤ х ≤ 1.6, n = 1 aт. %), методом ДСК, а также разработка методики обработки ДСК-пиков посредством унифицированной модели кристаллизации и ее использование для минимизации кристаллизации при получении оптических стекол и световодов с достаточной фазовой чистотой.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Исследовали кристаллизацию стекол составов: GeS_1.25 + 0.01Bi, GeS_1.35 + 0.01Bi, GeS_1.4 + 0.01Bi, GeS_1.6 + 0.01Bi. Методика их получения и сведения о чистоте образцов приведены в работах [12, 13].

Для измерений готовилась серия образцов массой 30–40 мг. Контактирующие с дном тигля поверхности образцов подвергались шлифовке для обеспечения воспроизводимого контакта с последующими ультразвуковой очисткой в дистиллированной воде и сушкой. Для измерений использовались предварительно отожженные алюминиевые тигли как наиболее химически инертные по отношению к стеклу Ge–S.

ДСК-кривые для четырех изученных образцов (рис. 2) в ходе линейного повышения температуры последовательно представляют участки стеклообразного состояния, заканчивающиеся соответствующими “ступенями” расстекловывания в интервале температур 351–381 К, и следующие за ними интервалы вязкотекучего или переохлажденного жидкого состояния, в которых “проявляются” соответствующие пики кристаллизации. Результаты стандартной обработки ДСК-кривых (температура стеклования определялась по точке перегиба в интервале стеклования, а температуры кристаллизации и плавления – по началу пика, определяемого пересечением касательной переднего фронта пика с линией основания пика) представлены в табл. 1. Табличные данные демонстрируют также установленную зависимость температур кристаллизации от состава переохлажденного расплава GeS_x + 0.01Bi. При х = 1.25, 1.35, 1.4 последовательно кристаллизуются GeS и GeS₂, а при х = 1.6 образуется только кристалл GeS₂. Такой характер кристаллизации соответствует фазовой диаграмме Ge–S. Возможное фазовое превращение β-GeS₂ в α-GeS₂ не наблюдается [12].

Рис. 2.

ДСК-кривые сульфид-германатных стекол: 1 – GeS_1.25 + 0.01Bi, 2 – GeS_1.35 + 0.01Bi, 3 – GeS_1.4 + + 0.01Bi, 4 – GeS_1.6 + 0.01Bi при скорости нагревания 10 К/мин.

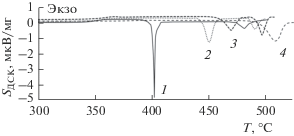
Таблица 1.

Температуры стеклования (T_g) в стеклообразующем расплаве GeS_x + 0.01Bi в зависимости от содержания серы (х), а также температуры кристаллизации (Т_cr) GeS и GeS₂ из переохлажденных расплавов (скорость нагревания 10 К/мин)

x	T_g, °С	Т_cr, °С		ΔT = T_cr – T_g
x	T_g, °С	GeS	GeS₂	GeS	GeS₂
1.25	350.9	401.1	472.9	50.2	122
1.35	355.9	443.2	488.8	87.3	132.9
1.40	356.3	460.6	491.2	104.3	134.9
1.5*				135**	135**
1.60	381.3	–	489.1	–	107.8

* Экстраполированное значение содержания серы. ** Стекло с одновременной и совмещенной кристаллизацией GeS и GeS₂.

Определяемые методом ДСК температуры стеклования и кристаллизации часто используются для качественной оценки стабильности стекла к кристаллизации посредством эмпирического критерия ΔT = T_cr – T_g (табл. 1), величина которого пропорциональна кристаллизационной устойчивости. Однако детальную и полную информацию о скоростях кристаллизационных процессов можно получить после анализа и обработки участков ДСК-кривых, соответствующих пикам кристаллизации.

МЕТОДИКА ОБРАБОТКИ КРИСТАЛЛИЗАЦИОННЫХ ДСК-ПИКОВ

Кристаллизацию стекла А можно представить квазихимической реакцией А → *А, которая определяет текущее изменение энтальпии процесса ∆Н [14] мольной координатой ξ и энтальпией реакции кристаллизации ∆_rH

(1)

$\Delta Н = {\text{ }}\xi {{\Delta }_{r}}H = {\text{ }}\alpha {{n}_{0}}{{\Delta }_{r}}H = {\text{ }}\alpha {{m}_{0}}({{{{\Delta }_{r}}H} \mathord{\left/ {\vphantom {{{{\Delta }_{r}}H} M}} \right. \kern-0em} M}).$

Второе и третье выражения в цепочке (1) записаны с использованием степени кристаллизации α = ξ/n₀ как доли текущего числа молей ξ от начального количества n₀ = m₀/M исходной (маточной) фазы; m₀ и М – соответственно начальная и мольная масса кристаллизующегося вещества.

Деление уравнения (1) на m₀ определяет взаимосвязь указанных энтальпий и теплот в удельных, т.е. отнесенных к единице массы, величинах:

$\frac{{\Delta H}}{{{{m}_{0}}}} = \alpha \frac{{{{\Delta }_{r}}H}}{M},\,\,\,\,{{Q}_{m}} = \alpha {{Q}_{{rM}}}.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1')$

Второе из уравнений (1') связывает текущую удельную теплоту Q_m = –∆Н/m₀ с удельной теплотой реакции А → *А Q_rM = –∆_rH/M.

В определенных пределах независимым от массы образца в приборах “ДСК теплового потока” принято [15] считать сигнал, пропорциональный удельному тепловому потоку

(2)

${{S}_{{{\text{ДСК}}}}} = C{{\dot {Q}}_{m}} = С\dot {\alpha }{{Q}_{{rM}}} = {{C}_{N}}\dot {\alpha },$

где поток $\frac{{{\text{d}}{{Q}_{m}}}}{{{\text{d}}t}}$ = ${{\dot {Q}}_{m}}$ = $\dot {\alpha }{{Q}_{{rM}}}$ получен дифференцированием по времени второго из уравнений (1'). Таким образом, форма кристаллизационного пика при постоянных $\dot {С}$ и ${{Q}_{{rM}}}$ определяется скоростью кристаллизации $\dot {\alpha }$ = $\frac{{{\text{d}}\alpha }}{{{\text{d}}t}},$ а текущая площадь пика – интегралом от выражения (2), равным $С\alpha {{Q}_{{rM}}}.$ Очевидно, что площадь всего пика после окончания кристаллизации образца (α = 1) равна $С{{Q}_{{rM}}}.$

Подобные рассуждения справедливы и для пиков плавления, по которым производится калибровка прибора. Поэтому для калиброванного прибора (С = 1) значение и размерность приборной или нормировочной константы ${{С}_{N}}$ = $С{{Q}_{{rM}}}$ соответствуют величине и размерности удельной теплоты процесса ${{Q}_{{rM}}}$ (Дж/г), обеспечивая размерность ДСК-сигнала (Дж/(г с)) как удельного потока тепла или удельной мощности.

При размерности сигнала прибора [S_ДСК] = = мкВ/мг размерность нормировочной константы равна $\left[ {{{С}_{N}}} \right]$ = $\left[ {\frac{{{{S}_{{{\text{ДСК}}}}}}}{{\dot {\alpha }}}} \right]$ = $\frac{{{\text{мкВ с}}}}{{{\text{мг}}}}.$

Температурная и временная зависимость степени кристаллизации в наиболее распространенной модели Джонсона–Мейла–Аврами (ДМА), которая является значительным упрощением теории Колмогорова–Джонсона–Мейла, имеет вид

(3)

$\alpha (t,Т) = 1--{\text{exp}}(--{{\tau }^{n}}).$

Здесь τ = kt, k = A exp(–E_a/(RT)) – константа скорости кристаллизации в представлении Аррениуса, A – предэкспоненциальный множитель, E_a – энергия активации, n – степенной параметр ДМА, качественно соответствующий т. н. размерному параметру теории Колмогорова–Джонсона–Мейла. Интегральной форме модели ДМА (3) соответствует ее дифференциальная форма

(4)

$\begin{gathered} \dot {\alpha } = \frac{{d\alpha }}{{dt}} = k\alpha _{{\tau }}^{'}(\alpha ); \\ \alpha _{{\tau }}^{'}(\alpha ) = n(1 - \alpha ){{[ - \ln (1 - \alpha )]}^{{1 - {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}}}}, \\ \end{gathered} $

где для производной от α по безразмерному времени τ часто используется обозначение $\alpha _{{\tau }}^{'}(\alpha )$ = ${\text{f}}(\alpha ).$

Шестак и Берггрен (Sestak–Berggren) [16], а вслед за ними Малек [17] показали, что полуэмпирическая модель кристаллизации Ерофеева [18] является более точной для обработки ДСК-пиков кристаллизации по сравнению с моделью ДМА. Дифференциальная форма этой модели имеет вид

(5)

$\dot {\alpha } = {{k}_{{{\text{эф}}}}}{{\alpha }^{a}}{{(1 - \alpha )}^{b}}.$

Однако отсутствие решения α (t, Т) дифференциального уравнения (5) в аналитической форме осложняет численную обработку результатов эксперимента, учет неизотермичности ДСК-измерений и, как следствие, заметно ограничивает предсказательные возможности модели. Другим существенным недостатком полуэмпирической модели является скрытое в эмпирических степенных параметрах a и b смысловое содержание, а также эффективный характер константы скорости k_эф. Последние факторы затрудняют выявление деталей механизма кристаллизации с позиции представлений Колмогорова–Джонсона–Мейла.

Отмеченные недостатки устраняются в предлагаемой унифицированной модели кристаллизации (УМК), интегральная и дифференциальная форма которой имеют вид

(6)

$\alpha (t,T) = \frac{1}{{{{{(1 + {1 \mathord{\left/ {\vphantom {1 {{{\tau }^{n}}}}} \right. \kern-0em} {{{\tau }^{n}}}})}}^{p}}}},$

(7)

$\dot {\alpha } = \alpha _{{\tau }}^{'}\tau _{t}^{'} = k\alpha _{{\tau }}^{'} = knp{{\alpha }^{{1 - {1 \mathord{\left/ {\vphantom {1 {(np)}}} \right. \kern-0em} {(np)}}}}}{{(1 - {{\alpha }^{{{1 \mathord{\left/ {\vphantom {1 p}} \right. \kern-0em} p}}}})}^{{1 + {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}}}}.$

Сопоставление формул (3), (4) и (6), (7) показывает, что при едином способе определения температурно-временной зависимости α (t, Т) только через произведение τ = kt роль важного для модели ДМА параметра n, эффективным образом определяющего механизм кристаллизации, в УМК переходит к произведению np. Наконец, сравнение формул (5) и (7) показывает, что УМК раскрывает содержание как степенных параметров a и b полуэмпирической модели, так и эффективной константы скорости k_эф.

При нагревании с постоянной скоростью β температура измерительной ячейки, отсчитываемая от начала пика кристаллизации Т₀, является линейной функцией времени:

(8)

$T = {{T}_{0}} + \beta t.$

Результат дифференцирования в формулах (4) и (7) с учетом (8) при аррениусовой форме k

(9)

$\dot {\alpha } = \frac{{{\text{d}}\alpha }}{{{\text{d}}t}} = \alpha _{{\tau }}^{'}\tau _{t}^{'} = \alpha _{{\tau }}^{'}k\left( {1 + \frac{{(T - {{T}_{0}})\theta }}{{{{T}^{2}}}}} \right)$

отличается от выражений (4) и (7) только сомножителем в скобках и при естественном отнесении его к “неизотермической” константе скорости

(10)

$\bar {k} = k\left( {1 + \frac{{(T - {{T}_{0}})\theta }}{{{{T}^{2}}}}} \right)$

повторяет их с заменой $k$ на $\bar {k}.$

Наличие в УМК явного выражения для степени кристаллизации существенно упрощает решение задачи параметризации при обработке кристаллизационных ДСК-пиков, сводя ее к нелинейной регрессии со стандартными процедурами минимизации среднеквадратичного отклонения экспериментальных и рассчитанных по уравнениям (2)–(4), (6), (7), (10) значений ДСК-сигнала.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Методика обработки данных ДСК должна учитывать изменение температуры во время измерения. Игнорирование неизотермичности условий определения кинетических констант, как показано в работе [19], может привести к погрешностям определения температурно-временной зависимости степени кристаллизации α (T, t) 10% и более.

Обработка методом наименьших квадратов (нелинейная регрессия) кристаллизационных пиков (рис. 3) по отражающим неизотермичность измерений уравнениям (6)–(10) дает параметры (табл. 2), в которых вычисленная энергия активации E_a дополнительно контролировалась уравнением Киссинджера. Кроме “технических” констант (Т₀, C_N), кинетические параметры кристаллизации не зависят от скорости сканирования, что в свою очередь повышает достоверность определения α (T, t).

Рис. 3.

Измеренные (значки) и рассчитанные (линии) по уравнениям (2), (6)–(10) значения ДСК-сигнала при скоростях нагревания 10 К/мин: (×) и (- - -) и 15 К/мин: (⚪) и (· - · -); пикам кристаллизации соответствуют синхронизированные со временем температурные зависимости степени кристаллизации (α) для стеклообразующих расплавов GeS_x + 0.01Bi с х = = 1.25 (a), 1.35 (б), 1.4 (в), 1.6 (г).

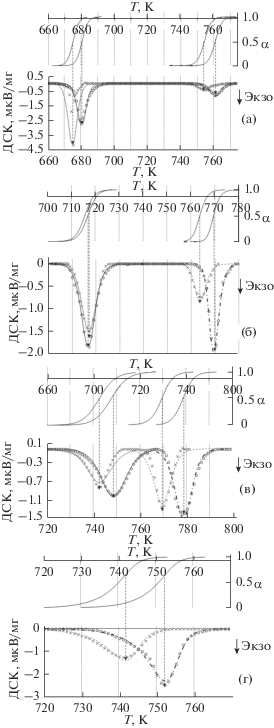
Таблица 2.

Кинетические параметры УМК стекол GeS_x + 0.01Bi (E_a – энергия активации, s – натуральный логарифм предэкспоненциального множителя, n, p – степенные параметры)

х	E_a, кДж/моль	s = ln(A/с^–1)	n	p	Т₀		C_N, мкВ/мг
х	E_a, кДж/моль	s = ln(A/с^–1)	n	p	10*	15*	10*	15*
Образование фазы GeS
1.25	324.8	52.82	4.64	0.86	650.1	656.6	180.42	81.72
1.35	483.1	74.90	4.15	0.91	640.94	663.97	71.61	56.93
1.40	322.2	45.88	3.50	1.01	651.1	658.2	60.57	58.48
Образование фазы GeS₂
1.25	494.6	72.38	4.28	0.93	646.9	678.6	24.60	29.65
1.35	644.9	97.05	3.13	1.28	747.0	757.7	31.26	42.82
1.40	417.4	58.63	4.64	0.86	652.9	697.1	67.21	56.08
1.60	312.3	44.41	6.57	0.32	670.6	699.8	98.24	104.65

Примечание. Произведение np по форме вхождения в уравнение (7) соответствует параметру n в модели ДМА (см. уравнение (4)); составы стекол, близкие к эвтектическому, характеризуются более высокой энергией активации. * Скорость нагревания, К/мин.

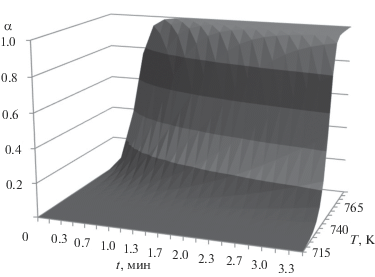
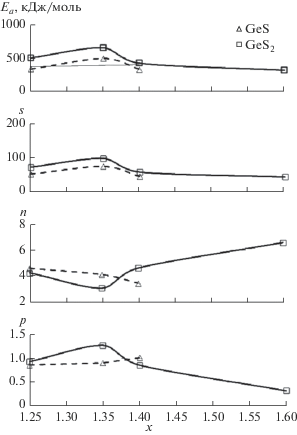
Графическая зависимость кристаллизационных параметров E_a, s, n, p от состава стекол представлена на рис. 4. Рассчитанные по этим параметрам температурно-временные диаграммы α (t, Т) (рис. 5) – основа прогнозирования температурно-временных режимов обработки стекол, минимизирующих кристаллизацию, а значит ее вклад в оптические потери.

Рис. 4.

Зависимости кинетических параметров кристаллизации (табл. 2) E_a, s, n, p фаз GeS и GeS₂ от содержания серы в стеклообразующем расплаве GeS_x + + 0.01Bi (x = 1.25–1.6).

Рис. 5.

ТТТ (Time–Temperature–Transition)-диаграмма стекла GeS_1.6 + 0.01Bi.

Кристаллизация из переохлажденного расплава GeS_x + 0.01Bi (x = 1.25–1.6) с небольшими, в первом приближении не влияющими на процесс, добавками Bi происходит при температурах ниже линии солидуса диаграммы Ge–S. Конечным состоянием в этом случае является смесь кристаллов GeS + GeS₂. В отличие от обычных переходов, соответствующих диаграмме плавкости, кристаллизация из переохлажденного расплава для ряда исследованных стекол: слева от эвтектического (х = 1.25), эвтектического (х = 1.35) и следующего за ним (х = 1.40) происходит следующим образом. При повышении температуры после расстекловывания следующие друг за другом пики кристаллизации соответствуют образованию рентгенографически подтвержденных кристаллов GeS, а затем GeS₂. Температурный интервал между пиками при их общем сдвиге в область высоких температур уменьшается, по оценке стремясь к совпадению при x = 1.5 (рис. 2, 3 а–3в). При х > 1.5, как это наблюдается для текла с x = 1.60, кристаллизуется индивидуальная фаза GeS₂ (рис. 2, 3 г). Возвращаясь к табл. 1 и примечанию к ней, отметим, что при максимальном содержании серы x = 1.5, при котором совмещаются кристаллизационные пики образования GeS и GeS₂, судя по соответствующему значению эмпирического критерия ΔT = T_cr – T_g, достигается максимальная устойчивость к кристаллизации. Для стекла с x = 1.60, в котором образуется единственная фаза GeS₂ и наблюдается один пик кристаллизации, критерий ΔT(x) уменьшается от ΔT(1.5) = = 135 К до ΔT(1.6) = 107.8 К (см. табл. 1).

ЗАКЛЮЧЕНИЕ

По эмпирическому критерию с использованием полученных температур стеклования и кристаллизации в стеклообразующих расплавах GeS_x + 0.01Bi (х = 1.25, 1.35, 1.4, 1.6) выявлен максимально устойчивый к кристаллизации состав стекла с содержанием серы х = 1.5. Менее стойкими к кристаллизации оказываются стекла как с меньшим содержанием серы, так и с бóльшим. С повышением температуры при х ≤ 1.5 поочередно выделяются кристаллы GeS и GeS₂. При x ≥ 1.5 наблюдается единственный пик кристаллизации с образованием фазы GeS₂.

Обработка кристаллизационных пиков по методике, использующей УМК, позволила определить инвариантные к скорости термосканирования параметры кристаллизации фаз GeS и GeS₂ для всех образцов GeS_x + 0.01Bi (x = 1.25, 1.35, 1.4, 1.6). При этом набор четырех основных кинетических параметров E_a, s, n, p определяет температурно-временную зависимость доли (степени) α (t, Т) образования каждой из кристаллизующихся фаз – GeS и GeS₂. Полученные зависимости дают возможность прогнозирования параметров кристаллизации, а значит, и α (t, Т) для стекол неизученных составов.

Графическое представление степени кристаллизации α (t, Т) – Time–Temperature–Transition (ТТТ)-диаграмма, которая определяет режим вытяжки волокна в виде линии пересечения поверхности ТТТ-диаграммы с горизонтальной плоскостью на уровне α, соответствующем требуемой фазовой чистоте.

БЛАГОДАРНОСТЬ

Исследование выполнено по плану работ в рамках госзадания ИХВВ РАН (тема № 0095-2018-0007).

Список литературы

Plotnichenko V.G., Philippovskiy D.V., Sokolov V.O., Sukhanov M.V., Velmuzhov A.P., Churbanov M.F., Dianov E.M. Infrared Luminescence in Bi-Doped Ge–S and As–Ge–S Chalcogenide Glasses and Fibers // Opt. Mater. Express. 2014. V. 4. № 2. P. 366–374. https://doi.org/10.1364/OME.4.000366
Dianov E.M. Amplification in Extended Transmission Bands Using Bismuth-Doped Optical Fibers // J. Lightwave Technol. 2013. V. 31. № 4. P. 681–688. https://doi.org/10.1109/JLT.2012.2211569
Simons D.R., Faber A.J., Waal H. GeS_x Glass for Pr³⁺-Doped Fiber Amplifiers at 1.3 m // J. Non-Cryst. Solids. 1995 V. 185 P. 283–288. https://doi.org/10.1016/0022-3093(94)00700-4
Kawamoto Y., Tsuchinashi S. Thermal Analysis of Ge–S Glasses // J. Am. Ceram. Soc. 1971. V. 54. P. 526–527. https://doi.org/10.1111/j.1151-2916.1971.tb12194.x
Borisova Z.U. Glassy semiconductors. New York: Plenum, 1981. P. 505. https://doi.org/10.1007/978-1-4757-0851-6
Виноградова Г.З. Стеклообразование и фазовые равновесия в халькогенидных системах. Двойные и тройные системы. М.: Наука, 1984. 176 с.
Liu C.H., Pashinkin A.S., Novoselova A.V. An Investigation of the Germanium-Sulphur System // Dokl. Akad. Nauk SSSR. 1963. V. 151. P. 1335–1338.
Frumar M., Ticha H., Koudelka L., Faimon J. Semiconducting Glasses of the Ge–Bi–S System // Mater. Res. Bull. 1976. V. 11. P. 1389–1396. https://doi.org/10.1016/0025-5408(76)90050-7
Tichy L., Ticha H., Benes L., Malek J. The Glass-Forming Region and Electrical Conductivity of Ge–Bi–S Glasses // J. Non-Cryst. Solids. 1990. V. 116. P. 206–218. https://doi.org/10.1016/0022-3093(90)90694-H
Voigt B. Über Glasbildung und Eigenschaften von Chalkogenidsystemen. XVII. Zur Glaschemie des Germaniumdisulfides // Z. Anorg. Allg. Chem. 1978. V. 447. P. 153–160. https://doi.org/10.1002/zaac.19784470117
Malek J., Klikorka J. Crystallization Kinetics of Glassy GeS₂ // J. Therm. Anal. 1987. V. 32. P. 1883–1893. https://doi.org/10.1007/BF01913981
Iskhakova L.D., Ermakov R.P., Sukhanov M.V., Voronov V.V., Velmuzhov A.P., Philippovskiy D.V., Plotnichenko V.G., Churbanov M.F. The Study of Phase Formation Processes in GeS_x:Bi (1 < x < 2) Chalcogenide Glasses // J. Non-Cryst. Solids. 2015. V. 428. P. 132–137. https://doi.org/10.1016/j.jnoncrysol.2015.08.021
Plotnichenko V.G., Philippovskiy D.V., Sokolov V.O., Sukhanov M.V., Velmuzhov A.P., Churbanov M.F., Dianov E.M. Infrared Luminescence in Bi-Doped Ge–S and As–Ge–S Chalcogenide Glasses and Fibers // Opt. Mater. Express. 2014. V. 4. P. 366–373. https://doi.org/10.1364/OME.4.000366
Пригожин И., Кондепуди Д. Современная термодинамика. От тепловых двигателей до диссипативных структур: Пер. с англ. Данилова Ю.А. и Белого В.В. М.: Мир, 2002. С. 461.
Borchard H.J., Daniels F. The Application of Differential Thermal Analysis to the Study of Reaction Kinetics // J. Am. Chem. Soc. 1957. V. 79. P. 41–46. https://doi.org/10.1021/ja01558a009
Sestaik J., Berggren G. Study of the Kinetics of Mechanism of Solid-State Reactions at Increasing Temperatures // Thermochim. Acta. 1971. V. 3. P. 1–12. https://doi.org/10.1016/0040-6031(71)85051-7
Malek J., Zmrhalova Z., Bartak J., Honcova P. A Novel Method to Study Crystallization of Glasses // Thermochim. Acta. 2010. V. 511. P. 67–73. https://doi.org/10.1016/j.tca.2010.07.026
Янг Д. Кинетика разложения твердых веществ: Пер. с англ. Печерской К.А.; Под ред. Ерофеева Б.В. М.: Мир, 1969. С. 263.
Malek J. The Kinetic Analysis of Non-Isothermal Data // Thermochim. Acta. 1992. V. 200. P. 257–269. https://doi.org/10.1016/0040-6031(92)85118-F

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Неорганические материалы

Архивы выпусков Информация о журнале Отправить рукопись в журнал

Неорганические материалы, 2019, T. 55, № 10, стр. 1101-1107

Исследование кристаллизационной устойчивости оптически активных стекол GeS_x〈Bi〉