Неорганические материалы, 2019, T. 55, № 9, стр. 994-998
Сопоставление полупроводниковых и электрохимических параметров двойного электрического слоя на границе магнетит/электролит
И. Г. Горичев 1, А. Д. Изотов 2, А. В. Кузин 1, Е. Г. Гололобова 1, *
1 Московский педагогический государственный университет
129164 Москва, ул. Кибальчича, 6, Россия
2 Институт общей и неорганической химии им. Н.С. Курнакова Российской академии наук
119991 Москва, Ленинский пр., 31, Россия
* E-mail: ggg777.79@mail.ru
Поступила в редакцию 11.02.2019
После доработки 19.04.2019
Принята к публикации 22.04.2019
Аннотация
Проведен сравнительный анализ электрохимических и полупроводниковых свойств магнетита на границе полупроводник/электролит. Установлено, что в твердой фазе оксида образуется объемная зона, приводящая к распределению заряда и потенциала как в объемной фазе, так и в растворе электролита. Наличие объемной зоны на поверхности магнетита доказывается линеризацией экспериментальных данных в координатах $\frac{1}{{{{C}^{2}}}}{\kern 1pt} - E$ (C – емкость, Е – потенциал).
ВВЕДЕНИЕ
При контакте оксидов железа с раствором электролитов происходит адсорбция потенциалопределяющих ионов Н+ и ОН–, образующихся в том числе и в результате диссоциативной хемосорбции воды [1, 2]. Энергия взаимодействия оксидов железа с водой составляет 3.5 × 10–5 Дж/см2, что соизмеримо с энергией диссоциации воды [2]. Адсорбция ионов Н+ и ОН– и сопровождающая их соадсорбция катионов и анионов фона происходят на активных центрах. Процесс растворения оксидов, коррозия металлов начинается с адсорбции потенциалопределяющих ионов Н+ или ОН–, а также анионов или катионов из раствора электролита в зависимости от рН среды. В результате возникают скачок потенциала (φ0) и заряд (q0), которые оказывают существенное влияние на кинетику растворения оксидов металлов. При соприкосновении оксидов с растворами электролитов скачок распределяется довольно сложным образом.
Как видно из рис. 1, на границе твердая фаза/раствор возникают три области распределения потенциала и заряда: область объемного заряда (в оксидной фазе), область скачка в слое Гельмгольца, диффузная область.
Рис. 1.
Строение двойного электрического слоя на границе раздела фаз оксид (1)/электролит (2). 1 – твердые фазы: I – металл, II – оксид, III – область пространственного заряда в оксиде; 2 – электролит: IV – слой Гельмгольца, V – слой Гуи. Частицы, создающие ДЭС: а – ориентированные диполи воды; б – избыточные ионы растворов; в – адсорбированные ионы на оксиде, создающие поверхностные состояния; г – ионные состояния. Энергетические характеристики полупроводника (оксида): А – зона проводимости, В – некомпенсированные ионы доноров, С – валентная зона; Ψ1, Ψ2, Ψ3 – Гальвани-потенциал раствора, поверхностных состояний оксидной фазы и металла соответственно.
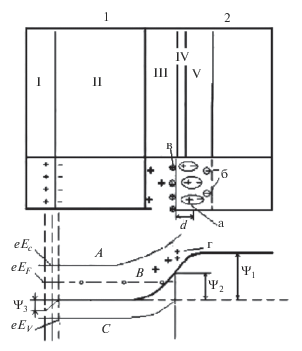
Общий скачок потенциала относительно раствора (потенциал раствора принимается за ноль) имеет следующий вид:
(1)
${{\varphi }_{0}} = \left( {{{\varphi }_{0}} - {{\psi }_{s}}} \right) + \left( {{{\psi }_{s}} - {{\varphi }_{1}}} \right) + \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right) + {{\varphi }_{2}},$Падение скачка потенциала в зоне объемного заряда описывается уравнением [3–5]
(2)
$\begin{gathered} \left( {{{\varphi }_{0}} - {{\psi }_{s}}} \right) = \frac{{{{d}_{0}}{{\varepsilon }_{1}}}}{{{{\varepsilon }_{0}}}}{{\left( {\frac{{8\pi kT{{n}_{1}}}}{{{{\varepsilon }_{1}}}}} \right)}^{{\frac{1}{2}}}}F\left( {\lambda ,Y} \right), \\ F\left( {\lambda ,Y} \right) = {{\left[ {\lambda \left( {{{e}^{{ - Y}}} - 1} \right) + {{\lambda }^{{ - 1}}}\left( {{{e}^{Y}} - 1} \right) + \left( {\lambda - {{\lambda }^{{ - 1}}}} \right)Y} \right]}^{{\frac{1}{2}}}}, \\ \end{gathered} $В области Гельмгольца и диффузном слое величины заряда и скачка потенциала можно рассчитать, используя уравнения [1–5]
(3)
$\begin{gathered} {{\varphi }_{0}} = \left( {{{\varphi }_{0}} - {{\psi }_{s}}} \right) + \left( {{{\psi }_{s}} - {{\varphi }_{1}}} \right) + \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right) + \\ + \,\,{{\varphi }_{2}} = \frac{{{{q}_{s}}}}{{{{K}_{s}}}} + \frac{{{{q}_{0}}}}{{{{K}_{{01}}}}} - \frac{{{{q}_{1}}}}{{{{K}_{{12}}}}} + {{\varphi }_{2}}, \\ {{\varphi }_{2}} = \frac{{2RT}}{F}{\text{arcsh}}(\frac{{{{q}_{2}}}}{{2A\sqrt {{{c}_{{{\text{эл}}}}}} }}), \\ А = {\text{ }}5.86 \times {{10}^{{--7}}}{{{\text{Кл }}{{{\text{л}}}^{{{\text{0}}{\text{.5}}}}}} \mathord{\left/ {\vphantom {{{\text{Кл }}{{{\text{л}}}^{{{\text{0}}{\text{.5}}}}}} {\left( {{\text{с}}{{{\text{м}}}^{{\text{2}}}}{\text{мол}}{{{\text{ь}}}^{{{\text{0}}{\text{.5}}}}}} \right)}}} \right. \kern-0em} {\left( {{\text{с}}{{{\text{м}}}^{{\text{2}}}}{\text{мол}}{{{\text{ь}}}^{{{\text{0}}{\text{.5}}}}}} \right)}}. \\ \end{gathered} $Здесь q0 – суммарный заряд на границе магнетит/раствор, q2 – заряд диффузной части ДЭС (Кл/см2), K01, K12 – емкости плотной и диффузной частей ДЭС (в растворе) (Ф/см2), cэл – молярная концентрация электролита (моль/ л).
На адсорбционные равновесия влияет в основном скачок потенциала со стороны раствора (ионная часть ДЭС).
Цель работы состояла в нахождении зависимости положения уровня Ферми магнетитового электрода в широком диапазоне значений рН и сопоставлении энергетических параметров магнетита с электрохимическими характеристиками процессов на границе оксид/электролит, а также изучении возможности расчета электрохимических и полупроводниковых свойств магнетита на границе электролит/полупроводник.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Для определения потенциала плоских зон магнетита применяли метод импедансных измерений. Объектом экспериментального исследования служил электрод, приготовленный спеканием порошкообразного магнетита, подвергнутого прессованию (0.2 ГПа) и последующему прокаливанию в атмосфере обескислороженного аргона в течение 4 ч при температуре 1300°С.
Импедансные измерения выполняли при частоте 20 кГц с использованием моста переменного тока Р-5021. Электрохимическую поляризацию магнетитового электрода проводили при помощи потенциостата П5827 М в потенциостатическом режиме. Электродом сравнения служил насыщенный хлорсеребряный электрод (потенциал по водородной шкале +0.201 В). Необходимое значения рН создавали буферными растворами. Измерения были выполнены в деаэрированных гелием растворах при температуре 25°С. Значения дифференциальной емкости рассчитывали по параллельной схеме.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Рис. 2.
Зависимости обратного квадрата емкости от потенциала магнетитового электрода при различных величинах рН раствора: 11.0 (1), 9.0 (2).
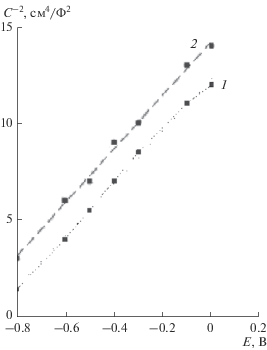
Результаты измерения емкости при различных потенциалах электрода и разных рН приведены на рис. 2. Из рис. 2 следует, что в области потенциалов плоских зон от +0.2 до –0.6 В наблюдается линейная зависимость величины $\frac{1}{{{{C}^{2}}}}$ магнетита от потенциала (Е), что указывает на процессы, протекающие в объемной зоне полупроводника.
Представляет интерес сопоставить параметры, которые описывают свойства магнетита и электрохимические характеристики равновесий, возникающих на границе электролит/оксид. Раствор характеризуется следующими параметрами: eE0 – величина, эквивалентная энергии Ферми, eEox и eEred – средние энергии уровня окислителя и восстановителя соответственно.
Связь между этими параметрами выражается уравнением
(4)
$e{{E}_{{\text{0}}}} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}(e{{E}_{{ox}}}--e{{E}_{{red}}}).$Магнетит как полупроводник характеризуется следующими параметрами: eEv – максимальная энергия валентной зоны; eEF – энергия Ферми; eEc – энергия дна зоны проводимости. Особый интерес представляют величины потенциала (eEfb) и толщины (d) плоских зон.
Величина потенциала плоских зон (eEfb) магнетита была определена с использованием уравнения Мотта–Шоттки [1, 3, 4, 6]
(5)
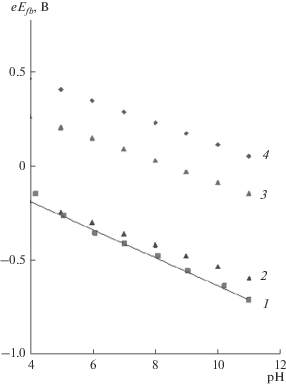
$\frac{1}{{{{C}^{2}}}} = \frac{2}{{e{{\varepsilon }_{0}}\varepsilon {{N}_{a}}}}\left( {E - e{{E}_{{fb}}} - \frac{{kT}}{e}} \right),$Из тангенса угла наклона зависимости $\frac{1}{{{{C}^{2}}}}{\kern 1pt} - E$ (рис. 2) была определена величина Na, которая составляет 2.8 × 1016 см–3. При С → 0 получили зависимости потенциалов плоских зон магнетита от рН, которые сопоставлялись с данными [2–6], приведенными на рис. 3. Из данных рис. 3 следует, что имеется линейная зависимость между потенциалом плоских зон магнетита и рН
Рис. 3.
Зависимости величины потенциала плоских зон различных оксидных полупроводников от рН: 1 – магнетит, 2 – TiO2, 3 – Fe2O3, 4 – WO3.
Средняя величина электростатического потенциала внешней плоскости Гельмгольца с учетом q2= –(q0+ q1) равна
где K12 = ε0ε/(х2 – х1) – интегральная емкость ионной части двойного слоя между х1 и х2. Соответственно, дифференциальные емкости С01 и С12 равны(8)
${{C}_{{01}}} = {{\left[ {\frac{{\partial {{q}_{0}}}}{{\partial ({{\varphi }_{0}} - {{\varphi }_{1}})}}} \right]}_{{{{c}_{{{\text{эл}}}}}}}} \approx {{K}_{{01}}},$(9)
$\begin{gathered} {{C}_{{12}}} = {{\left[ {\frac{{\partial {{q}_{2}}}}{{\partial \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right)}}} \right]}_{{_{{{{c}_{{{\text{эл}}}}}}}}}} = \\ = {{\left[ { - \frac{{\partial ({{q}_{0}} + {{q}_{1}})}}{{\partial \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right)}}} \right]}_{{{{c}_{{{\text{эл}}}}}}}} = {{\left[ {\frac{{\partial {{q}_{1}}}}{{\partial \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right)}}} \right]}_{q}} \approx {{K}_{{12}}}. \\ \end{gathered} $Предполагается, что дифференциальная емкость не зависит от потенциала, т.е. С01= K01, С12 = K12, где K01, K12 – интегральные емкости плотной и диффузной частей ДЭС на границе раздела оксид/электролит. Для дальнейших расчетов имеем
(10)
$\begin{gathered} ({{\varphi }_{0}} - {{\varphi }_{1}}) = \frac{{{{q}_{0}}}}{{{{K}_{{01}}}}}\,\,\,\,{\text{и}}\,\,\,\,({{\varphi }_{1}} - {{\varphi }_{2}}) = \\ = - \frac{{{{q}_{2}}}}{{{{K}_{{12}}}}} = \frac{{{{q}_{0}} + {{q}_{1}}}}{{{{K}_{{12}}}}}, \\ \end{gathered} $(11)
$\begin{gathered} {{\varphi }_{0}} = \left( {{{\varphi }_{0}} - {{\varphi }_{1}}} \right) + \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right) + {{\varphi }_{2}} = \\ = \frac{{{{q}_{0}}}}{{{{K}_{{01}}}}} - \frac{{{{q}_{2}}}}{{{{K}_{{12}}}}} + \xi ,\,\,\,\,{{\varphi }_{{\text{2}}}} = \xi . \\ \end{gathered} $В результате устанавливаются адсорбционные равновесия, которые и определяют заряд поверхности оксида и ионной части ДЭС. Согласно модели кислотно-основных равновесий на границе раздела оксид/раствор возникают следующие равновесия [7–9]:
(12)
$\begin{gathered} S - {\text{OH}}_{{2s}}^{ + } = S - {\text{OH}}_{s}^{0} + {{{\text{H}}}^{ + }}, \\ {{K}_{1}} = K_{1}^{0}\exp \left[ {\frac{{{{\varphi }_{0}}F}}{{RT}}} \right] = \frac{{[S - {\text{OH}}_{s}^{0}][{{{\text{H}}}^{ + }}]}}{{[S - {\text{OH}}_{{2s}}^{ + }]}}, \\ \end{gathered} $(13)
$\begin{gathered} S - {\text{OH}}_{s}^{0} = S - {\text{O}}_{S}^{ - } + {{{\text{H}}}^{ + }}, \\ {{K}_{2}} = K_{2}^{0}\exp \left[ {\frac{{{{\varphi }_{0}}F}}{{RT}}} \right] = \frac{{\left[ {S - {\text{O}}_{s}^{ - }} \right]\left[ {{{{\text{H}}}^{ + }}} \right]}}{{\left[ {S - {\text{OH}}_{s}^{0}} \right]}}, \\ \end{gathered} $(14)
$\begin{gathered} S - {\text{OH}}_{2}^{ + }...A_{s}^{ - } = S - {\text{OH}}_{s}^{0} + {{{\text{H}}}^{ + }} + {{A}^{ - }}, \\ {{K}_{3}} = K_{3}^{0}\exp \left[ {\frac{{({{\varphi }_{0}} - {{\varphi }_{1}})}}{{RT}}} \right] = \frac{{\left[ {S - {\text{OH}}_{s}^{0}} \right]\left[ {{{{\text{H}}}^{ + }}} \right]\left[ {{{A}^{ - }}} \right]}}{{\left[ {S - {\text{OH}}_{2}^{ + }...A_{s}^{ - }} \right]}}, \\ \end{gathered} $(15)
$\begin{gathered} S - {\text{OH}}_{s}^{0} + {{{\text{M}}}^{ + }} = S - {{{\text{O}}}^{ - }}...{\text{M}}_{s}^{ + } + {{{\text{H}}}^{ + }}, \hfill \\ {{K}_{4}} = K_{4}^{0}\exp \left[ {\frac{{({{\varphi }_{0}} - {{\varphi }_{1}})F}}{{RT}}} \right] = \frac{{[S - {{{\text{O}}}^{ - }}...{\text{M}}_{s}^{ + }]}}{{[S - {\text{OH}}_{s}^{0}][{{{\text{M}}}^{ + }}]}}, \hfill \\ \end{gathered} $Таблица 1.
Кислотно-основные константы и параметры на границе магнетит/электролит [10]
| Оксид | Ns, мкКл/см2 | K01, мкФ/см2 | ${\text{p}}K_{1}^{0}$ | ${\text{p}}K_{2}^{0}$ | ${\text{p}}K_{3}^{0}$ | ${\text{p}}K_{4}^{0}$ | рНт.н.з. |
|---|---|---|---|---|---|---|---|
| Fe3O4 | 96 | 140 | 4.4 | 9.0 | 6.2 | 7.2 | 6.7 |
C помощью кислотно-основной модели можно конкретизировать выражения для зарядов различных плоскостей ионной части ДЭС:
Суммарная концентрация всех частиц на поверхности оксида равна
(17)
$\begin{gathered} {{N}_{s}} = F([S - {\text{OH}}_{{2,s}}^{ + }] + [S - {\text{OH}}_{2}^{ + }...A_{5}^{ - }] + \\ + \,\,[S - {\text{OH}}_{s}^{0}] + [S - {\text{O}}_{s}^{ - }] + [S - {{{\text{O}}}^{ - }}...{\text{M}}_{s}^{ + }]). \\ \end{gathered} $Концентрация адсорбированных частиц сi зависит от величины потенциала в этой точке (φi) и определяется уравнением Больцмана
(18)
${{c}_{i}} = {{c}_{{i0}}}\exp ({{ - zF{{\varphi }_{i}}} \mathord{\left/ {\vphantom {{ - zF{{\varphi }_{i}}} {RT}}} \right. \kern-0em} {RT}}),$Полупроводниковая модель строения ДЭС на границе раздела фаз оксид/электролит также позволяет объяснить другие полупроводниковые свойства [11].
Отметим некоторые актуальные задачи дальнейших исследований в области строения ДЭС и явлений адсорбции ионов на границе раздела фаз оксид/электролит:
1) разработка детальной модели ДЭС с двумя внутренними плоскостями Гельмгольца с учетом дискретности и специфической адсорбции ионов;
2) объединение кислотно-основной теории Грема–Парсона и полупроводниковой модели строения ДЭС на границе раздела оксид/электролит;
3) разработка и применение методов ЯМР, ПМР, ИК-спектроскопии, РФЭС, импедансных измерений для описания адсорбции ионов на поверхности оксидов железа.
4) квантово-механическое описание адсорбционных явлений на границе раздела оксид/электролит на основе кластерных фрагментов.
Список литературы
Гуревич Ю.Я., Плесков Ю.В. Фотоэлектрохимия полупроводников. М.: Наука, 1983. 312 с.
Стрельцов Е.А. Электрохимия полупроводников. Минск: БГУ, 2012. 159 с.
Дамаскин Б.Б. и др. Электрохимия. М.: Химия, 2008. 672 с.
Батенков В.А. Электрохимия полупроводников. Барнаул: Изд-во Алт. ун-та, 2002. 162 с.
Плесков Ю.В. Фотохимическое преобразование солнечной энергии М.: Химия, 1990. 176 с.
The International Encyclopedia of Physical Chemistry and Chemical Physics / Ed. Eley D.D. Chapter 5. Semiconductor Surfaces the Electrical Double Layer / Sparnaay M.J. Oxford: Pergamon Press, 1972. P. 273–373.
Горичев И.Г., Федченко М.А., Якушева Е.А., Изотов А.Д. Влияние строения двойного электрического слоя на адсорбцию ионов на оксидах и гидроксидах железа. М.: МПГУ, 2005. 101 с.
Горичев И.Г., Батраков В.В., Изотова О.В., Панкратов Д.В. Расчет термодинамических констант кислотно-основных равновесий на границе оксид/электролит из экспериментальных зависимостей электрокинетического потенциала от рН // Неорган. материалы. 2010. Т. 46. № 7. С. 843–849.
Гололобова Е.Г., Горичев И.Г., Лайнер Ю.А., Скворцова И.В. Расчет констант кислотно-основных равновесий на границе оксид алюминия/электролит по зависимости адсорбции однозарядных ионов (Na, Cl) от pH // Металлы. 2011. № 3. С. 15–20.
Горичев И.Г., Батраков В.В. Зависимость заряда поверхности от потенциала на границе оксид/электролит // Электрохимия. 1992. Т. 28. Вып. 1. С. 14–20.
Киселев В.Ф., Козлов С.Н., Зотеев А.В. Основы физики поверхности твердого тела. М.: Изд-во МГУ, 1999. 284 с.
Дополнительные материалы отсутствуют.
Инструменты
Неорганические материалы


