1. На главную
  2. Электронные версии
  3. Неорганические материалы
  4. T. 55, № 9, 2019

Неорганические материалы, 2019, T. 55, № 9, стр. 999-1006

Структура параметра порядка топологических сверхпроводников на основе оксидов 3d- и 4d-элементов

В. Г. Яржемский 1, *, А. Д. Изотов 1

1 Институт общей и неорганической химии им. Н.С. Курнакова Российской академии наук
119991 Москва, Ленинский пр., 31, Россия

* E-mail: vgyar@igic.ras.ru

Поступила в редакцию 31.01.2019
После доработки 05.03.2019
Принята к публикации 12.04.2019

Полный текст (PDF)

Аннотация

Рассмотрены экспериментальные данные по структуре параметра порядка сверхпроводников La2CuO4 и Sr2RuO4 со структурой слоистого перовскита. Анализ экспериментальных данных проведен с применением пространственно-группового подхода к двухэлектронным состояниям в кристаллах. Для Sr2RuO4 из кристаллической симметрии получены двухэлектронные функции симметрии Eu с нулевыми плоскостями, соответствующие экспериментальным данным. В случае La2CuO4 и ВТСП-материалов параметр порядка соответствует неприводимому представлению B1g скрытой симметрии D4h. Показано также, что волны зарядовой плотности, обнаруженные в состояниях псевдощели ВТСП-материалов, можно рассматривать как двухэлектронные состояния эквивалентных электронов с отличным от нуля импульсом.

Ключевые слова: оксиды 3d- и 4d-элементов, структура слоистого перовскита, топологические сверхпроводники, триплетные куперовские пары, синглетные куперовские пары, волны зарядовой плотности

ВВЕДЕНИЕ

Открытие сверхпроводимости c температурой перехода Tc = 30 K в La2 –xBaxCuO4 (сверхпроводники на основе оксидов меди называют купратами или ВТСП) [1] и Sr2RuO4 [2] (Tc = 0.93 К), имеющих структуру слоистого перовскита, положило начало исследованиям новых типов сверхпроводников, получивших название “необычных” из-за существенных отличий от известных ранее металлических сверхпроводников, описывающихся теорией Бардина–Купера–Шифера (БКШ) [3]. Наибольшая величина Tc = 116 K для нетоксичного состава (т.е. без Hg и Tl) ВТСП была достигнута в (Cu,C)Ba2Ca3Cu4O11 + δ [4].

Следует отметить, что ещё до появления работы Мюллера и Беднорца в работе И.С. Шаплыгина, Б.Г. Кахана, В.Б. Лазарева [5] были синтезированы кристаллы состава, соответствующего ВТСП, и установлены необычные свойства проводимости при температуре выше Tc, однако измерения ниже Tc не проводились. Были также получены экспериментальные данные для других типов сверхпроводников с низкими Tc, не совпадающие с постулатами теории БКШ [3]. На примере CeCu2Si2 (Tc = 0.5 K) было впервые показано, что сверхпроводимость может существовать в материалах с магнитными полями, в частности, с взаимодействиями, связанными с наличием незаполненной f-оболочки [6].

Согласно теории БКШ, сверхпроводящая щель изотропна и не обращается в нуль, поэтому температурные зависимости многих физических величин носят экспоненциальный характер. Степенная (T  2) температурная зависимость затухания ультразвука в UPt3 была объяснена триплетной сверхпроводимостью со сверхпроводящей щелью, обращающейся в нуль на ферми-поверхности (ФП) [7]. На основании степенной (T3) температурной зависимости удельной теплоемкости UBe13 (Tc = 0.8 K) в сверхпроводящем состоянии был сделан вывод о триплетном характере сверхпроводимости [8]. Такие сверхпроводники называют также узловыми из-за наличия узловых плоскостей сверхпроводящего параметра порядка (СПП) или топологическими из-за его сложной пространственной структуры.

В настоящей работе представлен обзор экспериментальных данных, указывающих на необычную структуру СПП в купратах и Sr2RuO4. Для описания структуры СПП применен пространственно-групповой подход к волновой функции куперовской пары [9–14] и получена структура СПП Sr2RuO4, согласующаяся с экспериментом.

ВТСП-МАТЕРИАЛЫ НА ОСНОВЕ ОКСИДОВ МЕДИ

Sr2RuO4 имеет симметрию D4h [2], а симметрия купратов – D2h, причем отличие параметров решетки a и b невелико [15], поэтому можно говорить о скрытой симметрии D4h в купратах [16]. Важной симметрийной особенностью СПП в купратах является то, что узловая (нулевая) диагональная плоскость не является плоскостью симметрии кристаллической группы D2h и СПП имеет симметрию, подобную сферическим функциям ${{d}_{{{{x}^{2}} - {{y}^{2}}}}}$ [15]. Электронное строение купратов характеризуется образованием т.н. псевдощели при T  * > Tc, что было установлено по изменению сдвига Найта в спектах ЯМР при переходе через T  * [17]. Исследования методом фотоэлектронной спектроскопии с угловым разрешение [18–20] купратных сверхпроводников показали, что как волновая функция псевдощели (для T  * > Tc), так и СПП (для T < Tc) обращаются в нуль на диагонали квадрата в плоскости связи Cu–O.

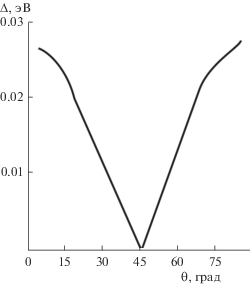
Угловая зависимость фотоэлектронного спектра ВТСП-материала схематически показана на рис. 1. Круговой дихроизм в фотоэлектронном спектре был интерпретирован как свидетельство нарушения симметрии с обращением времени [18]. Нарушение симметрии с обращением времени происходит между двумя областями, разделенными диагональю квадрата. Следует отметить, что наблюдаемые особенности фотоэлектронных спектров можно объяснить также другими причинами [19]. Объяснение природы псевдощелевой фазы является одной из основных проблем в попытках понять природу высокотемпературной сверхпроводимости. Определение симметрий, нарушающихся в фазе псевдощели, т.е. при T  * > T > Tc, важно для понимания природы сверхпроводимости. Измерения дифракции поляризованных нейтронов [21, 22] и эффекта Керра [23] подтверждают данные фотоэлектронной спектроскопии [18] о нарушении симметрии относительно обращения времени при T < T  *. Возникновение магнитного порядка при температуре псевдощели является признаком скрытого параметра порядка [22].

Рис. 1.

Угловая зависимость щели сверхпроводимости в ВТСП-материалах по данным фотоэлектронной спектроскопии [18–20, 27].

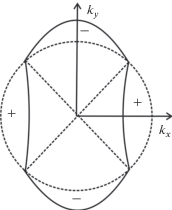
Исследования анизотропии эффекта Нернста в системе Y–Ba–Cu–O обнаружили нарушение вращательной симметрии C4 [24] при переходе через T  *. Был сделан вывод, что изменение электронного строения в недостаточно допированных оксидах меди при охлаждении происходит в два этапа: при T*, когда нарушается вращательная симметрия, при T < T*/2, когда нарушается трансляционная симметрия и наблюдается статический порядок спиновой плотности [25]. Данные фотоэлектронной спектроскопии с угловым разрешением [18] и результаты экспериментов, чувствительных к фазе [26], позволяют сделать вывод, что СПП меняет знак на диагонали [27], что схематически показано на рис. 2.

Рис. 2.

Схематическое изображение щели сверхпроводимости d-типа в ВТСП-материалах [27] (пунктир изображает ФП).

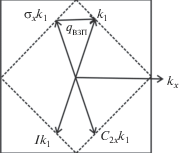
Дифракция рентгеновского излучения показала наличие волн зарядовой плотности (ВЗП) в нормальном состоянии сверхпроводника YBa2Cu3O6.67 (Tc = 67 K) [28]. Ниже Tc магнитное поле подавляет сверхпроводимость и увеличивает ВЗП. Из этого следует, что сверхпроводимость и ВЗП являются конкурирующими явлениями, в которых участвуют одни и те же носители [28]. В ВЗП спариваются электроны (дырки) с импульсами, сумма которых отлична от нуля, и в результате такая пара имеет полный момент, отличный от нуля. Схематически это изображено на рис. 3.

Рис. 3.

Волновой вектор ВЗП как сумма волновых векторов электронов.

Для единого описания куперовских пар и ВЗП используют SU(2)-симметрию [29–31]. Следует отметить, что SU(2) – это группа симметрии электронного спина, но в данном случае рассматриваются операторы с правилом коммутации таким же, как и у спиновых операторов, но которые действуют на волновые функции пар электронов и дырок. Параметр порядка ВЗП при таком подходе обычно записывают через операторы $С_{{k,\sigma }}^{\dag }$ рождения (или уничтожения) электронов с импульсом k и спином σ в виде:

(1)
${{\Delta }_{0}} = \frac{1}{2}\sum\limits_{k,\sigma } {{{C}_{{k + Q,\sigma }}}C_{{k,\sigma }}^{ + }} ,$
(2)
${{\Delta }_{1}} = \frac{1}{{\sqrt 2 }}\sum\limits_k {{{C}_{{k \downarrow }}}} {{C}_{{ - k \uparrow }}}.$

При такой записи параметра порядка три величины – ${{\Delta }_{0}},$ ${{\Delta }_{1}}$ и ${{\Delta }_{{ - 1}}} = \Delta _{1}^{\dag }$ – преобразуются по группе SU(2).

ЭКСПЕРИМЕНТАЛЬНАЯ СТРУКТУРА СПП Sr2RuO4

После открытия сверхпроводимости в слоистом перовските Sr4RuO4 [2] было установлено много необычных свойств его СПП. Отсутствие изменений сдвига Найта в спектре ЯМР 17O при переходе через Tc подтверждает нечетность СПП Sr2RuO4 [32]. Измерения критического тока в квантовом интерфейсе Sr2RuO4 с синглетным сверхпроводником AuIn выявили изменение фазы СПП на π при инверсии, что также указывает на нечетность СПП [33]. Результаты экспериментов по релаксации спинов мюонов в сверхпроводящем Sr2RuO4 указывают на наличие спонтанных внутренних магнитных полей, т.е. на нарушение симметрии относительно обращения времени [34]. Степенные зависимости глубины проникновения магнитного поля указывают на узловые линии СПП [35]. Авторы констатировали: “степенная зависимость предполагает, что функция щели имеет нули, что несовместимо со сверхпроводимостью p-типа” [35]. Однако было показано [14], что эти экспериментальные результаты не согласуются не со сверхпроводимостью p-типа, а с выводами феноменологических подходов, основанных на анализе произвольно заданных полиномов [36]. В частности, для описания хирального состояния Eu был предложен полином

(3)
$d(k) = \hat {z}\left( {{{k}_{x}} \pm i{{k}_{y}}} \right),$
где $\hat {z}$ обозначает компоненту триплетного спина ${{m}_{s}} = 0,$ которая принадлежит неприводимому представлению (НП) A2g. Такая запись правильно отражает физику явления – хиральная триплетная пара, в которой спины противоположно направлены, – но не учитывает кристаллическую симметрию.

Результаты исследования затухания ультразвука в Sr2RuO4 показывают, что СПП имеет узлы в вертикальной или горизонтальной плоскостях [37], но авторы также пишут, что эти результаты исключают возможность сверхпроводимости в виде p-волн. При измерениях удельной теплоемкости Sr2RuO4 были установлены четырехкратные колебания и минимум сверхпроводящей щели в активной зоне вдоль направления [100] [38], но авторы также обсуждают “противоречия” между спин-триплетной сверхпроводимостью в Sr2RuO4 и узловой структурой СПП. Недавние измерения теплопроводности на монокристаллах Sr2RuO4 выявили узлы СПП на вертикальных линиях [39]. Авторы пишут: “мы столкнулись с ситуацией, когда в Sr2RuO4, сверхроводимость p-типа имеет структуру щели с d-типа” [39]. Это утверждение связано теоремой Блунта [40], согласно которой в триплетном случае обращение в нуль СПП на линиях ФП крайне маловероятно. Результаты измерений эффекта Керра с высоким разрешением в Sr2RuO4 [41] подтверждают нарушение симметрии относительно обращения времени в сверхпроводящем состоянии и соответствуют СПП (3).

Таким образом, имеются противоречия между экспериментальными данными, указывающими на триплетный (или p-) тип сверхпроводимости Sr2RuO4, СПП которого обращается в нуль на вертикальных линиях, и выводами точечно-группового подхода [36, 40] о бесщелевом характере СПП p-типа.

ФП Sr2RuO4 состоит из трех зон – α, β и γ. Наибольшая щель в зоне γ составляет 0.005 эВ, в зонах α и β – около 0.0015 эВ. Нули СПП в зоне γ находятся на вертикальных координатных плоскостях, а в зонах α и β – на диагональных плоскостях [42].

В настоящей работе для описания симметрии двухэлектронных состояний применен пространственно-групповой подход [9–14] и показано, что для НП Eu, которое обычно связывают с СПП Sr2RuO4, существуют различные типы вертикальных нулевых плоскостей. Показано также, что СПП в купратах описывается скрытой симметрией D4h и НП B1g.

ТЕОРИЯ

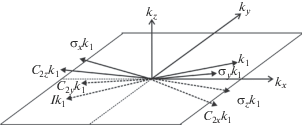
Волновая функция электрона в кристалле описывается звездой волнового вектора k, лучи которой образуются действием всех вращений и вращений с инверсией $\hat {G},$ входящих в пр. гр. $G.$ На рис. 4 изображена звезда вектора k для группы симметрии D2h, которая в общей точке зоны Бриллюэна (ЗБ) состоит из восьми лучей. На симметричных направлениях пространственная группа разлагается в левые смежные классы по группе H волнового вектора:

(4)
$\hat {G} = \sum\limits_{i = 1}^n {{{s}_{i}}} \hat {H},{\text{ }}n = {{\left| {\hat {G}} \right|} \mathord{\left/ {\vphantom {{\left| {\hat {G}} \right|} {\left| {\hat {H}} \right|}}} \right. \kern-0em} {\left| {\hat {H}} \right|}},$
где знак модуля обозначает число элементов в группе.

Рис. 4.

Звезда волнового вектора при симметрии D2h (ВТСП-материалы).

НП пространственной группы получаются индуцированием неприводимых представлений Dk группы волнового вектора [43]:

(5)
$\left( {{{D}^{k}} \uparrow G} \right)(g){}_{{i\mu ,jv}} = {{D}^{k}}{{\left( {s_{i}^{{ - 1}}g{{s}_{j}}} \right)}_{{\mu v}}}\delta (s_{i}^{{ - 1}}g{{s}_{j}}),$
где $\delta \left( {s_{i}^{{ - 1}}g{{s}_{j}}} \right) = \left\{ {\begin{array}{*{20}{c}} {1,\,\,еслиs_{i}^{{ - 1}}g{{s}_{j}} \in G} \\ {0,\,\,еслиs_{i}^{{ - 1}}g{{s}_{j}} \notin G} \end{array}} \right..$

Волновая функция двух эквивалентных электронов равна квадрату волновой функции одного электрона и в данном случае имеет размерность 64. Разложение этого пространства на неприводимые дает все возможные состояния двух электронов. Для такого разложения можно воспользоваться теоремой Макки–Брэдли [44].

Структура квадрата НП пространственной группы определяется разложением пр. гр. G в двойные классы по группе волнового вектора H:

(6)
$G = \sum\limits_\delta {H{{d}_{\delta }}H} .$

Из уравнения (6) видно, что в общей точке ЗБ имеется $\left| {\hat {G}} \right|$ членов разложения волновой функции двух электронов. Для самообратимых двойных классов, т.е. таких, где $H{{d}_{\alpha }}H = Hd_{\alpha }^{{ - 1}}H$, строятся характеры симметризованных и антисимметризованных квадратов по следующим формулам:

(7)
$\chi \left[ {P_{\delta }^{{k \pm }}(m)} \right] = \chi \left[ {{{D}^{k}}\left( m \right)} \right]\chi \left[ {{{D}^{k}}\left( {d_{\delta }^{{ - 1}}m{{d}_{\delta }}} \right)} \right],$
(8)
$\chi \left( {P_{\alpha }^{{k + }}\left( {{{d}_{\alpha }}m} \right)} \right) = \chi \left( {{{D}^{k}}\left( {{{d}_{\alpha }}m{{d}_{\alpha }}m} \right)} \right),$
(9)
$\chi \left( {P_{\alpha }^{{k - }}\left( {{{d}_{\alpha }}m} \right)} \right) = - \chi \left( {{{D}^{k}}\left( {{{d}_{\alpha }}m{{d}_{\alpha }}m} \right)} \right),$
где $m \in {{M}_{\delta }} = {{d}_{\delta }}Hd_{\delta }^{{ - 1}} \cap H,$ знак + (–) соответствует симметризованному (антисимметризованному) квадрату, т.е. пространственной части синглетной (триплетной) пары. Далее эти характеры индуцируются в группу G по формуле (5), где в качестве подгруппы берется ${{d}_{\delta }}{{M}_{\delta }} + {{M}_{\delta }}.$

Для куперовской пары рассматривается двойной класс, определяемый инверсией. В этом случае сумма волновых векторов равна нулю и формулы (7)–(9) дают характеры НП точечной группы. В общей точке ЗБ для синглетных пар возможны все четные НП точечной группы, а для триплетных пар – все нечетные. На плоскости симметрии ЗБ некоторые НП Γf не появляются при разложении представлений (7)–(9), индуцируемых в G. Пересечение такой плоскости с ФП дает линию, где Γf запрещено. Тогда говорят, что Γf имеет симметрийную линию нулей. Однако, как было показано в [12, 14], для двумерных НП такие выводы не всегда однозначны и нули СПП определяются дополнительными квантовыми числами. В настоящей работе применяется численный метод определения нулей СПП [45], основанный на расчете интерференции волновых функций пары на плоскостях симметрии.

В общей точке ЗБ группа волнового вектора H состоит только из единичного элемента, и волновые функции синглетной и триплетной пар можно записать в виде:

(10)
$\psi _{1}^{s} = {{\varphi }_{{{{k}_{1}}}}}\left( {{{r}_{1}}} \right){{\varphi }_{{I{{k}_{1}}}}}\left( {{{r}_{2}}} \right) + {{\varphi }_{{{{k}_{1}}}}}\left( {{{r}_{2}}} \right){{\varphi }_{{I{{k}_{1}}}}}\left( {{{r}_{1}}} \right),$
(11)
$\psi _{{{{k}_{1}}}}^{t} = {{\varphi }_{{{{k}_{1}}}}}\left( {{{r}_{1}}} \right){{\varphi }_{{I{{k}_{1}}}}}\left( {{{r}_{2}}} \right) - {{\varphi }_{{{{k}_{1}}}}}\left( {{{r}_{2}}} \right){{\varphi }_{{I{{k}_{1}}}}}\left( {{{r}_{1}}} \right).$

Полный базис для пары (синглетной или триплетной) для группы D4h изображен на рис. 5. Поскольку инверсия включена в формулы (10) и (11), полное число двухэлектронных базисных функций для группы D4h равно 8, т.е. вдвое меньше числа лучей в звезде вектора k1. Когда k1 пробегает базисную ЗБ (в данном случае сектор от 0° до 45°), полный базис пробегает всю ЗБ. Пространственные части триплетных и синглетных пар преобразуются по 8-мерным приводимым представлениям – нечетному и четному соответственно. Неприводимые базисы, полученные проектированием этих приводимых базисов на некоторые из НП группы D4h, приведены в табл. 1. Большинство исследователей сходятся во мнении, что СПП Sr2RuO4 преобразуется по НП Eu. Существуют две формы для НП Eu: действительная (или x–y) и комплексная (хиральная) [43]. Нетрудно проверить, что умножение НП Eu на любое из четных одномерных НП A2g, B1g и B2g дает тоже НП Eu. В табл. 1 приведены базисные функции для Eu, $E_{u}^{b} = {{E}_{u}} \times {{A}_{{2g}}}$ и хирального НП [43], обозначенного $E_{u}^{c}.$ В полученных таким образом линейных комбинациях функции, принадлежащие разным секторам в k-пространстве, приобретают относительную фазу. На плоскости симметрии функции соседних секторов могут сливаться друг с другом или сокращаться. Второй случай соответствует нулевым плоскостям.

Рис. 5.

Базис для волновой функции куперовской пары при симметрии D4h (Sr2RuO4) (все векторы имеют одинаковую компоненту kz).

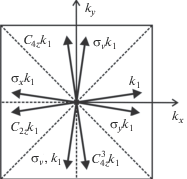
Таблица 1.  

Волновые функции триплетных и синглетных пар для некоторых НП группы D4h*

НП Волновая функция пары Рисунок
$E_{u}^{{}}$ $\begin{array}{*{20}{c}} {\psi _{1}^{t} + \psi _{{27}}^{t} - \psi _{4}^{t} - \psi _{{26}}^{t}} \\ {\psi _{{14}}^{t} + \psi _{{37}}^{t} - \psi _{{15}}^{t} - \psi _{{40}}^{t}} \end{array}$ 6а
$E_{u}^{b}$ $\begin{array}{*{20}{c}} {\psi _{1}^{t} - \psi _{{27}}^{t} - \psi _{4}^{t} + \psi _{{26}}^{t}} \\ {\psi _{{14}}^{t} - \psi _{{37}}^{t} - \psi _{{15}}^{t} + \psi _{{40}}^{t}} \end{array}$ 6б
$E_{u}^{c}$ $\begin{gathered} \psi _{1}^{t} - \psi _{4}^{t} + i\psi _{{14}}^{t} - i\psi _{{15}}^{t} \hfill \\ - \psi _{{27}}^{t} + \psi _{{26}}^{t} + i\psi _{{40}}^{t} - i\psi _{{37}}^{t} \hfill \\ \end{gathered} $ 6в
B1g $\psi _{1}^{s} + \psi _{4}^{s} - \psi _{{14}}^{s} - \psi _{{15}}^{s} + \psi _{{26}}^{s} + \psi _{{27}}^{s} - \psi _{{37}}^{s} - \psi _{{40}}^{s}$ 7

* $\psi _{1}^{s}$ и $\psi _{1}^{t}$ даются формулами (10) и (11) соответственно; $\psi _{i}^{{s(t)}} = {{h}_{i}}\psi _{1}^{{s(t)}},$ hi – операторы точечной группы в обозначениях [43] (см. рис. 5).

Для графического представления вертикальных нулевых плоскостей через каждый угловой градус строились гауссианы шириной, большей величины шага. Для каждого НП вклады от всех гауссианов суммировались в каждой точке и нормировались на единицу. В результате при деструктивной интерференции на плоскостях симметрии получались нулевые значения, соответствующие нулевым вертикальным плоскостям СПП. Результаты для различных форм Eu приведены на рис. 6. Имеются два типа нулевых плоскостей для двумерного НП. На нулевой плоскости первого типа сокращаются функции каждой из строк в отдельности, а на нулевой плоскости второго типа сокращаются функции двух строк. НП Eu не имеет нулей первого типа (рис. 6а), НП $E_{u}^{b} = {{E}_{u}} \times {{A}_{{2g}}}$ (рис. 6б) имеет нули первого типа на вертикальных координатных плоскостях, и оба НП имеют нули второго типа на одной из двух диагональных плоскостей (причем на разных). Результаты для ${{E}_{u}} \times {{B}_{{1g}}}$ и ${{E}_{u}} \times {{B}_{{2g}}}$ аналогичны и не приводятся.

Рис. 6.

Теоретическая структура СПП Sr2RuO4 для НП Eu в плоскости, перпендикулярной оси kz: Eu (а), $E_{u}^{b}$ (б), $E_{u}^{c}$ (в) (см. табл. 1).

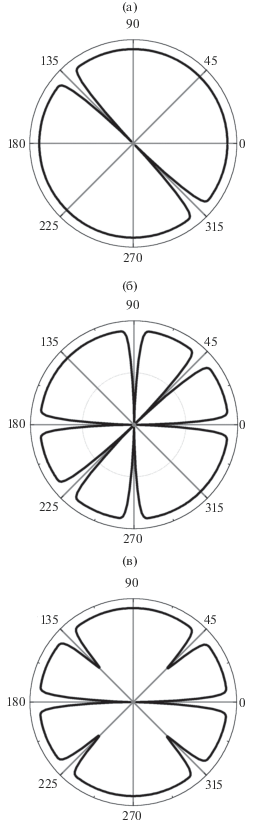
Хиральный базис $E_{u}^{c}$ не имеет нулей первого типа, но имеет одну нулевую плоскость (010) второго типа (см. рис. 6в). На рис. 6в видны также минимумы на диагональных плоскостях, связанные с отсутствием интерференции действительных и мнимых функций, находящихся по разные стороны от плоскости. Поскольку в группе D4h вертикальные координатные и диагональные плоскости равноправны, во всех полученных выводах их можно поменять местами. Таким образом, теоретически получено, что вертикальные нулевые плоскости СПП Sr2RuO4, установленные экспериментально [37–39], следуют из кристаллической симметрии. Наличие спиновой части триплетного спина $\hat {z}$ (см. формулу (3)), имеющего симметрию A2g, не меняет результатов, т.к. рассматривались произведения Eu на все четные одномерные НП.

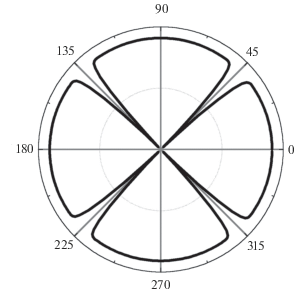
В случае ВТСП-материалов диагональная плоскость не является элементом симметрии группы D2h и нулевые плоскости не могут быть получены из кристаллической симметрии. В этом случае симметрия СПП определяется НП B1g скрытой симметрии D4h (см. табл. 1 и рис. 7).

Рис. 7.

Теоретическая структура СПП ВТСП-материалов для НП B1g скрытой симметрии D4h в плоскости, перпендикулярной оси kz.

Пространственно-групповой подход позволяет описать и СПП, и ВЗП. Действительно, рассмотрим в формуле (6) двойной класс, определяемый вращением на 180° вокруг оси y. В этом случае паре будет соответствовать волновой вектор, направленный по оси y, и звезда для пары будет состоять из двух векторов (Ky, –Ky). (Для обозначения импульса пары используется большая буква K.) Разложение прямого произведения содержит также пару (Kx, –Kx). Эти результаты соответствуют стандартному описанию ВЗП, приведенному на рис. 3.

Таким образом, куперовские пары и ВЗП в ВТСП-материалах можно рассматривать как разные состояния двух эквивалентных электронов. При таком рассмотрении переходы между ВЗП и куперовскими парами (“конкуренция” [28] между ними) аналогичны переходам между термами двух эквивалентных электронов.

ЗАКЛЮЧЕНИЕ

Применение пространственно-группового подхода к двухэлектронным состояниям в кристаллах позволило установить, что нулевые плоскости СПП Sr2RuO4 симметрии Eu имеют вертикальные нулевые плоскости, причем существуют различные базисы, имеющие различные вертикальные нулевые плоскости. Таким образом, устранено существовавшее ранее противоречие между экспериментальной структурой СПП Sr2RuO4 [37–39] и выводами точечно-группового подхода [36, 40]. В ВТСП-материалах структура СПП не может быть получена из группы симметрии D2h и соответствует НП B1g скрытой симметрии D4h. Показано также, что волны зарядовой плотности и в ВТПС-материалах могут быть представлены как состояния двух эквивалентных электронов.

БЛАГОДАРНОСТЬ

Работа выполнена в рамках государственного задания ИОНХ РАН в области фундаментальных научных исследований.

Список литературы

  1. Bednorz J.G., Müller K.A. Possible high Tc superconductivity in the Ba–La–Cu–O systems // Z. Phys. B. 1986. V. 64. № 2. P. 189–193.

  2. Maeno Y., Hashimoto H., Yoshida K., Nishizaki S., Fujita T., Bednorz J.G., Lichtenberg F. Superconductivity in Layered Perovskite without Copper // Nature. 1994. V. 372. P. 532–534.

  3. Bardeen J.L., Cooper N., Schriffer J.R. Theory of Superconductivity // Phys. Rev. 1957. V. 108. № 5. P. 1175–1204.

  4. Zhang Y., Liu W., Zhu X., Zhao H., Hu Z., He C., Wen H.-H. Unprecedented High Irreversibility Line in the Nontoxic Cuprate Superconductor (Cu,C)Ba2Ca3Cu4O11 + δ // Sci. Adv. 2018. V. 4. 0192 (1–5).

  5. Шаплыгин И.С., Кахан Б.Г., Лазарев В.Б. Получение и свойства некоторых твердых растворов Ln2CuO4 (Ln–La, Pr, Nd, Sm, Eu, Gd) // Журн. неорган. химии. 1979. Т. 24. № 6. С. 1478–1485.

  6. Steglich F., Aarts J., Bredl C.D., Lieke W., Meschede D., Franz W., Schafer H. Superconductivity in the Presence of Strong Pauli Paramagnetism: CeCu2Si2 // Phys. Rev. Lett. 1979. V. 43. P. 1892–1895.

  7. Bishop D.J., Varma C.M., Batlogg B., Bucher E., Fisk Z., Smith J.L. Ultrasonic attenuation in UPt3 // Phys. Rev. Lett. 1984. V. 53. № 10. P. 1009–1011.

  8. Ott H.R., Rudiger H., Rice T.M., Ueda K., Fisk Z., Smith J.L. p-Wave Superconductivity in UBe13 // Phys. Rev. Lett. 1984. V. 52. № 21. P. 1915–1918.

  9. Yarzhemsky V.G., Murav’ev E.N. Space Group Approach to the Wavefunction of a Cooper Pair // J. Phys.: Condens. Matter. 1992. V. 4. P. 3525–3532.

  10. Yarzhemsky V.G. Space-Group Approach to the Nodal Structure of Superconducting Order Parameter in UPt3 // Phys. Status. Solidi B. 1998. V. 209. P. 101–107.

  11. Яржемский В.Г., Нефедов В.И. Симметрия двухэлектронных состояний в необычных сверхпроводниках // Неорган. материалы. 2005. T. 41. № 12. C. 1415–1424.

  12. Yarzhemsky V.G. Nodal Quantum Numbers for Two-Electron States in Solids // Few-Body Systems. 2012. V. 53. № 3. P. 499–504.

  13. Yarzhemsky V.G. Wavefunction of a Cooper pair in crystals of $D_{{2h}}^{1}$ and $D_{{4h}}^{{17}}$ symmetry // Z. Phys. B: Condens. Matter. 1995. V. 99. № 1. P. 19–23.

  14. Yarzhemsky V.G. Group Theoretical Lines of Nodes in Triplet Chiral Supercondictor Sr2RuO4 // J. Phys. Soc. Jpn. 2018. V. 87. 114711 (1–8).

  15. Tsuei C.C., Kirtley J.R. Pairing Symmetry in Cuprate Superconductors // Rev. Mod. Phys. 2000. V. 72. P. 969–1017.

  16. Яржемский В.Г., Нефедов В.И. Кристаллическая симметрия и структура двухэлектронных состояний в высокотемпературных сверхпроводниках // Докл. РАН. 2005. Т. 404. № 4. С. 481–485.

  17. Alloul H., Ohno T., Mendels P. 89Y NMR Evidence for a Fermi-Liquid Behavior in YBa2Cu3O6 + x // Phys. Rev. Lett. 1989. V. 63. P. 1700–1703.

  18. Kaminski A., Rosenkranz S., Fretwell H.M., Campuzano J.C., Li Z., Raffy H., Cullen W.G., You H.C., Olson G., Varma C.M., Höchst H. Spontaneous Breaking of Time-Reversal Symmetry in the Pseudogap State of a High-Tc Superconductor // Nature. 2002. V. 416. P. 610–612.

  19. Borisenko S.V., Kordyuk A.A., Koitzsch A., Kim T.K., Nenkov K.A., Knupfer M., Fink J., Grazioli C., Turchini S., Berger H. Circular Dichroism in Angle-Resolved Photoemission Spectra of Under- and Overdoped Pb-Bi2212 // Phys. Rev. Lett. 2004. 92. 207001 (1–4).

  20. He J., Mion T.R., Gao S., Myers G.T., Arita M., Shimada K., Gu G.D., He R.H. Angle-Resolved Photoemission with Circularly Polarized Light in the Nodal Mirror Plane of Underdoped Bi2Sr2CaCu2O8 + δ Superconductor // Appl. Phys. Lett. 2016. V. 109. 182601 (1–5).

  21. Fauqué B., Sidis Y., Hinkov V., Pailhès S., Lin C.T., Chaud X., Bourges P. Magnetic Order in the Pseudogap Phase of High-Tc Superconductors // Phys. Rev. Lett. 2006. V. 96. 197010 (1–4).

  22. Li Y., Baledent V., Yu G., Barisic N., Hradil K., Mole R.A., Sidis Y., Steffens P., Zhao X., Bourges P., Greven M. Hidden Magnetic Excitation in the Pseudogap Phase of a High-Tc Superconductor // Nature Lett. 2010. V. 468. P. 283–285.

  23. Xia J., Schemm E., Deutscher G., Kivelson S.A., Bonn D.A., Hardy W.N., Liang R., Siemons W., Koster G., Fejer M.M., Kapitulnik A. Polar Kerr Effect of the High-Temperature Superconductor YBa2Cu3O6 + x: Evidence of Broken Symmetry near the Pseudogap Temperature // Phys. Rev. Lett. 2008. V. 100. 127002 (1–4).

  24. Daou R., Chang J., Le Boeuf D., Cyr-Choiniere O., Laliberte F., Doiron-Leyraud N., Ramshaw B.J., Liang R., Bonn D.A., Hardy W.N., Taillefer L. Broken Rotational Symmetry in the Pseudogap Phase of a High-Tc Superconductor // Nature. 2010. V. 463. P. 519–522.

  25. Hinkov V., Haug D., Fauqué B., Bourges P., Sidis Y., Ivanov A., Bernhard C., Lin C.T., Keimer B. Electronic Liquid Crystal State in the High-Temperature Superconductor YBa2Cu3O6.45 // Science. 2008. V. 319. P. 597–600.

  26. Van Harlingen D.J. Phase-Sensitive Tests of the Symmetry of the Pairing State in the High-Temperature Superconductors – Evidence for ${{d}_{{{{x}^{{\text{2}}}} - {{y}^{{\text{2}}}}}}} $ Symmetry // Rev. Mod. Phys.1995. V. 67. № 2. P. 515.

  27. Hashimoto M.M., Vishik I.M., He R.H., Devereaux T.P., Shen Z. Energy Gaps in High-Transition-Temperature Cuprate Superconductors // Nature Phys. 2014. V. 10. P. 483–495.

  28. Chang J., Blackburn E., Holmes A.T., Christensen N.B., Larsen J., Mesot J., Ruixing Liang R., Bonn D.A., Hardy W.N., Watenphul A., Zimmermann M.V., Forgan E.M., Hayden S.M. Direct Observation of Competition between Superconductivity and Charge Density Wave Order in YBa2Cu3Oy // Nature Phys. 2012. V. 8. P. 871–876.

  29. Montiel X., Kloss T., Pépin C. Effective SU(2) Theory for the Pseudogap State // Phys. Rev. B. 2017. V. 95. 104510.

  30. Montiel X., Kloss T., Pépin C. Local Particle-Hole Pair Excitations by SU(2) Symmetry Fluctuations // Sci. Rep. 2017. V. 7. P. 3477.

  31. Morice C., Chakraborty D., Pèpin C. Collective Mode in the SU(2) Theory of Cuprates // Phys. Rev. B. 2018. V. 98. 224514.

  32. Ishida K., Mukuda H., Kitaoka Y., Asayama K., Mao Z.Q., Mori Y., Maeno Y. Spin-Triplet Superconductivity in Sr2RuO4 Identified by 17O Knight Shift // Nature. 1998. V. 96. P. 658–660.

  33. Nelson K.D., Mao Z.Q., Maeno Y., Liu Y. Odd-parity superconductivity in Sr2RuO4 // Science. 2004. V. 306. № 5699. P. 1151–1154.

  34. Luke G.M., Fudamoto Y., Kojima K.M., Larkin M.I., Merrin J., Nachumi B., Uemura Y.J., Maeno Y., Mao Z.Q., Mori Y., Nakamura H., Sigrist M. Time-Reversal Symmetry-Breaking Superconductivity in Sr2RuO4 // Nature 1998. V. 394. P. 558–561.

  35. Bonalde I., Yanoff B.D., Salamon M.B., Van Harlingen D.J., Chia E.M.E., Mao Z.Q., Maeno Y. Temperature Dependence of the penetration depth in Sr2RuO4: Evidence for Nodes in the Gap Function // Phys. Rev. Lett. 2000. V. 85. P. 4775–4778.

  36. Rice T.M., Sigrist M. Sr2RuO4: an Electronic Analogue of 3He // J. Phys. Condens. Matter. 1995. V. 7. P. L643–L648.

  37. Lupien C., MacFarlane W.A., Proust C. Taillefer L., Mao Z.Q., Maeno Y. Ultrasound Attenuation in Sr2RuO4: an Angle-Resolved Study of the Superconducting Gap Function // Phys. Rev. Lett. 2001. V. 86. P. 5986–5986.

  38. Deguchi K., Mao Z.Q., Maeno Y.J. Determination of the Superconducting Gap Structure in All Bands of the Spin-Triplet Superconductor Sr2RuO4 // Phys. Soc. Jpn. 2004. V. 73. P. 1313–1321.

  39. Hassinger E., Bourgeois-Hope P., Taniguchi H., René de Cotret S., Grissonnanche G., Anwar M.S., Maeno Y., Doiron-Leyraud N., Taillefer L. Vertical Line Nodes in the Superconducting Gap Structure of Sr2RuO4 // Phys. Rev. X. 2017. V. 7. 011032 (1–9).

  40. Blount E.I. Symmetry Properties of Triplet Superconductors // Phys. Rev. B. 1985. V. 32. P. 2935–2944.

  41. Xia J., Maeno Y., Beyersdorf P.T., Fejer M.M., Kapitulnik A. High Resolution Polar Kerr Effect Measurements of Sr2RuO4: Evidence for Broken Time Reversal Symmetry in the Superconducting State // Phys. Rev. Lett. 2006. V. 97. 167002 (1–4).

  42. Maeno Y., Kittaka S., Nomura T., Yonezava S., Ishida K. Evaluation of Spin-Triplet Superconductivity in Sr2RuO4 // J. Phys. Soc. Jpn. 2012. V. 81. 011009 (1–29).

  43. Ковалев О.В. Неприводимые и индуцированные представления пространственных групп. М.: Наука, 1985. 386 с.

  44. Bradley C.J., Davies B.L. Kronecker Products and Symmetrized Squares of Irreducible Representations of Space Groups // J. Math. Phys. 1970. V. 11. P. 1536–1552.

  45. Яржемский В.Г., Изотов А.Д., Изотова В.О. Структура параметра порядка в сверхпроводящих материалах на основе пниктидов железа // Неорган. материалы. 2017. Т. 53. № 9. С. 943–949. https://doi.org/10.7868/S0002337X17090068

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Неорганические материалы

Архивы выпусков Информация о журнале Отправить рукопись в журнал