Неорганические материалы, 2020, T. 56, № 8, стр. 906-913

ВВЕДЕНИЕ

В подавляющем большинстве технологических процессов создание аморфных материалов связано с быстрым охлаждением вещества из жидкого (например, спиннингование) или газообразного состояния (процессы в вакууме – термическое испарение или варианты ионного распыления с последующим нанесением на подложку). В последнее время обсуждается возможность аморфизации в твердом состоянии, активируемой в процессе интенсивной деформации.

Аморфные материалы используются в современных технологиях, но полная характеризация их структуры затруднена, что является следствием ограниченных возможностей дифракционных методов, успешно реализуемых применительно к кристаллическим веществам и материалам. Это отразилось и на определении этого класса веществ: от предельно расплывчатого “хаотическое расположение атомов и молекул” [1] или “полностью разупорядоченная структура” [2] до “состоят из осколков кристаллической структуры” [3]. Наиболее используемая характеристика их атомной структуры – “наличие ближнего и отсутствие дальнего порядка” [4, 5]. Если исходить из того, что реализуемая скорость охлаждения 10⁶–10⁵ К/с, а элементарные процессы атомной перестройки 10^–14–10^–12 с^–1, нельзя исключать вероятность образования зародышей кристаллических фаз, ожидаемых для заданного элементного состава расплава; следует учитывать и немаловажную особенность классических аморфных веществ и материалов: в отличие от кристаллических материалов их переход из твердого состояния в жидкое не сопровождается скачкообразным изменением свойств [4].

Ограничение метода рентгеновской дифрактометрии заключается в качественной характеризации структуры как “рентгеноаморфная” и даже “дифракционно аморфная” [6] исходя из дифрактограммы в виде гало.

В основе анализа ближнего порядка аморфных веществ методами рентгеновской дифрактометрии лежит сопоставление экспериментальной функции радиального распределения атомов и соответствующего набора межатомных расстояний в кристалле того же состава или с заданной моделью структурных единиц. Разработанные подходы обобщены в монографии [7] и подтверждают ближний порядок в пределах первых двух координационных сфер не только в твердой фазе, но и в соответствующих расплавах. Ограничения этого подхода должны проявляться в анализе многокомпонентных “аморфных” структур.

Для конкретизации и обоснования структуры ближнего порядка “аморфных” металлов и металлических сплавов используют разные варианты атомного моделирования, в том числе и метод молекулярной динамики (например, [8–11]). Для металлических аморфных систем развиваются представления о среднем порядке, характеризующемся икосаэдрической упаковкой кластеров [12–17]. Принципиальные ограничения, неучет направленности связей, исключают применимость метода молекулярной динамики ко многим практически важным системам.

В энциклопедическом представлении “аморфного состояния” [1] отмечается, что в “обычном стекле”, в плавленом кварце содержатся фрагменты кристаллов размером 10^–7–10^–6 см. Там же высказана надежда, что “дальнейшие исследования должны сгладить резкую грань в наших представлениях аморфных стеклообразных веществ и обычных кристаллических твердых тел”.

Определения “квазиаморфные тела” [18] или “состоящие из осколков кристаллической структуры” [3] вполне могут “сгладить эту грань”, если считать вещества состоящими из структурных элементов – зародышей кристаллических фаз, соответствующих элементному составу материала. Последнее согласуется с выводами работы [6] о структуре аморфного сплава Al–Ni–La, где анализ проведен в рамках т. н. фрагментарной модели [19]. В ней представлено развитие подхода, базирующегося на сопоставлении экспериментальной функции радиального распределения атомов сплава с идеализированной структурой аморфного вещества, атомная структура которого представлена возможными для соответствующего элементного состава зародышами кристаллических фаз (без учета граничной фазы).

Обращение к данной теме вызвано следующими фактами: положение профиля гало на оси 2θ дифрактограммы в большинстве случаев соответствует положению совокупности наиболее интенсивных отражений для соответствующих кристаллических фаз (возможны гало с многоуровневым профилем распределения интенсивности, например, для металлических сплавов, получаемых быстрым охлаждением расплава [20–22]); в работах [23, 24] расслоение гало таких сплавов представлено как следствие “двухфазной аморфной структуры” без конкретизации аморфных фаз; в исследовании реальной структуры “аморфных” объектов методами рентгеновской дифрактометрии (РД) и дифракции быстрых электронов не рассматривалась информативность гало с учетом размерного эффекта дифракции, проявляющегося в изменении пространственного распределения интенсивности, т.е. в расширении узлов обратной решетки с ограничением размера или с сильно выраженной анизотропией формы области когерентного рассеяния [25, 26]. Целесообразность учета размерного эффекта следует и из результатов работы [27], в которой был представлен подход к анализу ультрадисперсных систем, основанный на моделировании дифракционных картин от ансамбля наночастиц заданных структуры, размера и формы, с расчетом интенсивности по формуле Дебая в каждой точке профиля.

Цель настоящей работы – установить возможную природу и, с учетом размерного эффекта, оценить информативность дифрактограмм в виде гало, наблюдаемых при исследовании “аморфных” металлических сплавов и сложных оксидных систем.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Объектами анализа служили: дифрактограммы полученного быстрым охлаждением из расплава “аморфного” сплава состава Fe₇₈P₂₀Si₂ в виде лент толщиной 30–40 мкм (спиннингование) и после формирования в приповерхностном слое следов локальной деформации методом наноиндентирования¹¹; пленок системы Li–Nb–O состава, близкого к стехиометрии LiNbO₃ (LN), толщиной до 1.5 мкм, нанесенных на ненагреваемую подложку в процессе ионно-лучевого распыления (ИЛР) мишени из монокристалла LN²²; пленок фосфата кальция толщиной ~1.5 мкм, нанесенных в процессе ИЛР керамической мишени гидроксиапатита (ГА) – Ca₁₀(PO₄)₆(OH)₂.

Исследование методом РД проводили на приборе ARL X`TRA в геометрии Брэгга–Брентано. Съемку проводили в режиме θ–θ, при этом образцы помещали на кремниевую пластину с “нулевым фоном”. В качестве источника использовали рентгеновскую трубку с медным анодом (CuK_α), а дискриминацию неупруго рассеянного излучения осуществляли полупроводниковым энергодисперсионным детектором разрешением 250 эВ с охладителем на элементах Пельтье. Прибор был откалиброван по стандартному образцу NIST SRM-1976a, средняя погрешность положения рефлексов на оси 2θ относительно эталона не превышала 0.005°. Модельные профили рентгеновских дифрактограмм рассчитывали по методу Ритвельда [28] в программе HighScore Plus 3.0 [29]. Инструментальная функция прибора была рассчитана в приближении фундаментальных параметров [30]. Кристаллографические данные фаз (*.cif формат) были взяты из базы Springer Materials [31].

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

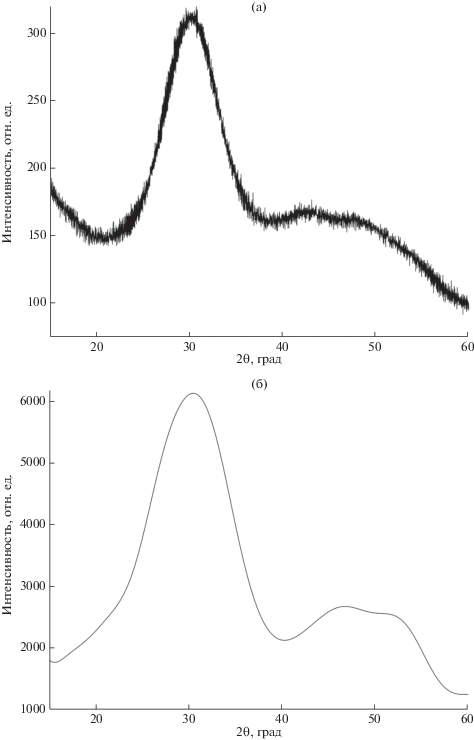
На рис. 1а приведены фрагменты дифрактограмм исходного образца (1) сплава Fe₇₈P₂₀Si₂ и после формирования областей множественной локальной деформации методом наноиндентирования (2), активирующей кристаллизацию [21]. Сопоставление гало со спектром отражений для возможных кристаллических фаз согласно диаграмме состояния показывает, что в интервале 2θ от 36° до 55° находится 11 отражений наибольшей интенсивности фазы Fe₃P, 6 отражений фазы Fe₂P и одно отражение α-Fe. Асимметрия гало на экспериментальной дифрактограмме 1 (рис. 1а) соответствует угловому распределению интенсивности отражений; она более выражена для дифрактограммы 2 (рис. 1а) вследствие развития процесса кристаллизации, на вершине гало проявляются заметные флуктуации интенсивности в области, соответствующей отражениям 201 (Fe₂P), 420 (Fe₃P) и 110 (α-Fe).

С учетом размерного эффекта дифракции, проявляющегося в расширении пространственного распределения интенсивности дифрагированной волны, представляемого в [26] функцией

где t₁, t₂, t₃ – размеры трехмерной области когерентного рассеяния; s₁, s₂, s₃ – проекции вектора отклонения от точного выполнения условия Вульфа–Брэгга (текущие координаты в обратном пространстве). Таким образом, гало можно рассматривать как результат суммирования предельно размытых отражений кристаллических фаз.

Соответственно, модель строения “аморфного” (квазиаморфного) материала, которая следует из учета размерного эффекта дифракции, может быть представлена состоящей из нанокристаллических областей размером в несколько периодов кристаллической решетки, полученных “измельчением” макроскопических кристаллов, соответствующих ожидаемым кристаллическим фазам для данного элементного состава. В отличие от нанопорошков нанозерна в данной модели разделены зернограничной фазой, т.е. соединены химическими связями того же типа, что и в микрокристаллических поликристаллах. Следует отметить, что в таком материале сохраняется достаточный объем когерентно рассеивающего кристаллического пространства³³ для формирования достаточной интенсивности рассеяния при случайной ориентации нанозерен (т.е. для каждой заданной ориентации нанозерен относительно первичного пучка есть множество других аналогично ориентированных нанозерен).

Интервал 2θ экспериментального гало на рис. 1 соответствует интервалу длин векторов возможных отражений $\left| {{{{\vec {g}}}_{{hkl}}}} \right| = {1 \mathord{\left/ {\vphantom {1 {{{d}_{{hkl}}}}}} \right. \kern-0em} {{{d}_{{hkl}}}}}$ для фазы Fe₇₈P₂₀Si₂ от 4 до 6 нм^–1. Для размера кристаллических зародышей фаз около 2 нм (даже для Fe₃P это 16 ячеек Бравэ) ширина соответствующего дифракционного пика на половине высоты составляет 2.5 нм^–1. При характерной для кристаллов Fe₂P и Fe₃P высокой плотности заселения отражениями рассматриваемого интервала углов их перекрытие должно приводить к образованию гало. Следует отметить, что форма наблюдаемого гало отражает интенсивность рефлексов каждой фазы, зависящую от ее доли. В частности, доля фазы Fe₃P увеличивается в результате ее продолжающегося синтеза за счет уменьшения доли метастабильной фазы Fe₂P и фазы α-Fe [32].

В соответствии с составом сплава была построена модельная дифрактограмма (рис. 1б) исходя из полного расхода фосфора на синтез фаз Fe₂P, Fe₃P, остающейся доли α-Fe и размера зародышей каждой фазы около 2 нм. Видно хорошее соответствие с экспериментальной дифрактограммой (рис. 1а). Из этого следует, что вывод авторов [33] о “сходстве” структуры этого сплава со структурой α-Fe был преждевременным, поскольку гало отображает наличие в составе сплава и образующихся интерметаллидов.

Обсуждаемая природа многоуровневого гало наиболее выразительно проявляется для сложных оксидов, например в пленках системы Li–Nb–O или фосфата кальция, формируемых в процессе ИЛР на неподореваемых подложках.

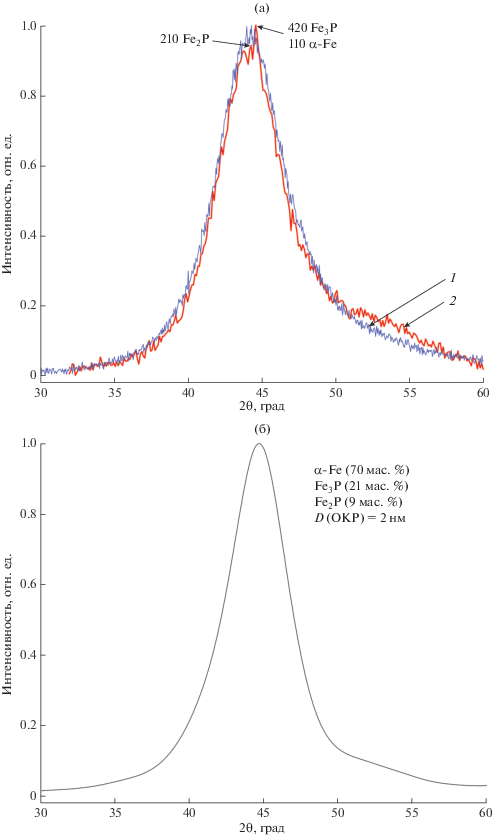
На рис. 2а приведен фрагмент рентгеновской дифрактограммы пленки фосфата кальция состава, близкого к ГА. Профиль интенсивности гало перекрывает интервал углов 2θ, на который приходятся 6 наиболее интенсивных отражений кристаллического ГА (в скобках относительная интенсивность): 0002 (174), 12$\overline 3 $0 (360), 12$\overline 3 $1 (999), 11$\overline 2 $2 (532), 30$\overline 3 $0 (614), 20$\overline 2 $2 (209) по данным [34]. Модельная дифрактограмма (рис. 2б), построенная с учетом размерного эффекта (размер области когерентного рассеяния (ОКР) взят равным 1.5 нм, т.е. удвоенный период вдоль оси с), качественно согласуется с экспериментальной.

Традиционное описание строения аморфного фосфата кальция Са_х(РО₄)_y · zH₂O (АФК, Са/Р = = х/у = 1.33–1.67) базируется на случайной упаковке областей ближнего порядка – кластеров Познера Са₉(РО₄)₆, размер которых примерно 0.95 нм [35]. В модели упорядоченной или случайной упаковки хиральных кластеров Познера с внeдрением в промежутки между ними ионов Са²⁺ и ОН^–(Н₂О) [36] удается описать соответственно кристаллические и аморфные фосфаты кальция в интервале составов Са/Р = 1.5–1.67. Таким образом, для моделирования дифрактограммы АФК заданного состава необходимо “измельчить” ОКР соответствующего фосфата кальция, в рассматриваемом примере это – ГА. Поскольку из растворов чаще всего осаждают АФК с Са/Р = 1.5, максимум гало для которого находится при 2θ ≈ 30° (съемка с использованием CuK_α-излучения, см., например, [37]), в этом случае для моделирования АФК с Са/Р = 1.5, по-видимому, следует в качестве макроскопического прототипа выбрать структуру α-Ca₃(PO₄)₂, поскольку при нагревании АФК первоначально кристаллизуется именно α‑Ca₃(PO₄)₂ [38].

Следует подчеркнуть, что при построении моделей дифрактограмм не учтены возможные анизотропия формы кристаллических зародышей, распределение их по размерам, объемная доля зернограничной фазы. При учете толщины межзеренных границ (для равновесной структуры границ зерен чистых металлов это два параметра кристаллической решетки [39–43]) объемная доля зернограничной фазы при предполагаемом размере зародышей кристаллической фазы может достигать 50%; особенности атомного строения зернограничной фазы могут проявиться в рассеянии и, следовательно, модулировать интенсивность фона.

На рис. 3 приведены рентгеновские дифрактограммы, характеризующие структуру исходной пленки системы Li–Nb–O (1), после ее термообработки при 425°С на воздухе в течение 1 (2) и 2 ч (3) непосредственно в высокотемпературной камере Anton Paar 1200N рентгеновского дифрактометра. Можно сделать вывод о том, что исходные пленки состоят из предельно наноструктурированных предшественников – зародышей кристаллических фаз: оксидов ниобия, оксида лития и продукта синтеза – LiNbO₃, поскольку три уровня гало дифрактограммы 1 перекрывают интервал интенсивных линий, отвечающих кристаллическим структурам Nb₂O₅ (левый и средний), NbO₂, LiNbO₃ (средний и правый) и Li₂O (правый уровень).

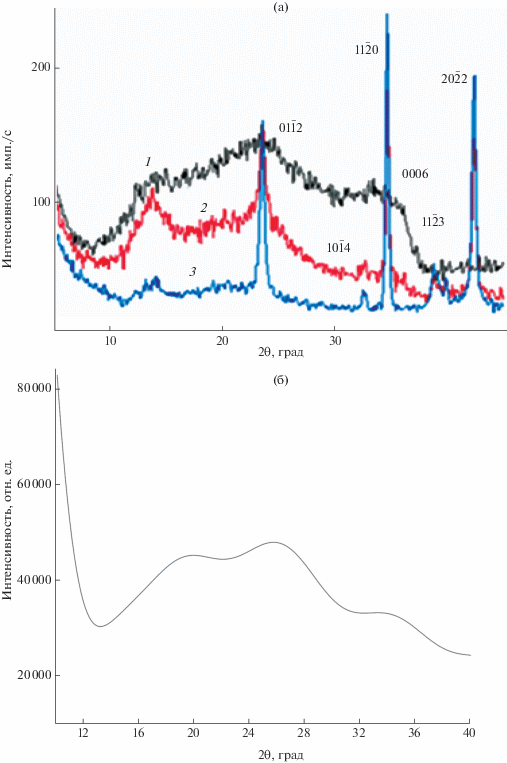
В процессе термической обработки проявляются основные отражения от кристаллической фазы LiNbO₃ (отмечены соответствующими индексами), при последующем отжиге их доля увеличивается. Снижение уровня общего фона дифрактограммы свидетельствует о расходовании исходных наноразмерных фаз в процессе синтеза LiNbO₃, что хорошо видно по изменению интенсивности пика при 2θ ~ 14°, наиболее вероятно отвечающего нанокристаллическому оксиду Nb₂O₅. Модельная дифрактограмма (рис. 3б), построенная с учетом размерного фактора (3 × 3 × 3 ячейки для каждой фазы), показала, что исходная пленка может состоять из продукта синтеза (LiNbO₃), а также оксидов LiNbO₂ [44] и Nb₂O₅.

ЗАКЛЮЧЕНИЕ

Свойственная достаточно большим кристаллам когерентность упруго рассеянных волн в рассмотренных структурах утрачена вследствие произвольной взаимной ориентации кристаллических зародышей соответствующих фаз предельно малых размеров. Поэтому ограниченная предельно малыми размерами взаимно разориентированных ОКР трансляционная симметрия – наиболее прозрачная характеристика природы таких (квазиаморфных) структур для систем с сильной межатомной связью.

При моделировании дифрактограмм квазиаморфных материалов возможен подход, при котором для соответствующих им по составу и структуре кристаллических фаз (прототипов) производится уменьшение размера ОКР до нескольких параметров кристаллической решетки.

Квазиаморфные структуры можно рассматривать как один из вариантов предельного наноструктурирования кристаллических веществ. Поэтому их “кристаллизацию” можно считать развитием процесса собирательной рекристаллизации, характерного, например, для наноструктурированных пленок металлов. В квазиаморфных объектах, например в соответствующих металлических сплавах, этот процесс проявляется формированием рекристаллизованных областей, разделенных относительно большими (протяженными) промежутками исходной структуры (распространенная характеристика таких металлических структур – “аморфно-кристаллические”). Развитие процесса собирательной рекристаллизации может тормозиться отторжением на его фронт атомов, избыточных относительно стехиометрического состава фазы.