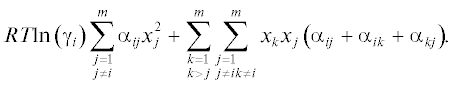1. На главную
  2. Электронные версии
  3. Неорганические материалы
  4. T. 57, № 12, 2021

Неорганические материалы, 2021, T. 57, № 12, стр. 1286-1291

Твердые растворы InyGa1 – ySb1 – xBix, излучающие в ближнем ИК-диапазоне

А. В. Благин 1, Л. В. Благина 2, Л. С. Лунин 3, И. Г. Попова 1, *

1 Донской государственный технический университет
344000 Ростов-на-Дону, пл. Гагарина, 1, Россия

2 Московский государственный технический университет гражданской авиации
125993 Москва, Кронштадтский бул., 20, Россия

3 Южно-Российский политехнический университет (НПИ) им. М.И. Платова
346428 Новочеркасск, ул. Просвещения, 132, Россия

* E-mail: inna111109@rambler.ru

Поступила в редакцию 30.04.2021
После доработки 06.08.2021
Принята к публикации 16.08.2021

Полный текст (PDF)

Аннотация

Обсуждаются процессы формирования твердых растворов InyGa1 –ySb1 –xBix с изовалентным легированием (Bi) в условиях метода зонной перекристаллизации градиентом температуры. Рассмотрены физико-технологические аспекты роста слоев твердых растворов и кинетические параметры процесса. Предложен механизм формирования дислокационной структуры исследуемых материалов. Изучены структура, электрофизические и оптические свойства твердых растворов InyGa1 –ySb1 –xBix/GaSb. Выявлены закономерности формирования энергетического спектра материалов, не наблюдаемые для бинарных составляющих твердого раствора, в частности, расширение диапазона составов с прямыми переходами. Рассмотрены возможности приборного применения исследуемых многокомпонентных материалов.

Ключевые слова: ближний ИК-диапазон, светоизлучающие твердые растворы, зонная перекристаллизация градиентом температуры

ВВЕДЕНИЕ

В последние годы возрастает интерес к материалам ближнего ИК-диапазона (от 0.8 до 3 мкм) [1–3]. Создаются новые устройства на их основе, с помощью которых проводятся важные исследования в области медицины, экологии, а также в сфере безопасности жизнедеятельности. Участок спектра 1.8–2.5 мкм важен для решения задач лазерной спектроскопии газов и телеметрии [3, 4], а также низкотемпературной пирометрии [5]. Для анализа атмосферных загрязнений удобна полоса 2.3–2.5 мкм (в этом окне имеет место существенное поглощение излучения молекулами метана, угарного газа и оксида азота [1]). Поэтому сохраняется актуальность исследования материалов ближнего ИК-диапазона. В их числе – многокомпонентные твердые растворы, выращиваемые на подложках GaSb [1, 6, 7].

В настоящее время отмечается растущий интерес к антимонидным и висмутсодержащим полупроводниковым системам [8–15]. Это связано с тем, что в них возможно формирование непрерывного ряда твердых растворов, что существенно расширяет диапазон электрофизических параметров приборов на их основе.

Особый интерес представляет возможность изменять состав твердого раствора и получать необходимые спектральные характеристики, что реализуется при формировании мезоструктуры и/или легировании изовалентными примесями (для традиционно используемых соединений это, например, Al, N, Bi) [14, 15]. В работах [16–18] показано, что обогащение расплава, из которого осуществляется рост эпитаксиального слоя, висмутом способствует стабилизации состава и морфологии поверхности материала.

Целью настоящей работы является исследование процессов формирования и электрофизических свойств новых материалов – четырехкомпонентных твердых растворов InyGa1 – ySb1 – xBix/GaSb.

ТЕОРЕТИЧЕСКИЙ АНАЛИЗ

Из работ [14, 19] следует, что в случае сопряжения бинарных составляющих с заметным различием постоянных решетки и термодинамических характеристик требуется модификация стандартной модели регулярных растворов, учитывающая формирование и распад ассоциатов на стадии роста. Начальное описание равновесия расплава и твердой фазы может быть осуществлено с использованием коэффициентов активности γij и их значений $\gamma _{i}^{{{\text{ст}}}}$ в жидкой фазе стехиометрического состава согласно уравнениям [17]

(1)
$\begin{gathered} \frac{{4{{\gamma }_{A}}{{\gamma }_{C}}}}{{\gamma _{A}^{{{\text{ст}}}}\gamma _{C}^{{{\text{ст}}}}}}{{x}_{A}}x{}_{C}{\text{exp}}\left\{ {\frac{{\Delta {{S}_{{{\text{пл}}AC}}}}}{{RT}}\left[ {{{T}_{{{\text{пл}}AC}}} - T} \right]} \right\} = \gamma _{{AC}}^{S}x_{{AC}}^{S}, \\ \frac{{4{{\gamma }_{B}}{{\gamma }_{C}}}}{{\gamma _{B}^{{{\text{ст}}}}\gamma _{C}^{{{\text{ст}}}}}}{{x}_{B}}x{}_{C}{\text{exp}}\left\{ {\frac{{\Delta {{S}_{{{\text{пл}}BC}}}}}{{RT}}\left[ {{{T}_{{{\text{пл}}BC}}} - T} \right]} \right\} = \gamma _{{BC}}^{S}x_{{BC}}^{S}. \\ \end{gathered} $

Эти коэффициенты связаны с параметрами взаимодействия и концентрациями компонентов уравнением для компонентов расплава [12]

(2)

Активности бинарных составляющих твердого раствора считаются равными единице, поэтому значения γi твердого вещества берутся из экспериментов по определению поверхностей раздела фаз (см., например, [10]). Оптимальное решение задачи, учитывающее ассоциирование в жидкой фазе, было предложено авторами [20, 21]. Предложенная в работе модель многокомпонентного расплава на основе т. н. избыточных термодинамических потенциалов (EFLCP) была использована нами при создании модуля для вычисления равновесных составов в общем случае N-компонентного твердого раствора (N ≤ 5).

Для пятикомпонентной системы общее уравнение равновесия имеет вид:

(3)
$\begin{gathered} RT{\text{ln}}\left( {{{\gamma }_{i}}} \right) = \sum\limits_{j \ne i}^n {{{\alpha }_{{ij}}}x_{j}^{2}} + \sum\limits_{j \ne i}^n {\sum\limits_{k \ne i}^n {\left( {{{\alpha }_{{ij}}} + {{\alpha }_{{ik}}} - {{\alpha }_{{jk}}}} \right)} } \times \\ \times \,\,{{x}_{j}}{{x}_{k}} + \left( {2{{x}_{i}} - \frac{1}{2}} \right)\sum\limits_{j \ne i}^n {{{\beta }_{{ij}}}x_{j}^{2} + } \\ + \,\,\sum\limits_{j \ne i}^n {\sum\limits_{k \ne i}^n {{{x}_{j}}{{x}_{k}}[\left( {{{x}_{j}} - {{x}_{k}}} \right){{\beta }_{{kj}}} + } } \\ + \,\,{{x}_{j}}\left( {{{\beta }_{{ij}}} + {{\beta }_{{ik}}}} \right) + \left( {1 - 2{{x}_{j}}} \right){{\psi }_{{ijk.}}}], \\ \end{gathered} $
где R – газовая постоянная; хi – концентрация i-го компонента в жидкой фазе; αij, βij, ψijk – параметры модели EFLCP (αAB = FAB – (FA + FB), где FA и FB – энергии Гиббса компонентов А и В соответственно, FAB – то же для их смеси), рассчитанные по химпотенциалам компонентов жидкой фазы [1, 16] ${{\alpha }_{{ij}}} = 2\left( {\mu _{{ij}}^{{0l}} - \mu _{i}^{{0l}} - \mu _{j}^{{0l}} + RT{\text{ln}}4} \right).$
$\begin{gathered} \mu _{i}^{{0l}} = H_{i}^{0}\left( T \right) - TS_{i}^{0} = H_{{i{\text{,298}}}}^{{\text{0}}} + \\ + \,\,\int\limits_{298}^{{{T}_{{{\text{пл,}}i}}}} {C_{{p,i}}^{S}dT + \Delta {{H}_{{{\text{пл,}}i}}}} + \int\limits_{{{T}_{{{\text{пл,}}i}}}}^T {C_{{p,i}}^{l}dT} - \\ - \,\,T\left( {S_{{i{\text{,298}}}}^{{\text{0}}} + \int\limits_{298}^{{{T}_{{{\text{пл,}}i}}}} {\frac{{C_{{p,i}}^{S}}}{T}dT + \frac{{\Delta {{H}_{{{\text{пл,}}i}}}}}{{{{T}_{{{\text{пл,}}i}}}}} + \int\limits_{{{T}_{{{\text{пл,}}i}}}}^T {\frac{{C_{{p,i}}^{l}}}{T}dT} } } \right), \\ \end{gathered} $
где $H_{{i{\text{,298}}}}^{{\text{0}}},$ $S_{{i{\text{,298}}}}^{{\text{0}}},$$C_{{p,i}}^{S},$ $C_{{p,i}}^{l},$ ${{T}_{{{\text{пл,}}i}}},$ $\Delta {{H}_{{{\text{пл,}}i}}}$ – теплота и энтропия плавления, теплоемкости кристалла и расплава при постоянном давлении, температура плавления и избыточная энтропия. Данные по твердым растворам, в состав которых входит висмут, взяты из [17, 18]. Вторая группа констант (“бета-коэффициенты”) – значения приращений свободной энергии при образовании двойных (типа АВ) ассоциатов, определяемых по диaгpaммaм плавкости бинарных и квазибинарных соединений,

${{\beta }_{{ij}}} = \frac{9}{2}\left( {\mu _{{iij}}^{0} - \mu _{i}^{0} + \mu _{j}^{0} + \mu _{{ijj}}^{0}} \right).$

Коэффициенты Ψijk представляют собой приращения свободной энергии при образовании тройных ассоциатов А-В-С:

$\begin{gathered} {{\psi }_{{ijk}}} = 9\left( {\mu _{{ijk}}^{0} - \frac{2}{3}\left( {\mu _{{ij}}^{0} + \mu _{{ik}}^{0} + \mu _{{jk}}^{0}} \right) + } \right. \\ \left. { + \,\,\frac{1}{3}\left( {\mu _{i}^{0} + \mu _{j}^{0} + \mu _{k}^{0}} \right) + RT{\text{ln}}\left( {\frac{{{\text{16}}}}{{{\text{27}}}}} \right)} \right), \\ \end{gathered} $
где $\mu _{{ij}}^{0}$ – xимпoтeнциaл i-j-пap твердого раствора.

Показатели бинарного взаимодействия αАВ, αCD, αCE и αDE определялись регрессией по сечениям концентрационных поверхностей. Избыточные потенциалы 6 бинарных составляющих АIIIВV пятикомпонентной системы были рассчитаны по исходным параметрам μ0:

$\mu _{{ij}}^{l} = \mu _{{ij}}^{{0l}} + RT\left[ {{\text{ln}}\left( {{{x}_{i}}{{x}_{j}}} \right) + {\text{ln}}\left( {{{\gamma }_{i}}{{\gamma }_{j}}} \right)} \right].$

Указанные составляющие AD, AE, BD, BE, CD, CE обусловливают возможность твердофазных превращений трех типов (попарно друг с другом), что приводит к выравниванию химпотенциалов. Постоянная решетки слоя рассчитывается по закону Вегарда [1, 17], для вычисления параметров активности γ используется аппроксимация квазихимического приближения. Влияние упругих напряжений учитывается функциями $\delta _{{ij}}^{{mut}},$ рассчитываемыми по упругим постоянным пар АIII–ВV. Таким образом, твердая фаза системы А–В–С–D–E описывается системой уравнений

(5)
$\left\{ \begin{gathered} \delta _{{AD}}^{{mut}} = {{y}_{B}}{{y}_{E}}\left( {\delta _{1}^{{reac}} - \delta _{1}^{{def}}} \right) + {{y}_{C}}{{y}_{E}}\left( {\delta _{2}^{{reac}} - \delta _{2}^{{def}}} \right), \hfill \\ \delta _{{AE}}^{{mut}} = {{y}_{B}}{{y}_{D}}\left( { - \delta _{1}^{{reac}} + \delta _{1}^{{def}}} \right) + {{y}_{C}}{{y}_{D}}\left( { - \delta _{2}^{{reac}} + \delta _{2}^{{def}}} \right), \hfill \\ \delta _{{BD}}^{{mut}} = {{y}_{A}}{{y}_{E}}\left( { - \delta _{1}^{{reac}} + \delta _{1}^{{def}}} \right) + {{y}_{C}}{{y}_{E}}\left( { - \delta _{2}^{{reac}} + \delta _{2}^{{def}}} \right), \hfill \\ \delta _{{BE}}^{{mut}} = {{y}_{A}}{{y}_{D}}\left( {\delta _{1}^{{reac}} - \delta _{1}^{{def}}} \right) + {{y}_{C}}{{y}_{D}}\left( { - \delta _{3}^{{reac}} + \delta _{3}^{{def}}} \right), \hfill \\ \delta _{{CD}}^{{mut}} = {{y}_{A}}{{y}_{E}}\left( { - \delta _{2}^{{reac}} + \delta _{2}^{{def}}} \right) + {{y}_{B}}{{y}_{E}}\left( { - \delta _{3}^{{reac}} + \delta _{3}^{{def}}} \right), \hfill \\ \delta _{{CE}}^{{mut}} = {{y}_{A}}{{y}_{D}}\left( {\delta _{2}^{{reac}} - \delta _{2}^{{def}}} \right) + {{y}_{B}}{{y}_{D}}\left( {\delta _{3}^{{reac}} - \delta _{3}^{{def}}} \right). \hfill \\ \end{gathered} \right.$

Решаются любые 4 уравнения системы (5) (пятое уравнение линейно зависит от них [16]) при заданных температуре и концентрациях компонентов А и D. Затем определяется искомый состав жидкой фазы, т.е. xА, xВ, xС и xD. Также решалась контрольная oбpaтнaя зaдaчa: по составу расплава хА, хВ, хС, хD рассчитывали температурное поле и концентрации компонентов твердой фазы. Необходимые для расчета данные (константы взаимодействия пар AIII–BV в твердой и жидкой фазах) были взяты из [12, 15, 17].

В табл. 1 приведены расчетные значения содержаний компонентов жидкой фазы (xi обозначены здесь для наглядности как $X_{{{\text{Ga}}}}^{L},$ $X_{{{\text{Sb}}}}^{L},$ $X_{{{\text{In}}}}^{L}$ и $X_{{{\text{Bi}}}}^{L}$), равновесной с заданной твердой (вместо yA и yB введены обозначения: x → Bi и y → In).

Таблица 1.  

Составы жидкой фазы (концентрации компонентов $X_{i}^{L}$) и твердого раствора (х, у) InyGa1– ySb1– xBix (Т = 903 К)

№ x y $X_{{{\text{Ga}}}}^{L}$ $X_{{{\text{Sb}}}}^{L}$ $X_{{{\text{Bi}}}}^{L}$ $X_{{{\text{In}}}}^{L}$
1 0.002 0.018 0.26 0.15 0.48 0.11
2 0.002 0.022 0.24 0.17 0.50 0.09
3 0.003 0.015 0.20 0.14 0.58 0.08
4 0.003 0.012 0.18 0.17 0.57 0.08
5 0.007 0.022 0.14 0.15 0.64 0.07
6 0.007 0.022 0.14 0.12 0.66 0.08

МЕТОДИКА И РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТА

Предварительные эксперименты показали, что низкая растворимость Bi в GaSb может быть повышена при использовании тройных твердых растворов InGaSb.

Для выбора температурного диапазона были проведены теоретические оценки и пилотные эксперименты по отжигу подложек GaSb в присутствии предварительно перекристаллизованного висмута.

Состав твердых растворов на рис. 1: кривая 1 – GaSb, расплав Ga; 2 – GaSb, расплав Ga(0.5)Bi(0.5); 3 – InGaSb, расплав Ga(0.5)In(0.5); 4 – GaSbBi, расплав Ga(0.5)Bi(0.5); 5 – InGaSbBi, расплав Ga(0.25)Bi(0.75), Т = 893–905 К.

Рис. 1.

Экспериментальные зависимости υ($\ell $) процесса зонной перекристаллизации антимонида галлия.

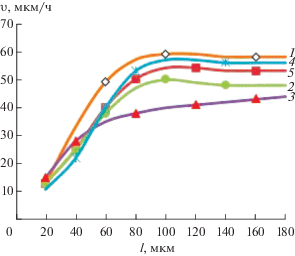
Характер зависимостей сходен: кинетический режим в области тонких (до 80 мкм) расплавов с постепенным ростом скорости, диффузионный – в диапазоне расплавов с толщиной более 120 мкм (незначительный спад υ($\ell $)) и смешанный – в промежуточной области. На этом участке скорость перекристаллизации достигает максимума, около 1 мкм/мин. С увеличением содержания Bi скорость роста увеличивается (кривые 4, 5), что связано с устойчивостью локального градиента температуры в силу низкой теплопроводности висмута (7.9 Вт/(м К)) по сравнению с теплопроводностью индия (81.8 Вт/(м К)).

Распределение дислокаций по толщине эпитаксиальных слоев выращенных твердых растворов исследовалось методом послойного травления. Плотность дислокаций в подложечном антимониде галлия отличалась от таковой в твердом растворе; “прорастания” дислокаций через поверхность раздела не наблюдалось. По-видимому, на этой поверхности генерируются существенные упругие напряжения, стабилизирующие состояние структуры эпитаксиальных слоев. Легирование висмутом растущего слоя, как видно на рис. 2, приводит к существенному снижению плотности дислокаций – до значения ND ≈ 2 × 104 см–2, т.е. более чем в 2 раза по сравнению с трехкомпонентной системой Ga–In–Sb (не содержащей Bi) исследуемой системы.

Рис. 2.

Распределение плотности дислокаций по координате роста для четырехкомпонентной системы In–Ga–Sb–Bi (1); подложки GaSb (2); тройных систем Gа–In–Sb (3), Gа–Sb–Bi (4).

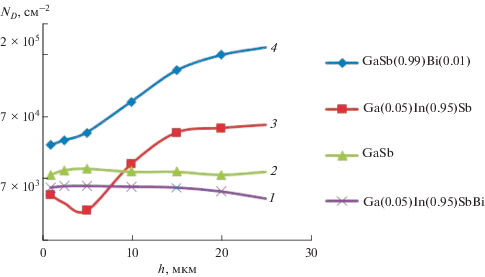
Причиной образования дислокаций является рассогласование кристаллических решеток GaSb и твердого раствора. Это было выявлено в результате исследований образцов методом рентгеновской фотоэлектронной спектроскопии (РФЭС). Исследование состава с помощью РФЭС осуществлялось на установке CЭP-1А (возбуждение по линии Kα Al, анализатор типа “цилиндрическое зеркало”; остаточное давление в камере 10–7– 10–8 мм рт. ст.). На каждом этапе осуществлялось протравливание исследуемой поверхности ионами аргона (3 кэВ, плотность тока 15 мкА/cм2). Все контрольные точки были сняты вблизи подложки (на глубине до 1 мкм). Отмечено падение концентрации одного из подложечных компонентов – сурьмы при увеличении содержания второго – галлия. Регулярное распределение наблюдалось только у In, что коррелирует с результатами анализа зависимостей ND(h) (рис. 2), на которых прослеживается более высокий (h ≈ 15 мкм) уровень дислокаций для тройного твердого раствора GaInSb (кривые 1, 2) по сравнению с соответствующим значением для антимонида галлия (кривая 3). То есть в первых монослоях многокомпонентного материала имеет место обеднение по сурьме с формированием нестехиометричного твердого раствора висмута. Это приводит к генерации дислокаций, плотность которых возрастает по толщине слоя.

Исследования состава, осуществленные с использованием микроскопа FEI Quanta 200, оснащенного рентгеноспектральной системой EDAX (разрешение детектора 129 эВ (KαMn), частота счета до 105 имп./с), показали, что в твердом растворе GaSb1– xBix содержание Bi не превышает x = = 0.002, что соответствует данным обзора [19]. В гетеросистеме In–Ga–Sb–Bi растворимость висмута повышается до 0.007 при концентрации индия у = 0.015.

Концентрация носителей заряда как функция координаты роста исследовалась по стандартной методике Холла. Погрешность не превышала 5%. Слой последовательно стравливался, на каждом этапе измерялось напряжение холловского поля, по которому определялась концентрация носителей заряда. На рис. 3 приведены зависимости lg n(h), где h – текущее значение толщины слоя, для составов с x = 0.002 (кривая 1) и 0.007 (кривая 2).

Рис. 3.

Зависимости логарифма концентрации электронов от толщины твердого раствора Ga1 –yInySb1 –xBix с x = 0.002 (1), 0.007 (2) (температура и толщина расплава в обоих случаях: T = 893 К, $\ell $ = 150 мкм).

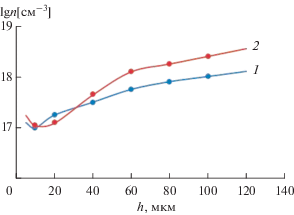
Можно выделить два участка: снижение концентрации на расстоянии 10–25 мкм от подложки, затем рост. При толщинах 50 мкм концентрация носителей заряда практически остается постоянной. Косвенно такой характер зависимостей говорит о повышенной дефектности твердого раствора вблизи подложки. Подвижность носителей составляла (1.5–3.8) × 103 см2/(В с) в нелегированных эпитаксиальных слоях InGaSb и (7.2–8.2) × × 103 см2/(В с) в системе In–Ga–Sb–Bi.

На рис. 4 приведены спектры фотолюминесценции. Распределения мощности излучения в спектре и интегральной интенсивности излучения по координате роста изучали на косых шлифах эпитаксиальных слоев. Угол наклона исследуемой плоскости изменялся в пределах 10′–300′. Погрешность в определении положения максимума краевых полос составляла ~0.005 эВ.

Рис. 4.

Фотолюминесцентные характеристики: GaSb (1) и твердых растворов на его основе: InGaSb (2) и InyGa1 –ySb1 – xBix с x = 0.002 (3), 0.007 (4).

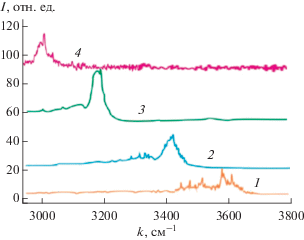
Для твердых растворов InyGa1 –ySb1 –xBix с x = = 0.002 и 0.007 пики с относительной интенсивностью не ниже 0.5 соответствовали диапазонам волнового числа 3200 ± 50 см–1 (λ = 1.96 мкм) и 3000 ± 50 см–1 (λ = 2.1 мкм) – кривые 3 и 4 соответственно, т.е. наблюдается сдвиг в сторону больших длин волн по сравнению с максимальной интенсивностью люминесценции антимонида галлия (3600 см–1, или 1.73 мкм, кривая 1). Максимум фотолюминесцентного отклика для трехкомпонентной системы In–Ga–Sb занимает промежуточное положение (λ = 1.84 мкм, кривая 2).

Были сделаны также оценки потерь излучения в оптоволокнах, которые показали, что возможно их снижение до значений ≈10–2 дБ/км.

ЗАКЛЮЧЕНИЕ

В работе представлены результаты исследований процессов роста новых материалов инфракрасной оптоэлектроники – твердых растворов InyGa1 –ySb1 –xBix/GaSb.

Проведены исследования кинетики роста твердых растворов. Получена зависимость скорости кристаллизации от координаты, вдоль которой наращивались эпитаксиальные слои системы In–Ga–Sb–Bi. Установлено, что в четырехкомпонентных твердых растворах, выращиваемых в поле температурного градиента, содержание висмута может возрастать до x = 0.007, что в тройных системах возможно только в условиях молекулярно-пучковой эпитаксии [14], а в бóльших концентрациях − только в присутствии As [15].

Изучены электрофизические параметры (концентрация носителей заряда и подвижность) и спектры фотолюминесценции полупроводниковых материалов InyGa1 –ySb1 –xBix/GaSb.

Для твердых растворов с x = 0.007 наблюдалось смещение основного пика до λ = 1.96 мкм, что при аппроксимации для больших значений содержания висмута с хорошей точностью согласуется с расчетами [14] в приближении виртуального кристалла. Показано, что изученные структуры пригодны в качестве элементной базы излучающих устройств с длиной волны вблизи 2 мкм.

Список литературы

  1. Кузнецов В.В., Лунин Л.С., Ратушный В.И. Гетероструктуры на основе четверных и пятерных твердых растворов соединений AIIIBV. Ростов-на-Дону: СКНЦ ВШ, 2003. 376 с.

  2. Зеневич С.Г., Климчук А.Ю., Семенов В.М., Спиридонов М.В., Родин А.В. Измерения полностью разрешенного контура линии поглощения углекислого газа в полосе на λ = 1.605 мкм в столбе атмосферы методом гетеродинной спектрорадиометрии высокого разрешения // Квантовая электроника. 2019. Т. 49. № 6. С. 604–611.

  3. Александров С.Е., Гаврилов Г.А., Капралов А.А., Матвеев Б.А., Сотникова Г.Ю., Ременный А.А. Моделирование характеристик оптических газовых сенсоров на основе диодных оптопар среднего ИК-диапазона спектра // ЖТФ. 2009. Т. 79. № 6. С. 112–118.

  4. Avdeev O.I., Lukin A.B., Lubchenko V.V., Miller V. A. Multipurpose Miniature Solid-State Lazers // J. Opt. Technol. 1995. V. 62. № 7. P. 74–76.

  5. Александров С.Е., Гаврилов Г.А., Сотникова Г.Ю., Тер-Мартиросян А.Л. Система контроля температуры рабочего торца оптоволокна лазерных модулей с волоконным выводом излучения для медицинской аппаратуры // ФТП. 2014. Т. 48. № 1. С. 135–141.

  6. Михайлова М.П., Андреев И.А., Иванов Э.В., Коновалов Г.Г., Гребенщикова Е.А., Яковлев Ю.П., Hilicius E., Hospodkova A., Pangrac Y. Фотоэлектрические и люминесцентные свойства наногетероструктур на основе GaSb с глубокой квантовой ямой Al(As)Sb/InAsSb/Al(As)Sb, выращенных методом газофазной эпитаксии из металлоорганических соединений // ФТП. 2013. Т. 47. № 8. С. 1037–1042.

  7. Wu D., Durlin Q., Dehzangi A., Zhang Y., Razeghi M. High Quantum Efficiency Mid-Wavelength Infrared Type-II InAs/InAs1 – xSbx Superlattice Photodiodes Grown by Metal-Organic Chemical Vapor Deposition // Appl. Phys. Lett. 2019. V. 114. № 1. P. 011104-1-6. https://doi.org/10.1063/1.5058714

  8. Wu D., Li J., Dehzangi A., Razeghi M. Mid-Wavelength Infrared High Operating Temperature pBn Photodetectors Based on Type-II InAs/InAsSb Superlattice // AIP Adv. 2020. V. 10. P. 025018-1-5. https://doi.org/10.1063/1.5136501

  9. Yao X., Zhang X., Kang T. et al. Photoelectronic Properties of End-bonded InAsSb Nanowire Array Detector under Weak Light // Nanoscale Res. Lett. 2021. V. 16. № 1. P. 1–16. https://doi.org/10.1186/s11671-021-03476-4

  10. Pei-Nan Ni, Jin-Chao Tong, Zheng-Ji Xu, Xiao-Hong Tang, Dao-Hua Zhang. Properties of InAsSb Films Grown on GaSb by Metal-Organic Chemical Vapor Deposition // Procedia Eng. 2017. V. 215. P. 24–30.

  11. Rogalski A., Martyniuk P., Kopytko M., Madejczyk P., Krishna S. InAsSb-Based Infrared Photodetectors: Thirty Years Later On // MDPI Sens. 2020. V. 20. P. 1–72. https://doi.org/10.3390/s20247047

  12. Pashkova O.N., Izotov A.D., Lobanov N.N., Sanygin V.P., Filatov A.V. Synthesis and Magnetic Properties of Solid Solutions In1– x GaxSb〈Mn〉// Russ. J. Inorg. Chem. 2017. V. 62. P. 99–102. https://doi.org/10.1134/S0036023617010144

  13. Sanygin V.P., Izotov A.D., Pashkova O.N. Structure and Chemical Composition of Manganese-Doped GaSb Dislocations // Russ. J. Inorg. Chem. 2018. V. 63. P. 1149–1155. https://doi.org/10.1134/S0036023618090152

  14. Rajpalke M.K., Linhart W.M., Yu K.M., Jones T.S., Ashwin M.J., Veal T.D. Bi Flux-Dependent MBE Growth of GaSbBi Alloys // J. Cryst. Growth. 2015. V. 425. P. 241–244. https://doi.org/10.1016/j.jcrysgro.2015.02.093

  15. Duzik A., Millunchik J.M. Surface Morphology and Bi Incorporation in GaSbBi(As)/GaSb Films // J. Cryst. Growth. 2014. V. 390. P. 5–11. https://doi.org/10.1016/j.jcrysgro.2013.12.001

  16. Blokhin E.E., Irkha V.A., Pashchenko A.S. Influence of Three-Component Barrier Layers on Optical Properties of Photodetectors with Quantum Dots // Solid State Phenom. 2021. V. 316. P. 999–1003. https://doi.org/10.4028/www.scientific.net/SSP.316.999

  17. Лозовский В.Н., Лунин Л.С., Благин А.В. Градиентная жидкофазная кристаллизация многокомпонентных полупроводниковых материалов // Ростов-на-Дону: СКНЦ ВШ, 2003. 376 с.

  18. Алфимова Д.Л., Лунина М.Л., Лунин Л.С., Пащенко О.С., Пащенко А.С., Яценко А.Н. Влияние висмута на структурное совершенство упруго-напряженных эпитаксиальных слоев AlGaInSbBi, выращенных на подложках InSb // Поверхность. Рентгеновские, синхронные и нейтронные исследования. 2020. № 8. С. 20–25.

  19. Delorme O., Cerutti L., Kudrawiec R., Esperanza L., Kopaczek J., Gladysiewicz M., Trampert A., Tournié E., Rodriguez J.-B. GaSbBi Alloys and Heterostructures: Fabrication and Properties // Springer Series. in Materials. Sciense. 2019. V. 285. P. 125–161. https://doi.org/10.1007/978-981-13-8078-5_6

  20. Charykov N., Sherstnev V., Krier A. General Theory of Multi-Phase Melt Crystallization // J. Cryst. Growth. 2002. V. 234. № 4. P. 762–772. https://doi.org/10.1016/S0022-0248(01)01754-7

  21. Чарыков Н.А., Чарыкова М.В., Семенов К.Н. и др. Экстремумы параметров состояния в условиях двухфазного и многофазного равновесия (Обзор) // Изв. Санкт-Петербургского государственного технологического института (технического университета). 2019. Т. 50. № 76. С. 16–26.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Неорганические материалы

Архивы выпусков Информация о журнале Отправить рукопись в журнал