Неорганические материалы, 2021, T. 57, № 3, стр. 243-249
Термодинамические свойства халькогенидных фаз в системе Bi–Te–S
Э. Дж. Ахмедов 1, *, Д. М. Бабанлы 1, 2, С. З. Имамалиева 1, Д. Б. Тагиев 1, М. Б. Бабанлы 1
1 Институт катализа и неорганической химии им. академика М. Нагиева Национальной академии наук Азербайджана
AZ1143 Баку, пр. Г. Джавида, 113, Азербайджан
2 Азербайджанский государственный университет нефти и промышленности, Французско-азербайджанский университет
AZ-1101 Баку, пр. Азадлыг, 6/21, Азербайджан
* E-mail: elvin.ehmedov.2014@mail.ru
Поступила в редакцию 19.06.2020
После доработки 23.10.2020
Принята к публикации 26.10.2020
Аннотация
Методом электродвижущих сил изучена система Bi–S–Te в области составов Bi2S3–Bi2Te3–Те–S в интервале температур 300–450 К. Рассчитаны относительные парциальные молярные функции висмута в сплавах, на основании которых получены взаимосогласованные комплексы значений стандартных свободной энергии Гиббса и энтальпии, а также стандартных энтропий для соединений Bi2S3, Bi2Тe3, Bi2Te2S и твердого раствора состава Bi2Te1.8S1.2 на основе последнего. Проведен сравнительный анализ полученных данных для Bi2S3 и Bi2Тe3 с литературными. Для фаз Bi2Te2S и Bi2Te1.8S1.2 термодинамические функции определены впервые.
ВВЕДЕНИЕ
Минерал тетрадимит и его структурные аналоги представляют большой интерес в связи с уникальными функциональными свойствами. Эти соединения, твердые растворы и допированные фазы интенсивно изучаются с середины прошлого столетия как термоэлектрические и оптические материалы [1–3]. В последнее десятилетие установлено, что указанные фазы являются топологическими изоляторами [4–8] и чрезвычайно перспективны для разнообразных приложений, начиная от спинтроники и кончая медициной и системами безопасности [9, 10]. Кроме того, нанокристаллы Bi2S3 благодаря уникальным оптическим свойствам перспективны для использования в широкополосных фотодетекторах и оптических транзисторах [11, 12].
Термодинамические функции соединений являются их фундаментальными характеристиками и в совокупности с фазовыми диаграммами составляют основу для выращивания кристаллов, а также для оптимизации условий разработки новых материалов на их основе [10, 13]. Термодинамические свойства бинарных соединений Bi2S3 и Bi2Te3 исследованы в многочисленных работах, результаты которых обобщены в фундаментальных справочниках и электронных базах данных [14–16]. Однако нами не обнаружены данные по термодинамическим функциям тетрадимита и твердых растворов на его основе.
Целью настоящей работы явилось исследование твердофазных равновесий в системе Bi–S–Te в области составов Bi2S3–Bi2Tе3–Te–S и термодинамических свойств образующихся в ней халькогенидных фаз методом ЭДС.
Указанный метод широко применяется для исследования бинарных и сложных халькогенидов металлов. При этом измерения ЭДС целесообразно проводить в температурном интервале ниже солидуса фазовой диаграммы соответствующей системы. Глицериновые растворы солей щелочных металлов оказались наиболее подходящими электролитами для подобных низкотемпературных измерений [17–21]. Как показано в [22, 23], при изучении подобных систем в качестве электролита могут быть использованы также ионные жидкости.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
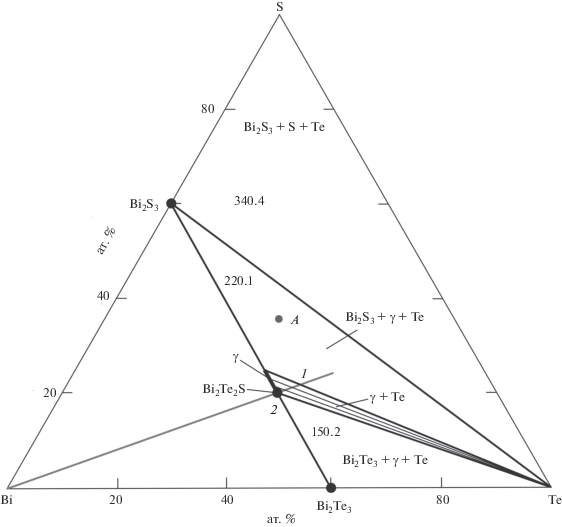
Для планирования экспериментов по термодинамическому исследованию системы Bi–S–Te нами с использованием литературных данных построена ее диаграмма твердофазных равновесий в области составов Bi2S3–Bi2Tе3–Te–S. Согласно изотермическому сечению фазовой диаграммы системы Bi–S–Te при 673 К, приведенному в [24], в вышеуказанной области соединение Bi2S3 и γ‑фаза переменного состава на основе тетрадимита связаны конодами с элементарным теллуром. Эти данные показывают, что ниже точки плавления серы фазовая диаграмма подсистемы Bi2S3–Bi2Tе3–Te–S должна выглядеть, как показано на рис. 1. Она состоит из трехфазных областей: Bi2S3 + + Te + S, Bi2S3 + Te + γ и Bi2Te3 + Te + γ (γ – твердые растворы на основе Bi2Te2S). Последние две области разграничены двухфазной областью γ + Те.
Рис. 1.
Диаграмма твердофазных равновесий системы Bi–Te–S в области составов Bi2S3–Bi2Tе3–Te–S при 300 К: цифры в трехфазных областях – значения ЭДС (мВ) цепей типа (1); А – сплав, порошковая дифрактограмма которого приведена на рис. 2.
Для термодинамического исследования системы Bi–S–Te методом ЭДС были составлены концентрационные цепи типа
(1)
$( - )~~{\text{Bi (тв}}{\text{.}})\left| {{\text{ионная жидкость}} + {\text{B}}{{{\text{i}}}^{{3 + }}}} \right|{\text{Bi}}{\kern 1pt} --{\kern 1pt} {\text{S}}{\kern 1pt} --{\kern 1pt} {\text{Te (тв}}{\text{.}})~( + )~.$В качестве левого электрода использовали элементарный висмут, а в качестве правых электродов – равновесные сплавы из трехфазных областей Bi2S3 + Te + S, Bi2S3 + Te + γ, Bi2Te3 + Te + γ, а также из области гомогенности γ-фазы с добавлением 0.5 мол. % избытка теллура. Сплавы готовили из предварительно синтезированных и идентифицированных бинарных соединений, а также элементарных серы и теллура высокой степени чистоты в вакуумированных (~10–2 Пa) кварцевых ампулах. После сплавления при 1000 К образцы охлаждали до 700 К и выдерживали в течение 500 ч, а затем дополнительно при 380 К 100 ч.
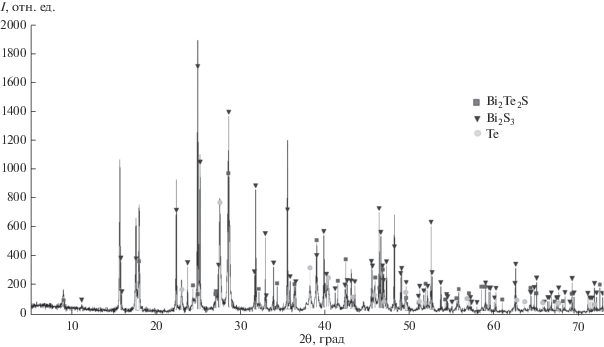
Соответствие фазовых составов полученных образцов диаграмме состояния (рис. 1) контролировали методом РФА. Порошковые дифрактограммы снимали на дифрактометре Bruker D8 (CuKα-излучение). На рис. 2 представлена дифрактограмма сплава состава (ат. %): 32Bi + 32Te + + 36S (рис. 1, точка А). Как видно, дифракционная картина этого сплава состоит из совокупности рефлексов Te, Bi2S3 и тетрадимита, что соответствует трехфазной области Bi2S3 + Te + γ на фазовой диаграмме.
В цепях типа (1) в качестве электролита использовали ионную жидкость (формиат морфолина) с добавлением BiCl3. Для получения ионной жидкости использовали морфолин, муравьиную кислоту и безводный BiCl3 (Alfa Aesar). Ионную жидкость получали по методике [23]: морфолин вливали в трехгорлую круглодонную колбу, которую погружали в ледяную баню, оснащенную обратным холодильником, капельной воронкой для добавления кислоты и термометром для контроля температуры. Муравьиную кислоту добавляли по каплям в течение 1 ч при интенсивном перемешивании. Учитывая экзотермичность этой реакции, температуру смеси поддерживали ниже 25°С. Перемешивание продолжали в течение 4 ч. Остаточный амин или кислоту выпаривали при пониженном давлении (1–5 мм рт. ст.), а оставшуюся жидкость дополнительно сушили при 80°C при тех же условиях.
Методики сборки электрохимических цепей типа (1) и проведения измерений ЭДС подробно описаны в [18, 23].
Первые равновесные значения ЭДС были получены после выдерживания ячейки при ∼350 К в течение 40–60 ч, последующие – через каждые 3–4 ч после установления определенной температуры. Равновесными считали значения ЭДС, которые не отличались друг от друга при неоднократном измерении при данной температуре более чем на 0.2 мВ, независимо от направления изменения температуры.
Для сплавов из трехфазной области Bi2S3 + S + Te измерения ЭДС проводили в интервале температур 300–380 К, для остальных сплавов – в интервале 300–450 К.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Измерения показали, что в пределах каждой их трехфазных областей Bi2S3 + Te + S, Bi2S3 + Te + γ, Bi2Te3 + Te + γ ЭДС имеет постоянные значения независимо от валового состава электрод-сплава (рис. 1), а в двухфазной области Te + γ изменяется с изменением состава γ-фазы. При этом для всех изученных сплавов температурные зависимости ЭДС оказались линейными (рис. 3). Учитывая это, экспериментальные значения пар Е и Т обработали с помощью компьютерной программы Microsoft Office Excel 2003 методом наименьших квадратов и получили линейные уравнения типа E = a + bT. Ход расчетов для трехфазной области Bi2S3 + Bi2Te1.8Se1.2(γ) + Te приведен в табл. 1.
Рис. 3.
Температурные зависимости ЭДС цепей типа (1) в системе Bi–S–Te; фазовые области: 1 – Bi2S3 + Te + S; 2 – Bi2S3 + Bi2Te1.8Se1.2(γ) + Te; 3 – Bi2Te2Se(γ) + Te; 4 – Bi2Te3 + Bi2Te2Se(γ) + Te.
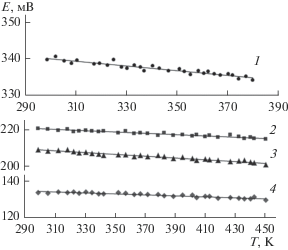
Таблица 1.
Результаты компьютерной обработки результатов измерений ЭДС для образца из области Bi2S3 + + Bi2Te1.8Se1.2(γ) + Te системы Bi2S3–Bi2Te3
| Ti, K | Ei, мВ | ${{T}_{i}} - \bar {T}$ | Ei(${{T}_{i}} - \bar {T}$) | ${{({{T}_{i}} - \bar {T})}^{2}}$ | $\tilde {E}$ | ${{E}_{i}} - \tilde {E}$ | ${{({{E}_{i}} - \tilde {E})}^{2}}$ |
|---|---|---|---|---|---|---|---|
| 298.7 | 340.12 | –42.85 | –14574.14 | 1836.12 | 340.49 | –0.37 | 0.14 |
| 302.1 | 340.96 | –39.45 | –13450.87 | 1556.30 | 340.27 | 0.69 | 0.48 |
| 305.5 | 339.84 | –36.05 | –12251.23 | 1299.60 | 340.05 | –0.21 | 0.05 |
| 308.3 | 339.21 | –33.25 | –11278.73 | 1105.56 | 339.87 | –0.66 | 0.44 |
| 310.4 | 340.08 | –31.15 | –10593.49 | 970.32 | 339.74 | 0.34 | 0.12 |
| 317.2 | 339.03 | –24.35 | –8255.38 | 592.92 | 339.31 | –0.28 | 0.08 |
| 319.4 | 339.27 | –22.15 | –7514.83 | 490.62 | 339.16 | 0.11 | 0.01 |
| 322.6 | 338.65 | –18.95 | –6417.42 | 359.10 | 338.96 | –0.31 | 0.10 |
| 324.8 | 340.11 | –16.75 | –5696.84 | 280.56 | 338.82 | 1.29 | 1.67 |
| 328 | 338.25 | –13.55 | –4583.29 | 183.60 | 338.62 | –0.37 | 0.13 |
| 330.3 | 337.91 | –11.25 | –3801.49 | 126.56 | 338.47 | –0.56 | 0.31 |
| 333.1 | 338.62 | –8.45 | –2861.34 | 71.40 | 338.29 | 0.33 | 0.11 |
| 335.5 | 338.13 | –6.05 | –2045.69 | 36.60 | 338.14 | –0.01 | 0.00 |
| 336.9 | 337.16 | –4.65 | –1567.79 | 21.62 | 338.05 | –0.89 | 0.79 |
| 340.2 | 338.51 | –1.35 | –456.99 | 1.82 | 337.84 | 0.67 | 0.46 |
| 342.9 | 337.82 | 1.35 | 456.06 | 1.82 | 337.66 | 0.16 | 0.02 |
| 346.6 | 337.14 | 5.05 | 1702.56 | 25.50 | 337.43 | –0.29 | 0.08 |
| 350.8 | 337.66 | 9.25 | 3123.36 | 85.56 | 337.16 | 0.50 | 0.25 |
| 352.7 | 336.97 | 11.15 | 3757.22 | 124.32 | 337.04 | –0.07 | 0.00 |
| 355.1 | 336.24 | 13.55 | 4556.05 | 183.60 | 336.88 | –0.64 | 0.41 |
| 358.3 | 337.22 | 16.75 | 5648.44 | 280.56 | 336.68 | 0.54 | 0.29 |
| 360.4 | 336.53 | 18.85 | 6343.59 | 355.32 | 336.54 | –0.01 | 0.00 |
| 362.2 | 336.95 | 20.65 | 6958.02 | 426.42 | 336.43 | 0.52 | 0.27 |
| 364.6 | 336.32 | 23.05 | 7752.18 | 531.30 | 336.28 | 0.04 | 0.00 |
| 366.9 | 336.07 | 25.35 | 8519.37 | 642.62 | 336.13 | –0.06 | 0.00 |
| 370.1 | 336.41 | 28.55 | 9604.51 | 815.10 | 335.92 | 0.49 | 0.24 |
| 371.9 | 335.95 | 30.35 | 10196.08 | 921.12 | 335.81 | 0.14 | 0.02 |
| 374.2 | 334.98 | 32.65 | 10937.10 | 1066.02 | 335.66 | –0.68 | 0.47 |
| 377 | 335.72 | 35.45 | 11901.27 | 1256.70 | 335.48 | 0.24 | 0.06 |
| 379.8 | 334.64 | 38.25 | 12799.98 | 1463.06 | 335.30 | –0.66 | 0.44 |
| $\bar {T}$ = 341.55 | $\bar {E}$ = 337.75 |
Полученные линейные уравнения представлены в табл. 2 в рекомендованном в [17] виде
(2)
$E = a + bT \pm t{{\left[ {\frac{{\delta _{E}^{{\text{2}}}}}{n} + \delta _{b}^{{\text{2}}}{{{{\text{(}}T - \bar {T}{\text{)}}}}^{{\text{2}}}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$Таблица 2.
Уравнения температурных зависимостей ЭДС цепей типа (1) в некоторых фазовых областях системы Bi2S3–Bi2Tе3–Te–S
| № | Фазовая область | $E,\,{\text{мВ}} = a + bT \pm t{{\delta }_{E}}\left( T \right)$ |
|---|---|---|
| 1 | Bi2S3 + S + Те | $359.58 - 0.0639Т \pm 2{{\left[ {\frac{{0.25}}{{30}} + 1.4 \times {{{10}}^{{ - 5}}}{{{(Т - 341.55)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ |
| 2 | Bi2S3 + Bi2Te1.8S1.2(γ) + Te | $230.53 - 0.0347Т \pm 2{{\left[ {\frac{{0.21}}{{30}} + 3.5 \times {{{10}}^{{ - 6}}}{{{(Т - 375.5)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ |
| 3 | Bi2Te2S(γ) + Te | $223.34 - 0.0489Т \pm 2{{\left[ {\frac{{0.22}}{{30}} + 3.6 \times {{{10}}^{{ - 6}}}{{{(Т - 375.5)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ |
| 4 | Bi2Te3 + γ + Te | $142.18 - 0.0266Т \pm 2{{\left[ {\frac{{0.20}}{{30}} + 3.3 \times {{{10}}^{{ - 6}}}{{{(Т - 375.5)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ |
Из данных табл. 2 по соотношениям
(4)
${{\overline {\Delta S} }_{{{\text{Bi}}}}} = zF{{\left( {\frac{{\partial E}}{{\partial T}}} \right)}_{p}} = zFb{\text{,}}$(5)
${{\overline {\Delta H} }_{{{\text{Bi}}}}} = - zF\left[ {E - T{{{\left( {\frac{{\partial E}}{{\partial T}}} \right)}}_{p}}} \right] = - zFa$были рассчитаны относительные парциальные молярные функции висмута в сплавах (табл. 3).
Таблица 3.
Парциальные молярные функции висмута в сплавах системы Bi2S3–Bi2Tе3–Te–S при 298 К
| Фазовая область | $ - \Delta {{\overline G }_{{{\text{Bi}}}}}$ | $ - \Delta {{\bar {H}}_{{{\text{Bi}}}}}$ | $\Delta {{\bar {S}}_{{{\text{Bi}}}}}$, Дж/(моль K) |
|---|---|---|---|
| кДж/моль | |||
| Bi2S3 + S + Те | 98.568 ± 0.073 | 104.08 ± 0.50 | –18.50 ± 1.47 |
| Bi2S3 + Bi2Te1.8S1.2(γ) + Te | 63.736 ± 0.064 | 66.73 ± 0.27 | –10.04 ± 0.72 |
| Bi2Te2S(γ) + Te | 60.428 ± 0.066 | 64.65 ± 0.28 | –14.16 ± 0.73 |
| Bi2Te3 + γ + Te | 38.855 ± 0.063 | 41.15 ± 0.26 | –7.71 ± 0.70 |
Согласно фазовой диаграмме (рис. 1), парциальные молярные функции висмута в трехфазных областях Bi2S3 + S + Те и Bi2Te3 + γ + Te являются термодинамическими функциями следующих потенциалобразующих реакций:
(6)
${\text{Bi}} + 1.5{\text{S}} = 0.5{\text{B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{S}}}_{{\text{3}}}},$(7)
${\text{Bi}} + 1.5{\text{Te}} = 0.5{\text{B}}{{{\text{i}}}_{{\text{2}}}}{\text{T}}{{{\text{e}}}_{3}}.$Также нетрудно показать, что данные табл. 3 для трехфазной области Bi2S3 + Bi2Te1.8S1.2(γ) + Te отвечают потенциалобразующей реакции
(8)
${\text{Bi}} + {\text{B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{S}}}_{3}} + 1.5{\text{Te}} = {\text{B}}{{{\text{i}}}_{{\text{2}}}}{\text{T}}{{{\text{e}}}_{{{\text{1}}{\text{.8}}}}}{{{\text{S}}}_{{{\text{1}}{\text{.2}}}}}.$В соответствии с уравнениями реакций (6)–(8) стандартные интегральные термодинамические функции образования и стандартные энтропии Bi2S3, Bi2Te3 и γ-фазы с максимальным содержанием серы (Bi2Te1.8S1.2) вычислены по следующим соотношениям:
(9)
${{\Delta }_{f}}{{Z}^{0}}({\text{B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{S}}}_{3}}) = 2\Delta {{\bar {Z}}_{{{\text{Bi}}}}},$(10)
${{\Delta }_{f}}{{Z}^{0}}({\text{B}}{{{\text{i}}}_{2}}{\text{T}}{{{\text{e}}}_{3}}) = 2{{\bar {Z}}_{{{\text{Bi}}}}},$(11)
${{\Delta }_{f}}{{Z}^{0}}({\text{B}}{{{\text{i}}}_{{\text{2}}}}{\text{T}}{{{\text{e}}}_{{{\text{1}}{\text{.8}}}}}{{{\text{S}}}_{{1.2}}}) = 1.2{{\bar {Z}}_{{{\text{Bi}}}}} + 0.4{{\Delta }_{f}}{{Z}^{0}}({\text{B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{S}}}_{3}}),$(12)
${{S}^{0}}({\text{B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{S}}}_{{\text{3}}}}) = 2\Delta {{\bar {S}}_{{{\text{Bi}}}}} + 2{{S}^{0}}({\text{Bi}}) + 3{{S}^{0}}(S),$(13)
${{S}^{0}}({\text{B}}{{{\text{i}}}_{{\text{2}}}}{\text{T}}{{{\text{e}}}_{{\text{3}}}}) = 2\Delta {{\bar {S}}_{{{\text{Bi}}}}} + 2{{S}^{0}}({\text{Bi}}) + 3{{S}^{0}}({\text{Te}}),$(14)
$\begin{gathered} {{S}^{0}}({\text{B}}{{{\text{i}}}_{{\text{2}}}}{\text{T}}{{{\text{e}}}_{{{\text{1}}{\text{.8}}}}}{{{\text{S}}}_{{1.2}}}) = 1.2\Delta {{{\bar {S}}}_{{{\text{Bi}}}}} + 1.2{{S}^{0}}({\text{Bi}}) + \\ + \,\,0.4{{S}^{0}}({\text{B}}{{{\text{i}}}_{{\text{2}}}}{{{\text{S}}}_{3}}) + 1.8{{S}^{0}}({\text{Te}}). \\ \end{gathered} $В выражениях (9)–(11) Z ≡ G(H).
Интегральные термодинамические функции для γ-фазы стехиометрического состава Bi2Te2S рассчитали графическим интегрированием уравнения Гиббса–Дюгема по лучевому разрезу от Bi-вершины концентрационного треугольника в интервале составов 1–2 (рис. 1).
Полученные результаты представлены в табл. 4. Погрешности находили методом накопления ошибок. При расчетах интегральных термодинамических функций помимо данных табл. 3 были использованы значения стандартных энтропий висмута (56.7 ± 0.5 Дж/(моль К), серы (31.9 ± 0.2 Дж/(моль К) и теллура (49.5 ± ± 0.2 Дж/(моль К) [16].
Таблица 4.
Стандартные интегральные термодинамические функции фаз системы Bi–S–Tе
| Фазовая область | $ - {{\Delta }_{f}}{{G}^{0}}(298\,\,{\text{K}})$ | $ - {{\Delta }_{f}}{{H}^{0}}(298\,\,{\text{K}})$ | ${{S}^{0}}(298\,\,{\text{K}})$ | Источник, метод |
|---|---|---|---|---|
| кДж/моль | Дж/(моль К) | |||
| Bi2S3 | 197.1 ± 0.2 | 208.2 ± 1.1 | 172.2 ± 4.7 | НР, ЭДС |
| 198.9 ± 7.5 | 201.7 ± 4.2 | 200.4 ± 8.6 | [15] | |
| 143.1 | 140.4 | 200.4 | [14] | |
| 152.9 | 155.6 | 200.4 ± 8.4 | [16] | |
| Bi2Te1.8S1.2 | 155.3 ± 0.2 | 163.4 ± 0.8 | 214.0 ± 2.9 | НР, ЭДС |
| Bi2Te2S | 151.5 ± 0.3 | 159.7 ± 0.9 | 217.3 ± 2.8 | НР, ЭДС |
| Bi2Te3 | 77.7 ± 0.2 | 82.3 ± 0.6 | 246.5 ± 3.1 | НР, ЭДС |
| 77.9 ± 0.6 | 80.0 ± 4.4 | [25], ЭДС | ||
| 89.5 ± 0.9 | 99.5 ± 9.5 | [26], ЭДС | ||
| 84.1 ± 3.2 | [27], калориметрия | |||
| 80.5 ± 5.0 | [28], давление пара | |||
| 77.1 | 77.4 | 260.9 | [14] | |
| 78.7 ± 2.1 | 261.1 ± 8.4 | [15] | ||
| 75.3 ± 1.7 | 78.6 ± 0.2 | 251.0 ± 8.4 | [16] | |
В табл. 4 также приведены литературные данные по термодинамическим функциям Bi2S3 и Bi2Te3.
Значения свободной энергии Гиббса и энтальпии образования соединения Bi2S3, приведенные в справочниках [14–16], сильно различаются. Наши результаты практически совпадают с данными, рекомендованными в [15]. Для Bi2Te3 наши и полученные в [25, 27, 28] различными экспериментальными методами результаты, а также рекомендованные в справочниках [14–16] величины хорошо согласуются между собой (табл. 4). Данные [26], полученные методом ЭДС, несколько завышены. Термодинамические функции тетрадимита и твердого раствора состава Bi2Te1.8S1.2 на его основе определены нами впервые.
ЗАКЛЮЧЕНИЕ
Система Bi–S–Te изучена методом ЭДС в области составов Bi2S3–Bi2Te3–Те–S и интервале температур 300–450 К. Из данных измерений ЭДС вычислены относительные парциальные молярные функции висмута в сплавах. На основании диаграммы твердофазных равновесий подсистемы Bi2S3–Bi2Te3–Те–S определены потенциалобразующие реакции, с использованием которых получены новые взаимосогласованные комплексы значений стандартных свободной энергии Гиббса и этальпии, а также стандартных энтропий для соединений Bi2S3, Bi2Тe3, Bi2Te2S и твердого раствора состава Bi2Te1.8S1.2. Полученные результаты для Bi2S3 и Bi2Тe3 дополняют и уточняют имеющиеся в литературе термодинамические данные, а термодинамические функции тройных фаз определены впервые.
Список литературы
Шевельков А.В. Химические аспекты создания термоэлектрических материалов // Успехи химии. 2008. Т. 77. № 1. С. 3–21.
Joo S.J., Ryu B., Son J.H. et al. Highly Anisotropic Thermoelectric Transport Properties Responsible for Enhanced Thermoelectric Performance in the Hot-Deformed Tetradymite Bi2Te2S // J. Alloys Compd. 2019. V. 783. P. 448–454. https://doi.org/10.1016/j.jallcom.2018.12.340
Liu W., Kevin C.L., Kenneth McEnaney et al. Studies on the Bi2Te3–Bi2Se3–Bi2S3 System for Mid-Temperature Thermoelectric Energy Conversion // Energy Environ. Sci. 2013. V. 6. № 2. P. 552–560. https://doi.org/10.1039/c2ee23549h
Kanagaraj M., Pawbake A., Sarma S.C. et al. Structural, Magnetotransport and Hall Coefficient Studies In Ternary Bi2Te2Se, Sb2Te2Se and Bi2Te2S Tetradymite Topological Insulating compounds // J. Alloys Compd. 2019. V. 794. P. 195–202. https://doi.org/10.1016/j.jallcom.2019.04.226
Annese E., Okuda T., Schwier E.F. et al. Electronic and Spin Structure of the Wide-Band-Gap Topological Insulator: Nearly Stoichiometric Bi2Te2S // Phys. Rev. B. 2018. V. 97. P. 205113–205118. https://doi.org/10.1103/PhysRevB.97.205113
Hogan C., Holtgrewe K., Ronci F. et al. Temperature Driven Phase Transition at the Antimonene/Bi2Se3 van der Waals Heterostructure // ACS Nano. 2019. V. 13. № 9. P. 10481–10489. https://doi.org/10.1021/acsnano.9b04377
Mamedov N.T., Alizade E.H., Jahangirli Z.A. et al. Infrared Spectroscopic Ellipsometry and Optical Spectroscopy of Plasmons in Classic 3D Topological Insulators // J. Vac. Sci. Technol. B. 2019. V. 37. P. 062602–062607. https://doi.org/10.1116/1.5122776
Estyunin D.A., Klimovskikh I.I., Shikin A.M. et al. Signatures of Temperature Driven Antiferromagnetic Transition in the Electronic Structure of Topological Insulator MnBi2Te4 // APL Mater. 2020. V. 8. P. 021105-7. https://doi.org/10.1063/1.5142846
Viti L., Coquillat D., Politano A. et al. Plasma-Wave Terahertz Detection Mediated by Topological Insulators Surface States // Nano Lett. 2016. V. 16. P. 80−87. https://doi.org/10.1021/acs.nanolett.5b02901
Babanly M.B., Chulkov E.V., Aliev Z.S. et al. Phase Diagrams in Materials Science of Topological Insulators Based on Metal Chalkogenides // Russ. J. Inorg. Chem. 2017. V. 62. № 13. P. 1703–1729. https://doi.org/10.1134/S0036023617130034
Liang F.X., Ge C.W., Zhang T.F. et al. Plasmonic Hollow Gold Nanoparticles Induced High-Performance Bi2S3 Nanoribbon Photodetector // Nanophonotics. 2017. V. 6. № 2. P. 1–8. https://doi.org/10.1515/nanoph-2016-0024
Shan Y., Li Z., Ruan B. et al. Two-Dimensional Bi2S3-Based All-Optical Photonic Devices with Strong Nonlinearity due to Spatial Self-Phase Modulation // Nanophonotics. 2019. V. 8. № 12. P. 2225–2234. https://doi.org/10.1515/nanoph-2019-0231
Babanly M.B., Mashadiyeva L.F., Babanly D.M. et al. Some Issues of Complex Investigation of the Phase Equilibria and Thermodynamic Properties of the Ternary Chalcogenide Systems by the EMF Method // Russ. J. Inorg. Chem. 2019. № 13. P. 1649–1671. https://doi.org/10.1134/S0036023619130035
Barin I. Thermochemical Data of Pure Substances, Third Edition // United States: Wiley, 2008. 1936 p.
Kubaschewski O., Alcock C.B., Spenser P.J. Materials Thermochemistry // United Kingdom: Pergamon Press, 1993. 512 p.
База данных термических констант веществ. 2006. Электронная версия / Под ред. Юнгмана В.С. http://www.chem.msu.ru/cgi-bin/tkv.pl?show=welcome.html/welcome.html
Морачевский А.Г., Воронин Г.Ф., Гейдерих В.А., Куценок И.Б. Электрохимические методы исследования в термодинамике металлических систем ИЦК. М.: Академкнига Москва, 2003. 334 с.
Бабанлы М.Б., Юсибов Ю.А. Электрохимические методы в термодинамике неорганических систем. Баку: ЭЛМ, 2011. 306 с.
Имамалиева С.З., Мехдиева И.Ф., Бабанлы Д.М. и др. Твердофазные равновесия в системе Tl2Te–Tl2Te3–TlErTe2 и термодинамические свойства соединений Tl9ErTe6 и TlErTe2 // Журн. неорган. химии. 2020. Т. 65. № 11. С. 1550–1557.
Имамалиева С.З., Бабанлы Д.М., Гасанлы Т.М. и др. Термодинамические свойства Tl9GdTe6 and TlGdTe2 // Журн. физ.химии. 2018. Т. 92. № 11. С. 1684–1690.
Бабанлы Д.М., Машадиева Л.Ф., Бабанлы М.Б. Уточнение фазовой диаграммы системы Tl–I и изучение термодинамических свойств иодидов таллия // Неорган.материалы. 2017. Т. 53. № 5. С. 524–529.
Aliev Z.S., Musayeva S.S., Imamaliyeva S.Z., Babanly M.B. Thermodynamic Study of Antimony Chalcoiodides by EMF Method with an Ionic Liquid // J. Therm. Anal. Calorim. 2018. V. 133. № 2. P. 1115–1120. https://doi.org/10.1007/s10973-017-6812-4
Imamaliyeva S.Z., Musayeva S.S., Babanly D.M. et al. Determination of the Thermodynamic Functions of Bismuth Chalcoiodides by EMF Method with Morpholinium Formate as Electrolyte // Thermochim. Acta. 2019. V. 679. P. 178319–178325. https://doi.org/10.1016/j.tca.2019.178319
Kitakaze A. Phase Relation of Some Sulfide Systems-(3) // Mem. Fac. Eng. Yamaguchi Univ. 2017. V. 68. № 1. P. 1–31. https://doi.org/10.13140/RG.2.2.21198.15685
Герасимов Я.И., Никольская А.В. Термодинамические свойства теллурида висмута (Bi2Te3) и теллурида сурьмы (Sb2Te3) // Металлургия и физика полупроводников. М., 1961. С. 30–33.
Sidorko V.R., Goncharuk L.V., Antonenko R.V. Thermodynamic Properties of Bismuth Sesquiselenide and Sesquitelluride and Their Solid Solutions // Powder Metall. Met. Ceram. 2008. V. 47. P. 234–241. https://doi.org/10.1007/s11106-008-9009-3
Vecher A.A., Mechkovski L.A., Skoropanov A.S. Formation Heats of Some Tellurides // Neorg. Mater. Izv. AN SSSR. 1974. V. 10. № 12. P. 2140–2143.
Boncheva-Mladenova Z., Pashinkin A.S., Novoselova A.V. Pressure of Saturated Steam of Solid Bismuth Telluride // Neorg. Mater. Izv. AN SSSR. 1968. V. 4. № 2. P. 291–292.
Дополнительные материалы отсутствуют.
Инструменты
Неорганические материалы