Журнал неорганической химии, 2019, T. 64, № 3, стр. 281-287

Корреляция между молярными объемами нестехиометрических M₁ _{– x}R_xF₂ _{+ x} (0 ≤ x ≤ 0.5) и упорядоченных M_mR_nF_2m _{+ 3n} (m/n = 8/6, 9/5) фаз в системах MF₂–RF₃ (M = Ca, Sr, Ba, Pb; R – редкоземельные элементы)

Н. И. Сорокин^1, *

¹ Институт кристаллографии им. А.В. Шубникова ФНИЦ “Кристаллография и фотоника” РАН
119333 Москва, Ленинский пр-т, 59, Россия

^* E-mail: nsorokin1@yandex.ru

Поступила в редакцию 21.06.2018
После доработки 15.08.2018
Принята к публикации 30.07.2018

DOI: 10.1134/S0044457X1903019X

Полный текст (PDF)

Аннотация

В системах MF₂–RF₃ (M = Ca, Sr, Ba, Pb; R – редкоземельные элементы Y, La−Lu) обнаружена корреляция между молярными объемами нестехиометрических фаз M₁_{– x}R_xF₂_{+ x} (0 ≤ x ≤ 0.5) со структурой типа флюорита (CaF₂) и упорядоченных фаз M_mR_nF_2m_{+ 3n} (m/n = 8/6, 9/5) с производной от флюорита структурой. Эта корреляция подтверждает справедливость кластерной концепции атомного строения нестехиометрических кристаллов M₁ _– xR_xF₂_{+ x}, согласно которой, их структура построена из матричных фрагментов {M₁₄F₆₄} и октаэдро-кубических кластеров {M₈B₆F_68–69}, где в роли катионов 6B выступают редкоземельные катионы (6R) или смесь катионов (5R + M).

Ключевые слова: фториды, редкоземельные элементы, нестехиометрические фазы, структура флюорита, дефекты

ВВЕДЕНИЕ

В бинарных системах MF₂–RF₃ (M = Ca, Sr, Ba, Pb; R = 16 редкоземельных элементов (РЗЭ): Y, La−Lu) образуются нестехиометрические фазы M_{1 –}_xR_xF₂₊_x на основе матриц MF₂ со структурой типа флюорита (CaF₂), которые занимают лидирующее положение по численности и степени нарушения стехиометрии среди других фторидных систем [1]. Значительные нарушения флюоритовой стехиометрии (отношения концентрации катионов к анионам [M, R] : [F] ≠ 1 : 2) в них связаны с появлением избыточных (междоузельных) ионов фтора ${\text{F}}_{{\operatorname{int} }}^{ - }$ в процессе замещения матричных катионов M²⁺ на катионы РЗЭ R³⁺. Области гомогенности нестехиометрических фаз M_{1 –}_xR_xF₂₊_x простираются при нормальном давлении до 50 ± 2 мол. % RF₃ (мольная доля x = 0.50 ± 0.02). Кристаллы M_1 –_xR_xF₂₊_x являются многофункциональными фторидными материалами с разупорядоченным атомным строением (суперионные проводники, оптические элементы, люминофоры, сцинтилляторы).

В результате изоморфных замещений катионов M²⁺ на R³⁺ в нестехиометрических флюоритовых кристаллах образуются большие концентрации примесно-индуцированных дефектов (катионы РЗЭ в позициях матричных катионов $R_{{\text{M}}}^{ - }$, междоузельные ионы фтора ${\text{F}}_{{\operatorname{int} }}^{ - }$, анионные вакансии ${\text{V}}_{{\text{F}}}^{ + }$), химические взаимодействия между которыми приводят к появлению ближнего порядка – формированию комплексов дефектов (кластеров) [2–7]. Всесторонняя аттестация дефектной (кластерной) структуры кристаллов M_{1 –}_xR_xF₂₊_x необходима, поскольку эта структура в значительной степени влияет на их свойства.

Непосредственные структурные исследования кристаллов нестехиометрических фаз M_{1 –}_xR_xF₂₊_x не дают надежной информации, химический состав кластеров остается дискуссионным. Комбинируя несколько типов кластеров в разных пропорциях, можно сколь угодно близко подогнать рассчитанные заселенности структурных позиций к экспериментальным. Изучение дефектной структуры и поиск конфигурации и состава структурных кластеров нестехиометрических флюоритов M_{1 –}_xR_xF₂₊_x остаются актуальной задачей для исследователей.

С ростом редкоземельного компонента кластеры способны к агломерации вплоть до образования упорядоченных фаз M_mR_nF_2m_{+ 3n} (m, n – натуральные числа) с производной от флюорита структурой [1, 8–15]. В упорядоченных фазах M_mR_nF_2m _+ 3n появляется дальний порядок в расположении кластеров, которые становятся структурными фрагментами, непосредственно фиксируемыми рентгено- и нейтронодифракционными методами. По этой причине наиболее строгое доказательство конфигурации и состава кластеров дают исследования упорядоченных фаз с производной от флюорита структурой.

Особый интерес среди этих объектов представляют ромбоэдрические фазы M₄R₃F₁₇ (гомологическая серия M_nF_2n_{+ 6} при n = 14) и M₉R₅F₃₃ (гомологическая серия M_nF_2n_{+ 5} при n = 14) с общей формулой M_mR_nF_2m_{+ 3n} при m/n = 8/6, 9/5 (в классификации Грейса [15] такие фазы обозначаются rhα). Эти упорядоченные фазы обнаружены в системах CaF₂–RF₃ (R = Y, Yb) [16, 17], SrF₂–RF₃ (R = Y, Gd–Lu) [11, 15], BaF₂–RF₃ (R = Y, Ce–Lu) [12, 14, 18] и PbF₂–RF₃ (R = Y, Sm−Lu) [19, 20].

К настоящему времени структура определена только для четырех ромбоэдрических фаз Ba₄R₃F₁₇ (R = Yb, Y) [21], Pb₈Y₆F₃₂O [22] и Sr₄Lu₃F₁₇ [23]. Эти упорядоченные фазы относятся, по классификации Голубева [6], к структурам с выделяемыми октаэдро-кубическими кластерами {M₈B₆F₆₈₋₆₉}, где в роли катионов 6B выступают катионы РЗЭ (6R) или статистическая смесь катионов (M + 5R) в расчете на каждый кластер. Образование статистической смеси катионов 6B связано с особенностями гетеровалентного замещения M²⁺ на R³⁺ и необходимостью компенсации избыточного положительного заряда для сохранения электронейтральности структуры в целом. Двойной индекс 68−69 для F использован из-за возможности существования кластеров с пустым центральным анионным кубооктаэдром {F₁₂} (68 анионов) или заполненным еще одним анионом {F₁₃} (69 анионов). Как кластеры {M₈R₆F₆₉} в кристаллах M₄R₃F₁₇, так и кластеры {M₉R₅F₆₈} в кристаллах M₉R₅F₃₃ изолированы друг от друга и объединяются только за счет анионов; между ними не остается катионов M²⁺, не входящих в состав кластеров.

Цель работы – исследование закономерностей изменения объема нестехиометрических флюоритовых фаз M_{1 –}_xR_xF₂₊_x (M = Ca, Sr, Ba, Pb; R = = РЗЭ) и упорядоченных фаз M_mR_nF_2m _+ 3n (m/n = = 8/6, 9/5) от их состава.

КОНЦЕНТРАЦИОННЫЕ ЗАВИСИМОСТИ ОБЪЕМА ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ НЕСТЕХИОМЕТРИЧЕСКИХ ФЛЮОРИТОВЫХ ФАЗ M_1 – _xR_xF_2 + _x

Объем элементарной ячейки флюоритовых кристаллов M₁_{– x}R_xF₂_{+ x} находится по формуле V = a³, где a – параметр кубической решетки. Приведенные в разных исследованиях значения параметров решетки для нестехиометрических фаз M₁_{– x}R_xF₂_{+ x} отличаются друг от друга и зависят от условий синтеза и термической предыстории образцов. В дальнейшем для расчетов будем использовать параметры решеток a(x), полученные твердофазным синтезом образцов с последующей закалкой в рамках одной экспериментальной методики [24].

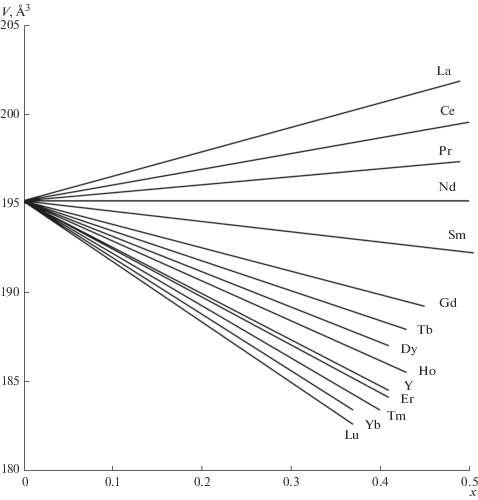
Построены зависимости V(x) для всех 64 флюоритовых фаз M₁_{– x}R_xF₂_{+ x} в системах MF₂−RF₃ (M = Ca, Sr, Ba, Pb; R = Y, La−Lu). На рис. 1 в качестве примера показаны концентрационные кривые V(x) для семейства флюоритовых фаз Sr₁_{– x}R_xF₂_{+ x}. Зависимость объемов элементарных ячеек от состава удовлетворяет линейным уравнениям (правило Ретгерса):

(1)

$V = {{V}_{0}} + {{k}_{V}}x,\quad$

где V₀ = $a_{0}^{3}$ относится к объему элементарной ячейки флюоритовой матрицы MF₂. Коэффициент k_V принимает как положительные, так и отрицательные значения в зависимости от соотношения ионных радиусов катионов M²⁺ и R³⁺.

Рис. 1.

Зависимость объема элементарных ячеек V кристаллов нестехиометрических флюоритовых фаз Sr_{1 –}_xR_xF₂₊_x (R = РЗЭ) от состава (x).

Значения коэффициента k_V определяли следующим образом. По рентгенографическим данным [24], параметры решетки практически для всех синтезированных при нормальном давлении флюоритовых фаз M₁ _– xR_xF₂ _+ x (исключение составляет небольшая группа фаз Ca₁_{– x}R_xF₂_{+ x} с R = = La–Ho при x > 0.2) линейно зависят от концентрации редкоземельного компонента RF₃ (правило Вегарда):

(2)

$a = {{a}_{0}} + {{k}_{a}}x.$

Поскольку параметр кубической решетки связан с объемом элементарной ячейки зависимостью a = = V^1/3, разложение функции a(x) = (a₀³+ k_Vx)^1/3 в ряд Тейлора в окрестности точки x = 0 имеет вид:

(3)

$a\left( x \right) = {\text{ }}{{a}_{0}} + \left( {{{{{k}_{V}}} \mathord{\left/ {\vphantom {{{{k}_{V}}} {3a_{0}^{2}}}} \right. \kern-0em} {3a_{0}^{2}}}} \right)x - \left( {{{k_{V}^{2}} \mathord{\left/ {\vphantom {{k_{V}^{2}} {9a_{0}^{5}}}} \right. \kern-0em} {9a_{0}^{5}}}} \right){{x}^{2}} + \quad...$

Первые три слагаемых в разложении (3) дают квадратичное уравнение для зависимости a(x), которое справедливо для фаз Ca₁_{– x}R_xF₂_{+ x} с R = = La–Ho.

Если ограничиться в разложении (3) первыми двумя слагаемыми, то приходим к линейному уравнению (1) с ${{k}_{a}} = {{{{k}_{V}}} \mathord{\left/ {\vphantom {{{{k}_{V}}} {3a_{0}^{2}}}} \right. \kern-0em} {3a_{0}^{2}}}.$ Взяв значения коэффициента k_a, приведенные в [24], можно рассчитать значения коэффициента k_V из условия ${{k}_{V}} = 3a_{0}^{2}{{k}_{a}}.$ Параметры V₀ и k_V в уравнениях (1) для 64 флюоритовых фаз M₁_{– x}R_xF₂_{+ x} в 4 рядах систем MF₂–RF₃ (M = Ca, Sr, Ba, Pb) приведены в табл. 1.

Таблица 1.

Значения коэффициента k_V в уравнениях V(x) = V₀ + k_Vx для нестехиометрических флюоритовых фаз M₁_{– x}R_xF₂_{+ x}

Флюоритовые фазы	Ca₁_{– x}R_xF₂_{+ x}	Sr₁_{– x}R_xF₂_{+ x}	Ba₁_{– x}R_xF₂_{+ x}	Pb₁_{– x}R_xF₂_{+ x}
Объем V₀, Å³	163.04	195.11	238.33	209.58
R	Значения коэффициента k_V при разном R, Å³
La	53.45	13.69	–34.98	0.33
Ce	50.32	8.66	–40.87	–4.55
Pr	43.24	4.50	–43.57	–10.01
Nd	40.74	0	–46.67	–14.95
Sm	33.57	–5.75	–60.51	–23.06
Gd	28.65	–13.30	–65.61	–28.80
Tb	27.76	– 6.84	–71.59	–33.78
Dy	24.17	–20.09	–72.63	–36.04
Ho	19.25	–22.69	–76.10	–41.43
Er	15.76	–27.29	–80.12	–45.15
Tm	12.89	–29.81	–82.10	–47.86
Yb	10.03	–32.28	–87.62	–47.25
Lu	7.88	–34.74	−	–48.04
Y	17.10	–14.44	–78.88	–41.47

КОРРЕЛЯЦИЯ МЕЖДУ МОЛЯРНЫМИ ОБЪЕМАМИ КРИСТАЛЛОВ M₁ _– xR_xF₂ _+ x (0 ≤ x ≤ 0.5) и M_mR_nF_2m_{+ 3n} (m/n = 8/6, 9/5)

Число структурных единиц в элементарных ячейках кристаллов M₁ _– xR_xF₂_{+ x} и M₄R₃F₁₇ различно (Z = 4 и 42 соответственно), поэтому рассмотрим их молярные объемы V ^mol, содержащие одинаковое число структурных единиц N_A (N_A – постоянная Авогадро). Молярные объемы флюоритовых фаз M₁_{– x}R_xF₂_{+ x} (пр. гр. Fm3m) и ромбоэдрических фаз M₄R₃F₁₇ и M₉R₅F₃₃ (пр. гр. R3, гексагональная установка) найдены соответственно по формулам

(4)

${{V}^{{{\text{mol}}}}} = {{a}^{3}}{{{{N}_{{\text{A}}}}} \mathord{\left/ {\vphantom {{{{N}_{{\text{A}}}}} 4}} \right. \kern-0em} 4},$

(5)

$V_{{{\text{rh}}\alpha }}^{{{\text{mol}}}} = 0.866\,\,{{a}^{2}}c{{{{N}_{{\text{A}}}}} \mathord{\left/ {\vphantom {{{{N}_{{\text{A}}}}} {42}}} \right. \kern-0em} {42}},$

где a и c – параметры кристаллической решетки.

К настоящему времени структура определена для четырех упорядоченных фаз M₄R₃F₁₇: Ba₄R₃F₁₇ (R = Yb, Y) [21], Pb₈Y₆F₃₂O [22] и Sr₄Lu₃F₁₇ [23], структурными фрагментами которых являются октаэдро-кубические кластеры типа {M₈B₆F₆₈₋₆₉}. Остановимся подробнее на этих упорядоченных фазах и соответствующих им нестехиометрических флюоритовых фазах Ba₁_{– x}R_xF₂_{+ x} (R = Yb, Y), Pb₁_{– x}Y_xF₂_{+ x} и Sr₁_{– x}Lu_xF₂_{+ x}. Вследствие большой разницы между объемами замещающихся ионов Ba²⁺ и Y³⁺ (Yb³⁺), Pb²⁺ и Y³⁺, Sr²⁺ и Lu³⁺ в роли катионов сорта 6B в октаэдро-кубических кластерах {M₈B₆F_68–69} выступают только трехзарядные катионы РЗЭ. Это приводит к образованию кластеров типа {M₈R₆F₆₉}.

Зависимость молярного объема кристаллов флюоритовых фаз M₁ _– xR_xF₂_{+ x} (в том числе Ba₁ _{– x}Y_xF₂_{+ x}, Ba₁_{– x}Yb_xF₂_{+ x}, Pb₁_{– x}Y_xF₂_{+ x} и Sr₁ _‒ xLu_xF₂_{+ x}) от состава имеет линейный вид:

(6)

${{V}^{{{\text{mol}}}}} = V_{0}^{{{\text{mol}}}} + {{K}_{V}}x,$

где молярный объем матрицы MF₂$V_{0}^{{{\text{mol}}}}$ = V₀N_A/4 и коэффициент K_V = k_VN_A/4.

В табл. 2 приведены экспериментальные значения объемов $V_{{{\text{rh}}\alpha }}^{{{\text{mol}}}}$ кристаллов Ba₄R₃F₁₇ (R = Yb, Y), Pb₈Y₆F₃₂O и Sr₄Lu₃F₁₇ и экстраполируемые (через двухфазную область на шкале составов в системах MF₂–RF₃) по уравнению (6) значения объема V^mol для нестехиометрических фаз M₁_{– x}R_xF₂_{+ x} при x = 3/7, отвечающие составу ромбоэдрической фазы M₄R₃F₁₇ (x = 0.428). Результаты показывают, что экстраполируемые значения объема V^mol(x = = 0.428) флюоритовых фаз Ba₁_{– x}R_xF₂_{+ x} (R = Yb, Y), = Pb₁_{– x}Y_xF₂_{+ x} и Sr₁_{– x}Lu_xF₂_{+ x} совпадают с молярными объемами $V_{{{\text{rh}}\alpha }}^{{{\text{mol}}}}$ кристаллов Ba₄R₃F₁₇ (R = Yb, Y), Pb₈Y₆F₃₂O и Sr₄Lu₃F₁₇ с изученной структурой. На рис. 2 показаны корреляции между молярными объемами этих кристаллов M₁_{– x}R_xF₂_{+ x} и M₄R₃F₁₇ (коэффициент корреляции R² = 0.99), которые носят весьма нетривиальный характер. Предельные составы флюоритовых нестехиометрических фаз M₁_{– x}R_xF₂_{+ x} отделены от упорядоченных фаз M₄R₃F₁₇ двухфазной областью. Например, для системы BaF₂–YF₃ насыщенная нестехиометрическая фаза Ba_0.68Y_0.32F_2.32 (x = 0.32) отделена от упорядоченной Ba₄Y₃F₁₇ (x = = 0.428) интервалом в 10.8 мол. % YF₃.

Таблица 2.

Молярные объемы нестехиометрических фаз M₁_{– x}R_xF₂_{+ x} и соединений M₄R₃F₁₇ в системах MF₂–RF₃ (M−R = Ba−Yb, Ba−Y, Pb−Y, Sr−Lu)

Система	Молярный объем, $V_{0}^{{{\text{mol}}}}$	Коэффициент, K_V	Молярный объем, V ^mol, см³/моль
Система	см³/моль		по уравнению (6) при x = 3/7	кристаллы M₄R₃F₁₇ [21–23]
BaF₂–YbF₃	35.88	–12.762	30.40	30.44
BaF₂–YF₃	35.88	–11.507	31.03	31.03
PbF₂–YF₃	31.55	–6.104	28.95	28.94
SrF₂–LuF₃	29.37	–5.119	27.19	27.35

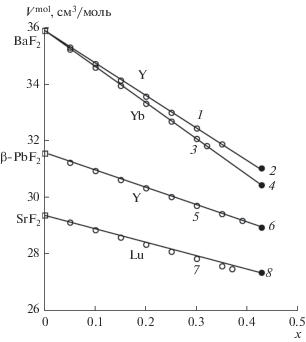
Рис. 2.

Корреляции между молярными объемами V^mol(x) кристаллов нестехиометрических фаз Ba_1 ‒ xY_xF₂₊_x (1), Ba_{1 –}_xYb_xF₂₊_x (3), Pb_{1 –}_xY_xF_{2 +}_x (5), Sr₁ _–_xLu_xF₂₊_x (7) и упорядоченных фаз Ba₄Y₃F₁₇ (2), Ba₄Yb₃F₁₇ (4), Pb₈Y₆F₃₂O = = Pb₄Y₃(F,O)₁₇ (6), Sr₄Lu₃F₁₇ (8).

Для других упорядоченных фаз M₄R₃F₁₇ и M₉R₅F₃₃ известны только их параметры решетки: Ca₉Y₅F₃₃ [16], Ca₉Yb₅F₃₃ [17], Sr₉R₅F₃₃ (R = Gd–Lu, Y) [21, 25], Sr₄R₃F₁₇ (R = Gd−Lu, Y) [11], Ba₄R₃F₁₇ (R = Ce−Lu, Y) [12], Pb₄R₃F₁₇ (R = Sm−Lu, Y) [19, 20, 26]. С учетом данных [11, 12, 16, 17, 19–21, 24–26] были рассчитаны молярные объемы $V_{{{\text{rh}}\alpha }}^{{{\text{mol}}}}$ ромбоэдрических фаз M_mR_nF_2m_{+ 3n} (m/n = 8/6, 9/5) по уравнению (5) и молярные объемы V^mol(x) нестехиометрических фаз M₁_{– x}R_xF₂_{+ x} по уравнению (6) при x = 3/7 (M₄R₃F₁₇) и x = 5/14 (M₉R₅F₃₃). Результаты расчетов объемов V^mol(x = 3/7), V^mol(x = = 5/14) и $V_{{{\text{rh}}\alpha }}^{{{\text{mol}}}}$ приведены в табл. 3.

Таблица 3.

Молярные объемы кристаллов M₁_{– x}R_xF₂_{+ x} и M_mR_nF_2m_{+ 3n} (m/n = 8/6, 9/5) в системах MF₂–RF₃ (M = = Ca, Sr, Ba, Pb; R = РЗЭ)

Система	Молярный объем, V^mol, см³/моль
Система	по уравнению (6) при x = 5/14	кристаллы M₉R₅F₃₃ [11, 16, 17]	по уравнению (6) при x = 3/7	кристаллы M₄R₃F₁₇ [11, 12, 19, 20]
CaF₂–RF₃, R: Yb Y	25.09 25.47	25.06 25.44
SrF₂–RF₃, R: Gd Tb Dy Ho Er Tm Yb Lu Y	28.66 28.48 28.31 28.17 27.92 27.80 27.67 27.55 27.99	28.53 28.42 28.22 28.10 27.89 27.72 27.63 27.48 27.98	28.52 28.30 28.10 27.93 27.65 27.65 27.34 27.19 27.71	28.59 28.34 28.17 28.02 27.80 27.67 27.45 27.29 27.90
BaF₂–RF₃, R: Ce Pr Nd Sm Gd Tb Dy Ho Er Tm Yb Y			33.31 33.14 32.95 32.10 31.81 31.45 31.39 31.19 30.95 30.84 30.40 31.03	33.33 32.99 32.64 32.21 31.71 31.46 31.22 31.02 30.88 30.59 30.51 30.97
PbF₂–RF₃, R: Sm Gd Tb Dy Ho Er Tm Yb Lu Y			30.09 29.73 29.42 29.28 28.95 28.73 28.56 28.60 28.55 28.95	30.24 29.78, 29.79 29.37 29.24 29.05 28.63 , 28.97 28.42, 28.80 28.47, 28.59 28.23, 28.41 28.97, 28.94

При фиксированном катионном составе (M, R) наблюдается совпадение между объемами V^mol(x = 3/7) или V^mol(x = 5/14) для неупорядоченной фазы M₁_{– x}R_xF₂_{+ x} и объемами $V_{{{\text{rh}}\alpha }}^{{{\text{mol}}}}$ для упорядоченных фаз M_mR_nF_2m_{+ 3n} (m/n = 8/6 или 9/5), что указывает на существование взаимосвязи между молярными объемами нестехиометрической и упорядоченной фаз. Эта взаимосвязь выражается в том, что уравнение (6), выведенное для молярных объемов кристаллов неупорядоченной фазы M₁_{– x}R_xF₂_{+ x}, остается справедливым и в случае упорядоченных фаз M₄R₃F₁₇ с отношением катионов M²⁺ и R³⁺ = 4 : 3 или M₉R₅F₃₃ с соотношением катионов M²⁺ и R³⁺ = 9 : 5.

Эта корреляция подтверждает справедливость кластерной концепции [6] атомного строения нестехиометрических кристаллов M₁_{– x}R_xF₂_{+ x}, согласно которой структура рассмотренных нестехиометрических кристаллов M₁_{– x}R_xF₂_{+ x} состоит из матричных фрагментов {M₁₄F₆₄} и октаэдро-кубических кластеров типа {M₈B₆F₆₈₋₆₉}, где в роли катионов 6B выступают катионы РЗЭ (6R) или статистическая смесь катионов (5R + M). Внешние грани кластеров {M₈B₆F₆₈₋₆₉} являются фрагментами флюоритовой матрицы, поэтому октаэдро-кубические кластеры соединяются между собой, а также с матричными кластерами {M₁₄F₆₄} с сохранением общего кубического мотива катионной упаковки. При изоморфных замещениях такое встраивание кластеров во флюоритовую матрицу (блочный изоморфизм [27]) сопровождается минимальными структурными искажениями, что делает тип флюорита необычно изоморфноемким по отношению к трифторидам РЗЭ RF₃. При этом разрешенные способы соединения кластеров {M₈B₆F₆₈₋₆₉} в зависимости от степени их конденсации, взаимного проникновения друг в друга и наличия матричных фрагментов структуры флюорита, установленные в [6], задают строго определенные составы упорядоченных фаз M_mR_nF_2m _+ 3n с производной от флюорита структурой.

ЗАКЛЮЧЕНИЕ

Для всех флюоритовых фаз M₁_{– x}R_xF₂_{+ x} в системах MF₂−RF₃ (M = Ca, Sr, Ba, Pb; R = Y, La–Lu) зависимость объемов элементарных ячеек от их состава удовлетворяет линейным уравнениям (правило Ретгерса). Указана причина отклонения зависимости параметра решетки a(x) для некоторых флюоритовых фаз M₁_{– x}R_xF₂_{+ x} от правила Вегарда.

Обнаружено, что при фиксированном составе (M, R) уравнение (6) для концентрационной зависимости молярного объема нестехиометрической флюоритовой фазы M₁_{– x}R_xF₂_{+ x} применимо также к кристаллам упорядоченных фаз M_mR_nF_2m_{+ 3n} (m/n = 8/6, 9/5) с производной от флюорита структурой. Этот факт подтверждает справедливость кластерной концепции [6] атомного строения кристаллов M₁_{– x}R_xF₂_{+ x}, согласно которой их структура построена из матричных фрагментов {M₁₄F₆₄} и октаэдро-кубических кластеров{M₈B₆F₆₈₋₆₉}, где в роли катионов 6B выступают редкоземельные катионы (6R) или статистическая смесь катионов (M + 5R). Именно блочный тип изоморфных замещений матричных флюоритовых структурных фрагментов на кластеры дефектов является причиной протяженных областей гомогенности флюоритовых гетеровалентных фаз M₁_{– x}R_xF₂_{+ x} по отношению к трифторидам РЗЭ.

БЛАГОДАРНОСТЬ

Работа выполнена при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию ФНИЦ “Кристаллография и фотоника” РАН.

Список литературы

Sobolev B.P. The Rare Earth Trifluorides. Part 1. The High Temperature Chemistry of Rare Earth Trifluorides. Institute of Crystallography, Moscow and Institut d’Estudis Catalans., Barcelona, 2000.
Cheetham A.K., Fender B.E.F., Steele D. et al. // Solid State Commun. 1970. V. 8. № 3. P. 171.
Bevan D.J.M., Greis O., Strahle J. // Acta Crystallogr. A. 1980. V. 36. P. 889.
Мурадян Л.А., Максимов Б.А., Симонов В.И. // Коорд. химия. 1986. Т. 12. № 10. С. 1398.
Fedorov P.P. // Bull. Soc. Cat. Cien. 1991. V. 12. № 2. P. 349.
Соболев Б.П., Голубев А.М., Эрреро П. // Кристаллография. 2003. Т. 48. № 1. С. 148.
Hull S. // Rep. Prog. Phys. 2004. V. 67. P. 1233.
Tkachenko N.L., Garashina L.S., Izotova O.E. et al. // J. Solid State Chem. 1973. V. 8. № 3. P. 213.
Fedorov P.P., Izotova O.E., Alexandrov V.B., Sobolev B.P. // J. Solid State Chem. 1974. V. 9. № 4. P. 368.
Sobolev B.P., Fedorov P.P. // J. Less-Common Metals. 1978. V. 60. № 1. P. 33.
Sobolev B.P., Seiranian K.B., Garashina L.S., Fedorov P.P. // J. Solid State Chem. 1979. V. 28. № 1. P. 51.
Kieser M., Greis O. // Z. Anorg. Allg. Chem. 1980. B. 469. S. 164.
Greis O., Kieser M. // Z. Anorg. Allg. Chem. 1981. B. 479. S. 165.
Sobolev B.P., Tkachenko N.L. // J. Less-Common Metals. 1982. V. 85. № 12. P. 155.
Greis O., Haschke J.M. Rare earth fluorides // Handbook on the physics and chemistry of rare earths / Eds. Gscheidner K.A., Eyring L. North-Holland, Amsterdam: 1982. V. 5. Ch. 45. P. 387.
Gettmann W., Greis O. // J. Solid State Chem. 1978. V. 26. № 3. P. 255.
Lechtenbohmer C., Greis J. // J. Less-Common Metals. 1978. V. 61. № 2. P. 177.
Greis O., Kieser M. // J. Less-Common Metals. 1980. V. 75. № 1. P. 119.
Dib A., Aleonard S., Roux M.T. // J. Solid State Chem. 1984. V. 52. P. 292.
Greis O., Uwais B.M., Horne W. // Z. Kristallogr. 1989. B. 186. S. 104.
Максимов Б.А., Соланс Х., Дудка А.П. и др. // Кристаллография. 1996. Т. 41. № 1. С. 51.
Dib A., Aleonard S. // J. Solid State Chem. 1986. V. 64. № 2. P. 148.
Сульянова Е.А., Молчанов В.Н., Верин И.В. и др. // Кристаллография. 2009. Т. 54. № 3. С. 554.
Федоров П.П., Соболев Б.П. // Кристаллография. 1992. Т. 37. № 5. С. 1210.
Sobolev B.P. The rare earth trifluorides. Part 2. Introduction to materials science of multicomponent metal fluoride crystals. Institute of Crystallography, Moscow and Institut d’Estudis Catalans., Barcelona, 2001.
Reau J.M., Fedorov P.P., Rabardel L. et al. // Mater. Res. Bull. 1983. V. 16. P. 1235.
Fedorov P.P. // Russ. J. Inorg. Chem. 2000. V. 45. Suppl. 3. P. S268.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал неорганической химии

Архивы выпусков Информация о журнале Отправить рукопись в журнал

Журнал неорганической химии, 2019, T. 64, № 3, стр. 281-287

ВВЕДЕНИЕ

КОНЦЕНТРАЦИОННЫЕ ЗАВИСИМОСТИ ОБЪЕМА ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ НЕСТЕХИОМЕТРИЧЕСКИХ ФЛЮОРИТОВЫХ ФАЗ M_1 – _xR_xF_2 + _x

(1)

Рис. 1.

(2)

(3)

Таблица 1.

Значения коэффициента k_V в уравнениях V(x) = V₀ + k_Vx для нестехиометрических флюоритовых фаз M₁_{– x}R_xF₂_{+ x}

КОРРЕЛЯЦИЯ МЕЖДУ МОЛЯРНЫМИ ОБЪЕМАМИ КРИСТАЛЛОВ M₁ _– xR_xF₂ _+ x (0 ≤ x ≤ 0.5) и M_mR_nF_2m_{+ 3n} (m/n = 8/6, 9/5)

(4)

(5)

(6)

Таблица 2.

Молярные объемы нестехиометрических фаз M₁_{– x}R_xF₂_{+ x} и соединений M₄R₃F₁₇ в системах MF₂–RF₃ (M−R = Ba−Yb, Ba−Y, Pb−Y, Sr−Lu)

Рис. 2.

Таблица 3.

Молярные объемы кристаллов M₁_{– x}R_xF₂_{+ x} и M_mR_nF_2m_{+ 3n} (m/n = 8/6, 9/5) в системах MF₂–RF₃ (M = = Ca, Sr, Ba, Pb; R = РЗЭ)

ЗАКЛЮЧЕНИЕ

БЛАГОДАРНОСТЬ

Свяжитесь с нами

Время работы

Журнал неорганической химии, 2019, T. 64, № 3, стр. 281-287

ВВЕДЕНИЕ

КОНЦЕНТРАЦИОННЫЕ ЗАВИСИМОСТИ ОБЪЕМА ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ НЕСТЕХИОМЕТРИЧЕСКИХ ФЛЮОРИТОВЫХ ФАЗ M1 – xRxF2 + x

(1)

Рис. 1.

(2)

(3)

Таблица 1.

Значения коэффициента kV в уравнениях V(x) = V0 + kV x для нестехиометрических флюоритовых фаз M1– xRxF2+ x

КОРРЕЛЯЦИЯ МЕЖДУ МОЛЯРНЫМИ ОБЪЕМАМИ КРИСТАЛЛОВ M1 – xRxF2 + x (0 ≤ x ≤ 0.5) и MmRnF2m+ 3n (m/n = 8/6, 9/5)

(4)

(5)

(6)

Таблица 2.

Молярные объемы нестехиометрических фаз M1– xRxF2+ x и соединений M4R3F17 в системах MF2–RF3 (M−R = Ba−Yb, Ba−Y, Pb−Y, Sr−Lu)

Рис. 2.

Таблица 3.

Молярные объемы кристаллов M1– xRxF2+ x и MmRnF2m+ 3n (m/n = 8/6, 9/5) в системах MF2–RF3 (M = = Ca, Sr, Ba, Pb; R = РЗЭ)

ЗАКЛЮЧЕНИЕ

БЛАГОДАРНОСТЬ

Свяжитесь с нами

Время работы

КОНЦЕНТРАЦИОННЫЕ ЗАВИСИМОСТИ ОБЪЕМА ЭЛЕМЕНТАРНОЙ ЯЧЕЙКИ НЕСТЕХИОМЕТРИЧЕСКИХ ФЛЮОРИТОВЫХ ФАЗ M_1 – _xR_xF_2 + _x

Значения коэффициента k_V в уравнениях V(x) = V₀ + k_Vx для нестехиометрических флюоритовых фаз M₁_{– x}R_xF₂_{+ x}

КОРРЕЛЯЦИЯ МЕЖДУ МОЛЯРНЫМИ ОБЪЕМАМИ КРИСТАЛЛОВ M₁ _– xR_xF₂ _+ x (0 ≤ x ≤ 0.5) и M_mR_nF_2m_{+ 3n} (m/n = 8/6, 9/5)

Молярные объемы нестехиометрических фаз M₁_{– x}R_xF₂_{+ x} и соединений M₄R₃F₁₇ в системах MF₂–RF₃ (M−R = Ba−Yb, Ba−Y, Pb−Y, Sr−Lu)

Молярные объемы кристаллов M₁_{– x}R_xF₂_{+ x} и M_mR_nF_2m_{+ 3n} (m/n = 8/6, 9/5) в системах MF₂–RF₃ (M = = Ca, Sr, Ba, Pb; R = РЗЭ)